Сочетания и размещения | План-конспект урока по алгебре (11 класс) на тему:
Тема урока № 7 : «Комбинаторика. Сочетания»
Предмет: алгебра и начала анализа.
Класс: 11.
Тип урока: комбинированный.
Цель урока: рассмотреть основные понятия теории комбинаторики — сочетания.
Задачи урока:
- образовательные: научить воспроизводить общие правила комбинаторики и типы соединений — сочетания, уметь применять теоретические знания при решении задач;
- воспитательные: воспитание умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, настойчивости в достижении цели и заинтересованности в конечном результате труда;
- развивающие: развитие умения анализировать, обобщать изучаемые факты, выделять и сравнивать существенные признаки, выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия; контроль и оценка процесса и результатов деятельности.

Используемые технологии: развивающее обучение, ИКТ, элементы исследовательской деятельности
Оборудование и материалы для урока: компьютер, проектор, видеоурок «Сочетания» сайт https://videouroki.net/blog/sochetaniya.html , экран, карточки с заданиями.
План урока:
1) Организационный момент.
2) Устный счет.
3) Изучение нового материала – просмотр видеоурока.
4) Решение задач по теме «Сочетания».
5) Итоги урока.
6) Домашнее задание.
Ход урока
1. Организационный момент
Приветствие учеников, сообщение темы и цели урока
2. Устный счет (ПК) – 6 класс – действия с десятичными дробями
3. Изучение нового материала
Просмотр видеоурока «Сочетания» источник сайт Видеоуроки.ru
План видеоурока:
- Примеры размещений и сочетаний. Задача: «Составить букеты из 5 различных цветов по 3 цветка. Сколько таких букетов можно составить?»
- Формула вычисления сочетаний
- Примеры вычисления сочетаний по формуле
- Задача 1: «Турист запланировал взять с собой в поездку 8 футболок, при этом всего у него их насчитывается 12.
 Сколькими способами он может сделать выбор?»
Сколькими способами он может сделать выбор?» - Задача 2: «В чемпионате принимали участие 8 команд. Каждая команда сыграла с каждой только один раз. Сколько всего было игр?»
- Задача 3. «Сколькими способами для участия в конкурсе можно выбрать 2 мальчиков и 4 девочек, если в классе 11 мальчиков и 13 девочек?»
4. Решение задач в группах.
- А теперь перейдем к работе в группах. Ваша задача: решить задачи, оформить их в тетрадях и рассказать о проделанной совместной работе. Листочки с заданиями на столах. Помогайте друг другу при решении. (Учитель, в процессе работы учащихся, оказывает помощь каждой группе).
Задача 2: «В чемпионате принимали участие 8 команд. Каждая команда сыграла с каждой только один раз. Сколько всего было игр?»
Задача 3. «Сколькими способами для участия в конкурсе можно выбрать 2 мальчиков и 4 девочек, если в классе 11 мальчиков и 13 девочек?»
Дополнительные задачи:
Задача № 4. Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?
Решение:
Два юноши не могут одновременно пригласить одну и ту же девушку. И
И
варианты, при которых одни и те же девушки танцуют с разными юношами,
считаются разными, поэтому:
Ответ: 360.
Задача № 5. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только один раз?
Решение:
В условии задачи предложено подсчитать число всевозможных комбинаций из трех цифр, взятых из предположенных девяти цифр, причём порядок
расположения цифр в комбинации имеет значение (например, числа 132 и 231 различные). Иначе говоря, нужно найти число размещений из девяти элементов по три. По формуле числа размещений находим:
Ответ: 504 трехзначных чисел.
Задача №6. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
Решение:
Чтобы рассмотреть все возможные комиссии, нужно рассмотреть все возможные 3 – элементные подмножества множества, состоящего из 7 человек. Искомое число способов равно
Ответ: 35 способов.
Озвучивание решений групп, затем просмотр их решений в видеоуроке.
5. Итоги урока
Ученики проговаривают, что нового узнали на уроке. Учитель оценивает работу ребят. При выходе из кабинета каждый ученик выбирает прямоугольник по цвету, соответствующему надписями “всё понятно и усвоено”, “трудно и не всё понятно”, “не понятно и не усвоено”, и опускает в соответствующий конверт.
6. Домашнее задание РГР-1 «Комбинаторика»
Литература
Задача В10. Открытый банк заданий по математике. ЕГЭ 2018.
интернет – источники:
https://www.youtube.com/watch?v=zu73D0v74i4 видеоуроки.net
http://festival.1september.ru/articles/595703/;
http://www.testsoch.com/urok-sochetaniya-i-razmeshheniya/.
https://math-ege.sdamgia.ru/
Урок 7
«Комбинаторика. Сочетания»
Задача 2: «В чемпионате принимали участие 8 команд. Каждая команда сыграла с каждой только один раз. Сколько всего было игр?»
Задача 3. «Сколькими способами для участия в конкурсе можно выбрать 2 мальчиков и 4 девочек, если в классе 11 мальчиков и 13 девочек?»
Дополнительные задачи:
Задача № 4. Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?
Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?
Задача № 5. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только один раз?
Задача №6. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
Урок 7
«Комбинаторика. Сочетания»
Задача 2: «В чемпионате принимали участие 8 команд. Каждая команда сыграла с каждой только один раз. Сколько всего было игр?»
Задача 3. «Сколькими способами для участия в конкурсе можно выбрать 2 мальчиков и 4 девочек, если в классе 11 мальчиков и 13 девочек?»
Дополнительные задачи:
Задача № 4. Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?
Задача № 5. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только один раз?
Задача №6. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
Урок 7
«Комбинаторика. Сочетания»
Задача 2: «В чемпионате принимали участие 8 команд. Каждая команда сыграла с каждой только один раз. Сколько всего было игр?»
Задача 3. «Сколькими способами для участия в конкурсе можно выбрать 2 мальчиков и 4 девочек, если в классе 11 мальчиков и 13 девочек?»
Дополнительные задачи:
Задача № 4. Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?
Задача № 5. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только один раз?
Задача №6. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
Урок 7
«Комбинаторика. Сочетания»
Задача 2: «В чемпионате принимали участие 8 команд. Каждая команда сыграла с каждой только один раз. Сколько всего было игр?»
Задача 3.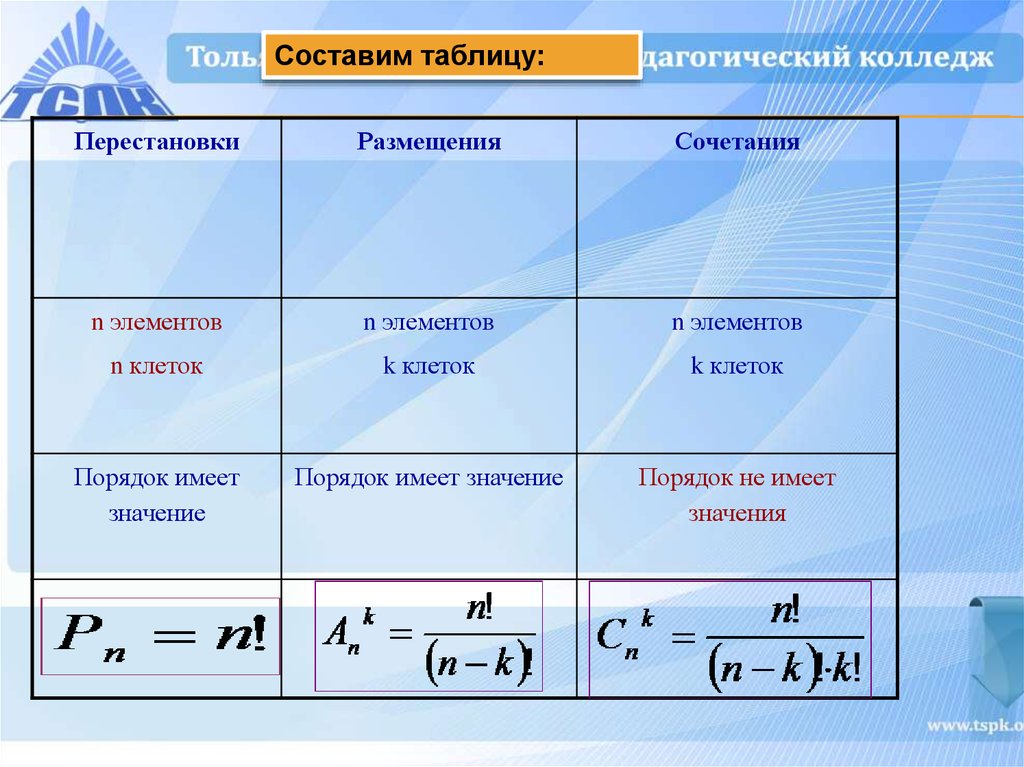 «Сколькими способами для участия в конкурсе можно выбрать 2 мальчиков и 4 девочек, если в классе 11 мальчиков и 13 девочек?»
«Сколькими способами для участия в конкурсе можно выбрать 2 мальчиков и 4 девочек, если в классе 11 мальчиков и 13 девочек?»
Дополнительные задачи:
Задача № 4. Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?
Задача № 5. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только один раз?
Задача №6. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
Самостоятельная работа
1 вариант.
Решить задачи:
1. Сколькими способами можно из 6 человек составить комиссию, состоящую из двух человек?
2. В соревновании участвуют 10 человек. Сколькими способами могут распределиться между ними места?
3. Сколькими способами можно расставить на полке 4 различные книги?
4. Сколько различных словарей необходимо переводчику, чтобы он мог переводить с любого из 5 языков – русского, английского, немецкого, французского, испанского – на любой другой из этих языков?
5. Пять человек обменялись друг с другом фотографиями. Сколько всего фотографий было?
Пять человек обменялись друг с другом фотографиями. Сколько всего фотографий было?
6. На плоскости отмечены 6 точек. Каждые две точки соединили отрезком. Сколько получилось отрезков?
2 вариант
Решить задачи:
1. Сколькими способами можно переставить 5 различных геометрических фигур?
2. Пять человек пожали друг другу руки. Сколько было рукопожатий?
3. За свои рисунки ученик получил две положительные оценки. Какими они могут быть? Сколько вариантов?
4. Сколько флагов можно составить из трех разных цветов, если имеются полосы синего, белого, красного цветов?
5. В понедельник в пятом классе 5 уроков. Сколькими способами можно составить расписание на понедельник?
6. Из десяти учащихся надо выбрать старосту, физорга и культорга. Сколькими способами это можно сделать?
Ответы и решения:
I вариант | II вариант |
1. 2. 3. Pn=4!=24 4. Pn=5!=120 5. Pn=5!=120 6. | 1. Pn=5!=120 2. 3. положительные оценки: 4, 5. 22=4 4. Рn=3!=6 5. Pn=5!=120 6. |
Урок 7
«Комбинаторика. Сочетания»
Самостоятельная работа
1 вариант.
Решить задачи:
1. Сколькими способами можно из 6 человек составить комиссию, состоящую из двух человек?
2. В соревновании участвуют 10 человек. Сколькими способами могут распределиться между ними места?
3. Сколькими способами можно расставить на полке 4 различные книги?
4. Сколько различных словарей необходимо переводчику, чтобы он мог переводить с любого из 5 языков – русского, английского, немецкого, французского, испанского – на любой другой из этих языков?
5. Пять человек обменялись друг с другом фотографиями. Сколько всего фотографий было?
6. На плоскости отмечены 6 точек. Каждые две точки соединили отрезком. Сколько получилось отрезков?
Каждые две точки соединили отрезком. Сколько получилось отрезков?
2 вариант
Решить задачи:
1. Сколькими способами можно переставить 5 различных геометрических фигур?
2. Пять человек пожали друг другу руки. Сколько было рукопожатий?
3. За свои рисунки ученик получил две положительные оценки. Какими они могут быть? Сколько вариантов?
4. Сколько флагов можно составить из трех разных цветов, если имеются полосы синего, белого, красного цветов?
5. В понедельник в пятом классе 5 уроков. Сколькими способами можно составить расписание на понедельник?
6. Из десяти учащихся надо выбрать старосту, физорга и культорга. Сколькими способами это можно сделать?
Урок 7
«Комбинаторика. Сочетания»
Самостоятельная работа
1 вариант.
Решить задачи:
1. Сколькими способами можно из 6 человек составить комиссию, состоящую из двух человек?
2. В соревновании участвуют 10 человек. Сколькими способами могут распределиться между ними места?
3. Сколькими способами можно расставить на полке 4 различные книги?
Сколькими способами можно расставить на полке 4 различные книги?
4. Сколько различных словарей необходимо переводчику, чтобы он мог переводить с любого из 5 языков – русского, английского, немецкого, французского, испанского – на любой другой из этих языков?
5. Пять человек обменялись друг с другом фотографиями. Сколько всего фотографий было?
6. На плоскости отмечены 6 точек. Каждые две точки соединили отрезком. Сколько получилось отрезков?
2 вариант
Решить задачи:
1. Сколькими способами можно переставить 5 различных геометрических фигур?
2. Пять человек пожали друг другу руки. Сколько было рукопожатий?
3. За свои рисунки ученик получил две положительные оценки. Какими они могут быть? Сколько вариантов?
4. Сколько флагов можно составить из трех разных цветов, если имеются полосы синего, белого, красного цветов?
5. В понедельник в пятом классе 5 уроков. Сколькими способами можно составить расписание на понедельник?
6. Из десяти учащихся надо выбрать старосту, физорга и культорга. Сколькими способами это можно сделать?
Из десяти учащихся надо выбрать старосту, физорга и культорга. Сколькими способами это можно сделать?
Задачи для решения на закрепление нового материала
Задача № 1. Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?
Решение:
Р5 = 5!= 1 ∙2 ∙3 ∙4 ∙5 = 120 способов.
Ответ: 120 способов.
Задача №2. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз?
Решение:
Число всех перестановок из трех элементов равно Р3=3!, где 3!=1 · 2 · 3=6. Значит, существует шесть трехзначных чисел, составленных из цифр 1,2,3.
Ответ: 6 чисел.
Задача № 3. Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?
Решение:
Два юноши не могут одновременно пригласить одну и ту же девушку. И
варианты, при которых одни и те же девушки танцуют с разными юношами,
считаются разными, поэтому:
Ответ: 360.
Задача № 4. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только один раз?
Решение:
В условии задачи предложено подсчитать число всевозможных комбинаций из трех цифр, взятых из предположенных девяти цифр, причём порядок
расположения цифр в комбинации имеет значение (например, числа 132 и 231 различные). Иначе говоря, нужно найти число размещений из девяти элементов по три. По формуле числа размещений находим:
Ответ: 504 трехзначных чисел.
Задача №5. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
Решение:
Чтобы рассмотреть все возможные комиссии, нужно рассмотреть все возможные 3 – элементные подмножества множества, состоящего из 7 человек. Искомое число способов равно
Ответ: 35 способов.
Задача № 6. В соревновании участвуют 12 команд. Сколько существует вариантов распределения призовых (1, 2, 3) мест?
Решение:
А123 = 12 ∙11 ∙10 = 1320 вариантов распределения призовых мест.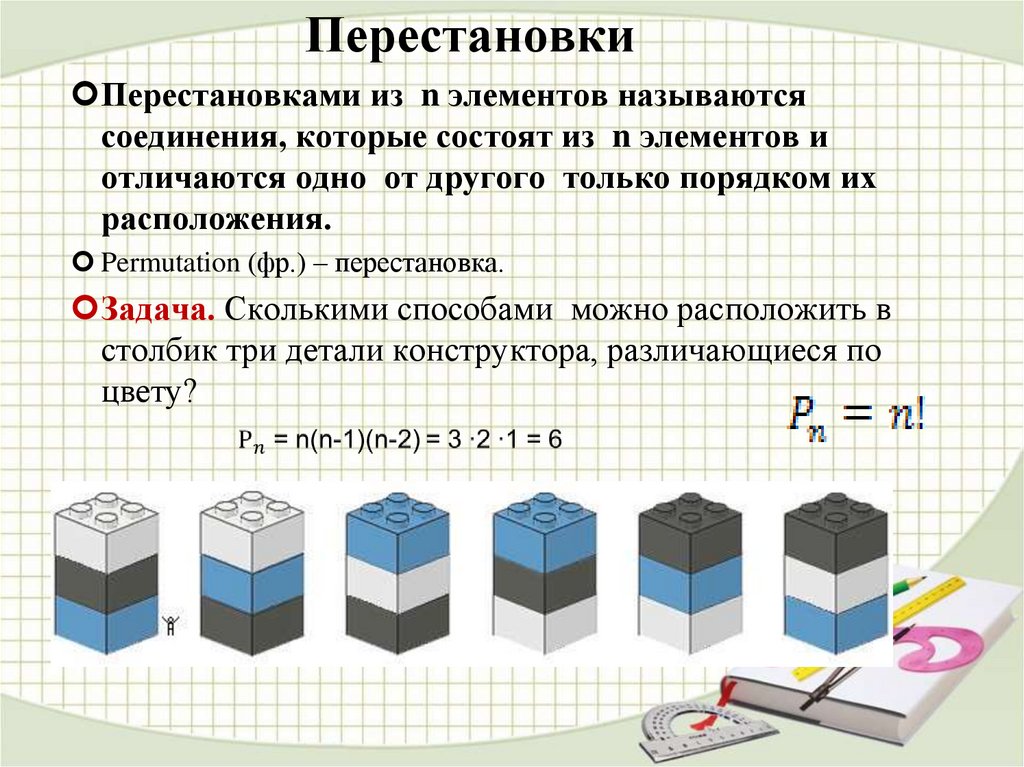
Ответ: 1320 вариантов.
Задача № 7. На соревнованиях по лёгкой атлетике нашу школу представляла команда из 10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете 4×100 м на первом, втором, третьем и четвёртом этапах?
Решение:
Выбор из 10 по 4 с учётом порядка: способов.
Ответ: 5040 способов.
Задача № 8. Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?
Решение:
На первое место можно поставить любой из четырех шариков (4 способа), на
второе – любой из трех оставшихся (3 способа), на третье место – любой из
оставшихся двух (2 способа), на четвертое место – оставшийся последний шар.
Всего 4 · 3 · 2 · 1 = 24 способа. Р4 = 4! = 1 · 2 · 3 · 4 = 24. Ответ: 24 способа.
Задача № 9. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?
Решение:
Выбор 6 из 10 без учёта порядка: способов.
Ответ: 210 способов.
Задача № 10. В 9 классе учатся 7 учащихся, в 10 — 9 учащихся, а в 11 — 8 учащихся. Для работы на пришкольном участке надо выделить двух учащихся из 9 класса, трех – из 10, и одного – из 11 . Сколько существует способов выбора учащихся для работы на пришкольном участке?
Решение:
Выбор из трёх совокупностей без учёта порядка, каждый вариант выбора из
первой совокупности (С72) может сочетаться с каждым вариантом выбора из
второй (С93) и с каждым вариантом выбора третьей (С81) по правилу умножения получаем:
Ответ: 14 112 способов.
Задача № 11. Девятиклассники Женя, Сережа, Коля, Наташа и Оля побежали на перемене к теннисному столу, за которым уже шла игра. Сколькими способами подбежавшие к столу пятеро девятиклассников могут занять очередь для игры в настольный теннис?
Решение:
Первым в очередь мог встать любой девятиклассник, вторым – любой из оставшихся троих, третьим – любой из оставшихся двоих и четвёртым – девятиклассник, подбежавший предпоследним, а пятым – последний. По правилу умножения у пяти учащихся существует 5· 4⋅3⋅2⋅1=120 способов занять очередь.
По правилу умножения у пяти учащихся существует 5· 4⋅3⋅2⋅1=120 способов занять очередь.
Ответ: 120 способов.
Отчет групп о проделанной работе.
4. Итоги урока
Ученики проговаривают, что нового узнали на уроке. Учитель оценивает работу ребят. При выходе из кабинета каждый ученик выбирает прямоугольник по цвету, соответствующему надписями “всё понятно и усвоено”, “трудно и не всё понятно”, “не понятно и не усвоено”, и опускает в соответствующий конверт.
5. Домашнее задание
1 вариант.
Решить задачи:
1. Сколькими способами можно из 6 человек составить комиссию, состоящую из двух человек?
2. В соревновании участвуют 10 человек. Сколькими способами могут распределиться между ними места?
3. Сколькими способами можно расставить на полке 4 различные книги?
4. Сколько различных словарей необходимо переводчику, чтобы он мог переводить с любого из 5 языков – русского, английского, немецкого, французского, испанского – на любой другой из этих языков?
5. Пять человек обменялись друг с другом фотографиями. Сколько всего фотографий было?
Пять человек обменялись друг с другом фотографиями. Сколько всего фотографий было?
6. На плоскости отмечены 6 точек. Каждые две точки соединили отрезком. Сколько получилось отрезков?
2 вариант
Решить задачи:
1. Сколькими способами можно переставить 5 различных геометрических фигур?
2. Пять человек пожали друг другу руки. Сколько было рукопожатий?
3. За свои рисунки ученик получил две положительные оценки. Какими они могут быть? Сколько вариантов?
4. Сколько флагов можно составить из трех разных цветов, если имеются полосы синего, белого, красного цветов?
5. В понедельник в пятом классе 5 уроков. Сколькими способами можно составить расписание на понедельник?
6. Из десяти учащихся надо выбрать старосту, физорга и культорга. Сколькими способами это можно сделать?
Ответы и решения:
I вариант
II вариант
1.
2.
3. Pn=4!=24
4. Pn=5!=120
5. Pn=5!=120
6.
1. Pn=5!=120
2.
3. положительные оценки: 4, 5.
22=4
4. Рn=3!=6
5. Pn=5!=120
6.
Сочетания и некоторые свойства сочетаний
Сочетания из n по m m-элементные подмножества n-элементного множества.
Пример: Решим следующую задачу. Пусть в коробке находится пять пронумерованных шаров {1, 2, 3, 4, 5}. Перечислите все способы выбора двух шаров из этих пяти.
Каждому способу выбора двух шаров из пяти соответствует некоторое двухэлементное подмножество пятиэлементного множества. Перечислим эти подмножества:
Обратите внимание, что подмножества (2,1) и (1,2) содержат один и тот же набор элементов и поэтому отождествляются. Итак, у пятиэлементного множества 10 двухэлементных подмножеств.
Рассмотрим все подмножества, состоящего из трех элементов {a, b, c}.
Их восемь:
- Ø – пустое множество, как принадлежащее любому множеству;
- {a}, {b}, {c} – одноэлементные 3 множества;
- {a, b}, {a, c}, {b, c} – двухэлементные 3 множества;
- {a, b, c} – одно множество из трех элементов, то есть полное рассматриваемое множество.

В сумме получили 8 различных подмножеств.
Число подмножеств, m элементов в каждом, содержащихся во множестве из n элементов, обозначается Cnm (читается «це из эн по эм») Буква C выбрана для обозначения числа сочетаний в связи тем, что по-французски слово «сочетание» — «combinaison» — начинается с этой буквы.
C52 = 10
В комбинаторике конечные множества называются сочетаниями.
В сочетаниях нас интересует только сами элементы множества и не интересует их порядок.
Важно, какие конкретно элементы множества входят в каждое соединение.
Число сочетаний, перестановок и размещений связаны по формуле:
Действительно, чтобы получить все размещения из n элементов по m надо:
1) взять n-элементное множество;
2) выделить m-элементное подмножество. Это можно сделать Cnm — способами. Всего получим Cnm упорядоченных множеств, так как в каждом m – элементном подмножестве возможно установить Рm порядков, где Рm – число перестановок из m элементов.
Следовательно, | , а | . |
Подставив сюда уже известные нам выражения
и Рm = m!, m ≤ n и Cn0 = 1, получим
что можно записать иначе: |
Сочетания с повторениями
Сочетание с повторениями – каждый элемент, входящий в соединение, может быть представлен более чем одним элементом:
В дальнейшем сочетание без повторений мы будем называть одним словом – «сочетание».
Задача: В классе 22 учащихся. Двух из них следует назначить дежурными. Сколькими способами это можно сделать?
Замечание
При решении задач по комбинаторике следует обращать внимание, учитывается ли порядок в сочетаниях. Если порядок учитывается, то есть составляются упорядоченные множества, то это – размещения. Если порядок не учитывается, то есть составляются множества, то это – сочетания.
Если порядок учитывается, то есть составляются упорядоченные множества, то это – размещения. Если порядок не учитывается, то есть составляются множества, то это – сочетания.
IV этап: Закрепление и проверка усвоения материала
Цель: Закрепить в памяти учащихся те знания и умения, которые необходимы им для самостоятельной работы по новому материалу. Добиться в ходе закрепления повышения уровня осмысления материала, глубины его понимания.
Ю.М. Колягин Алгебра и начала анализа стр. 135 №329; стр. 137 №337.
Типичные задачи, в которых обычно путаются учащиеся
Сочетания | Размещения |
1. Сколько рукопожатий получится, если здороваются 5 человек? | 1. |
Перестановки | |
1. Сколькими способами n человек могут сесть на одной скамейке? | 2. Сколькими способами n человек могут сесть за круглым столом? |
Самостоятельная работа по вариантам
1. Сколько различных экзаменационных комиссий по 3 человека можно составить, если на кафедре 20 преподавателей? | 4. В нашем распоряжении есть 5 разноцветных флагов. Сколько различных сигналов, состоящих из 3 флагов, можно поднять на флаг штоке? | 7. Сколькими способами можно выбрать 6 различных пирожных в кондитерской, где имеется 11 сортов пирожных? |
2. | 5. Имеется 7 путевок в различные дома отдыха и 7 кандидатов. Сколькими способами можно распределить эти путевки? | 8. В шахматном турнире участвуют 12 человек. Каждый из участников должен сыграть с каждым из остальных по две партии. Сколько всего партий должны сыграть участники турнира? |
3. Сколькими способами можно расставить 5 книг на полке? | 6. В колоде 52 карты. Раздаются 3 карты. Сколько может быть случаев появления одного туза среди розданных карт? | 9. Сколькими способами из 30 человек может выбрать собрание председателя и секретаря? |
V Домашняя работа
Сообщить учащимся о домашнем задании, разъяснить методику его выполнения, мотивировать необходимость выполнения работы.
По карточкам.
20 приемов использования в Python модуля itertools
В декабре 2019 года мы подробно рассказали о модуле collections. Другой важный компонент стандартной библиотеки – itertools.
Модуль itertools содержит строительные блоки итераторов, основанные на конструкциях из языков программирования APL, Haskell и SML. Ниже мы опишем набор быстрых и эффективных в отношении памяти инструментов, полезных как самостоятельно, так и в сочетании. Вместе они образуют «алгебру итераторов» для программ на чистом Python.
Цель публикации – в сжатой форме рассмотреть распространённые примеры и шаблоны использования модуля itertools.
Начнем с импорта:
import itertools
Чтобы лучше запомнить функции модуля, мы не станем использовать конструкцию from ., а будем обращаться к методам модуля через его имя.
Если вы владеете Jupyter Notebook, блокнот этой статьи доступен на GitHub. Соответственно код легко запустить в интерактивном режиме с помощью Colab.
Функция itertools.count(start=0, step=1) создаёт бесконечный итератор. Можно задать начальное значение и шаг итерирования.
>>> cnt = itertools.count(start=2020, step=4)
>>> next(cnt)
2020
>>> next(cnt)
2024
>>> next(cnt)
2028
Пример использования итератора в zip-функции:
>>> days = [366]*4
>>> list(zip(itertools.count(2020, 4), days))
[(2020, 366), (2024, 366), (2028, 366), (2032, 366)]
Чтобы продолжить счёт при прерывании выполнения программы передайте последнее значение новому объекту итератора в виде параметра start.
Если необходимо подсчитывать число вхождений элементов в список или кортеж, обратите внимание на Counter() из модуля collections.
Если последовательности имеют неодинаковую длину, zip() ограничивается самой короткой:
>>> list(zip(range(0, 10), range(0, 5)))
[(0, 0), (1, 1), (2, 2), (3, 3), (4, 4)]
Но такое сокращение может быть неудобно из-за потери информации. Чтобы сохранить обе последовательности, используйте itertools.zip_longest():
for (i, j) in itertools.zip_longest(range(0, 10), range(0, 5)): print(i, j)
0 0
1 1
2 2
3 3
4 4
5 None
6 None
7 None
8 None
9 None
Вместо None функция может подставлять значение, переданное аргументу fillvalue.
Суммирование нарастающим (накопительным) итогом – вид сложения последовательности чисел. Например, так считается квартальная прибыль Каждый элемент складывается с суммой всех предшествовавших элементов. В следующем примере 1 и 2 даёт 3, сумма 1, 2 и 3 равна 6 и т. д. Описанный тип работы с последовательностью воплощен в
Например, так считается квартальная прибыль Каждый элемент складывается с суммой всех предшествовавших элементов. В следующем примере 1 и 2 даёт 3, сумма 1, 2 и 3 равна 6 и т. д. Описанный тип работы с последовательностью воплощен в itertools.accumulate(iterable, func=operator.add, *, initial=None):
>>> list(itertools.accumulate(range(1, 10)))
[1, 3, 6, 10, 15, 21, 28, 36, 45]
Чтобы вывести данные, мы используем список. При печати самого итератора выводится только его ссылка.
По умолчанию к элементам применяется operator.add. Можно, например, указать оператор умножения:
>>> import operator
>>> list(itertools.accumulate(range(1, 10), operator.mul))
[1, 2, 6, 24, 120, 720, 5040, 40320, 362880]
С помощью itertools.cycle() создаётся кольцевой итератор. Прийдя к последнему значению, он вновь начинает с первого:
Прийдя к последнему значению, он вновь начинает с первого:
>>> waltz = itertools.cycle(['и раз', 'и два', 'и три'])
>>> next(waltz)
'и раз'
>>> next(waltz)
'и два'
>>> next(waltz)
'и три'
>>> next(waltz)
'и раз'
itertools.repeat() это вырожденный случай itertools.cycle(). Вместо последовательности повторяется одно и то же значение. Бесконечно или times раз:>>> s = "Птица Говорун отличается умом и сообразительностью"
>>> rep = itertools.repeat(s, times=2)
>>> next(rep)
'Птица Говорун отличается умом и сообразительностью'
>>> next(rep)
'Птица Говорун отличается умом и сообразительностью'
>>> next(rep)
StopIteration...
Классический пример использования itertools.repeat() – итератор для map():
>>> nums = range(10) >>> squares = map(pow, nums, itertools.Все числа последовательностиrepeat(2)) >>> list(squares) [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
nums возведены в степень 2. Итератор вызывается столько раз, сколько необходимо, не нужно думать о числе элементов в последовательности.Раз мы заговорили о map(), полезно рассказать и о itertools.starmap(). Этот метод принимает функцию и список кортежей аргументов. Как если бы использовался оператор *, отсюда и название:
>>> squares = itertools.starmap(pow, [(0, 2), (1, 2), (2, 2)])
>>> list(squares)
[0, 1, 4]
Модуль itertools позволяет решать программные задачи, построенные на структурах комбинаторики.
Сочетания – выбранные из множества n объектов комбинации m объектов, отличающиеся хотя бы одним объектом.
Например, мы хотим составить трёхцветный флаг из лент цветных тканей. Есть четыре цвета лент. Все варианты выбора тканей без учёта их расположения:
colors = ['белый', 'жёлтый', 'синий', 'красный']
for item in itertools.combinations(colors, 3):
print(item)
('белый', 'жёлтый', 'синий')
('белый', 'жёлтый', 'красный')
('белый', 'синий', 'красный')
('жёлтый', 'синий', 'красный')
Порядок следования не имеет значения, поэтому все тройки цветов уникальны.
Размещения – те же сочетания, для которых важен порядок следования элементов. В продолжение предыдущего примера определим все варианты как мы можем составить флаг с учётом порядка следования цветов:
for item in itertools.permutations(colors, 3):
print(item)
('белый', 'жёлтый', 'синий')
('белый', 'жёлтый', 'красный')
('белый', 'синий', 'жёлтый')
('белый', 'синий', 'красный')
('белый', 'красный', 'жёлтый')
('белый', 'красный', 'синий')
('жёлтый', 'белый', 'синий')
('жёлтый', 'белый', 'красный')
('жёлтый', 'синий', 'белый')
('жёлтый', 'синий', 'красный')
('жёлтый', 'красный', 'белый')
('жёлтый', 'красный', 'синий')
('синий', 'белый', 'жёлтый')
('синий', 'белый', 'красный')
('синий', 'жёлтый', 'белый')
('синий', 'жёлтый', 'красный')
('синий', 'красный', 'белый')
('синий', 'красный', 'жёлтый')
('красный', 'белый', 'жёлтый')
('красный', 'белый', 'синий')
('красный', 'жёлтый', 'белый')
('красный', 'жёлтый', 'синий')
('красный', 'синий', 'белый')
('красный', 'синий', 'жёлтый')
Как и ожидалось, число комбинаций с учетом порядка элементов гораздо больше.
Размещение с повторениями (выборка с возвращением) – это комбинаторное размещение объектов, в котором каждый объект может участвовать в размещении несколько раз.
Например, есть пин-код из четырех цифр. На каждой позиции стоит цифра от 0 до 9. Позиции не зависят друг от друга. Переберем все возможные коды:
digits = range(10)
pincode_vars = itertools.product(digits, repeat=4)
for var in pincode_vars:
print(var)
(0, 0, 0, 0)
(0, 0, 0, 1)
(0, 0, 0, 2)
...
(9, 9, 9, 8)
(9, 9, 9, 9)
Рассмотрим также случай обычного размещения, когда элементы могут повторяться, но каждое сочетание встречается только один раз:
letters = 'ABCD'
code_vars = itertools.combinations_with_replacement(letters, 2)
for var in code_vars:
print(var)
('A', 'A')
('A', 'B')
('A', 'C')
('A', 'D')
('B', 'B')
('B', 'C')
('B', 'D')
('C', 'C')
('C', 'D')
('D', 'D')
Метод itertools. можно использовать не только для размещений с повторениями. product()
product()
Декартово (прямое) произведение – множество, элементами которого являются все возможные упорядоченные пары элементов исходных множеств.
Например, найдём обозначения всех полей шахматной доски:
import string
letters = list(string.ascii_lowercase[:8])
digits = range(1, 9)
for (letter, digit) in itertools.product(letters, digits):
print(letter+str(digit), end=' ')
a1 a2 a3 a4 a5 a6 a7 a8 b1 b2 b3 b4 b5 b6
b7 b8 c1 c2 c3 c4 c5 c6 c7 c8 d1 d2 d3 d4
d5 d6 d7 d8 e1 e2 e3 e4 e5 e6 e7 e8 f1 f2
f3 f4 f5 f6 f7 f8 g1 g2 g3 g4 g5 g6 g7 g8
h2 h3 h4 h5 h5 h6 h7 h8
Иногда необходимо использовать нескольков итераторов. И независимо, и цепочкой один за другим. Для объединения итераторов используйте itertools.chain(*iterables).
Например, мы хотим использовать для отрисовки игральных карт независимые итераторы обозначений в углу поля карты:
>>> num_cards = [str(i) for i in range(2, 11)]
>>> face_cards = ['В', 'Д', 'К', 'Т']
>>> list(itertools.chain(num_cards, face_cards))
['2', '3', '4', '5', '6', '7', '8', '9', '10', 'В', 'Д', 'К', 'Т']
С помощью itertools.chain() также можно добавлять отдельные элементы в начало итератора:
>>> def prepend(value, iterator):
... return itertools.chain([value], iterator)
...
>>> list(prepend(1, [2, 3, 4]))
[1, 2, 3, 4]
Альтернативным конструктором itertools.chain() служит itertools.chain.from_iterable(). Метод принимает один итерируемый объект. Сравните их вызовы:
>>> list(itertools.chain('ABC', 'DEF')) ['A', 'B', 'C', 'D', 'E', 'F'] >>> list(itertools.chain.from_iterable(['ABC', 'DEF'])) ['A', 'B', 'C', 'D', 'E', 'F']
Последний конструктор удобно использовать для объединения списков:
>>> list_of_lists = [[1, 2], [3, 4, 5], [6, 7, 8, 9]]
>>> list(itertools.chain.from_iterable(list_of_lists))
[1, 2, 3, 4, 5, 6, 7, 8, 9]
Срез – удобный инструмент списков, который доступен и для итераторов с помощью itertools.islice().
Например, нам достаточно читать из крупного файла только три первых строки:
with open('test.txt', 'r') as f:
header = itertools.islice(f, 3)
for line in header:
print(line, end = '')
Строка 1
Строка 2
Строка 3
Функция itertools. позволяет итерироваться по любым объектам в формате среза. Например, следующая функция возвращает  islice()
islice()n первых элементов итерируемого объекта в виде списка:
def take(n, iterable):
return list(islice(iterable, n))
Функция compress() оставляет из итерируемых данных только те, что соответствуют позициям булевых селекторов:
>>> numbers = [0, 1, 2, 3, 2, 1, 0]
>>> selectors = [True, True, False, True]
>>> list(itertools.compress(numbers, selectors))
[0, 1, 3]
Метод itertools.filterfalse() дополняет обычный фильтр filter():
def filter_func(n):
if n < 2:
return True
return False
print(list(filter(filter_func, numbers)))
print(list(itertools.filterfalse(filter_func, numbers)))
[0, 1, 1, 0]
[2, 3, 2]
Если необходимо отобрать объекты, стоящие после неудовлетворяющего условию элемента, используем itertools.: dropwhile()
dropwhile()
>>> list(itertools.dropwhile(filter_func, numbers))
[2, 3, 2, 1, 0]
Метод itertools.takewhile() наоборот выведет элементы, удовлетворяющие условию вплоть до объекта, прерывающего цепочку истинных элементов:
>>> list(itertools.takewhile(filter_func, numbers))
[0, 1]
Инструмент itertools.groupby() объединяет смежные словари в группы по общему ключу. Например, сгруппируем студентов с одинаковой оценкой:
people = [{"Имя": "Петр",
"Отчество": "Петрович",
"Фамилия": "Петров",
"Оценка":5},
{"Имя": "Ольга",
"Отчество": "Алексеевна",
"Фамилия": "Иванова",
"Оценка":5},
{"Имя": "Николай",
"Отчество": "Николаевич",
"Фамилия": "Николаев",
"Оценка":4},
{"Имя": "Федор",
"Отчество": "Владимирович",
"Фамилия": "Иванов",
"Оценка":3},
{"Имя": "Владимир",
"Отчество": "Федорович",
"Фамилия": "Иванов",
"Оценка":3}]
def get_mark(person):
return person['Оценка']
person_marks = itertools. groupby(people, get_mark)
for key, group in person_marks:
print(key)
for person in group:
print(person)
print()
groupby(people, get_mark)
for key, group in person_marks:
print(key)
for person in group:
print(person)
print()
5
{'Имя': 'Петр', 'Отчество': 'Петрович', 'Фамилия': 'Петров', 'Оценка': 5}
{'Имя': 'Ольга', 'Отчество': 'Алексеевна', 'Фамилия': 'Иванова', 'Оценка': 5}
4
{'Имя': 'Николай', 'Отчество': 'Николаевич', 'Фамилия': 'Николаев', 'Оценка': 4}
3
{'Имя': 'Федор', 'Отчество': 'Владимирович', 'Фамилия': 'Иванов', 'Оценка': 3}
{'Имя': 'Владимир', 'Отчество': 'Федорович', 'Фамилия': 'Иванов', 'Оценка': 3}
Обратите внимание, что группировка работает только со смежными объектами. Предварительно отсортируйте данные.
Функция itertools.tee() создаёт из одного итерируемого объекта два итератора:
>>> letters = 'abc'
>>> it1, it2 = itertools.tee(letters)
>>> next(it1)
'a'
>>> next(it1)
'b'
>>> next(it2)
'a'
Эти итераторы соответствуют одной последовательности, но независимы друг от друга.
Волшебная сила itertools – в умении комбинировать итераторы, чтобы писать быстрый, эффективный и ясный код.
Например, сочетание itertools.chain() и itertools.from_iterable() даёт ограниченный вариант бесконечного itertools.cycle():
def ncycles(iterable, n):
return itertools.chain(itertools.from_iterable(repeat(tuple(iterable), n)))
Напоследок напишем функцию, выводящую все уникальные элементы в том же порядке, как они появлялись в исходной последовательности. Опциональный аргумент – ссылка на функцию определения эквивалентов, представленных по-разному. Например, заглавных и строчных букв.
def unique_everseen(iterable, key=None):
seen = set()
seen_add = seen.add
if key is None:
for element in itertools.filterfalse(seen.__contains__, iterable):
seen_add(element)
yield element
else:
for element in iterable:
k = key(element)
if k not in seen:
seen_add(k)
yield element
>>> list(unique_everseen('Абракадааааабра'))
['А', 'б', 'р', 'а', 'к', 'д']
>>> list(unique_everseen('Абракадааааабра', str. lower))
['А', 'б', 'р', 'к', 'д']
lower))
['А', 'б', 'р', 'к', 'д']
Описывая приёмы использования itertools, мы попутно определили основные функции модуля.
Итераторы полезны для обработки крупных файлов и потоков данных, для доступа к содержимому объектов без раскрытия их полного внутреннего представления.
Модуль itertools обеспечивает ключевые структуры итераторов Python. Другие шаблоны вы найдёте в специальной библиотеке примеров more-itertools:
pip install more-itertools
Понимание перестановок и комбинаций
При решении задач «Шесть сигм» часто важно рассчитать вероятность того, что произойдет комбинация событий или упорядоченная комбинация событий. Понимание некоторых основных концепций вероятности дает практикам инструменты для прогнозирования событий или комбинаций событий. Это обеспечивает хорошую основу для понимания распределения вероятностей, доверительных интервалов и проверки гипотез. Перестановки и комбинации — две важные концепции для создания этой основы.
Перестановки и комбинации — две важные концепции для создания этой основы.
Но перестановки и комбинации вызывают много путаницы: «Какой из них какой?» и «Какой из них я использую?» являются общими вопросами.
Перестановки
Если я покупаю салат на обед, это может быть смесь листьев салата, помидоров, моркови и редиски. Меня не особо волнует, в каком порядке кладут овощи в миску. Меня волнует только то, что у меня есть салат из листьев салата, помидоров, моркови и редиски. Салат может состоять из «моркови, помидоров, редиски и салата» или «редиса, помидоров, моркови и салата». Для меня это все тот же салат.
Как насчет ПИН-кода для моего банковского счета? «ПИН-код моей учетной записи — 8-9-10». Если я хочу получить доступ к своему банковскому счету через банкомат, мне нужно позаботиться о порядке этих цифр. «10-9-8» не будет получать доступ к моей учетной записи. Как и «9-10-8». Должно быть ровно 8-9-10. Порядок важен.
Детали имеют значение для перестановок – каждая мелочь. Для перестановки красный/желтый/зеленый отличается от зеленого/желтого/красного. Порядок важен, и его необходимо соблюдать.
Для перестановки красный/желтый/зеленый отличается от зеленого/желтого/красного. Порядок важен, и его необходимо соблюдать.
Комбинации
С комбинациями гораздо проще уживаться — детали не имеют большого значения. В комбинации красный/желтый/зеленый выглядит так же, как зеленый/желтый/красный.
Перестановки предназначены для списков (где порядок имеет значение), а комбинации — для групп (где порядок не имеет значения). Другими словами: перестановка — это упорядоченная комбинация.
Примечание. «Комбинированный» замок на самом деле следует называть «перестановочным», потому что порядок, в котором вы ставите числа, имеет значение. Настоящий «комбинированный» замок открывается с использованием либо 10-17-23, либо 23-17-10. На самом деле, любая комбинация из 10, 17 и 23 откроет настоящий «комбинационный» замок.
Перестановки: Детали, Детали, Детали
Перестановки — это все возможные способы расположения элементов множества. Мы будем заботиться о каждой мельчайшей детали, включая порядок каждого элемента. Перестановки рассматривают различные упорядоченные расположения как разные ответы.
Перестановки рассматривают различные упорядоченные расположения как разные ответы.
Допустим, у нас есть пять человек, участвующих в конкурсе барбекю: Энди, Боб, Чарли, Дэвид и Эрик.
Сколькими способами мы можем раздать ленточки за первое, второе и третье место (синюю, красную и желтую) среди 5 участников?
Поскольку важен порядок вручения лент, нам нужно использовать перестановки.
Вот разбивка:
- Голубая лента: Есть пять вариантов: A B C D E. Допустим, А выигрывает синюю ленту.
- Красная ленточка: Осталось четыре варианта: B C D E. Допустим, B выиграет красную ленточку.
- Желтая лента: Осталось три варианта: C D E. Допустим, C выиграет желтую ленту.
В этом примере мы выбрали определенных людей для победы, но на самом деле это не имеет значения. Важно лишь то, что мы понимаем, что сначала у нас было пять вариантов, затем четыре, а потом три. Всего вариантов было 5 × 4 × 3 = 60 . Пришлось заказывать трех человек из пяти. Для этого мы начинали со всех пяти вариантов, затем убирали их по одному (четыре, потом три и т. д.), пока не кончились ленты.
Для этого мы начинали со всех пяти вариантов, затем убирали их по одному (четыре, потом три и т. д.), пока не кончились ленты.
Пятифакториал (пишется 5!) это: 5! = 5 × 4 × 3 × 2 × 1 = 120 .
Но 120 слишком много! Это сработало бы, если бы у нас было пять лент. Но мы этого не делаем; у нас есть три ленты. Нам нужно всего 5 × 4 × 3 (общее количество вариантов). Как заставить факториал «остановиться» на 3? Нам нужно избавиться от 2 × 1. Что мы называем 2 × 1? 2-факториал! Это то, что осталось после того, как мы выберем трех победителей из пяти участников.
Если разделить 5! на 2!, получаем: 5! / 2! = (5 × 4 × 3 × 2 × 1) / (2 × 1) = 5 × 4 × 3 = 60 (поскольку 2 × 1 в числителе и знаменателе компенсируют друг друга).
Лучше (проще) записать это так: 5! / (5 – 3)!
Это говорит: «Используйте первые три числа из 5!»
В более общих чертах, если у нас всего n предметов и мы хотим выбрать k в определенном порядке, мы получим:
n! / (н – к)!
А это формула перестановки: Число способов, которыми k элементов можно заказать из n элементов:
P(n,k) = n! / (н – к)!
Комбинации: Заказ не требуется
У каждого из нас есть спокойный родственник. Ничто их не беспокоит. Они просто живут своей жизнью, как будто ничего не имеет значения.
Ничто их не беспокоит. Они просто живут своей жизнью, как будто ничего не имеет значения.
Комбинации — беспечные родственники перестановок. Порядок для них не имеет значения. Вы можете смешать заказ, и они все равно будут счастливы. Мир кажется им одинаковым, упорядочен он или нет.
Допустим, вместо того, чтобы награждать синей, красной и желтой ленточками за наш конкурс барбекю, мы награждаем тройку лучших ленточками «участника». Сколькими способами я могу наградить тремя лентами участника пять человек?
В этом случае порядок не имеет значения. Если я подарю ленточку участника Энди, Бобу и Чарли, это будет то же самое, что подарить ленточку участника Чарли, Энди и Бобу. В любом случае, все они будут одинаково разочарованы.
Минуточку! Энди/Боб/Чарли = Чарли/Боб/Энди. У нас тут есть повторы. Не обращайте на это внимания, давайте просто подсчитаем, сколькими способами мы можем переставить трех человек.
У нас есть три варианта для первого лица, два для второго и только один для последнего. Итак, у нас есть 3*2*1 способа переставить трех человек.
Итак, у нас есть 3*2*1 способа переставить трех человек.
Но это похоже на перестановку – так оно и есть! Если у вас N человек, и вы хотите знать, сколько аранжировок есть для всех, это просто N -факториал или N !
Итак, если нам нужно раздать три ленты участников, их будет 3! равно шести вариантам для каждого выбора, который мы выбираем. Если мы хотим выяснить, сколько у нас комбинаций, мы создаем все перестановки и делим на все избыточности. В нашем случае мы получаем 336 перестановок ( 8 x 7 x 6 ), и делим на шесть избыточностей для каждой перестановки и получаем 336/6 = 56 .
Таким образом, общая формула комбинации:
C(n,k) = P(n,k) / k!
Это означает: «Найти все способы выбрать k человек из n и разделить на k ! варианты». Записав это, мы получим нашу формулу комбинирования, или количество способов комбинирования k элементов из набора n:
C(n,k) = n! / (н-к)! × к!
Заключение
Более важно понять, почему перестановки и комбинации работают, чем запомнить формулы. Вы всегда можете найти формулы, если забудете их.
Вы всегда можете найти формулы, если забудете их.
Только помните:
- Если порядок не имеет значения, это комбинация.
- Если порядок имеет значение, то это перестановка.
Методы подсчета, перестановки и комбинации
Методы подсчета — обычно называемые в материалах GMAT «комбинациями и перестановками» — обычно представляют собой область математики с самой низкой доходностью в тесте. Под «самой низкой отдачей» я подразумеваю, что улучшение вашего результата на тесте невелико по сравнению с количеством усилий, которые вы должны приложить к теме. Если у вас есть сильное словесное представление, вы определенно можете побить 700 или 720 без знаний, кроме правил счета № 1 и № 2 ниже. Тем не менее, если вы стремитесь покорить раздел «Количественный анализ» и справились с текстовыми задачами и вопросами по геометрии, пришло время обратиться к методам счета.
Как упоминалось ранее в нашем обсуждении факториалов, на GMAT мы иногда должны подсчитывать возможности. В некоторых вопросах мы делаем это для того, чтобы вычислить вероятность, а в некоторых — потому, что нас об этом прямо просят.
В некоторых вопросах мы делаем это для того, чтобы вычислить вероятность, а в некоторых — потому, что нас об этом прямо просят.
В некоторых случаях мы можем подсчитать возможности, просто перечислив их исчерпывающе — перечислив. Этот метод прост и хорошо работает со многими вопросами GMAT. В других случаях нам придется вычислить количество возможностей чего-то, не имея возможности подсчитать все возможности, либо потому, что мы имеем дело с переменной, либо потому, что количество возможностей слишком велико для перечисления.
Правило продукта
Группы независимых возможностей, если рассматривать их совместно, увеличиваются в числе. Если существует 90 142 и 90 143 способов сделать одно действие и 90 142 и 90 143 способов сделать другое, то существует 90 142 и 90 143 способов выполнить оба действия.
Предположим, вы решили заказать пиццу. Сначала необходимо выбрать тип корочки: тонкое или глубокое блюдо (2 варианта). Затем вы выбираете начинку: сыр, пепперони или колбасу (3 варианта). Используя правило произведения, вы знаете, что существует (2)(3) = 6 возможных комбинаций заказа пиццы.
Используя правило произведения, вы знаете, что существует (2)(3) = 6 возможных комбинаций заказа пиццы.
Думая об этом примере в обозначениях: если начинки {A,B,C}, а варианты корочки {X,Y}, то возможные общие варианты выбора {AX,AY,BX,BY,CX,CY} . В этом примере правило гласит: умножьте 3 на 2, чтобы получить 6.
Ключ к правилу произведения состоит в том, что две категории возможности учитываются или получаются одновременно . Другими словами, ваша пицца будет иметь тип корочки и топпинг . Вот почему вы умножаете. Когда вы рассматриваете взаимоисключающие категории, вы используете «Правило суммы».
Правило суммы
Правило суммы, как и правило произведения, является основным принципом счета. Это идея о том, что если у нас есть 90 142 a 90 143 способов сделать что-то и 90 142 b 90 143 способов сделать что-то другое, и мы не можем делать и то, и другое одновременно, то есть 90 142 a + b 90 143 способов выбрать одно из действий.
Рассмотрим модификацию примера с пиццей. Скажем, пицца, которую вы заказываете, по умолчанию представляет собой пиццу на тонком тесте без начинки. Без дополнительной платы вы можете получить одно «улучшение» к пицце: толстое тесто или одну начинку — сыр, пепперони или колбасу. Правила пиццерии в этом случае другие. Можем выбрать толстую корочку или топпинг, но не оба. Поскольку возможности исключительны, применяется правило суммы: есть 1 + 3 = 4 способа выбрать одно бесплатное дополнение для вашей пиццы.
Скажем, пицца, которую вы заказываете, по умолчанию представляет собой пиццу на тонком тесте без начинки. Без дополнительной платы вы можете получить одно «улучшение» к пицце: толстое тесто или одну начинку — сыр, пепперони или колбасу. Правила пиццерии в этом случае другие. Можем выбрать толстую корочку или топпинг, но не оба. Поскольку возможности исключительны, применяется правило суммы: есть 1 + 3 = 4 способа выбрать одно бесплатное дополнение для вашей пиццы.
Упражнения
1. Томас идет в ресторан и решает приготовить свой собственный бургер. У него есть 2 разных вида сыра, 3 разных хлеба и 3 разных соуса, из которых он может выбирать, но он может выбрать только один из каждой категории. Сколькими способами он может приготовить этот бургер?
2. Диана заказывает пиццу для своей семьи. Есть 4 различных возможных размера пиццы. Кроме того, она должна выбрать одну из 5 начинок для пиццы и один из 3 разных видов сыра для пиццы. Кроме того, она должна выбрать один из 3 различных видов корочки. Сколькими способами она может съесть свою пиццу?
Сколькими способами она может съесть свою пиццу?
3. а) Сколько трехзначных чисел можно составить из цифр 2, 3, 4, 5, 7 и 9?
б) Сколько из этих чисел меньше 400?
Ответы
1.
2.
3. а) Поскольку имеется шесть доступных цифр, ответ будет
б) Чтобы значение трехзначного числа было меньше 400, мы только есть два варианта для первой цифры, а именно 2 или 3. После этого мы можем свободно выбирать две другие цифры. Таким образом, ответ
Зависимые события и факториалы
Есть n ! различные способы расположения n различных объектов в последовательность, перестановки этих объектов.
Предположим, Джон работает в библиотеке. Он должен поставить 5 книг на полку в любом порядке. Сколькими способами он может расположить книги на полке? В отличие от независимых событий, здесь, когда Джон кладет книгу на полку, это исключает одну книгу из оставшихся вариантов книг, которые можно поставить на полку следующей; поэтому они называются зависимыми событиями. Сначала у него есть 5 различных вариантов, поэтому первым числом в задаче на умножение будет 5. Теперь, когда одно число отсутствует, число уменьшается до 4. Затем оно уменьшается до 3 и так далее. Итак, общее количество способов заказать 5 книг:
Сначала у него есть 5 различных вариантов, поэтому первым числом в задаче на умножение будет 5. Теперь, когда одно число отсутствует, число уменьшается до 4. Затем оно уменьшается до 3 и так далее. Итак, общее количество способов заказать 5 книг:
Допустим, на собачьем соревновании участвуют 10 собак. Сколькими способами можно выбрать победителей первого и второго места? Мы можем начать с первого места. Есть 10 разных собак, поэтому 10 разных способов выбрать первое место. Далее, сколько собак осталось, чтобы выбрать второе место? В любом случае, независимо от того, кто был выбран на первое место, есть 9 способов выбрать второе место. Итак, что в сумме? Есть 10 способов выбрать первое место, а есть 9способов выбрать второе место для каждого способа выбрать первое место, поэтому есть 10 раз по 9 или 90 способов выбрать первое и второе место из 10 собак. Фраза «для каждого» здесь и часто является намеком на то, что мы должны умножать.
Правила подсчета
Правило 1: Повторные испытания одного типа. Если любое из k взаимоисключающих и исчерпывающих событий может произойти в каждом из n испытаний, то существует
Если любое из k взаимоисключающих и исчерпывающих событий может произойти в каждом из n испытаний, то существует
различных последовательностей, которые могут возникнуть в результате набора таких испытаний.
Пример: Подбросьте монету три раза, чтобы найти количество возможных последовательностей. Так как у медали две стороны, есть два возможных исхода, и k = 2. Подбросов три, поэтому n = 3. Следовательно,
Правило 2: Испытания смешанных типов. Если числа
являются числами возможностей на n стадиях событий, то количество различных полных последовательностей событий, которые могут произойти, равно произведению этих чисел:
.
Пример: Подбросьте монету и бросьте кубик, чтобы найти количество возможных последовательностей. Количество различных итоговых результатов:
Правило 1 и Правило 2 по существу являются одним и тем же правилом. Например, если вы рассматриваете применение правила 2, в котором вы просто делаете одно и то же n раз, так что все k равны, то вы получите k к n . силовые возможности. Вы также можете смешивать правила. Например, если вы трижды подбросите монету, а затем бросите шестигранный кубик, количество возможных исходов равно 9.0003
Например, если вы рассматриваете применение правила 2, в котором вы просто делаете одно и то же n раз, так что все k равны, то вы получите k к n . силовые возможности. Вы также можете смешивать правила. Например, если вы трижды подбросите монету, а затем бросите шестигранный кубик, количество возможных исходов равно 9.0003
.
Правило 3: Перестановка. Расположение по порядку называется перестановкой. Число различных способов, которыми n различных вещей могут быть упорядочены (или расположены вдоль линии или относительно одного измерения), равно
То есть есть n ! способы заказа n товаров по одному измерению.
Пример: Расположите 10 предметов по порядку, найдя количество возможных способов. Количество возможных аранжировок
Пример: Мы хотим вычислить количество перестановок S = {1,2,3}. Поскольку множество S состоит из трех элементов, в нем 3! = 6 перестановок.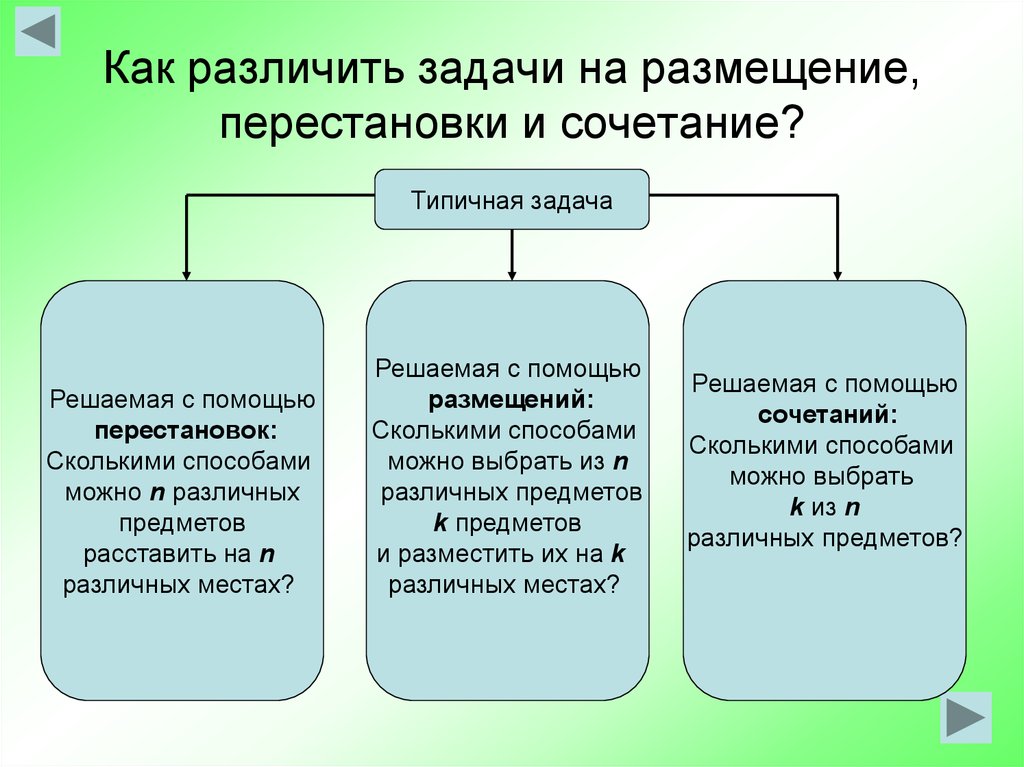 Их можно перечислить как 123, 132, 213, 231, 312, 321. Этот пример изображен графически ниже:
Их можно перечислить как 123, 132, 213, 231, 312, 321. Этот пример изображен графически ниже:
Возможные перестановки 3 элементов
Правило 4: k -Permutation Количество способов выбора и расположения тыс. объектов из числа n различных объектов:
или, как видно на калькуляторе или написано от руки, [nPk].
Пример: выберите 3 предмета из 10 и разложите их по порядку. В таком случае n = 10, k = 3, поэтому общее количество общих исходов, выборов и расстановок равно
числа 10!/7! значительно упростили, сократив его до (10)(9)(8). Упрощение такого рода всегда будет возможно при применении этого правила или приведенного ниже правила. Всегда будет факториал в числителе и меньший факториал в знаменателе, а множители большего факториала всегда полностью включают меньший факториал.
Возможно, вы сможете решить этот вопрос и другие k -перестановки, не используя приведенную выше формулу, а используя правило произведения, обсуждавшееся выше. Обратите внимание, что приведенное выше очень похоже на пример, который мы обсуждали с выставкой собак с двумя победителями, только в этом случае у нас есть три победителя. Для решения этого вопроса можно использовать ту же методику, которую мы использовали для решения вопроса о выставке собак.
Обратите внимание, что приведенное выше очень похоже на пример, который мы обсуждали с выставкой собак с двумя победителями, только в этом случае у нас есть три победителя. Для решения этого вопроса можно использовать ту же методику, которую мы использовали для решения вопроса о выставке собак.
Пример: Недавно созданная музыкальная группа может сыграть четыре оригинальных песни. Их просят исполнить две песни на музыкальном фестивале. Мы хотим вычислить количество аранжировок, которые группа может предложить на концерте. Абстрактно это эквивалентно вычислению количества 2-перестановок четырех песен. Таким образом, количество различных аранжировок равно 4!/2! = 12.
Возможные варианты выбора-2 из 4 элементов
0142 k » перестановка n элементов аналогична простой перестановке n элементов, о которой мы говорили в предыдущем правиле. Здесь есть дополнительная логическая ошибка, заключающаяся в том, что мы не выбираем все элементы для упорядочения.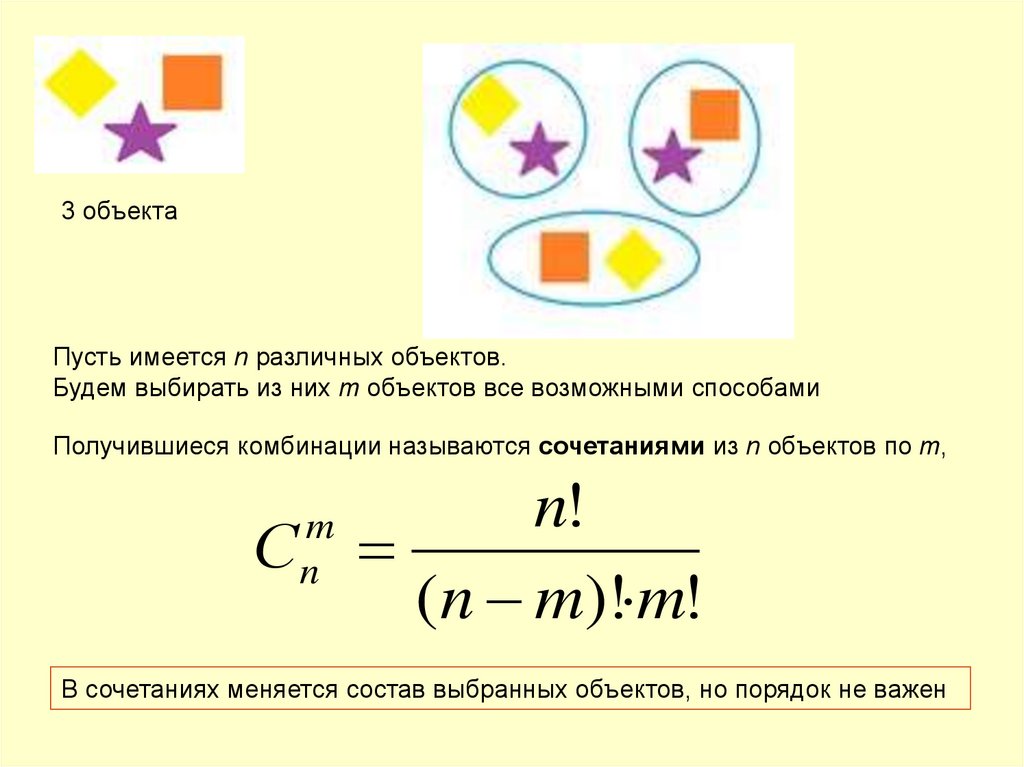 Другой способ представить это состоит в том, что простая перестановка n элементов, описанная в предыдущем правиле, подобна перестановке k n элементов, в которой вы выбираете все n элементов, так что к = п . Подставив это в приведенную выше формулу, мы получим
Другой способ представить это состоит в том, что простая перестановка n элементов, описанная в предыдущем правиле, подобна перестановке k n элементов, в которой вы выбираете все n элементов, так что к = п . Подставив это в приведенную выше формулу, мы получим
Как и следовало ожидать, мы вернулись к предыдущему правилу, которое гласит, что существует n ! способы заказа n шт.
Правило 5: Комбинация. Общее количество способов выбора k различных комбинаций из n объектов, независимо от порядка (т. е. мы не упорядочиваем элементы после выбора k, , а только делаем выбор), составляет:
или, как показано на калькуляторе, [nCr]. Этот выбор называется «комбинацией» , чтобы отличить его от перестановки выше.
Пример: Выберите 3 предмета из 10 в любом порядке, где n = 10, k = 3. Общее количество способов сделать выбор равно
Один из способов запомнить Правило № 5: что оно представляет вычисление, аналогичное вычислению в правиле 4, но в правиле 5 количество уменьшено на по подразделениям. В этом правиле Правило 5 порядок нам не важен, количество возможных способов выбора будет меньше, поэтому делим на к !.
В этом правиле Правило 5 порядок нам не важен, количество возможных способов выбора будет меньше, поэтому делим на к !.
Пример: Мы можем рассмотреть приведенный выше пример в модифицированном виде. У недавно созданной музыкальной группы есть четыре оригинальных песни, которые они могут сыграть. Их просят исполнить две песни на музыкальном фестивале. Если мы хотим вычислить количество аранжировок песен, которые группа может предложить на концерте, игнорируя порядок, число комбинаций 4!/(2!) разделить на 2!, или 6.
Количество комбинаций 2-х элементов, выбранных из 4
(Пунктирные линии означают, что комбинации не упорядочены.)
Иногда полезно знать, что
Мы можем видеть это непосредственно из определения
Обратите внимание, что два члена в знаменателе в сумме дают n . Так, например,
и
Этот факт может пригодиться на GMAT, когда вас спросят об одной такой комбинации, но с эквивалентной комбинацией работать проще.


 Сколькими способами он может сделать выбор?»
Сколькими способами он может сделать выбор?»

 Сколькими способами пять человек могут обменяться фотографиями?
Сколькими способами пять человек могут обменяться фотографиями? Сколькими способами можно окрасить трехкомнатную квартиру (каждая комната окрашивается одной краской, все комнаты окрашиваются в разные цвет), если имеется 10 различных красок?
Сколькими способами можно окрасить трехкомнатную квартиру (каждая комната окрашивается одной краской, все комнаты окрашиваются в разные цвет), если имеется 10 различных красок? repeat(2))
>>> list(squares)
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
repeat(2))
>>> list(squares)
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
 chain('ABC', 'DEF'))
['A', 'B', 'C', 'D', 'E', 'F']
>>> list(itertools.chain.from_iterable(['ABC', 'DEF']))
['A', 'B', 'C', 'D', 'E', 'F']
chain('ABC', 'DEF'))
['A', 'B', 'C', 'D', 'E', 'F']
>>> list(itertools.chain.from_iterable(['ABC', 'DEF']))
['A', 'B', 'C', 'D', 'E', 'F']
 groupby(people, get_mark)
for key, group in person_marks:
print(key)
for person in group:
print(person)
print()
groupby(people, get_mark)
for key, group in person_marks:
print(key)
for person in group:
print(person)
print()
 lower))
['А', 'б', 'р', 'к', 'д']
lower))
['А', 'б', 'р', 'к', 'д']