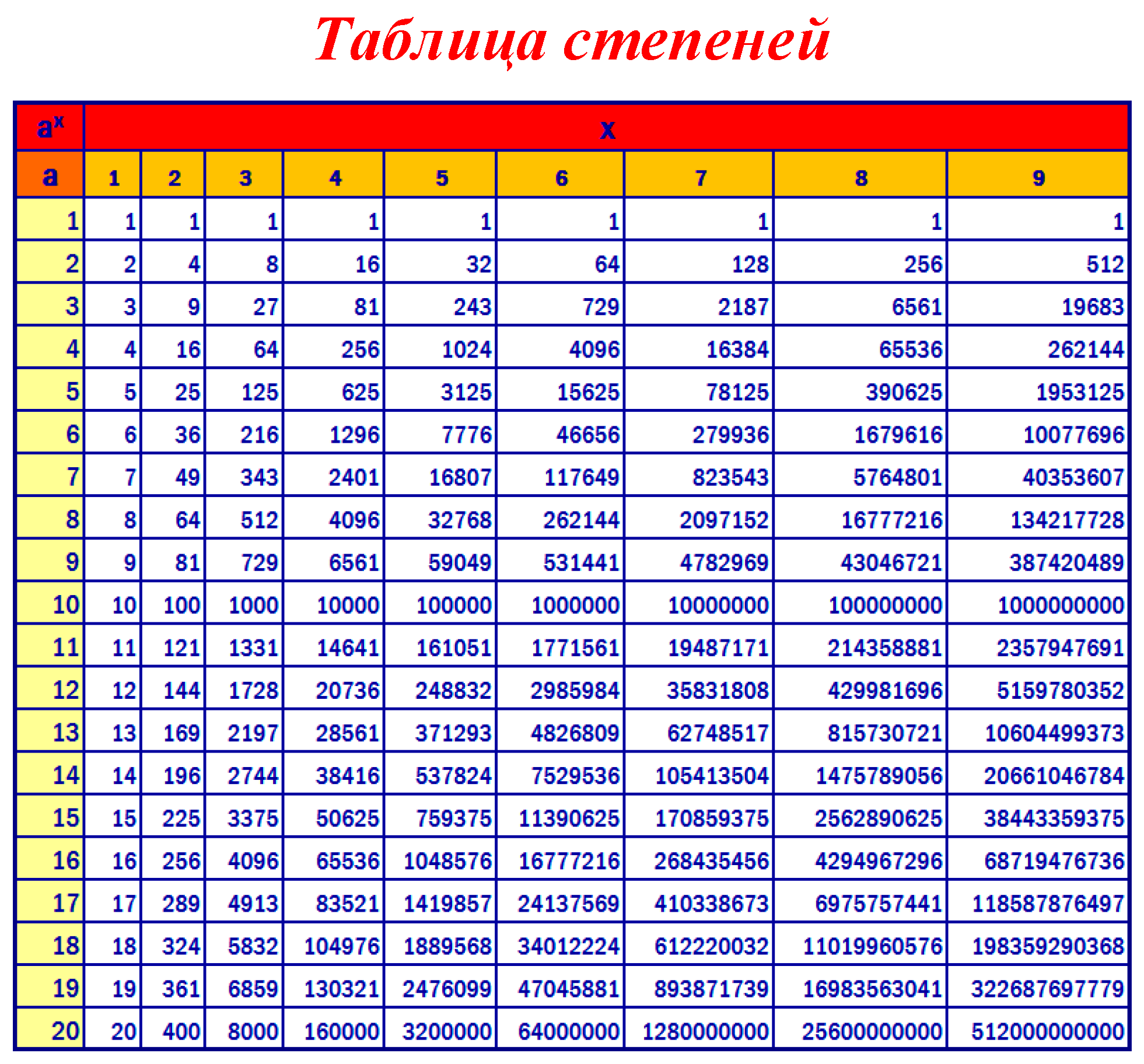
Как понять математику с нуля: Математика с нуля. Это возможно? — Офтоп на vc.ru

Содержание

Дроби

Дроби это тема об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.

Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые.

Но есть и хорошие новости. Если вы наберётесь терпения и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным.

А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину.

Что такое дробь?

Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.

Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.

Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.

Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия:

Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:

А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:

Такие записи называют дробями. Дробь состоит из числителя и знаменателя.

Число, которое записывается сверху, называется числителем дроби.

Число, которое записывается снизу, называется знаменателем дроби.

В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы.

Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь?

Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):

Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли».

Теперь представьте, что пиццу мы разделили не на четыре части, а на три.

Допустим мы съели один кусок этой пиццы. Как записать такую дробь?

Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:

Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть».

Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:

Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам»:

Допустим, из этих двух кусков мы съели один кусок. Как записать такую дробь?

Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:

Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина».

Дроби, которые мы сейчас рассмотрели, называют обыкновенными.

Вообще, дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже.

Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.

На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4.

Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли (одну часть из двух), или как говорят в народе «половину» пиццы.

С помощью переменных дробь можно записать так:

где a — это числитель, b — знаменатель.

Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильными и неправильными.

Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:

Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём (одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.

С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:

Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.

Теперь возьмём к примеру неправильную дробь и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.

Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например:

Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь . Применим её к нашей пицце.

Допустим, мы хотим съестьпиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим этупиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.

Дробь означает деление

Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.

Например, рассмотрим дробь . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:

Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:

Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».

Выделение целой части дроби

Вычислим дробь . Пять разделить на два будет два и один в остатке:

5 : 2 = 2 (1 в остатке)

Проверка: (2 × 2) + 1 = 4 + 1 = 5

Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде. Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.

Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?

Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой:

Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом. Очевидно, что каждому досталось по два целых яблока и по половинке яблока.

Теперь возвращаемся к дроби и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:

Схематически это выглядит так:

Процедуру, которую мы сейчас провели, называют выделением целой части дроби.

В нашем примере мы выделили целую часть дроби и получили новую дробь . Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.

В нашем примере целая часть это 2, а дробная часть это

Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь.

Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и у них выделена целая часть:

Чтобы выделить целую часть, достаточно знать, как делить числа уголком. Например, выделим целую часть у дроби . Записываем уголком данное выражение и решаем:

После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Важно понимать, что куда относить. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части.

В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.

Но если вы только начинаете изучать математику, советуем записывать каждую мелочь.

Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть дроби

Записываем уголком данное выражение и решаем. Потом собираем смешанную дробь:

Получили:

Перевод смешанного числа в неправильную дробь

Любое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь . Если выделить в ней целую часть, то получается

Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученный результат будет числителем новой дроби, а знаменатель останется без изменений.

Например, переведём смешанное число в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:

2 × 3 = 6

Затем к 6 прибавляем числитель дробной части:

6 + 1 = 7

Полученная семёрка будет числителем новой дроби, а знаменатель 3 останется без изменений:

Подробное решение выглядит так:

А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:

Пример 2. Перевести смешанное число в неправильную дробь.

Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменений:

Основное свойство дроби

Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится.

Например, рассмотрим дробь . Умножим её числитель и знаменатель на одно и то же число, например на число 2

Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:

Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (один кусок из двух), а второй иллюстрирует дробь (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.

Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.

Рассмотрим дробь . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2

Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (четыре куска из восьми), а второй иллюстрирует дробь (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.

Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.

Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!

Сокращение дробей

Дроби можно сокращать. Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь .

Если при решении примеров получается большая и некрасивая дробь, то нужно попытаться её сократить.

Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби.

Деление числителя и знаменателя на их наибольший общий делитель называется сокращением дроби.

Пример 1. Сократить дробь

Итак, нужно разделить числитель и знаменатель дроби на наибольший общий делитель чисел 2 и 4.

В данном случае дробь простая и для неё НОД ищется легко. НОД чисел 2 и 4 это число 2. Значит, числитель и знаменатель дроби надо разделить на 2

В результате дробь обратилась в более простую дробь . Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число. А это действие, как было указано ранее, не меняет значение дроби.

На рисунке представлены дроби и в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному.

Пример 2. Сократим дробь

Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40.

НОД чисел 20 и 40 это число 20. Поэтому делим числитель и знаменатель дроби на 20

Пример 3. Сократим дробь

Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36.

НОД чисел 32 и 36 это число 4. Поэтому делим числитель и знаменатель дроби на 4

Если в числителе и знаменателе располагаются простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми:

Напомним, что простыми называются числа, которые делятся только на единицу и самих себя.

Второй способ сокращения дроби

Второй способ является короткой версией первого способа. Суть его заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель.

К примеру, вернёмся к дроби . Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4

Теперь представьте, что в данном выражении отсутствует конструкция , и сразу записан ответ . Получится следующее выражение:

Суть в том что число, на которое разделили числитель и знаменатель, хранят в уме. В нашем случае числитель и знаменатель делят на 4 — это число и будем хранить в уме.

Сначала делим числитель на число 4. Полученный ответ записываем рядом с числителем, предварительно зачеркнув его:

Затем таким же образом делим знаменатель на число 4. Полученный ответ записываем рядом со знаменателем, предварительно зачеркнув его:

Затем собираем новую дробь. В числитель отправляем новое число 8 вместо 32, а в знаменатель отправляем новое число 9 вместо 36

Происходит своего рода замена одной дроби на другую. Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.

Также, дроби можно сокращать, предварительно разложив на простые множители числитель и знаменатель.

Например, сократим дробь , предварительно разложив на простые множители числитель и знаменатель:

Итак, мы разложили числитель и знаменатель дроби на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.

Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение:

Сократить можно ещё по тройке в числителе и в знаменателе:

Дальше сокращать больше нéчего. Последнюю тройку в знаменателе просто так сократить нельзя, поскольку в числителе нет множителя, который можно было бы сократить вместе с этой тройкой.

Записываем новую дробь, в числителе и в знаменателе которой будут новые множители.

Получили ответ . Значит, при сокращении дроби получается новая дробь .

Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на простые множители числителя и знаменателя, если человек только нáчал изучать математику. Практика показывает, что это оказывается сложным на первых этапах.

Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решён старым способом и будет выглядеть так:

Сравните это выражение с выражением, которое мы получили, когда пользовались вторым способом:

Первое выражение намного понятнее, аккуратнее и короче. Не правда ли?

Задания для самостоятельного решения

Задание 1. Запишите в виде дроби следующий рисунок:

Показать решение

Задание 2. Запишите в виде дроби следующий рисунок:

Показать решение

Задание 3. Запишите в виде дроби следующий рисунок:

Показать решение

Задание 4. Запишите в виде дроби следующий рисунок:

Показать решение

Задание 5. Запишите в виде дроби следующий рисунок:

Показать решение

Задание 6. Выделите целые части в следующих дробях:

Показать решение

Задание 7. Выделите целые части в следующих дробях:

Показать решение

Задание 8. Переведите смешанные дроби в неправильные:

Показать решение

Задание 9. Переведите смешанные дроби в неправильные, не расписывая как целая часть умножается на знаменатель дробной части и полученный результат складывается с числителем дробной части

Показать решение

Задание 10. Сократите следующую дробь на 3

Показать решение

Задание 11. Сократите следующую дробь на 3 вторым способом

Показать решение

Задание 12. Сократите следующую дробь на 5

Показать решение

Задание 13. Сократите следующую дробь на 5 вторым способом

Показать решение

Задание 14. Сократите следующие дроби:

Показать решение

Задание 15. Сократите следующие дроби вторым способом:

Показать решение

Задание 16. Запишите в виде дроби следующий рисунок:

Показать решение

Задание 17. Запишите в виде дроби следующий рисунок:

Показать решение

Задание 18. Запишите в виде дроби следующий рисунок:

Показать решение

Задание 19. Запишите в виде дроби следующий рисунок:

Показать решение

Задание 20. Запишите в виде дроби следующий рисунок:

Показать решение

Задание 21. Изобразите в виде рисунка следующую дробь:

Показать решение

Задание 22. Изобразите в виде рисунка следующую дробь:

Показать решение

Задание 23. Изобразите в виде рисунка следующую дробь:

Показать решение

Задание 24. Изобразите в виде рисунка следующую дробь:

Показать решение

Задание 25. Изобразите в виде рисунка следующую дробь:

Показать решение

Задание 26. Изобразите в виде рисунка следующую дробь:

Показать решение

Задание 27. Изобразите в виде рисунка следующую дробь:

Показать решение

Задание 28. Изобразите в виде рисунка следующую дробь:

Показать решение

Задание 29. Изобразите в виде рисунка следующую дробь:

Показать решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

как научиться работе с цифрами

Этого не должно было случиться, но почему-то произошло: 11 класс остался в далеком прошлом, а вы стали вовсе не художником или рок-звездой, а интернет-маркетологом. И школьная учительница оказалась права: математика еще пригодится, вот увидишь!

Где учиться цифрам с нуля, как не сойти с ума от цифр и почему в школе было так сложно (а сейчас легче не станет).

Почему математика такая страшная

В любой вещи, которую вы не понимаете, мало приятного. Но математику особенно не любят. Или даже боятся ее.

Дело не только в том, что у учительницы по алгебре был слишком грозный вид. Математическая тревожность — явление, которое исследуют ученые. И под тревожностью имеют в виду все ее проявления: панику, дрожь в руках. Непонятно, что появляется раньше: неспособности к математике и, как следствие, страх перед ней или же сам страх не дает научиться вычислениям.

Хорошая новость в том, что математическая тревожность слабо коррелирует с результатами тестов IQ.

Что мы знаем про способности к математике

Наверняка вы говорили о себе: «У меня нет математических способностей». И вообще закончили гуманитарный класс.

Большинство ученых с вами согласятся, но лишь потому, что в принципе не доказано существование врожденных способностей к математике. Исследователи много лет пытаются узнать о наследуемости этого навыка. Пока одним из самых громких за последнее время стала работа ученых из университета Питтсбурга (США). Они доказали, что есть корреляция между способностями к математике у детей и родителей. Но ее причина — не только в генетике, но и в социальных факторах.

Кроме способностей к математике, существует математическое чувство, и оно наследуется. Это благодаря ему мы определяем самую короткую очередь, не считая количество людей. Ученые из США сравнили, как дети в шесть месяцев и три с половиной года воспринимают цифры и количество предметов. Оказалось, что малыши, которые в раннем возрасте демонстрировали лучшие математические способности, показали лучший результат и спустя три года, причем общий уровень развития не коррелировал с математическими способностями.

Но выдыхать рано (вы наверняка уже решили, что оказались бы в этом эксперименте среди детей с заурядными результатами). Другая группа исследователей проверила, можно ли развить математические способности и научиться работе с цифрами во взрослом возрасте. Оказалось, что можно. Добровольцы решали задачи, а затем половина участников эксперимента тренировали математические навыки, а контрольная группа — нет, как и полагается контрольной группе. После этого все участники снова решили арифметические примеры.

Занимавшаяся математикой группа показала результаты гораздо выше, чем контрольная.

Как выучить математику во взрослом возрасте

Сначала решите, для чего вам нужна математика, какие темы нужно знать и как вы оцените, что цель выполнена. Для повседневной работы в маркетинге вам вряд ли понадобятся линал или понимание задач тысячелетия. Быстрое вычисление, работа с процентами, понимание математических функций.

Полезные курсы по математике

Проект «Математика с нуля»

Текстовые уроки по основным темам.

Интернет-Урок:

(Математика, 1-6 класс)
(Алгебра, 7-11 класс)

Уроки школьной программы по математике в формате видео. Рассчитаны на детей и подростков, но разве это вас остановит?

Stepik. Основы статистики

На практике пригодится чаще, чем основы по математике. Если вы не помните из статистики ничего, пройдите курс перед изучением веб-аналитики.

Stepik.

Теория вероятностей

Курс по теории вероятностей посвящен базовым вероятностным методам, которые можно использовать в работе и повседневной жизни.

Открытый университет. Теория игр

Теория игр полезна для многих специальностей. Развивает способность к анализу информации, постановке целей и созданию стратегий.

Вводный курс по матанализу

Если вы уже готовы к высшей математике, но плохо помните университетскую программу.

Khana Academy

Курсы разделены темам и по уровням. Дается сразу теория и тренажер, обучение геймифицировано. Уроки только на английском языке.

Книги по изучению математики с нуля

http://www.alleng.ru/

Подборка школьных учебников, если скучаете по ним.

Математика для взрослых. Кьяртан Поскитт

Не научит теории, но избавит от ежедневных страданий, когда нужно сделать простые вычисления.

Если вы аналитик и занимаетесь, например, аналитикой в Instagram или других соцсетях удобней всего использовать Popsters.

Итого:

Многие люди и правда боятся математику. Ученые не понимают: страх из-за незнания или незнание от страха.
Чувство числа наследуется от родителей. А вот математические способности можно развить.
Взрослые люди могут с нуля выучить математику. Для этого есть бесплатные курсы и книги.

Полезная статья на похожую тему:

Подборка лучших книг по маркетингу.

Как научить себя математике

Немногие предметы вызывают столько воспоминания о боли и беспокойстве, как уроки математики. Сбивающие с толку символы, сложные процедуры и страшные графики и диаграммы.

Кое-кто теперь даже предполагает, что изучение математики может быть травмирующим опытом, чем-то выжившим, чем выученным.

Болезненная история многих людей с математикой — это позор, потому что математика невероятно полезна. Многие из лучших профессий выходят из областей STEM и полагаются на понимание математики. Понимание новостей и событий в мире все больше становится уроком статистики. Наконец, правильно понятая математика позволяет вам решать многие из ваших собственных проблем.

В этой статье я хотел бы объяснить, как вы можете самостоятельно изучить любую математику, будь то статистика, алгебра или алгоритмы.

Шаг первый: начните с объяснения

Первый шаг к изучению любой математики — получить предварительное объяснение темы.

Эту информацию можно получить во многих местах. Вот несколько хороших ресурсов, охватывающих широкий спектр тем:

KhanAcademy — огромный бесплатный ресурс видео практически по всем темам математики
MIT OCW — они начинаются на университетском уровне, но они решают много сложной математики
Coursera — множество полных уроков по математике

Кроме того, существуют и специализированные ресурсы. Они, как правило, не охватывают все мыслимые темы, но часто более интересны, интуитивны и полезны для тех, кто ими занимается:

BetterExplained — отличные статьи, дающие интуитивное представление об исчислении, алгебре, экспонентах и многом другом
3Blue1Brown — отличные видеоролики на YouTube, подробно изучающие математические концепции
Numberphile – Беседы с математиками на интересные математические темы

Где бы вы ни получили свое объяснение, ваш первый шаг — посмотреть его один раз, чтобы почувствовать, что вы понимаете основы того, как оно работает.

Что делать, если я не понимаю объяснение?

Если вы посмотрели объяснение, но не поняли его, возможны две проблемы:

Вам не хватает некоторых предпосылок для понимания этой части математики
. Это означает, что вам нужно сделать резервную копию и пройти ее снова. Если вам кажется, что все «пошло слишком быстро» или вы не понимаете, что делает учитель, возможно, вам придется вернуться на несколько уроков назад и лучше выучить их, прежде чем продолжить.
Вы пытаетесь охватить слишком много без практики . Хороший способ — посмотреть кусок объяснения, а затем попробовать самому. Если вы только смотрите, но никогда не тренируетесь, это немного похоже на просмотр видео о катании на лыжах и никогда не катание по склонам. В конце концов объяснения перестанут иметь смысл, потому что у вас не будет личного опыта.

Попробуйте следующее: просмотрите объяснение один раз полностью в качестве отправной точки.

Шаг второй: Решайте задачи

Математика — это не то, что вы смотрите и запоминаете, а то, что вы делаете.

Если вы тратите все свое время на просмотр видео, а затем получаете набор задач, вам может быть очень трудно применить свои математические знания. Это может привести к ощущению, что вы «плохо разбираетесь в математике», хотя проблема лишь в том, что вы используете паршивый метод ее изучения.

Вы можете исправить это, приступив к решению проблем как можно скорее. Хорошая задача должна казаться сложной, но не невозможной. Если вы видите решение и даже не понимаете, как они его получили, скорее всего, вы слишком торопитесь — вернитесь и изучите некоторые основы, прежде чем двигаться дальше.

Что делать, если у меня нет проблем, которые нужно решать?

Если у вас нет предложенных задач, вы можете сделать несколько вещей:

Решить задачи, указанные в объяснении, но не глядя на ответ.
Создайте свои собственные проблемы и попытайтесь их решить.
Попробуйте доказать понятия в классе. Это продвинутая техника, но она необходима для того, чтобы по-настоящему понять более сложную математику.

Попробуйте следующее: после просмотра объяснения выполните достаточное количество задач, чтобы чувствовать себя комфортно и понимать процедуру.

Шаг третий: поймите, почему математика работает

Интуитивное понимание очень важно для математики, в отличие от других предметов. Хотя интуиция для словарного запаса слов на иностранном языке может помочь, их все равно нужно запоминать. Однако заучивание математики может быть опасным, если оно заставляет вас учить ее без понимания.

Следующий шаг — убедить себя, что вы знаете, почему математика работает. Моя любимая техника для этого — Техника Фейнмана, которую я демонстрирую здесь:

Техника Фейнмана требует некоторого времени, поэтому вам не нужно полностью применять ее к каждому аспекту каждой математической задачи, с которой вы сталкиваетесь. Скорее применяйте его выборочно к наиболее важным понятиям и тем, которые кажутся вам запутанными, несмотря на достаточную практику.

Попробуйте следующее: определите основные понятия математики, которые вы изучаете, и используйте метод Фейнмана, чтобы убедить себя, что вы их понимаете.

Шаг четвертый: играйте с математикой

Практика — это хорошо, лучше понимать, но лучше всего играть с математикой.

После того, как вы решили некоторые заданные вам вопросы и убедились, что понимаете их, естественным продолжением этого будет попытка поиграть с математикой, которую вам дали. Как все меняется, когда вы пытаетесь изменить числа или применить их к другим задачам?

Допустим, вы только недавно научились рассчитывать сложные проценты. Вы можете выполнять простые расчеты процентов самостоятельно, и вы понимаете, почему они работают. Как вы могли играть с этой математикой?

Вы могли видеть, что происходит по мере увеличения скорости начисления процентов.
Что произойдет, если проценты будут отрицательными?
Вы можете попытаться подсчитать собственные сбережения, если инвестируете их по разным ставкам.
Попробуйте представить, сколько процентов по ипотеке вы платите по сравнению с основной суммой.

Excel — это хороший способ поэкспериментировать с математикой, так как вы можете вводить формулы напрямую, без необходимости выполнять алгебраические операции или повторять вычисления.

Попробуйте следующее: возьмите тему математики, которую вы недавно изучали, и посмотрите, как вы можете изменить переменные, применить их к разным вещам и изменить формулы.

Шаг пятый: применение математики вне класса

В конечном счете, целью изучения математики должно быть ее использование, а не просто сдача теста. Однако для этого вам нужно освободить свое понимание от примеров из учебника и применить его к реальным ситуациям.

Это сложнее, чем просто решить проблему. Когда вы решите проблему, вы начнете запоминать схему решения. Это часто позволяет вам решать проблемы без реального понимания принципов их работы.

Применение математики в реальной жизни, напротив, требует осознания ситуации, перевода ее в математику и решения созданной вами проблемы. Это сложнее, чем решать проблемы, поэтому, если вы хотите действительно использовать то, чему научились, вам нужно практиковаться.

Попробуйте следующее: возьмите тему, которую вы недавно изучали по математике, и попытайтесь найти реальную ситуацию, в которой вы могли бы вычислить ее, используя свои собственные числа или оценки, если они недоступны.

Похоже, это слишком много работы!

Выполнение всех этих пяти шагов по каждой теме, которую вы изучаете по математике, займет много времени. Это нормально, вам не нужно делать это для каждой мелочи, которую вам нужно выучить.

Вместо этого думайте об этом как о индикаторе выполнения. Каждое математическое понятие, которое вы изучаете, может проходить с первого по пятый этапы, углубляя ваши знания и увеличивая полезность математики каждый раз.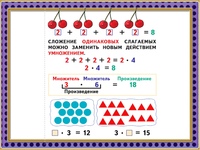 Некоторые концепции будут достаточно важными, чтобы вы захотели их тщательно применить. Другие будут достаточно редкими, чтобы просто смотреть объяснения — это все время, которое вы можете сэкономить.

В частности, постарайтесь сосредоточиться на наиболее важных концепциях каждой идеи. Математика имеет тенденцию быть глубокой, поэтому часто в классе полного семестра может быть только несколько действительно больших идей, а все остальные идеи являются просто различными проявлениями этой базовой концепции.

Большинство курсов по математическому анализу для первого года обучения, например, сосредоточены на понятии производной, а все, что преподается, представляет собой просто различные расширения и приложения этой основной идеи. Если вы действительно понимаете, что такое дериватив и как он работает, вам будет намного легче выучить другие части.

Соотношения в математике

A Соотношение — это некоторые отношения между сущностями в нашем мире. Это могут быть числа, физические величины, предметы, продукты или даже люди.

В математике отношение чаще используется как «сколько раз одно число содержит другое».

Например, если есть четыре яблока и две груши, то отношение «четыре к двум» (то есть 4∶2, что эквивалентно отношению 2∶1), или если мы поменяем местами яблоки и груши , «от двух до четырех».

Отношение выражается как a к b (где вместо a и b любые числа), но чаще можно увидеть так a : b . Существуют различные способы прочтения этого обозначения:

от a до b
отношение a к b

Запишем соотношение четырех яблок и двух груш, используя символ соотношения ( двоеточие ):

4 : 2

Это соотношение можно прочитать как «четыре к двум» или « соотношение четырех яблоки к двум грушам » или « четыре яблока к двум грушам ».

Если мы поменяем местами яблоки и груши, мы получим соотношение 2 : 4. Это соотношение можно прочитать как «два к четырем» или «две груши к четырем яблокам». «.

Что такое отношение?

Соотношение, как упоминалось ранее, записывается в виде a:b. Его также можно записать в виде дроби. А мы знаем, что такое обозначение в математике означает деление. Тогда результатом отношения является частное чисел a и b. Частное означает «сколько раз» и происходит от латыни.

Отношение в математике — это частное двух чисел. Равные частные соответствуют равным отношениям.

Отношение позволяет узнать, сколько раз одно число содержит другое

Вернемся к соотношению четырех яблок к двум грушам (4 : 2). Это соотношение позволяет нам узнать, сколько яблок приходится на единицу груши. Под одной мы подразумеваем одну грушу. Сначала запишем отношение 4 : 2 в виде дроби:

Это отношение есть деление числа 4 на число 2. Если мы произведем это деление, то получим ответ на вопрос « Каково соотношение яблок и груш?»

Получили 2.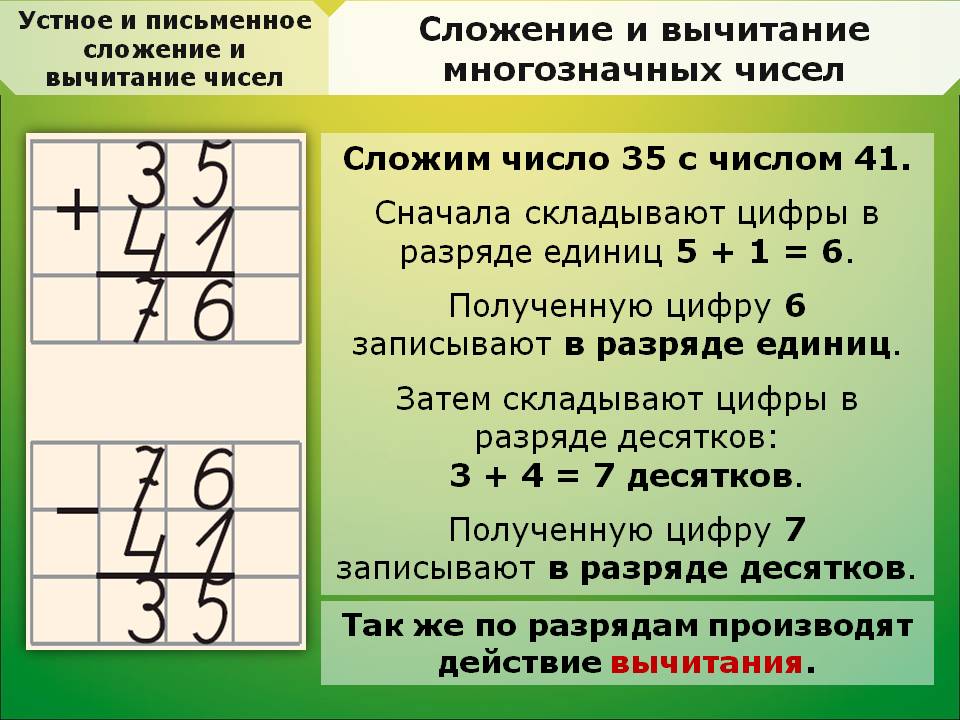 Итак, четыре яблока на две груши (4 : 2)

На диаграмме показано, как четыре яблока и две груши связаны друг с другом Вы видите, что на каждую грушу приходится два яблока.

Соотношение можно изменить, написав его как . Тогда мы получим отношение двух груш к четырем яблокам, или » отношение двух груш к четырем яблокам «. Это соотношение покажет, сколько груш приходится на единицу яблока. Под единицей яблока мы подразумеваем одно яблоко.

Чтобы найти значение дроби нужно вспомнить как делить меньшее число на большее

Получили 0,5. Преобразуем эту десятичную дробь в обыкновенную:

Уменьшим полученную дробь на 5

Ответ: (половина груши). Таким образом, две груши и четыре яблока (2 : 4) относятся друг к другу так, что одно яблоко составляет половину груши

На рисунке показано, каково отношение между двумя грушами и четырьмя яблоками. Вы видите, что на каждое яблоко приходится половинка груши.

Числа, составляющие отношение, называются членами отношения .

Например, в отношении 4 : 2 членами отношения являются числа 4 и 2
4 — предшествующие и 2 — 90 042 следствие

Учитывать другие примеры соотношений. Рецепт предназначен для приготовления чего-либо. Рецепт основан на соотношении продуктов. Например, для овсянки обычно требуется чашка хлопьев на две чашки молока или воды. Соотношение 1:2 (« один к двум » или « одна чашка хлопьев к двум чашкам молока «).

Преобразуем соотношение 1 : 2 в дробь, получим . Подсчитав эту дробь, получим 0,5. Итак, один стакан хлопьев а два стакана молока связаны друг с другом таким образом, что один стакан молока равен половине стакана хлопьев

Если мы инвертируем соотношение 1 : 2, то получим соотношение 2 : 1 («два к одному»). » или «два стакана молока на один стакан каши»). Преобразуем соотношение 2 : 1 в дробь, получим . Подсчитав эту дробь, получим 2. Значит, два стакана молока и один стакан каши связаны друг к другу таким образом, что на один стакан хлопьев приходится два стакана молока.

Пример 2. В классе 15 учеников. Из них 5 мальчиков и 10 девочек. Мы можем записать соотношение девочек и мальчиков 10:5 и преобразовать это соотношение в дробь. Если мы посчитаем эту дробь, то получим 2. Вот и все, девочки и мальчики связаны друг с другом таким образом, что на каждого мальчика приходится две девочки

На рисунке показано, как связаны между собой десять девочек и пять мальчиков другой. Вы видите, что на каждого мальчика приходится две девочки.

Не всегда возможно перевести отношение в дробь и найти частное. В некоторых случаях это будет нелогично.

Итак, если вы перевернете соотношение, вы получите , то есть соотношение мальчиков и девочек. Если вы вычислите эту дробь, вы получите 0,5. Получается, что пять мальчиков относятся к десяти девочкам так, что каждая девочка наполовину мальчик. Математически, конечно, это правильно, но с точки зрения реальности не совсем разумно, потому что мальчик — живой человек и его нельзя просто так взять и разделить, как грушу или яблоко.

Умение построить правильное соотношение является важным навыком при решении задач. Итак, в физике отношение пройденного расстояния ко времени есть скорость движения.

Расстояние обозначается переменной S , время переменной t , а скорость символом v . Тогда фраза «отношение пройденного пути ко времени есть скорость движения» будет описываться следующим выражением:

Предположим, автомобиль проехал 100 километров за два часа. Тогда отношение пройденных ста километров к двум часам будет скоростью автомобиля:

Скоростью обычно называют расстояние, пройденное телом за единицу времени. Единицей времени является 1 час, 1 минута или 1 секунда. А соотношение, как упоминалось ранее, позволяет узнать, сколько одного объекта приходится на единицу другого объекта. В нашем примере отношение ста километров к двум часам показывает, сколько километров приходится на один час движения. Мы видим, что на каждый час движения приходится 50 километров

Следовательно, скорость измеряется в км/ч, м/мин, м/с . Символ дроби (/) указывает на отношение расстояния ко времени: километров в час, метров в минуту и метров в секунду соответственно.

Пример 2. Отношение стоимости товаров к их количеству равно цене одной единицы товара

Если мы взяли в магазине пять шоколадных пирожных и их общая стоимость составила 100 долларов, то мы можем определить цена одного торта. Для этого нам нужно найти отношение ста долларов к количеству пирожных. Тогда мы получаем, что один торт стоит 20 долларов.

Сравнение величин

Ранее мы узнали, что соотношение между величинами различных форм природы является новой величиной. Например, отношение пройденного пути ко времени есть скорость движения. Отношение стоимости товара к его количеству есть цена одной единицы товара.

Но соотношение также можно использовать для сравнения значений. Результатом соотношения является число, показывающее, во сколько раз первое значение больше второго.

Чтобы узнать, во сколько раз первое значение больше второго, запишите большее значение в числитель, а меньшее — в знаменатель.

Чтобы узнать, какая часть первого значения является второй, запишите в числитель меньшее значение, а в знаменатель большее значение.

Рассмотрим числа 20 и 2. Выясним, во сколько раз число 20 больше числа 2. Для этого найдем отношение числа 20 к числу 2. Запишем число 20 в числитель и цифра 2 в знаменателе

Значение этого отношения равно десяти

Отношение числа 20 к числу 2 составляет число 10. Это число показывает, во сколько раз число 20 больше числа 2. Таким образом, число 20 в десять раз число 2.

Пример 2. В классе 15 учеников. Из них 5 мальчиков и 10 девочек. Определите, во сколько раз девочек больше, чем мальчиков.

Запишите соотношение девочек и мальчиков. Запишите количество девочек в числителе и количество мальчиков в знаменателе:

Значение этого отношения равно 2. Таким образом, в классе из 15 учащихся вдвое больше девочек, чем мальчиков.

Вопрос о том, сколько девочек приходится на одного мальчика, больше не стоит. В этом случае соотношение используется для сравнения числа девочек и числа мальчиков.

Пример 3. Какая часть числа 20 равна числу 2.

Найдите отношение 2 к 20. Запишите число 2 в числителе и число 20 в знаменателе

Чтобы найти значение этого отношения, нужно вспомнить, как делить меньшее число на большее

Значение отношения числа 2 к числу 20 равно числу 0,1

В этом случае десятичную 0,1 можно преобразовать в правильную дробь. Этот ответ будет легче понять:

Таким образом, число 2 из 20 составляет одну десятую.

Вы можете сделать тест. Для этого нужно найти число 20. Если мы все сделали правильно, то должно получиться число 2

20 : 10 = 2

2 × 1 = 2

Мы получили число 2. Значит одна десятая от 20 это число 2. Отсюда делаем вывод, что задача решена правильно.

Пример 4. В классе 15 человек. Из них 5 мальчиков и 10 девочек. Определить, какую часть от общего числа учащихся составляют мальчики.

Запишите долю мальчиков к общему количеству учащихся. Запишите пять мальчиков в числителе и общее количество учеников в знаменателе. Всего учеников 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения 9 запишем 15.0003

Чтобы найти значение этого отношения, нужно вспомнить, как делить меньшее число на большее. В этом случае число 5 делится на число 15.

Разделив 5 на 15, мы получим периодическую дробь. Преобразуем эту дробь в обыкновенную

Уменьшим полученную дробь на 3

Окончательный ответ . Итак, мальчики составляют треть класса.

Из рисунка видно, что в классе из 15 учеников треть класса составляют 5 мальчиков.

Если мы найдем из 15 учеников, которых нужно проверить, мы получим 5 мальчиков

15 : 3 = 5

5 × 1 = 5

Пример 5. Во сколько раз 35 больше 901 80 , чем число 5 ?

Напишите отношение числа 35 к числу 5. Запишите число 35 в числителе и число 5 в знаменателе, но не наоборот.

Значение этого отношения равно 7. Таким образом, число 35 в семь раз больше , чем число 5.

Пример 6. В классе 15 человек. Из них 5 мальчиков и 10 девочек. Определите, какую часть от общего числа составляют девочки.

Запишите соотношение девушек к общему количеству учащихся. Запишите в числителе коэффициента десять девочек, а в знаменателе — общее количество студентов. Общее количество учеников 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения

запишем 15 Чтобы найти значение этого отношения, нужно вспомнить, как делить меньшее число на большее. В этом случае число 10 нужно разделить на число 15

Деление 10 на 15 дает периодическую дробь. Преобразуем эту дробь в обыкновенную

Уменьшим полученную дробь на 3

Окончательный ответ . Итак, девочки составляют две трети класса.

Из рисунка видно, что в классе из 15 учеников две трети класса составляют 10 девочек.

Если мы найдем 15 школьников для проверки, мы получим 10 девочек

15 : 3 = 5

5 × 2 = 10

Пример 7. Какая часть 25 сантиметров равна 10 сантиметрам?

Запишите отношение десяти сантиметров к двадцати пяти сантиметрам. Запишите в числителе 10 см, а в знаменателе 25 см

Чтобы найти значение этого отношения, нужно вспомнить, как делить меньшее число на большее. В этом случае нам нужно число 10 разделить на число 25

Преобразовать полученную десятичную дробь в обыкновенную дробь

Уменьшим полученную дробь на 2

Получили окончательный ответ . Значит 10 см это 25 см.

Пример 8. Во сколько раз 25 см больше 10 см

Запишите отношение двадцати пяти сантиметров к десяти сантиметрам. Запишем 25 см в числителе и 10 см в знаменателе

Найдем значение этого отношения

Ответ 2,5. Итак, 25 см в 2,5 раза больше 10 см (в два с половиной раза).

Важное примечание. При нахождении соотношения одноименных физических величин эти величины должны быть выражены в одной и той же единице измерения , иначе ответ будет неверным.

Например, если мы имеем дело с двумя длинами и хотим узнать, во сколько раз первая длина больше второй, то сначала обе длины должны быть выражены в одной единице (км, м, мили).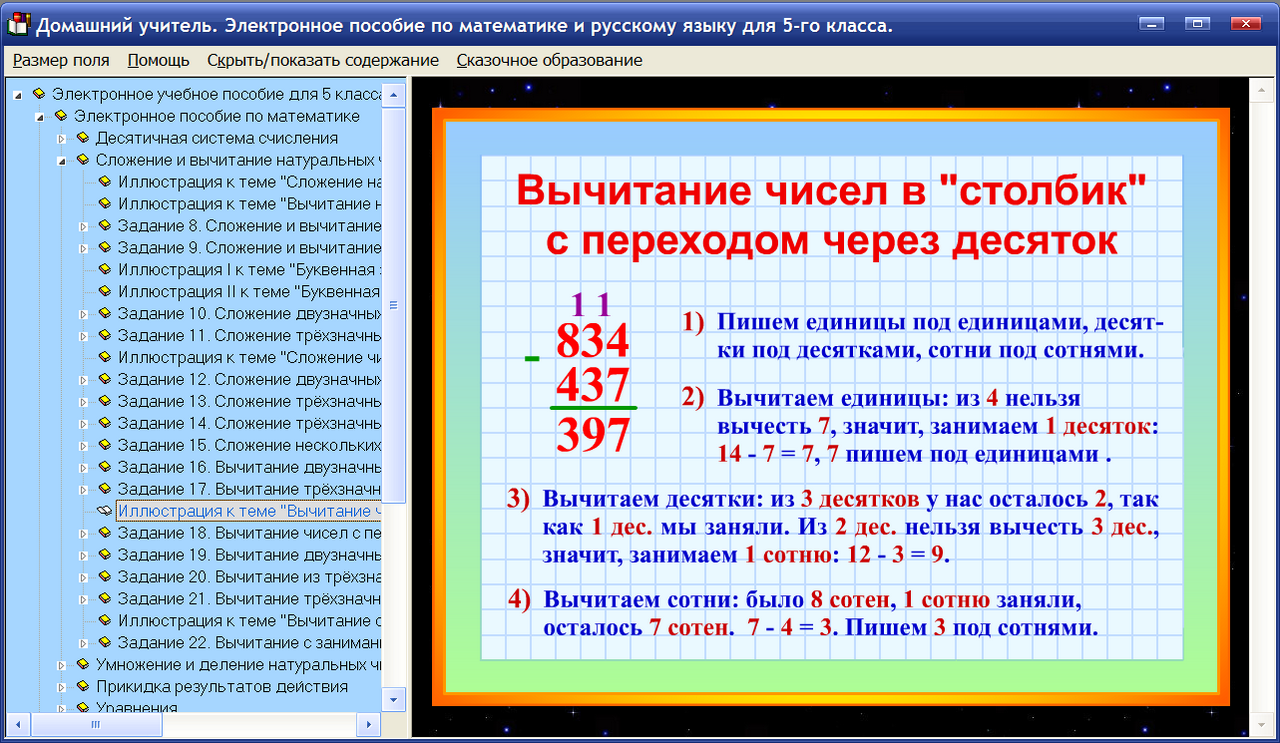

Пример 9. Во сколько раз 150 см больше 1 метра?

Во-первых, давайте выразим обе длины в одной единице. Для этого переведем 1 метр в сантиметры. Один метр — это сто сантиметров.

1 м = 100 см

Теперь найдем отношение ста пятидесяти сантиметров к ста сантиметрам. Запишем в числителе 150 сантиметров, а в знаменателе 100 сантиметров

Найдем значение этого отношения

Ответ: 1,5. Значит 150 см в 1,5 раза больше 100 см (в полтора раза).

А если бы мы не переводили метры в сантиметры, а сразу попытались найти отношение 150 см к одному метру, то мы бы имели следующее:

Получилось бы, что 150 см в сто пятьдесят раз больше более одного метра, и это неправильно. Поэтому необходимо обратить внимание на единицы физических величин, которые участвуют в соотношении. Если эти величины выражены в разных единицах, то для того, чтобы найти отношение этих величин, необходимо перейти к одной единице измерения.

Пример 10. В прошлом месяце зарплата директора банка составляла 25 000 долларов, а в этом месяце зарплата увеличилась до 27 000 долларов. Определите, во сколько раз новая заработная плата больше старой.

Запишите соотношение двадцать семь тысяч к двадцати пяти тысячам. Запишем 27000 в числителе и 25000 в знаменателе

Найдем значение этого отношения

Ответ был 1,08. Это означает, что заработная плата увеличилась на 1,08. В дальнейшем, когда мы познакомимся с процентами, такие показатели, как заработная плата, будем выражать в процентах.

Пример 11. Жилой дом имеет ширину 80 метров и высоту 16 метров. Каково соотношение между шириной дома и его высотой?

Запишите отношение ширины дома к его высоте:

Значение этого отношения равно 5. Значит, ширина дома в пять раз больше его высоты.

Свойства из Соотношение
Отношение остается неизменным, если его члены умножаются или делятся на одно и то же ненулевое число ,
a/b = pa/pb = qa/qb , p, q ≠0
a/b = (a/p) / (b/p) = (a/q) / (b/q) , p, q ≠0
Два отношения в представлении дробей можно сравнивать так же, как мы сравниваем действительные числа .
a/b = p/q ⟺ aq = bp
a/b > p/q ⟺ aq > bp
a/b < p/q ⟺ aq < bp
Если два отношения a/b и c/d равны
a/b = c/d ⟹ b/a = d/c (Invertendo)
a/b = c/d ⟹ a/c = b/d (Альтернэндо)
a/b = c/d ⟹ (a+b)/b = (c+d)/d (Componendo)
a/b = c/d ⟹ (a-b)/b = (c-d)/d (дивидендо)

Отношение не изменится, если его члены умножить или разделить на одно и то же число.
Это одно из наиболее важных свойств следующего соотношения. Мы знаем, что если частное и делитель умножить или разделить на одно и то же число, то частное не изменится. А так как отношение есть не что иное, как деление, то свойство частного работает и на него.

Вернемся к соотношению девочек и мальчиков (10 : 5). Это соотношение показывает, что на каждого мальчика приходится две девочки. Проверим, как работает свойство отношения, а именно попробуем умножить или разделить его члены на одно и то же число.
В нашем примере удобнее делить члены отношения на их наибольший общий делитель (НОД).
НОД членов 10 и 5 равен числу 5. Следовательно, можно разделить члены отношения на число 5
У нас есть новый коэффициент . Это соотношение два к одному (2:1). Это соотношение, как и предыдущее соотношение 10:5, показывает, что на каждого мальчика приходится две девочки.
На рисунке показано соотношение 2 : 1 (два к одному). Как и в прошлом соотношении 10:5, на одного мальчика приходится две девочки. Другими словами, соотношение не изменилось.
Пример 2. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз девочек в первом классе больше, чем мальчиков? Во сколько раз девочек во втором классе больше, чем мальчиков?
В обоих классах девочек в два раза больше, чем мальчиков, потому что отношения и равны .
Свойство ratio позволяет создавать разные модели, имеющие параметры, схожие с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 м и высоту 10 м.
Чтобы нарисовать подобный дом на бумаге, нужно нарисовать его в том же соотношении 30 : 10.
Разделим оба члена этого соотношения на число 10. Тогда получим соотношение 3 : 1. Это отношение равно 3, как и предыдущее отношение равно 3
Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров.
3 м = 300 см
1 м = 100 см
Соотношение 300 см : 100 см. Разделим слагаемое этого соотношения на 100. Получится соотношение 3 см : 1 см. Теперь мы можем нарисовать дом шириной 3 см и высотой 1 см.
Конечно, нарисованный дом намного меньше реального дома, но соотношение ширины и высоты остается прежним. Это позволило нам нарисовать дом максимально похожим на настоящий дом
Отношение можно понимать и по-другому. Изначально было сказано, что настоящий дом имеет ширину 30 метров и высоту 10 метров. Итого 30+10, то есть 40 метров.
Эти 40 метров можно представить как 40 частей. Соотношение 30 : 10 означает, что 30 частей относятся к ширине и 10 частей к высоте.
Затем члены соотношения 30 : 10 поделили на 10. Получилось соотношение 3 : 1. Это соотношение можно понимать как 4 части, три из которых — ширина, а одна — высота. В этом случае обычно требуется знать, сколько конкретных метров приходится на ширину и высоту.
Другими словами, нужно узнать, сколько метров в 3 частях и сколько метров в 1 части. Для начала нужно узнать, сколько метров приходится на одну деталь. Для этого разделите сумму 40 метров на 4, так как в соотношении 3 : 1 всего четыре части
40 м : 4 = 10 м
Затем с помощью умножения определите, сколько метров приходится на ширину и высоту . В качестве коэффициента используются условия, которые приведены в соотношении.
Определить, сколько метров приходится на ширину:
10 м × 3 = 30 м
Определим, сколько метров приходится на высоту:
10 м × 1 = 10 м
Несколько членов в соотношении
Если в соотношении дано более одного члена , их можно понимать как части чего-то.

Пример 1. Купили 18 яблок. Яблоки раздали маме, папе и дочке в соотношении 2 : 1 : 3. Сколько яблок получил каждый?
Соотношение 2 : 1 : 3 означает, что мама получила 2 части, папа – 1 часть, а дочь – 3 части. Другими словами, каждый член соотношения 2 : 1 : 3 представляет собой определенную долю 18 яблок:
Если сложить члены отношения 2 : 1 : 3, то можно узнать, сколько всего частей:
2 + 1 + 3 = 6 (частей)
Давайте узнаем, сколько яблок на одну часть. Для этого 18 яблок разделим на 6
18 : 6 = 3 (яблоки на одну часть)
Теперь определим, сколько яблок получил каждый человек. Умножив три яблока на каждого члена соотношения 2 : 1 : 3, можно определить, сколько яблок досталось маме, сколько яблок досталось папе и сколько яблок досталось дочери.
Посмотрим, сколько яблок получила мама:
3 × 2 = 6 (яблок)
Посмотрим, сколько яблок получил папа:
3 × 1 = 3 (яблок)
Посмотрим, сколько яблок Дочь получила:
3 × 3 = 9 (яблоки)
Пример 2. Новое серебро (альпака) — сплав никеля, цинка и меди в соотношении 3 : 4 : 13. Сколько килограммов каждый металл должен быть взят, чтобы сделать 4 кг нового серебра?
4 килограмма нового серебра будут содержать 3 части никеля, 4 части цинка и 13 частей меди. Сначала узнаем общее количество частей в четырех килограммах серебра:
3 + 4 + 13 = 20 (деталей)
Определим, сколько килограммов будет в одной части:
4 кг : 20 = 0,2 кг
Определим, сколько килограммов никеля будет содержаться в 4 кг новой серебро. Соотношение 3 : 4 : 13 указывает на то, что три части сплава содержат никель. Поэтому умножаем 0,2 на 3:
0,2 кг × 3 = 0,6 кг никеля
Теперь определим, сколько килограммов цинка будет содержаться в 4 кг нового серебра. Соотношение 3 : 4 : 13 указывает на то, что четыре части сплава содержат цинк. Поэтому умножаем 0,2 на 4:
0,2 кг × 4 = 0,8 кг цинка
Теперь определим, сколько килограммов меди будет содержаться в 4 килограммах нового серебра. Соотношение 3 : 4 : 13 говорит о том, что тринадцать частей сплава содержат медь. Поэтому умножаем 0,2 на 13:
0,2 кг × 13 = 2,6 кг меди
Итак, чтобы получить 4 кг нового серебра, нужно взять 0,6 кг никеля, 0,8 кг цинка и 2,6 кг меди.
Пример 3. Латунь – это сплав меди и цинка, масса которого составляет 3:2. Для изготовления куска латуни требуется 120 г меди. Сколько цинка требуется для изготовления этого куска латуни?
Определить, сколько граммов сплава в одной детали. В условии сказано, что для изготовления куска латуни требуется 120 граммов меди. Там же сказано, что три части сплава содержат медь. Если 120 разделить на 3, то узнаем, сколько граммов сплава в одной детали:
120 : 3 = 40 грамм на деталь
Теперь определим, сколько цинка нужно для изготовления куска латуни. Для этого умножьте 40 граммов на 2, так как соотношение 3 : 2 указывает на то, что две части содержат цинк:
40 г × 2 = 80 г цинка
Пример 4.
No related posts.