Как посчитать натуральный логарифм на калькуляторе: Как считать логарифм с калькулятором 🚩 как считать на инженерном калькуляторе 🚩 Математика

Содержание

Разбираемся с натуральным логарифмом.

Это может быть, например, калькулятор из базового набора программ операционной системы Windows. Ссылка на его запуск упрятана довольно в главное меню ОС — раскройте его щелчком по кнопке «Пуск», затем откройте его раздел «Программы», перейдите в подраздел «Стандартные», а затем в секцию «Служебные» и, наконец, щелкните пункт «Калькулятор». Можно вместо мыши и перемещений по меню использовать клавиатуру и диалог запуска программ — нажмите сочетание клавиш WIN + R, наберите calc (это имя исполняемого файла калькулятора) и нажмите клавишу Enter.

Переключите интерфейс калькулятора в расширенный режим, позволяющий осуществлять . По умолчанию он открывается в «обычном» виде, а вам нужен «инженерный» или « » (в зависимости от версии используемой ОС). Раскройте в меню раздел «Вид» и выберите соответствующую строку.

Введите аргумент, натуральный которого нужно вычислить. Это можно сделать как с клавиатуры, так и щелкая мышкой соответствующие кнопки в интерфейсе калькулятора на экране.

Кликните кнопку с надписью ln — программа рассчитает логарифма по основанию e и покажет результат.

Воспользуйтесь каким-либо из -калькуляторов в качестве альтернативного вычисления значения натурального логарифма. Например, тем, который размещен по адресу http://calc.org.ua . Его интерфейс предельно прост — есть единственное поле ввода, куда вам надо впечатать значение числа, логарифм от которого надо вычислить. Среди кнопок найдите и щелкните ту, на которой написано ln. Скрипт этого калькулятора не требует отправки данных на сервер и ответа, поэтому результат вычисления вы получите практически мгновенно. Единственная особенность, которую следует учитывать — разделителем между дробной и целой частью вводимого числа здесь обязательно должна быть точка, а не .

Термин «логарифм » произошел от двух греческих слов, одно из которых обозначает «число», а другое — «отношение». Им обозначают математическую операцию вычисления переменной величины (показателя степени), в которую надо возвести постоянное значение (основание), чтобы получить число, указанное под знаком

логарифм а.

Если основание равно математической константе, называемое числом «e», то логарифм называют «натуральным».

Вам понадобится

Доступ в интернет, Microsoft Office Excel или калькулятор.

Инструкция

Воспользуйтесь во множестве представленными в интернете -калькуляторами — это, пожалуй, и простой способ вычисления натурального а. Поиском соответствующего сервиса вам заниматься не придется, так как многие поисковые системы и сами имеют встроенные калькуляторы, вполне пригодные для работы с логарифм ами. Например, перейдите на главную страницу самого крупного сетевого поисковика — Google. Никаких кнопок для ввода значений и выбора функций здесь не потребуется, просто наберите в поле ввода запроса нужное математическое действие. Скажем, для вычисления

логарифм а числа 457 по основанию «e» введите ln 457 — этого будет вполне достаточно, чтобы Google отобразил с точностью до восьми знаков после запятой (6,12468339) даже без нажатия кнопки отправки запроса на сервер.

Используйте соответствующую встроенную функцию, если необходимость вычисления значения натурального логарифм а возникает при работе с данными в популярном табличном редакторе Microsoft Office Excel. Эта функция здесь вызывается с использованием общепринятого обозначения такого логарифм а в верхнем регистре — LN. Выделите ячейку, в которой должен быть отображен результат вычисления, и введите знак равенства — так в этом табличном редакторе должны начинаться записи в ячейках, содержащих в подразделе «Стандартные» раздела «Все программы» главного меню. Переключите калькулятор в более функциональный режим, нажав сочетание клавиш Alt + 2. Затем введите значение, натуральный

логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит результат.

Видео по теме

Совсем неплохо, правда? Пока математики подбирают слова, чтобы дать вам длинное путанное определение, давайте поближе посмотрим на это простое и ясное.

Число e означает рост

Число e означает непрерывный рост. Как мы видели в прошлом примере, e x позволяет нам увязать процент и время: 3 года при росте 100% есть то же самое, что и 1 год при 300%, при условии «сложных процентов».

Можно подставлять любые значения процента и времени (50% на протяжении 4 лет), но лучше задать процент как 100% для удобства (получается 100% на протяжении 2 лет). За счёт перехода к 100% мы можем сфокусироваться исключительно на компоненте времени:

e x = e процент * время = e 1.0 * время = e время

Очевидно, что e x означает:

насколько вырастет мой вклад через x единиц времени (при условии 100%-го непрерывного роста).
например, через 3 промежутка времени я получу в e 3 = 20.08 раз больше «штуковин».

e x — это масштабирующий коэффициент, показывающий, до какого уровня мы вырастем за x отрезков времени.

Натуральный логарифм означает время

Натуральный логарифм — это инверсия числа e, такой причудливый термин для обозначения противоположности. Кстати, о причудах; по латыни он называется logarithmus naturali , отсюда и появилась аббревиатура ln.

И что эта инверсия или противоположность означает?

e x позволяет нам подставить время и получить рост.

ln(x) позволяет нам взять рост или доход и узнать время, необходимое для его получения.

Например:

e 3 равняется 20.08. Через три отрезка времени у нас будет в 20.08 раз больше того, с чего мы начали.
ln(20.08) будет примерно 3. Если вас интересует рост в 20.08 раз, вам понадобится 3 промежутка времени (опять же, при условии стопроцентного непрерывного роста).

Всё ещё читаете? Натуральный логарифм показывает время, нужное, чтобы достичь желаемого уровня.

Этот нестандартный логарифмический счёт

Вы проходили логарифмы — это странные существа. Как им удалось превратить умножение в сложение? А деление в вычитание? Давайте посмотрим.

Чему равняется ln(1)? Интуитивно понятно, что вопрос стоит так: сколько нужно ждать, чтобы получить в 1 раз больше того, что у меня есть?

Ноль. Нуль. Нисколько. У вас уже это есть единожды. Не требуется нисколько времени, чтобы от уровня 1 дорости до уровня 1.

ln(1) = 0

Хорошо, что насчёт дробного значения? Через сколько у нас останется 1/2 от имеющегося количества? Мы знаем, что при стопроцентном непрерывном росте ln(2) означает время, необходимое для удвоения. Если мы обратим время вспять (т.е. подождём отрицательное количество времени), то получим половину от того, что имеем.

ln(1/2) = -ln(2) = -0.693

Логично, правда? Если мы вернёмся назад (время вспять) на 0.693 секунды, то обнаружим половину имеющегося количества. Вообще можно переворачивать дробь и брать отрицательное значение: ln(1/3) = -ln(3) = -1.09. Это означает, что, если мы вернёмся в прошлое на 1.09 отрезков времени, то обнаружим только треть от нынешнего числа.

Ладно, а как насчёт логарифма отрицательного числа? Сколько времени нужно, чтобы «вырастить» колонию бактерий от 1 до -3?

Это невозможно! Нельзя получить отрицательное число бактерий, не так ли? Вы можете получить максимум (эээ.

.. минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.

ln(отрицательное число) = неопределено

«Неопределено» означает, что нет такого промежутка времени, который надо было бы прождать, чтобы получить отрицательное значение.

Логарифмическое умножение — просто умора

Сколько времени займёт четырёхкратный рост? Конечно, можно просто взять ln(4). Но это слишком просто, мы пойдём другим путём.

Можно представить четырёхкратный рост как удвоение (требующее ln(2) единиц времени) и затем снова удвоение (требующее ещё ln(2) единиц времени):

Время на 4х рост = ln(4) = Время на удвоится и затем ещё раз удвоится = ln(2) + ln(2)

Интересно. Любой показатель роста, скажем, 20, можно рассматривать как удвоение сразу после 10-кратного увеличения. Или роста в 4 раза, и затем в 5 раз. Либо же утроение и затем увеличение в 6.666 раз. Видите закономерность?

ln(a*b) = ln(a) + ln(b)

Логарифм от A, умноженного на B, есть log(A) + log(B). Это отношение сразу обретает смысл, если оперировать в терминах роста.

Если вас интересует 30-кратный рост, вы можете подождать ln(30) за один присест, либо же подождать ln(3) Для утроения, и затем ещё ln(10) для удесятирения. Конечный результат тот же самый, так что конечно время должно оставаться постоянным (и остаётся).

Что на счёт деления? В частности, ln(5/3) означает: сколько времени понадобится для того, чтобы вырасти в 5 раз, и затем получить 1/3 от этого?

Отлично, рост в 5 раз есть ln(5). Рост в 1/3 раза займёт -ln(3) единиц времени. Итак,

ln(5/3) = ln(5) – ln(3)

Сие означает: дайте вырасти в 5 раз, и затем «вернитесь во времени» к той отметке, где останется всего треть от того количества, так что у вас получится 5/3 рост. В общем получается

ln(a/b) = ln(a) – ln(b)

Я надеюсь, что странная арифметика логарифмов начинает обретать для вас смысл: умножение показателей роста становится сложением единиц времени роста, а деление превращается в вычитание единиц времени. Не надо запоминать правила, попробуйте осознать их.

Использование натурального логарифма при произвольном росте

Ну конечно, — скажете вы, — это всё хорошо, если рост 100%-ный, а что в случае 5%, которые я получаю?»

Нет проблем. «Время», которое мы рассчитываем с помощью ln(), на самом деле является комбинацией процентной ставки и времени, тот самый Х из уравнения e x . Мы всего лишь решили задать процент как 100% для простоты, но мы вольны использовать любые числа.

Допустим, мы хотим достичь 30-кратного роста: берём ln(30) и получаем 3.4 Это означает:

e x = рост
e 3.4 = 30

Очевидно, это уравнение означает «100%-ная доходность на протяжении 3.4 лет даёт рост в 30 раз». Мы можем записать это уравнение в таком виде:

e x = e ставка*время
e 100% * 3.4 года = 30

Мы можем менять значения «ставки» и «времени», лишь бы ставка * время оставалось 3.4. Например, если нас интересует 30-кратный рост — сколько нам придётся ждать при процентной ставке 5%?

ln(30) = 3. 4
ставка * время = 3.4
0.05 * время = 3.4
время = 3.4 / 0.05 = 68 лет

Я рассуждаю так: «ln(30) = 3.4, значит, при 100%-ном росте это займёт 3.4 года. Если я удвою скорость роста, необходимое время уменьшится вдвое».

100% за 3.4 года = 1.0 * 3.4 = 3.4
200% за 1.7 года = 2.0 * 1.7 = 3.4
50% за 6.8 года = 0.5 * 6.8 = 3.4
5% за 68 года = .05 * 68 = 3.4 .

Здорово, правда? Натуральный логарифм может использоваться с любыми значениями процентной ставки и времени, поскольку их произведение остаётся постоянным. Можете перемещать значения переменных сколько душе угодно.

Отпадный пример: Правило семидесяти двух

Правило семидесяти двух — математический приём, позволяющий оценить, сколько времени понадобится, чтобы ваши деньги удвоились. Сейчас мы его выведем (да!), и более того, мы попробуем уяснить его суть.

Сколько времени понадобится, чтобы удвоить ваши деньги при 100% ставке, нарастающей ежегодно?

Оп-па. Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.

Теперь вопрос прост: Как быстро можно удвоиться при 100%-ном росте? ln(2) = 0.693. Нужно 0.693 единиц времени (лет — в нашем случае), чтобы удвоить нашу сумму с непрерывным ростом 100%.

Так, а что если процентная ставка — не 100%, а скажем, 5% или 10%?

Легко! Поскольку ставка * время = 0.693, мы удвоим сумму:

ставка * время = 0.693
время = 0.693 / ставка

Получается, если рост 10%-ный, это займёт 0.693 / 0.10 = 6.93 лет на удвоение.

Чтобы упростить вычисления, давайте домножим обе части на 100, тогда можно будет говорить «10», а не «0. 10″:

время на удвоение = 69.3 / ставка, где ставка выражена в процентах.

Теперь черёд удваиваться при ставке 5%, 69.3 / 5 = 13.86 лет. Однако 69.3 — не самое удобное делимое. Давайте выберем близкое число, 72, которое удобно делить на 2, 3, 4, 6, 8 и другие числа.

время на удвоение = 72 / ставка

что и является правилом семидесяти двух. Всё шито-крыто.

Если вам нужно найти время для утроения, можете использовать ln(3) ~ 109.8 и получить

время на утроение = 110 / ставка

Что является ещё одним полезным правилом. «Правило 72» применимо росту по процентным ставкам, росту населения, культур бактерий, и всего, что растёт экспоненциально.

Что дальше?

Надеюсь, натуральный логарифм теперь приобрёл для вас смысл — он показывает время, необходимое для роста любого числа при экспоненциальном росте. Я думаю, натуральным он называется потому, что e — универсальная мера роста, так что ln можно считать универсальным способом определения, сколько времени нужно для роста.

Каждый раз, когда вы видите ln(x), вспоминайте «время, нужное, чтобы вырасти в Х раз». В предстоящей статье я опишу e и ln в связке, так что свежий аромат математики заполнит воздух.

Дополнение: Натуральный логарифм от e

Быстрая викторина: сколько будет ln(e)?

математический робот скажет: поскольку они определены как инверсия одна другой, очевидно, что ln(e) = 1.
понимающий человек: ln(e) это число времени, чтобы вырасти в «е» раз (около 2.718). Однако число e само по себе является мерой роста в 1 раз, так что ln(e) = 1.

Мыслите ясно.

9 сентября 2013

Что такое логарифм?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно — уравнения с логарифмами.

Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 — 20 минут вы:

1. Поймете, что такое логарифм .

2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.

3. Научитесь вычислять простые логарифмы.

Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень…

Чувствую, сомневаетесь вы… Ну ладно, засекайте время! Поехали!

Для начала решите в уме вот такое уравнение:

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

1.1. Определение степени для целого показателя степени

X 1 = X
X 2 = X * X
X 3 = X * X * X
…
X N = X * X * … * X — N раз

1.2. Нулевая степень.

По определению принято считать, что нулевая степень любого числа равна 1:

1.3. Отрицательная степень.

X -N = 1/X N

1.4. Дробная степень, корень.

X 1/N = корень степени N из Х.

Например: X 1/2 = √X.

1.5. Формула сложения степеней.

X (N+M) = X N *X M

1.6.Формула вычитания степеней.

X (N-M) = X N /X M

1.7. Формула умножения степеней.

X N*M = (X N) M

1.8. Формула возведения дроби в степень.

(X/Y) N = X N /Y N

2. Число e.

Значение числа e равно следующему пределу:

E = lim(1+1/N), при N → ∞.

С точностью 17 знаков число e равно 2.71828182845904512.

3. Равенство Эйлера.

Это равенство связывает пять чисел, играющих особую роль в математике: 0, 1, число e, число пи, мнимую единицу.

E (i*пи) + 1 = 0

4. Экспоненциальная функция exp (x)

exp(x) = e x

5. Производная экспоненциальной функции

Экспоненциальная функция обладает замечательным свойством: производная функции равна самой экспоненциальной функции:

(exp(x))» = exp(x)

6.

Логарифм.

6.1. Определение функции логарифм

Если x = b y , то логарифмом называется функция

Y = Log b (x).

Логарифм показывает в какую степень надо возвести число — основание логарифма (b), чтобы получить заданное число (X). Функция логарифм определена для X больше нуля.

Например: Log 10 (100) = 2.

6.2. Десятичный логарифм

Это логарифм по основанию 10:

Y = Log 10 (x) .

Обозначается Log(x): Log(x) = Log 10 (x).

Пример использования десятичного логарифма — децибел .

6.3. Децибел

Пункт выделен в отдельную страницу Децибел

6.4. Двоичный логарифм

Это логарифм по основанию 2:

Y = Log 2 (x).

Обозначается Lg(x): Lg(x) = Log 2 (X)

6.5. Натуральный логарифм

Это логарифм по основанию e:

Y = Log e (x) .

Обозначается Ln(x): Ln(x) = Log e (X)
Натуральный логарифм — обратная функция к экспоненциальной функции exp (X).

6.6. Характерные точки

Log a (1) = 0
Log a (a) = 1

6.

7. Формула логарифма произведения Log a (x*y) = Log a (x)+Log a (y)

6.8. Формула логарифма частного

Log a (x/y) = Log a (x)-Log a (y)

6.9. Формула логарифма степени

Log a (x y) = y*Log a (x)

6.10. Формула преобразования к логарифму с другим основанием

Log b (x) = (Log a (x))/Log a (b)

Пример:

Log 2 (8) = Log 10 (8)/Log 10 (2) =
0.903089986991943552 / 0.301029995663981184 = 3

7. Формулы полезные в жизни

Часто возникают задачи пересчета объема в площадь или в длину и обратная задача — пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича .

Разрешается использовать материалы сайта при условии установки активной ссылки на источник.

Как рассчитать ln? – Обзоры Вики

Общая формула для вычисления Ln(x) с логарифмической функцией: Ln(x) = Log(x)/Log(e)или эквивалентно Ln(x) = Log(x)/0. 4342944819.

Как нажимать ln E на калькуляторе? Для этого используются самые простые научные калькуляторы,

введите номер,
затем нажмите кнопку реверса (inv) или Shift.
нажмите кнопку журнала (или ln). Его также можно обозначить как 10 ^x (или е ^x ) кнопку.

Как решить ln 5?

Вы можете раздать лн? Чтобы ответить на вопрос в вашем заголовке, нельзя «разложить» ln на сумму, потому что ln не является фактором. cos, ln и √ — функции, для функций нет дистрибутивного свойства.

Как преобразовать ln в журнал?

Чтобы преобразовать натуральное число в обычный логарифм, используйте уравнение ln(x) = log(x) ÷ log(2.71828).

Что является основанием ln 3?

Кроме того, ln3 означает логарифм 3 с e в качестве основания и e = 2.71828, и, следовательно, ln3 =1.0986 (используя научный калькулятор) и, следовательно, ln3≠1 .

Как сокращаются ln и e?

Подставьте базовое число e в обе части уравнения. e и ln отменить друг друга оставив нам квадратное уравнение. x = 0 невозможно, так как нет возможности записать 0 как степень. Запишите левую часть как один логарифм.

Что означает ln в математике?

Когда вы видите ln, это означает натуральный логарифм (мы определим натуральные логарифмы ниже). В этом курсе будут использоваться только десятичные и натуральные логарифмы.

Может ли ln быть отрицательным? Функция натурального логарифма ln(x) определена только для x>0. Таким образом, натуральный логарифм отрицательное число не определено.

Как вы конвертируете ln в ex? Если вам нужно преобразовать между логарифмами и натуральными логарифмами, используйте следующие два уравнения: журнал ₁₀ (х) = ln (x) / ln (10)
…
Чем натуральные логарифмы отличаются от других логарифмов?

Логарифмические правила	в правилах
журнал (х / у) = журнал (х) — журнал (у)	ln (x / y) = ln (x) −ln (y)
журнал (х ^a )= алог(х)	ln(x ^a )= альн(х)
журнал (10 ^x ) = х	лн(е ^x ) = х
10 ^журнал⁽^x⁾ = х	e ^ln⁽^x⁾ = х

• 17 января 2020 г.

Что такое В Эльне стоит?

Таким образом, натуральный логарифм e равен равный одному.

Что такое ln значение? Ln называется натуральным логарифмом. Его также называют логарифмом по основанию e. Здесь константа e обозначает число, являющееся трансцендентным числом и иррациональным, которое приблизительно равно значению 2.71828182845. Натуральный логарифм (ln) может быть представлен как ln x или logex. .

Как переписать ln?

Каково значение ln 10? Значение журнала от 1 до 10 для базы журнала e

Натуральный логарифм числа (log _e x)	LnValue
пер (7)	1.94591
пер (8)	2.079442
пер (9)	2.197225
пер (10)	2. 302585

Какова ценность LNX?

Натуральный логарифм числа — это его логарифм по основанию математической константы e, которая является иррациональным и трансцендентным числом, приблизительно равным 2.718281828459. Натуральный логарифм x обычно записывается как ln x, log_e x, а иногда, если основание e неявно, просто log x.

Что такое lne2? таким образом, пер(е2)=2. Другой способ — использовать свойство логарифмов, которое гласит: ln(ab)=b⋅ln(a). В этом случае a=e и b=2. Таким образом, ln(e2)=2⋅ln(e)=2⋅1=2.

Как упростить e 3lnx?

Что такое ln и e в математике?

Натуральный бревно, или ln, является обратным e.

Буква «e» представляет собой математическую константу, также известную как натуральный показатель степени. Как и π, e является математической константой и имеет заданное значение. Значение e равно примерно 2.71828. … Итак, ln(x) = log_e(Икс). Например, ln (5) = log_e(5) = 1.609.

Почему e повышается до ln, отменяется?

Причина в том, что из-за определения самого логарифма. Логарифм — это операция, обратная возведению в степень, так же как деление — операция, обратная умножению, и наоборот.

Где Lnx undefined? Действительная функция натурального логарифма ln(x) определена только для х> 0. Таким образом, натуральный логарифм нуля не определен.

Калькулятор натурального журнала | Определение | Формула

Представляем вам Калькулятор натурального логарифма , который можно использовать для вычисления натурального логарифма чисел. CalCon разработал этот калькулятор, чтобы пользователям было проще вычислять натуральный логарифм . В дополнение к калькулятору на нашем веб-сайте вы можете загрузить наше приложение калькулятора CalCon из Google Play и App Store и запустить калькулятор на своем мобильном устройстве или планшете.

Узнайте больше о натуральном логарифме, константе Эйлера, основных правилах и способах его вычисления далее в этой статье. Мы также покажем вам, где чаще всего применяется натуральный логарифм, как вычисляется вывод, график функции натурального логарифма, связь с показательной функцией и поделимся другими интересными вещами.

Что такое натуральное бревно?

Натуральные логарифмы могут показаться сложными, но как только вы поймете несколько фундаментальных правил, вы сможете решать даже задачи, которые кажутся очень сложными.

натуральный логарифм , или ln , является обратной функцией e . Буква e представляет собой математическую константу, известную как натуральный показатель степени. Точно так же число π , e является математической константой с фиксированным значением. Это может быть представлено приведенными ниже уравнениями. 9y = x

Тогда основание e логарифма x и стандартное обозначение:

 \ln(x) = \log_e(x) = y

Постоянная Эйлера или Число Эйлера и приблизительно:

 e \ приблизительно2,71828183

Число e появляется во многих случаях в математике, включая сценарии сложной процентной ставки, уравнения роста и уравнения распада. Например, логарифм ln(x) — это время, необходимое для роста до x , а e ^x — это рост после x .

Поскольку e часто используется в математике и экономике, специалистам в этих областях часто приходится логарифмировать на основе e , чтобы решить уравнение или найти значение. Натуральный логарифм был создан как способ записи и вычисления логарифма с основанием e . Это позволяет людям, столкнувшимся с проблемой, узнать, как решить логарифм с основанием 9.0018 и . Таким образом, \ln(x) = \log_e (x) . Например, \ln (3) = \log_e (3) = 1,099 .

Где мы его используем?

Натуральные логарифмы встречаются в каждом процессе, где связан период, постоянный рост или затухание количественно определяемого явления.

Используется в расчетах задач радиоактивного распада и выхода с фиксированной скоростью. Натуральные логарифмы появляются при расчете роста и распада популяций бактерий, животных и растений, скорости распада заряженного конденсатора или изменения температуры объекта и связаны с показателем степени 9.0018 e со многими другими явлениями.

Примеры реальных ситуаций

Таким образом, натуральный логарифм дает вам время, необходимое для достижения определенного уровня роста. Связь между функцией натурального логарифма и экспоненциальной функцией показана следующим образом:

	Натуральный логарифм = время	Экспонента = рост
Время/перспектива роста	ln (x) is Время мы нужно вырасти до х	e ^x равно Сумма роста со временем x

Предположим, у вас есть инвестиции в криптовалюту с процентной ставкой 100% годовых, которая постоянно растет. Если вы хотите 10-кратного роста, предполагая непрерывное начисление сложных процентов, вы должны ждать только ln (10), что равно 2302 годам.

ln и e близнецы:

e ^x это количество которое мы имеем после начала 1.0 и непрерывного роста на x единиц времени
ln(x) – это время, необходимое для достижения суммы x , если предположить, что мы непрерывно увеличиваемся от 1,0

Чтобы уточнить, натуральный логарифм дает нам время, необходимое для достижения желаемый рост. Узнайте больше об экспоненциальном росте с помощью этого калькулятора экспоненциального роста.

Ключевые правила натурального логарифма

Есть 4 основных правила , которые вам необходимо знать при работе с натуральными логарифмами, и вы всегда будете встречать каждое из них снова и снова в своих математических задачах. Эти 4 правила необходимы, и вам нужно хорошо их знать, потому что они могут сбивать с толку, когда вы впервые их видите. Кроме того, это поможет вам убедиться, что у вас есть базовые знания, прежде чем переходить к более сложным темам логарифмирования.

Правило произведения

Натуральный логарифм умножения x и y является суммой ln x и ln y .

 \ln{(x\cdot y)} = \ln (x) + \ln (y)

Правило частных

Натуральный логарифм деления x и y есть разность ln от x и ln от y .

 \ln{ (\frac x y)} = \ln (x) - \ln (y) 9y) = y \cdot \ln (x)

Доп.

9 0117

Имя правила/свойства	Правило/свойство
Интеграл от ln	\int {\ln (x) \cdo t dx} = x \cdot (\ln (x) — 1) + константа
ln отрицательного числа	\ln(x) \; для \; x \leqslant 0 не определено
ln из нуля	\ln(0) не определено
ln из одного	ln(1) = 0
ln бесконечности	\displaystyle \lim_{ x \to ∞} \ln (x) = ∞
Тождество Эйлера	\ln(-1) = i \cdot π

Как рассчитать натуральный бревно ?

Вы можете вычислить натуральный логарифм числа с помощью нашего калькулятора натурального логарифма. Калькулятор не сложен, и все, что вам нужно ввести в поле Натуральный логарифм из , это число, необходимое для вычисления ln из. Результат отобразится в поле ниже, равно .

В фоновом режиме по существу размещено и разрешено следующее выражение:

\ln (x) = \log_e(x) = y

Пример: Найдите натуральный логарифм числа 20 93 = 20

с учетом округления чисел.

Как и в случае с обыкновенным логарифмом и антилогарифмом, для натурального логарифма существует производная таблица, состоящая из столбцов x и ln(x) .

Производная натурального логарифма

Производная функции натурального логарифма является обратной функцией.

 f(x)=\ln (x)

 f'(x)=\frac {1} {x}

График натурального логарифма

Логарифм Непера 9Функция 0004 (другое название Natural log) определяется для любого числа, принадлежащего интервалу [0,+∞]. Таким образом, функция определяется от нуля до положительной бесконечности.

Функция натурального логарифма обычно записывается как:

 y = \ln(x) \; или \; f(x) = \ln (x)

Некоторые из основных свойств функции ln следующие:

Функция определяется, когда аргумент x больше нуля в точке (1, 0)
Функция имеет вертикальную асимптоту: линия x = 0.

Для построения графика логарифмической функции y = \ln(x) необходимо выполнить следующие действия:

Начертить координату оси и выберите единицы измерения
Для каждого x > 0 вычисляем ln(x) с помощью нашего калькулятора или таблицы0135

Откуда взялось число е?

Одной из основных математических констант является число e . Оно называется либо числом Эйлера, либо константой Непье, а также представляет собой основу натурального логарифма.

Тем не менее, Леонард Эйлер получил больше заслуг, основанных на том факте, что буква, которую Эйлер использовал для выражения этой константы, — это то, что мы обозначаем сегодня. Кроме того, Эйлер был первым, кто вычислил e со значительным числом знаков после запятой, но он не был первым, кто это открыл. Константа была открыта швейцарским математиком Якобом Бернулли при изучении сложных процентов.

Часто задаваемые вопросы

Натуральный логарифм 0?

Технически \ln(0) не определено. Вот почему существует понятие бесконечности; поэтому мы можем количественно оценить вещи, которые находятся за пределами нашего воображения.
Если мы присоединимся к концепции бесконечности, мы увидим, что если мы продолжаем использовать значения ближе к нулю (0,1, 0,01, 0,001,…), то \ln становится все больше и больше в отрицательном смысле.
Следовательно, в предельном случае
\ln(0) = -бесконечность

Натуральный логарифм 2?

При использовании калькулятора натурального логарифма \ln(2) = 0,69+} \ln (x) = ∞

Как найти производную от ln?

Производная функции натурального логарифма является обратной функцией.
f ‘(x) = 1 / x

В чем основное различие между log и ln?

Основное различие между натуральными логарифмами и другими логарифмами заключается в используемом основании. Например, логарифмы (log) имеют основание 10 (хотя может быть и другое значение, которое будет указано), а натуральные логарифмы всегда будут иметь основание и .

Кроме того, проверьте наш Калькулятор логарифма и Калькулятор антилогарифма.

Натуральный логарифм

Горячая математика
натуральный логарифм числа Икс это логарифм на базу е , где е это математическая константа примерно равно 2,718 . Обычно записывается с использованием сокращенной записи п Икс , вместо бревно е Икс как вы могли ожидать . Вы можете переписать натуральный логарифм в экспоненциальная форма следующее:
п Икс «=» а ⇔ е а «=» Икс
Пример 1:
Находить п 7 .
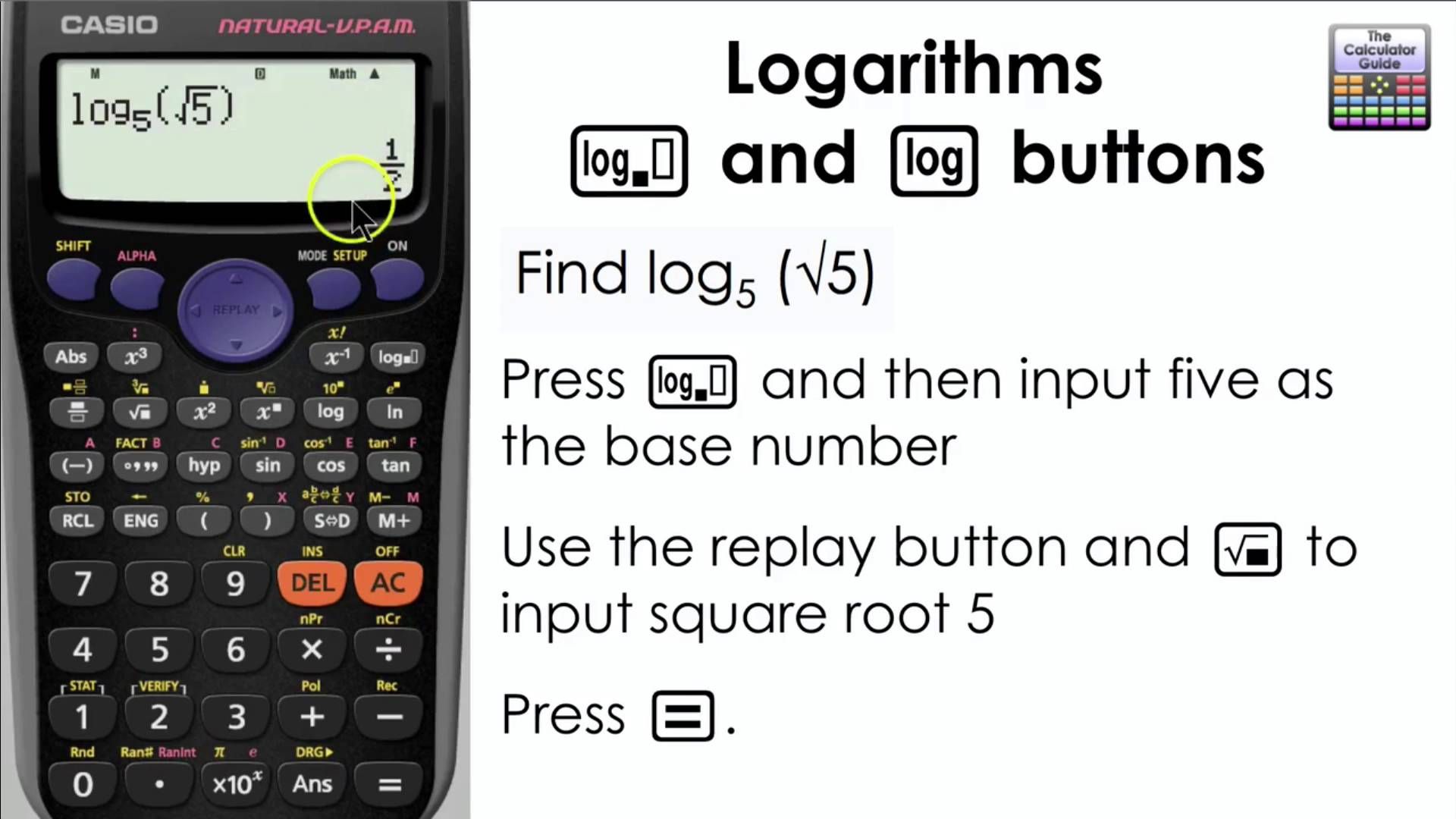
На научном калькуляторе вы можете просто нажать [ 7 ] с последующим [ п ] чтобы получить ответ: примерно 1,946 .
Экспоненциальная форма уравнения, которое вы решаете, имеет вид
е а «=» 7 2,718 1,954 ≈ 7
Пример 2:
Решите уравнение. Округлить до тысячных.
п Икс «=» − 5,5
Сначала перепишем уравнение в экспоненциальной форме.
е − 5,5 «=» Икс
Используйте калькулятор. (Большинство научных калькуляторов имеют кнопку, которая дает хорошее приближение для е ; если у вас его нет, используйте 2,71828 . )
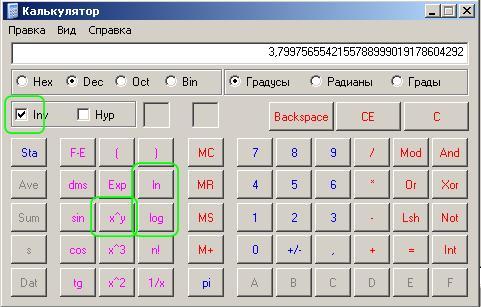Икс ≈ 0,004
Обычно свойства логарифмов верны и для натурального логарифма.
Пример 3:
Упрощать.
п ( 3 д ) 2
Следующее свойство позволяет упростить логарифмы степени:
бревно б Икс у «=» у бревно б Икс
Так,
п ( 3 д ) 2 «=» 2 п ( 3 д )
Теперь используйте свойство, согласно которому лог продукта равен сумме логов.
бревно б Икс у «=» бревно б Икс + бревно б у
Так,
2 п ( 3 д ) «=» 2 ( п 3 + п д ) ≈ 2.
No related posts.