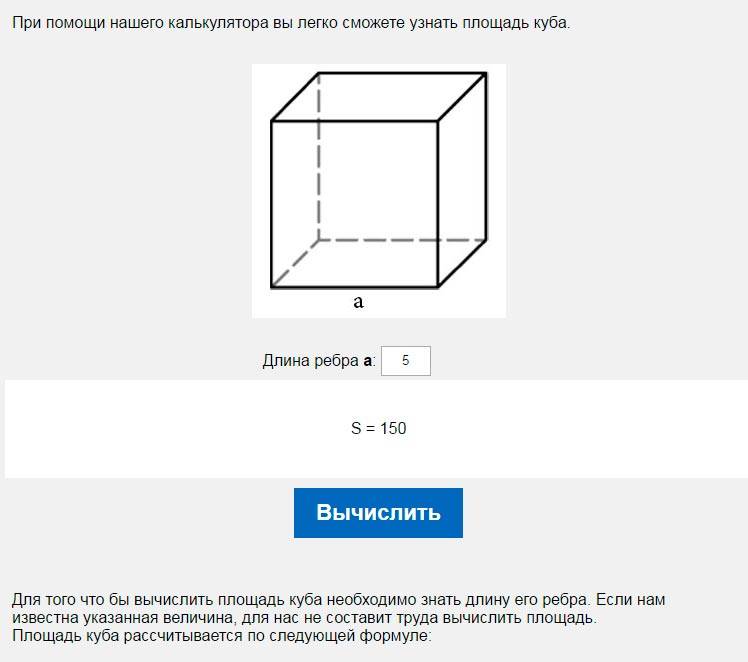
Площадь поверхности куба формула и калькулятор онлайн
На этой странице мы собрали формулы, которые помогут найти площадь полной и боковой поверхности куба. А чтобы упростить расчет у нас есть калькулятор, который сделает это быстро и точно.
В дополнение на сайте можно найти объем куба.
Куб — фигура, представляющая собой правильный многогранник, все грани которого являются квадратами. Все ребра (стороны) куба равны между собой.
Содержание:
- калькулятор площади поверхности куба
- площадь полной поверхности куба
- формула площади полной поверхности куба через ребро
- формула площади полной поверхности куба через диагональ грани
- формула площади полной поверхности куба через диагональ куба
- формула площади полной поверхности куба через периметр грани
- формула площади полной поверхности куба через периметр куба
- формула площади полной поверхности куба через объем
- формула площади полной поверхности куба через площадь вписанного шара
- площадь боковой поверхности куба
- формула площади боковой поверхности куба через ребро
- формула площади боковой поверхности куба через диагональ грани
- формула площади боковой поверхности куба через диагональ куба
- формула площади боковой поверхности куба через периметр грани
- формула площади боковой поверхности куба через периметр куба
- формула площади боковой поверхности куба через объем
- примеры задач
Что такое площадь полной поверхности куба
Куб состоит из сторон, которые называют гранями.
2 = 4 \cdot 16 = 64 \: см²
Ответ: 64 см²
Проверка .
Площадь куба: онлайн калькулятор, формулы, примеры решений
Фигура {$ main.figures[data.figure] $}
Рассчитываем {$ main.types[data.type] $}
Введите 1 величину
Сторона A
Диагональ фигуры (D)
Диагональ грани (d)
Введите 1 величину
Радиус (r)
Диаметр (d)
Введите 3 величины
Сторона A
Сторона B
Сторона C
Диагональ фигуры (d)
Введите 2 величины (радиус и диаметр основания приняты за одну величину)
Высота (h)
Образующая конуса (s)
Радиус (r)
Диаметр (d)
Введите H и 1 величину
Высота (h)
Радиус (r)
Диаметр (d)
Введите 3 величины
Количество сторон (n)
Высота (h)
Сторона a
Количество сторон (n)
Введите 2 величины
Сторона основания (a)
Высота (h)
Длина бокового ребра (s)
Угол (α)Между стороной и плоскостью основания
{$ main.
angles[data.angle] $}Результат расчёта
- Объём: {$ result.v|number:4 $}
- Площать: {$ result.s|number:4 $}
- Площать: {$ result.s $}
Куб — это правильный шестигранник, каждая грань которого является квадратом. Кубические фигуры часто встречаются в реальной жизни, поэтому на работе или в быту вам может понадобиться вычислить объем или площадь поверхности объекта, который имеет форму кубика.
Геометрия куба
Куб или правильный гексаэдр — это частный случай шестигранной прямоугольной призмы, все грани которой представляют собой квадраты. Кроме того, куб — это и частный случай прямоугольного параллелепипеда, у которого длина, ширина и высота абсолютно равны. Куб — уникальная фигура, существующая в разных многомерных пространствах.
К примеру, нульмерный куб — это точка, одномерный — отрезок, двухмерный — квадрат, а четырехмерный — тессеракт. В нашем родном трехмерном пространстве куб встречается повсеместно, к примеру, в форме детских кубиков, рафинированного сахара, картонных коробок, газетных киосков или предметов интерьера.
Кубы широко используются в программировании, аналитике, научных изысканиях и прочих высоких материях. Идеальная форма геометрической фигуры позволяет при помощи разномерных кубов выражать массивы данных, измерять объемы или визуализировать данные. Кубические фигуры часто встречаются в реальности и абстрактных задачах, поэтому вам может понадобиться рассчитать объем или площадь поверхности кубика для решения самых разных проблем.
Площадь поверхности куба
Площадь кубической фигуры — это сумма площадей всех граней. Каждая грань куба — это квадрат. Площадь квадрата, то есть одной грани, определяется по простой формуле как:
Sg = a2
Куб — это гексаэдр, то есть шестигранник.
Таким образом, площадь поверхности кубической фигуры представляет собой сумму шести квадратов:
S = 6 Sg = 6 a2
Определить площадь куба можно не только при помощи длины его ребра: для расчета площади поверхности вы можете использовать диагональ самого куба или диагональ одной грани.
Диагональ куба — это отрезок, который находится внутри пространства куба и соединяет две противоположные вершины. Проведенная диагональ разделяет куб на два прямоугольных треугольника. Согласно теореме Пифагора квадрат ребра куба равен одной трети от квадрата диагонали D, следовательно, формула площади полной поверхности приобретает вид:
S = 2 D2
Площадь поверхности куба легко определить и с помощью диагонали одной грани. Площадь квадрата через диагональ равна:
S = 0,5 d2.
Так как у куба 6 граней, общая площадь поверхности составит сумму шести граней куба, то есть:
S = 6 × 0,5 d2 = 3 d2
Таким образом, чтобы определить площадь поверхности кубической фигуры вам достаточно ввести в форму-онлайн калькулятора всего один параметр на выбор:
- длину ребра;
- диагональ куба;
- диагональ квадрата.
Рассмотрим примеры использования данных формул в реальной жизни.
Примеры из жизни
Ящик
Представьте, что вы хотите соорудить из листов ДСП ящик для хранения инструментов в форме куба. Вы знаете, что он отлично впишется в пространство на чердаке высотой 50 см. Сколько же квадратных метров ДСП вам понадобится для создания такого контейнера? Зная высоту, равную a = 0,5 м вы можете легко подсчитать площадь общей поверхности куба, введя данный параметр в онлайн-калькулятор. Вы получите ответ в виде:
S = 1,5
Таким образом, вам понадобится всего 1,5 квадратных метра ДСП для создания ящика для инструментов. Зная всего один параметр, вы без труда порежете листы на грани куба и соорудите нужную конструкцию.
Контейнер
Допустим, вы хотите обработать антикоррозионным покрытием грузовые контейнеры, которые имеют кубическую форму. Для правильного расчета параметров покрытия вам необходимо знать площадь обрабатываемой поверхности. Вы знаете, что диагональ грани стандартного контейнера равняется d = 3 м.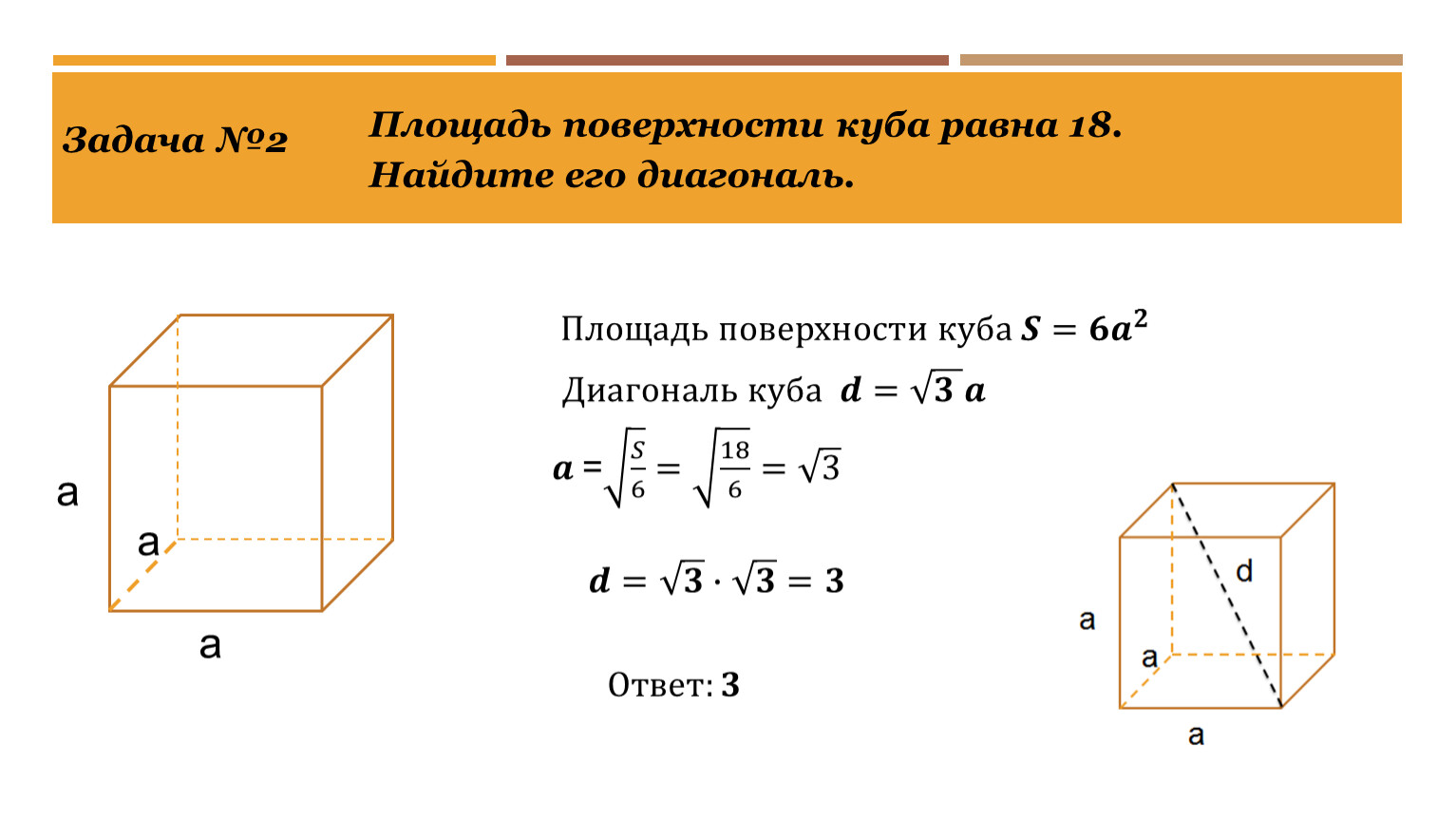
Зная этот параметр, вы легко рассчитаете площадь кубической поверхности, которая равна
S = 18
Зная общую площадь покрытия, вы без проблем определите необходимое количество антикоррозионной жидкости.
Заключение
Куб встречается в реальной жизни не так часто, как призматические фигуры или параллелепипеды, однако в любом случае вам может понадобиться удобный калькулятор, при помощи которого вы определите площадь полной поверхности кубического объекта. Наш сервис поможет решить вам бытовые, производственные или школьные задачи мгновенно и без ошибок.
Площадь поверхности куба: Формула и примеры
Давайте узнаем, как определить площадь поверхности куба .
Что такое куб? Единственный правильный шестигранник, куб представляет собой трехмерный объект с шестью квадратными поверхностями или сторонами одинакового размера, 12 ребрами и 8 вершинами. Учитывая, что его квадратные стороны равны, отсюда следует, что длина, ширина и высота куба также равны.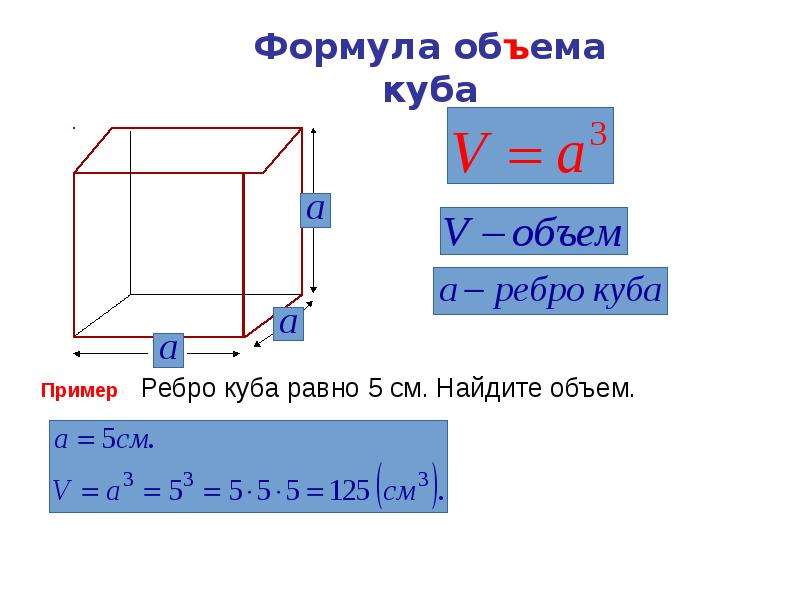
Примерами объектов в форме куба являются игральные кости, шкатулки для драгоценностей, кубики льда, кубики сахара и кубики Рубика.
Вот иллюстрация куба. Обратите внимание, как в развернутом виде он образует 6 равных квадратных поверхностей или сторон. Получающаяся двумерная форма, когда куб разворачивается, называется сетью куба .
Как найти площадь поверхности куба :Напомним, что площадь поверхности трехмерной фигуры относится к общей площади, занимаемой поверхностью фигуры. Чтобы лучше понять площадь поверхности, посмотрите на сеть или плоскую компоновку куба на иллюстрации ниже.
Площадь поверхности куба , равная , равна сумме площадей всех его шести квадратных сторон. Напомним, что площадь квадрата вычисляется путем умножения длины каждой стороны ( на ) на себя: на или на ². Просто умножьте площадь стороны квадрата на 6, и вы получите площадь поверхности куба.
Используйте эту формулу, чтобы найти общую площадь поверхности куба: SA = 6 a ²
, где a = длина одной стороны куба и a ² = площадь одной квадратной стороны куба.
Примечание: Не забывайте, что площади поверхности измеряются в квадратных единицах, таких как см 2 , м 2 , км 2 и 2 .
Краткое руководство по нахождению площади поверхности куба :Шаг 1. Запишите данные числа. Вам понадобится длина стороны куба, чтобы найти площадь поверхности. Убедитесь, что все единицы измерения одинаковы. Если нет, преобразуйте любой из них, чтобы он соответствовал другому.
Шаг 2. Подставьте цифры в формулу.
Шаг 3. Выполните операции. Не забудьте указать квадратную единицу площади поверхности.
Пример #1:
Найдите площади поверхности куба ниже.
Решение для примера №1:
Шаг 1. Запишите данное измерение, a = 8 м .
Шаг 2. Подставьте 8m вместо a в формуле для площадь поверхности .
SA = 6 a ²
SA = 6(8m)²
Шаг 3. Упростите и решите уравнение.
SA = 6(64 м²)
SA = 384 м²
Таким образом, площадь равна 384 м² .
Хотите узнать, как найти объем этого куба?
Связанные материалы: Объем куба – формула и примеры
Найдите площади поверхности куба длиной 4 метра.
Шаг 1. Запишите данное измерение, a = 4м .
Шаг 2. Замените 4 м на a в формуле для площади поверхности .
SA = 6 a ²
SA = 6(4m)²
Шаг 3. Упростите и решите уравнение.
SA = 6(16м²)
SA = 96 м²
Следовательно, площадь поверхности равна 96 м² .
Спасибо, что прочитали. Мы надеемся, что это эффективно! Всегда не стесняйтесь возвращаться на эту страницу, если у вас возникнут вопросы о площади поверхности куба .
Ознакомьтесь с некоторыми другими сообщениями в нашем блоге или инвестируйте в свое будущее с помощью одного из наших курсов самообучения!
Нажмите здесь, чтобы ознакомиться с руководством по подготовке к экзамену AP Calculus AB 2021 !Нажмите здесь, чтобы ознакомиться с руководством по подготовке к экзамену AP Calculus BC 2021 !Как найти площадь поверхности куба
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
ACT Math Help » Геометрия » Твердая геометрия » Кубики » Как найти площадь поверхности куба
Если площадь поверхности куба равна 96, какова длина одной стороны куба?
Возможные ответы: Правильный ответ:4
Пояснение: Площадь поверхности куба = 6a 2 , где a — длина стороны каждого ребра куба.
Иными словами, поскольку все стороны куба равны, а — это просто длина одной стороны куба.
У нас есть 96 = 6a 2
→ a 2 = 16, так что это площадь одной грани куба.Решив, мы получим √16, так что a = 4
Сообщить об ошибке
Сторона куба имеет длину . Какова общая площадь поверхности куба?
Возможные ответы: Правильный ответ: Пояснение:Куб имеет 6 граней. Площадь каждой грани находится путем возведения в квадрат длины стороны.
Умножьте площадь одной грани на количество граней, чтобы получить общую площадь поверхности куба.
Сообщить об ошибке
Какова площадь поверхности куба, если его высота 3 см?
Возможные ответы: Правильный ответ: Объяснение:Площадь одной грани равна длине стороны в квадрате.
Площадь шести граней равна шестикратной площади одной грани: 54 см 2 .
Сообщить об ошибке
Сфера объемом вписана в куб, как показано на диаграмме ниже.
Какова площадь поверхности куба в ?
Возможные ответы: Правильный ответ: Пояснение:Сначала мы должны найти радиус сферы, чтобы решить эту задачу. Поскольку мы уже знаем объем, для этого воспользуемся формулой объема.
Имея в руках радиус сферы, мы можем применить его к кубу. Радиус сферы равен половине расстояния от вершины до низа куба (или половине расстояния от одной стороны до другой). Следовательно, радиус представляет собой половину длины стороны квадрата. Так что в данном случае
Формула площади поверхности куба:
Площадь поверхности куба
Сообщить об ошибке
Что такое площадь поверхности четырехугольника в квадратных дюймах дюймовый куб?
Возможные ответы: Правильный ответ: Пояснение: Чтобы ответить на этот вопрос, нам нужно найти площадь поверхности куба.
Для этого нужно найти площадь одной грани и умножить ее на , потому что у куба есть грани квадратной формы и одинакового размера.
Чтобы найти площадь квадрата, нужно умножить его длину на ширину. (Обратите внимание, что длина и ширина квадрата одинаковы.) Следовательно, для этих данных:
Теперь мы должны умножить площадь одной грани на 6, чтобы получить общую поверхность куба.
Таким образом, поверхность представляет собой четырехдюймовый куб.
Сообщить об ошибке
Какова площадь поверхности куба с объемом ? При необходимости округлите ответ до сотых
Сначала нам нужно найти длину стороны куба. Сделайте это, взяв кубический корень из объема.
=
Затем подставьте длину стороны в формулу площади поверхности куба:
Сообщить об ошибке
Какова площадь поверхности куба с измеряемыми сторонами в квадратных дюймах?
Возможные ответы: Правильный ответ: Объяснение: Площадь поверхности куба — это мера общей площади поверхностей всех сторон этого куба.
Поскольку куб содержит квадратные стороны, площадь поверхности умножается на площадь квадратной стороны.
Площадь одной стороны квадрата равна длине стороны длины стороны, или в данном случае. Таким образом, площадь поверхности этого куба равна квадратным дюймам.
Сообщить об ошибке
Какова длина стороны куба, площадь поверхности которого равна объему?
Возможные ответы:Недостаточно информации для определения ответа.
Правильный ответ: Объяснение:Чтобы найти длину стороны куба, площадь поверхности которого равна его объему, приравняйте уравнения площади поверхности и объема куба, решите длину стороны:
Установите эти две формулы, равные друг другу и решить для s.
Сообщить об ошибке
Какова площадь поверхности куба со стороной длиной?
Возможные ответы: Правильный ответ: Объяснение: Чтобы найти площадь поверхности куба с заданной длиной стороны, используйте формулу:
Сообщить об ошибке
Найдите площадь поверхности куба, длина стороны которого равна .