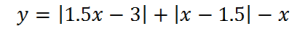Построение функций, содержащих модули
Здравствуйте, уважаемые посетители! В этой статье мы попробуем подробно разобраться, как построить график функции, если эта функция содержит модуль. В статье разобраны различные примеры с пошаговым построением и подробным объяснением, как получен тот или иной график.
1. Начнем с построения графика

В “основе” его лежит график функции

и все мы знаем, как он выглядит:

Теперь построим график


Теперь необходимо умножить на два все ординаты, чтобы получить график функции


Наконец, сдвигаем график вверх на две единицы:


Последнее, что нам осталось сделать, это построить график данной функции, если она заключена под знак модуля. Для этого отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту часть, что лежит ниже оси х):

2. Теперь построим график функции

Выражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так:

При х>2/3 функция запишется так:

То есть точка х=2/3 делит нашу координатную плоскость на две области, в одной из которых (правее) мы строим функцию

а в другой (левее) – график функции

Строим:

3. Следующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля:

Посмотрим, в каких точках подмодульные выражения меняют знак:

Расставим знаки для подмодульных выражений на координатной прямой:

Раскрываем модули на первом интервале:

На втором интервале:

На третьем интервале:

Таким образом, на интервале (-∞; 1.5] имеем график, записанный первым уравнением, на интервале [1.5; 2] – график, записанный вторым уравнением, и на интервале [2;∞) – график по третьему уравнению:

Строим:

4. Теперь можем построить график, похожий на один из предыдущих, и все же отличающийся:

В основе опять знакомый нам график функции

но, если в знаменателе x стоит под знаком модуля,

то график имеет вид:

Теперь произведем сдвиг на три единицы,

при этом сдвинутся обе части: правая – вправо, левая – влево (своеобразное зеркало : отходишь дальше – видно больше)

График этой функции, умноженной на два,

выглядит так:

Теперь можно поднять график по оси у:

и тогда он будет таким:
Наконец, строим окончательный вид графика, отражая все, что ниже оси абсцисс, вверх:


5.Очень интересно выглядит график функции

В точках 2 и (-2) знак подмодульного выражения меняет знак, поэтому функция состоит из трех кусков (точки 2 и (-2) выколоты). На участках (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) – второе:


6. Две следующие функции отличаются знаком, и графики их выглядят по-разному:




7. Еще два похожих графика, вид которых меняется в зависимости от х в показателе степени:
Первый:


Второй:


8.Теперь построим график такой функции:

Здесь точкой перемены знака подмодульного выражения является х=4. Тогда на интервале (-∞; 4] функция выглядит так:

А на интервале [4; ∞) так:

Точка вершины первой параболы (2;-12), она обращена вниз ветвями, точка вершины второй параболы (6, -20), ветви ее обращены вверх. В итоге имеем:

9. Построим график функции, которая, на первый взгляд, выглядит устрашающе:

Однако многочлен в числителе раскладывается на множители:

Точки перемен знака подмодульных выражений – 4 и (-2). Точки эти (они выколоты) разбивают числовую прямую на три интервала, на которых данная функция будет выглядеть:
На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

Строим:

Внесем небольшие изменения, добавив двойку в знаменатель исходной функции:

Тогда точки перемены знака остаются те же, но функция выглядит иначе на разных интервалах:
На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

График изменится:

10. Наконец, последний график мы построим для функции

Начнем построение с “базовой” для этого графика функции

она выглядит так:

Далее добавим знак модуля под корень:


Теперь опустим этот график вниз на 4 единицы по оси у:


“Опрокинем” все, что ниже оси х, вверх,

и не забудем поделить все ординаты на 2:


Методы построения графиков функций содержащих модуль
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока:
- повторить построение графиков функций содержащих знак модуля;
- познакомиться с новым методом построения графика линейно-кусочной функции;
- закрепить новый метод при решении задач.
Оборудование:
- мультимедиа проектор,
- плакаты.
Ход урока
Актуализация знаний
На экране слайд 1 из презентации.
Что является графиком функции y=|x| ? (слайд 2).
(совокупность биссектрис 1 и 2 координатных углов)
Найдите соответствие между функциями и графиками, объясните ваш выбор (слайд 3).
Рисунок 1
y=| x+3|
y=| x| +3
y=-2| x| -2
y=6-| x-5|
y=1/3| x-6| -3
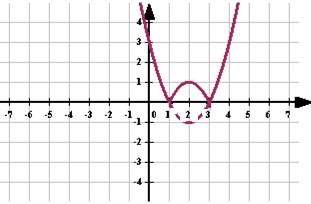
Расскажите алгоритм построения графиков функций вида y=|f(x)| на примере функции y=|x2-2x-3| (слайд 4)
Ученик: чтобы построить график данной функции нужно
— построить параболу y=x2-2x-3
— часть графика над ОХ сохранить, а часть графика расположенную ниже ОХ отобразить симметрично относительно оси ОХ (слайд 5)
Рисунок 2
Рисунок 3
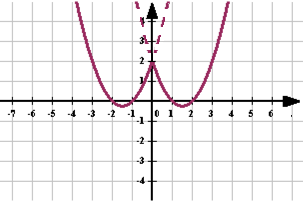
Расскажите алгоритм построения графиков функций вида y=f(|x|) на примере функции y=x2-2|x|-3 (слайд 6).
Ученик: Чтобы построить график данной функции нужно:
— построить параболу.
— часть графика при х 0 сохраняется и отображается симметрии относительно оси ОУ (слайд 7)
Рисунок 4
Расскажите алгоритм построения графиков функций вида y=|f(|x|)| на примере функции y=|x2-2|x|-3| (слайд 8).
Ученик: Чтобы построить график данной функции нужно:
— нужно построить параболу у=x2-2x-3
— строим у= x2-2|x|-3, часть графика сохраняем и симметрично отображаем относительно ОУ
— часть над ОХ сохраняем, а нижнюю часть симметрично отображаем относительно ОХ (слайд 9)
Рисунок 5
Следующее задание выполняем письменно в тетрадях.
1. Построить график линейно-кусочной функции у=|х+2|+|х-1|-|х-3|
Ученик на доске с комментарием:
— находим нули подмодульных выражений х1=-2, х2=1, х3=3
— разбиваем ось на промежутки
— для каждого промежутка запишем функцию
при х < -2, у=-х-4
при -2 х<1, у=х
при 1 х<3, у = 3х-2
при х 3, у = х+4
— строим график линейно-кусочной функции.
Мы с вами построили график функции используя определение модуля (слайд 10).
Рисунок 6
Предлагаю вашему вниманию “метод вершин”, который позволяет строить график линейно-кусочной функции (слайд 11). Алгоритм построения дети записывают в тетрадь.
Метод вершин
Алгоритм:
- Найдем нули каждого подмодульного выражения
- Составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа
- Нанесем точки на координатную плоскость и соединим последовательно
2. Разберем этот метод на той же функции у=|х+2|+|х-1|-|х-3|
Учитель на доске, дети в тетрадях.
Метод вершин:
— найдем нули каждого подмодульного выражения;
— составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа
х -3 -2 1 3 4
у -1 -2 1 7 8
— нанесем точки на координатную плоскость и соединим последовательно.
Графиком линейно-кусочной функции является ломанная с бесконечными крайними звеньями (слайд 12) .
Рисунок 7
Каким же методом график получается быстрее и легче?
3. Чтобы закрепить данный метод предлагаю выполнить следующее задание:
При каких значения х функция у=|х-2|-|х+1| принимает наибольшее значение.
Следуем алгоритму; ученик на доске.
у=|х-2|-|х+1|
х1=2, х2=-1
у(-2)=4-1=3
у(-1)=3
у(2)=-3
у(3)=1-4=3, соединяем последовательно точки.
унаиб = 3
4. Дополнительное задание
При каких значениях а уравнение ||4+x|-|x-2||=a имеет два корня.
5. Домашняя работа
а) При каких значениях Х функция у =|2x+3|+3|x-1|-|x+2| принимает наименьшее значение.
б) Построить график функции y=||x-1|-2|-3| .
Обучение учащихся построению графиков функций с модулем
Обучение учащихся построению графиков функций с модулем
Построение графиков, содержащих модуль, осуществляется двумя способами:
На основании определения модуля
Построение графика функции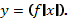
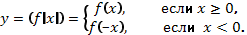
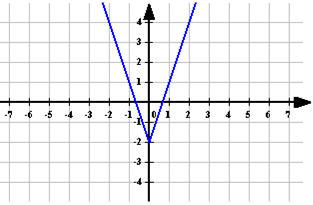
Приведем пример построения графика функции 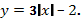
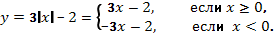
П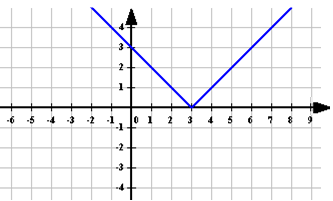 остроение графика функции
остроение графика функции 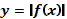
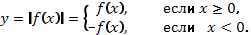
Приведем пример построения графика функции 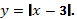

На основании правил геометрического преобразования графиков функций.
Какие геометрические преобразования, можно использовать при построении графиков функций? (параллельный перенос вдоль осей ОХ и ОУ, симметричное отображение относительно осей или точки)
Построение графика 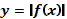 .
.
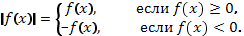
 Чтобы построить график функции
Чтобы построить график функции 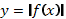 , если известен график функции
, если известен график функции 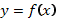 , нужно оставить на месте ту его часть, где
, нужно оставить на месте ту его часть, где 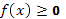 , и симметрично отобразить относительно оси Х другую его часть, где
, и симметрично отобразить относительно оси Х другую его часть, где 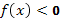 .
.
Алгоритм построения графика:
1. Построить график функции 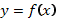 ,
,
2. Часть графика 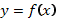 , лежащая над осью ОХ, сохраняется, а часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ.
, лежащая над осью ОХ, сохраняется, а часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ.
Построение графика 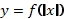 .
.
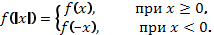
 Чтобы построить график функции
Чтобы построить график функции 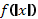 , если известен график функции
, если известен график функции 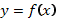 , нужно оставить на месте ту его часть, где
, нужно оставить на месте ту его часть, где 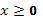 , а при
, а при 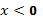 отобразить построенную часть симметрично относительно оси ОУ.
отобразить построенную часть симметрично относительно оси ОУ.
Алгоритм построения графика:
Построить график функции 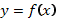 ,
,
При 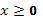 график сохраняется, а при
график сохраняется, а при 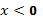 отображается построенная часть симметрично относительно оси ОУ.
отображается построенная часть симметрично относительно оси ОУ.
В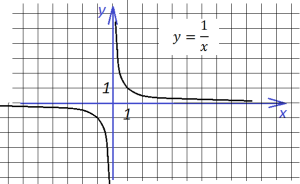 “основе” его лежит график функции
“основе” его лежит график функции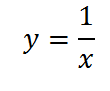 , он выглядит так :
, он выглядит так :
Теперь построим график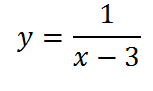
Ч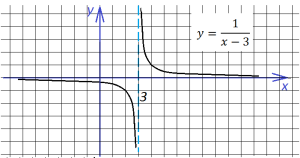 тобы получить этот график, достаточно всего лишь сдвинуть полученный ранее график на три единицы вправо. Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то мы сдвинули бы график влево:
тобы получить этот график, достаточно всего лишь сдвинуть полученный ранее график на три единицы вправо. Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то мы сдвинули бы график влево:
Т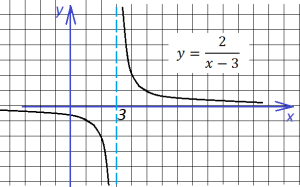 еперь необходимо умножить на два все ординаты, чтобы получить график функции
еперь необходимо умножить на два все ординаты, чтобы получить график функции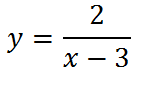
Наконец, сдвигаем график вверх на две единицы:
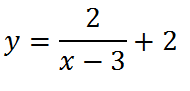
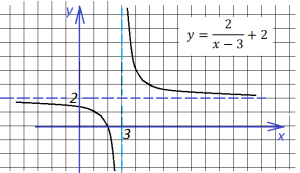
Последнее, что нам осталось сделать, это построить график данной функции, если она заключена под знак модуля. Для этого отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту часть, что лежит ниже оси х):
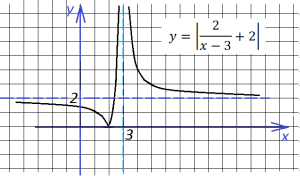
В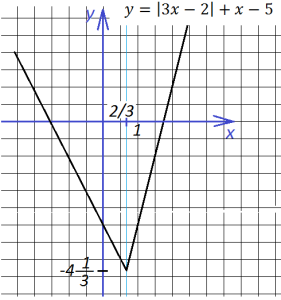 ыражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так:
ыражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так: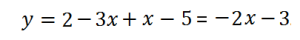
При х>2/3 функция запишется так: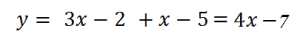
То есть точка х=2/3 делит нашу координатную плоскость на две области, в одной из которых (правее) мы строим функцию 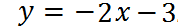 ,
,
а в другой (левее) – график функции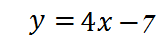
С
 ледующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля:
ледующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля: 
Посмотрим, в каких точках подмодульные выражения меняют знак:
Расставим знаки для подмодульных выражений на координатной прямой:
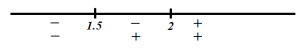
Раскрываем модули на первом интервале: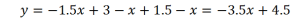
На втором интервале: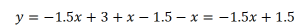
На третьем интервале: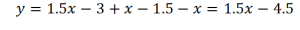
Таким образом, на интервале (-∞; 1.5] имеем график, записанный первым уравнением, на интервале [1.5; 2] – график, записанный вторым уравнением, и на интервале [2;∞) — график по третьему уравнению:
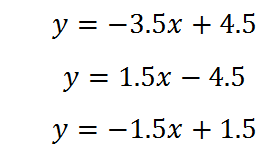
Строим:
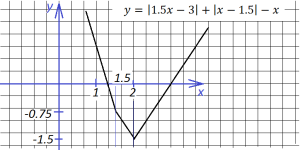
4. Теперь можем построить график, похожий на один из предыдущих, и все же отличающийся:
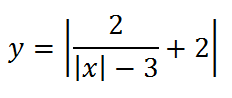
В основе опять знакомый нам график функции
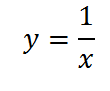
но, если в знаменателе x стоит под знаком модуля,
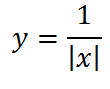
то график имеет вид:
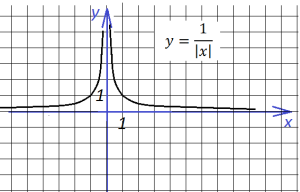
Теперь произведем сдвиг на три единицы,
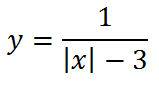
при этом сдвинутся обе части: правая — вправо, левая — влево (своеобразное зеркало : отходишь дальше — видно больше)
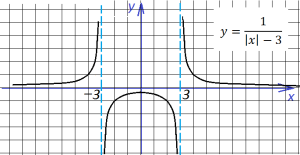
График этой функции, умноженной на два,
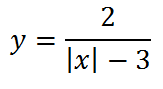
выглядит так:
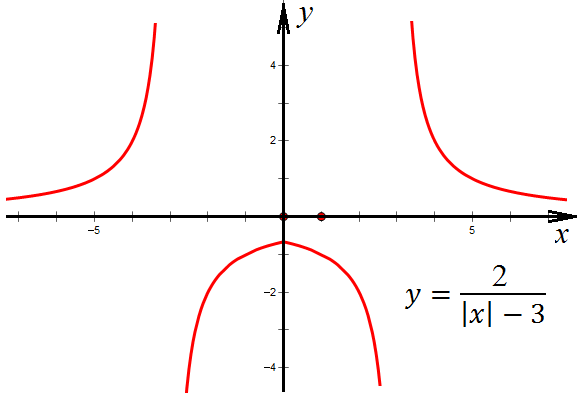
Теперь можно поднять график по оси у:
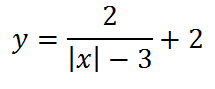
и тогда он будет таким: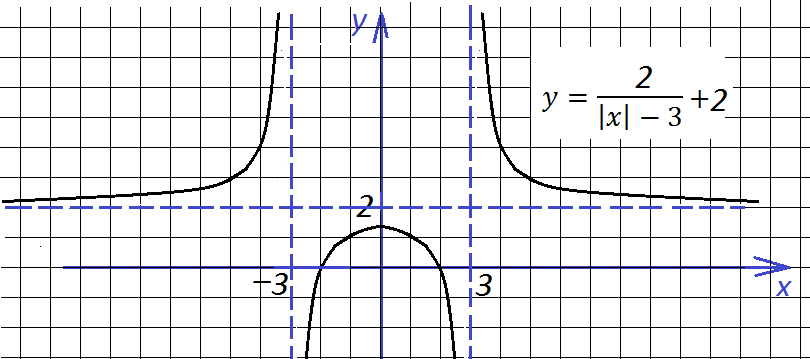
Наконец, строим окончательный вид графика, отражая все, что ниже оси абсцисс, вверх:
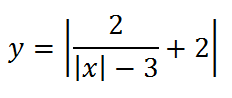
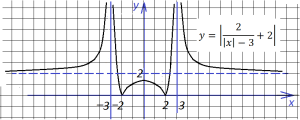
5.Очень интересно выглядит график функции
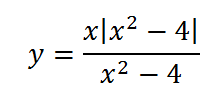
В точках 2 и (-2) знак подмодульного выражения меняет знак, поэтому функция состоит из трех кусков (точки 2 и (-2) выколоты). На участках (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) — второе:
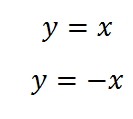
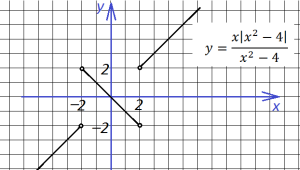
6. Две следующие функции отличаются знаком, и графики их выглядят по разному:
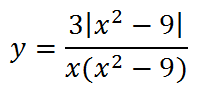
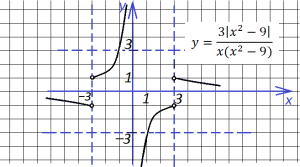
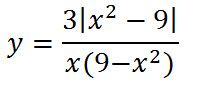
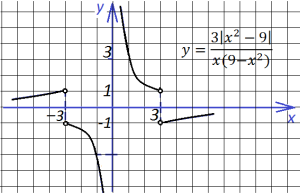
7. Еще два похожих графика, вид которых меняется в зависимости от х в показателе степени:
Первый:
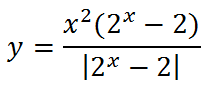
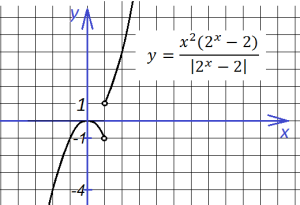
Второй:
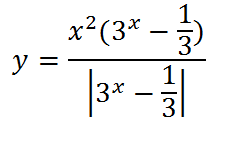
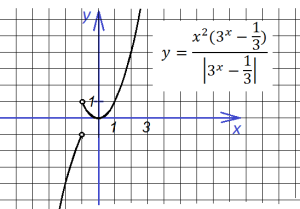
8.Теперь построим график такой функции:
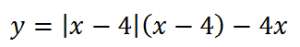
Здесь точкой перемены знака подмодульного выражения является х=4. Тогда на интервале (-∞; 4] функция выглядит так:
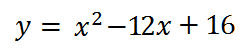
А на интервале [4; ∞) так:
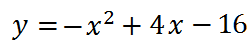
Точка вершины первой параболы (2;-12), она обращена вниз ветвями, точка вершины второй параболы (6, -20), ветви ее обращены вверх. В итоге имеем:
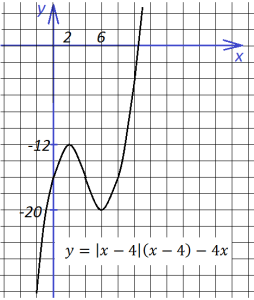
9. Построим график функции, которая, на первый взгляд, выглядит устрашающе:
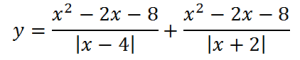
Однако многочлен в числителе раскладывается на множители:
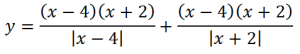
Точки перемен знака подмодульных выражений – 4 и (-2). Точки эти (они выколоты) разбивают числовую прямую на три интервала, на которых данная функция будет выглядеть:
На первом интервале (-∞; -2):
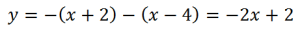
На втором интервале (-2;4):

На третьем интервале (4;∞):
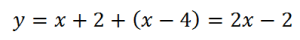
Строим:

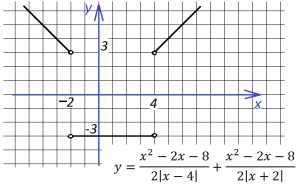
Внесем небольшие изменения, добавив двойку в знаменатель исходной функции:

Тогда точки перемены знака остаются те же, но функция выглядит иначе на разных интервалах:
На первом интервале (-∞; -2):
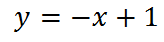
На втором интервале (-2;4):
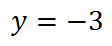
На третьем интервале (4;∞):
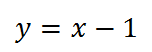
График изменится:
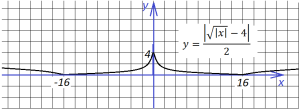
10. Наконец, последний график мы построим для функции
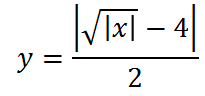
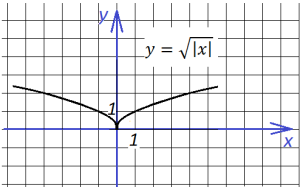
Начнем построение с “базовой” для этого графика функции
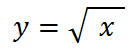
она выглядит так:
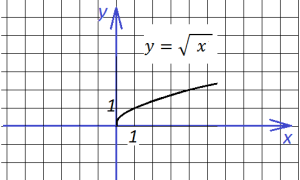
Далее добавим знак модуля под корень:
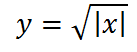
Теперь опустим этот график вниз на 4 единице по оси у:
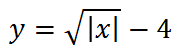
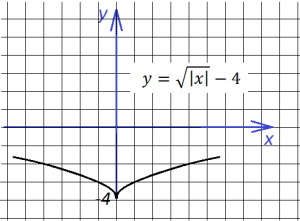
“Опрокинем” все, что ниже оси х, вверх,
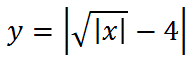
и не забудем поделить все ординаты на 2:
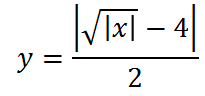
Графики прямой, параболы, гиперболы, с модулем
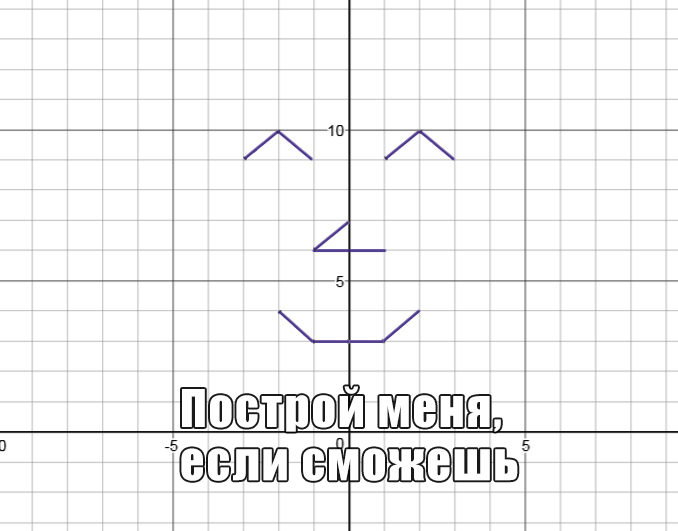
Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
Для понимания друг друга введу немного «обзываний» системы координат:

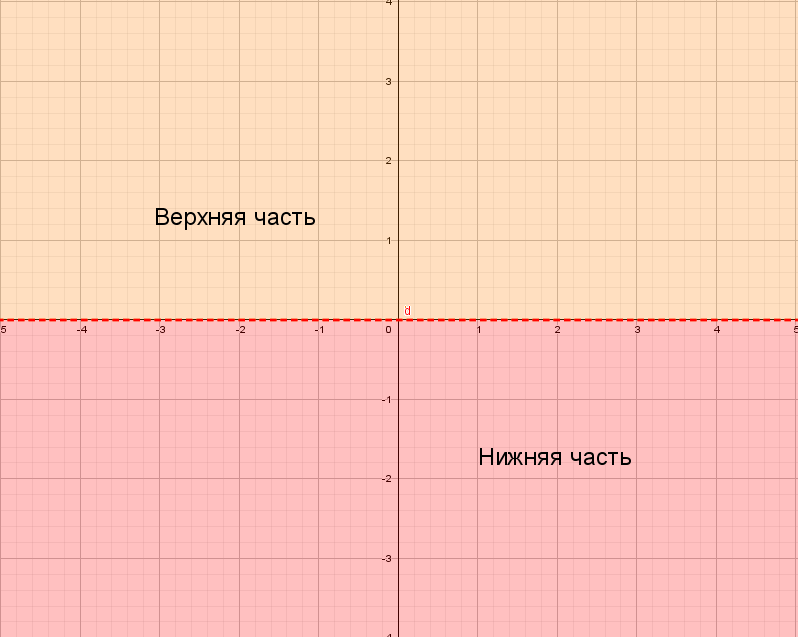

Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:

А если теперь добавить модуль y = |2x − 1|.
Модуль — это всегда положительное значение, получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).
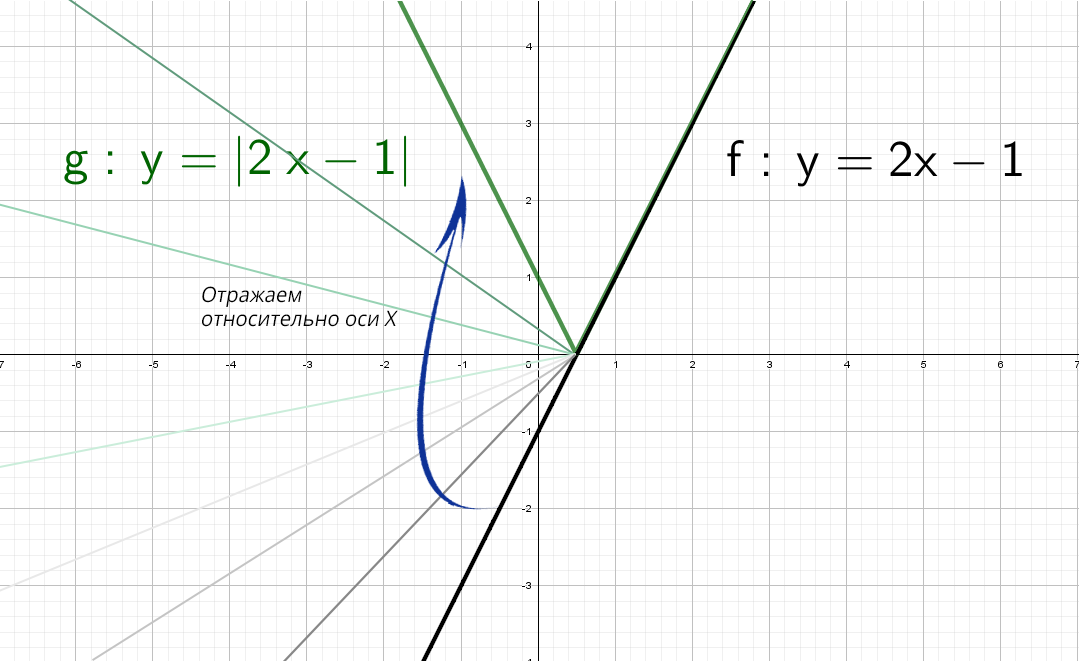 Получается такая зеленая «галочка».
Получается такая зеленая «галочка».
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
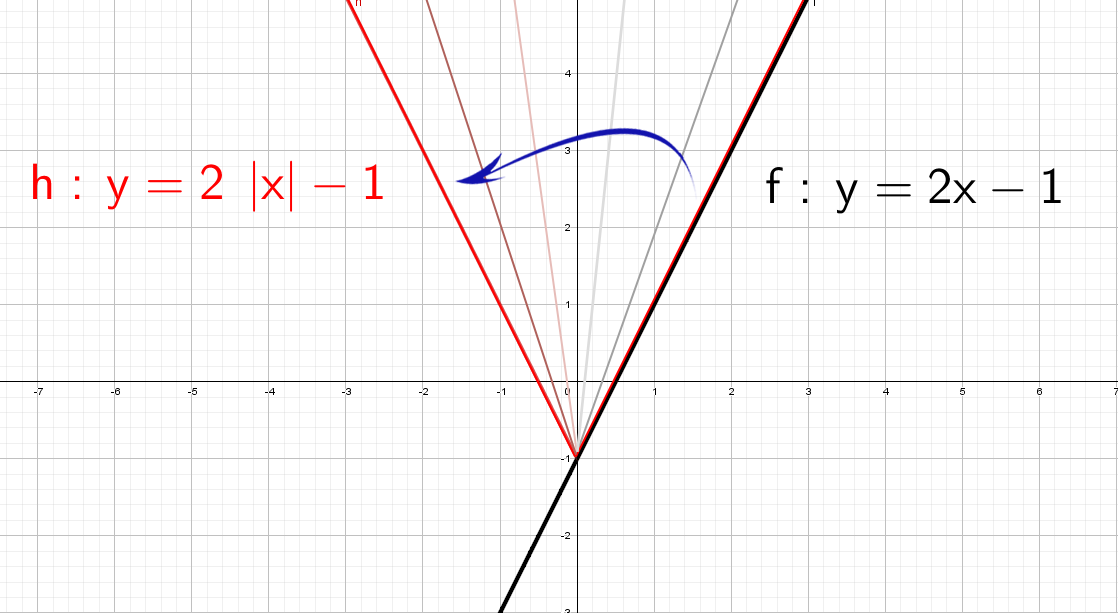
Здесь отражаем относительно оси «y». Такая же галочка, только теперь через другую ось.
Смертельный номер: y = |2|x| − 1|.
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!
А после этого отражаем относительно оси «y» то, что мы получили справа налево:

Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x₁ = 1 и x₂ = -2.
Можно найти вершину у параболы и взять пару точек для точного построения.
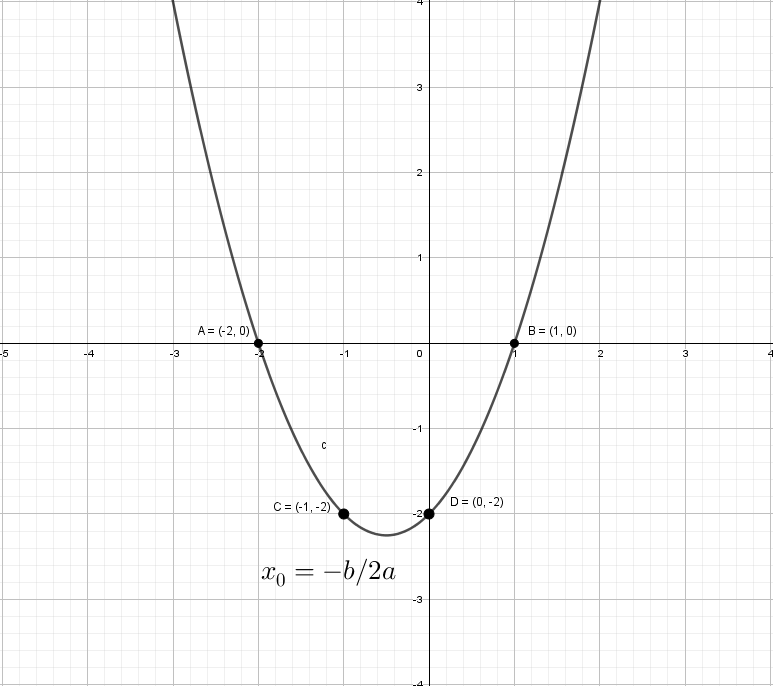
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
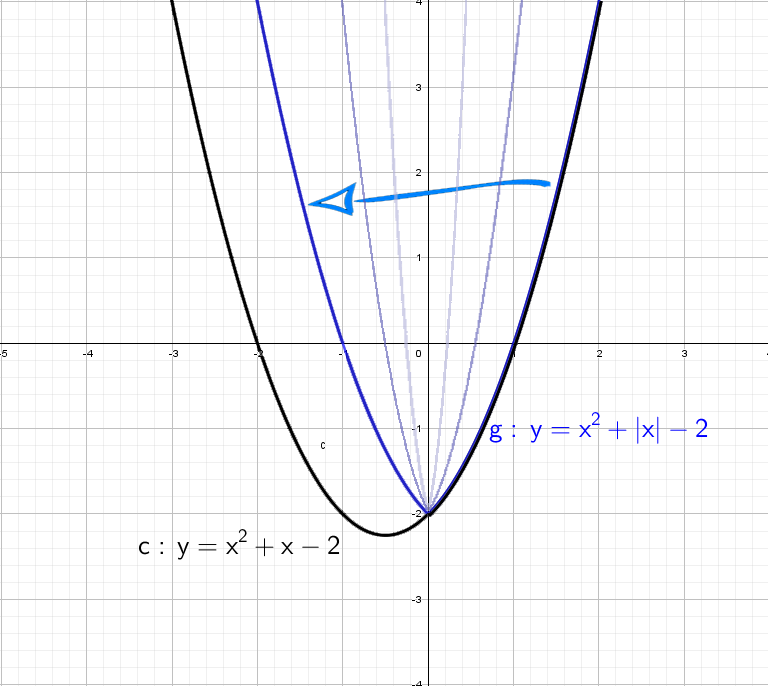
А дальше что мелочиться: рассмотри сразу остальные графики с модулем!
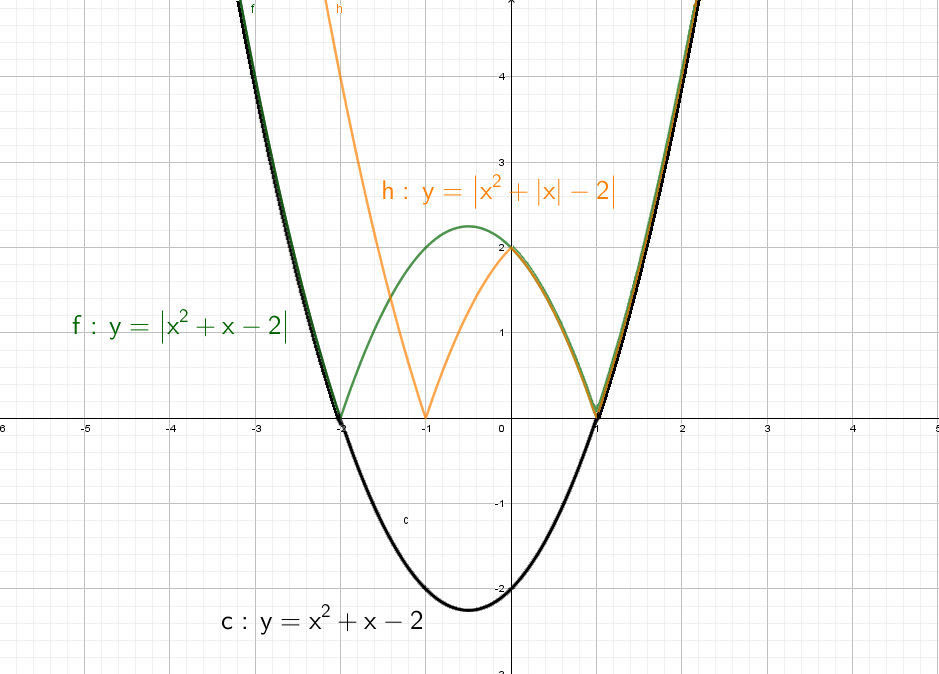
Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
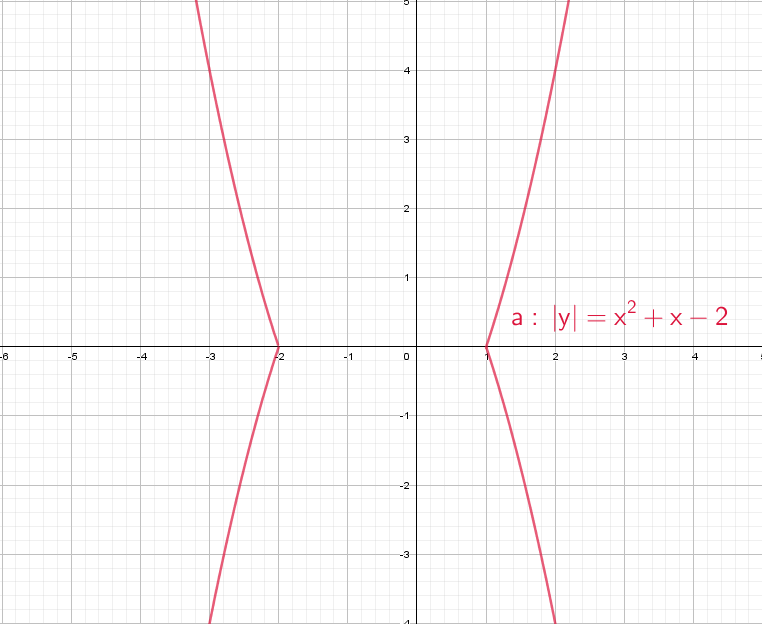
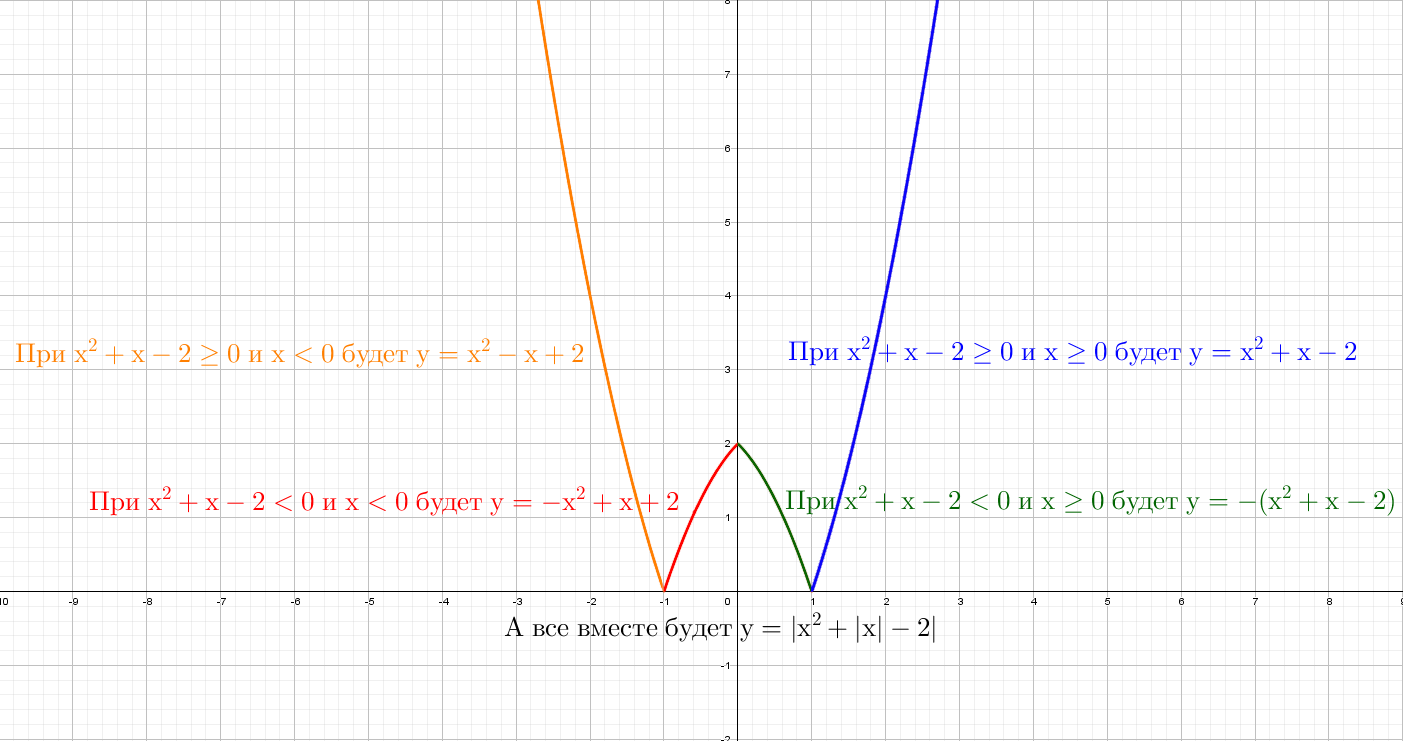
А теперь сразу комбо:
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.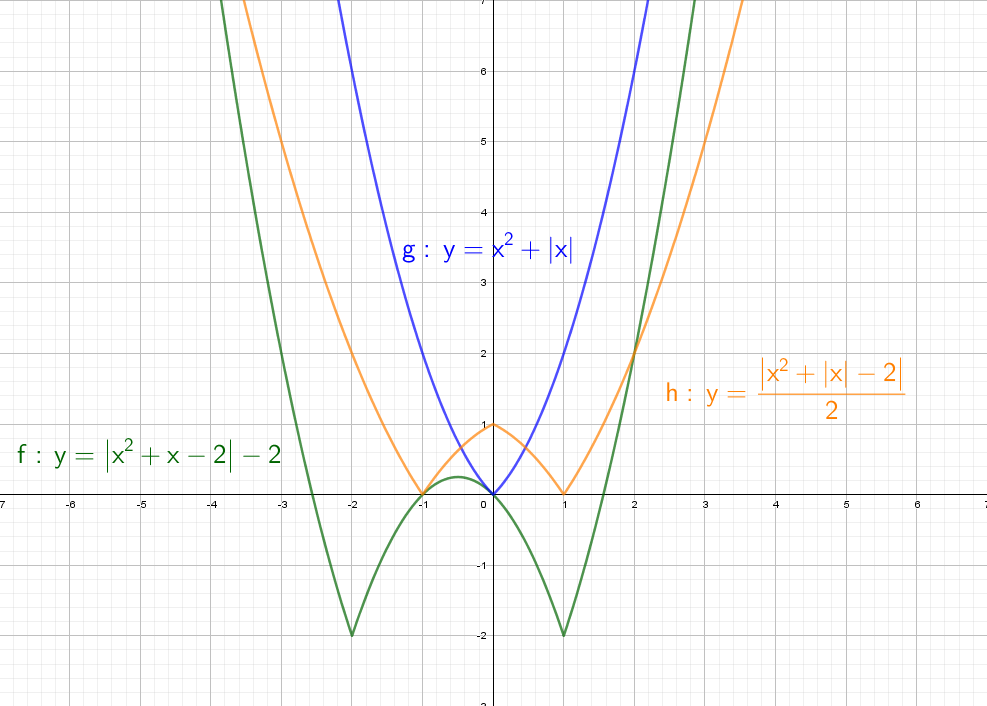
Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум, потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
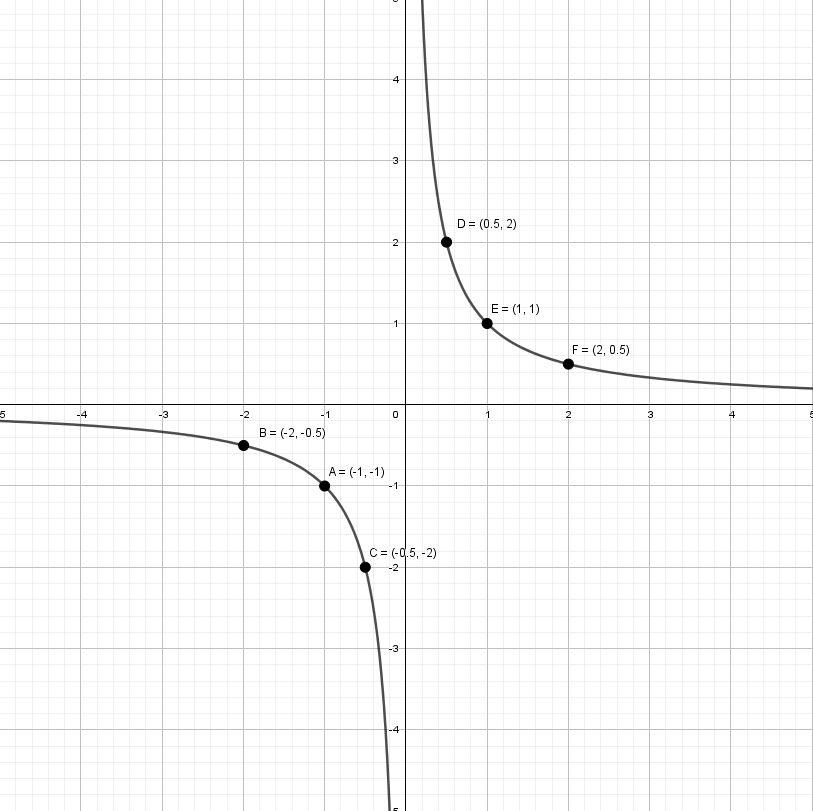
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
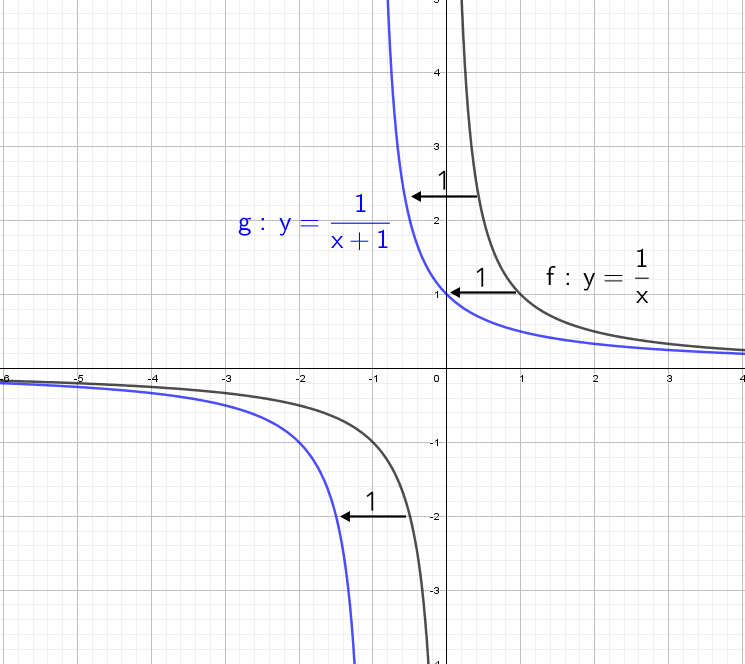
А что будет, если мы добавим в знаменателе «−1»? График сдвинется вправо на единицу.
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!
 Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!
Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
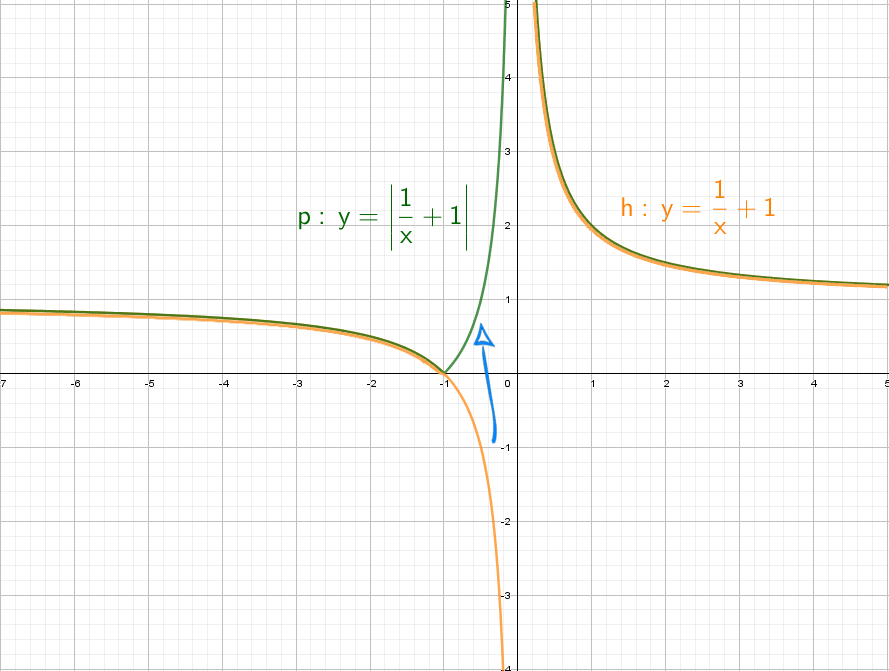
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
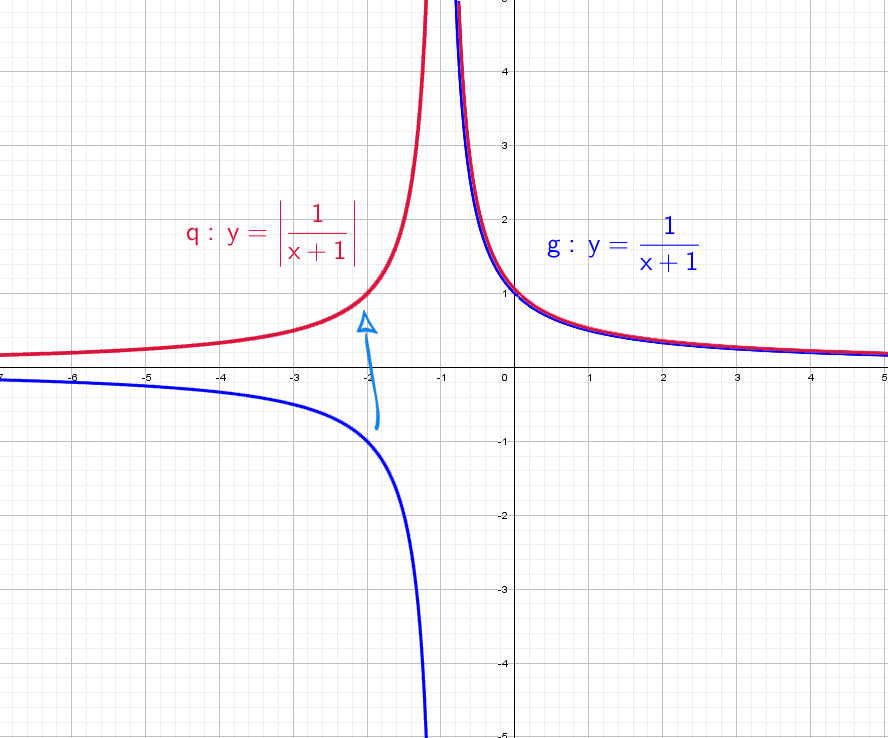
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.
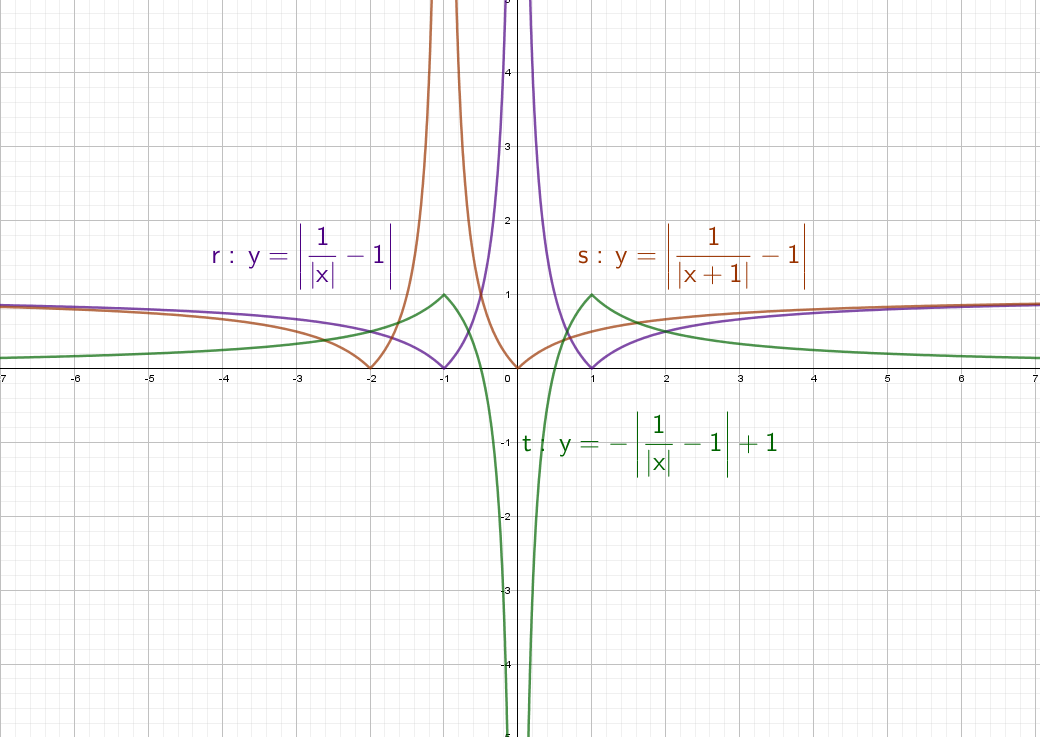
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
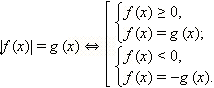
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
Для параболы с одним модулем будет два кусочно-заданных графика: 
C двумя модулями кусочно-заданных графиков будет четыре:
 Таким способом, медленно и кропотливо можно построить любой график!
Таким способом, медленно и кропотливо можно построить любой график!
Выводы:
- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль.
- Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Будь в курсе новых статеек, видео и легкого математического юмора.
График функции с модулем и дробью
График функции с модулем и дробью — ещё одна группа заданий номера 23 ОГЭ по математике.
Подобно функциям с переменной в знаменателе, графики таких функций могут содержать выколотую точку. Как и при построении графиков функций с модулем, рассматриваем два варианта раскрытия модуля.
1) Построить график функции
и определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:
Так как x²=|х|², формулу, задающую функцию, перепишем в виде
В знаменателе общий множитель |х| вынесем за скобки
Найдём область определения функции.
|х|(|х|-1)≠0
|х|≠0; |х|-1≠0
x≠0; |х|≠1
x≠0, x≠±1.
D(y):x∈(-∞;-1)∪(-1;0)∪(0;1)∪(1;∞).
Сократив дробь на (|х|-1), получаем
При x>0 |х|=x,
— функция обратной пропорциональности. График — гипербола. Для построения гиперболы возьмём несколько точек (включая выколотую x=1):
При x<0 |х|=-x,
— функция обратной пропорциональности.
Прямая y=kx не имеет с графиком общих точек, если она проходит через выколотые точки либо совпадает с осью Ox, то есть при k=±1 и k=0:
Ответ: -1; 0; 1.
2)Постройте график функции
и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.
Решение:
В числителе вынесем за скобки общий множитель 0,25x:
Ищем область определения функции.
x+2≠0
x≠-2.
D(y):x∈(-∞;-2)∪(-2;∞).
Сокращаем дробь на (x+2):
Получили функцию, содержащую переменную под знаком модуля (при условии x≠-2).
При x=0, y=0,25·0·|0|=0.
При x>0 |х|=x, y=0,25·x·|x|= y=0,25·x·x=0,25x².
y=0,25x² или
— квадратичная функция. График — парабола, полученная из параболы y=x² сжатием к оси Ox в 4 раза.
При x<0 |х|=-x, y=0,25·x·|x|= y=0,25·x·(-x)=-0,25x².
— квадратичная функция. График — парабола, полученная из параболы y=-x² сжатием к оси абсцисс в 4 раза.
Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку, то есть при m=-1:
Ответ: -1.
3) Построить график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
Найдём область определения функции: x≠0.
D(y):x∈(-∞;0)∪(0;∞).
Если
то есть при x∈[-4;0)∪[4;∞), то
y=x/4 -функция прямой пропорциональности. График — прямая, проходящая через начало координат.
Для построения прямой достаточно взять одну точку, например, при x=4 y=4/4=1. Вторая точка — точка O — на графике выколотая, так как x≠0. Для более точного построения прямой лучше взять ещё одну точку: при x=-4 y=-4/4=-1.
Если
то есть при x∈(-∞;-4)∪(0;4), то
y=4/x — функция обратной пропорциональности. График — гипербола.
Для построения гиперболы возьмём несколько точек из промежутков (-∞;-4)∪(0;4) (-4 и 4 также лучше взять для уточнения построения графика).
Прямая y=m имеет с графиком ровно одну общую точку при m=1 и m=-1:
Ответ: -1; 1.
Модуль в модуле. Графический метод
Распространенными примерами с модулями является уравнение типа модуль в модуле. Двойной модуль можно записать в виде формулы
||a*x-b|-c|=k*x+m.
Если k=0 то такое уравнение с модулем легче решать графическим методом. Классическое раскрытия модулей в таких ситуациях громоздкое и не дает желаемого эффекта (экономии времени) на контрольных и тестах. Графический метод позволяет за короткое время выполнить построение модульных функций и найти количество корней уравнения.
Алгоритм построения двойного, тройного модуля достаточно прост и из приведенных ниже примеров понравится многим. Для закрепления методики внизу приведены примеры для самостоятельного вычисления.
Пример 1. Решить уравнение модуль в модуле ||x-3|-5|=3.
Решение: Решим уравнение с модулями классическим методом и графически. Найдем ноль внутреннего модуля
x-3=0 x=3.
В точке x=3 уравнения с модулем разделяется на 2. Кроме того, ноль внутреннего модуля является точкой симметрии графика модулей и если правая сторона уравнения равна постоянной, то корни лежат на одинаковом расстоянии от этой точки. То есть можно решить одно уравнение из двух, а остальные корней вычислить из этого условия.
Раскроем внутренний модуль для x>3
|x-3-5|=3; |x-8|=3.
Полученное уравнение при раскрытии модуля делится на 2
Под модульная функция >0
x-8=3; x=3+8=11;
и для значений < 0 получим
-(x-8)=3; x=8-3=5.
Оба корня уравнения удовлетворяют условию x>3, то есть являются решениями.
Учитывая записано выше правило симметрии решений уравнения с модулями, можно не искать корни уравнения для x< 3, которое имеет вид
|-(x-3)-5|=3; |-x-2|=3,
а вычислить их.
Значение симметрично относительно x=3 для x=11 равно
x=3-(11-3)=6-11=-5.
По той же формуле находим второе решение
x=3-(5-3)=6-5=1.
Заданное уравнение модуля в модуле имеет 4 решения
x=-5; x=1; x=5; x=11.
Теперь найдем решения уравнения с модулями графическим методом. С внутреннего модуля |x-3| следует что график стандартной модуль функции является смещен по оси Ох вправо на 3.
Дальше — отнять 5 означает что график необходимо опустить на 5 клеток по оси Oy. Чтобы получить модуль полученной функции симметрично отражаем все что находится ниже оси Ox.
И напоследок выполняем построение прямой y=3, параллельной оси Ox. Лучше всего для вычислений уравнений с модулями графически использовать тетрадь в клеточку, поскольку в ней удобно строить графики.
Окончательный вид графика модулей имеет вид
Точки пересечения модуль функции и прямой y=3 и является искомыми решениями x=-5;x=1; x=5;x=11.
Преимущество графического метода над раскрытием модулей для простых уравнений очевидно. Однако графически неудобно искать корни когда правая сторона имеет вид k*x+m, то есть является прямой наклоненной к оси абсцисс под углом.
Здесь таких уравнений рассматривать не будем.
Пример 2. Сколько корней имеет уравнение ||2x-3|-2|=2?
Решение: Правая сторона равна постоянной, поэтому скорее найти решение можно графическим методом. Внутренний модуль обращается в нуль
|2x-3|=0 x=3/2=1,5
в точке x=1,5.
Значит в эту точку смещаем график функции y=|2x|. Для того, чтобы его построить подставьте несколько точек и проведите через них прямые. От полученной функции вычитаем 2 то есть график опускаем на двойку вниз и, чтобы получить модуль переносим отрицательные значения (y< 0) симметрично относительно оси Ox.
Далее остается построить правую сторону (прямую y=2) и подсчитать количество точек пересечения. График модуль функции и прямой приведен ниже
Видим, что заданное уравнение имеет три решения.
Пример 3. При каком значении параметра a уравнение с модулем |||x+1|-2|-5|=a имеет 5 решений?
Решение: Имеем уравнение с тремя вложенными модулями. Найдем ответ с графического анализа. Начнем, как всегда, из внутреннего модуля. Он обращается в нуль
|x+1|=0 x=-1
в точке x=-1.
Строим график модуль функции в этой точке
Далее график опускаем вниз на двойку и отрицательные значения (y< 0) симметрично переносим вверх. Получим график функции
y=||x+1|-2|
Повторно выполним смещение графика модуль функции вниз на 5 и симметрично переносим отрицательные значения функции. В результате получим левую сторону уравнения с модулями
y=|||x+1|-2|-5|.
Параметр а соответствует значению параллельной прямой, которая должна пересечь график модуль функции в 5 точках. Сначала проводим такую прямую, далее ищем точку пересечения ее с осью Oy.
Это прямая y=3, то есть искомый параметр равен a=3.
Методом раскрытия модулей данную задачу можно было решать целый урок, если не больше. Здесь все свелось к нескольким графикам.
Ответ: a=3.
Пример 4. Сколько решений имеет уравнение |||3x-3|-2|-7|=x+5 ?
Решение: Раскроем внутренний модуль уравнения
|3x-3|=0 <=> x=3/3=1.
Строим график функции y=|3x-3|. Для этого на одну клетки изменения x от н
График функции с модулем | Алгебра
Построить график функции с модулем — один из видов задания 23 ОГЭ по математике.
Рассмотрим примеры таких заданий.
1) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
Область определения функции D(y): x∈R.
1)Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:
x-2=0, x=2.
Найдём значение функции при x=2.
y(2)=5·0-2²+5∙2-3∙0-6=0.
Получили точку (2;0).
2) Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает положительные значения.
Если x-2>0, то есть при x>2, |х-2|=x-2,
y=5|х-2|-x²+5x-6=5(х-2)-x²+5x-6=5х-10-x²+5x-6=-x²+10x-16.
y=-x²+10x-16 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).
Координаты вершины параболы
то есть вершина параболы — точка (5;9). От вершины строим график функции y=-x² (так как a=-1).
3)Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает отрицательные значения.
Если x-2<0, то есть при x<2, |х-2|=-(x-2),
y=5|х-2|-x²+5x-6=-5(х-2)-x²+5x-6=-5х+10-x²+5x-6=-x²+4.
y=-x²+4 — квадратичная функция. График — парабола ветвями вниз.
Координаты вершины параболы
то есть вершина параболы — точка (0;4). От вершины строим график функции y=-x².
Прямая x=2 разбивает координатную плоскость на две полуплоскости. Слева от неё, для x<2, строим параболу y=-x²+4, справа, для x>2 — параболу y=-x²+10x-16:
График функции с модулем можно рассматривать и как график кусочной функции:
Прямая y=m имеет с графиком ровно три общие точки при m=0 и m=4:
Ответ: 0; 4.
2) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:
|6x+1|=6x+1 и y=x²-(6x+1)=x²-6x-1.
y=x²-6x-1 — квадратичная функция. График — парабола ветвями вверх (поскольку a=1>0).
Координаты вершины параболы
Так как a=1, от вершины (3;-10) строим график y=x².
|6x+1|=-(6x+1) и y=x²+(6x+1)=x²+6x+1.
y=x²+6x+1 — квадратичная функция. График — парабола ветвями вверх.
Координаты вершины параболы
от вершины (-3;-8) строим график y=x².
Или:
Прямая y=m имеет с графиком ровно три общие точки при m=1/30 и m=-8:
Ответ: -8; 1/36.
3) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Если x=0, y=|0|·0+3·|0|-5·0=0.
2) Если x>0, |x|=x, y=x·x+3·x-5·x=x²-2x.
y=x²-2x — квадратичная функция. График — парабола ветвями вверх (a=1>0).
Координаты вершины параболы
От вершины (1;-1) строим параболу y=x² (так как a=1).
3) Если x<0, |x|=-x, y=-x·x+3·(-x)-5·x=-x²-8x.
y=-x²-8x — квадратичная функция. График — парабола ветвями вниз (a=-1<0).
Координаты вершины параболы
От вершины (-4;16) строим параболу y=-x² (так как a=-1).
Таким образом, график данной функции представляет собой комбинацию двух парабол: справа от прямой x=0 (оси Oy) — y=x²-2x, слева — y=-x²-8x:
Альтернативный вариант:
Прямая y=m имеет с графиком ровно две общие точки, когда она проходит через вершины парабол, то есть при m=-1 и m=16:
Ответ: -1; 16.
4) Построить график функции y=|x²+2x-3|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Решение:
Область определения функции D(y): x∈R.
Построим график функции y=x²+2x-3.
Эта функция — квадратичная. Её графиком является парабола, ветви которой направлены вверх.
Координаты вершины параболы
, то есть вершина параболы — точка (-1;-4).
От вершины строим график функции y=x²:
График функции y=|x²+2x-3| может быть получен из графика функции y=x²+2x-3 следующим образом: часть графика, расположенную выше оси Ox, сохраняем. Часть, расположенную ниже оси Ox, отображаем симметрично относительно оси Ox.
Или y=|x²+2x-3|
Вершина параболы (-1;-4) при этом переходит в точку (-1;4):
Наибольшее число общих точек, которое график данной функции может иметь с прямой, параллельной оси абсцисс, равно 4 (например, прямая y=3 пересекает график в четырёх точках).
Ответ: 4.
модулей JavaScript: руководство для начинающих
от Preethi Kasireddy
Источник: https://www.flickr.com/photos/qubodup/16258492451Если вы новичок в JavaScript, используйте жаргон вроде «сборщики модулей против загрузчиков модулей», «Webpack против Browserify» и «AMD против CommonJS» может быстро стать подавляющим.
Модульная система JavaScript может показаться пугающей, но понимание ее жизненно важно для веб-разработчиков.
В этом посте я расскажу вам эти модные словечки на простом английском языке (и несколько примеров кода).Надеюсь, вы сочтете это полезным!
Примечание: для простоты этот раздел будет разделен на два раздела: Часть 1 будет посвящена объяснению, что такое модули и почему мы их используем. Во второй части (опубликованной на следующей неделе) будет рассмотрено, что означает объединение модулей и различные способы сделать это.
Часть 1: Кто-нибудь, пожалуйста, объясните, какие модули снова?
Хорошие авторы делят свои книги на главы и разделы; хорошие программисты делят свои программы на модули.
Подобно главе книги, модули — это просто скопления слов (или кода, в зависимости от случая).
Хорошие модули, однако, в высшей степени автономны с различными функциями, что позволяет их перемешивать, удалять или добавлять по мере необходимости, не нарушая работу системы в целом.
Зачем нужны модули?
Использование модулей дает множество преимуществ в пользу разветвленной взаимозависимой кодовой базы. Самыми важными, на мой взгляд, являются:
1) Ремонтопригодность: По определению, модуль является автономным.Хорошо спроектированный модуль нацелен на максимальное уменьшение зависимости от частей кодовой базы, чтобы она могла расти и улучшаться независимо. Обновить отдельный модуль намного проще, если модуль отделен от других частей кода.
Возвращаясь к нашему примеру с книгой, если вы хотите обновить главу в своей книге, было бы кошмаром, если бы небольшое изменение в одной главе потребовало, чтобы вы настраивали и каждую другую главу. Вместо этого вам нужно написать каждую главу таким образом, чтобы можно было вносить улучшения, не затрагивая другие главы.
2) Пространство имен: В JavaScript переменные, не входящие в область действия функции верхнего уровня, являются глобальными (то есть каждый может получить к ним доступ). Из-за этого часто возникает «загрязнение пространства имен», когда совершенно несвязанный код использует глобальные переменные.
Совместное использование глобальных переменных между несвязанным кодом является большим запретом в разработке.
Как мы увидим позже в этом посте, модули позволяют избежать загрязнения пространства имен, создавая личное пространство для наших переменных.
3) Возможность повторного использования: Давайте будем честными: мы все скопировали код, который мы ранее писали, в новые проекты в тот или иной момент. Например, представим, что вы скопировали некоторые служебные методы, написанные из предыдущего проекта, в текущий проект.
Это все хорошо, но если вы найдете лучший способ написать часть этого кода, вам придется вернуться и не забыть обновить его везде, где вы его написали.
Очевидно, это огромная трата времени. Разве не было бы намного проще, если бы существовал — подождите — модуль, который мы можем использовать снова и снова?
Как можно встраивать модули?
Есть много способов встраивать модули в ваши программы.Давайте рассмотрим несколько из них:
Шаблон модуля
Шаблон модуля используется для имитации концепции классов (поскольку JavaScript изначально не поддерживает классы), чтобы мы могли хранить как общедоступные, так и частные методы и переменные внутри одного объект — аналогично тому, как классы используются в других языках программирования, таких как Java или Python. Это позволяет нам создавать общедоступный API для методов, которые мы хотим предоставить миру, при этом инкапсулируя частные переменные и методы в области закрытия.
Есть несколько способов выполнить шаблон модуля. В этом первом примере я буду использовать анонимное закрытие. Это поможет нам достичь нашей цели, поместив весь наш код в анонимную функцию. (Помните: в JavaScript функции — единственный способ создать новую область видимости.)
Пример 1: Анонимное закрытие
(function () {
// Мы сохраняем эти переменные закрытыми внутри этой области закрытия
var myGrades = [93, 95, 88, 0, 55, 91];
var average = function () {
var total = myGrades.reduce (функция (аккумулятор, артикул .javascript — в узле js при создании модуля, как использовать функцию, определенную в модуле?
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Загрузка…
- Авторизоваться зарегистрироваться
6. Модули — документация Python 3.8.5
Если вы выйдете из интерпретатора Python и войдете в него снова, определения вы сделали (функции и переменные) потеряны. Поэтому, если вы хотите написать несколько более длинная программа, вам лучше использовать текстовый редактор для подготовки input для интерпретатора и запускать его с этим файлом в качестве ввода. это называется созданием сценария . По мере того, как ваша программа становится длиннее, вы можете захотеть разделите его на несколько файлов для облегчения обслуживания.Вы также можете использовать удобная функция, которую вы написали в нескольких программах, не копируя ее определение в каждую программу.
Для поддержки этого в Python есть способ помещать определения в файл и использовать их в скрипт или в интерактивном экземпляре интерпретатора. Такой файл называется модуль ; определения из модуля могут быть импортированы в другие модули или в основной модуль (набор переменных, к которым у вас есть доступ в скрипт выполняется на верхнем уровне и в режиме калькулятора).
Модуль — это файл, содержащий определения и инструкции Python. Имя файла
— это имя модуля с добавленным суффиксом .py . Внутри модуля
имя модуля (в виде строки) доступно как значение глобальной переменной __name__ . Например, используйте свой любимый текстовый редактор для создания файла
называется fibo.py в текущем каталоге со следующим содержимым:
Теперь войдите в интерпретатор Python и импортируйте этот модуль со следующим command:
Это не вводит имена функций, определенных в fibo непосредственно в
текущая таблица символов; он вводит там только имя модуля fibo .С помощью
имя модуля вы можете получить доступ к функциям:
6.1. Подробнее о модулях
Модуль может содержать исполняемые операторы, а также определения функций. Эти операторы предназначены для инициализации модуля. Они исполняются только — первый раз, когда имя модуля встречается в операторе импорта. (Они также запускаются, если файл выполняется как сценарий.)
Каждый модуль имеет свою собственную таблицу частных символов, которая используется как глобальный символ.
table всеми функциями, определенными в модуле.Таким образом, автор модуля может
использовать глобальные переменные в модуле, не беспокоясь о случайных конфликтах
с глобальными переменными пользователя. С другой стороны, если вы знаете, что вы
вы можете прикоснуться к глобальным переменным модуля с той же записью, что и
обратитесь к его функциям, modname.itemname .
Модули могут импортировать другие модули. Обычно, но не обязательно размещать все импортировать операторов в начале модуля (или сценария, для этого
иметь значение).Имена импортированных модулей помещаются в глобальную
таблица символов.
Существует вариант оператора import , который импортирует имена из
модуль прямо в таблицу символов импортирующего модуля. Например:
>>> из fibo import fib, fib2 >>> фиб (500) 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377
Это не вводит имя модуля, из которого берется импорт в
таблица локальных символов (поэтому в примере fibo не определена).
Существует даже вариант импорта всех имен, определяемых модулем:
>>> из импорта fibo * >>> фиб (500) 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377
Импортируются все имена, кроме тех, которые начинаются с подчеркивания ( _ ).
В большинстве случаев программисты Python не используют эту возможность, поскольку она вводит
неизвестный набор имен в интерпретаторе, возможно, скрывающий некоторые вещи
вы уже определились.
Обратите внимание, что в целом практика импорта * из модуля или пакета
не одобряют, поскольку это часто приводит к плохо читаемому коду.Однако это нормально
используйте его, чтобы сохранить набор текста в интерактивных сеансах.
Если после имени модуля идет как , то имя
следующий за , поскольку привязан непосредственно к импортированному модулю.
>>> импортировать fibo как fib >>> fib.fib (500) 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377
Это эффективно импортирует модуль так же, как import fibo подойдет, с той лишь разницей, что он доступен как fib .
Его также можно использовать при использовании из с аналогичными эффектами:
>>> из fibo import fib as fibonacci >>> фибоначчи (500) 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377
Примечание
Из соображений эффективности каждый модуль импортируется только один раз на интерпретатор.
сессия. Следовательно, если вы меняете свои модули, вы должны перезапустить
интерпретатор — или, если это только один модуль, который вы хотите протестировать в интерактивном режиме,
используйте importlib.reload () , e.грамм. import importlib;
importlib.reload (имя модуля) .
6.1.1. Выполнение модулей как скриптов
Когда вы запускаете модуль Python с
python fibo.py <аргументы>
код в модуле будет выполнен, как если бы вы его импортировали, но с __name__ установлен на "__main__" . Это означает, что, добавив этот код в
конец вашего модуля:
, если __name__ == "__main__":
import sys
выдумка (Int (SYS.ARGV [1]))
вы можете сделать файл пригодным для использования как скрипт, а также как импортируемый модуль, потому что код, который анализирует командную строку, запускается только в том случае, если модуль выполняется как «главный» файл:
$ python fibo.py 50 0 1 1 2 3 5 8 13 21 34
Если модуль импортирован, код не запускается:
Это часто используется либо для обеспечения удобного пользовательского интерфейса для модуля, либо для в целях тестирования (запуск модуля в качестве сценария выполняет набор тестов).
6.1.2. Путь поиска модуля
Когда импортируется модуль с именем spam , интерпретатор сначала ищет
встроенный модуль с таким именем. Если не найден, то ищет файл
с именем spam.py в списке каталогов, заданном переменной
node.js — вызвать «локальную» функцию в module.exports из другой функции в module.exports?
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- реклама Обратитесь к разработчикам и технологам со всего мира
- О компании

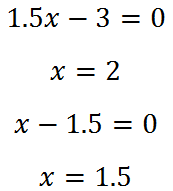 ледующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля:
ледующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля: