Тема консультации для учителей математики 8 класса по учебнику Л. Г. Петерсон, Н. Х. Агаханова, А. Ю. Петровича, О. К. Подлипского, М. В. Рогатовой, Б. В. Трушина. на январь: «КВАДРАТИЧНАЯ ФУНКЦИЯ»
Тема консультации для учителей математики 8 класса
по учебнику Л. Г. Петерсон, Н. Х. Агаханова, А. Ю. Петровича, О. К. Подлипского, М. В. Рогатовой, Б. В. Трушина.
на январь:
«КвадраТИЧНАЯ ФУНКЦИЯ»
1. Дидактической основой непрерывного курса математики «Учусь учиться» является дидактическая система деятельностного метода обучения «Школа 2000…». Ее главной особенностью является то, что знания не даются учащимся в готовом виде, а организуется их самостоятельное открытие детьми. Такой подход обеспечивает высокий уровень математической подготовки, развивает мышление учащихся, их способности, повышает интерес к изучению математики, обеспечивают личностные и метапредметные результаты образования, соответствующие ФГОС.
2. В соответствии с планированием учебного материала по курсу математики «Учусь учиться» для 8 класса в январе заканчивается изучение первого параграфа главы «Квадратичная функция» (см. консультацию на декабрь) и начинается изучение ее второго параграфа.
3. Тематическое планирование
В соответствии с принципом минимакса дидактической системы деятельностного метода «Школа 2000…» организовать работу по данному учебнику возможно в условиях различных учебных планов образовательных учреждений.
Программа 8 – 9 класса строится так, что она может быть использована для изучения школьного курса алгебры на основном и предпрофильном (углубленном) уровнях. Заметим, что предложенное учебное содержание обеспечивает возможность работы по курсу алгебры «Учусь учиться» для 8–9 классов учащихся разного уровня подготовки. Благодаря увлекающей форме подачи материала и нарастающей сложности задач, предлагаемых как для разбора в классе, так и для самостоятельной проработки дома, каждый учитель или сам ученик может выбрать тот уровень, который необходим и достаточен для достижения поставленных индивидуальных целей.
Это может быть как довольно поверхностное понимание изучаемых вопросов математики, которое обеспечит лишь успешную сдачу государственной итоговой аттестации, так и более глубокая проработка, позволяющая заложить прочный фундамент для более глубокого понимания сложных разделов не только основной, но и старшей школы.
Тематическое планирование по изучению курса 8 класса разработано в двух вариантах на 102 ч и на 170 ч. Вы можете скачать тематическое планирование на 3 ч в неделю и на 5 ч в неделю, обратившись к содержанию консультации на сентябрь.
Отметим, что на сегодняшний момент этот учебник может стать дополнительным в работе учителя.
4. Методические рекомендации к организации учебного процесса
Глава 4. Квадратичная функция
§2. Квадратичная функция
Четвертая глава посвящена изучению ключевой для школьного курса функции – квадратичной. Эта функция рассматривается в неразрывной взаимосвязи следующих вопросов: квадратное уравнение – квадратичная функция – квадратное неравенство.
Это позволяет получить учащимся целостную картину: они понимают, как решение квадратных уравнений связано с графиком квадратичной функции, видят, как свойства квадратичной функции помогают при решении квадратных неравенств.
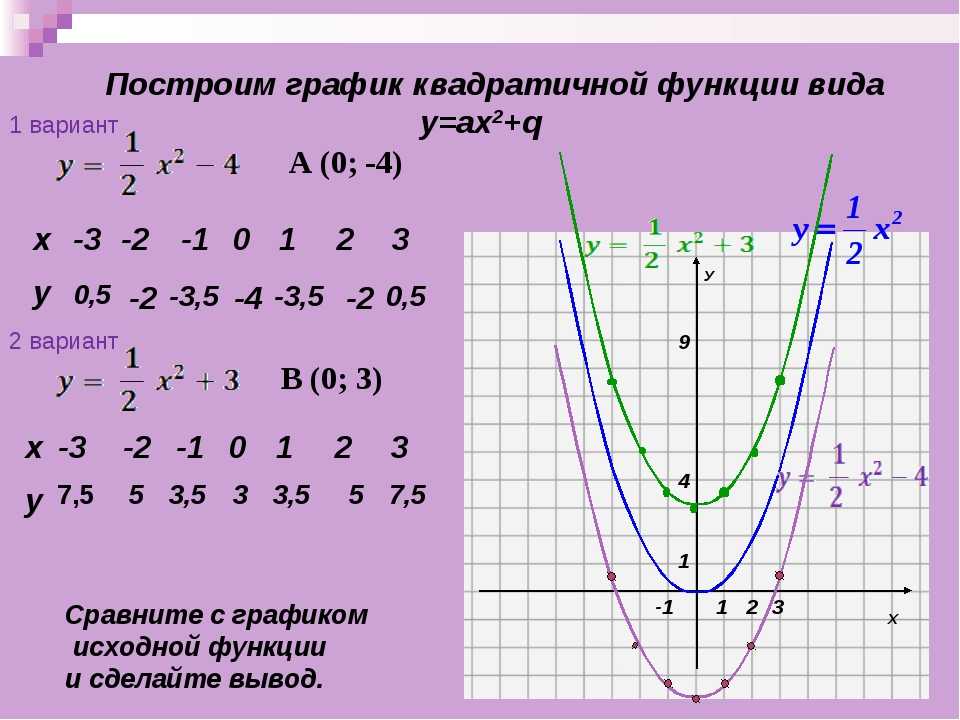
Во втором параграфе четвертой главы учащиеся изучают квадратичную функцию. Учащиеся уже знакомы с функцией y = x2, теперь они изучают функции вида y = ax2; y = ax2 + h; y = a (x– d)2 , после чего знакомятся с квадратичной функцией y = ax2 + bx + c. Учащиеся выявляют два способа построения графика квадратичной функции: с помощью выделения полного квадрата и с помощью вычисления координат вершины параболы. В соответствии с принципом вариативности при построении графика квадратичной функции учащиеся могут использовать любой из выявленных ими способов. При углубленном изучении курса восьмиклассники учатся находить наибольшее и наименьшее значения квадратных трехчленов на заданном отрезке.
При этом они опираются на изученные ими свойства графика квадратичной функции.
5. Основные содержательные цели. Организация самостоятельной деятельности учащихся по открытию новых знаний.
§2. Квадратичная функция
4.2.1. Функции y = ax2; y = ax2 + h; y = a (x– d)2 их графики.
Основные содержательные цели:
1) Познакомить учащихся с функциями y = ax2, y = ax2 + h и y = a (x– d)2; выявить свойства этих функций.
2) Сформировать умение строить график функций y = ax2 + h, y = a (x– d)2 и y = a(x – d)2 + h путем сдвига вдоль координатных осей графика функции y = ax2.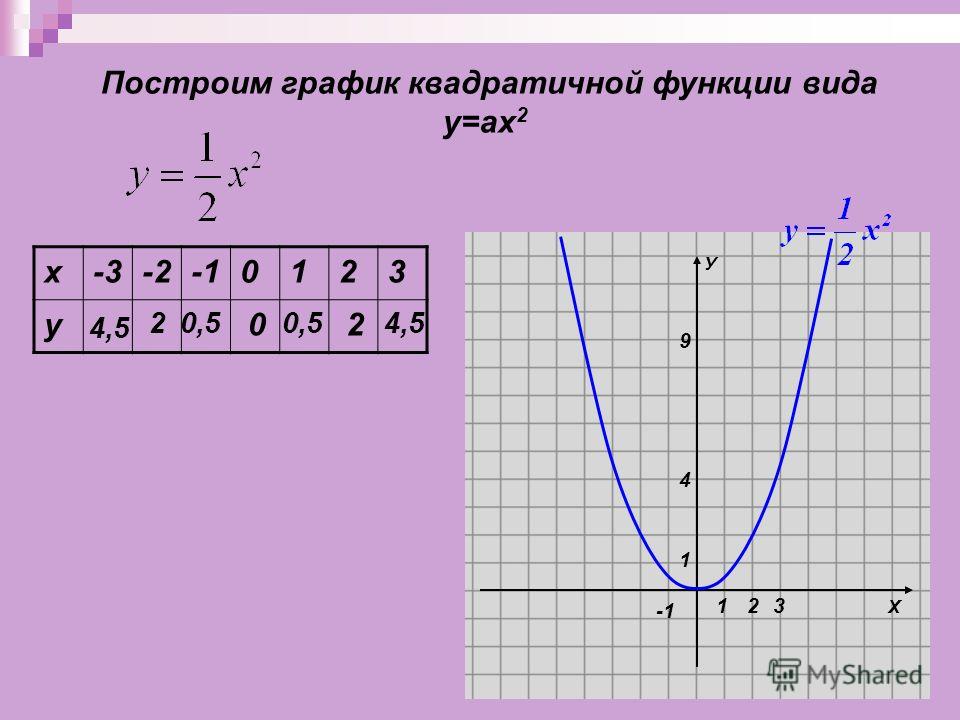
3) Тренировать умение решать текстовые задачи, сводящиеся к квадратным уравнениям и закрепить умение выполнять преобразование выражений с корнями, строить кусочно-заданные функции.
Для актуализации понятия параболы и свойств функции y = x2 можно использовать №444. Для самостоятельного открытия функции y = ax2 и выявления ее свойств рекомендуется использовать № 445. Для самостоятельного открытия способа построения графика функции y = ax2 + h рекомендуется использовать № 447, а функции y = a (x– d)2 – №448.
П. 4.2.2. Квадратичная функция y = ax2 + bx + c.
Основные содержательные цели:
1) Сформировать понятие квадратичной функции y = ax2 + bx + c.
2) Выявить свойства квадратичной функции и сформировать умение строить график функции.
3) Познакомить учащихся со способом вычисления координат вершины параболы.
4) Сформировать опыт применения понятий: промежутки возрастания и убывания функции, четность функции.
5) Подготовить изучение способа решения квадратных неравенств.
6) Повторить способ построения графиков функций y = ax2 + h, y = a (x– d)2 и y = a(x – d)2 + h и закрепить умение решать системы линейных неравенств с одним и двумя неизвестными.
Для введения понятия квадратичной функции можно использовать №462 – №463. Для самостоятельного открытия способа построения графика квадратичной функции путем выделения полного квадрата рекомендуется выполнить № 464 – №465.
П.4.2.3.* Наибольшее и наименьшее значение квадратного трехчлена
Основные содержательные цели:
1) Построить алгоритм нахождения наименьшего (наибольшего) значения квадратного трехчлена на отрезке [А; В] и сформировать умение его применять
2) Подготовить изучение способа решения квадратных неравенств.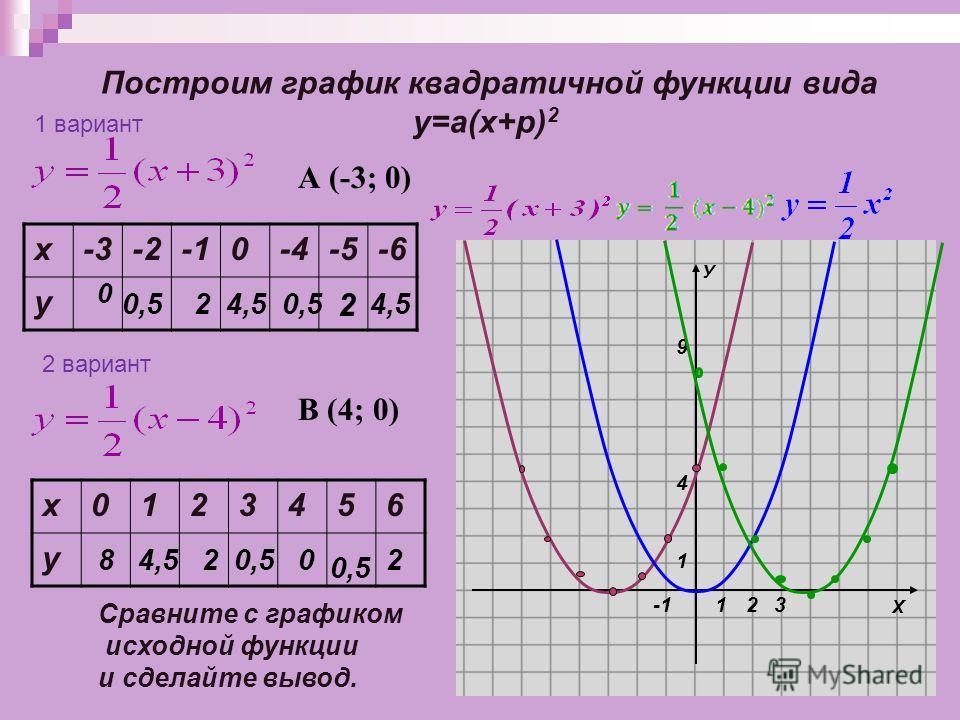
3) Тренировать умение вычислять координаты вершины параболы. Закрепить умение выполнять преобразования выражений с корнями.
Для самостоятельного открытия учащимися способа нахождения наименьшего (наибольшего) значения квадратного трехчлена на отрезке рекомендуется выполнить №482 – №484.
Мы предлагаем скачать примеры решения заданий второго параграфа данной главы.
6. Методические рекомендации по планированию уроков
При изучении второго параграфа четвертой главы планированием предусмотрены уроки ОНЗ, структура которых обеспечивает выполнение учащимися целого комплекса универсальных учебных действий. Рассмотрим способ организации урока ОНЗ на примере содержания пункта 4.2.1. «Функция у=аx² , у=аx² + h, у=k(x – d)² и их графики».
В этом пункте учащиеся знакомятся с функциями у = ax2, y = ax2 + h и y = a (x– d)2; выявляют свойства этих функций.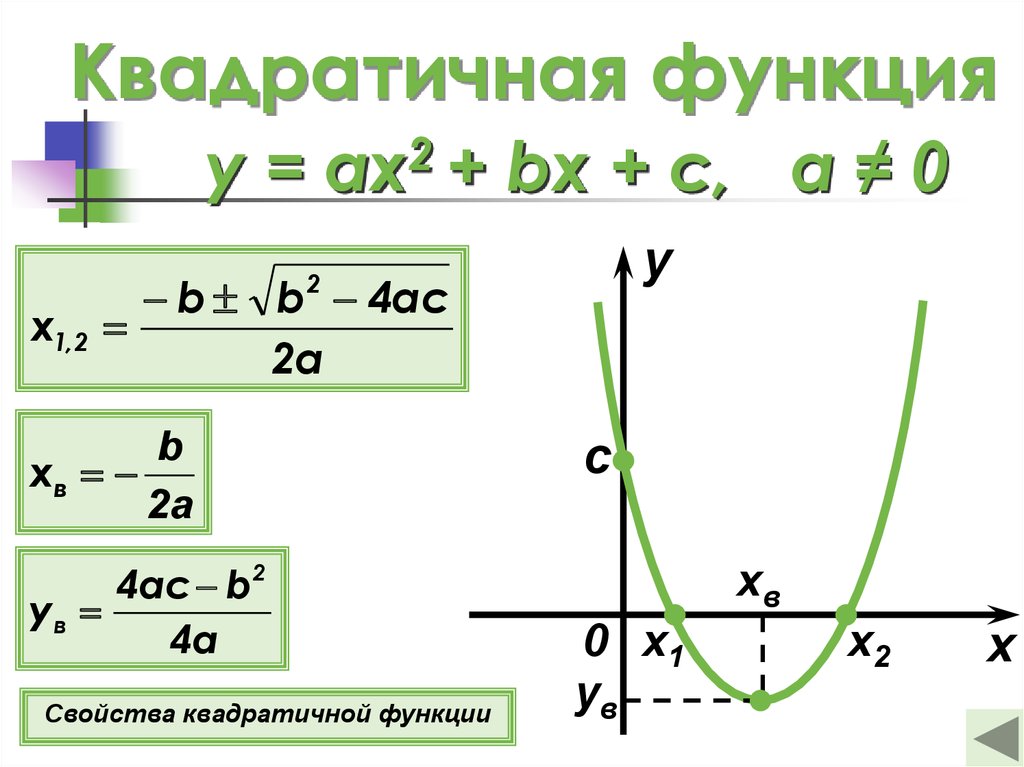
Они учатся строить график функций y = ax2 + h, y = a (x– d)2 и y = a(x – d)2 + h путем сдвига вдоль координатных осей графика функции y = ax2.
Урок открытия новых знаний выстраивается в соответствии с требованиями технологии деятельностного метода Л.Г. Петерсон. На этапе мотивации учитель может предложить пояснить смысл высказывания Галилея, из всех возможных ответов учеников следует остановиться на понятии функции. Далее учитель может попросить учащихся сделать предположения о тематических рамках урока.
После чего учитель организует актуализацию нужных для открытия знаний с помощью выполнения задания №444. Далее учащихся следует познакомить с функцией у = ax2 (для организации побуждающего диалога можно использовать задания № 445 (1, 2)) и ее свойствами (используется текст учебника на стр.114 – 115).
Для самостоятельного открытия способа построения графиков функций y = a(x – d)2 и у = ax2 + h рекомендуется использовать систему заданий №№ 447 – 448. При этом на этапе реализации проекта можно разбить учащихся на группы и поставить перед ними различные задачи: часть класса составляет способ построения графика y = ax2 + h, а другая часть – способ построения y = a (x– d)2. После чего на этапе защиты полученных ими результатов способы, составленные учащимися, объединяются в единый эталон. В менее подготовленном классе можно поступить иначе: учащиеся будут открывать самостоятельно только способ построения графика y = ax2 + h, а со способом построения графика функции y = a (x– d)2 учитель познакомит учащихся в подводящем диалоге (можно использовать текст учебника).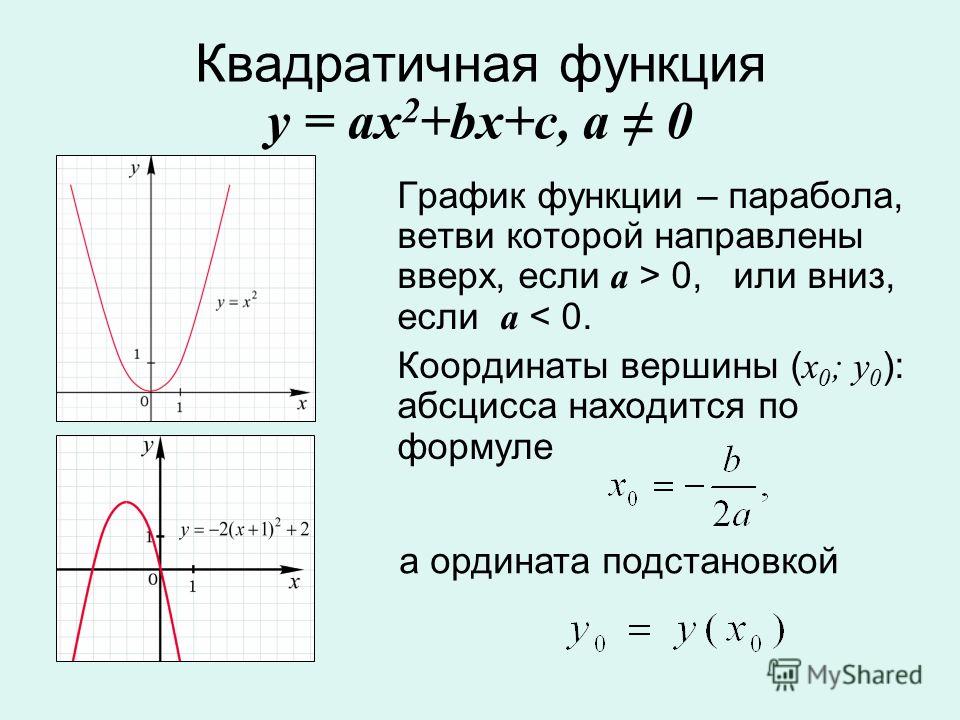
Рассмотрим пример структуры открытия нового знания:
1. Новое знание: способ построения графиков функций y = a(x – d)2 и у = ax2 + h путем сдвига графика у = ax2.
2. Актуализация.
Повторить: понятие функции y = x2.
Ввести: понятие функции y = аx2 ; свойства функции у = ax2 и ее графика.
3. Задание на пробное действие:
Укажите способ построения графика функции у = 2(х – 1)2 и y = 2x2 + 5 без использования таблицы.
4. Фиксация затруднения:
Я не могу указать способ построения графика функции у = 2(х – 1)2 и y = 2x2 + 5 без использования таблицы.
Я не могу обосновать, что указанный мною способ верный.
5. Фиксация причины затруднения:
Не известен способ построения графиков функций y = a(x – d)2 и у = ax2 + h без использования таблицы.
6. Цель учебной деятельности:
Выявить еще один способ построения графиков функций y = a(x – d)2 и у = ax2 + h.
7. Фиксация нового знания:
Учащиеся должны выявить способ построения графиков функций y = a(x – d)2 и у = ax2 + h путем сдвига вдоль координатных осей графика функции y = ax2.
Открыть новое знание учащиеся могут, анализируя частные примеры формул y = ax2 + h, y = a (x– d)2 с формулой y = ax2 и сравнивая графики этих функций, построенные по точкам. Организовать это открытие можно с использованием текста заданий №№ 447 – 448. Сначала учащиеся используют №447 (способ построения графика y = ax2 + h), затем №446 (способ построения y = a (x– d)2).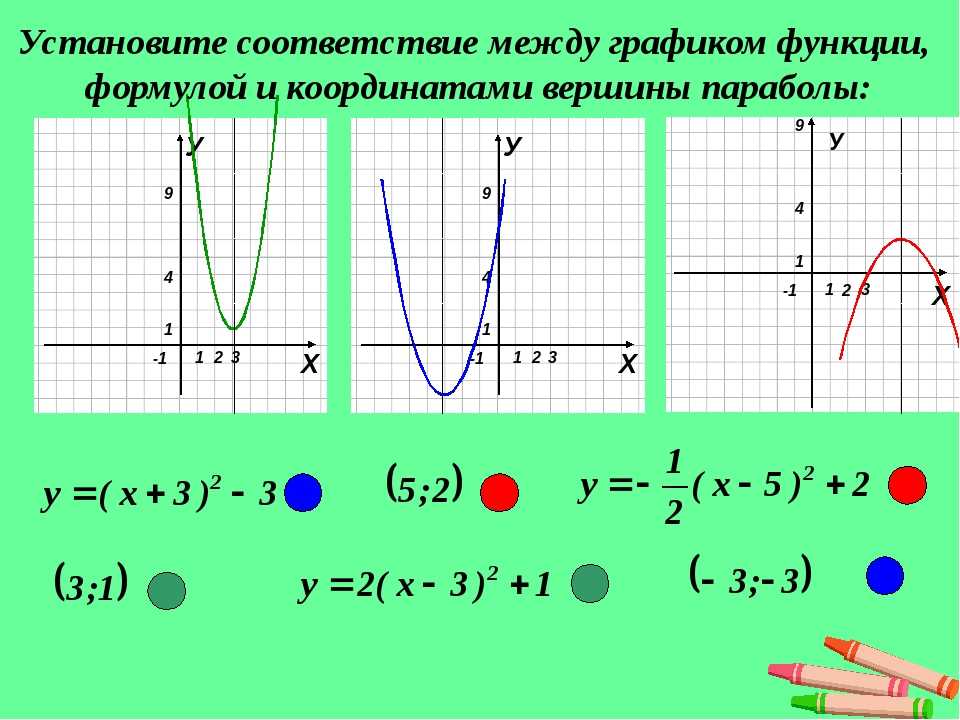
На этапе первичного закрепления рекомендуется выполнить задание №450 (а, б), 451 (а), для самостоятельной работы учащимся можно предложить №450 (в), 451 (б).
На этапе включения в систему знаний учитель предлагает учащимся № 451 (в), после чего формулируется алгоритм построения графика y = a(x – d)2 + h . Затем можно выполнить № 452(а), а в более подготовленном классе можно выполнить № 452 (б).
На этапе рефлексии можно вернуться к эпиграфу и предложить учащимся прокомментировать его с точки зрения содержания сегодняшнего урока. После чего учащимся предлагается оценить процесс и результат своей работы на уроке.
При наличии времени рекомендуется разбить рассмотренный выше урок на два урока, тогда на первом учащиеся будут самостоятельно открывать функцию у = ax2 и ее свойства (для организации открытия рекомендуется использовать задание № 445). Второй урок будет посвящен открытию способа построения графика y = a(x – d)2 + h.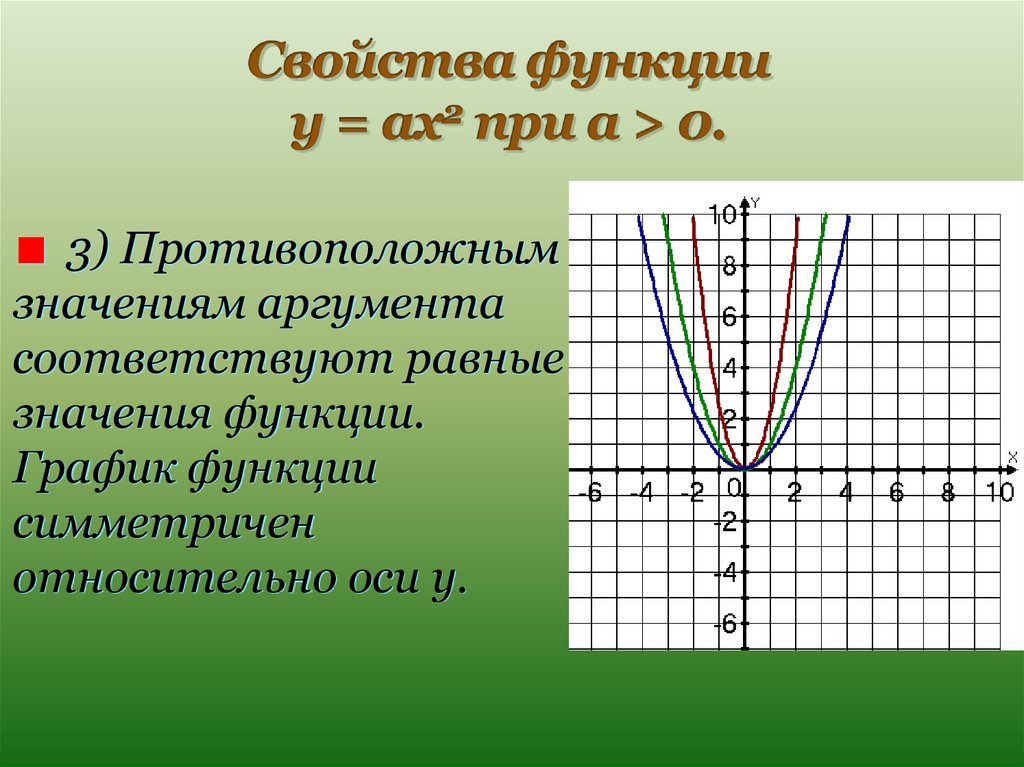
Сначала учащиеся используют №447 (способ построения графика y = ax2 + h), затем №446 (способ построения y = a (x– d)2). Далее, используя задание №449, или в побуждающем диалоге составляется алгоритм построения графика y = a(x – d)2 + h.
Кроме урока открытия нового знания, основные структурные элементы которого рассмотрены выше, планированием предусмотрены и другие типы уроков: уроки рефлексии тренировочного и коррекционного типа, где учащиеся вырабатывают и закрепляют свое умение применять новые понятия и способы действий, учатся самостоятельно выявлять и исправлять свои ошибки, корректировать свою учебную деятельность.
Уважаемые коллеги! Предлагаем вам скачать решение некоторых задач на смекалку, которые входят в данный параграф.
2 + bx + c = 0$Где a ≠ 0, b, c — действительные числа.
Так как каждая функция имеет свой особый график, то и квадратичная тоже.
График любого квадратного уравнения представляет собой параболу . Парабола — это набор точек на плоскости, которые все одинаково удалены от заданной линии, называемой директрисой, и заданный фокус точки не находится на этой линии.
На поведение этого графа влияет множество аспектов, поэтому начнем с самого простого.
Обратите внимание, что у нас только старший коэффициент отличен от нуля. И он равен ровно единице. Поскольку мы до сих пор не знаем, как именно выглядит этот график, мы начнем с рисования множества точек и посмотрим, куда это нас приведет. 92$. И это именно тот результат, которого мы могли ожидать, потому что, если вы возьмете большое число в качестве своего старшего коэффициента, функция будет быстро расти, а значит, она будет выглядеть уже.
Вершина параболы с одним старшим коэффициентом всегда будет в точке (0, 0).
С другой стороны, если ваш ведущий коэффициент будет числом меньше единицы (но все же положительным числом), ваш график будет выглядеть шире, потому что значения функции будут расти намного медленнее.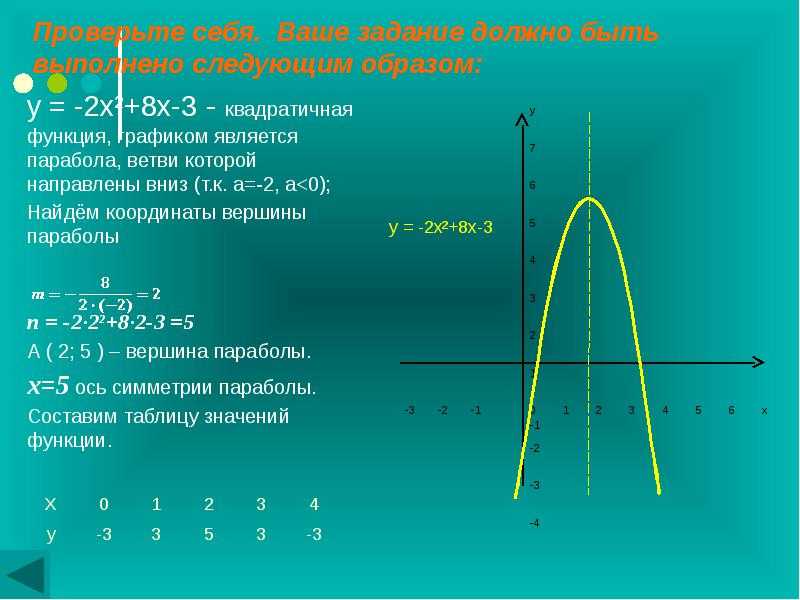
Теперь нарисуем график функции 92 – 2x$
Снова возьмем некоторое множество точек и посчитаем в них значение функции.
Отсюда мы не можем точно нарисовать нашу параболу, потому что мы мало о ней знаем. В первом случае, который мы показали, мы знали, что вершина параболы будет в центре и что ее график будет симметричен относительно оси y. Теперь мы знаем, что ничего из этого не относится к этому графику.
Первое, что вам нужно сделать, это найти вершину. x – координата вершины параболы любого вида находится по формуле:
$ V_x = – \frac{b}{2a}$
Когда вы знаете координату x, вы можете просто ввести ее в функцию и получить координату y.
Для этой функции: $\a = 1$, $\b = – 2$, значит
$V_x = 1$
и
$V_y = f(V_x) = 1$
Второе. что полезно знать при построении графика квадратного уравнения — это нули. Нули — это точки, в которых график делит ось x пополам.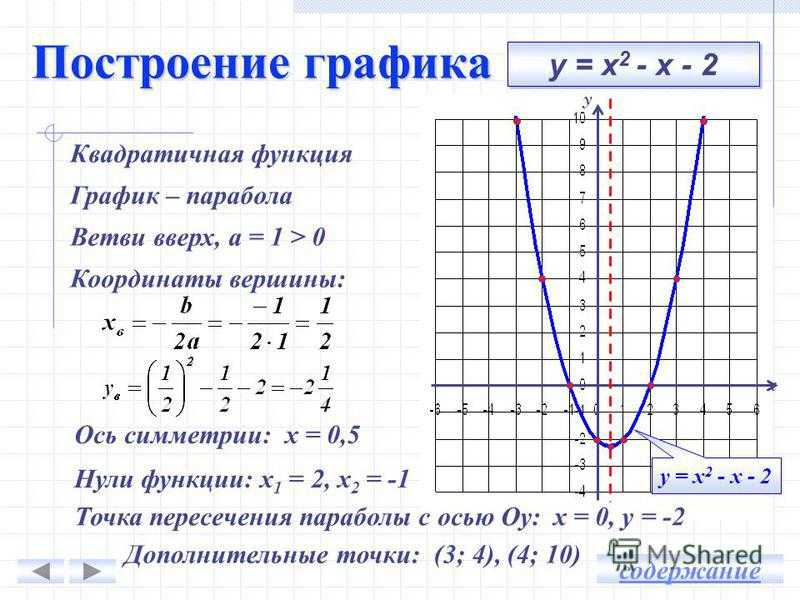
Вы получаете эти очки, вычисляя f(x) = 0 и вычисляя нули полученного вами квадратного уравнения. 92 – 4x + 3 = 0$
$\ x = \frac{(4 +- \sqrt[2](16-24))}{4}$
Мы получили мнимые решения. Это всегда будет означать, что наш график не делит ось x пополам. Поскольку вы уже знаете свою вершину, вы знаете линию, относительно которой симметричен ваш график. Все, что вам нужно, это еще несколько точек, которые вы вычисляете, и вы можете нарисовать свой график. Чтобы быть точным, вы также можете рассчитать, где ваш график будет пересекать ось Y пополам в точке, где x = 0, или, в нашем случае, в точке (0, 3).
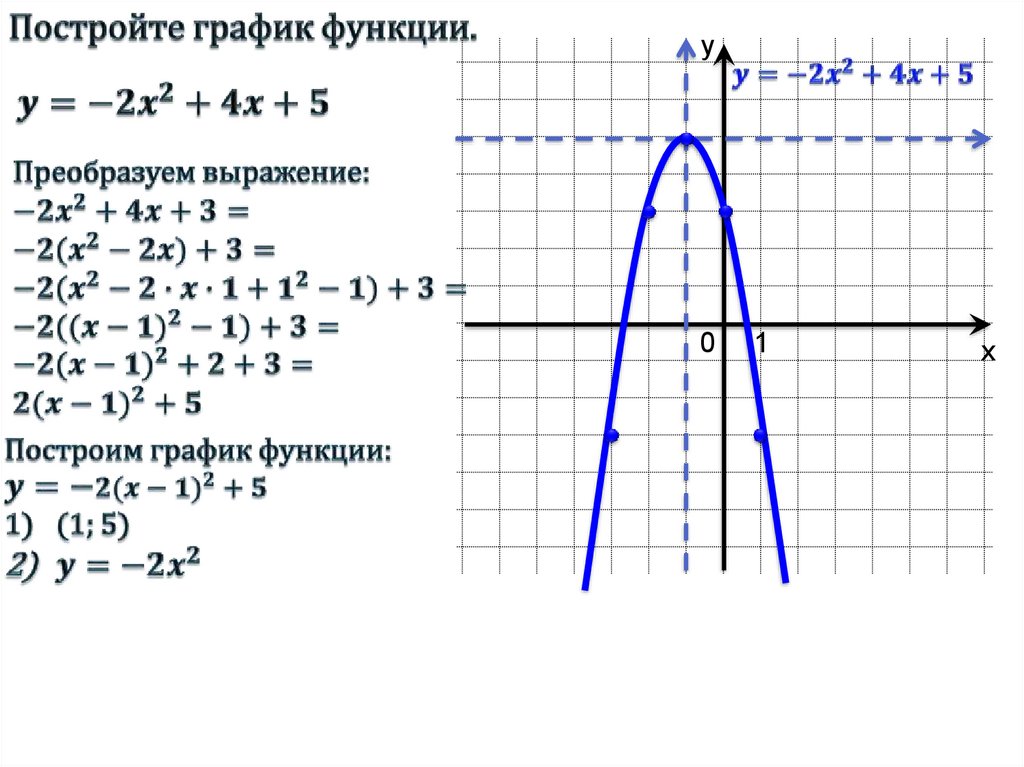
92$ переводится на 1 вправо по оси x и на 3 по оси y – вверх.График Квадратичные функции — Стандартная форма (1,7 миб, 975 попаданий)
График Квадратичные функции — Форма вершины (1,8 миб, 956 хиты)
График. 854 просмотров)
Пошаговое руководство по построению графика квадратичной функции
от Каталин Дэвид
Чтобы нарисовать график функции в декартовой системе координат
системы нам нужны две перпендикулярные линии xOy (где O –
точка пересечения x и y), называемая «координатными осями».
и единица измерения.
Точка в этой системе имеет две координаты.
M(x, y): M — название точки, x — абсцисса, отсчитываемая от Ox, а y — ордината, отсчитываемая от Oy.
Две координаты представляют расстояния от точки до двух осей.
Если рассмотреть функцию f: A -> B (A — область определения определение, B — домен), то точка, найденная на графике функция имеет вид P(x, f(x)).
Пример 92-\frac{\Delta}{4a}$
, где Δ = b 2 — 4ac
Если a > 0, минимальное значение f(x) будет $-\frac{\Delta}{4a}$, которое получается, если $x=-\frac{b}{2a}$.
Граф будет
Если a < 0, максимальное значение f(x) будет $-\frac{\Delta}{4a}$
который получается, если $x=-\frac{b}{2a}$.
График будет вогнутая парабола с вершиной $V(-\frac{b}{2a};-\frac{\Delta}{4a})$.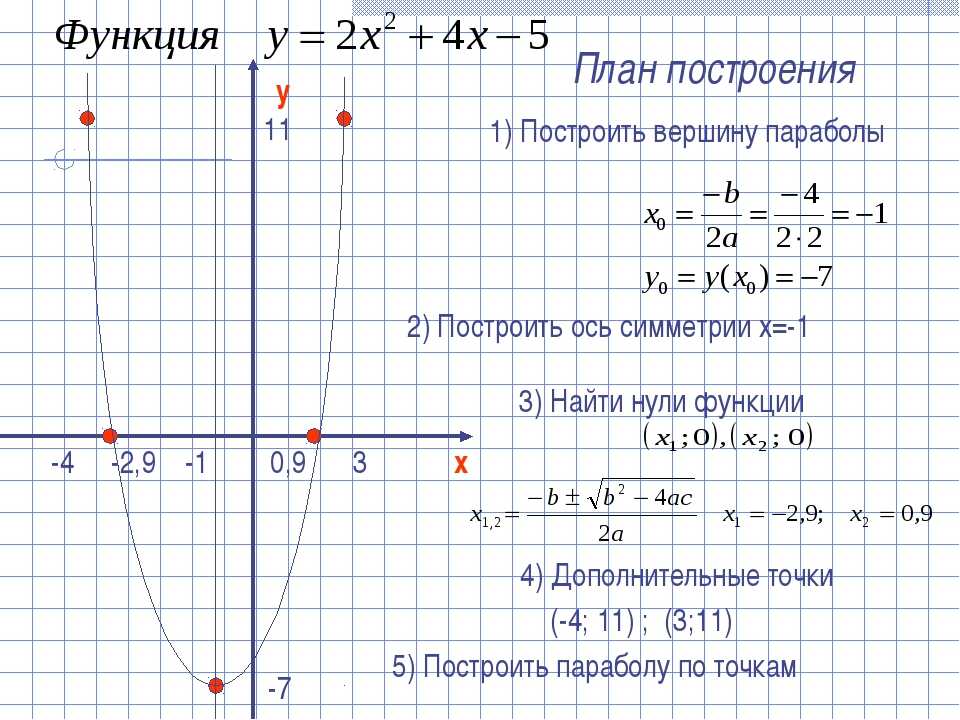
Парабола симметрична относительно прямой, пересекающей $x=-\frac{b}{2a}$,
которая называется «осью симметрии» .
Вот почему, когда мы присваиваем значения x , мы
выбирать значения, симметричные относительно $-\frac{b}{2a}$.
При построении графика очень важны точки пересечения с осями координат.
|. Точка найдена на Ox ось имеет вид P(x, 0) , потому что расстояние от нее до Ox
равно 0. Если точка найдена и на Ox , и на графике функции, то она также форма P(x, f(x)) ⇒ f(x) = 0 .Таким образом, чтобы найти координаты точек пересечения Ox с осью , мы должны решить уравнение f(x)=0 . Получаем уравнение a 2 + bx + c = 0 .
Решения уравнения зависят от знака Δ = б 2 — 4ас .
Имеем следующие ситуации:
1) Δ < 0
уравнение не имеет решений в R (множество действительных чисел) график не пересекает Ox .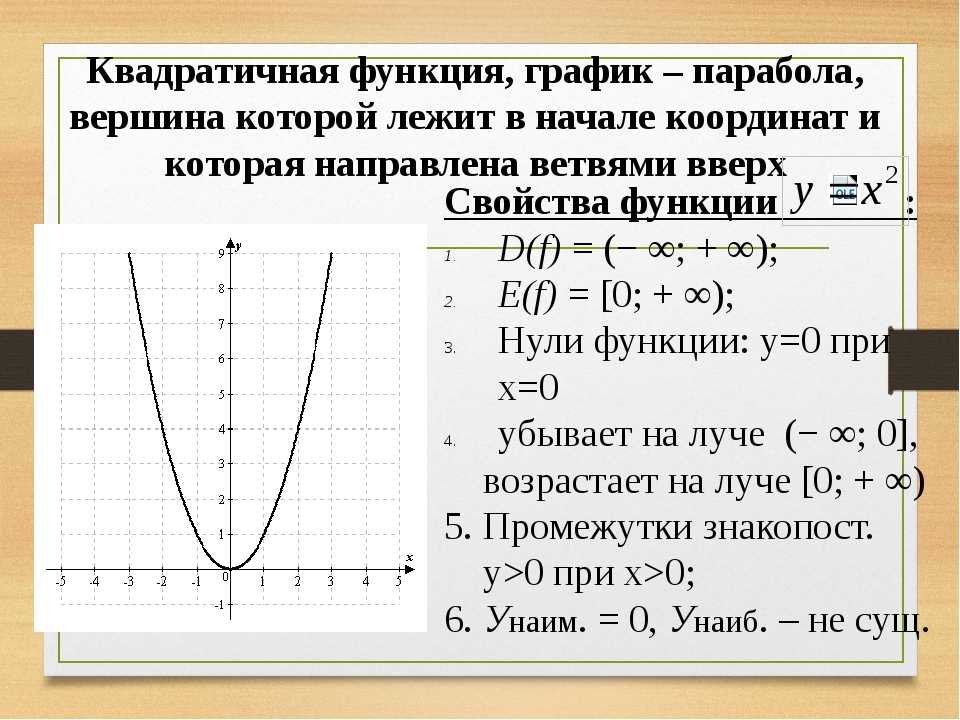
Форма графика будет:
или
2) Δ = 0
уравнение имеет два равных решения $x_1=x_2=-\frac{b}{2a}$
График касается оси Ox в вершине параболы. Форма графика:
3) Δ > 0
уравнение будет иметь два разных решения.
$x_1=\frac{-b-\sqrt{\Delta}}{2a}$ и $x_2=\frac{-b+\sqrt{\Delta}}{2a}$
График функции будет пересекать ось Ох в точках М(х 1 и Ох . Вид графика будет:
или
||. Точка найдена на Oy 9Ось 0199 имеет форму R(0, y) , потому что расстояние от нее до Oy равно 0 . Если точка находится и на Oy , и на графике функции, то она также имеет вид R(x, f(x)) ⇒ x = 0 ⇒ R(0, f(0)) .
В случае квадратичной функции
f(0) = a×0 2 + b×0 + c ⇒ R(0, c).
Необходимые шаги для построения графика квадратичной функции
f: R → R
f(x) = ax 2 + бх + в
1.
Рисуем таблицу переменных, в которую записываем некоторые важные значения для x .
2. Находим координаты вершины $V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
3. Также запишем 0 в таблице и симметрию 0 относительно $-\frac{b}{2a}$.
или
4. Определяем точку пересечения Ох с осью, решая уравнение f(x)=0 и в таблице запишем х 1 и х 2 .
∆ > 0 ⇒
Δ < 0 ⇒ точек пересечения нет. В этом случае мы выберем два удобных значения, симметричных относительно $-\frac{b}{2a}$
Δ = 0 ⇒ граф касается Ox прямо в своей вершине. Мы снова выберем два удобных значения, симметричных относительно $-\frac{b}{2a}$. Чтобы лучше определить форму графика, мы можем также выбрать другие пары значений для 9.0196 x , но они также должны быть симметричны относительно $-\frac{b}{2a}$.
5. Записываем все эти значения в системе координат и строим график, соединяя точки.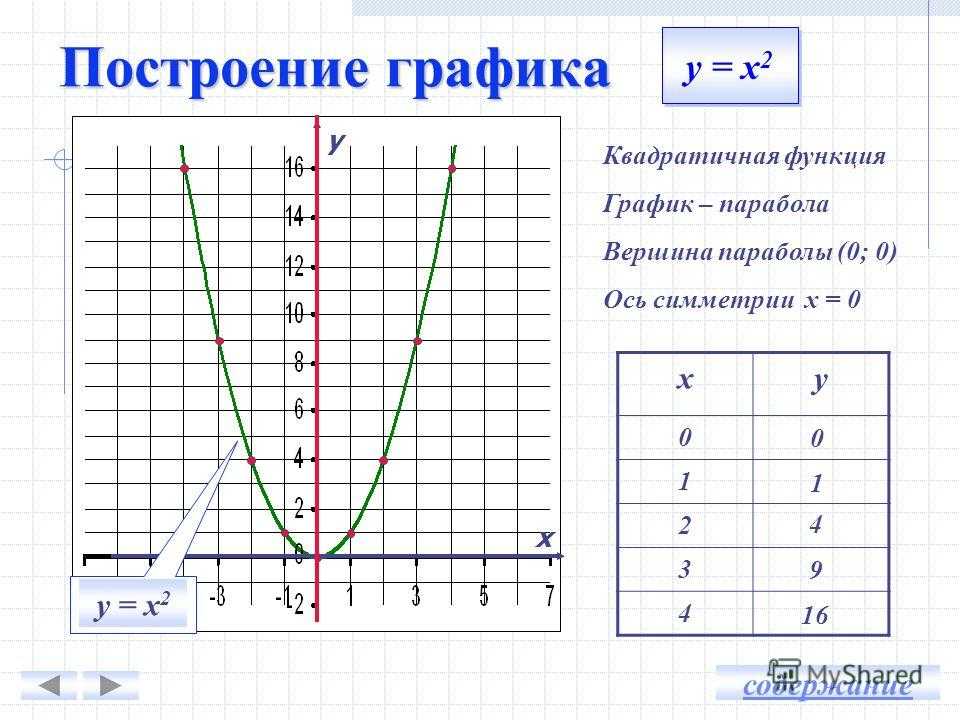
Пример 1
f: R → R
f(x) = x 2 — 2x — 3
a = 1, b = -2, c = -3
Δ = b 2 — 4×a×c = (-2) 2 — 4×1×(-3) = 16
$-\frac{b}{2a}=\frac{2}{2}=1$
⇒ V(1; -4)
1. $-\frac{\Delta}{4a}=-\frac{16}{4}=-4$
2. f(0) = -3
Симметрия 0 относительно 1 равна 2.
f(2) = -3
Δ = 16 > 0
$x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{2 -4}{2}=-1$
$x_1=\frac{2+4}{2}=3$
Мы нашли точки:
A(-1; 0)
B(0; -3)
V(1; -4)
C(2; -3)
D(3; 0)
График будет:
Пример 2
f: R → R
f(x) = -x 2 — 2x + 8
a = -1, b = -2, c = 8
Δ = b 2 — 4×a×c = (-2) 2 — 4×(-1)×8 = 36
$-\frac{b}{2a}=\frac{2}{-2}= -1$
⇒ V(-1; 9)
1. $-\frac{\Delta}{4a}=-\frac{-36}{-4}=9$
2. f(0) = 8
f(-2) = 8 (симметричность 0 относительно -1 равна -2)
3.
f(x) = 0 ⇒ -x 2 — 2x + 8 = 0
Δ = 36
x 1 = 2 и x 2 = -4
A(-4; 0)
B(-2; 8)
V(-1; 9)
C(0; 8)
D(2; 0)
Пример 3
f: R → R
f(x) = x 2 — 4x + 4
a = 1, b = -4, c = 4
Δ = b 2 — 4×a×c = (-4 ) 2 — 4×1×4 = 0
$-\frac{b}{2a}=\frac{4}{2}=2$
⇒ V(2; 0)
1. $-\frac{\Delta}{4a}=0$
2. f(0) = 4
f(4) = 4 (симметричность 0 относительно 2 равна 4)
3. f(x) = 0 ⇒ x 2 — 4x + 4 = 0
Δ = 0
x 1 = x 2 = $-\frac{b}{2a}$ = 2
А(-2; 9)
Б(0; 4)
С(4; 4)
Д(5; 9)
Пример 4
f: R → R
f(x) = -x 2 + 4x — 5
a = -1, b = 4, c = -5
Δ = b 2 — 4×a×c = 4 2 — 4×(-1)×(-5) = 16 — 20 = -4
$-\frac{b}{2a}=\frac{-4}{-2}=2$
⇒ V(2; -1)
1.