Ряды распределения — задачи
Ряды распределения — задачиСтатистика
Искать…
- Вы здесь:
- Главная
- Статистика
- Ряды распределения — задачи
Ряды распределения — задачи
Практическое занятие. Тема: Ряды распределения.
Задача с решением по рядам динамики
На экзамене по истории студенты получили оценки:
3 4 4 4 3 4
3 4 3 5 4 4
5 5 2 3 2 3
3 4 4 5 3 3
5 4 5 4 4 4
Построить дискретный вариационный ряд распределения студентов по баллам.
Ход решения задачи:
Строим дискретный вариационный ряд распределения:
|
Оценка |
Количество студентов получивших такую оценку |
В % к итогу |
|
2 |
2 |
6,7 |
|
3 |
9 |
30 |
|
4 |
13 |
43,3 |
|
5 |
6 |
20 |
|
Итого |
30 |
100 % |
Дискретный вариационный ряд изображается графически в виде полигона распределения:
Кол-во студентов
процент к итогу
оценка
1 2 3 4 5
Наибольшее количество студентов получило оценку 3 и 4.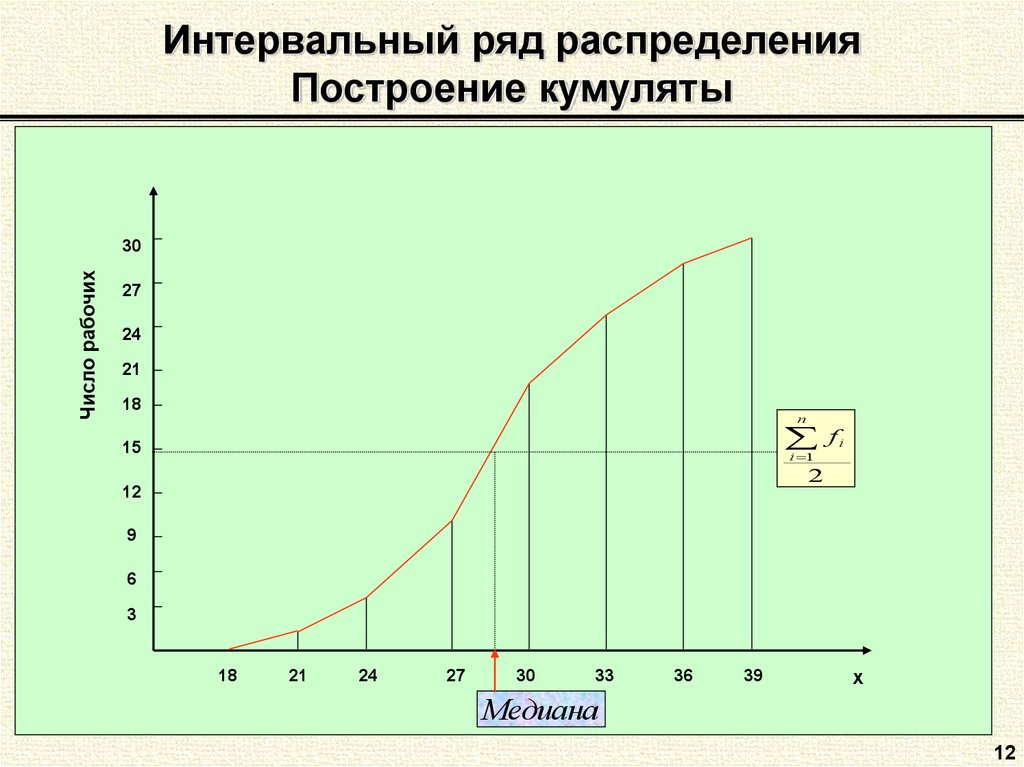
Теперь преобразуем дискретный ряд в интервальный, выделив для этого, например, 3 группы учащихся по полученным за экзамен оценкам; определяем величину интервала и группы:
1 гр. 2+1=3 (2-3)
2 гр. 3+1=4 (3-4)
3 гр. 4+1=5 (4-5)
|
Группы студентов по полученным оценкам |
Количество студентов |
В % к итогу |
Накопленные частоты |
|
2-3 |
11 |
36,7 |
11 |
|
3-4 |
13 |
43,3 |
24 |
|
4-5 |
6 |
20 |
30 |
|
Итого |
30 |
100 |
Гистограмма
Число студентов в % к итогу
нтервалы
интервалы 1 2 3 4 5
Кумулята
Накопленные частоты
интервалы 1 2 3 4 5
- Назад
- Вперед
Добавить комментарий
Задачи по темам:
5.
3. Решение задачПример 1. Производится три независимых опыта, в каждом из которых событие A появляется с вероятностью 0,4. Рассматривается случайная величина X – число появлений события A в трех опытах. Построить ряд и многоугольник распределения, функцию распределения случайной величины X. Найти: 1) вероятность событий: A={X<2}; B={}; C={}; 2) математическое ожидание , дисперсию , среднее квадратическое отклонение случайной величины X.
Решение. Случайная величина X может принимать значения ; ; ; . Соответствующие им вероятности найдем, воспользовавшись формулой Бернулли. При n=3, ; имеем: ; ;
; .
Отсюда ряд распределения случайной величины X имеет вид:
(Контроль: ).
Многоугольник распределения случайной величины X представлен на рис.6.
Рис. 6 Рис. 7
Найдем функцию распределения F(x). По определению функции распределения имеем: если , то ;
Если , то ;
Если , то ;
Если , то ;
Если , то
.
Итак,
График функции F(x) изображен на рис. 7.
1) Сначала вычислим искомые вероятности непосредственно:
;
;
.
Эти же вероятности найдем, воспользовавшись формулами:
и . Тогда ;
;
2) Найдем математическое ожидание случайной величины X. Используя формулу (3), получим . Вычислим дисперсию. По формуле (6) имеем:
=0,72. Тогда среднее квадратическое отклонение .
Пример 2. Дан ряд распределения дискретной случайной величины X:
Найти моду.
Решение. Так как дискретная случайная величина X принимает значение с наибольшей вероятностью по сравнению с двумя соседними значениями, то мода случайной величины X равна 20, т. е. .
Пример 3. Дана функция
Рис. 8
Показать, что может служить плотностью вероятности некоторой случайной величины X.. Найти математическое ожидание и дисперсию случайной величины X.
Решение. Используя свойство нормированности плотности распределения, найдем, что
,
Кроме того, .
Следовательно, может служить плотностью вероятности некоторой случайной величины. Так как прямая является осью симметрии соответствующей дуги кривой (см. рис.8), то математическое ожидание случайной величины X равно , т. е. . Найдем дисперсию, воспользовавшись формулой (8). Двукратным интегрированием по частям получим:
Пример 4. Дана плотность вероятности случайной величины X;
Найти функцию распределения F(X), вероятность попадания случайной величины X в промежуток , числовые характеристики величины X: .
Решение. Найдем функцию распределения случайной величины X, для этого воспользуется соотношением (1).
Если x < 0, то .
Если x > a, то .
Итак,
По формуле (*) имеем .
Найдем математическое ожидание случайной величины X. Согласно формуле (5)
.
Теперь отыщем дисперсию. По формуле (8)
Отсюда среднее квадратическое отклонение .
Пример 5. Найти моду, медиану, математическое ожидание и функцию распределения случайной величины X с плотностью вероятности
Решение.
Найдем точку максимума функции : ; отсюда при . Точка является точкой максимума функции , так как , если и , если . Следовательно, мода .
Медиану определим из условия (9): (или ).
В данном случае по формуле (2): , т. е. .
Таким образом, приходим к уравнению: или . Отсюда, .
Воспользовавшись формулой (5), вычислим математическое ожидание случайной величины X:
Найдем функцию распределения случайной величины X.
Прежде всего заметим, что если x < 0, то
Если же то т. е. .
| < Предыдущая | Следующая > |
|---|
Таблица распределения частот: Примеры, как ее составить
- Использование счетных меток
- Включая классы
См. также: Таблица распределения частот в Excel
Пример создания таблицы распределения частот с классами смотрите в видео:
Как составить таблицу распределения частот
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Частота говорит вам как часто что-то происходило . Частота наблюдения говорит вам, сколько раз наблюдение встречается в данных. Например, в следующем списке чисел частота числа 9 равна 5 (поскольку оно встречается 5 раз):
1, 2, 3, 4, 6, 9, 9, 8, 5, 1, 1, 9, 9, 0, 6, 9.
Таблицы могут отображать либо категориальные переменные (иногда называемые качественными переменными), либо количественные переменные (иногда называемые числовыми переменными). Вы можете думать о категориальных переменных как о категориях (таких как цвет глаз или марка собачьего корма), а количественные переменные — как о числах.
Если вы не совсем уверены в различии, см.: Качественное или количественное? Как сказать.
В следующей таблице показано, какие методы планирования семьи использовали подростки в Квененг, Западная Ботсвана. Левая колонка показывает категориальная переменная (Метод), а правый столбец — это частота — количество подростков, использующих этот конкретный метод (изображение предоставлено KSU).
Таблицы частотного распределения дают вам моментальный снимок данных, чтобы вы могли найти закономерности. Беглый взгляд на приведенную выше таблицу распределения частот показывает, что большинство подростков вообще не используют никаких противозачаточных средств.
Наверх
Пример 1
Контрольные метки часто используются для составления таблицы частотного распределения. Например, предположим, что вы проводите опрос нескольких домохозяйств и выясняете, сколько у них домашних животных. Результаты: 3, 0, 1, 4, 4, 1, 2, 0, 2, 2, 0, 2, 0, 1, 3, 1, 2, 1, 1, 3. Глядя на эту цепочку чисел, глаза разбегаются. глаз; таблица частотного распределения облегчит понимание данных.
Шаги
Чтобы составить таблицу распределения частот, сначала напишите категории в одном столбце (количество домашних животных):
Далее, подсчитайте числа в каждой категории (из результатов выше).
Например, число ноль встречается в списке четыре раза, поэтому поставьте четыре метки «||||»:
Наконец, подсчитайте метки и запишите частоту в последнем столбце. Частота просто общая. У вас есть четыре подсчета для «0», поэтому поставьте 4 в последней колонке:
Вернуться к началу
Как нарисовать таблицу частотного распределения (чуть более сложный пример)
Таблица частотного распределения — это один из способов организации данных, чтобы они имели больше смысла. Например, предположим, что у вас есть список оценок IQ для одаренного класса в определенной начальной школе. баллов IQ : 118, 123, 124, 125, 127, 128, 129, 130, 130, 133, 136, 138, 141, 142, 149, 150, 154. что-либо. Вы можете нарисовать таблицу частотного распределения , которая даст лучшее представление о ваших данных, чем простой список.
Как нарисовать таблицу распределения частот: шаги.
Нужна помощь с домашним заданием? Посетите нашу обучающую страницу!
Часть 1: Выбор классов
Шаг 1: Выясните, сколько классов (категорий) вам нужно.
Жестких правил о том, сколько классов выбрать, нет, но есть несколько общих рекомендаций:
- Выберите от 5 до 20 классов. Для приведенного выше списка IQ мы выбрали 5 классов.
- Убедитесь, что у вас есть несколько предметов в каждой категории. Например, если у вас есть 20 предметов, выберите 5 классов (4 предмета в каждой категории), а не 20 классов (что даст вам только 1 предмет в каждой категории).
Примечание : Существует более математический способ выбора классов. Формула: log(наблюдения)\log(2). Вы бы округлили ответ до следующего целого числа. Например, log17\log2 = 4,1 будет округлено до 5. (Спасибо Айману Масри за этот совет).
Часть 2: Сортировка данных
Шаг 2: Вычтите минимальное значение данных из максимального значения данных. Например, в нашем списке IQ выше было минимальное значение 118 и максимальное значение 154, поэтому:
154 – 118 = 36
Шаг 3: Разделите ответ на шаге 2 на количество классов, которое вы выбрали на шаге 1.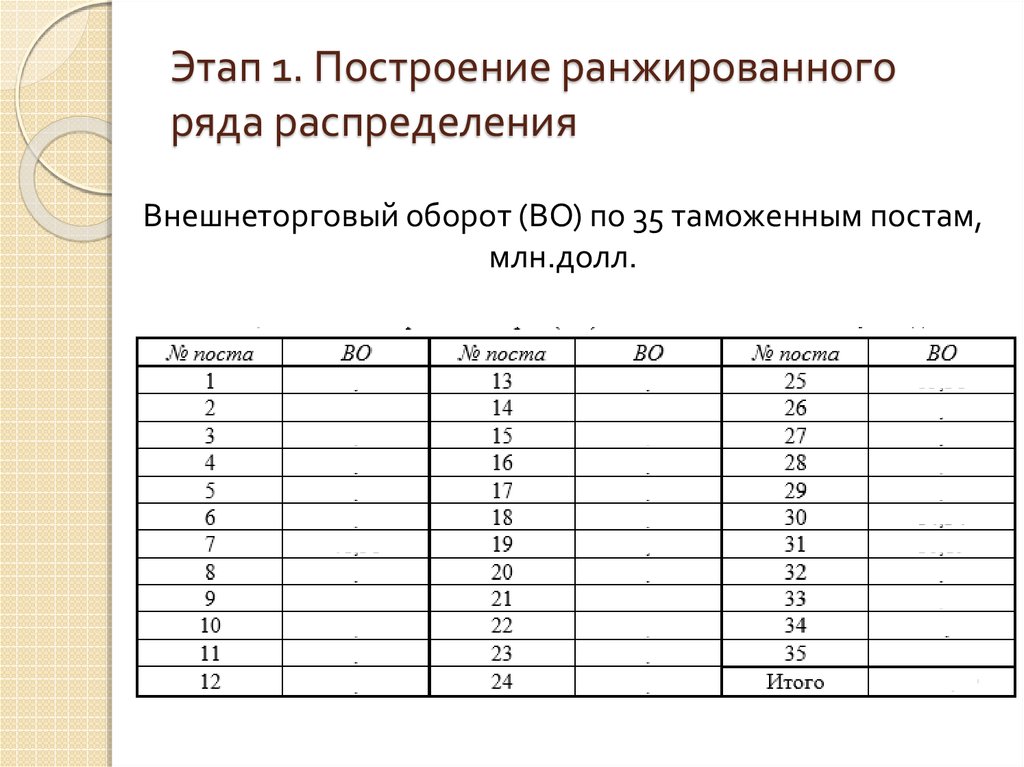
36 / 5 = 7,2
94:093 с шага 3 до целого числа, чтобы получить ширину класса. При округлении 7,2 становится 8 .
Шаг 5: Запишите наименьшее значение для первого минимального значения данных:
Наименьшее значение 118
Шаг 6: Добавьте ширину класса из Шага 4 в Шаг 5, чтобы получить следующий более низкий класс лимит:
118 + 8 = 126
Шаг 7: Повторите шаг 6 для других минимальных значений данных (другими словами, продолжайте добавлять ширину вашего класса к вашим минимальным значениям данных), пока вы не создадите количество классов, которые вы выбрали на шаге 1. Мы выбрали 5 классов, поэтому наши 5 минимальных значений данных: Шаг 8: Запишите верхние пределы класса. Это самые высокие значения, которые могут быть в категории, поэтому в большинстве случаев вы можете вычесть 1 из ширины класса и добавить это к минимальному значению данных.
Например:
118 + (8 — 1) = 125
118 — 125
126 — 133
134 — 141
142 — 149
150 — 157
3. Выполнение таблицы вверх
Шаг 9: Добавить второй столб количество предметов в каждом классе и пометьте столбцы соответствующими заголовками:
| IQ | Номер |
|---|---|
| 118-125 | |
| 126-133 | |
| 134-141 | |
| 142-149 | |
| 150-157 |
Шаг 10: Подсчитайте количество предметов в каждом классе и поместите общее количество во второй столбец. Список значений IQ: 118, 123, 124, 125, 127, 128, 129, 130, 130, 133, 136, 138, 141, 142, 149, 150, 154.
| IQ | Номер |
|---|---|
| 118-125 | 4 |
| 126-133 | 6 |
| 134-141 | 3 |
| 142-149 | 2 |
| 150-157 | 2 |
Вот как легко нарисовать таблицу распределения частот!
Нравится объяснение? Ознакомьтесь с нашей статистикой, как забронировать, с сотнями других пошаговых решений, таких как это!
Совет .
Если вы работаете с большими числами (например, сотнями или тысячами), округлите шаг 4 до большого целого числа, которое легко превратить в классы, например 100, 1000 или 10 000. То же самое с очень маленькими числами — вы можете округлить до 0,1, 0,001 или аналогичного деления.
Вернуться к началу
Ссылки
Гоник, Л. (1993). Мультяшный путеводитель по статистике. HarperPerennial.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Таблица распределения частот: примеры, как ее составить» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/descriptive-statistics/frequency-distribution-table/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области.
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Школа данных — Таблица 101: Как строить гистограммы
Таблица 101: Как строить гистограммы
Уильям Гишени
Всем привет!Эта неделя в Data School была полностью посвящена разбору всех расширенных функций Tableau. Лекции Энди были столь же поучительными, сколь и сложными, от выяснения всех изящных способов получить максимальную отдачу от табличных вычислений до создания нелепых вложенных операторов if с расчетами уровня детализации. Однако сегодняшнее руководство посвящено простому, но мощному типу диаграммы: гистограмме.
Гистограмма представляет собой диаграмму, состоящую из прямоугольников, площадь которых пропорциональна частоте переменной, а ширина равна интервалу классов. Другими словами, они показывают распределение ваших данных, разбивая их на ячейки одинакового размера и назначая каждой ячейке полосу, пропорциональную количеству точек данных, которые помещаются в эту ячейку.
Что еще круче в функциях Tableau, когда речь идет о гистограммах, так это возможность динамически изменять размер ячейки с помощью параметров. Да! Нет необходимости воссоздавать новую диаграмму, если вы хотите углубиться в распределение ваших данных или агрегировать их, вы можете просто использовать ползунок на вашем элементе управления параметрами. Имея все это в виду, давайте углубимся в суть: как вы все равно делаете эту диаграмму?
В сегодняшнем руководстве Tableau я буду использовать некоторые данные о рождаемости, которые дают информацию об общем количестве рождений, среднем возрасте их матерей и т. д. Наша цель будет состоять в том, чтобы создать гистограмму, показывающую распределение среднего числа рождений. масса.
Шаг 1. Создание бинов
Чтобы построить нашу гистограмму, нашим первым шагом будет создание бинов, в которых затем будут распределены наши точки данных.
- Этот шаг настолько прост, насколько это возможно: нажмите на значок курсора Измерьте интересующих вас элементов на панели данных — у меня это Средний вес при рождении в фунтах — прокрутите вниз до параметра Создать и выберите Корзины.
Шаг 2. Настройка управления параметрами Все, что вам нужно сделать, это щелкнуть меню Size of Bins и выбрать Создать новый параметр .
- После того, как вы нажмете Создать новый параметр , вам будет предложено другое окно конфигурации. Вы можете оставить все предварительно заполненные значения — Tableau оценит, какими должны быть минимальный, максимальный и размер шага — или настроить их по своему вкусу. Я собираюсь изменить минимальное значение и размер шага на 0,01 и оставить максимальное значение как есть. Это означает, что пользователь моей информационной панели сможет использовать элемент управления параметрами для настройки размера бинов с шагом 0,01, с минимальным размером 0,01 и максимальным размером 0,449..
- Не забудьте дать вашему параметру имя, чтобы ваш будущий пользователь мог легко понять, что он регулирует, когда он играет с ползунком!
- Нажмите «ОК», и вы должны увидеть, что ваш элемент управления параметрами появляется в правом верхнем углу экрана.
