Как правильно решать неравенства: Основные правила решения неравенств — урок. Алгебра, 9 класс.

Содержание

Учимся решать уравнения и неравенства

Учимся решать уравнения и неравенства
Л. Денищева, Н. Карюхина, Т. Михеева, Москва
10 – 11 классы

В течение всех лет обучения в школе решают различные виды уравнений и неравенств. Не сосчитать, сколько линейных, квадратичных, дробно-рациональных уравнений и неравенств решили ученики за эти годы. Однако в старших классах при решении показательных или логарифмических уравнений, когда после преобразований ученик переходит к алгебраическому уравнению, он все равно допускает ошибки. Это неудивительно: решение уравнений и неравенств – один из наиболее трудных вопросов. Действительно, чтобы правильно решить уравнение или неравенство, нужно уметь проводить тождественные преобразования входящих в него выражений, нужно уметь безошибочно вычислять, нужно знать, какие способы решения уравнений (неравенств) в каких случаях целесообразнее применить.
Очевидно, что уравнения и неравенства, изучаемые в старшей школе, осваиваются учащимися хуже, так как на их рассмотрение отводится незначительное количество часов, а при их решении ученику необходимо владеть комплексом умений, полученных в основной школе, а также новыми знаниями, связанными с каждым из новых видов уравнений.

Такого объема упражнений, который обычно предлагается в учебниках по алгебре и началам анализа для 10–11-х классов, явно недостаточно для формирования умения решать показательные, логарифмические и тригонометрические уравнения (неравенства). Восполнить этот пробел поможет пособие «Учимся решать уравнения и неравенства» (авторы: Л.О. Денищева, Н.В. Карюхина, Т.Ф. Михеева).

Это учебное пособие состоит из трех глав.

В главе 1, состоящей из пяти параграфов, рассматриваются стандартные методы решения тригонометрических, показательных и логарифмических уравнений и неравенств. В начале главы (§§ 1, 2) учащимся напоминается решение простейших уравнений и неравенств. Для приведения знаний в систему и для обеспечения их лучшего запоминания этот материал сведен в таблицу и снабжен графическими иллюстрациями.

Приведем фрагмент таблицы, относящийся к решению простейших тригонометрических неравенств.

Параграфы 1, 2 снабжены большим числом тренировочных упражнений. Например, учащимся предлагается решить 25 простейших тригонометрических неравенств, в которых задействованы все табличные значения тригонометрических функций. Выполнение этих заданий не должно затруднить учащихся и занять у них много времени, так как предполагается, что при решении школьники будут активно использовать рабочую таблицу и поэтому им не нужно каждый раз чертить тригонометрический круг и делать необходимый рисунок. Для решения неравенства учащийся из таблицы выбирает нужный рисунок («а» или «б»), вычисляет необходимое значение арксинуса (или другой тригонометрической функции) и записывает ответ.

В этих же параграфах (§§ 1, 2), кроме простейших, предлагается решить уравнения и неравенства, которые за один «шаг» (с помощью элементарных алгебраических преобразований) приводятся к простейшим. Здесь строится «лесенка сложности» заданий, в ходе выполнения которых закрепляется решение простейших уравнений и неравенств.

Например, тригонометрические уравнения здесь представлены следующими задачами. (Пояснение. Нумерация дана как в учебном пособии.)

Далее (§ 3) рассматривается применение при решении тригонометрических, показательных и логарифмических уравнений (неравенств) формул тождественных преобразований выражений. В теоретической части параграфа обсуждается вопрос о возможном расширении или сужении области определения выражения в ходе его тождественного преобразования. Даются примеры преобразований, приводящих к потере корней уравнения (неравенства).

Приведем пример, где учащимся показывается, какое преобразование нужно выполнить и как записать преобразованное выражение так, чтобы в ходе решения не потерять корни уравнения.

В § 3 содержится более 100 уравнений и неравенств, легко сводящихся к простейшим в результате тождественных преобразований выражений, входящих в уравнение (неравенство). Материал этого параграфа ориентирован таким образом, чтобы обеспечить обучающую функцию. В этой связи задания разбиты по содержательно-смысловым блокам. Выделены три тематических блока: показательные уравнения (неравенства), логарифмические уравнения (неравенства) и тригонометрические уравнения (неравенства). Каждый из названных блоков имеет свою структуру. Например, в блоке, содержащем логарифмические уравнения, выделены следующие содержательно-смысловые части:

применение основного логарифмического тождества, применение формул логарифма произведения или частного, применение формул логарифма степени. В соответствии с этим предлагается такая система уравнений.

Решите логарифмические уравнения

I. Примените основное логарифмическое тождество

II. Примените формулы логарифма произведения и частного

III. Примените формулу логарифма степени
В §§ 4, 5 представлены известные из основной школы методы решения уравнений: сведение исходного уравнения (с помощью замены) к квадратному и разложение на множители.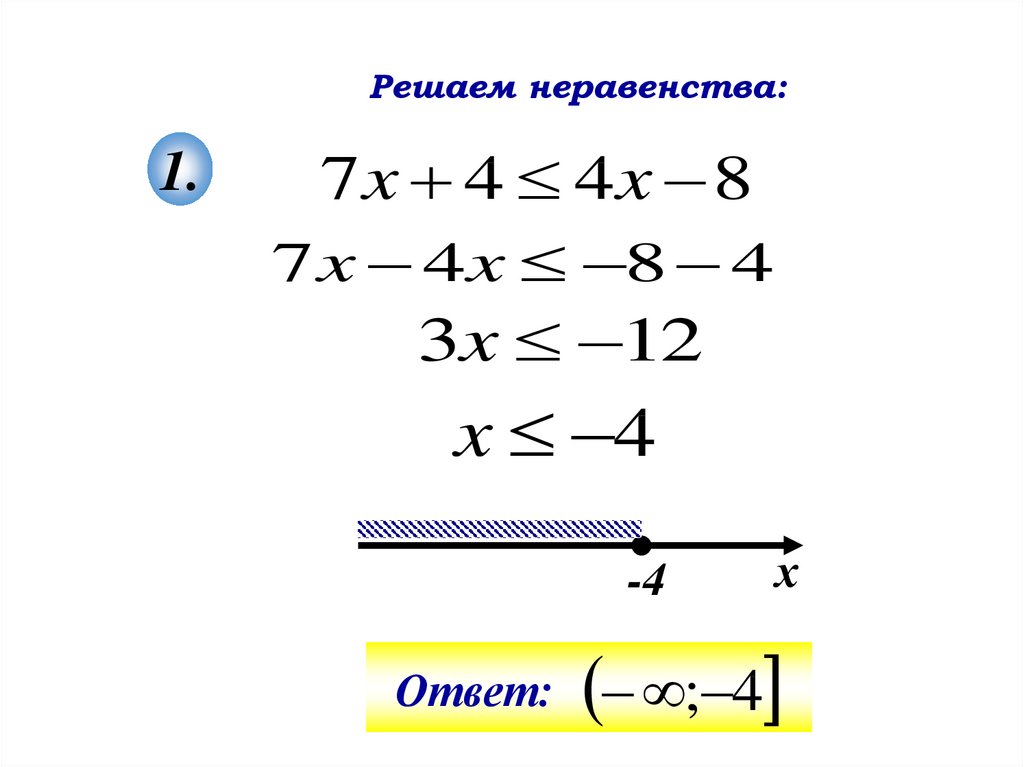
В теоретической части этих параграфов приводятся возможные образцы записи решений; вводятся алгоритмические предписания, в которых реализуется данный метод решения.
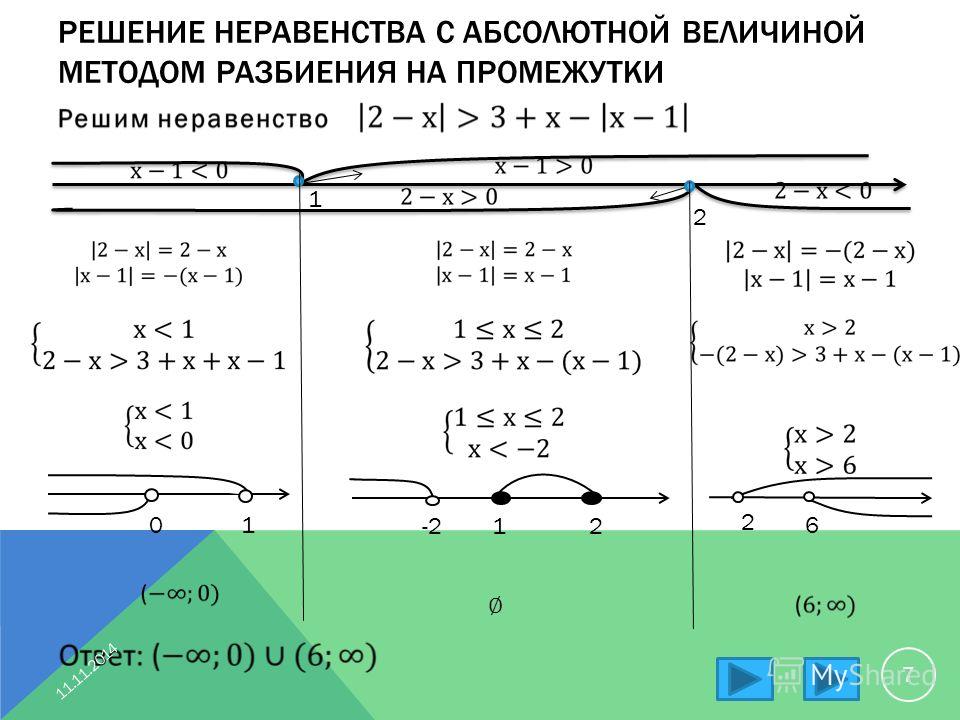
Поскольку в программе по математике и в практике преподавания меньше внимания уделяется решению неравенств, то в теоретической части этих параграфов сделан больший акцент на рассмотрение различных ситуаций, возникающих при решении неравенств. Так, например, показывается, что исходное неравенство может быть равносильно не только неравенству, но и системе неравенств, или совокупности неравенств.
Например, решим неравенство
Заметим, что 150 уравнений и неравенств, представленных в этих параграфах для самостоятельного решения, предполагают прямое применение указанных методов, вырабатывая на этом этапе обучения стереотип решения.
В главе 2 рассматриваются нестандартные методы решения уравнений и неравенств, основанные на использовании свойств функций. Здесь предложены два параграфа:

§ 1. Ограниченность; § 2. Монотонность. Заданиям для самостоятельного решения предпослан разъяснительный текст, в котором раскрывается сущность указанного метода, показывается образец рассуждений, в которых для нахождения корней уравнения (неравенства) используется свойство функции. Приведем фрагмент объяснения из § 2.
§ 2. Монотонность
Рассмотрим задание: найти положительные корни уравнения
2^x = – x² + 3.
Как и к уравнениям из предыдущего параграфа, к этому уравнению нельзя применить стандартные приемы решения. Однако один корень этого уравнения легко угадывается (x = 1). Если посмотреть на эскиз графиков функций y = 2^x и y = – x² + 3, то можно предположить, что на промежутке [0; Ч) найденное решение единственное. Действительно, на этом промежутке «получилась» единственная точка пересечения графиков функций (см.
рисунок).
Но нельзя считать задание выполненным, если не обосновать, что других положительных корней уравнение не имеет. Для доказательства заметим, что функция y = 2^x возрастает, а функция y = – x² + 3 убывает на промежутке [0; Ч), а значит каждое свое значение они принимают ровно один раз. Таким образом, «увиденный» нами корень x = 1 является единственным на заданном промежутке.
Рассмотрим неравенство
Областью определения данного неравенства является множество неотрицательных чисел. Очевидно, что на этом промежутке произведение принимает значение, равное 1, при
x = 9. Действительно,
Функции являются монотонно возрастающими, следовательно при x > 9 их значения будут больше, чем число 1, а значит и произведение также окажется большим единицы. Эти рассуждения приводят нас к заключению, что решением исходного неравенства будет промежуток [9; Ґ).
При решении этих двух заданий нами применялось свойство монотонности.
В главе 3 приведены материалы для подготовки учащихся к экзаменам – выпускному из школы и вступительному в вуз. Здесь собраны интересные и поучительные уравнения и неравенства, предлагавшиеся ранее на выпускных экзаменах за курс общеобразовательной школы и на вступительных экзаменах в педагогические и технические вузы. Задания этой главы распределены по уровню сложности, но выбор метода решения предстоит сделать ученику на основе анализа исходного уравнения или неравенства. Чтобы показать школьникам, какие наблюдения и рассуждения помогают выбрать рациональный метод решения, в начале параграфа обсуждаются подходы к решению нескольких уравнений и неравенств. Приведем пример.

Пример 3. Решить неравенство

Решение. при всех x, кроме так как Значит, исходное неравенство равносильно системе
Неравенству x² + 2x Ј 0 удовлетворяют значения промежутка [– 2; 0]. Остается исключить из него число вида Таким числом является при n = – 1 число

Эта глава содержит около 250 уравнений и неравенств, снабженных ответами, что должно помочь учащимся в проверке выполненной ими самостоятельной работы.

По вопросу приобретения данного пособия обращайтесь в издательство «Интеллект-центр».
Телефон (095) 158-66-05, или по адресу:
129515, Москва, а/я 70, Миндюку М.Б.
Решение задач с неравенствами на практике
Опубликовано 05 августа 2019
Со значением слов больше и меньше мы знакомы с ранних лет нашей жизни. Взрослея, мы учимся понимать превосходства объектов по размерам, количествам. Фактически мы учимся сравнивать числа, выясняем какое число больше либо меньше. Такие практические задачи решали еще с давних времен, тогда же и начали употреблять слова, которые обозначают результат сравнения одинаковых величин больше меньше, дешевле- дороже, легче- тяжелее, длиннее- короче, выше- ниже и т. д. На математическом языке все эти слова мы записываем с помощью общепринятых математических знаков строгого и нестрогого неравенства.
Хотя между уравнением и неравенством есть много общего, но основное отличие все таки существует- это то, что решением неравенства чаще всего бывают бесконечные множества чисел, которые при подстановке в исходное неравенство дадут правильный результат. Суметь найти все решения либо доказать, что таких решений нет- значит решить неравенство правильно. Сделать полную проверку ответов как в случае с уравнениями не возможно, поэтому при их решении нужно переходить к равносильным неравенствам, которые имеют одни и те же решения. Во избежание получения ненужных решений либо их потери, нужно всегда следить за равносильностью преобразований, которые дают возможность находить решения, выполняя такие действия с ними, которые приведут его к более простому решению.
Как решать неравенства мы учимся еще в первых классах, начиная с самых простых, постепенно переходя в старших классах школы к более сложным- линейным, квадратным, дробно-рациональным, логарифмическим, показательным, неравенствам с параметром.
Школьная программа математики изучает основные методы их решения такие, как метод интервалов для рациональных и дробно- рациональных функций, метод равносильных переходов, основные методы решения показательных и логарифмических решений, использование свойств функций при их решении.
Решение задач с неравенствами на практике так же довольно часто встречаются при решении экономических задач, которые сводятся к исследованию и решению системного линейного неравенства с большим числом переменных. При помощи решения такого рода неравенств экономистам стало возможно находить самые выгодные планы размещения ресурсов и моделировать процессы производства.
Что бы достойно сдать экзамены и поступить в престижное высшее учебное заведение, нужно систематически решать различного рода неравенства, так как такого рода задания разного уровня сложности присутствуют в ЕГЭ по математике. Для того, чтобы иметь достаточный уровень подготовки лучше обратиться к помощи высококвалифицированных преподавателей, которые с помощью современных научных методик смогут подготовить Вас онлайн к успешной сдаче экзаменов. Основным преимуществом занятий через интернет является то, что Вы сможете заниматься без ограничений в удобное для Вас время, в любом уголке нашей огромной страны.
Смотрите также:
Предыдущая новость Следующая новость
Другие матералы рубрики:
17.09.2018 Глава Рособрнадзора рассказал родителям об экзаменах и оценочных процедурах
10.10.2018 Стобалльники выскажут свое мнение о качестве школьного образования
27.02.2019 Глава Рособрнадзора рассказал о планах ввести в ЕГЭ оценку soft skills-креативности выпускников
Архив новостей
2023Последние новостиФевральЯнварь
Как решать неравенства с двумя переменными: алгебра
Привет всем и счастливой среды! Сегодня мы рассмотрим, как решать неравенства с двумя переменными. Вы можете услышать это в своем классе как «Одновременное неравенство» или «Система неравенства», все они означают одно и то же! Ключом к ответу на вопросы такого типа является умение отображать неравенства в виде графиков и знать, что решение всегда находится там, где две заштрихованные области на графике перекрывают друг друга. Мы рассмотрим пример шаг за шагом, затем в конце этого поста будут практические вопросы, которые вы можете попробовать самостоятельно. Удачных расчетов! 🙂

Как решать неравенства с двумя переменными :
Напомним, что при графическом построении линейных неравенств помните, что мы всегда хотим рассматривать неравенство как уравнение прямой в форме… за некоторыми исключениями:
1) В зависимости от того, какой тип знака неравенства мы отображаем, мы будем использовать либо пунктирную линию и незакрашенный кружок (< и >), либо сплошную линию и замкнутый кружок (> или <) и для правильного представления решения.
2) Затенение — еще одна важная особенность графического изображения неравенств. В зависимости от знака неравенства нам нужно будет либо заштриховать выше оси x ( > или > ), либо ниже оси x ( < или < ), чтобы правильно представить решение.
3) Решение: Чтобы найти решение системы неравенств, мы всегда будем искать, где перекрываются заштрихованные области обоих неравенств.
Теперь, когда мы знаем правила построения графиков одновременных неравенств, давайте взглянем на Пример !
Шаг 1: Сначала возьмем наше первое неравенство и приведем его к форме y=mx+b. Для этого нам нужно переместить 0,5х на другую сторону неравенства, вычитая его из обеих сторон. Как только мы это сделаем, мы сможем определить наклон и точку пересечения по оси Y.
Шаг 2: Прежде чем строить график, давайте теперь определим, какой тип неравенства мы здесь имеем. Так как мы работаем со знаком <, нам нужно будет использовать пунктирную линию и открытые кружки при построении графика.
Шаг 3: Теперь, когда мы определили всю необходимую информацию, давайте изобразим первое неравенство ниже:
Шаг 4: Теперь пришло время заштриховать наш график, так как это неравенство, нам нужно показать все наши потенциальные решения с затенением. Поскольку у нас есть знак «меньше» <, мы будем затенять ниже оси X. Обратите внимание, что все отрицательные значения y ниже включены слева от нашей строки. Здесь мы будем затенять.
Шаг 5: Теперь давайте начнем рисовать второе неравенство! Мы делаем это, беря второе уравнение и переводя его в форму y=mx+b. Для этого нам нужно 2x переместиться в другую часть неравенства, прибавив его к обеим частям. Затем мы можем еще больше упростить неравенство, разделив 2.
Шаг 6: Прежде чем строить график, давайте теперь определим, какой тип неравенства мы здесь имеем. Поскольку мы работаем со знаком >, нам нужно будет использовать сплошная линия и закрытые кружки при построении нашего графика.
Шаг 7: Теперь, когда мы определили всю необходимую информацию, давайте нарисуем второе неравенство ниже:
Шаг 8: Теперь пришло время заштриховать наш график. Так как у нас есть знак больше или равно >, мы будем затенять выше оси x. Обратите внимание, что все положительные значения y выше включены слева от нашей линии. Здесь мы будем затенять.
Где решение?!
Шаг 9: Решение находится там, где две заштрихованные области перекрываются. В этом случае мы видим, что две заштрихованные области перекрываются в фиолетовой части этого графика.
Шаг 10: Проверить! Теперь мы можем, наконец, проверить нашу работу. Для этого мы можем выбрать любую точку в нашей перекрывающейся фиолетовой заштрихованной области. Если выбранная нами координатная точка верна при подключении к обоим нашим неравенствам, тогда наш график правильный!
Возьмем точку (-4,-1) и подставим ее в оба исходных неравенства, где x=-4 и y=-1.
Практические вопросы:
Решения:
Остались вопросы? Без проблем! Не стесняйтесь комментировать любые вопросы ниже. Спасибо, что заглянули и удачных расчетов! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Ищу обзор графических линейных неравенств Посмотрите этот пост здесь!
Нравится:
Нравится Загрузка…
Как решать неравенства степени 3 и выше
Энциклопедия>Алгебра>Уравнения и неравенства>Неравенства>Другие виды неравенств>Как решать неравенства степени 3 и выше
При решении неравенств высших степеней используется тот же метод, что и с квадратными неравенствами, но иногда вам нужно найти хотя бы один нуль выражения, чтобы иметь возможность разложить выражение, которое вы получаете в левой части. Это можно исправить с помощью полиномиального длинного деления.
Правило
Неравенства высших степеней
1.
Соберите все члены с одной стороны, обычно с левой.
2.
Упростите выражение.
3.
Факторизация.
4.
Составьте таблицу знаков, чтобы прочитать решение. 9Пример 1 сторона руки. Затем вам нужно разложить на множители появившееся кубическое уравнение P(x). Вы делаете это, угадывая решение. Когда вы угадываете решение, естественной отправной точкой являются значения x=1,−1,2,−2,… ⁡. Вставив эти значения в кубическое выражение, вы обнаружите, что P(1)=0, что означает, что x=1 является нулем P(x). Затем вы можете использовать полиномиальное длинное деление, разделив P(x) на x−1, что даст вам квадратное выражение. Это выглядит так: x3+6×2−6>2×2−xx3+6×2−6−2×2+x>0x3+4×2+x−6>0
Решите это неравенство, как уравнение. Вы делаете это, устанавливая левую часть равной нулю. Здесь вы угадываете решение. Сначала попробуйте x=1: P(1)=(1)3+4(1)2+(1)−6=1+4+1−6=0.
К счастью, вам нужно было протестировать только одно решение. Теперь вы нашли, что x=1 является решением P(x)=0, что означает, что x=1 является нулем P(x).
No related posts.