правила сокращения, пояснение на примерах
Смысл сокращения алгебраической дроби
ОпределениеАлгебраическая дробь — дробь, числитель и знаменатель которой состоят из многочленов с буквенными множителями.
В алгебре принято считать, что обыкновенные дроби — частный случай алгебраических.
Из курса по обыкновенным дробям (математика за 3 — 5 классы) известно, что сокращение — это деление числителя и знаменателя на общий множитель. Это объяснение справедливо не только для обыкновенных дробей, но и для алгебраических. Разница заключается в том, что при сокращении алгебраической дроби общим делителем может быть не только число, но и переменная или выражение.
Часто алгебраическая дробь является сложной математической конструкцией. Сокращение позволяет упростить дальнейшие операции с дробью: сложение, умножение, сравнение и т. д.
Правило сокращения алгебраических дробей
ПравилоПри сокращении дроби руководствуются следующим правилом: числитель и знаменатель можно делить на одинаковое число, одноименные буквы или на одинаковые множители — многочлены.
Нельзя сокращать дробь на разноименные буквенные обозначения. Также нельзя делить числитель и знаменатель на переменную или цифру, входящую в многочлен, если ее нельзя вынести как общий множитель выражения.
Приведем пример правильного сокращения дроби:
и неправильного:
Вынесение общего множителя при сокращении дробей
Если числитель и знаменатель представляют собой многочлены, то при сокращении дробей общий множитель удобнее вынести за скобки, после чего разделить на него числитель и знаменатель.
Вынесение общего множителя — это запись выражения F в виде произведения PQ, где P — общий множитель, Q — результат деления выражения F на P.
Отметим, что общим делителем может быть как число или переменная, так и целое выражение.
Если при сокращении необходимо изменить знаки в выражении на противоположные, выносят (-1).
Сокращение алгебраических дробей с помощью формул сокращенного умножения
На практике часто встречаются дроби, в числителе и знаменателе которых имеются выражения в различной степени, например, квадратные, кубические.
Для таких выражений используют формулы сокращенного умножения.
Приведем упомянутые тождества:
Формула 1Разность квадратов: a2-b2=(a-b)(a+b)
Формула 2Квадрат суммы: (a+b)2=a2+2ab+b2
Формула 3Квадрат разности: (a-b)2=a2-2ab+b2
Формула 4Сумма кубов: a3+b3=(a+b)(a2-ab+b2)
Формула 5Разность кубов: a3-b3=(a-b)(a2+ab+b2)
Формула 6Куб суммы: (a+b)3=a3+3a2b+3ab2+b3
Формула 7Куб разности: (a-b)3=a3-3a2b+3ab2-b3
Сокращение алгебраических дробей с многочленами
Сокращение алгебраической дроби, числитель и знаменатель которой представляют собой многочлены, сводится к вынесению общего делителя в числителе и знаменателе. При работе с такими дробями используют один (или комбинируют оба) из представленных выше способов:
- вынесение общего множителя;
- применение формул сокращенного умножения.
Однако не все многочлены можно преобразовать по формулам сокращенного умножения или поделить на общий множитель. Если дробь нельзя упростить, то говорят, что дробь несократима.
Пояснение на примерах
Рассмотрим решения нескольких контрольных примеров по упрощению дробей. В качестве подготовки можно попробовать решить предлагаемые примеры самостоятельно.
Пример 1Тренажер. Соедините соответствующие карточки с формулами сокращенного умножения.
Пример 2Упростить дробь: 5a+25b+10a+5b+2
Решение.
Общий множитель выражения в числителе — число 5. Вынесем его за скобки: 5(a+5b+2)a+5b+2
Получили одинаковый трехчлен в числителе и знаменателе. Сократим дробь на общий делитель.
Ответ: 5
Пример 3Упростить дробь: 9×2+12xy+4y2(9x+6y)(x-y)
Решение.
Обратим внимание на числитель. Под корнем находится выражение, которое можно преобразовать в квадрат суммы. В знаменателе в множителе (9x+6y) можно вынести за скобку число 3. Выполним перечисленные операции:
(3x+2y)23(3x+2y)(x-y)
Вынесем квадрат суммы из-под корня, получим:
3x+2y3(3x+2y)(x-y)
Теперь у числителя и знаменателя есть общий делитель (3x+2y), сократим на него дробь.
Ответ: 13(x-y)
Пример 4Упростить дробь:
(4ab-a2-4b2)(5a-10b)5(a3b-6a2b2+6ab3-8b4)
Решение.
Начнем с преобразования числителя. Из первого выражения в скобках можно получить формулу квадрата разности. Для этого вынесем (-1) за скобку и поменяем знаки на противоположные. Из второго выражения можно вынести общий множитель — число 5. Перепишем дробь в виде:
(-1)·5(a-2b)2(a-2b)5(a3b-6a2b2+6ab3-8b4)
В числителе получили два одинаковых выражения, при их умножении показатели степени складываются, то есть:
-5(a-2b)35(a3b-6a2b2+6ab3-8b4)
Теперь преобразуем знаменатель. Вынесем общий множитель выражения в скобках — переменную b:
-5(a-2b)35b(a3-6a2b+6ab2-8b3)
Теперь многочлен в скобках представляет собой формулу куба разности. Перепишем дробь:
-5(a-2b)35b(a-2b)3
У числителя и знаменателя два общих делителя: число 5 и куб разности. Сократим дробь на общие множители.
Ответ: -1b
Пример 5Упростить дробь:
a2+3a3+5b2b-5a+11ac
Решение.
В числителе и знаменателе нет формул сокращенного умножения, также у числителя и знаменателя нет общего делителя. Дальнейшие преобразования невозможны.
Ответ: дробь несократима
Как писать дроби с помощью клавиатуры iPhone
Будь то письмо, документ, презентация, математическая задача или рецепт чего-либо, в какой-то момент вам может понадобиться записать десятичные дроби. Не лучше ли написать жене письмо, что нам нужно ½ кг картошки, вместо полкило картошки, не правда ли, дроби выглядят более профессионально и легче читать прямо так, научитесь делать дроби выглядят более профессионально и их легче читать непосредственно с клавиатуры.
На клавиатуре iOS нет возможности писать дроби 1/2, 1/4, 3/4 или любую другую дробь, кроме как с использованием числа, затем косой черты, а затем другого числа, и получатель должен понимать, что это означает, или вы должны написать это буквами, половина, четверть, ценник и так далее. Предполагается писать так ½ или ¼ или ¾ по крайней мере. Возможно, вам придется каждый раз копировать эти дроби из Интернета, чтобы написать их правильно.
Возможно, вам придется каждый раз копировать эти дроби из Интернета, чтобы написать их правильно.
Круто то, что на iPhone уже давно есть какое-то сочетание клавиш, а именно замена текста. Его настройка требует немного усилий, но после этого вы в любой момент можете написать дробь обычным способом, например 1/2, и она автоматически заменит ее правильной дробью. А если вам не нравится замена текста, есть другой способ.
Создавайте дроби с помощью сочетаний клавиш
Перейдите в «Настройки» — «Основные» — «Клавиатура» — затем «Замена текста».
Щелкните значок плюса (+), чтобы создать новый ярлык.
В текстовом поле «Фраза» введите дробь, которую вы вводите обычным способом, например 1/2.
В поле Аббревиатура правильно введите дробь. Нажмите «Сохранить», когда закончите.
Повторите эти шаги для любых других дробей, которые должны отображаться правильно.
Затем всякий раз, когда вы вводите дробь обычным способом и нажимаете клавишу пробела, она будет напрямую перезаписываться дробью, сохраненной в сочетаниях клавиш.
Вот наиболее распространенные дроби, которые можно использовать для замены текста.
¼
½
¾
⅐
⅑
⅒
⅓
⅔
⅕
⅖
⅗
⅘
⅙
⅚
⅛
⅜
⅝
⅞
А если вы не хотите использовать сочетание клавиш, вы можете использовать приложения для клавиатуры, которые поддерживают десятичные дроби, и это сэкономит вам усилия и время.
Или вы также можете использовать приложение клавиатуры-хамелеона, как вы знаете, приложение клавиатуры-хамелеона позволяет вам сделать свою собственную клавиатуру, и я сделал специальную клавиатуру для дробей, Вы можете скачать это здесь Затем откройте его через приложение-хамелеон.
Узнайте больше о приложении клавиатуры хамелеон в этой статье.
клавиатура хамелеон клавиатура
| Разработчик | i4islam |
Используете ли вы дроби в письме? И как ты это написал? Сообщите нам в комментариях.
المصدر:
ios.гаджетхаки
Статьи по теме
Теги:
клавиатура ВерблюдПошаговое руководство — Психометрический успех
Обновлено 16 февраля 2023 г.
Что такое дроби?
Дроби — это числовые величины, представляющие значения меньше единицы. Также известные как дробные числа, они обычно используются для измерения частей целого, например:
- Половина (1/2)
- Одна пятая (1/5)
- Две трети (2/3)
Дроби
Дроби состоят из двух чисел, одно над и одно под разделительной чертой.
Нижнее число известно как знаменатель и относится к отдельным частям целого.
Когда мы говорим о знаменателе, мы используем порядковые числительные, то есть числа, определяющие положение, например «третье» или «четвертое».
Верхнее число дроби называется числителем и указывает на то, со сколькими частями целого мы имеем дело.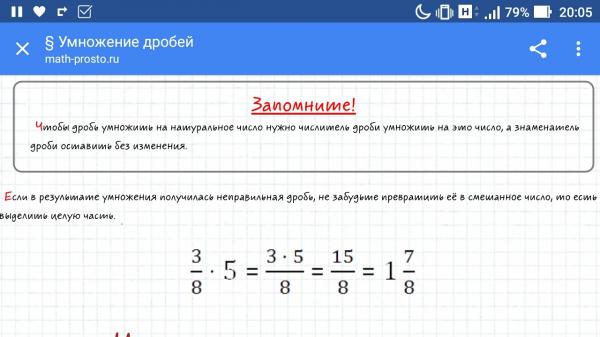
Самый простой способ определить дробь — представить себе круг, разделенный поровну на шесть частей.
Сам пирог представляет собой единое целое, а отдельные ломтики — его части. Поскольку у нас есть шесть равных частей одного целого, наш знаменатель здесь равен 6.
Если мы возьмем один кусок пирога, у нас будет одна шестая (1/6). Два среза эквивалентны двум шестым (2/6) и так далее.
Само по себе это довольно просто понять. Однако существуют разные типы дробей и разные методы для выполнения каждого типа дробного уравнения.
Ключевые факты о фракциях
Чтобы понять, как вычислять дроби, важно усвоить основы. Во-первых, давайте рассмотрим три разных типа дробей:
Определения и примеры дробей
Правильная дробь – Правильная дробь – это дробь, в которой числитель меньше знаменателя. 1/2, 10/15 и 85/100 — все это примеры правильных дробей. Общее значение правильной дроби всегда меньше единицы.
Неправильная дробь – В неправильной дроби значение числителя больше значения знаменателя.
6/3, 25/18 и 50/20 — все это примеры неправильных дробей. Общее значение неправильной дроби всегда больше единицы.
Смешанные дроби – Смешанная дробь представлена целым числом, за которым следует дробное число, например 2⅔, 6⅘ или 25⅝. Смешанные дроби также известны как смешанные числа.
Подготовьтесь к любому экзамену по оценке работы с помощью JobTestPrep
Ключевые термины
Теперь, когда мы знаем различные типы дробей, давайте посмотрим на некоторые другие ключевые термины и фразы:
Эквивалентные дроби – это дроби, которые кажутся разными, но имеют одинаковое значение. Например, 2/3 равно 4/6.
Упрощенные дроби – это дроби, приведенные к наименьшей форме. По сути, низший эквивалент высшей дроби. Итак, в приведенном выше примере 2/3 — это упрощенная версия 4/6.
Обратные числа — Здесь дробь переворачивается путем размещения знаменателя над числителем.

Дроби также могут быть представлены в виде десятичных знаков и процентов . Мы рассмотрим, как преобразовать дроби в приведенных ниже примерах уравнений.
10 простых дробей и способы их решения
Ниже приведены десять примеров дробных уравнений и рекомендации по их решению. Если вы работаете с дробями на экзамене, обязательно покажите свой метод.
1. Как преобразовать смешанную дробь в неправильную дробь
Как уже говорилось, смешанная дробь состоит из целого числа, за которым следует дробное число. В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную численно как 7⅘.
При запросе на преобразование смешанной дроби в неправильную:
- Сначала умножьте целое число на знаменатель дробной части.
- Возьмите полученное число и добавьте его к числителю дроби.

- Возьмите эту последнюю цифру в качестве нового числителя и поместите ее над первоначальным знаменателем. Это дает вам неправильную дробь.
Пример:
Пример вопроса
Преобразуйте 7⅘ в неправильную дробь.
2. Как преобразовать дробь в десятичную
Поскольку оба используются для определения значений меньше единицы, десятичная дробь — это просто другой способ представления дроби.
Метод, используемый для преобразования дроби в десятичную, представляет собой простое деление: вы просто делите числитель на знаменатель.
Пример:
Пример вопроса
Преобразование 3/10 в десятичную дробь.
Подготовьтесь к любому аттестационному тесту с помощью JobTestPrep
3. Как преобразовать дробь в проценты
Существует три простых способа преобразования дроби в проценты. Мы рассмотрим их все здесь, используя одну и ту же дробь 7/20.
Первый метод:
Разделите числитель на знаменатель, затем умножьте полученное число на 100, чтобы получить процентное преобразование:
7 ÷ 20 = 0,35
Умножить числитель на 100, затем разделить полученное число на знаменатель:
7 x 100 = 700
700 ÷ 20 = 35%
Метод третий:
3 десятичная точка вашего ответа на два знака вправо:
7 ÷ 20 = 0,35
Перемещение десятичной точки дает преобразование 35%.
При преобразовании дроби в процент всегда не забывайте включать в свой ответ знак %.
Если вам нужно подготовиться к ряду различных тестов при приеме на работу и вы хотите перехитрить конкурентов, выберите Премиум-членство от JobTestPrep .
Вы получите доступ к трем пакетам PrepPack на ваш выбор из базы данных, которая охватывает всех основных поставщиков тестов и работодателей, а также специализированные пакеты профессий.
Подготовьтесь к любому экзамену по оценке работы с помощью JobTestPrep
4. Как складывать дроби
Процесс сложения дробей прост, если знаменатели совпадают.
В качестве базового примера возьмем 1/6 + 3/6. В этом случае у вас равные знаменатели, поэтому просто сложите числители обеих дробей, придерживаясь нижней цифры 6:
1 + 3 = 4
Итак, 1/6 + 3/6 = 4/6
При сложении дробей, в которых меньшие числа не совпадают, вам сначала нужно найти наименьший общий знаменатель . Это наименьшее число, которое полностью делится на оба существующих знаменателя.
Это наименьшее число, которое полностью делится на оба существующих знаменателя.
Пример:
Пример вопроса
1/4 + 2/3
5. Как вычитать дроби
Как и при сложении, вычитание дробей легко, когда знаменатели одинаковы. Нужно просто вычесть второй числитель из первого, сохранив нижнее число тем же.
Пример:
Пример Вопрос
4/7 – 3/7.
Теперь давайте посмотрим на вычитание дробей с различными знаменателями .
Пример:
Пример вопроса
4/5 – 2/3
6. Как делить дроби
Чтобы разделить одну дробь на другую, сначала нужно превратить делимую дробь в обратную, переключив переключатель знаменатель и числитель.
Пример:
Пример вопроса
Возьмем пример 1/2 ÷ 1/5, последняя дробь как обратная 5/1.
Теперь умножьте первую дробь на обратную:
1/2 x 5/1
Для этого умножьте числители и знаменатели:
1 x 5 = 5 (числители)
2 x 1 = 2 (знаменатели)
Таким образом, 1/2 x 5/1 = 5/2
7.
 Как умножать дроби
Как умножать дробиПроцесс вычисления дробей путем умножения друг на друга очень прост:
- Умножение ваши числители
- Умножьте ваши знаменатели
- Напишите новый числитель над новым знаменателем
Пример:
Пример вопроса
На примере уравнения 1/2 x 1/6:
1 x 1 = 1 (числители)
2 x 6 = 12 (знаменатели)
Как сделать Упростить дробь
Упростить дробь означает привести ее к самой простой форме. По сути, найти наименьшую возможную эквивалентную дробь.
Сначала найдите наибольший общий делитель . Это наибольшее целое число, на которое делятся и числитель, и знаменатель.
Для этого запишите все множители для обеих частей вашей дроби, как показано ниже на примере 32/48:
Пример вопроса
- Множители 32: 1, 2, 4, 8, 16, 32
- Коэффициенты 48: 1, 2, 3, 4, 8, 12, 16, 24, 48
Наибольший общий множитель здесь: 16
Теперь разделите числитель и знаменатель на это число, чтобы найти упрощенную дробь:
32 ÷ 16 = 2 (числители)
48 ÷ 16 = 3 (знаменатели)
Заполняя любую форму дробного уравнения, всегда упрощайте свой ответ до наименьшей возможной формы.
9. Как вычислять дроби величин
Когда вам представят количество и попросят вычислить дробную часть, просто разделите данное количество на знаменатель дроби, а затем умножьте это число на числитель.
Пример:
Пример вопроса
У вас есть 55 конфет, две пятых из которых вы хотите отдать соседу, чтобы он забрал его домой. Сколько конфет она возьмет?
Разделите полученную сумму на знаменатель дроби: 55 ÷ 5 = 11
Умножьте эту цифру на числитель: 11 x 2 = 22
другой, либо умножить, либо разделить обе части одной дроби на одно и то же целое число.
Если ваши ответы также являются целыми числами, то дробь сохраняет свое значение и эквивалентна.
Пример:
Пример Вопрос
Чтобы определить, эквивалентно ли 12/15 4/5, разделите 12 и 15 на целое число:
12 ÷ 2 = 6
15 ÷ 2 = 7,5
Поскольку у вас нет целую цифру в качестве ответа здесь, перейдите к следующему основному числу:
12 ÷ 3 = 4
15 ÷ 3 = 5
Вы также можете сделать это в обратном порядке, умножив обе части младшей дроби:
4 x 3 = 12
5 x 3 = 15
По существу, если одна дробь является упрощенной версией другой, то они эквивалентны.
Подготовьтесь к любому аттестационному тесту с помощью JobTestPrep
Резюме
Дроби — это числовые величины, которые помогают нам измерять равные части целого.
Они бывают в виде правильных, неправильных и смешанных дробей и могут быть легко преобразованы в десятичные точки и проценты.
Методы, используемые в дробных уравнениях, различаются в зависимости от решаемой задачи, и каждый из них необходимо практиковать с осторожностью, убедившись, что вы полностью понимаете вопрос, и показывая, как вы работаете.
Хотя поначалу они могут показаться пугающими, время, потраченное на понимание основных правил, должно помочь вам научиться с легкостью вычислять дроби.
Пошаговое руководство — Психометрический успех
Обновлено 16 февраля 2023 г.
Что такое дроби?
Дроби — это числовые величины, представляющие значения меньше единицы. Также известные как дробные числа, они обычно используются для измерения частей целого, например:
- Половина (1/2)
- Одна пятая (1/5)
- Две трети (2/3)
Дроби
Дроби состоят из двух чисел, одно над и одно под разделительной чертой.
Нижнее число известно как знаменатель и относится к отдельным частям целого.
Когда мы говорим о знаменателе, мы используем порядковые числительные, то есть числа, определяющие положение, например «третье» или «четвертое».
Верхнее число дроби называется числитель и указывает на то, со сколькими частями целого мы имеем дело.
Самый простой способ определить дробь — представить себе круг, разделенный поровну на шесть частей.
Сам пирог представляет собой единое целое, а отдельные кусочки являются его частями. Поскольку у нас есть шесть равных частей одного целого, наш знаменатель здесь равен 6.
Если мы возьмем один кусок пирога, у нас будет одна шестая (1/6). Два среза эквивалентны двум шестым (2/6) и так далее.
Само по себе это довольно просто понять. Однако существуют разные типы дробей и разные методы для выполнения каждого типа дробного уравнения.
Ключевые факты о дробях
Чтобы понять, как вычислять дроби, важно разобраться с основами. Во-первых, давайте рассмотрим три разных типа дробей:
Во-первых, давайте рассмотрим три разных типа дробей:
Определения и примеры дробей
Правильная дробь – Правильная дробь – это дробь, в которой числитель меньше знаменателя. 1/2, 10/15 и 85/100 — все это примеры правильных дробей. Общее значение правильной дроби всегда меньше единицы.
Неправильная дробь – В неправильной дроби значение числителя больше значения знаменателя. 6/3, 25/18 и 50/20 — все это примеры неправильных дробей. Общее значение неправильной дроби всегда больше единицы.
Смешанные дроби – Смешанная дробь представлена целым числом, за которым следует дробное число, например 2⅔, 6⅘ или 25⅝. Смешанные дроби также известны как смешанные числа.
Подготовьтесь к любому экзамену по оценке работы с помощью JobTestPrep
Ключевые термины
Теперь, когда мы знаем различные типы дробей, давайте посмотрим на некоторые другие ключевые термины и фразы:
Эквивалентные дроби – это дроби, которые кажутся разными, но имеют одинаковое значение.
 Например, 2/3 равно 4/6.
Например, 2/3 равно 4/6.Упрощенные дроби – это дроби, приведенные к наименьшей форме. По сути, низший эквивалент высшей дроби. Итак, в приведенном выше примере 2/3 — это упрощенная версия 4/6.
Обратные числа — Здесь дробь переворачивается путем размещения знаменателя над числителем. Например, обратное 2/3 равно 3/2. Обратные числа используются при делении и умножении дробей (5 ÷ 1/5 равно 5 х 5/1 или 5 х 5).
Дроби также могут быть представлены в виде
10 простых дробей и способы их решения
Ниже приведены десять примеров дробных уравнений и рекомендации по их решению. Если вы работаете с дробями на экзамене, обязательно покажите свой метод.
1. Как преобразовать смешанную дробь в неправильную дробь
Как уже говорилось, смешанная дробь состоит из целого числа, за которым следует дробное число. В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную численно как 7⅘.
В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную численно как 7⅘.
При запросе на преобразование смешанной дроби в неправильную:
- Сначала умножьте целое число на знаменатель дробной части.
- Возьмите полученное число и добавьте его к числителю дроби.
- Возьмите эту последнюю цифру в качестве нового числителя и поместите ее над первоначальным знаменателем. Это дает вам неправильную дробь.
Пример:
Пример вопроса
Преобразуйте 7⅘ в неправильную дробь.
2. Как преобразовать дробь в десятичную
Поскольку оба используются для определения значений меньше единицы, десятичная дробь — это просто другой способ представления дроби.
Метод, используемый для преобразования дроби в десятичную, представляет собой простое деление: вы просто делите числитель на знаменатель.
Пример:
Пример вопроса
Преобразование 3/10 в десятичную дробь.
Подготовьтесь к любому аттестационному тесту с помощью JobTestPrep
3. Как преобразовать дробь в проценты
Существует три простых способа преобразования дроби в проценты. Мы рассмотрим их все здесь, используя одну и ту же дробь 7/20.
Первый метод:
Разделите числитель на знаменатель, затем умножьте полученное число на 100, чтобы получить процентное преобразование:
7 ÷ 20 = 0,35
Умножить числитель на 100, затем разделить полученное число на знаменатель:
7 x 100 = 700
700 ÷ 20 = 35%
Метод третий:
3 десятичная точка вашего ответа на два знака вправо:
7 ÷ 20 = 0,35
Перемещение десятичной точки дает преобразование 35%.
При преобразовании дроби в процент всегда не забывайте включать в свой ответ знак %.
Если вам нужно подготовиться к ряду различных тестов при приеме на работу и вы хотите перехитрить конкурентов, выберите Премиум-членство от JobTestPrep .
Вы получите доступ к трем пакетам PrepPack на ваш выбор из базы данных, которая охватывает всех основных поставщиков тестов и работодателей, а также специализированные пакеты профессий.
Подготовьтесь к любому экзамену по оценке работы с помощью JobTestPrep
4. Как складывать дроби
Процесс сложения дробей прост, если знаменатели совпадают.
В качестве базового примера возьмем 1/6 + 3/6. В этом случае у вас равные знаменатели, поэтому просто сложите числители обеих дробей, придерживаясь нижней цифры 6:
1 + 3 = 4
Итак, 1/6 + 3/6 = 4/6
При сложении дробей, в которых меньшие числа не совпадают, вам сначала нужно найти наименьший общий знаменатель . Это наименьшее число, которое полностью делится на оба существующих знаменателя.
Пример:
Пример вопроса
1/4 + 2/3
5. Как вычитать дроби
Как и при сложении, вычитание дробей легко, когда знаменатели одинаковы. Нужно просто вычесть второй числитель из первого, сохранив нижнее число тем же.
Нужно просто вычесть второй числитель из первого, сохранив нижнее число тем же.
Пример:
Пример Вопрос
4/7 – 3/7.
Теперь давайте посмотрим на вычитание дробей с различными знаменателями .
Пример:
Пример вопроса
4/5 – 2/3
6. Как делить дроби
Чтобы разделить одну дробь на другую, сначала нужно превратить делимую дробь в обратную, переключив переключатель знаменатель и числитель.
Пример:
Пример вопроса
Возьмем пример 1/2 ÷ 1/5, последняя дробь как обратная 5/1.
Теперь умножьте первую дробь на обратную:
1/2 x 5/1
Для этого умножьте числители и знаменатели:
1 x 5 = 5 (числители)
2 x 1 = 2 (знаменатели)
Таким образом, 1/2 x 5/1 = 5/2
7. Как умножать дроби
Процесс вычисления дробей путем умножения друг на друга очень прост:
- Умножение ваши числители
- Умножьте ваши знаменатели
- Напишите новый числитель над новым знаменателем
Пример:
Пример вопроса
На примере уравнения 1/2 x 1/6:
1 x 1 = 1 (числители)
2 x 6 = 12 (знаменатели)
Как сделать Упростить дробь
Упростить дробь означает привести ее к самой простой форме. По сути, найти наименьшую возможную эквивалентную дробь.
По сути, найти наименьшую возможную эквивалентную дробь.
Сначала найдите наибольший общий делитель . Это наибольшее целое число, на которое делятся и числитель, и знаменатель.
Для этого запишите все множители для обеих частей вашей дроби, как показано ниже на примере 32/48:
Пример вопроса
- Множители 32: 1, 2, 4, 8, 16, 32
-
Наибольший общий множитель здесь: 16
Теперь разделите числитель и знаменатель на это число, чтобы найти упрощенную дробь:
32 ÷ 16 = 2 (числители)
48 ÷ 16 = 3 (знаменатели)
Заполняя любую форму дробного уравнения, всегда упрощайте свой ответ до наименьшей возможной формы.
9. Как вычислять дроби величин
Когда вам представят количество и попросят вычислить дробную часть, просто разделите данное количество на знаменатель дроби, а затем умножьте это число на числитель.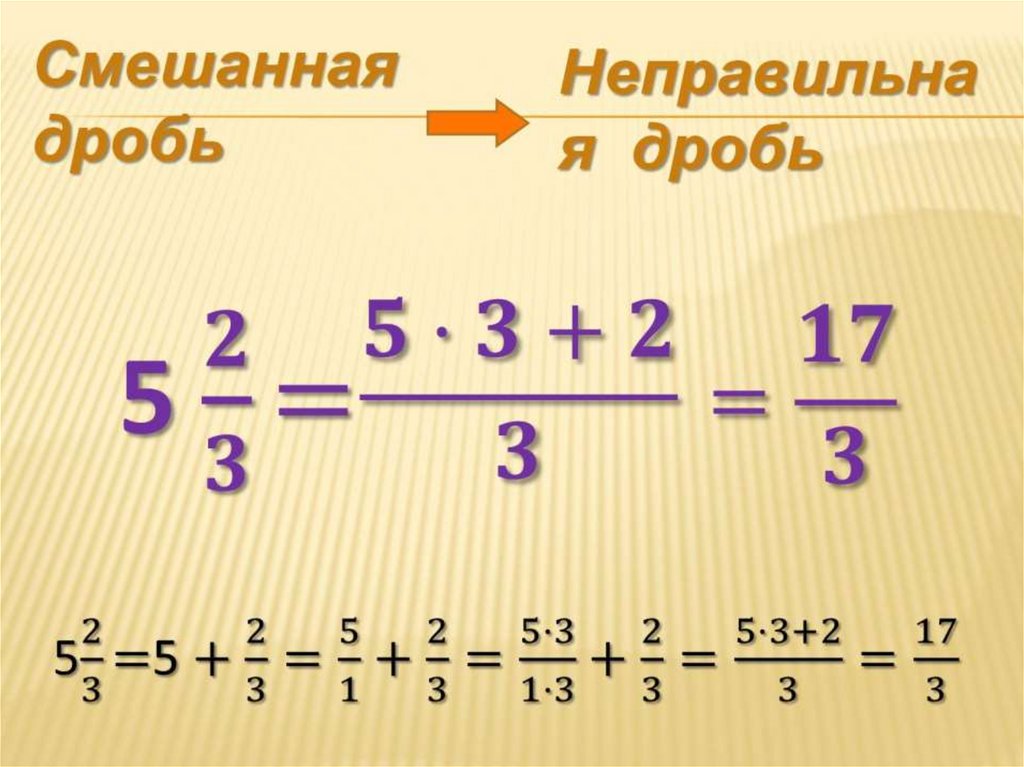
Пример:
Пример вопроса
У вас есть 55 конфет, две пятых из которых вы хотите отдать соседу, чтобы он забрал его домой. Сколько конфет она возьмет?
Разделите полученную сумму на знаменатель дроби: 55 ÷ 5 = 11
Умножьте эту цифру на числитель: 11 x 2 = 22
другой, либо умножить, либо разделить обе части одной дроби на одно и то же целое число.
Если ваши ответы также являются целыми числами, то дробь сохраняет свое значение и эквивалентна.
Пример:
Пример Вопрос
Чтобы определить, эквивалентно ли 12/15 4/5, разделите 12 и 15 на целое число:
12 ÷ 2 = 6
15 ÷ 2 = 7,5
Поскольку у вас нет целую цифру в качестве ответа здесь, перейдите к следующему основному числу:
12 ÷ 3 = 4
15 ÷ 3 = 5
Вы также можете сделать это в обратном порядке, умножив обе части младшей дроби:
4 x 3 = 12
5 x 3 = 15
По существу, если одна дробь является упрощенной версией другой, то они эквивалентны.




 Например, 2/3 равно 4/6.
Например, 2/3 равно 4/6.