Как правильно строить графики функций: Как построить график функции у = f(x) + m, если известен график функции у = f(x) — урок. Алгебра, 8 класс.

2-4, -1<x≤2. \end {cases}$

Содержание

Построение в Excel графиков математических и тригонометрических функций — Трюки и приемы в Microsoft Excel

Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.

Построение графиков математических функций с одной переменной

Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.

Рис. 140.1. Диаграмма представляет собой график функции SIN(x)

Функция выражается в таком виде: у = SIN(x). 2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)

Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.

Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂

Построение графиков математических функций с двумя переменными

Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)

На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.

Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными

Значения х находятся в диапазоне А2:А22, а значения у — в диапазоне B1:V1.

Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1).

Чтобы создать диаграмму, выполните приведенные ниже действия.

Выделите диапазон A1:V22.
Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
Выберите макет диаграммы, который вам нравится, а затем настройте его.

Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2)) =SIN($A2)*COS($A2*B$1) =COS($A2*B$1)

Как набросать любой график на глаз

Уравнения в математике полезны, но они также неэффективны — для каждого значения x вам нужно выполнить отдельный расчет, чтобы выяснить, что такое y.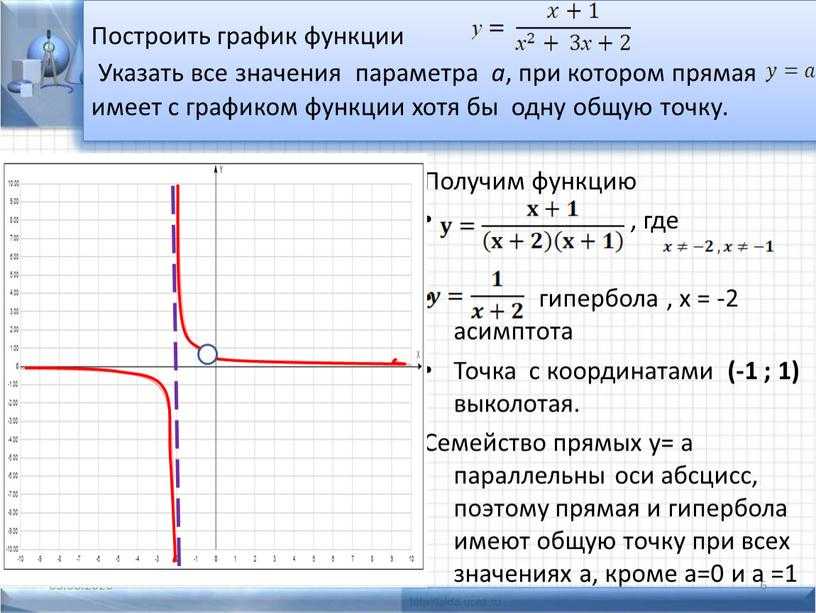 Графики берут это уравнение и превращают его в визуальное представление, на которое вы можете смотреть и сразу же видеть, что происходит при различных значениях x, как изменяется функция и многое другое!

Однако, когда вы впервые изучаете графики, все сводится к запоминанию основных уравнений и того, как будут выглядеть их графики, начиная с линейных уравнений в форме пересечения наклона. Однако по мере того, как вы переходите к более сложным уравнениям, таким как квадратные уравнения и тригонометрия, вас часто просят запомнить формы таких уравнений —

— где вы должны запомнить точную настройку уравнения и то, что означает каждый член на графике, будь то вершина, наклон, точки пересечения, масштабирование, горизонтальные или вертикальные сдвиги и многое другое!

Но зачем запоминать все эти а, в, к и з, если это будет полезно только в нескольких конкретных случаях?!

Вместо этого в следующий раз, когда вам понадобится узнать, как должен выглядеть график функции, попробуйте выполнить эти шаги, чтобы быстро набросать любой график!

Для демонстрации воспользуемся уравнением:

Это похоже на полиномиальные уравнения, которые вы, возможно, видели в классе, но они кубические, поэтому у нас нет очевидных форм уравнений, которые можно было бы использовать для построения графика.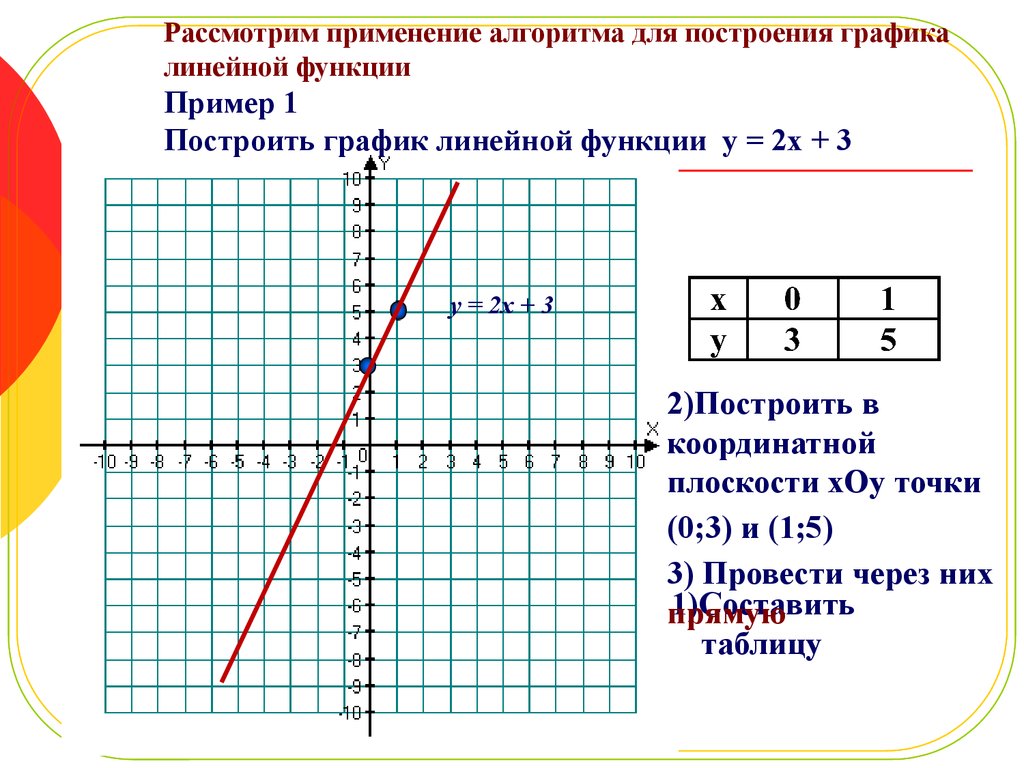 Итак, как построить график этой функции?

1. График x = 0

Первое, что мы хотим сделать, это получить несколько точек на нашем графике, поэтому мы хотим выбрать те, которые будет легко вычислить. Практически для любого уравнения подставить x = 0 и решить для y можно быстро и легко сделать на глаз, и почти всегда можно обойтись без калькулятора. Для нашего примера уравнения:

Итак, первая точка, которую мы поместим на наш график, это (0, -4).

а. Если вы можете легко найти его, постройте график y = 0

Далее, в некоторых случаях y = 0 тоже довольно легко решить. Если вы можете быстро решить y = 0 , это еще один хороший момент, который нужно решить сразу. В данном случае:

Итак, теперь у нас есть точка (-2, 0) для добавления к нашему графику!

б. Бонус: нанесите несколько простых для расчета точек, таких как x = 1 и x = -1

. В зависимости от графика может быть легко подставить небольшие целые числа, такие как 1 или -1.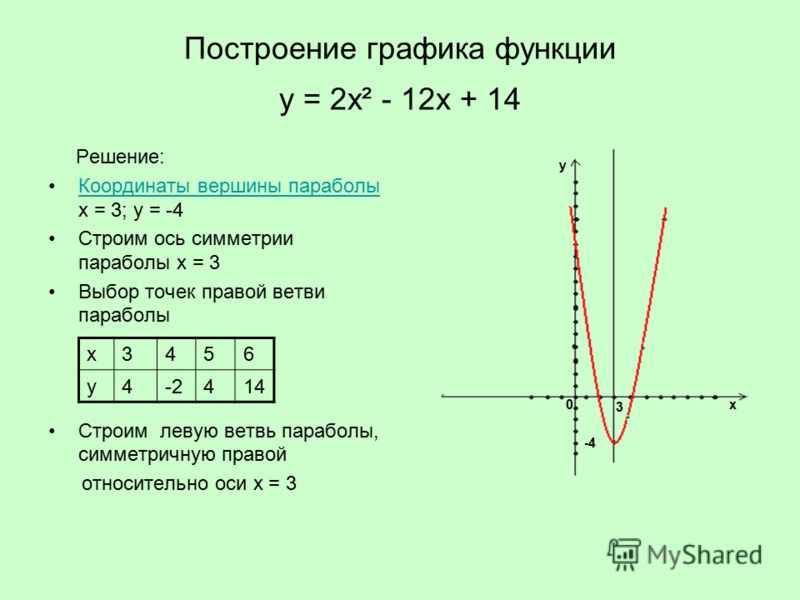 Чем больше точек вы можете добавить к своему графику, тем лучше вы сможете увидеть, какую форму он в конечном итоге примет. Однако придерживайтесь точек, которые легко рассчитать. Цель этого метода — быстро найти всего несколько точек — если вы собираетесь вычислять каждую точку на графике, вы не экономите время!

Для этого уравнения мы получим:

Итак, теперь у нас есть четыре точки: (0,-4), (-2,0), (1,-18) и ( -1, -2). Давайте нанесем эти точки и посмотрим, как они выглядят!

Мы можем начать видеть, как график обретает форму, но нам понадобится больше информации, прежде чем мы закончим.

2. Выяснить, что происходит, когда x действительно велико (в положительном и отрицательном направлении)

Любая линия, которую мы рисуем, должна заканчиваться стрелками на обоих концах, чтобы мы знали, что происходит по мере продвижения. далее по оси x как в положительном, так и в отрицательном направлении. Это то, что называется «конечным поведением». Чтобы выяснить, что это такое, мы подставим два числа в исходное уравнение — большое положительное число и большое отрицательное число. Теперь мы на самом деле не собираемся выбирать число и использовать наш калькулятор, чтобы выяснить, что произойдет, мы просто посмотрим, как части уравнения повлияют на конечный результат.

Например, подставив большое положительное число в нашу кубическую функцию, мы получим:

Добавление 1 к большому положительному числу почти не изменит его — затем, когда мы возведем его в куб, оно станет действительно большим положительным числом.

Однако действительно большое положительное число станет отрицательным при умножении на -2, а вычитание 2 не будет иметь большого значения, поэтому конечным результатом будет действительно большое отрицательное число.

Если мы попробуем то же самое для другой стороны графика, подставив вместо x большое отрицательное число, мы получим:

Большое отрицательное число в кубе — это действительно большое отрицательное число, но на этот раз, когда оно умножается на -2, оно становится действительно большим положительным числом.

o, для нашего графика мы нашли, что при больших положительных x, y большие и отрицательные, а при больших отрицательных x, y большие и положительные. Давайте добавим это к нашему графику со стрелками.

3. Опционально: ищите любые «значимые» значения x

Некоторые уравнения имеют необычные особенности или особые точки, которые вы можете заметить, взглянув на уравнение – обратите особое внимание на любые точки, в которых большая часть уравнения может стать нулем. Это может помочь вам найти корни, асимптоты или другие места, где форма графика изменяется необычным образом.

Например, в уравнении, которое мы рассматривали,

Этот термин интересен тем, что если x = -1, вся часть уравнения станет равной нулю. Конечно, мы уже нашли эту точку ранее, но это говорит нам о том, что x = -1 — это «особая» точка в уравнении — возможно, здесь форма графика как-то сдвинется.

4. Соедини точки и закончи!

На данный момент мы сделали все, что могли — у нас есть несколько точек на графике, мы знаем, как он будет выглядеть на концах, и мы определили любые необычные точки или особенности.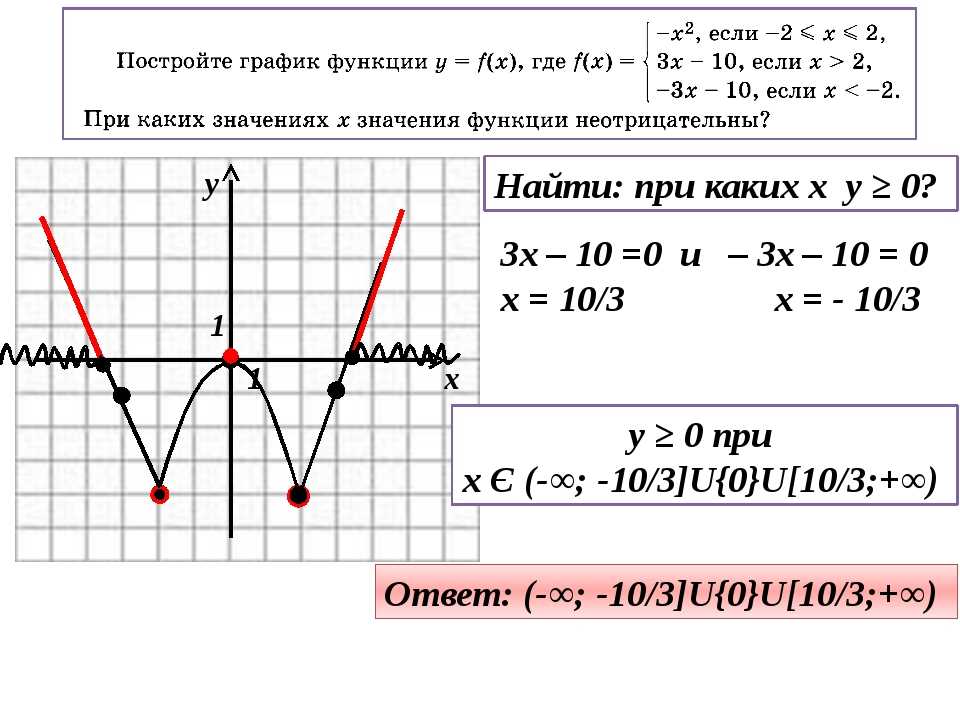 Мы можем не знать точно, что это такое, но мы готовы что-то нарисовать.

Возможно, мы до сих пор не знаем точно, какова форма графика, но здесь вы можете использовать основы для каждого основного уравнения. Мы знаем, что наша линия будет гладкой и максимально простой, но при этом будет попадать во все точки. Если мы в целом знаем, какого рода это уравнение (полиномиальное, радикальное, экспоненциальное), у нас есть хотя бы некоторое предположение, какова будет его общая форма.

В нашем примере у нас достаточно точек, чтобы набросать одну сторону нашего уравнения, но отрицательная сторона немного неясна, поэтому давайте подумаем, что мы можем сказать о другом типе многочлена, квадратном уравнении.

Для нашей кубической функции мы знаем, что квадратичные функции всегда симметричны относительно своей вершины, но это не совсем работает, потому что мы знаем, что в одном направлении мы получим положительное значение, а в другом нам нужно стать отрицательным.

Итак, давайте предположим что-то подобное — может быть, наша «особая» точка при x = -1 — это , как вершина, но в этой точке форма графика такая же, но движется в противоположном направлении. (Для справки я нарисовал пунктирную линию на x = — 1, но, конечно, это не будет частью настоящего окончательного графика.)

Поехали! Это не идеальный график, но за несколько быстрых шагов мы, по крайней мере, в общих чертах знаем, как этот график будет выглядеть. Если вам интересно, вот как это уравнение выглядит, когда оно построено на компьютере.

Этот метод работает для огромного количества функций — многочленов, радикалов, экспонент, логарифмов, тригонометрических функций и многого другого! Просто будьте осторожны, когда вы доберетесь до функций с несколькими y или членами: в этих случаях графики будут необычными, сложными формами, поэтому нарисуйте много точек (x, y), прежде чем пытаться соединить все точки!

5 шагов для графического отображения преобразований функций в алгебре | Эрнест Вулф | countdown.education

5 шагов для графического отображения преобразований функций в алгебре | Эрнест Вулф | обратный отсчет.образование | Средний

1. Определите родительскую функцию

Все, что вы должны построить на графике самостоятельно, основано на более простом графике (родительской функции), который вам НЕОБХОДИМО запомнить
Посмотрите на изображение выше и проверьте с вашим учителем, чтобы узнать, за что вы отвечаете

2. Отразить по оси X или оси Y

Если за скобками есть отрицательное значение, то отразить по оси X или по вертикали (все значения Y становятся отрицательными)
пример: f(x) = -x2
Если в круглых скобках есть отрицательное значение, то отразите его по оси y по горизонтали (все значения x станут отрицательными) и вынесите отрицательное значение
ex: f(x) = 1 / (-x+3) становится f(x) = 1 / (-(x-3)) **ЭТО СЛОЖНО**

3. Сдвиг (перевод) по вертикали или горизонтали

Если за скобками добавляется число, сдвиньте его вверх по вертикали на указанную величину, а если число вычитается, сдвиньте его вниз
пример: f (x) = x2–2 уменьшается 2
Если в круглых скобках добавляется число, сдвиньте его влево на эту величину, а если число вычитается, сдвиньте его вправо (вопреки ожидаемому)
пример: f(x) = (x-2)2 сдвинут вправо на 2 единицы

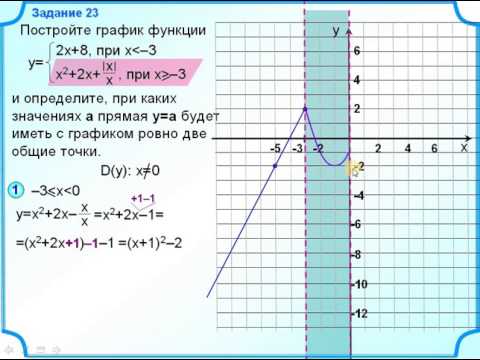4. Вертикальное и горизонтальное растяжение/сжатие

Если за скобками указан целочисленный коэффициент, умножьте значения y всех точек на этот коэффициент и посмотрите на график растяжения по вертикали
пример: f( x) = 4×2 растягивается по вертикали в 4 раза
Если за скобками стоит дробный коэффициент, то умножьте значения y всех точек на этот коэффициент и посмотрите, как график сжимается по вертикали
пример: f(x) = 1/2 x2 сжато по вертикали в 2 раза
Если в скобках указан целочисленный коэффициент, то умножьте значения x всех точек на величину, обратную (!), что
пример: f(x) = (4x)2 сжато по горизонтали в 4 раза
Если в скобках дробный коэффициент, то умножить x-значения всех точек обратным (!) этому коэффициенту, и посмотрите, как график сжимается по горизонтали (противоположно тому, что вы ожидаете)
пример: f(x) = (1/2 x — 4)2 становится (1/2 (x — 8))2 растягивается по горизонтали в 2 раза

5. Подключите пару ваших координаты в родительскую функцию, чтобы дважды проверить свою работу

ПОМНИТЕ: ГРАФИК ЭТО ПРОСТО НАБОР ТОЧЕК, КОТОРЫЙ УДОВЛЕТВОРЯЕТ УРАВНЕНИЮ
Это означает, что вы всегда можете проверить свою работу, подставив значение x (я рекомендую x= 0 и посмотрите, соответствует ли значение y значению y вашего графика)

БЫСТРЫЙ ОБЗОР :

Отражение > Сдвиг > Растяжение
Внутренние круглые скобки = подумайте об обратном для растяжек и сдвигов и FACTOR (при необходимости) по оси x)

Алгебра

Технология

Сжатие

Константа

Кубический корень

переосмыслить образование

Подробнее на сайте countdown.education