Деление дробей с разными знаменателями – примеры и правила (5 класс, математика)
4.6
Средняя оценка: 4.6
Всего получено оценок: 260.
4.6
Средняя оценка: 4.6
Всего получено оценок: 260.
Дроби неприятны тем, что большое воздействие на действия с ними оказывают знаменатели. Часто ученики 5 класса приходят в ступор при виде дробей с разными знаменателями, начиная выполнять, лишние действия и терять время. А ведь не для всех действий с дробями требуется наличие одинакового знаменателя, поговорим подробнее о данном вопросе.
Действия с дробями
Необходимость приведения к одному знаменателю зависит от выполняемых действий. Разобьем возможные действия на группы и разберемся с каждой из групп в отдельности.
Сложение и вычитание
Сложение и вычитание дробей основано на вынесении общего множителя. Рассмотрим на примере, как выглядит сложение дробей в подробности:
$${3\over{13}}+{5\over{13}}={1\over{13}}*(3+5)={8\over{13}}$$
Это значит, что сложение и вычитание дробей возможно только при условии наличия одинакового знаменателя.
Если не привести дроби к одному знаменателю, то общий множитель просто не получится вынести, а принцип сложение осуществить не получится. Поэтому вычитание или сложение дробей с разными знаменателями невозможно. Это непреложное правило.
Умножение
Умножение дробей не требовательно к знаменателю. Здесь используется совершенно иной принцип. Дело в том, что дробную черту можно заменить знаком деления. Тогда:
${3\over{5}}*{2\over{3}}=3:5*2:3=(3*2):(5*3)={6\over{15}}$ – для того, чтобы перемножить две дроби нужно умножить числитель на числитель, а знаменатель на знаменатель. Получившаяся дробь будет результатом умножения.
Деление
Деление использует те же принципы, что и умножение:
${3\over{5}}:{2\over{3}}=(3:5):(2:3)=3:5*3:2=9:10={9\over{10}}$ – для того, чтобы разделить одну дробь на другую необходимо перевернуть дробь-делитель. Для этого числитель меняется на знаменатель, а знаменатель на числитель.
Одинаковый знаменатель ни для деления, ни для умножения дробей не требуется. Помните, что каждое действие в математике имеет свое основание.
Основанием для сложения и умножения является общий множитель. Значит нужно, чтобы этот общий множитель был. Поэтому требуется одинаковый знаменатель у двух дробей. Основание для деления и умножения – математический смысл дроби.
Этот принцип работает вне зависимости от значения знаменателя, поэтому деление дробей с разными знаменателями и деление дробей с одинаковым знаменателем не отличается. Последовательность действий при решении примеров деления дробей с разными знаменателями одна и та же.
Что мы узнали?
Мы поговорили о действиях с дробями. Выделили отдельные группы действий с дробями. Привели обоснование каждому из действий. Объяснили, когда необходимо наличие одинакового знаменателя, а когда нет.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 260.
А какая ваша оценка?
Умножение алгебраических дробей. Умножение и деление алгебраических дробей Умножение алгебраических дробей с разными знаменателями
Мы умеем выполнять умножение и деление арифметических дробей, например:
если буквы a, b, c и d обозначают арифметические целые числа.
Возникает вопрос, не остаются ли в силе эти равенства, если a, b, c и d будут обозначать: 1) какие-нибудь арифметические числа и 2) любые относительные числа.
Прежде всего придется рассмотреть сложные дроби, например:
Этих примеров уже достаточно, чтобы убедиться в справедливости равенств, относящихся к умножению и делению дробей, когда числа a, b, c
и d
какие угодно (целые или дробные) арифметические.
Заметим, что основных равенств лишь 2, а именно:
Остается теперь рассмотреть, останутся ли справедливыми эти равенства, если некоторые из чисел a, b, c и d предположить отрицательными: если, например, a отрицательное число, b, c и d – положительные, то дробь отрицательна, а дробь положительна; поэтому, например, от деления на должно получиться отрицательное число, но мы видим, что, согласно нашему предположению, и выражение должно выразить отрицательное число, т. е. равенство оправдывается и в этом случае. Легко также рассмотреть и другие предположения для знаков числе a, b, c и d . Результатом этого рассмотрения является убеждение в справедливости равенств
и для случая, когда a, b, c и d выражают любые относительные числа, т. е. для умножения и деления алгебраических дробей остаются в силе те же правила, как и для арифметических.
Теперь мы можем выполнять умножение и деление алгебраических дробей. Наибольшие затруднения представляет здесь вопрос о сокращении дробей, получаемых после умножения или деления.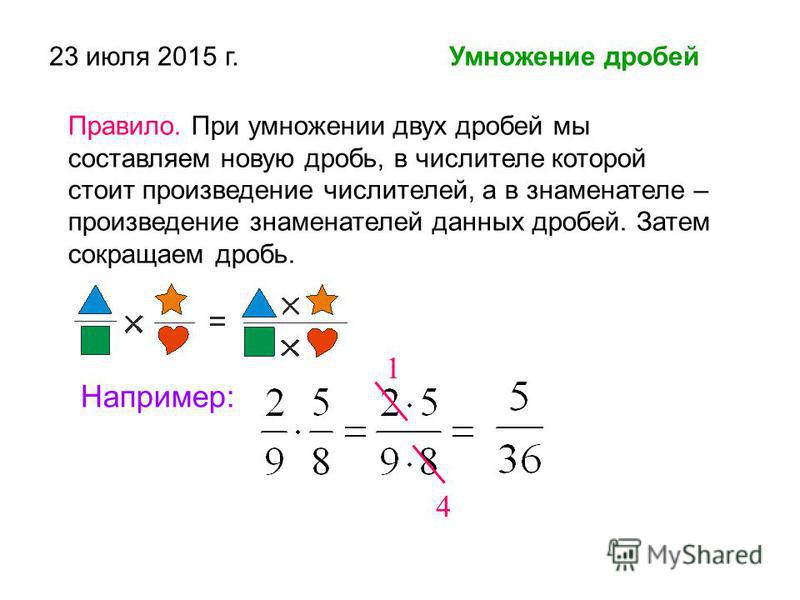
Если алгебраические дроби одночленные, то сокращение полученного результата не представит затруднений, а если дроби алгебраические, то является необходимым предварительно числителя и знаменателя каждой из данных дробей разлагать на множители.
На данном уроке будут рассмотрены правила умножения и деления алгебраических дробей, а также примеры на применение данных правил. Умножение и деление алгебраических дробей не отличается от умножения и деления обыкновенных дробей. Вместе с тем, наличие переменных приводит к несколько более сложным способам упрощения полученных выражений. Несмотря на то, что умножение и деление дробей выполняется проще, чем их сложение и вычитание, к изучению данной темы необходимо подойти крайне ответственно, поскольку в ней существует много «подводных камней», на которые обычно не обращают внимания. В рамках урока мы не только изучим правила умножения и деления дробей, но и разберём нюансы, которые могут возникнуть при их применении.
Тема: Алгебраические дроби.
Арифметические операции над алгебраическими дробями
Урок: Умножение и деление алгебраических дробей
Правила умножения и деления алгебраических абсолютно аналогичны правилам умножения и деления обыкновенных дробей. Напомним их:
То есть, для того, чтобы умножить дроби, необходимо умножить их числители (это будет числитель произведения), и умножить их знаменатели (это будет знаменатель произведения).
Деление на дробь — это умножение на перевёрнутую дробь, то есть, для того, чтобы разделить две дроби, необходимо первую из них (делимое) умножить на перевёрнутую вторую (делитель).
Несмотря на простоту данных правил, многие при решении примеров по данной теме допускают ошибки в ряде частных случаев. Рассмотрим подробнее эти частные случаи:
Во всех этих правилах мы пользовались следующим фактом: .
Решим несколько примеров на умножение и деление обыкновенных дробей, чтобы вспомнить, как пользоваться указанными правилами.
Пример 1
Примечание: при сокращении дробей мы пользовались разложением числа на простые множители. Напомним, что простыми числами называются такие натуральные числа, которые делятся только на и на само себя. Остальные числа называются составными . Число не относится ни к простым, ни к составным. Примеры простых чисел: .
Пример 2
Рассмотрим теперь один из частных случаев с обыкновенными дробями.
Пример 3
Как видим, умножение и деление обыкновенных дробей, в случае правильного применения правил, не является сложным.
Рассмотрим умножение и деление алгебраических дробей.
Пример 4
Пример 5
Отметим, что сокращать дроби после умножения можно и даже нужно по тем же правилам, которые мы до этого рассматривали на уроках, посвящённых сокращению алгебраических дробей. Рассмотрим несколько простых примеров на частные случаи.
Пример 6
Пример 7
Рассмотрим теперь несколько более сложных примеров на умножение и деление дробей.
Пример 8
Пример 9
Пример 10
Пример 11
Пример 12
Пример 13
До этого мы рассматривали дроби, в которых и числитель, и знаменатель являлись одночленами. Однако в ряде случаев необходимо перемножить или поделить дроби, числители и знаменатели которых являются многочленами. В этом случае правила остаются такими же, а для сокращения необходимо использовать формулы сокращённого умножения и вынесение за скобки.
Пример 14
Пример 15
Пример 16
Пример 17
Пример 18
На данном уроке будут рассмотрены правила умножения и деления алгебраических дробей, а также примеры на применение данных правил.
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Умножение и деление алгебраических дробей
Правила умножения и деления алгебраических дробей абсолютно аналогичны правилам умножения и деления обыкновенных дробей. Напомним их:
То есть, для того, чтобы умножить дроби, необходимо умножить их числители (это будет числитель произведения), и умножить их знаменатели (это будет знаменатель произведения).
Деление на дробь — это умножение на перевёрнутую дробь, то есть, для того, чтобы разделить две дроби, необходимо первую из них (делимое) умножить на перевёрнутую вторую (делитель).
2. Частные случаи применения правил умножения и деления дробейНесмотря на простоту данных правил, многие при решении примеров по данной теме допускают ошибки в ряде частных случаев. Рассмотрим подробнее эти частные случаи:
Во всех этих правилах мы пользовались следующим фактом: .
3. Примеры умножения и деления обыкновенных дробейРешим несколько примеров на умножение и деление обыкновенных дробей, чтобы вспомнить, как пользоваться указанными правилами.
Пример 1
Примечание: при сокращении дробей мы пользовались разложением числа на простые множители. Напомним, что простыми числами называются такие натуральные числа, которые делятся только на и на само себя. Остальные числа называются составными . Число не относится ни к простым, ни к составным.
Примеры простых чисел: .
Пример 2
Рассмотрим теперь один из частных случаев с обыкновенными дробями.
Пример 3
Как видим, умножение и деление обыкновенных дробей, в случае правильного применения правил, не является сложным.
4. Примеры умножения и деления алгебраических дробей (простые случаи)Рассмотрим умножение и деление алгебраических дробей.
Пример 4
Пример 5
Отметим, что сокращать дроби после умножения можно и даже нужно по тем же правилам, которые мы до этого рассматривали на уроках, посвящённых сокращению алгебраических дробей. Рассмотрим несколько простых примеров на частные случаи.
Пример 6
Пример 7
Рассмотрим теперь несколько более сложных примеров на умножение и деление дробей.
Пример 8
Пример 9
Пример 10
Пример 11
Пример 12
Пример 13
5.
Примеры умножения и деления алгебраических дробей (сложные случаи) До этого мы рассматривали дроби, в которых и числитель, и знаменатель являлись одночленами. Однако в ряде случаев необходимо перемножить или поделить дроби, числители и знаменатели которых являются многочленами. В этом случае правила остаются такими же, а для сокращения необходимо использовать формулы сокращённого умножения и вынесение за скобки.
Пример 14
Тема: Умножение и деление алгебраических дробей
Образование есть то, что остается, когда все выученное уже забыто
Лауэ
Цели:
Образовательные:
закрепить ЗУН по теме
провести первичный текущий контроль знаний
работать над пробелами
Развивающие:
способствовать развитию коммуникативной компетенции, т.е. умению эффективно сотрудничать с другими людьми.
способствовать развитию кооперативной компетенции, т.е. умению работать в парах.
способствовать развитию проблемной компетенции, т.е. умению понимать неизбежности возникновения трудностей в ходе любой деятельности.
Воспитательные:
прививать умение адекватно оценивать работу, проделанную товарищем;
при работе в парах воспитывать качества взаимопомощи, поддержки.
Методические:
создание условий для проявления индивидуальности, познавательной активности учащихся;
показать методику проведения урока с проектированием результатов учебной деятельности и способам их исследования на основе компетентностного подхода.
Оборудование: доска, цветной мел. Таблица «Умножение и деление алгебраических дробей»; карточки для индивидуальной работы, карточки-«памятки». Задание в свободную минуту.
Ход урока
Организационный момент
План урока записан на доске:
Устная разминка.
Индивидуальная работа.
Решение заданий.
Парная работа.
Итог урока.
Домашнее задание.
Учитель: В старину на Руси считалось, что если человек был сведущ в математике, то это означало высшую степень учености. А умение правильно видеть и слышать первый шаг к мудрости. Хочется, чтобы сегодня все ученики вашего класса показали насколько они мудры и насколько сведущие люди в алгебре 7 класса.
Итак, тема урока «Умножение и деление алгебраических дробей» На прошлом уроке вы начали изучать данную тему, и мы обсуждали, зачем ее изучаем. Давайте вспомним, где она нам пригодится уже через несколько уроков.
Учащиеся: Для совместных действий с алгебраическими дробями, для решения уравнений, а значит и задач.
Учитель: Еще в старину на Руси говорили, что умноженье — мученье, а с делением — беда. Тот, кто умел быстро и безошибочно умножать и делить считался большим математиком.
Какие вы цели поставите перед собой?
Учащиеся: Продолжить изучать тему, научиться быстро и безошибочно умножать и делить.
Учитель: Чтобы достичь поставленных целей мы (открывает план, записанный на доске, проговаривает его)
1. Устная разминка: (в это время 3 — 4 человека решают тренажер по сокращению дробей в парах) разложите на множители, заполнив пропуски
1= (у-1) (…), 5а+5b=… (a+b), ху-х=х (…), 14-2х=…
сократите дробь
Дроби, дроби, дроби бей сокращай их не жалей.
найдите ошибку, допущенную при умножении и делении алгебраических дробей
Учитель: Где допущена ошибка? Почему ошибка допущена? Какого правила, ученик не знал? Какое знал? Как надо правильно сделать?
2. Работа в тетради, № из учебника 488 (1) Анализ, решение, проверка.
Учитель: А сейчас вам представится возможность показать свои знания при выполнении теста, а чтобы воодушевить вас на работу прочитаю стишок «Чтоб записал учитель «5» в твой дневник числитель на числитель сумей умножить вмиг, а чтоб преподаватель доволен был тобой, ты первый знаменатель умножишь на второй»
Самопроверка, взаимопроверка.
По критериям (вывешены на доске) В-1 (321), В-2 (132) по правильным кодам оценивание в парах. Первоначальный результат. Оценки.
Работа над ошибками в парах «ученик-учитель»
Если в парах нет ошибок делают задание в свободную минуту.
Упростите выражение и найдите его значение при
5. Итог урока
В заключение урока, мне хотелось бы узнать у вас, какие виды работы вызвали у вас затруднения? Как вы думаете, почему? Что узнали нового? Кто из вас доволен своей работой на уроке? Как вы считаете, цели, поставленные в начале урока достигнуты?
Учитель: Закончить урок я хотела бы словами французского инженера-физика Лауэ: «Образование есть то, что остается, когда все выученное уже забыто»
Надеюсь, что этот материал вы не забудете, чтобы этого не случилось надо выполнить д/з №486,487,488 четные.
Видеоурок «Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень» — вспомогательное средство для ведения урока математики по данной теме.
С помощью видеоурока учителю легче сформировать у учеников умение выполнять умножение и деление алгебраических дробей. Наглядное пособие содержит подробное понятное описание примеров, в которых выполняются операции умножения и деления. Материал может быть продемонстрирован во время объяснения учителя или стать отдельной частью урока.
Чтобы сформировать умение решать задания на умножение и деление алгебраических дробей, по ходу описания решения даются важные комментарии, моменты, требующие запоминания и глубокого понимания выделяются с помощью цвета, жирного шрифта, указателей. С помощью видеоурока учитель может повысить эффективность урока. Данное наглядное пособие поможет быстро и эффективно достичь учебных целей.
Видеоурок начинается с представления темы. После этого указывается, что операции умножения и деления с алгебраическими дробями производятся аналогично операциям с обыкновенными дробями. На экране демонстрируются правила умножения, деления и возведения в степень дробей.
С помощью буквенных параметров демонстрируется умножение дробей. Отмечается, что при умножении дробей числители, а также знаменатели перемножаются. Так получается результирующая дробь a/b·c/d=ac/bd. Демонстрируется деление дробей на примере выражения a/b:c/d. Указывается, что для выполнения операции деления необходимо в числитель записать произведение числителя делимого и знаменателя делителя. Знаменателем частного становится произведение знаменателя делимого и числителя делителя. Таким образом, операция деления превращается в операцию умножения дроби делимого и дроби, обратной делителю. Возведение в степень дроби приравнивается дроби, в которой числитель и знаменатель возводятся в назначенную степень.
Далее рассматривается решение примеров. В примере 1 необходимо выполнить действия (5х-5у)/(х-у)·(х 2 -у 2)/10х. Чтобы решить данный пример, числитель второй дроби, входящей в произведение, раскладывается на множители. Используя формулы сокращенного умножения, делается преобразование х 2 -у 2 =(х+у)(х-у).
Затем числители дробей и знаменатели перемножаются. После проведения операций видно, что в числителе и знаменателе есть множители, которые можно сократить, используя основное свойство дроби. В результате преобразований получается дробь (х+у) 2 /2х. Здесь же рассматривается выполнение действий 7а 3 b 5 /(3a-3b)·(6b 2 -12ab+6a 2)/49a 4 b 5 . Все числители и знаменатели рассматриваются на предмет возможности разложения на множители, выделения общих множителей. Затем перемножаются числители и знаменатели. После умножения производятся сокращения. Результатом преобразования становится дробь 2(a-b)/7а.
Рассматривается пример, в котором необходимо выполнить действия (х 3 -1)/8у:(х 2 +х+1)/16у 2 . Чтобы решить выражение, предлагается преобразовать числитель первой дроби, используя формулу сокращенного умножения х 3 -1=(х-1)(х 2 +х+1). Согласно правилу деления дробей, первая дробь умножается на дробь, обратную второй. После перемножения числителей и знаменателей получается дробь, которая содержит в числителе и знаменателе одинаковые множители.
Они сокращаются. В результате получается дробь (х-1)2у. Здесь же описывается решение примера (a 4 -b 4)/(ab+2b-3a-6):(b-a)(a+2). Аналогично предыдущему примеру, для преобразования числителя применяется формула сокращенного умножения. Также преобразуется знаменатель дроби. Затем первая дробь перемножается с дробью, обратной второй дроби. После умножения выполняются преобразования, сокращения числителя и знаменателя на общие множители. В результате получается дробь -(a+b)(a 2 +b 2)/(b-3). Обращается внимание учеников, как меняются знаки числителя и знаменателя при умножении.
В третьем примере необходимо выполнить действия с дробями ((х+2)/(3х 2 -6х)) 3:((х 2 +4х+4)/(х 2 -4х+4)) 2 . В решении данного примера применяется правило возведения дроби в степень. И первая, и вторая дробь возведены в степень. Они преобразуются возведением в степень числители и знаменателя дроби. Кроме того, для преобразования знаменателей дробей применяется формула сокращенного умножения, выделение общего множителя.
Чтобы поделить первую дробь на вторую, необходимо умножить первую дробь на обратную дробь ко второй. В числителе и знаменателе образуются выражения, которые можно сократить. После преобразования получается дробь (х-2)/27х 3 (х+2).
Видеоурок «Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень» применяется для повышения эффективности традиционного урока математики. Материал может быть полезен учителю, осуществляющему обучение дистанционно. Детальное понятное описание решения примеров поможет ученикам, самостоятельно осваивающим предмет или требующим дополнительных занятий.
Как делить дроби с разными знаменателями
Когда вы складываете или вычитаете две дроби, обе дроби должны иметь одинаковые знаменатели. Но для умножения или деления дробей знаменатели вообще не имеют значения. Когда вы умножаете, вы просто работаете прямо над дробью, умножая все числители вместе, а затем все знаменатели вместе. Деление дробей работает точно так же, с добавлением еще одного шага в начале.
TL;DR (слишком длинный; не читал)
Чтобы разделить дроби независимо от знаменателей, переверните вторую дробь (делитель) вверх ногами и умножьте результат на первую дробь (делимое).
SO A / B ÷ C / D = A / B × D / C = ad / bc
Повторение: умножение дробей с разными знаменателями
Прежде чем перейти к делению дробей, найдите минутку, чтобы просмотреть процесс умножения дробей. Вам также понадобится этот навык для работы с задачами на деление.
Если перед вами стоит задача на умножение вида
\frac{a}{b} × \frac{c}{d}
, знаменатели не имеют значения. Все, что вам нужно сделать, это перемножить числители и записать их в качестве числителя вашего ответа; затем умножьте знаменатели вместе и умножьте их как знаменатель вашего ответа.
Пример 1: Вычислить
\frac{2}{5} × \frac{1}{3}
Помните, что для умножения не имеет значения, имеют ли ваши дроби одинаковые знаменатели.
Все, что вам нужно сделать, это умножить прямо поперек, что дает вам:
\frac{2 × 1}{5 × 3}
, что при упрощении дает вам:
\frac{2}{15}
Если вы можете упростить свой ответ, сократив множители из числителя и знаменателя, вы должен. Но в этом случае дальнейшее упрощение невозможно, поэтому полный ответ будет следующим:
\frac{2}{5} × \frac{1}{3} = \frac{2}{15}
Теперь о делении. Дроби
Теперь, когда вы рассмотрели, как умножать дроби, деление дробей работает почти так же — вам просто нужно добавить один дополнительный шаг. Переверните вторую дробь (также известную как делитель) вверх ногами, а затем измените операцию на умножение вместо деления.
Итак, если ваша первоначальная задача на деление выглядит так:
\frac{a}{b} ÷ \frac{c}{d}
Первое, что вы делаете, это переворачиваете вторую дробь вверх ногами, получая д / с ; затем измените знак деления на знак умножения, что даст вам:
\frac{a}{b} × \frac{d}{c}
И поскольку вы практиковались в умножении дробей, вы знаете, как решить эту задачу.
Просто умножьте числители и знаменатели, что даст вам результат:
\frac{a}{b} ÷ \frac{c}{d} = \frac{ad}{bc}
Два примера деления дробей
Теперь, когда вы знаете процесс деления дробей, пора попрактиковаться на паре примеров.
Пример 2: Вычислить
\frac{1}{3} ÷ \frac{8}{9}
Помните, что ваш первый шаг – перевернуть вторую дробь вверх ногами и изменить операцию на умножение. Это дает вам:
\frac{1}{3} × \frac{9}{8}
Теперь просто перемножьте и упростите:
\frac{1 × 9}{3 × 8} = \frac{9}{24} = \frac{3}{8}
Итак,
\frac{ 1}{3} ÷ \frac{8}{9} = \frac{3}{8}
Пример 3: Вычислить
\frac{11}{10} ÷ \frac{5}{ 7}
Обратите внимание, что одна из этих дробей неправильная (числитель больше знаменателя). Но это не меняет процесса деления дробей, поэтому переверните вторую дробь вверх ногами и измените операцию на умножение:
\frac{11}{10} × \frac{7}{5}
Как и прежде, умножьте и упростите, если сможете:
\frac{11 × 7}{10 × 5} = \frac{ 77}{50}
77 и 50 не имеют общих множителей, поэтому дальнейшее упрощение невозможно.
Итак, ваш окончательный ответ:
\frac{11}{10} ÷ \frac{5}{7} = \frac{77}{50}
Уловка для запоминания
Если вам трудно это запомнить , полезно вспомнить, что умножение и деление — взаимные операции; то есть одно отменяет другое. Когда вы переворачиваете дробь вверх ногами, это тоже называется обратной величиной. Итак, d / c является обратной величиной c / d , и наоборот.
Это означает, что когда вы делите дробь, вы фактически выполняете обратную операцию над обратной дробью . Чтобы проблема разрешилась, должны присутствовать обе эти взаимосвязи. Если бы у вас был только один из них — скажем, если бы вы выполнили обратную операцию (умножение), не взяв сначала обратное значение этой второй дроби — ваш ответ не был бы правильным.
Итак, есть ОДНО дополнительное правило, на которое следует обращать внимание, когда речь заходит о том, какие дроби можно делить, а какие нет.
Точно так же, как вы не можете делить целые числа на ноль, вы также не можете делить дробь на ноль; результат не определен. Если вы забудете об этом, вам довольно быстро напомнят, если вы попытаетесь решить такую задачу, как 5/6 ÷ 0/2. Это потому, что обычно вы переворачиваете вторую дробь и умножаете: 5/6 × 2/0. Но в знаменателе дроби не может быть нуля; это тоже считается неопределенным.
Точно так же, как вы не можете делить целые числа на ноль, вы также не можете делить дробь на ноль; результат не определен. Если вы забудете об этом, вам довольно быстро напомнят, если вы попытаетесь решить такую задачу, как 5/6 ÷ 0/2. Это потому, что обычно вы переворачиваете вторую дробь и умножаете: 5/6 × 2/0. Но в знаменателе дроби не может быть нуля; это тоже считается неопределенным.Как насчет деления смешанных чисел?
Если вас просят разделить смешанные числа, будьте осторожны – это ловушка! Прежде чем вы сможете продолжить, вы должны преобразовать это смешанное число в неправильную дробь. Как только это будет сделано, вы будете следовать точно такому же процессу, который вы бы использовали для правильных дробей. См. Пример 3 выше, иллюстрирующий, как это работает. Он включает неправильную дробь 11/10, которую также можно записать как смешанное число 1 1/10.
Умножение и деление дробей: примеры и методы
Джон был приглашен на день рождения Эми, и она пригласила в общей сложности 7 друзей, чтобы отпраздновать ее день рождения.
Чтобы получить одинаковые кусочки торта, каждый из участников должен иметь \(\frac{1}{8}\) торта. Случайно Эми уронила свой кусок пирога, поэтому Джон решил отдать ей часть своего. Он разделил свой кусок пирога на 2 и отдал половину Эми.
Можем ли мы посчитать, какая часть пирога досталась Эми в итоге? Ответ состоит в том, чтобы разделить дробь Джона на 2, то есть \(\dfrac{\dfrac{1}{8}}{2}=\dfrac{1}{16}\) торта.
В этой статье мы научимся выполнять операции умножения и деления с дробями.
Умножение и деление дробей шаг за шагом
Нас интересуют операции умножения и деления дробей. Прежде всего, давайте вспомним наши знания о дробях.
Дробь представляет часть целого . Он состоит из двух частей – числителя и знаменателя. Числитель пишется над чертой, а знаменатель — под чертой. Знаменатель не может быть равен нулю.
\(\dfrac{2}{3}, \dfrac{1}{2}, \dfrac{7}{8}, \cdots\) являются примерами дробей.
Мы знакомы с умножением и делением двух чисел.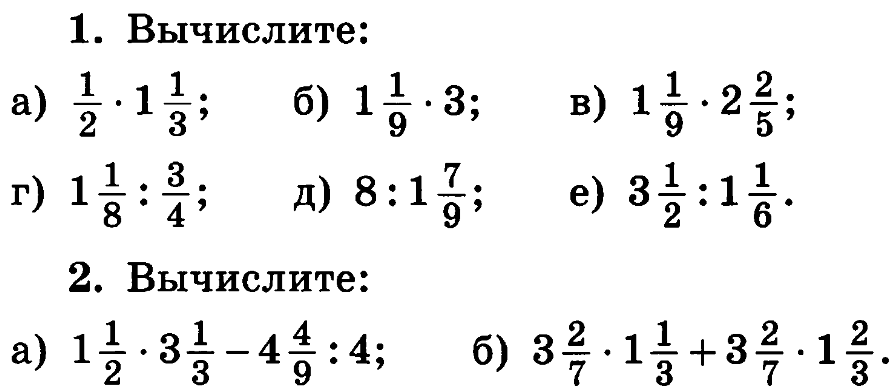
Теперь вопрос в том, как выполнять эти операции над дробями, а не над целыми числами.
Предположим, вам даны две дроби, скажем, \(\dfrac{a}{b}\) и \(\dfrac{c}{d}\), мы хотим знать, что мы подразумеваем под \(\dfrac{ a}{b}\times \dfrac{c}{d}\) и \(\dfrac{\dfrac{a}{b}}{\dfrac{c}{d}}.\)
Умножение и деление правила дробей
Правила умножения дробей
Чтобы умножить две дроби \(\dfrac{a}{b}\) и \(\dfrac{c}{d}\), необходимо умножить числители вместе и знаменатели вместе. Таким образом. имеем
\[\dfrac{a}{b}\times \dfrac{c}{d}=\dfrac{a\times b}{c\times d}.\]
Мы, по сути, следуем следующие шаги, чтобы умножить дроби вместе.
Шаг 1. Перемножьте числители двух дробей вместе и знаменатели вместе.
Шаг 2. Разделите полученные числа, чтобы получить новую дробь.
На этом мы можем остановиться. Однако, если числитель и знаменатель новой дроби имеют общие делители, мы переходим к следующему шагу, чтобы получить простейшую форму дроби.
Шаг 3. Найдите общий делитель числителя и знаменателя новой дроби. Разделите числитель и знаменатель на этот общий множитель. Это дает простейшую форму дроби.
Перемножьте дроби \(\dfrac{3}{7}\) и \(\dfrac{5}{11}\).
Решение
Шаг 1. Перемножая числители дробей, получаем \[3\times 5=15.\]
Перемножая знаменатели дробей вместе, получаем \[7\times 11=77.\]
Шаг 2. Деление полученных чисел дает новую дробь \(\dfrac{15}{77}.\)
Так как числитель и знаменатель новой дроби не имеют общих факторов, это самая простая форма.
Умножить\(\dfrac{2}{5}\) и \(\dfrac{7}{9}\).
Решение
Перемножая числители и знаменатели, получаем
\[\dfrac{2}{5}\times \dfrac{7}{9}=\dfrac{2\times 7}{5 \times 9}=\dfrac{14}{45}.\]
Умножить \(\dfrac{5}{8}\) и \(\dfrac{2}{3}.\)
Решение
Шаг 1. Перемножая числители двух дробей вместе, мы получаем
\(5 \times 2=10.\) Точно так же, делая то же самое со знаменателями, получаем \(8\times 3=24.\)
Шаг 2. Разделив полученные числа, мы получим новую дробь \(\dfrac{10}{24}.\)
Заметим, что числитель и знаменатель новой дроби имеют общий делитель 2.
Шаг 3. Мы получаем простейшую форму этой дроби путем деления общего делителя 2 из числителя 10 и знаменателя 24. Это дает нам \(10 \divsymbol 2=5\)и \(24\divsymbol 2=12\).
Таким образом, простейшая дробь равна \(\dfrac{5}{12}.\)
Правила деления дробей
Чтобы разделить две дроби, вы, по сути, инвертируете дробь, на которую делите, а затем умножаете ее на первую. Таким образом, деление двух дробей вида
\[\frac{a}{b}\divsymbol\frac{c}{d}=\frac{\frac{a}{b}}{\frac{c} {d}}\]
равносильно умножению дробей \[\frac{a}{b}\times \frac{d}{c}.\] Таким образом, мы имеем
\[\frac{a }{b}\divsymbol\frac{c}{d} =\frac{a}{b}\times\frac{d}{c}. \]
Поскольку мы уже видели, как умножать две дроби, просто следуйте этим шагам отсюда.
Таким образом, мы выполняем следующие шаги для выполнения деления на дроби,
Шаг 1. Переворачиваем делитель дроби – числитель становится знаменателем, а знаменатель становится числителем.
Шаг 2. После инверсии перемножьте полученные дроби вместе, используя шаги, описанные для умножения дробей.
Разделить \(\dfrac{5}{8}\) на \(\dfrac{2}{3}.\)
Решение
Шаг 1. Обратив делитель, получим \(\dfrac{3}{2}\).
Шаг 2. Теперь выполняем умножение полученных дробей,
\(\dfrac{5}{8}\) и \(\dfrac{3}{2}\), чтобы получить,
\ [\dfrac{5}{8}\times \dfrac{3}{2}=\dfrac{5\times 3}{8\times 2}=\dfrac{15}{16}.\]
Поскольку числитель и знаменатель не имеют общих делителей, это простейшая форма.
Найдите \(\dfrac{2}{5}\divsymbol \dfrac{3}{8}\).
Решение
Здесь \(\dfrac{2}{5}\) — дробь делимого, а \(\dfrac{3}{8}\) — дробь делителя.
Шаг 1. Инвертируем делитель, получаем \(\dfrac{8}{3}.\)
Шаг 2. Теперь умножаем полученные дроби,
\[\frac{2}{ 5}\divsymbol\frac{3}{8}=\frac{2}{5}\times \frac{8}{3}=\frac{2\times 8}{3\times 5} =\frac{ 16}{15}.\]
Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.
При умножении или делении дроби на целое число \(a\), \(a\) может быть записано как его эквивалентная форма \(\dfrac{a}{1}\), поэтому никаких изменений в процедуре не требуется .
Найти \(\dfrac{\dfrac{2}{5}}{3}.\)
Решение
Здесь \(\dfrac{2}{5}\) — доля делимого, а \( 3=\dfrac{3}{1}\) — делитель дроби.
Шаг 1. Переворачиваем делитель, получаем \(\dfrac{1}{3}\).
Шаг 2. Теперь умножьте дроби, чтобы получить
\[\dfrac{2}{5}\times \dfrac{1}{3}=\dfrac{2\times 1}{5\times 3 }=\dfrac{2}{15}. \]
Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.
Упростить \(\dfrac{4}{\dfrac{7}{9}}\).
Решение
Здесь \(4=\dfrac{4}{1}\) — дробь делимого, а \(\dfrac{7}{9}\) — дробь делителя.
Решение
Шаг 1. Переворачиваем делитель, получаем \(\dfrac{9}{7}\).
Шаг 2. Теперь перемножьте дроби, чтобы получить
\[\dfrac{4}{\dfrac{7}{9}}=\dfrac{4}{1}\times \dfrac{9} {7}=\dfrac{4\times 9}{1\times 7}=\dfrac{36}{7}.\]
Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.
Чтобы упростить нашу работу, избегая гигантских умножений, мы можем «отменить» общие множители между числителями и знаменателями в начале, прежде чем мы перемножим члены вместе. Это изменит шаги для умножения дробей на следующие:
Шаг 1. Если какие-либо числитель и знаменатель имеют общий множитель, разделите соответствующий числитель и знаменатель на общий множитель, чтобы «сократить» общий множитель. Делайте это до тех пор, пока между числителями и знаменателями не останется общих множителей.
Шаг 2. Выполнить умножение полученных дробей.
В следующих примерах мы использовали вышеупомянутый метод.
Примеры умножения и деления дробей
До сих пор мы рассматривали примеры операций умножения и деления двух дробей. Вы можете умножать / делить несколько дробей вместе, используя те же правила, что описаны выше. Если есть цепочка из нескольких умножений и делений, вы должны сначала инвертировать члены делителя.
Упростить \(\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}\)
Решение
Здесь умножаются три дроби. Первый шаг состоит в том, чтобы умножить числители дробей вместе \(5\умножить на 18\умножить на 21\) и знаменатели вместе \(9\умножить на 13\умножить на 20.\)
Здесь мы видим, что мы получаем умножение огромных чисел. Чтобы избежать этого, мы собираемся сначала отменить общие факторы, где это возможно.
Шаг 1 . Числители 5,18,21, а знаменатели 9,13,20. Мы видим, что 9 и 18 имеют 9 в качестве общего делителя, а 5 и 20 имеют 5 в качестве делителя, таким образом, мы имеем
\[\frac{5}{9}\times\dfrac{18}{13}\times\dfrac{ 21}{20}=\dfrac{1}{1}\times\dfrac{2}{13}\times\dfrac{21}{4}.\]
Далее, мы можем упростить 2 и 4, разделив на 2, чтобы получить
\[\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}=\dfrac{1}{13} \times\dfrac{ 21}{2}.\]
Шаг 2. И окончательный ответ:
\[\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}=\dfrac{21}{13\times 2 }=\dfrac{21}{26}.\]
Упростить \[\dfrac{14}{39}\times\dfrac{12}{35}\divsymbol\dfrac{8}{13}\times\dfrac {2}{9}\]
Решение
Шаг 1. Инвертируйте делитель, чтобы получить
\[\dfrac{14}{39}\times\dfrac{12}{35}\ divsymbol\dfrac{8}{13}\times\dfrac{2}{9}=\dfrac{14}{39}\times\dfrac{12}{35}\times\dfrac{13}{8}\times \dfrac{2}{9}\]
Шаг 2. Теперь попробуем привести термы к простейшему виду. Разделив 14 и 35 на 7, 13 и 39 на 13, 12 и 9 на 3, 2 и 8 на 2, получим
\[\dfrac{14}{39}\times\frac{12}{35}\ раз\dfrac{13}{8}\times\dfrac{2}{9}=\dfrac{2}{3}\times\dfrac{4}{5}\times\dfrac{1}{4}\times \dfrac{1}{3}\]
Шаг 3 . Отбросив 4, мы получим \[\dfrac{2}{3}\times\dfrac{4}{5}\times\dfrac{1}{4}\times\dfrac{1}{3}=\dfrac {2}{5}\times\dfrac{1}{5}\times \dfrac{1}{3}=\dfrac{2}{45}.\]
В следующем примере мы выполняем умножение и деление смешанных дробей.
Смешанная дробь представляет собой комбинацию целого числа и дроби. Чтобы умножить или разделить смешанные дроби, сначала преобразуйте их в неправильные дроби, а затем продолжите стандартный процесс.
Упростить
\[4\dfrac{2}{7}\times 2\dfrac{1}{3}\div \dfrac{3}{5}.\]
Решение
Преобразование смешанного дроби на неправильные дроби, получаем
\[4\dfrac{2}{7}\times 2\dfrac{1}{3}\div \frac{3}{5} = \dfrac{30}{7}\times \dfrac{7} {3} \div \dfrac{3}{5}.