Как решаются дробные уравнения? – 4 Метода — ЕГЭ/ОГЭ
Окт192020
Статьи
В статье расскажу, как решать дробные уравнения 4-мя разными способами. Объясню, почему в дробных уравнениях нужно ОДЗ, как найти корень по методу «креста» и научу мантре, которая спасет вас от провала на контрольной. Всего одна статья поможет вам стать экспертом в области дробных уравнений))
Содержание:
Введение
Виды дробных уравнений:
ложные дробные (линейные с дробями)
дробные рациональные
дробные иррациональные
Дробные уравнения – это уравнения, обязательно содержащие числитель и знаменатель. Но давайте разберемся, какого вида знаменатель это должен быть.
Посмотрите на эти 2 примера – только одно из них дробное. Как вы думаете какое?
ОДЗ: НЕТ
ОДЗ: x ≠ –3
Те, кто ответил, что второе – молодцы.
Почему же так?
Все дело в ОДЗ. В 1) его нет, во 2) есть
Знаменатель без переменных всегда можно представить как дробный множитель обычного линейного уравнения.
А вот второе уравнение как раз-таки дробное, потому что в знаменатели у него переменная.
Итак, запомнили: дробное уравнение обязательно содержит переменную в знаменателе.
С определением разобрались, пора начать их решать!
Виды дробных уравнений- Ложные дробные
метод пропорции
приведение к общему знаменателю
- Дробные рациональные
метод пропорции
приведение к общему знаменателю
разбиение на скобки
замена переменной
- Дробные иррациональные
Ложными дробными – я назвал все уравнения, которые имеют в своем составе дроби, но в знаменателях которых нет неизвестной.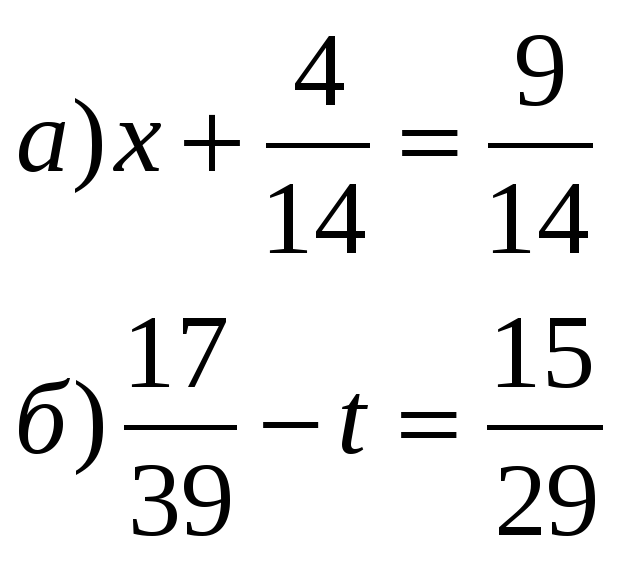
Дробь равна 0
Дробь равна числу
Несколько слагаемых
Просто числитель приравниваем к 0 😉
x – 2 = 0
x = 2
В обоих случаях нам необходимо избавиться от знаменателя ❗
x – 3 = 2
x = 5
Домножим все уравнение на общий знаменатель = 6
x – 1 + 2x + 3(x+1) = 0
6x + 2 = 0
6x = -2
x = –1/3
Дробные РациональныеОбщий алгоритм решения:
1) Выписать ОДЗ
2) Объединить все под 1 дробь
или Избавиться от вида дроби
3) Разбить на скобки → найти корни
4) Исключить из корней те, что не подходят под ОДЗ
1. Выпишем ОДЗ
ОДЗ:
x – 4 ≠ 0
x ≠ 4
2. Разложим числитель на скобки (Как я так легко и просто нашел корни квадратного уравнения знают те, кто читал мою статью с интересными способами решения квадратных уравнений, их аж 6! Пробуйте, решение квадратных уравнений в жизни пригодится…до конца института так точно))
3.
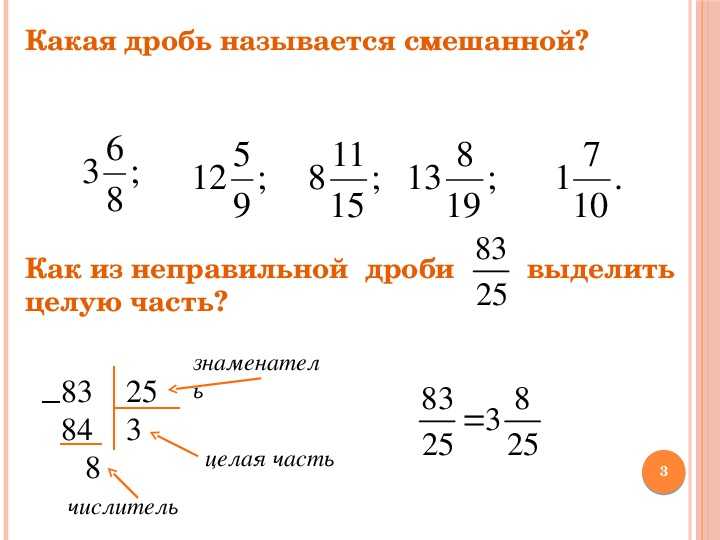Выпишем корни числителя
x – 5 = 0
x = 5
x – 4 = 0
x = 4
4. Сверимся с ОДЗ
x = 5
Подходит
x = 4
Не входит в ОДЗ
Ответ: 5
1. Выпишем ОДЗ
x – 2 ≠ 0
x ≠ 2
2. Метод пропорции «Крест на крест»
3. Выпишем корни
– x – 2 = 0
x = –2
4. Сверимся с ОДЗ
x = –2
Подходит
Ответ: –2
1. Выпишем ОДЗ
x – 2 ≠ 0
x ≠ 2
2.
Избавимся от знаменателя
Домножим все уравнения на общий знаменатель x(x – 2)
3. Выпишем корни
x = 2/3
4. Сверимся с ОДЗ
x = 2/3
Подходит
Ответ: 2/3
Очень Трудные (замена)
1. Выпишем ОДЗ
x + 2 ≠ 0
x ≠ –2
2. Заменим x + 2 на a
x + 2 = a
3. Приведем к общему знаменателю
4. Найдем корни числителя
(По разности квадратов)
5. Проведем обратную замену
a = x + 2
6. Сверимся с ОДЗ
Подходит
Ответ:
Автор: Venage
Алгоритм решения дробного рационального уравнения: определение и понятие, примеры.
2-4 \cdot 7 \cdot (-141) = 1225+3948 = 5173 $$$$ x = \frac{32 \pm \sqrt{5173}}{14} $$
Все три корня $x_1 = 1, x_{2,3} = \frac{32 \pm \sqrt{5173}}{14}$ подходят.
Ответ: $\{1; \frac{32 \pm \sqrt{5173}}{14}\}$
8.4 Решение уравнений с дробями или десятичными коэффициентами — Предварительная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Решение уравнений с дробными коэффициентами
- Решение уравнений с десятичными коэффициентами
Приготовься 8.10
Прежде чем начать, пройдите этот тест на готовность.
Умножить: 8·38,8·38.
Если вы пропустили эту проблему, просмотрите пример 4.28
Приготовься 8.11
Найдите ЖК-дисплей 56 и 14, 56 и 14.
Если вы пропустили эту проблему, просмотрите пример 4.63
Приготовься 8.12
Умножить: 4.784.78 на 100.100.
Если вы пропустили эту проблему, просмотрите пример 5.
Решение уравнений с дробными коэффициентами
Давайте воспользуемся представленной ранее общей стратегией решения линейных уравнений, чтобы решить уравнение 18x+12=14,18x+12=14.
| Чтобы изолировать член xx, вычтите 1212 с обеих сторон. | |
| Упростите левую сторону. | |
| Измените константы на эквивалентные дроби с помощью ЖК-дисплея. | |
| Вычесть. | |
| Умножьте обе части на обратное число 1818. | |
| Упрощение. |
Этот метод работал нормально, но многие ученики не чувствуют себя уверенно, когда видят все эти дроби. Итак, мы собираемся показать альтернативный метод решения уравнений с дробями. Этот альтернативный метод исключает дроби.
Мы применим свойство равенства умножения и умножим обе части уравнения на наименьший общий знаменатель всех дробей в уравнении. Результатом этой операции будет новое уравнение, эквивалентное первому, но без дробей. Этот процесс называется очистка уравнения дробей . Давайте снова решим то же уравнение, но на этот раз воспользуемся методом очистки дробей.
Пример 8,37
Решите: 18x+12=14,18x+12=14.
Решение
| Найдите наименьший общий знаменатель всех дробей в уравнении. | |
| Умножьте обе части уравнения на этот ЖК-дисплей, 8. Это очищает дроби. | |
| Использовать Распределительное свойство. | |
| Упростите — и заметьте, больше никаких дробей! | |
Решите, используя общую стратегию решения линейных уравнений. | |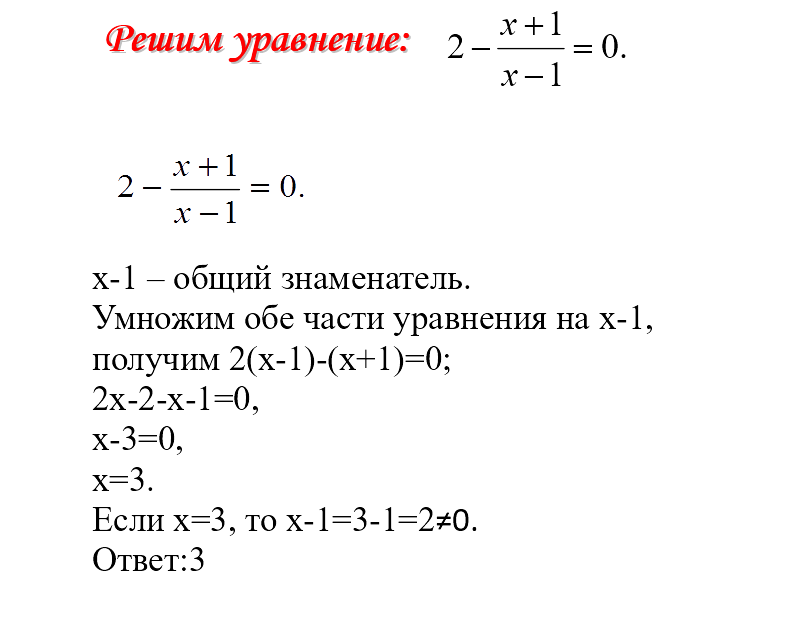
| Упрощение. | |
| Проверка: пусть x=−2x=−2 |
Попробуй это 8,73
Решите: 14x+12=58,14x+12=58.
Попробуй это 8,74
Решите: 16y−13=16,16y−13=16.
Обратите внимание, что в примере 8.37, как только мы очистили уравнение дробей, оно стало таким же, как те, которые мы решали ранее в этой главе. Мы изменили задачу на ту, которую уже знали, как решить! Затем мы использовали общую стратегию решения линейных уравнений.
Как
Решите уравнения с дробными коэффициентами, очистив дроби.
- Шаг 1. Найдите наименьший общий знаменатель числа все дроби в уравнении.
- Шаг 2. Умножьте обе части уравнения на этот ЖК-дисплей. Это очищает дроби.
- Шаг 3.
Решите, используя общую стратегию решения линейных уравнений.
Пример 8,38
Решите: 7=12x+34x−23x.7=12x+34x−23x.
Решение
Мы хотим очистить дроби, умножив обе части уравнения на LCD всех дробей в уравнении.
| Найдите наименьший общий знаменатель | |
| Умножьте обе части уравнения на 12. | |
| Распределить. | |
| Упростите — и заметьте, больше никаких дробей! | |
| Объедините похожие термины. | |
| Разделить на 7. | |
| Упрощение. | |
| Проверка: Пусть x=12.x=12. | |
Попробуй это 8,75
Решите: 6=12v+25v−34v.6=12v+25v−34v.
Попробуй это 8,76
Решите: −1=12u+14u−23u.
−1=12u+14u−23u.
В следующем примере у нас будут переменные и дроби с обеих сторон уравнения.
Пример 8,39
Решите: x+13=16x−12.x+13=16x−12.
Решение
| Найдите ЖК всех дробей в уравнении. | |
| Умножьте обе стороны на LCD. | |
| Распределить. | |
| Упрости — больше никаких дробей! | |
| Вычесть xx с обеих сторон. | |
| Упрощение. | |
| Вычтите 2 с обеих сторон. | |
| Упрощение. | |
| Разделить на 5. | |
| Упрощение. | |
| Проверить: Подставить x=−1.x=−1. | |
Попробуй это 8,77
Решите: a+34=38a−12.
a+34=38a−12.
Попробуй это 8,78
Решите: c+34=12c−14.c+34=12c−14.
В примере 8.40 мы начнем с использования свойства Distribution. Этот шаг сразу очистит дроби!
Пример 8.40
Решить: 1=12(4x+2).1=12(4x+2).
Решение
| Распределить. | |
| Упрощение. Теперь не нужно очищать дроби! | |
| Вычтите 1 с обеих сторон. | |
| Упрощение. | |
| Разделить на 2. | |
| Упрощение. | |
| Проверка: Пусть x=0.x=0. | |
Попробуй это 8,79
Решите: −11=12(6p+2).−11=12(6p+2).
Попробуй это 8,80
Решите: 8=13(9q+6).
Много раз, даже после распределения, все еще будут дроби.
Пример 8.41
Решите: 12(y−5)=14(y−1).12(y−5)=14(y−1).
Решение
| Распределить. | |
| Упрощение. | |
| Умножение на LCD, 4. | |
| Распределить. | |
| Упрощение. | |
| Соберите члены yy слева. | |
| Упрощение. | |
| Соберите константы справа. | |
| Упрощение. | |
| Проверить: заменить 99 на y.y. | |
Попробуй это 8,81
Решите: 15(n+3)=14(n+2).15(n+3)=14(n+2).
Попробуй это 8,82
Решите: 12(м-3)=14(м-7).
12(м-3)=14(м-7).
Решение уравнений с десятичными коэффициентами
В некоторых уравнениях есть десятичные дроби. Такое уравнение возникает, когда мы решаем задачи, связанные с деньгами и процентами. Но десятичные дроби — это еще один способ представления дробей. Например, 0,3=3100,3=310 и 0,17=17100,0,17=17100. Итак, когда у нас есть уравнение с десятичными дробями, мы можем использовать тот же процесс, который мы использовали для очистки дробей, — умножить обе части уравнения на наименьший общий знаменатель.
Пример 8,42
Решите: 0,8x−5=7,0,8x−5=7.
Решение
Единственный десятичный знак в уравнении — 0.8.0.8. Поскольку 0,8=810, 0,8=810, ЖК-дисплей равен 10,10. Мы можем умножить обе части на 1010, чтобы очистить десятичную дробь.
Умножьте обе стороны на LCD. | |
| Распределить. | |
| Умножьте и обратите внимание, больше нет десятичных знаков! | |
| Добавьте 50, чтобы получить все константы справа. | |
| Упрощение. | |
| Разделите обе части на 8. | |
| Упрощение. | |
| Проверка: Пусть x=15.x=15. | |
Попробуй это 8,83
Решите: 0,6x−1=11,0,6x−1=11.
Попробуй это 8,84
Решите: 1,2x−3=9,1,2x−3=9.
Пример 8,43
Решите: 0,06x+0,02=0,25x−1,5.0,06x+0,02=0,25x−1,5.
Решение
Посмотрите на десятичные дроби и придумайте эквивалентные дроби.
0,06=6100,0,02=2100,0,25=25100,1,5=15100,06=6100,0,02=2100,0,25=25100,1,5=1510
Обратите внимание, на ЖК-дисплее 100,100.
Путем умножения на ЖК-дисплее мы очистим десятичные дроби.
| Умножьте обе стороны на 100. | |
| Распределить. | |
| Умножьте, и больше никаких десятичных знаков. | |
| Соберите переменные справа. | |
| Упрощение. | |
| Соберите константы слева. | |
| Упрощение. | |
| Разделить на 19. | |
| Упрощение. | |
| Проверка: Пусть x=8.x=8. | |
Попробуй это 8,85
Решите: 0,14ч+0,12=0,35ч-2,4.
0,14ч+0,12=0,35ч-2,4.
Попробуй это 8,86
Решите: 0,65k−0,1=0,4k−0,35.0,65k−0,1=0,4k−0,35.
В следующем примере используется уравнение, типичное для тех, которые мы увидим в приложении к деньгам в следующей главе. Обратите внимание, что мы сначала распределим десятичную дробь, прежде чем очистим все десятичные дроби в уравнении.
Пример 8,44
Решите: 0,25x+0,05(x+3)=2,85.0,25x+0,05(x+3)=2,85.
Решение
| Сначала раздайте. | |
| Объедините похожие термины. | |
| Чтобы убрать десятичные дроби, умножьте на 100. | |
| Распределить. | |
| Вычтите 15 с обеих сторон. | |
| Упрощение. | |
Разделить на 30. | |
| Упрощение. | |
| Проверка: Пусть x=9.x=9. | |
Попробуй это 8,87
Решите: 0,25n+0,05(n+5)=2,95.0,25n+0,05(n+5)=2,95.
Попробуй это 8,88
Решите: 0,10d+0,05(d−5)=2,15.0,10d+0,05(d−5)=2,15.
Раздел 8.4 Упражнения
Практика ведет к совершенству
Решите уравнения с коэффициентами дробей
В следующих упражнениях решите уравнение, удалив дроби.
209.
14x−12=−3414x−12=−34
210.
34x−12=1434x−12=14
211.
56y−23=−3256y−23=−32
212.
56y−13=−7656y−13=−76
213.
12а+38=3412а+38=34
214.
58б+12=-3458б+12=-34
215.
2=13x−12x+23×2=13x−12x+23x
216.
2=35x−13x+25×2=35x−13x+25x
217.
14м-45м+12м=-114м-45м+12м=-1
218.
56n-14n-12n=-256n-14n-12n=-2
219.
х+12=23х-12х+12=23х-12
220.
х+34=12х-54х+34=12х-54
221.
13w+54=w−1413w+54=w−14
222.
32z+13=z−2332z+13=z−23
223.
12x−14=112x+1612x−14=112x+16
224.
12а-14=16а+11212а-14=16а+112
225.
13б+15=25б-3513б+15=25б-35
226.
13x+25=15x−2513x+25=15x−25
227.
1=16(12x−6)1=16(12x−6)
228.
1=15(15x−10)1=15(15x−10)
229.
14(р-7)=13(р+5)14(р-7)=13(р+5)
230.
15(q+3)=12(q−3)15(q+3)=12(q−3)
231.
12(х+4)=3412(х+4)=34
232.
13(х+5)=5613(х+5)=56
Решение уравнений с десятичными коэффициентами
В следующих упражнениях решите уравнение, очистив десятичные дроби.
233.
0,6г+3=90,6г+3=9
234.
0,4y−4=20,4y−4=2
235.
3,6j−2=5,23,6j−2=5,2
236.
2,1к+3=7,22,1к+3=7,2
237.
0,4х+0,6=0,5х-1,20,4х+0,6=0,5х-1,2
238.
0,7х+0,4=0,6х+2,40,7х+0,4=0,6х+2,4
239.
0,23х+1,47=0,37х-1,050,23х+1,47=0,37х-1,05
240.
0,48х+1,56=0,58х-0,640,48х+1,56=0,58х-0,64
241.
0,9x−1,25=0,75x+1,750,9x−1,25=0,75x+1,75
242.
1,2х-0,91=0,8х+2,291,2x−0,91=0,8x+2,29
243.
0,05n+0,10(n+8)=2,150,05n+0,10(n+8)=2,15
244.
0,05n+0,10(n+7)=3,550,05n+0,10(n+7)=3,55
245.
0,10d+0,25(d+5)=4,050,10d+0,25(d+5)=4,05
246.
0,10d+0,25(d+7)=5,250,10d+0,25(d+7)=5,25
247.
0,05(q-5)+0,25q=3,050,05(q-5)+0,25q=3,05
248.
0,05(q-8)+0,25q=4,100,05(q-8)+0,25q=4,10
Математика на каждый день
249.
Монеты У Тейлора есть $2,00$2,00 в десятицентовиках и пенни. Количество пенни на 22 больше, чем количество десятицентовиков. Решите уравнение 0,10d+0,01(d+2)=20,10d+0,01(d+2)=2 для d,d, количества десятицентовиков.
250.
Марки Трэвис купил на 9,45 долларов 9,45 долларов марок номиналом 49 центов49 центов и марок номиналом 21 цент21 цент. Количество марок номиналом 21 цент21 цент было на 55 меньше, чем количество марок номиналом 49 центов49 центов. Решите уравнение 0,49s+0,21(s−5)=9,450,49s+0,21(s−5)=9,45 для s,s, чтобы найти количество 49-центовых марок, купленных Трэвисом.
Письменные упражнения
251.
Объясните, как найти наименьший общий знаменатель чисел 38, 16 и 23.