Как решать графически систему уравнений: Графический метод — урок. Алгебра, 9 класс.

Математика: Справ. материалы

Математика: Справ. материалы

Гусев В. А., Мордкович А. Г. Математика: Справ. материалы: Кн. для учащихся.— М.: Просвещение, 1988.— 416 с. В книге дано краткое изложение основных разделов школьных курсов алгебры и начал анализа, геометрии. Книга окажет помощь в систематизации и обобщении знаний по математике. Оглавление СЛОВО К УЧАЩИМСЯ ГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел. 8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами. 29. Свойства арифметических действий над действительными числами. 30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку. 41. Правило извлечения квадратного корня из натурального числа. 42. Понятие о степени с иррациональным показателем. 43. Свойства степеней с действительными показателями. § 4. Комплексные числа 45. Арифметические операции над комплексными числами. 46. Алгебраическая форма комплексного числа. 47. Отыскание комплексных корней уравнений. ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 49. 3. 112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени. 130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 140. Системы и совокупности уравнений. 141. Уравнения, содержащие переменную под знаком модуля. 142. Понятие следствия уравнения. Посторонние корни. 143. Уравнения с переменной в знаменателе. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения. 149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными. 169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной 175. Графическое решение неравенств с одной переменной. 176. Линейные неравенства с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188. Неравенства и системы неравенств с двумя переменными. § 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21. Производная и ее применения 209. Определение производной. 210. Формулы дифференцирования. Таблица производных. 211. Дифференцирование суммы, произведения, частного. 212. Сложная функция и ее дифференцирование. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226. Правила вычисления первообразных. 227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. § 3. Геометрические построения на плоскости 22. Простейшие задачи на построение. 23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники. 49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76. Понятие движения. § 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ

графически решить систему

Вы искали графически решить систему? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и графически решить систему уравнений, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «графически решить систему».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как графически решить систему,графически решить систему уравнений,графический способ,графический способ решения,графическим способом решите систему уравнений ответ округлите до десятых,графическое решение системы уравнений,как графически решить систему уравнений,как графическим способом решить систему уравнений,как решать графически систему уравнений,как решать графическим способом систему уравнений,как решать систему уравнений графически,как решать систему уравнений графическим способом,как решить графически систему уравнений,как решить графическим способом систему уравнений,как решить систему уравнений графически,как решить систему уравнений графическим способом,как решить систему уравнений способом графическим,решение систем уравнений графическим способом,решение системы уравнений графическим способом,решите графическим способом систему уравнений,решите систему уравнений графическим способом,решить графически систему,решить графическим способом систему,решить графическим способом систему уравнений,решить систему графически,решить систему графическим способом,решить систему уравнений графически,решить систему уравнений графическим способом,система уравнений графическая,система уравнений графическим способом,системы уравнений решение графическим способом. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и графически решить систему. Просто введите задачу в окошко и нажмите «решить» здесь (например, графический способ).

Решить задачу графически решить систему вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Объяснение урока: графическое решение систем уравнений

В этом объяснении мы научимся решать систему из двух линейных уравнений или одного линейного и одного квадратного уравнения, рассматривая их графики и определение точки пересечения.

Когда мы изображаем любую функцию, скажем, 𝑦=𝑓(𝑥), 𝑥-координата любой точки на графике сообщает нам входное значение функции, а 𝑦-координата сообщает нам соответствующий результат. Другими словами, каждая точка на графике имеет вид (𝑥,𝑓(𝑥)). Точно так же, если мы нарисуем график уравнения, то координаты любой точки на графике удовлетворяют уравнению.

Мы можем использовать эту идею для решения систем уравнений, используя их графики. Если мы нарисуем графики двух уравнений на одной и той же паре осей координат, то любая точка, лежащая на обоих графиках уравнений, будет удовлетворять обоим уравнениям; это будет решением система.

Например, рассмотрим следующую систему линейных уравнений: 𝑦=3𝑥+2,𝑦=−4𝑥+16.

Мы можем решить эту систему, начертив обе линии на одной и той же паре координатных осей и найдя координаты точки пересечение. У нас есть несколько способов нарисовать прямую линию; например, один из способов — найти координаты двух точки на нем и соедините их вместе, продолжая линию вперед с обеих сторон. Подставляем 𝑥=0 и 𝑥=1 в каждое уравнение, чтобы найти две точки на каждой прямой: 𝑦=3(0)+2=2,𝑦=3(1)+2=5,𝑦=−4(0)+16=16,𝑦=−4(1)+16=12.

Таким образом, первая линия соединяет точки (0,2) и (1,5), а вторая линия соединяет точки (0,16) и (1,12). Мы можем нарисовать эти линии как следует.

Видим, что есть единственная точка пересечения линий с координатами (2,8). С он лежит на графиках обоих уравнений, 𝑥=2 и 𝑦=8 должны быть решениями обоих уравнений. Следовательно, это решение системы уравнений.

Стоит отметить, что каждое решение системы уравнений является точкой пересечения на графиках. Это означает, что, поскольку есть только одна точка пересечения, есть только одно решение системы.

В нашем первом примере мы идентифицируем решение системы уравнений, используя их графики.

Пример 1. Определение решений системы уравнений по их графикам

Используйте показанный график для решения заданных одновременных уравнений 𝑦=4𝑥−2,𝑦=−𝑥+3.

Ответ

Когда мы изображаем функцию, 𝑥- и 𝑦-координаты любой точки на графике уравнения сообщите нам значения 𝑥 и 𝑦, которые решают это уравнение. Поэтому любая точка, лежащая на обоих графики уравнений будут удовлетворять обоим уравнениям; это будет решением системы. Мы видим, что есть только одна точка пересечения, и мы можем прочитать координаты из графика.

Мы видим, что точка пересечения (1,2). Таким образом, 𝑥=1 и 𝑦=2 является решением обоих уравнений (поскольку точка лежит на обеих прямых).

Следовательно, 𝑥=1 и 𝑦=2 является решением системы уравнений.

В нашем следующем примере мы найдем решение системы линейных уравнений, нарисовав графики обоих уравнений и найдя точка пересечения.

Пример 2: построение линейной системы уравнений и ее решение

Построив графики 𝑦=𝑥−1 и 𝑦=5𝑥+7, найдите точку, которая оба уравнения одновременно.

Ответ

Если конкретная пара значений 𝑥 и 𝑦 удовлетворяет обоим уравнениям, то мы можем отметить, что точка с этими координатами должна лежать на пересечении обоих графиков. Это потому, что мы строим графики, строя значения 𝑥 и 𝑦, которые удовлетворяют уравнению, поэтому точка пересечения удовлетворяет оба уравнения.

Существует множество способов построения графиков прямых линий. Например, мы могли бы использовать тот факт, что обе строки даны в форме наклона-перехвата 𝑦=𝑚𝑥+𝑐. Итак, наклон каждой линии равен 𝑚, а 𝑦-перехват равен 𝑐.

Кроме того, мы можем начертить любую прямую линию, найдя координаты двух точек на линии, а затем соединив эти точки прямой линией. Заметим, что 𝑦-перехват 𝑦=𝑥−1 равен (0,−1), и мы можем подставить 𝑥=1 в уравнение, чтобы получить 𝑦=1−1=0.

Таким образом, график 𝑦=𝑥−1 проходит через (0,−1) и (1,0), поэтому мы можем соединить эти точки прямой линией, чтобы нарисовать ее график.

Проделываем тот же процесс для 𝑦=5𝑥+7. Заметим, что его 𝑦-перехват находится в точке (0,7), и мы подставляем 𝑥=1 в уравнение, чтобы получить 𝑦=5(1)+7=12.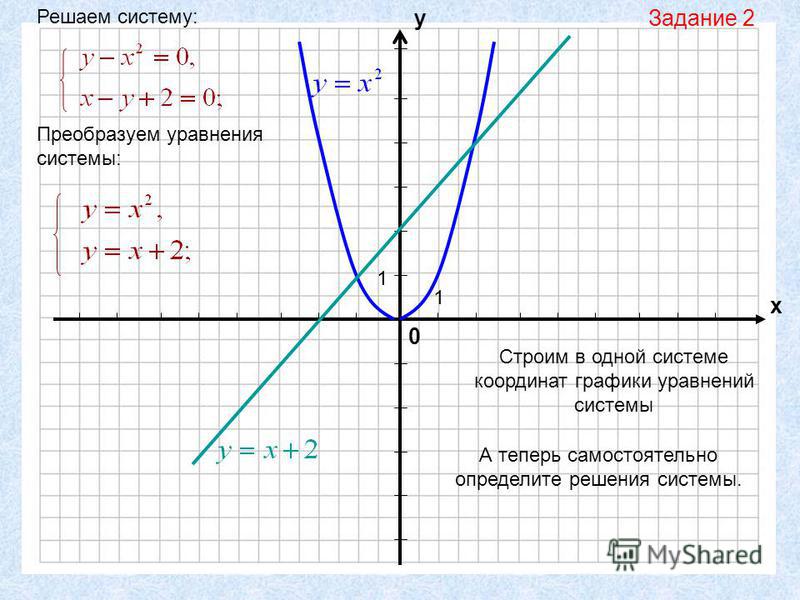

Таким образом, график 𝑦=5𝑥+7 проходит через (0,7) и (1,12), и мы можем соединить эти точки прямой линией, чтобы нарисовать ее график.

В нашем эскизе мы видим, что точка пересечения линий имеет координаты (−2,−3). Поскольку это только набросок, рекомендуется проверить, что эти значения удовлетворяют обоим уравнениям. Мы можем сделать это, заменив 𝑥=−2 и 𝑦=−3 в оба уравнения.

Для первого уравнения имеем 𝑦=𝑥−1−3=−2−1=−3, а для второго уравнения имеем 𝑦=5𝑥+7−3=5(−2)+7=−3.

Таким образом, 𝑥=−2 и 𝑦=−3 удовлетворяют обоим уравнениям. Следовательно, (−2,−3) является точкой пересечения линий.

Мы можем применять этот процесс до тех пор, пока мы можем построить уравнения. В нашем следующем примере мы определим решения для линейно-квадратичную систему уравнений с использованием их заданных графиков.

Пример 3. Определение решений системы уравнений по их графикам

Используйте показанный график для решения одновременных уравнений 𝑦=−2𝑥+1,𝑦=−𝑥−2𝑥+1. 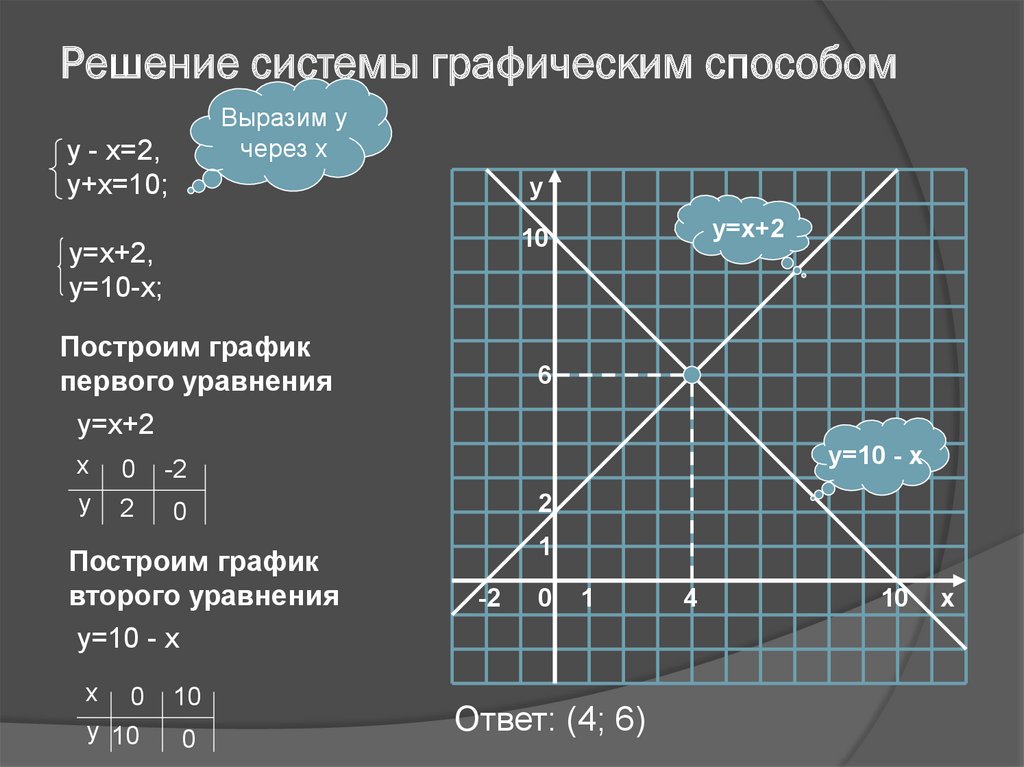

Ответ

Нам дали графики обоих уравнений и попросили использовать эти графики для решения одновременных уравнений. Мы можем сделать это вспомнив, что решение системы одновременных уравнений задается координатами точки пересечения между графиками уравнений.

На данном графике мы видим, что есть единственная точка пересечения в (0,1).

Поскольку каждое решение системы уравнений задается точками пересечения, мы можем заключить, что это единственное решение. Мы можем проверить это решение, подставив 𝑥=0 и 𝑦=1 в оба уравнения, чтобы проверить, что они удовлетворяют каждому уравнению.

Следовательно, единственным решением системы является 𝑥=0 и 𝑦=1.

В предыдущем примере мы видели, что данная линейно-квадратичная система уравнений имеет только одно решение. Мы можем доказать это вспомнив, что знак дискриминанта квадратичной функции говорит нам о количестве корней квадратичной функции.

Мы можем решить систему уравнений алгебраически, приравняв два выражения для 𝑦: −2𝑥+1=−𝑥−2𝑥+1. 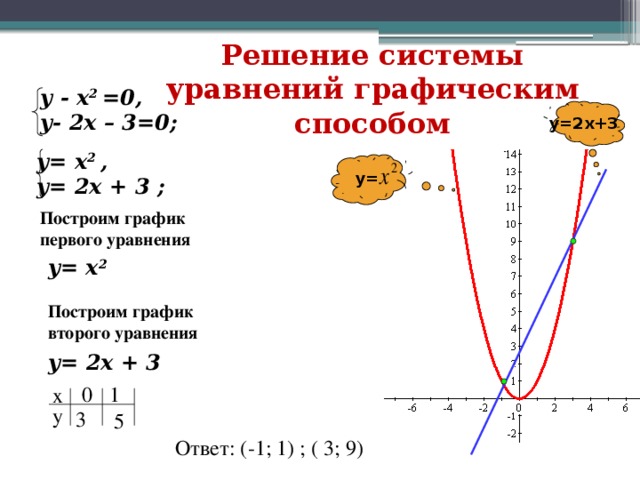

Затем мы можем переставить и собрать подобные члены: −2𝑥+1+𝑥+2𝑥−1=−𝑥−2𝑥+1+𝑥+2𝑥−1𝑥+(−2+2)𝑥+(1−1)=0,

После этого мы можем определить количество решений квадратного уравнения вида 𝑎𝑥+𝑏𝑥+𝑐=0 учитывая знак дискриминанта 𝑏−4𝑎𝑐. Имеем 𝑎=1, 𝑏=0, и 𝑐=0, поэтому 𝑏−4𝑎𝑐=(0)−4(1)(0)=0.

Поскольку дискриминант равен 0, мы можем заключить, что существует только 1 корень квадратного. Следовательно, существует только один решение системы уравнений.

В общем случае, если мы имеем линейно-квадратичную систему уравнений вида 𝑦=𝑝𝑥+𝑞,𝑦=𝑎𝑥+𝑠𝑥+𝑡, тогда мы можем установить выражения для 𝑦 равными друг другу, чтобы получить 𝑝𝑥+𝑞=𝑎𝑥+𝑠𝑥+𝑡.

Затем мы можем переставить, чтобы получить 𝑎𝑥+(𝑠−𝑝)𝑥+(𝑡−𝑞)=0.

Если мы перенумеруем коэффициенты, то увидим, что имеем 𝑎𝑥+𝑏𝑥+𝑐=0.

Предполагая, что 𝑎 не равно нулю, мы можем затем проверить знак дискриминанта, чтобы определить количество корней этого уравнения и, следовательно, количество решений системы уравнений:

• Если 𝑏−4𝑎𝑐>0, то система имеет 2 решения.
• Если 𝑏−4𝑎𝑐=0, то система имеет 1 решение.
• Если 𝑏−4𝑎𝑐0, то система не имеет действительных решений.

Мы можем увидеть каждый из этих случаев, рассмотрев, как мы можем набрасывать квадратные числа и прямые на плоскости.

Есть две точки пересечения, 𝑏−4𝑎𝑐>0; Итак, есть два реальных решения.

Имеется одна точка пересечения, 𝑏−4𝑎𝑐=0; Итак, есть одно реальное решение.

Нет точек пересечения, 𝑏−4𝑎𝑐0; так что реальных решений нет.

Это дает нам следующее свойство систем уравнений.

Свойство: число решений линейно-квадратичной системы

• Если мы можем преобразовать линейно-квадратичную систему уравнений в форму 𝑎𝑥+𝑏𝑥+𝑐=0, где 𝑎≠0, то
  • если 𝑏−4𝑎𝑐>0, то система имеет 2 решения;
  • если 𝑏−4𝑎𝑐=0, то система имеет 1 решение;
  • если 𝑏−4𝑎𝑐0, то система не имеет действительных решений.

В нашем следующем примере мы будем идентифицировать решения линейно-квадратичной системы уравнений, используя их заданные графики.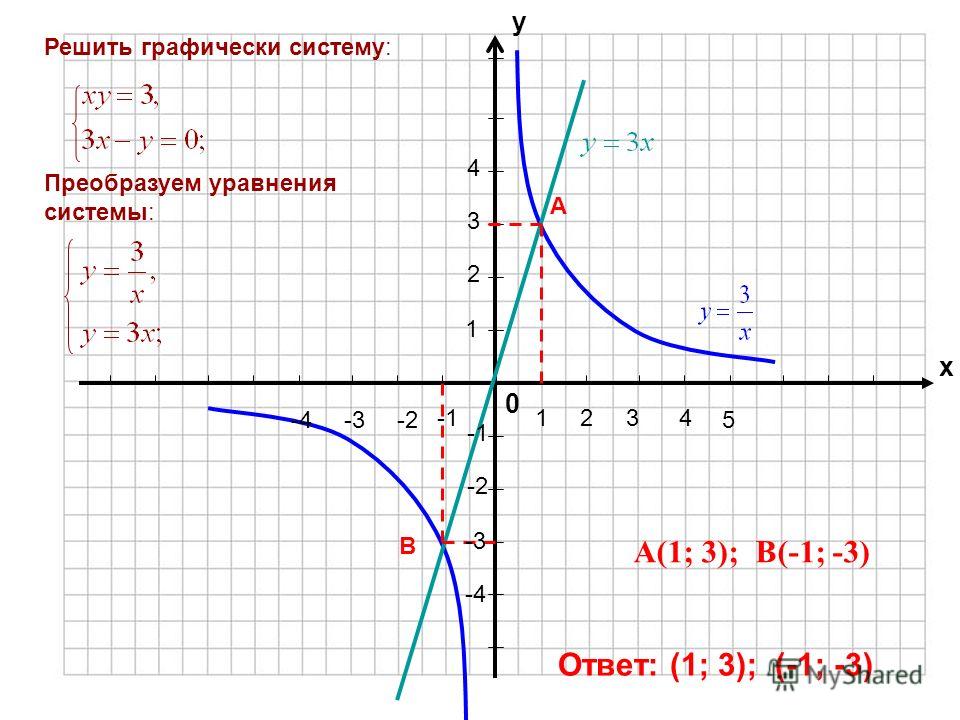

Пример 4. Определение решений системы уравнений по их графикам

Используйте показанный график, чтобы найти решения одновременных уравнений 𝑦=3𝑥−1,𝑦=3𝑥+2𝑥+1.

Ответ

Нам дали графики обоих уравнений и попросили использовать эти графики для решения одновременных уравнений. Мы можем сделать это вспомнив, что решения системы одновременных уравнений задаются координатами точки пересечения между графиками уравнений.

Из приведенной схемы видно, что графики двух уравнений не пересекаются. Мы можем сделать вывод, что поскольку существует нет точек пересечения, системы уравнений не имеют решений.

Стоит отметить, что мы можем показать, почему это так, рассмотрев алгебраический метод решения системы. Мы устанавливаем выражения для 𝑦 должны быть равны друг другу, чтобы получить 3𝑥−1=3𝑥+2𝑥+1.

Вычтем 3𝑥−1 из обеих частей уравнения, чтобы получить 0=3𝑥−𝑥+2.

Затем мы можем определить количество решений системы, найдя знак дискриминанта 𝑏−4𝑎𝑐 этого квадратичного уравнения. У нас есть (−1)−4(3)(2)=−23,

Так как дискриминант отрицателен, мы можем заключить, что квадратичная система не имеет действительных решений.

В нашем следующем примере мы найдем решения линейно-квадратичной системы уравнений, нарисовав график каждое уравнение и нахождение координат точек пересечения.

Пример 5. Нахождение множества точек пересечения двух графов

Нахождение множества точек пересечения графов 𝑥+𝑦=8 и 𝑥+𝑦=50.

Ответ

Сначала напомним, что точки пересечения двух графиков будут даны решением системы обоих уравнений: 𝑥+𝑦=8,𝑥+𝑦=50.

Эту систему можно решить двумя способами. Во-первых, можно вспомнить, что точки пересечения их графиков дадут решения к системе. Мы можем изобразить оба уравнения, используя графическое программное обеспечение.

На самом деле мы можем заметить, что уравнение 𝑥+𝑦=50 дает окружность радиуса √50 с центром по происхождению; видим, что есть две точки пересечения: (1,7) и (7,1).

Мы также можем решить систему алгебраически, чтобы найти точки пересечения. Сначала найдем выражение для 𝑦 вычитанием 𝑥 из обеих частей первого уравнения. Это дает нам 𝑦=8−𝑥.

Теперь подставим это во второе уравнение, чтобы получить 𝑥+(8−𝑥)=50.

Раскрывая скобки и упрощая выходы, получаем 𝑥+64−16𝑥+𝑥=502𝑥−16𝑥+14=0.

Мы можем заметить, что все три члена имеют общий коэффициент 2, поэтому мы можем разделить уравнение на 2, чтобы получить 𝑥−8𝑥+7=0,

Теперь мы можем решить это уравнение, разложив его на множители. Нам нужны два числа, произведение которых равно 7, а сумма -8. Мы можем обратите внимание, что эти числа равны -1 и -7, поэтому мы можем разложить квадратное число как (𝑥−1)(𝑥−7)=0.

Таким образом, решения 𝑥=1 и 𝑥=7. Это 𝑥-координаты двух точки пересечения графиков.

Мы можем подставить эти значения в уравнение для 𝑦, чтобы определить 𝑦-координаты этих два пункта: 𝑦=8−1=7,𝑦=8−7=1.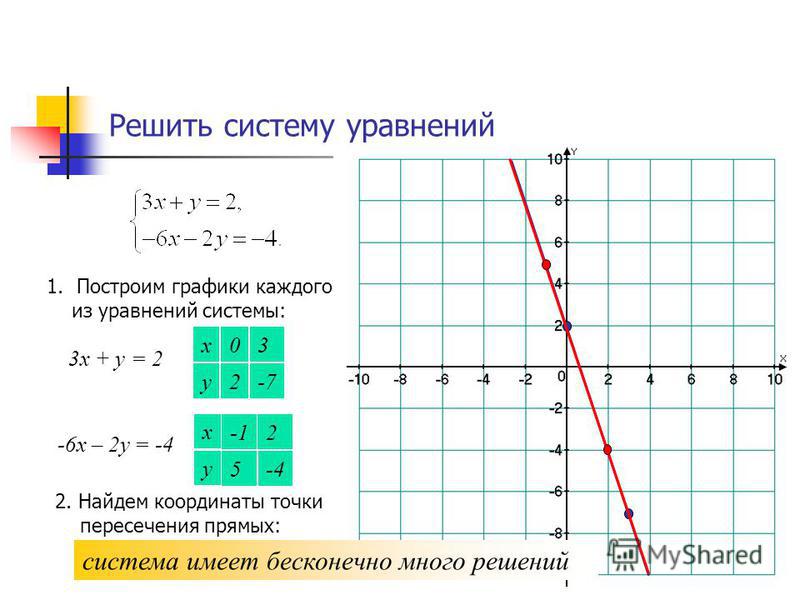

Отсюда мы нашли, что (7,1) и (1,7) — координаты точек пересечения.

Мы можем убедиться в этом, подставив координаты любой точки в уравнения обоих графиков. Например, давайте проверьте, что (7,1) является решением, подставив 𝑥=7 и 𝑦=1 в оба уравнения. Для первого уравнения имеем 𝑥+𝑦=87+1=8.

Для второго уравнения имеем 𝑥+𝑦=507+1=5049+1=50.

Поскольку выполняются оба уравнения, мы можем заключить, что (7,1) является точкой пересечения.

Следовательно, множество точек пересечения графиков равно {(7,1),(1,7)}.

В нашем следующем примере мы решим линейно-квадратичную систему уравнений, построив оба уравнения в виде графика.

Пример 6: графическое решение системы линейно-квадратичных уравнений

1. Что из следующего показывает график 𝑦=−𝑥+7 и 𝑦=𝑥+3𝑥+2?
2. Найдите решения системы уравнений 𝑦=−𝑥+7 и 𝑦=𝑥+3𝑥+2.

Ответ

Часть 1

Чтобы начертить линию 𝑦=−𝑥+7, мы можем найти координаты двух точек на линии и соединить их прямая линия.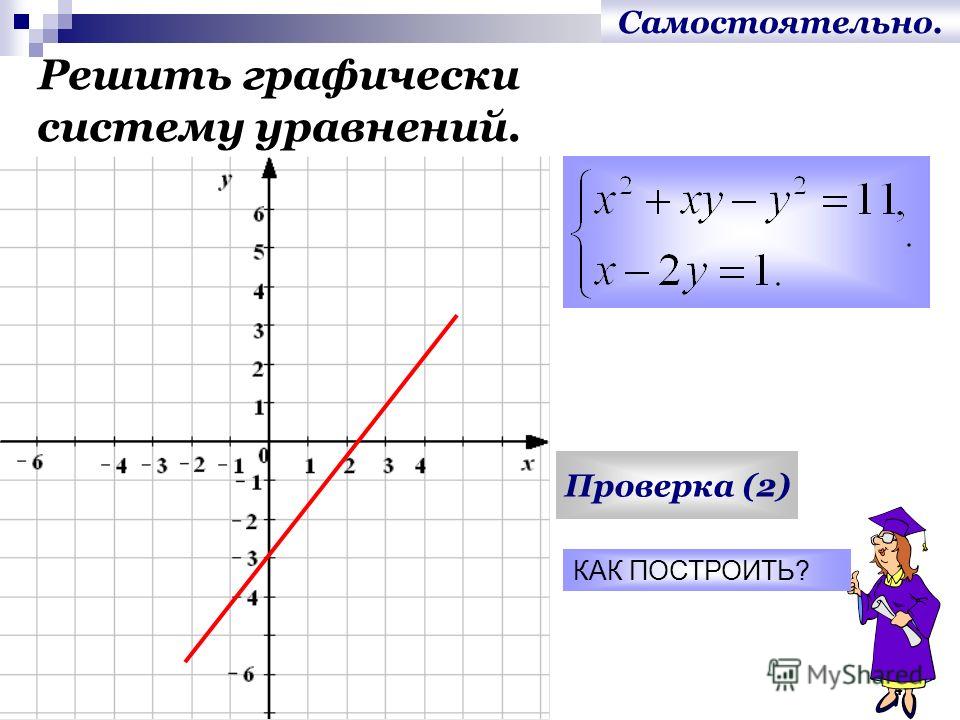 Подстановкой можно найти две точки на прямой.

Когда 𝑥=0, мы имеем 𝑦=−0+7=7.

Когда 𝑥=3, мы имеем 𝑦=−3+7=4.

Таким образом, прямая 𝑦=−𝑥+7 проходит через (0,7) и (3,4).

Чтобы нарисовать квадратное выражение 𝑦=𝑥+3𝑥+2, мы можем начать с факторизации правой части уравнения. Мы хотим найти два числа, которые при сложении дают 3 и при умножении дают 2, и мы находим, что это 1 и 2. Таким образом, 𝑥+3𝑥+2=(𝑥+1)(𝑥+2).

Следовательно, 𝑥-пересечения этого квадратного числа равны −1 и −2. Это квадратичным с положительным старшим коэффициентом, поэтому форма графика будет параболой, обращенной вверх. Мы можем найти 𝑦-перехват, подставив 𝑥=0 в уравнение. У нас есть 𝑦=0+3(0)+2=2.

Итак, нам нужно нарисовать параболу, выходящую вверх с 𝑥-пересечениями в точках −1 и −2 и 𝑦-перехват на 2.

Мы видим, что это соответствует ответу C.

Часть 2

Если конкретная пара значений 𝑥 и 𝑦 удовлетворяет обоим уравнениям, то можно заметить, что точка с этими координатами должна лежать на пересечении обоих графиков.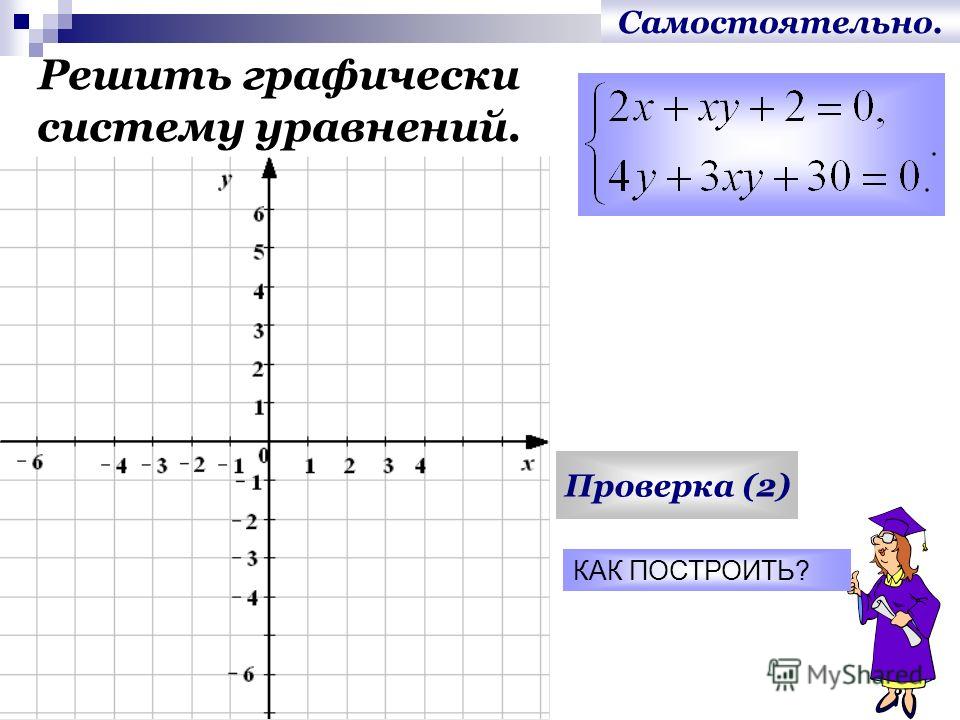 Следовательно, мы можем решить уравнения нахождение координат точек пересечения. Мы видим, что это точки (−5,12) и (1,6).

Следовательно, решениями системы уравнений являются 𝑥=−5, 𝑦=12 и 𝑥=1, 𝑦=6.

В нашем последнем примере мы решаем реальную задачу, набрасывая систему уравнений для поиска решений.

Пример 7. Решение реальной задачи с использованием системы уравнений

Строитель хочет построить треугольную балку с основанием длины 𝑥 м и высота длины 𝑥−2 м. Площадь этого треугольника определяется выражением 12𝑥(𝑥−2) м ² . Если Строитель хочет, чтобы площадь балки была в три раза больше длины основания, найдите длину основания.

Ответ

Если мы назовем площадь треугольной балки 𝑎, то заметим, что площадь треугольника определяется уравнением 𝑎=12𝑥(𝑥−2). Однако мы также хотим, чтобы площадь в три раза превышала длину основание, поэтому 𝑎=3𝑥.

Мы можем решить эту задачу, начертив оба графика и найдя координаты точек пересечения. Сначала мы известно, что график 𝑎=3𝑥 будет прямой линией, проходящей через начало координат с наклоном 3. Мы можем нарисуйте линию, проведя линию через начало координат и точку (1,3).

Мы можем нарисовать график 𝑎=12𝑥(𝑥−2), заметив, что это парабола с положительный ведущий коэффициент, поэтому он открывается вверх. Квадратное число факторизуется, поэтому мы можем решить каждый множитель, равный нулю, чтобы найти 𝑥-перехваты. 𝑥-перехваты находятся в 𝑥=0 и 𝑥=2, и мы также можем отметить, что это означает, что 𝑦-перехват также находится в 0,

Проводя эти графики по одной и той же паре координатных осей, находим, что координаты точек пересечения равны (0,0) и (8,24). У нас не может быть треугольника с основанием длины 0, поэтому только точка (8,24) является допустимым решением для нашего треугольника.

Мы можем проверить это решение, подставив 𝑥=8 в систему уравнений. У нас есть 𝑎=12𝑥(𝑥−2)𝑎=12(8)(8−2)=24,𝑎=3𝑥𝑎=3(8)=24.

Поскольку оба значения площади равны, мы убедились, что 𝑥=8 является решением задачи.

Следовательно, строителю нужно будет сделать основание треугольной балки 8 метров в длину.

Давайте закончим повторением некоторых важных моментов из этого объяснения.

Ключевые точки

• Мы можем решать системы одновременных уравнений, находя координаты точек пересечения на графиках уравнений. В частности, любая точка на всех графиках удовлетворяет всем уравнениям и любому решению задачи. система будет точкой пересечения графиков.
• Если мы можем преобразовать линейно-квадратичную систему уравнений в форму 𝑎𝑥+𝑏𝑥+𝑐=0, где 𝑎≠0, то
  • если 𝑏−4𝑎𝑐>0, то система имеет 2 решения;
  • если 𝑏−4𝑎𝑐=0, то система имеет 1 решение;
  • если 𝑏−4𝑎𝑐0, то система не имеет действительных решений.
• Мы можем подставить наши решения обратно в систему, чтобы убедиться, что они действительно являются решениями системы.

Видео-урок: Решение систем линейных уравнений графически

Расшифровка видео

В этом видео мы узнаем, как решить систему двух линейных уравнений, рассматривая их графики и определяя точка их пересечения.

Напомним прежде всего, что линейное уравнение — это уравнение, в котором наибольшая степень каждой входящей переменной равна один и нет условий, в которых переменные перемножаются вместе. Например, уравнение два 𝑥 плюс 𝑦 равно шести — это линейное уравнение.

Система двух линейных уравнений просто пара из двух таких уравнений. Например, если бы у нас также был 𝑥 плюс 𝑦 равняется двум уравнениям, теперь у нас есть система линейных уравнений, иногда называется парой одновременных уравнений. Есть много разных методов которые можно использовать для решения таких систем уравнений, но в этом видео мы ориентация на графический метод. В результате две буквы, которые мы используем для представления наших переменных часто будут 𝑥 и 𝑦, но это не обязательно должно быть случай.

Решение системы из двух линейные уравнения можно найти, построив график двух прямых представленные этими уравнениями, а затем определение координат их точки пересечения. Это связано с тем, что эта точка лежит на обе линии и, следовательно, удовлетворяет обоим уравнениям одновременно.

В нашем первом примере мы рассмотрим как найти уравнение прямой по ее графику. Это, в свою очередь, позволит нам определите систему линейных уравнений, которую можно решить с помощью данного графа.

Какой из следующих наборов одновременные уравнения могут быть решены с помощью данного графика? (A) 𝑦 равно двум 𝑥 минус четыре, 𝑦 равно 𝑥 плюс пять. (B) 𝑦 равно минус четырем 𝑥 плюс два, 𝑦 равно пяти 𝑥 минус один.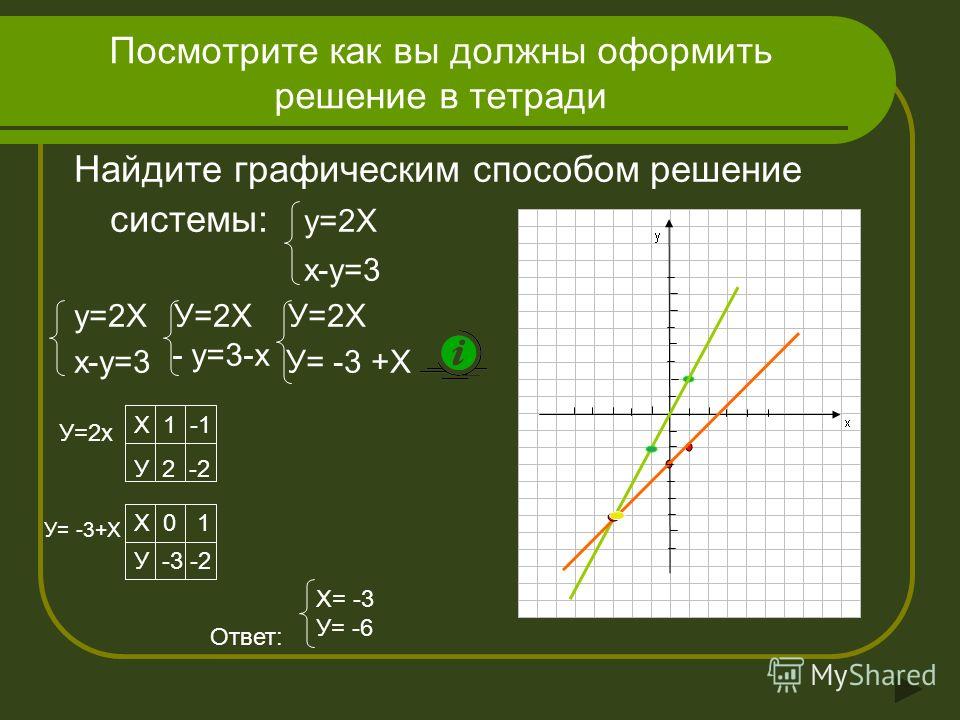 (C) 𝑦 равно двум 𝑥 минус четыре, 𝑦 равно отрицательному 𝑥 плюс пять. (D) 𝑦 равно двум 𝑥 плюс четыре, 𝑦 равно отрицательному 𝑥 плюс пять. Или (E) 𝑦 равняется отрицательным четырем 𝑥 плюс два, 𝑦 равно пяти 𝑥 плюс один.

Нам дан график из двух прямые линии. Назовем их 𝑙 один и 𝑙 два. Нас просят определить, какой пару одновременных уравнений, которые мы могли бы решить, используя этот график. Это означает, что нам необходимо определите уравнения двух прямых.

Для этого вспомним общая форма прямой линии в форме наклона и пересечения, 𝑦 равно 𝑚𝑥 плюс 𝑏. И напомним, что коэффициент 𝑥, то есть 𝑚, дает наклон линии. И постоянный член, это 𝑏, дает 𝑦-перехват графа. Это значение 𝑦, при котором линия пересекает ось 𝑦.

Мы можем определить оба этих значения из диаграммы.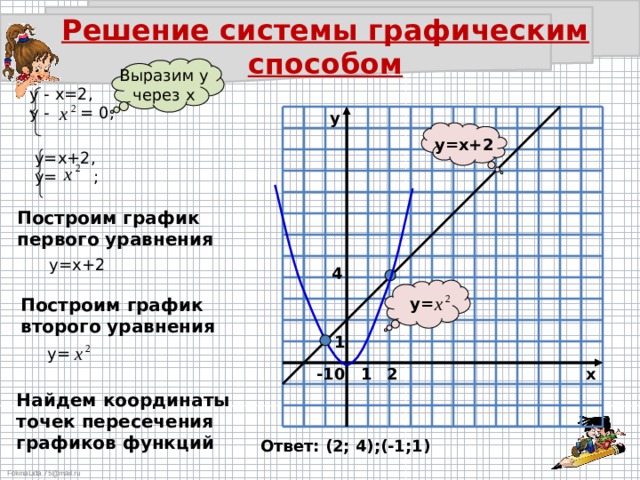 Во-первых, строка 𝑙 имеет 𝑦-пересечение пяти, а строка 𝑙 два имеет 𝑦-пересечение отрицательных четырех. Далее определяем наклон каждой линии, используя тот факт, что линия, проходящая через две координатные точки — 𝑥 один, 𝑦 один и 𝑥 два, 𝑦 два — имеет наклон 𝑚 равен 𝑦 два минус 𝑦 один больше 𝑥 два минус 𝑥 один. 𝑙 проходит через точки ноль, пять и один, четыре. Мы могли бы выбрать любые два точки от этой линии. Но нам будет легче работать, если мы выберите вторую точку рядом с 𝑦-перехватом.

Первая линия имеет наклон 𝑚 равно четыре минус пять на один минус ноль. Итак, наклон 𝑙 единицы отрицательный один. Вторая линия 𝑙 два прохода через точки ноль, минус четыре и один, минус два. Его наклон рассчитывается как 𝑚 равно минус четыре минус минус два больше нуля минус один. Итак, наклон 𝑙 два положителен два. Следовательно, в строке 𝑙 one 𝑏 равно до пяти и 𝑚 равно отрицательной единице. Его уравнение наклона и пересечения имеет вид 𝑦 равно отрицательному 𝑥 плюс пять, что является одним из уравнений, приведенных в варианте (C), и в варианте (Д).

Строка 𝑙 два имеет 𝑏 равно минус четыре и 𝑚 равно двум. Итак, его уравнение 𝑦 равно двум 𝑥 минус четыре. Это дает нам систему уравнения 𝑦 равно двум 𝑥 минус четыре, 𝑦 равно отрицательному 𝑥 плюс пять. Решения этой системы линейные уравнения, заданные координатами точки пересечения, равны 𝑥 три и 𝑦 равно двум. На данном графике показана система одновременные линейные уравнения в варианте (C): 𝑦 равно двум 𝑥 минус четыре, 𝑦 равно минус 𝑥 плюс пять.

Теперь рассмотрим второй пример.

Используйте показанный график, чтобы решить заданы одновременные уравнения: 𝑦 равно четырем 𝑥 минус два, 𝑦 равно отрицательному 𝑥 плюс три.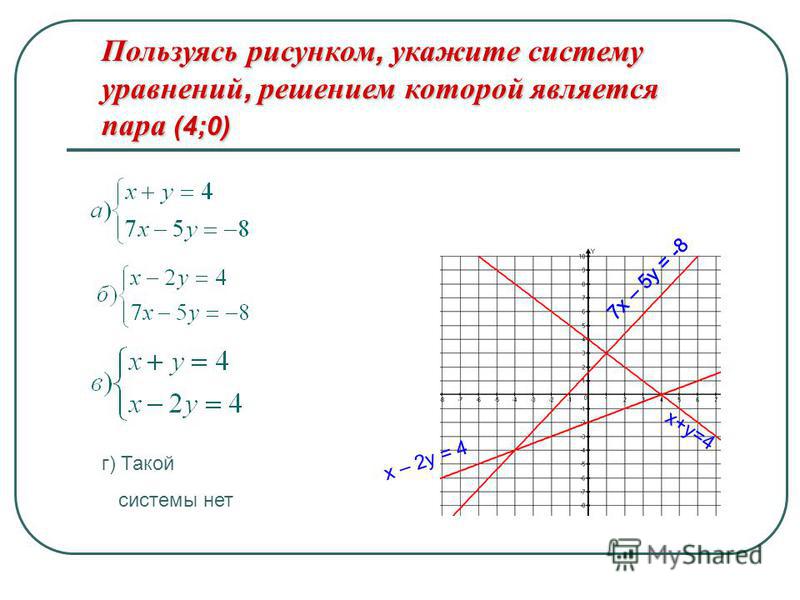

Напомним, что решение система уравнений задается координатами точки пересечения графики всех уравнений. Это означает, что координаты точка пересечения двух прямых говорит нам о решении задачи. одновременные уравнения. Мы видим, что 𝑥-координата эта точка равна единице, а 𝑦-координата равна двум. Это говорит нам, что 𝑥 равно единице, а 𝑦 равно двум является решением уравнений.

Мы можем проверить это, подставив эти значения в уравнения. Если мы подставим 𝑥 равно единице в первое уравнение, мы получаем 𝑦 равно четыре раза один минус два равно два, что согласен с нашим решением. Точно так же, если мы заменим 𝑥 равно единице во втором уравнении, мы получаем 𝑦 равно минус один плюс три равно два, что также согласуется с нашим решением. Поскольку оба уравнения верны, это подтверждает решение. Поскольку это единственная точка пересечение, это единственное решение одновременных уравнений. Следовательно, единственное решение 𝑥 равно единице, а 𝑦 равно двум.

В нашем следующем примере нам потребуется построить графики двух уравнений, которые мы хотим решить сами. Итак, напомним себе некоторые основных методов для этого.

Построив графики 𝑦 равных 𝑥 минус один и 𝑦 равно пяти 𝑥 плюс семь, найдите точку, которая удовлетворяет обоим уравнения одновременно.

Напомним, что если пара координаты 𝑥 и 𝑦 удовлетворяют обоим уравнениям одновременно, то точка должна лежать на графиках обоих уравнений. Следовательно, это их точка зрения пересечение, а значит, является решением системы уравнений. Следовательно, мы можем найти решения этой системы путем нахождения координат точек пересечение. Мы делаем это, рисуя оба графика на одной координатной плоскости. Отметим, что обе линии принадлежат форма 𝑦 равна 𝑚𝑥 плюс 𝑏. Напомним, что эта строка будет иметь 𝑦-пересечение 𝑏 и наклон 𝑚 при условии, что 𝑚 не равно нулю.

Мы можем интерпретировать важные информацию о каждой строке, обращаясь к этой формуле. Во-первых, строка 𝑦 равна 𝑥 минус у одного будет 𝑦-перехват отрицательной единицы. Мы знаем, что коэффициент при 𝑥 равно единице, поэтому наклон первой линии должен быть равен единице. Напомним, что наклон прямой это изменение 𝑦 по отношению к изменению 𝑥. Следовательно, наклон в одну представляет собой увеличение на единицу 𝑦 и увеличение на единицу 𝑥. После смены координаты, на одну вверх и одну вправо, получаем еще одну координатную точку на прямой: единицу, нуль. Соединение этих точек позволяет нам начертить линию с наклоном, равным единице, и 𝑦-перехватом, равным единице.

Переходим ко второй линейке уравнение, у нас есть 𝑦-перехват семь и наклон пять. Это означает изменение в 𝑦-координата равна пяти, а изменение 𝑥-координаты равно единице. Итак, начинаем с 𝑦-перехвата затем переместитесь вверх на пять и вправо. Однако из-за позиции 𝑦-перехват возле края нашей координатной плоскости, мы можем обратить эти направления по мере необходимости, чтобы найти точку на линии слева от нуля, семь. Итак, мы сдвинемся вниз на пять и влево один вместо. Мы нашли точку на прямой с координаты 𝑥 равны отрицательной единице, а 𝑦 равны двум.

Наконец, мы соединяем эти точки с нарисуйте линию 𝑦 равно пяти 𝑥 плюс семь. Мы видим, что обе строки содержат точка минус два, минус три. Это точка пересечения, означает, что 𝑥 равно отрицательному значению два, а 𝑦 равно отрицательному трем удовлетворяет оба уравнения.

Мы можем убедиться, что эти координаты удовлетворяют обоим уравнениям, заменяя 𝑥 равным отрицательным двум. Отметим, что оба уравнения дают 𝑦 равняется минус трем. Поскольку оба уравнения верны, это подтверждает решение, которое мы нашли с помощью графика. Следовательно, 𝑥 равно минус двум и 𝑦 равно минус трем удовлетворяет обоим уравнениям. И мы можем сказать, что дело в том, что удовлетворяет обоим уравнениям отрицательно два, отрицательно три.

Построить графики одновременных уравнения 𝑦 равно двум 𝑥 плюс семь, 𝑦 равно двум 𝑥 минус четыре, а затем решить система.

Напомним, что точки пересечение графиков обоих уравнений даст нам решения система уравнений. Это означает, что мы можем решить систему зарисовав оба уравнения на одной координатной плоскости. Так как это линейные уравнения заданных в форме наклона и пересечения, мы построим их графики, используя их наклон и 𝑦-перехваты.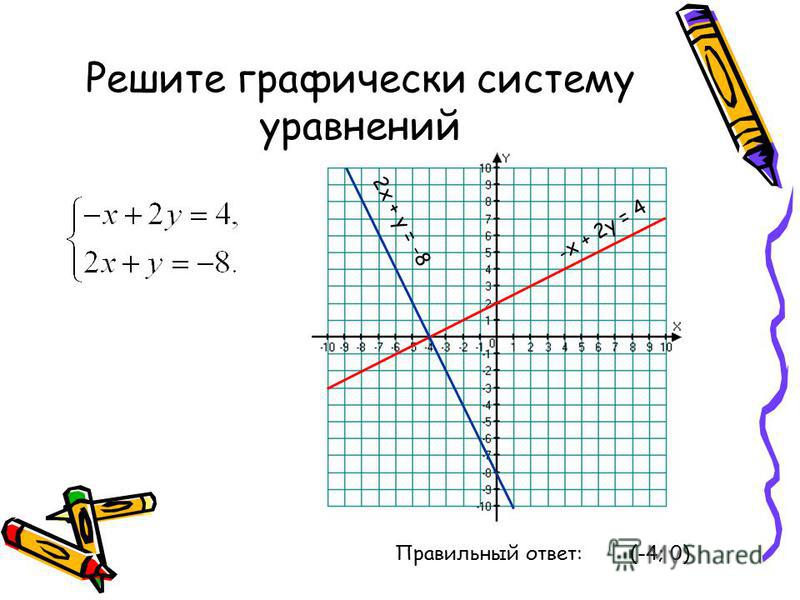

Начнем с первого уравнение, 𝑦 равно двум 𝑥 плюс семь. Мы видим, что два – это коэффициент числа 𝑥, а семь — константа. Это означает, что два — это наклон а семь — это 𝑦-перехват. Итак, мы строим 𝑦-перехват первая линия в семь. Вторая линия имеет тот же наклон как первая строка, но другой 𝑦-перехват, минус четыре.

А теперь вспомним, что наклон — это изменение 𝑦 относительно изменения 𝑥. Таким образом, наклон в два раза может быть интерпретируется как добавление двух к 𝑦-координате и добавление единицы к 𝑥-координата. Чтобы найти другую точку на втором линии, мы просто двигаемся вверх два и вправо один. Затем, чтобы построить график линии 𝑦 равно двум 𝑥 минус четыре, мы соединяем 𝑦-перехват с новой точкой прямая линия. Это линия, заданная уравнение 𝑦 равно двум 𝑥 минус четыре.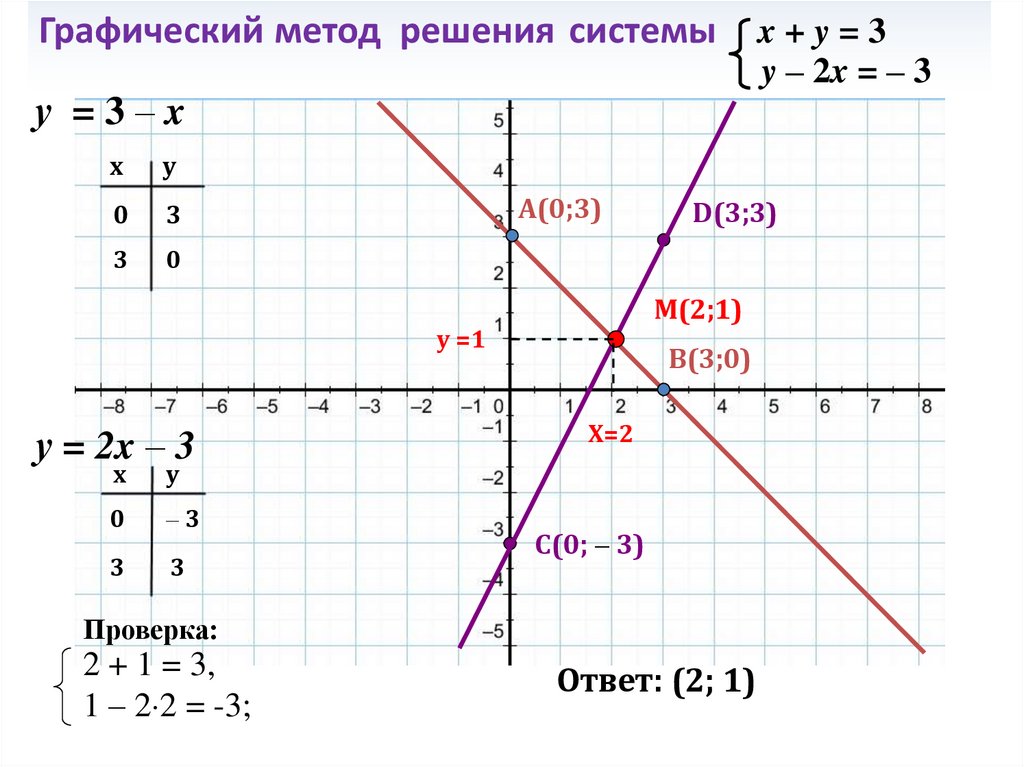

Так как первая строка имеет то же самое наклона второй линии, мы можем построить ее график, проведя параллельную линию через 𝑦-перехват семи. Это линия, заданная уравнение 𝑦 равно двум 𝑥 плюс семь. Видя, что эти строки бегут параллельно, мы знаем, что нет точек пересечения, поэтому эта система не имеет решения.

На самом деле, мы могли бы сэкономить себе усилия по рисованию графиков, просто внимательно изучив уравнения из двух строк. Мы видим, что обе строки имеют тот же наклон, но разные 𝑦-перехваты. Это говорит нам о том, что эти строки параллельно; у них одинаковый наклон. И они различны; они проходят через разные 𝑦-перехваты. Следовательно, прямые не пересекаются и система не имеет решений.

В наших примерах до сих пор мы видели две возможности. Во-первых, линии могли пересекаться в одной точке, и в этом случае существует одно решение системы линейных уравнения. Мы называем это независимой системой линейных уравнений. Во-вторых, линии могут быть параллельны, если они имеют одинаковый наклон и разные 𝑦-пересечения. В этом случае решения нет к системе одновременных уравнений, так как две линии никогда не пересекутся. Мы называем это несовместимой системой уравнений. Системы хотя бы с одним решением считаются непротиворечивыми, как и в первом случае.

На самом деле есть третий вариант. Предположим, нас попросили решить система уравнений 𝑦 равно два 𝑥 минус четыре и четыре 𝑥 минус два 𝑦 равно восемь. Если бы мы построили эти графики, мы бы можно увидеть, что эти два уравнения описывают одну и ту же прямую. Это потому, что если мы напишем второе уравнение в форме наклона и пересечения, мы получаем 𝑦 равно два 𝑥 минус четыре. Это означает, что второе уравнение эквивалентный способ записи уравнения первой линии. В этом случае строки описывается как совпадение. Одна линия лежит точно над другой. И каждый пункт в этом поэтому бесконечно длинная линия будет удовлетворять системе линейных уравнений. Поэтому мы говорим, что существуют бесконечно много решений. Мы называем это зависимой системой линейные уравнения, которые также считаются непротиворечивыми, потому что этот тип системы имеет решения.

Итак, это три варианта при решении пары линейных одновременных уравнений графически.

Давайте рассмотрим ключевые моменты, которые мы видно в этом видео. Во-первых, мы увидели, что системы линейные уравнения могут быть решены путем построения их графиков и определения координаты точек их пересечения. Однако мы также видели, что не все прямые пересекаются. Три возможности заключаются в том, что прямые пересекаются в одной точке, значит, существует одно решение, состоящее из 𝑥-координата и 𝑦-координата.