Как решать координаты вектора: Связь координат вектора и координат начальной и конечной точек вектора — урок. Геометрия, 9 класс.

Нахождение координат вектора через координаты точек. Как найти вектор по двум точкам

Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i→ должно совпадать с осью Ox, а направление вектора j→ с осью Oy.

Определение 1

Векторы i→ и j→ называют координатными векторами.

Координатные векторы неколлинеарны. Поэтому любой вектор p→ можно разложить по векторам p→=xi→+yj→. Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p→ по координатным векторам называются координатами вектора p→ в данной системе координат.

Координаты вектора записываются в фигурных скобках p→x; y. На рисунке вектор OA→ имеет координаты 2; 1, а вектор b→ имеет координаты 3;-2. Нулевой вектор представляется в виде 0→0; 0.

Если векторы a→ и b→ равны, то и y1=y2. Запишем это так: a→=x1i→+y1j→=b→=x2i→+y2j→, значит x1=x2, y1=y2 .

Таким образом, координаты равных векторов соответственно равны.

Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на Oxy заданы координаты точек начала и конца AB→: Axa, ya, Bxb, yb. Найти координаты заданного вектора.

Изобразим координатную ось.

Из формулы сложения векторов имеем OA→+AB→=OB→, где O – начало координат. Отсюда следует, что AB→=OB→-OA→.

OA→ и OB→ – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения OA→=xa, ya, OB→=xb, yb.

По правилу операций над векторами найдем AB→=OB→-OA→=xb-xa, yb-ya.

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.

Для нахождения координат вектора, необходимо найти разность его точек конца и начала.

Пример 1

Найти координаты OA→ и AB→ при значении координат точек A(2,-3), B(-4,-1).

Решение

Для начала определяется радиус-вектор точки A. OA→=(2,-3).

Чтобы найти AB→, нужно вычесть значение координат точек начала из координат точек конца.

Получаем: AB→=(-4-2,-1-(-3))=(-6, 2).

Ответ: OA→=(2,-3), AB→=(-6,-2).

Пример 2

Задано трехмерное пространство с точкой A=(3, 5, 7), AB→=(2, 0,-2). Найти координаты конца AB→.

Решение

Подставляем координаты точки A: AB→=(xb-3, yb-5, zb-7).

По условию известно, что AB→=(2, 0,-2).

Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: xb-3=2yb-5=0zb-7=-2

Отсюда следует, что координаты точки B AB→равны: xb=5yb=5zb=5 

Ответ:  B(5, 5, 5).

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Простейшие задачи в координатах 9 класс онлайн-подготовка на Ростелеком Лицей

Основные сведения о координатах вектора (напоминание)

 

Любой вектор  разлагается по векторам  и  однозначно:

 

.

Если известно начало вектора – точка  и конец вектора – точка то координаты вектора  то есть из координат конца нужно вычесть координаты начала.

Через координаты векторов мы умеем находить их сумму, разность и произведение на число.

Пользуясь всем этим, рассмотрим три опорные задачи:

 

Координаты середины отрезка

 

 

Задача 1. Координаты середины отрезка.

 

Дано: отрезок АВ; ; ; С – середина АВ.

Найти: координаты точки .

Решение (рис. 1):

Рис. 1. Иллюстрация к задаче

Построим векторы ,  и .

Найдем вектор :

Другим путем:

.

Сложим:

Так как С – середина отрезка и векторы  и  противонаправлены, то , следовательно .

Найдем координаты вектора

Координаты вектора  совпадают с координатами точки , координаты вектора  совпадают с координатами точки .

Координаты вектора   совпадают с координатами точки , следовательно

 

Определение длины вектора

 

 

Задача 2. Вычисление длины вектора по его координатам.

 

Дано: вектор

Найти: длину вектора .

Решение (рис. 2):

Рис. 2. Иллюстрация к задаче

Задан вектор , отложим его от начала координат, получим вектор  с началом в точке  и концом в точке .

  это проекция на ось ;

  это проекция на ось

По теореме Пифагора

Если вектор  задан своими координатами, то его длина находится по формуле:

 

Формула расстояния между точками

 

 

Задача 3. Вычисление расстояния между точками.

 

Дано: точки  и .

Найти: расстояние  между точками.

Решение (рис. 3):

Рис. 3. Иллюстрация к задаче

Рассмотрим вектор . Из координат конца вычтем координаты начала:

.

Теперь нужно найти длину этого вектора.

Для этого отложим его от начала координат (рис. 4).

Рис. 4. Иллюстрация к задаче

Получаем точки  и

;

Раз векторы равны, то координаты точки  ( равны координатам вектора .

(По формуле, полученной в задаче 2).

 

Решение задач

 

 

Задача 4.

 

Дано: отрезок , точка  и точка   середина .

Найти: координаты точки .

Решение (рис. 5):

Рис. 5. Иллюстрация к задаче

Каждая координата точки  равна полусумме соответствующих координат точек  

Находим :

  

Ответ:

Задача 5.

Дано:  .

Найти: расстояние =

Решение (рис. 6):

Рис. 6. Иллюстрация к задаче

Ответ:

 

Заключение

 

 

Итак, мы рассмотрели три простейшие опорные задачи и применили их для решения конкретных примеров. Эти опорные задачи далее будут использоваться при решении более сложных задач.

 

 

Список литературы

1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А. В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. E-science.ru (Источник).
2. E-science.ru (Источник).
3. Mathematics.ru (Источник).

 

Домашнее задание

1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010., №№ 936; 938; 940. 

 

Поиск вектора направления по двум точкам

Все ресурсы предварительного исчисления

12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

Precalculus Help » Матрицы и векторы » Алгебраические векторы и параметрические уравнения » Найдите вектор направления по двум точкам

Найдите вектор направления  если точки A и B равны  и , соответственно.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти вектор, точка A является конечной точкой, а точка B — начальной точкой.

Вектор направления можно определить путем вычитания начала из конечной точки.

Сообщить об ошибке

Найти вектор через точки

и .

Возможные ответы:

Правильный ответ:

Объяснение:

Правильный вектор получается вычитанием двух точек: .

Так как вычитание здесь покомпонентное, то оно дается формулой: .

В результате получается вектор .

Вектор тоже правильный, так как он является скалярным множителем вектора, помеченного как правильный. Он находится путем вычитания двух точек в обратном порядке.

Сообщить об ошибке

Найдите вектор, у которого есть начальная и конечная точки.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти вектор направления, вычтите координаты начальной точки из координат конечной точки.

Сообщить об ошибке

Найдите вектор направления с начальной точкой и конечной точкой.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти вектор направления, вычтите координаты начальной точки из координат конечной точки.

Сообщить об ошибке

Найти  если  и .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти вектор направления, идущий из  в , вычтите координаты x и y из .

Сообщить об ошибке

Найти  если  и .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти вектор направления от  к , вычтите координаты x и y из .

Сообщить об ошибке

Найдите вектор направления, который имеет начальную точку в  и конечную точку .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти вектор направления, вычтите координаты начальной точки из координат конечной точки.

Сообщить об ошибке

Найдите вектор направления, который имеет начальную точку в  и конечную точку в .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти вектор направления, вычтите координаты начальной точки из координат конечной точки.

Сообщить об ошибке

Найдите вектор направления с начальной точкой  и конечной точкой .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти вектор направления, вычтите координаты начальной точки из координат конечной точки.

Сообщить об ошибке

Найдите вектор направления, который имеет начальную точку в  и конечную точку в .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти вектор направления, вычтите координаты начальной точки из координат конечной точки.

Сообщить об ошибке

← Предыдущий 1 2 Следующий →

Уведомление об авторских правах

Все ресурсы Precalculus

12 Диагностические тесты 380 практических тестов Вопрос дня Карточки Learn by Concept

Видео с вопросами: Использование операций над векторами для нахождения координат неизвестной точки

На решетке, где 𝐀𝐂 = 〈3, 3〉, 𝐁𝐂 = 〈13, −7〉 и 2𝐂 + 2𝐀𝐁 = 〈−4, −4〉, найдите координаты точки 𝐶.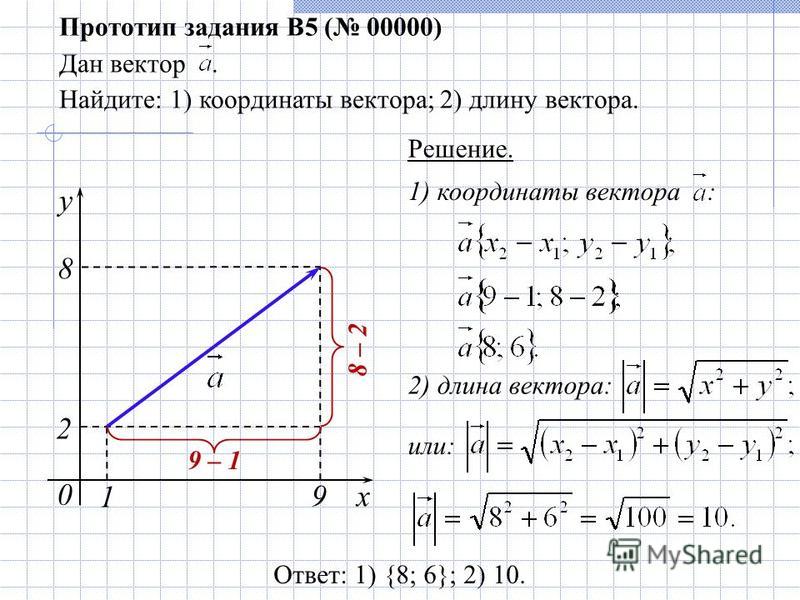

Стенограмма видео

На решетке, где вектор 𝐀𝐂 есть равно трем, трем; вектор 𝐁𝐂 равен 13, минус семь; и два 𝐂 плюс два 𝐀𝐁 равно минус четыре, минус четыре, найти координаты точки 𝐶.

Если мы начнем с рассмотрения три точки 𝐴, 𝐵 и 𝐶, показанные на диаграмме, мы знаем, что вектор 𝐀𝐂 равен до трех, до трех. Это означает, что мы двигаемся на три единицы в положительном 𝑥-направлении и три единицы в положительном 𝑦-направлении. Вектор 𝐁𝐂 равен 13, минус семь. Чтобы добраться из точки 𝐵 в точку 𝐶, мы перемещаемся на 13 единиц в положительном 𝑥-направлении и на семь единиц в отрицательном 𝑦-направление.

Мы можем использовать эту информацию, чтобы найти вектор 𝐀𝐁. Один из способов добраться из точки 𝐴 к точке 𝐵 будет через точку 𝐶. Чтобы сделать это, мы бы путешествовать по векторам 𝐀𝐂 и 𝐂𝐁. Мы знаем, что вектор 𝐀𝐂 равен трем, три. Вектор 𝐂𝐁 будет иметь то же самое величина как вектор 𝐁𝐂, но действует в противоположном направлении. Это означает, что вектор 𝐂𝐁 равно отрицательному 13, семь. Таким образом, вектор 𝐀𝐁 равен три, три плюс минус 13, семь.

Мы знаем, что можем сложить два вектора путем добавления соответствующих им компонентов. Три плюс минус 13 равно минус 10, а три плюс семь равно 10. Следовательно, вектор 𝐀𝐁 равен минус 10, 10. Если мы позволим точке 𝐶 иметь координаты 𝑥, 𝑦, то вектор положения точки 𝐶, также обозначаемый 𝐎𝐂, равен равно вектору 𝑥, 𝑦. Подставив это вместе с вектор 𝐀𝐁 в данное уравнение, мы имеем два, умноженные на 𝑥, 𝑦 плюс два умножить на минус 10, 10 равно минус четыре, минус четыре.

Вспомним, что мы можем умножать вектор на скаляр путем умножения каждого из компонентов на этот скаляр.