Урок 3. Неполное квадратное уравнение
Класс
1 класс
2 класс
- Английский язык
- Математика
3 класс
- Русский язык
- Английский язык
- Математика
4 класс
- Русский язык
- Английский язык
- Математика
5 класс
- Русский язык
- Английский язык
- Математика
- Биология
6 класс
- Русский язык
- Английский язык
- Математика
- Биология
7 класс
- Русский язык
- Английский язык
- Математика
- Биология
- Физика
- Химия
8 класс
- Русский язык
- Английский язык
- Математика
- Биология
- Физика
- Химия
9 класс
- Русский язык
- Английский язык
- Математика
- Биология
- Физика
- Химия
10 класс
- Английский язык
- Биология
- Физика
- Химия
11 класс
- Английский язык
- Биология
- Химия
8 КЛАСС
Урок 3.
 Неполное квадратное уравнение
Неполное квадратное уравнениеОпределение надо повторить в п.4.3 "Неполное квадратное уравнение".
Надо помнить, что квадрат любого числа всегда число положительное, поэтому уравнение под буквой а) может иметь либо два корня, либо не иметь корней.
Если произведение множителей равно нулю, значит каждый множитель может быть равен нулю. Пользуясь этим правилом, решаем уравнения данного упражнения.
Для каждого уравнения применяем правило вынесения общего множителя за скобку, затем применяем правило- каждый множитель может быть равен нулю, если произведение равно нулю..
Для решения неполных квадратных уравнений такого вида, применяем формулу сокращеного умножения-разность квадратов для разложения выражения на множители. Если квадрат переменной х равен отрицательному числу, такое уравнение корней не имеет.
Неполное квадратное уравнение, у которого коэффициент b равен нулю, всегда имеет два корня, равные по модулю, но противоположные по знаку.
Сначала надо выполнить равносильные преобразования, чтобы привести уравнение к виду неполного квадратного, у которого равен нулю свободный член. Такое уравнение решается методом вынесения общего множителя за скобки.
Повторить в п. 4.3 "Неполные квадратные уравнения", какой вид имеют и как решаются такого вида уравнения.
Повторить, какой вид имеет квадратное уравнение, у которого один из корней равен 0, а другой не равен 0, и также какой вид имеет квадратное уравнение, у которого два корня равны по модулю, но противоположны по знаку.
Для равносильных преобразований применяются формулы сокращенного умножения и правила умножения многочлена на многочлен. После упрощения уравнения принимают вид неполных квадратных уравнений.
Для каждого уравнения необходимо выполнить равносильные преобразования, чтобы привести к неполному квадратному уравнению. Для выполнения этого упражнения надо повторить формулы сокращеного умножения и приведение дробей к общему знаменателю.
Для ответа на вопрос пункта а) надо помнить, что любое число во 2-ой степени - число положительное. В пункте б) надо данный корень х = 0 подставить в уравнение и найти значение числа k.
По тексту задачи составить уравнение, получится неполное квадратное уравнение. Правила решений таких уравнений в п. 4.3.
Решая уравнения, в которых не даны конкретные значения коэффициентов квадратного уравнения, то надо рассматривать все возможные ситуации, при которых уравнение имеет корни и, при которых не может иметь корней.
Значения параметра а надо подбирать таким образом, чтобы в квадратном уравнении обращалось в ноль одно из слагаемых, содержащих переменную х. Так как таких слагаемых в уравнении два, поэтому и в ответе получаем два значения параметра а.
Вопросники:
Вопрос:
Вопрос:
Вопрос:
Вопрос:
Вопрос:
Вопрос:
Неполные квадратные уравнения | СПАДИЛО
ОпределениеКвадратным уравнением называется уравнение вида ax2+bx+c=0, где х – переменная, a, b, c некоторые числа, причем a≠0. Обычно его называют полным квадратным уравнением.
Обычно его называют полным квадратным уравнением.
Если в таком уравнении один из коэффициентов b или c равен нулю, либо оба одновременно равны нулю, то такое уравнение называется неполным квадратным уравнением.
Неполное квадратное уравнение при b=0: ax
2+c=0Для решения такого вида уравнения надо выполнить перенос коэффициента с в правую часть, затем найти квадрат переменной (делим обе части на одно и то же число), найти два корня уравнения, либо доказать, что корней нет (если х2 равен отрицательному коэффициенту; знаем, что квадрат любого числа равен только положительному числу).
Пример №1. Решить уравнение:
5х
Выполним перенос числа –45 в правую часть, изменяя знак на противоположный: 5х2=45; найдем переменную в квадрате, поделив обе части уравнения на 5: х2=9. Видим, что квадрат переменной равен положительному числу, поэтому уравнение имеет два корня, находим их устно, извлекая квадратный корень из числа 9, получим –3 и 3. Оформляем решение уравнения обычным способом:
Оформляем решение уравнения обычным способом:
5х2–45=0
5х2=45
х2=9
Ответ: х=±3 или можно записать ответ так: х1=–3, х2=3 (обычно меньший корень записывают первым). Пример №2. Решить уравнение:
–6х2–90=0
Выполним решение уже известным способом: –6х2=90. х2=–15 Здесь видим, что квадрат переменной равен отрицательному числу, а это значит, что уравнение не имеет корней. Ответ: нет корней. Пример №3. Решить уравнение:
х2–100=0
Здесь мы видим в левой части уравнения формулу сокращенного умножения (разность квадратов двух выражений). Поэтому, можем разложить данное выражение на множители, и найти корни уравнения: (х–10)(х+10)=0. Соответственно, вспомним, что произведение двух множителей равно нулю тогда, когда хотя бы один из множителей равен нулю, то есть х–10=0 или х+10=0. Откуда имеем два корня х1=10, х2=–10.
Откуда имеем два корня х1=10, х2=–10.
Неполное квадратное уравнение при с=0: ax
2+bx=0Данного вида уравнение решается способом разложения на множители – вынесением за скобки переменной. Данное уравнение всегда имеет два корня, один из которых равен нулю. Рассмотрим данный способ на примерах.
Пример №4. Решить уравнение:
х2+8х=0
Выносим переменную х за скобки: х(х+8)=0. Получаем два уравнения х=0 или х+8=0. Отсюда данное уравнение имеет два корня – это 0 и –8.
Пример №5. Решить уравнение:
3х2–12х=0
Здесь кроме переменной можно вынести за скобки еще и коэффициент 3, который является общим множителем для данных в уравнении коэффициентов. Получим: 3х(х–4)=0. Получаем два уравнения 3х=0 и х–4=0. Соответственно и два корня – нуль и 4.
Неполное квадратное уравнение с коэффициентами b и с равными нулю: ax
2=0Данное уравнение при любых значениях коэффициента а будет иметь один корень, равный нулю.
Пример №6. Решить уравнение:
–14х2=0
Обе части уравнения делим на (–14) и получаем х2=0, откуда соответственно и единственный корень – нуль. Пример №6. Решить уравнение:
23х2=0
Также делим обе части на 23 и получаем х2=0. Значит, корень уравнения – нуль.
Даниил Романович | Просмотров: 7.8k
квадратичные неравенства — математические подсказки
Этот раздел охватывает:
- График. Диаграмма (знаковая модель) Метод
- Реальное квадратичное неравенство
- Дополнительная практика
Точно так же, как мы решили и начертили линейных неравенств , мы можем сделать то же самое с квадратными неравенствами.
(См.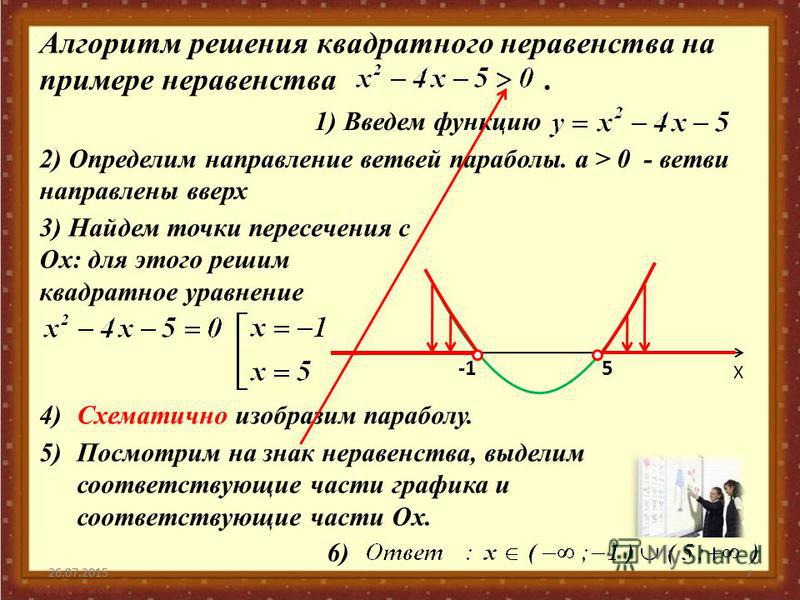 раздел «Решение неравенств » для получения информации о других неравенствах.)
раздел «Решение неравенств » для получения информации о других неравенствах.)
Мы научились строить графики неравенств с двумя переменными еще в разделе «Система координат» и «Графические линии «. Мы можем сделать то же самое с квадратиками, и затенение почти такое же: когда у нас есть «\(y<\) », мы всегда закрашиваем в под линией, которую мы рисуем, и когда у нас есть «\(y>\) », мы всегда затеняем выше линии, которую рисуем. Мы можем сделать это даже на графическом калькуляторе!
Опять же, мы всегда можем подключить упорядоченную пару, чтобы увидеть, отображается ли она в затененных областях (что означает, что это решение) или в незатененных областях (что означает, что это не решение). » и «\(>\)», мы рисуем пунктирную (или пунктирную) линию , чтобы указать, что мы на самом деле не включаем эту линию (но все до нее), тогда как с «\(\le \) » и «\(\ge \)», мы рисуем обычная строка , чтобы указать, что мы включаем ее в решение. Чтобы запомнить это, я думаю о том, что «\(<\)» и «\(>\)» имеют меньше карандашных пометок, чем «\(\le \)» и «\(\ge \)», так что там меньше карандаш используется, когда вы рисуете линии на графике. Вы также можете запомнить это, думая, что линия под «\(\le \)» и «\(\ge \)» означает, что вы рисуете сплошную линию на графике.
Чтобы запомнить это, я думаю о том, что «\(<\)» и «\(>\)» имеют меньше карандашных пометок, чем «\(\le \)» и «\(\ge \)», так что там меньше карандаш используется, когда вы рисуете линии на графике. Вы также можете запомнить это, думая, что линия под «\(\le \)» и «\(\ge \)» означает, что вы рисуете сплошную линию на графике.
Вот пример:
| Квадратное неравенство/Объяснение 9{2}}-3x+2\) . Так как у нас есть неравенство «\(y<\)», мы заштриховываем под график, т.к. он «сыпется дождем». Обратите внимание, что мы используем пунктирную линию, так как у нас есть «\(<\)».
Если бы у нас было «\(>\)», оно было бы заштриховано ( внутри параболы).
Давайте подставим \(\left( {0,0} \right)\) , чтобы увидеть, отображается ли это как решение. \(\left( {0,0} \right)\) находится в заштрихованной области , поэтому он удовлетворяет неравенству: \(0<5{{\left( 0 \right)}^{2}}- 3\влево(0\вправо)+2\). | |||||||
| Мы также можем построить это с помощью графического калькулятора. После ввода уравнения в \({{Y}_{1}}=\) используйте курсор для прокрутки до перед \({{Y}_{1}}=\) и продолжайте нажимать ВВОД , пока не появится значок. Затем нажмите ГРАФИК .
(Для калькулятора TI-84C вам нужно будет использовать курсор, чтобы прокрутить вниз от настройки Color: до Y , и использовать курсор прокрутки вправо, чтобы перейти к «\(<\) .) 9{2}}}\), вы можете переместить все на другую сторону, чтобы сделать его положительным, но будьте осторожны со знаками неравенства! Рекламные ссылки Вы можете решать квадратные неравенства, изображая две стороны неравенства в виде графика и определяя интервалы \(x\), где один график лежит ниже (\(<\)) или выше (\(> \)) другой. Вот несколько примеров использования графического калькулятора . Рекламные ссылки Мы поместим левую часть уравнения в \({{Y}_{1}}=\) и правую часть в \({{Y}_{2} }=\), посмотрите, где они пересекаются, и проверьте, какие интервалы больше или меньше, в зависимости от задачи:
При алгебраическом решении извлеките квадратный корень из каждой стороны, но нам нужно беспокоиться о неравенстве подписать. Когда вы возьмете квадратный корень из обеих частей, разделите уравнение на два уравнения . Мы получаем первое уравнение, просто убирая знак абсолютного значения слева. Самый простой способ получить второе уравнение — убрать знак абсолютного значения слева и сделать две вещи справа : поменять знак неравенства , а изменить знак всего справа (даже если там есть переменные). Помните, что с \(>\) у нас есть «или», а с \(<\) у нас есть «и». Вот пример: Вот пример, в котором у нас есть . Заполните квадрат First:
Итак, я хотел бы познакомить вас с таблицей знаков или методом шаблона знаков — методом, который вы будете использовать позже в алгебре, когда будете работать с Решение полиномиальных неравенств в Графики и нахождение корней полиномиальных функций и Рациональные неравенства в Графики рациональных функций, включая раздел Асимптоты . Таблица знаков или шаблон знаков — это просто числовая линия, которая разделена на части (или интервалы, или области) с граничными точками (называемые « критическими значениями »), которые вы получаете, установив квадратное значение на 0 (без неравенства) и нахождение \(x\) (корни). Диаграммы знаков просты и очень интересны, поскольку вы можете выбрать любую точку между критическими значениями и посмотреть, является ли весь квадрат положительным или отрицательным . Затем вы просто выбираете этот интервал (или интервалы), глядя на неравенство. Кроме того, рекомендуется поставить открытых или закрытых кружков на критических значений , чтобы напомнить себе, есть ли у нас включительно точек (неравенства со знаками равенства, такие как \(\le \) и \ (\ge \)) или 9{2}}-28x\le 0\\4x\left( {x-7} \right)\le 0\end{array}\) Проблема требует \(\le 0\), поэтому смотрим для знака(ов) минус , и наши ответы включают (жесткие скобки).
Ответ: \([0,7]\). | Первое, что нам нужно сделать, это получить все в левой части и 0 в правой части , чтобы мы могли посмотреть, можем ли мы разложить квадратное число. Затем мы делим на множитель квадратного числа (если можем). Если мы не можем, нам придется использовать квадратную формулу или завершить квадрат. Для этого квадратичного выражения выньте наибольший общий делитель (GCF).
Теперь мы нарисуем диаграмму знаков . Граничные точки, или критических значений , являются корнями (устанавливая коэффициенты равными 0 ) квадратного числа, как если бы это было равенство.
Поскольку корни равны 0 и 7 (мы игнорируем 4 , так как это фактор без переменной в нем), мы помещаем их на диаграмму знаков в качестве границ. Затем мы проверяем каждый интервал со случайными точками, чтобы увидеть, является ли факторизованная форма квадратного числа положительной или отрицательной 9.
Мне нравится использовать факторизованную форму для проверки, поскольку так немного проще проверить, являются ли случайные точки положительными или отрицательными. Например, мы можем попробовать –1 для крайнего левого интервала: \(4\left( {-1} \right)\left( {-1-7} \right)=32\), что равно \(+ \). Давайте попробуем 1 для среднего интервала: \(4\left( 1 \right)\left( {1-7} \right)=-24\), что равно \(-\). Давайте попробуем 8 для самого правого интервала: \(4\left( 8 \right)\left( {8-7} \right)=32\), что равно \(+\). Всегда пробуйте легкие числа, особенно 0 , если это не критическое значение!
Мы хотим \(\le \) из задачи, поэтому мы ищем интервалы со знаком \(-\) (отрицательный); интервал равен \([0,7]\). Нам нужны жесткие скобки (включение конечных точек), так как у нас есть \(\le \), а не \(<\). Смотрите - это не так уж и плохо! |
Примечание : Если нет квадратов любого из факторов (с переменными) в квадратичной факторизованной форме, 9Таблица знаков 0006 обычно представляет собой с чередованием минуса и плюса , например, плюс-минус-плюс или минус-плюс-минус.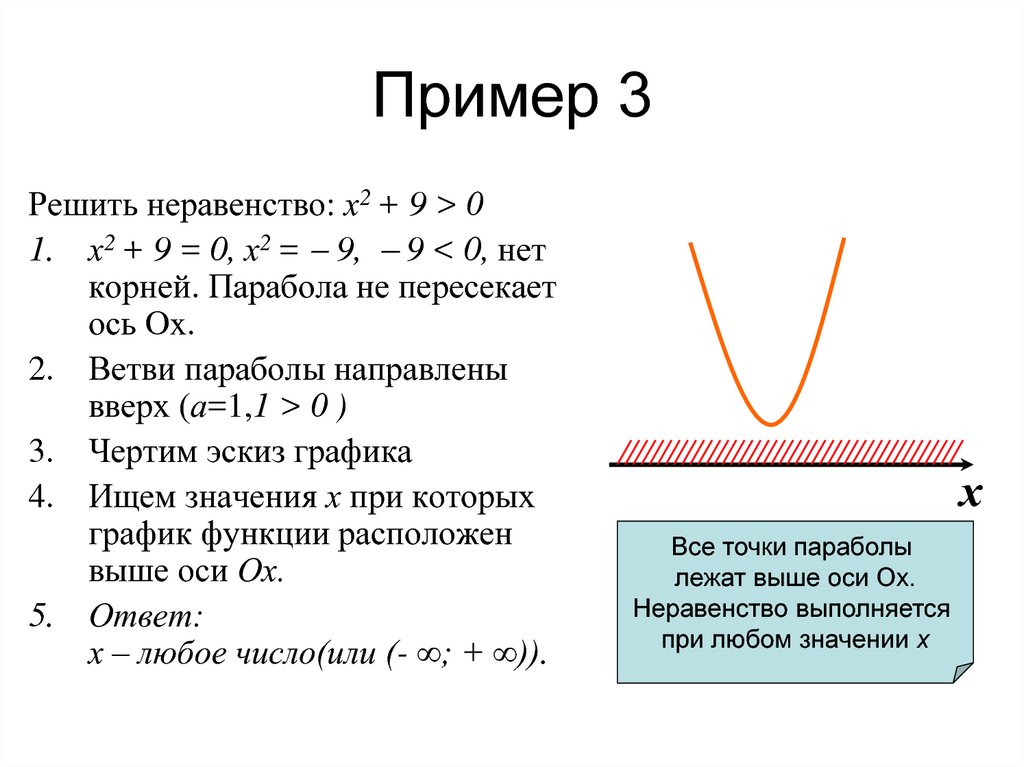 Если один из множителей возводится в четный множитель (например, в квадрат), то это указывает на « отскок » на графике, и в этой точке знаки не меняются.
Если один из множителей возводится в четный множитель (например, в квадрат), то это указывает на « отскок » на графике, и в этой точке знаки не меняются.
Вот еще примеры:
Задача квадратичного неравенства | Примечания 6 73 9007 | {2}}-7x+3>0\\\,\left( {2x-1} \right)\left( {x-3} \right)>0\end{массив}\) Первое, что нам нужно сделать, это получить все в левой части и 0 в правой части , чтобы мы могли посмотреть, можем ли мы разложить квадратное число.
Поскольку мы можем разложить квадратное число на множители, создадим диаграмму со знаками. Мы получаем границы, получая корни, как если бы это было равенством; критическими значениями являются \(\displaystyle \frac{1}{2}\) и 3 (установите для каждого фактора значение 0 и найдите \(x\)).
Затем мы проверяем каждый интервал со случайными точками, чтобы увидеть, является ли факторизованная форма квадратного числа положительной или отрицательной . Ставим знаки над интервалом. Обязательно используйте 0 в качестве контрольной точки , если можете!
Ищите интервалы \(+\) из-за \(>\). Интервал \(\displaystyle \left( {-\infty ,\frac{1}{2}} \right)\cup \left( {3,\infty } \right)\). 9{2}}\left( {3x+2} \right)<0\) Проблема требует \(<0\), поэтому мы ищем знак(и) минус и наши ответы исключающие (мягкие скобки). | Неравенство составлено так, чтобы сделать диаграмму со знаками, так как у нас есть 0 в правой части . Границы равны \(\displaystyle -\frac{2}{3}\) и 1 .
Проверьте каждый интервал случайными точками (используя « 0 ») и поставьте знаки над интервалом. 9{2}}\)). Это потому, что возведение в квадрат нечетного числа все равно дает четное число.
Ищите интервалы \(-\) из-за \(<\). Однако мы должны быть осторожны, поскольку мы не включаем граничные точки (у нас есть \(<\), а не \(\le \)). Тогда интервал равен \(\displaystyle \left( {-\frac{2}{3},1} \right)\cup \left({1,\infty} \right)\). |
И еще один пример, где мы не можем разложить:
| 9{2}}-4\влево( 1 \вправо)\влево( {-9} \вправо)}}}}{2}\\\,\,\,\,\,\,\,\,\, \,x=\frac{{-5-\sqrt{{61}}}}}{2}\приблизительно -6,41\,\,\,\,\,\,\,\,\,\,\,\ ,x=\frac{{-5+\sqrt{{61}}}}{2}\приблизительно 1,41\end{массив}\)
Проблема требует \(\le 0\), поэтому мы ищем знак(и) минус , и наши ответы включают (жесткие скобки). | Первое, что нам нужно сделать, это получить все в левой части , а 0 в правой части , поэтому мы можем увидеть, можем ли мы разложить квадратное число на множители.
Мы не можем факторизовать это, поэтому воспользуемся квадратным уравнением от до , чтобы найти корни (как если бы это было равенство).
Границами для таблицы знаков являются эти корни, которые приблизительно равны – 6,41 и 1,41 .
Ищите интервалы \(-\) из-за \(\le \). Интервал равен \(\displaystyle \left[ {\frac{{-5-\sqrt{{61}}}}}{2},\,\frac{{-5+\sqrt{{61}}}}}{ 2}} \справа]\). Десятичный (неточный ответ) равен \(\left[ {-6.41,\,1.41} \right]\). 9{2}}+6\), где \(t\) – время в секундах, а \(h\) – высота мяча. Ее подруга Райли должна поймать мяч между 2 футов и 5 футов над поверхностью воды (земли). Между какими двумя временами Райли должна попытаться поймать мяч? Решение: Поскольку нам нужно знать, когда (\(t\)) мяч должен быть пойман, нам нужно решить для \(t\), используя неравенство, так как оно может быть в любое время между 2 и 5 секунд.
Когда мы извлекаем квадратные корни, нам не нужно беспокоиться об отрицательных значениях, поскольку \(t\) не может быть отрицательный.
Райли должна попытаться поймать мяч между \(\displaystyle \frac{1}{4}\) и \(\displaystyle \frac{1}{2}\) секунд . Удачи, Райли! | Я использовал 2 nd TRACE (CALC) , 5 (пересечение), чтобы получить пересечение квадратичной и каждой из прямых. Когда калькулятор запрашивает Первая кривая? и вторая кривая? , просто перемещайте кнопки со стрелками, пока они не попадут на нужные вам кривые.
|
Изучите эти правила и практикуйтесь, практикуйтесь, практикуйтесь!
Нажмите «Отправить» (стрелка справа от проблемы), чтобы решить эту проблему. Вы также можете ввести другие проблемы или щелкнуть 3 точки в правом верхнем углу, чтобы просмотреть примеры проблем.
Если вы нажмете «Нажмите, чтобы просмотреть шаги», вы перейдете на сайт Mathway , где сможете зарегистрироваться для получения полной версии (включая шаги) программного обеспечения. Вы даже можете получить рабочие листы по математике.
Вы также можете пойти на Mathway сайт здесь, где вы можете зарегистрироваться, или просто использовать программу бесплатно без подробных решений. Существует даже приложение Mathway для вашего мобильного устройства. Наслаждаться!
На Quadratic Applications — все готово!
Неполные квадратные уравнения с примерами
Неполное квадратное уравнение — это квадратное уравнение, не содержащее ни одного члена вида ax²+bx+c=0 (при условии, что всегда присутствует член x²).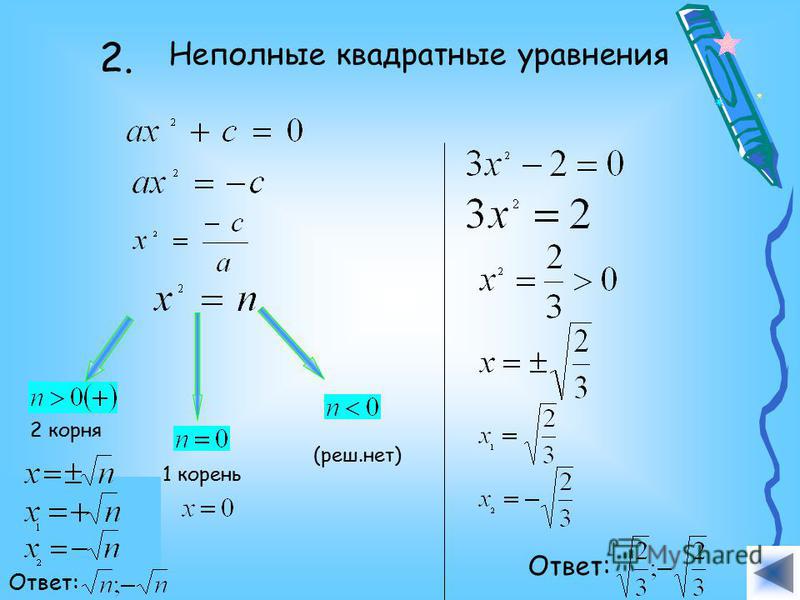 Эти уравнения обычно легче решить, чем полное квадратное уравнение. В зависимости от пропущенного члена у нас есть два типа неполных квадратных уравнений.
Эти уравнения обычно легче решить, чем полное квадратное уравнение. В зависимости от пропущенного члена у нас есть два типа неполных квадратных уравнений.
В этой статье мы подробно узнаем о двух типах неполных квадратных уравнений. Мы научимся решать эти типы уравнений и рассмотрим несколько практических примеров.
АЛГЕБРА
Актуально для …
Обучение решению неполных квадратных уравнений.
См. примеры
Содержание
АЛГЕБРА
Актуально для …
Обучение решению неполных квадратных уравнений. 92-7х=0$. Поэтому факторизуем его следующим образом:
$latex x(x-7)=0$
Теперь составим уравнение с каждым множителем и решим:
$latex x=0 ~~$ или $latex ~~ x-7=0$
$latex x=0 ~~$ или $latex ~~x=7$
Примечание: В этом типе уравнения одним из решений всегда будет $latex x=0$ .
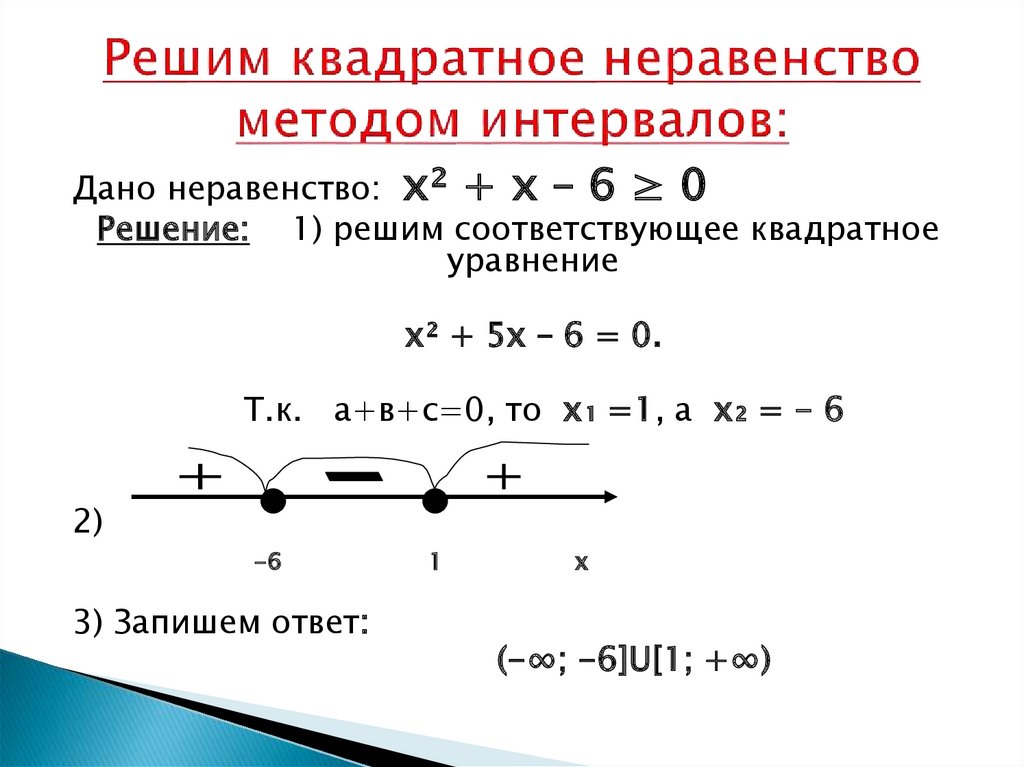
Неполные квадратные уравнения – Примеры с ответами
Методы решения обоих типов неполных квадратных уравнений используются в следующих примерах.




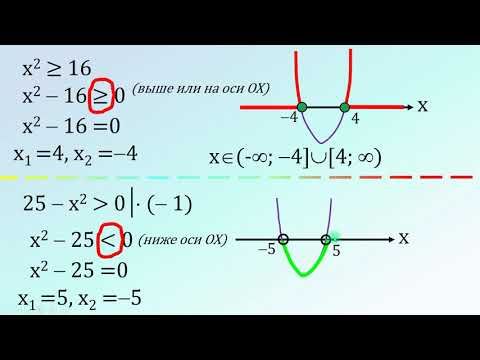 Вы должны увидеть « Первая кривая? » внизу. Затем нажмите 9{2}}-7x\) в \({{Y}_{1}}=\) и –3 в \({{Y}_{2}}=\) и график.
Вы должны увидеть « Первая кривая? » внизу. Затем нажмите 9{2}}-7x\) в \({{Y}_{1}}=\) и –3 в \({{Y}_{2}}=\) и график. Разбейте уравнение на два уравнения, как мы это делали в 9{2}}<4\), мы говорим, что абсолютное значение \(x\) меньше квадратного корня из 4 или \(\left| x \right|<2\). Это потому, что квадратный корень может быть либо положительным , либо отрицательным .
Разбейте уравнение на два уравнения, как мы это делали в 9{2}}<4\), мы говорим, что абсолютное значение \(x\) меньше квадратного корня из 4 или \(\left| x \right|<2\). Это потому, что квадратный корень может быть либо положительным , либо отрицательным . {2}}\) сам по себе. Теперь мы можем взять квадратный корень из обеих сторон .
{2}}\) сам по себе. Теперь мы можем взять квадратный корень из обеих сторон . Сначала это кажется трудным, но на самом деле совсем не так уж и плохо!
Сначала это кажется трудным, но на самом деле совсем не так уж и плохо!
 0007 . Ставим знаки над интервалом.
0007 . Ставим знаки над интервалом.

 Возможно, было бы проще просто использовать метод Completing the Square , описанный выше, но мы можем сделать это и таким образом.
Возможно, было бы проще просто использовать метод Completing the Square , описанный выше, но мы можем сделать это и таким образом.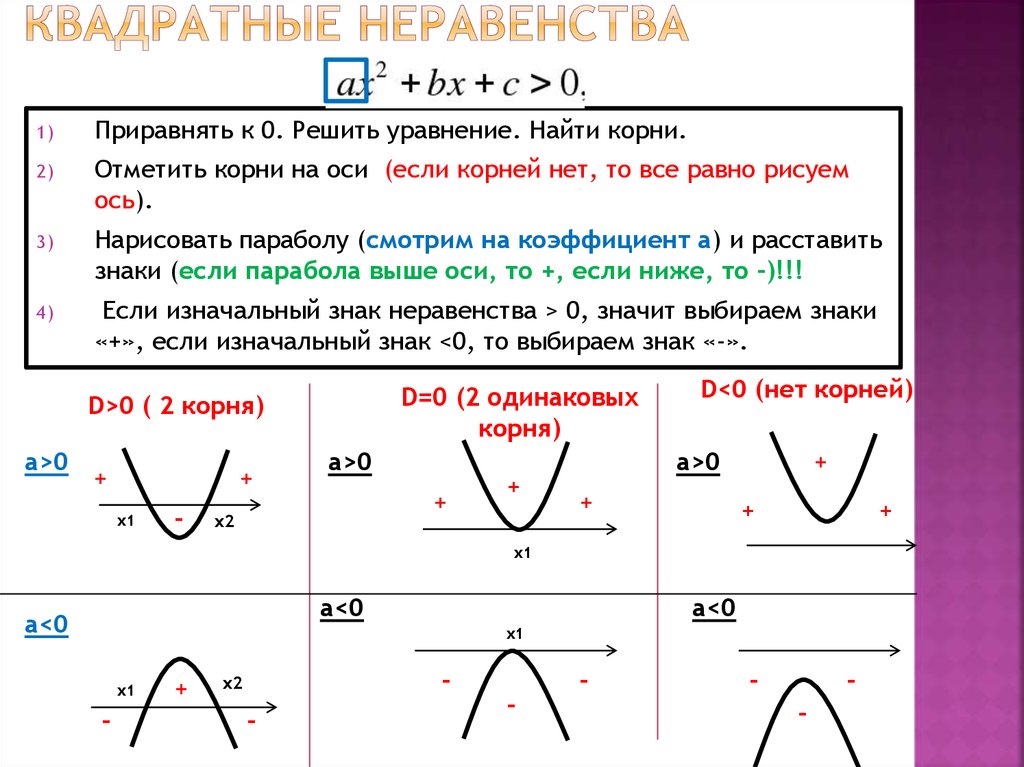 Мы будем использовать только знаки \(<\), поскольку в задаче сказано «между», а не «включительно». Решить: 9{2}}>\frac{1}{{16}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t <\frac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ ,\,\,\,\,\,\,\,\,t>\frac{1}{4}\\\,\,\,\,\,\,\,\,\,\,\ ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{4}<\,\, t<\frac{1}{2}\end{array}\)
Мы будем использовать только знаки \(<\), поскольку в задаче сказано «между», а не «включительно». Решить: 9{2}}>\frac{1}{{16}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t <\frac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ ,\,\,\,\,\,\,\,\,t>\frac{1}{4}\\\,\,\,\,\,\,\,\,\,\,\ ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{4}<\,\, t<\frac{1}{2}\end{array}\) Нажмите ВВОД после Угадайте? , чтобы получить перекрестки.
Нажмите ВВОД после Угадайте? , чтобы получить перекрестки.