Теорема Виета. В чём её смысл?
Теорема Виета в квадратных уравнениях — штука простая и очень-очень важная. Позволяет делать массу полезных вещей буквально в уме. Имеет смысл познакомиться и освоить, правда? Тем более это совсем просто. Сомневаетесь? Напрасно.) Сами увидите. Читаем дальше.
Что такое приведённое квадратное уравнение? Складываем и перемножаем корни…
Знакомство наше начнём с безобидного уравнения:
Обычное квадратное уравнение, ничего выдающегося. Коэффициенты a, b и c здесь следующие:
a = 1; b = -4; c = 3
Решаем тоже как обычно, безо всяких фокусов, через дискриминант и получаем два корня:
Уравнение как уравнение — и что с того? Ничего, сейчас интересно будет!)
Первым делом я возьму корни нашего уравнения и… сложу их.) Зачем? Так надо!
Итак:
Теперь проделаю ещё одну бесполезную (казалось бы!) штуку. Перемножу корни:
Перемножу корни:
Ну сложил, ну перемножил — и что? Спокойствие и терпение!
Выпишем ещё разок само уравнение, а прямо под ним напишем сумму и произведение корней:
И посмотрим на нашу запись. Внимательно посмотрим… Ничего не бросается в глаза? Ведь многие важные открытия в математике совершались на основе хорошей наблюдательности, между прочим! Не видите…
А вот так?)
Да! Сумма корней нашего квадратного уравнения равна коэффициенту b. Но, обратите внимание, не просто b, а с противоположным знаком! В уравнении коэффициент при икс (а это и есть буковка b) равен минус четыре. Сумма же корней даёт плюс четыре. То есть, –b.
А произведение корней даёт нам свободный член! Т.е. буковку c. Даёт со своим знаком! Как была в уравнении тройка (с=3), так в произведении корней тройкой же и осталась. )
)
Теперь я немного изменю уравнение. Поменяю в нём свободный член с тройки на четвёрку. Вот такое уравнение теперь решим:
Решаем точно так же, через дискриминант (здесь он равен нулю), и получаем единственное решение x=2.
Но мы с вами люди уже достаточно взрослые и понимаем, что это не один корень, а два одинаковых:
x1,2 = 2
Поэтому снова сосчитаем сумму и произведение корней:
И опять в сумме мы получили –b (-b=+4), а в произведении с (c=+4)!
А вот это уже крайне важно! Оказывается, такая забавная штука будет получаться всегда для любого квадратного уравнения! Если оно имеет корни, разумеется.) Правда, уравнения не какого попало, а такого, где квадрат икса чистый (т.е. коэффициент a=1). В математике такие квадратные уравнения имеют своё особое название — приведённые квадратные уравнения.
В математике такие квадратные уравнения имеют своё особое название — приведённые квадратные уравнения.
Запоминаем:
Квадратное уравнение, в котором коэффициент при х2 равен единице (а=1), называется приведённым квадратным уравнением. Весьма важная штука!
Как оно выглядит в общем виде? Очень просто. Подставим в общий вид квадратного уравнения
единичку вместо а и получим общий вид приведённого квадратного уравнения:
В некоторых учебниках коэффициенты b и с переобозначают другими буквами (чаще всего p и q) и получают вот такой общий вид
Но суть та же самая. Как говорится, хоть горшком назови… Лично я предпочитаю использовать традиционные буквы b и с. Для универсальности.)
Ну и что из этого? — спросите вы. Чем приведённые квадратные уравнения так выделяются на фоне остальных квадратных, неприведённых? А дело вот в чём.
Чем приведённые квадратные уравнения так выделяются на фоне остальных квадратных, неприведённых? А дело вот в чём.
Что такое теорема Виета?
Итак, мы выяснили, что в приведённом квадратном уравнении (любом!) сумма коэффициентов равна –b, а произведение равно с. Всегда. Ясное дело, если дискриминант неотрицательный и корни у уравнения имеются.
Математически эта фишка записывается вот так:
Этот любопытный факт — и есть теорема Виета! Собственной персоной.
А словами она звучит вот как:
Теорема Виета:
Если ПРИВЕДЁННОЕ квадратное уравнение имеет корни, то их сумма равна коэффициенту при икс, взятому с противоположным знаком (—b), а их произведение равно свободному члену (c).
Вот и всё, никаких премудростей.)
Хотите строгое доказательство? Пожалуйста! Флаг вам в руки!) Распишите общую формулу корней квадратного уравнения для a=1, составьте сумму и произведение корней в общем виде. Т.е. через буквы. И упростите. Попробуйте! Весьма полезно и познавательно, между прочим.)
Верна также и обратная теорема:
Если числа х1 и х2 таковы, что их сумма равна –b, а произведение равно c, то эти числа являются корнями приведённого квадратного уравнения x2 + bx + c = 0.
А по секрету скажу вам, что, на самом деле, именно обратной теоремой вы и пользуетесь, так умело подбирая в уме корни уравнения по сумме и произведению! Об этом подборе как раз дальше будет. )
)
Зачем нужна теорема Виета?
Полезная вещь первая — подбираем корни в уме!
Теорема Виета (обратная форма) позволяет искать корни многих квадратных уравнений гораздо быстрее и проще, чем традиционным путём через дискриминант. В буквальном смысле устно!
Вернёмся к нашему уравнению:
Теперь, вооружившись глубокими познаниями, прямо по теореме Виета, записываем системку для наших искомых корней:
Вопрос на сообразительность: какие же такие два числа в сумме дают четвёрку, а в произведении — тройку? Немного подумав головой, можно довольно быстро догадаться, что это чиселки 1 и 3.
Значит, можно смело записать:
x1 = 1
x2 = 3
Вот и всё. Это и будут корни нашего уравнения. Оба подходят.) Здорово, правда? И не нужно считать никаких дискриминантов, возиться с общей формулой корней. В которой, между прочим, можно и ошибок наляпать… Сразу, в уме, получен верный ответ!
Это и будут корни нашего уравнения. Оба подходят.) Здорово, правда? И не нужно считать никаких дискриминантов, возиться с общей формулой корней. В которой, между прочим, можно и ошибок наляпать… Сразу, в уме, получен верный ответ!
Возможно, кто-то уже приготовил мне вопрос. Очень грамотный вопрос, кстати. А всегда ли в случае приведённого квадратного уравнения можно вот так красиво и легко подобрать корни?
К сожалению, нет. Далеко не всегда. Например, я снова изменю в исходном уравнении свободный член, только вместо четвёрки напишу двойку. Вот такое уравнение пусть будет:
Уравнение приведённое, коэффициент а равен единичке, вроде бы, всё нормально. Пишем теорему Виета:
И снова пробуем подобрать иксы так, чтобы оба равенства сработали!
Гм… Что-то не подбирается, правда? Какие бы целые числа вы бы ни подбирали, ничего не выйдет.
Тут выход только один — решать через дискриминант. Ибо дискриминант — штука универсальная. Спасает всегда — и в приведённых уравнениях, и в обычных. Попробуйте. И вы убедитесь, что корни этого уравнения получаются иррациональными. Естественно, такие корни подобрать в уме несколько затруднительно, да…
Ибо дискриминант — штука универсальная. Спасает всегда — и в приведённых уравнениях, и в обычных. Попробуйте. И вы убедитесь, что корни этого уравнения получаются иррациональными. Естественно, такие корни подобрать в уме несколько затруднительно, да…
Догадываюсь, что вы сейчас спросите: Зачем же нам тогда городить огород, пробовать подобрать корни, если дискриминант всё равно надёжнее и с ним-то уж точно всё решится?
Да, надёжнее, но… Не всё так просто, как кажется!
Дело всё в том, что квадратные уравнения изучаются в 8-м классе, где народ тренируется на простых (иногда — совсем примитивных) задачках. И… привыкает к простоте.) Затем, в старших классах и особенно в институте, при изучении высшей математики, квадратные уравнения представляются как нечто само собой разумеющееся. Но при этом в коэффициентах зачастую возникают такие большие числа, что работать с ними большинство учеников… просто не готовы!
Попадётся вам, к примеру, такая задачка:
Из пункта А в пункт В, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 82 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 3 часа 25 минут позже автомобилиста. Ответ дайте в км/ч.
Известно, что в час автомобилист проезжает на 82 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 3 часа 25 минут позже автомобилиста. Ответ дайте в км/ч.
Это не моя разыгравшаяся фантазия, а вполне реальная задачка из ЕГЭ, между прочим.)
Кто в курсе, как решать текстовые задачи на движение, тот без труда составит вот такое уравнение:
Классическое дробно-рациональное уравнение. Здесь х — скорость велосипедиста. Немного повозившись с ним (избавившись от дробей и упростив всё до упора), получим вот такое квадратное уравнение:
Если начать решать это уравнение по-рабочекрестьянски, то получим, что дискриминант у него равен аж 13924! И… что? Как нам из такого здоровенного числа корень извлекать? Без калькулятора! Слабо? То-то…
Зато через теорему Виета это злое уравнение решается практически устно! Не верите? Что ж, смотрите сами…
Записываем сумму и произведение корней:
Осталось лишь догадаться, какие же числа дают в сумме минус 82, а в произведении минус 1800. Совсем чуточку подумав, довольно быстро получим, что:
Совсем чуточку подумав, довольно быстро получим, что:
Минус сто, ясное дело, нас не интересует (скорость не бывает отрицательной), а вот 18 км/ч — вполне себе правдоподобная велосипедная скорость.)
Вот и все дела.) И без долгих и утомительных вычислений, связанных с извлечением корня из пятизначного числа! Здорово, правда?
Посему, первые практические советы:
1. Если перед вами квадратное уравнение приведённого вида, то первым делом пробуем найти корни подбором. По теореме, ОБРАТНОЙ теореме Виета. В подавляющем большинстве заданий это срабатывает.
2. Не боимся уравнений с большими коэффициентами! Самое главное — не бросаемся считать дискриминант! Как правило, корни таких уравнений также довольно легко ищутся подбором.
Может, конечно, и не повезти, но зачем же такой шанс упускать, правда?)
Но есть у меня для вас хорошая новость.) Составители большинства заданий — люди гуманные. ) И стараются составить уравнение так, чтобы корни являлись целыми числами и их легко можно было бы подобрать. Пробуем делать это!
) И стараются составить уравнение так, чтобы корни являлись целыми числами и их легко можно было бы подобрать. Пробуем делать это!
Переходим к следующей полезной вещи.
Полезная вещь вторая — проверяем корни!
Теорему Виета можно применять не только для подбора корней, но и для проверки корней, найденных другим способом (через дискриминант, например). Решили уравнение — проверьте сумму и произведение корней! Всё срослось — значит, верно. Нет — значит, где-то накосячили. Ищите ошибку.)
Например, такое уравнение:
Дело нехитрое. Решаем себе через дискриминант, всё чин-чином, получаем корни:
x1 = -7
x2 = -3
Не бросаемся сразу же радостно писать ответ! Знаете поговорку доверяй, но проверяй?) Вот и не ленимся. Первым делом сложим наши корни:
Первым делом сложим наши корни:
Получили -10. Обратите внимание, не десять, а минус десять! Коэффициент b с противоположным знаком. Так уж теорема Виета устроена.)
Последняя (и окончательная) проверка — перемножим корни. Должен получиться свободный член:
Вот теперь всё хорошо.)
Более того, с этой благородной целью (проверка корней) теорему Виета можно применять и для неприведённых квадратных уравнений. Для любых. Да-да, я не шучу! Но эту фишку я оставлю на конец урока. На десерт.)
И что, думаете, только для подбора и проверки корней теорема Виета и нужна? Вовсе нет!
Полезная вещь третья — когда корни считать… не надо!
Вы спросите, а разве можно обойтись и вовсе без вычисления корней? Можно! Ещё как!)
Дискриминант — штука, безусловно, удобная, простая и понятная. С ним, как правило, всё легко и предсказуемо. Но… Может получиться какой-нибудь дурацкий дискриминант: 17 там, скажем, или 20. Что неизбежно приводит к появлению иррациональных корней, да…) А уж если в задании надо ещё что-то делать с корнями, то выражения с радикалами, даже для опытного ученика, могут перерасти в большую проблему. А для неопытного — вообще превратиться в полный ахтунг.
С ним, как правило, всё легко и предсказуемо. Но… Может получиться какой-нибудь дурацкий дискриминант: 17 там, скажем, или 20. Что неизбежно приводит к появлению иррациональных корней, да…) А уж если в задании надо ещё что-то делать с корнями, то выражения с радикалами, даже для опытного ученика, могут перерасти в большую проблему. А для неопытного — вообще превратиться в полный ахтунг.
Но теорема Виета иногда способна на настоящие чудеса!
Например, такое задание:
Дано квадратное уравнение:
Найдите сумму квадратов корней, не находя самих корней.
Если сейчас начать решать это задание «в лоб» — считать дискриминант и искать корни уравнения по общей формуле, то получим вот таких двух красавцев:
Нам нужна сумма их квадратов. И что нам теперь с такими лохматыми числами делать?! Возводить в квадрат, складывать… Нет, возвести и сложить можно, конечно, но… не каждый ученик дорешает до конца это задание без ошибок!
Не отчаиваемся и читаем ещё раз условие. Обратите внимание, нам вообще НЕ сказано «решать уравнение», НЕ сказано «находить корни». Более того, нам прямым текстом говорится: «Найти сумму квадратов корней, не находя самих корней«.
Обратите внимание, нам вообще НЕ сказано «решать уравнение», НЕ сказано «находить корни». Более того, нам прямым текстом говорится: «Найти сумму квадратов корней, не находя самих корней«.
Что делать? Как выкручиваться без поиска корней?
Посмотрим ещё раз на уравнение. Приведённое, между прочим.) Раз так, то, стало быть, для него справедлива теорема Виета!
Можно смело записать:
Вот так. Сумма корней — тройка, а произведение — единичка. Мы не знаем, чему равны сами эти корни, но у нас это и не спрашивают. Нас просят найти только сумму их квадратов.)
А вот теперь ключевой вопрос: А можно ли как-то расписать нужную нам сумму квадратов корней через сумму и произведение корней?
Да, можно! Кто на «ты» с формулами сокращённого умножения (а именно — с формулой квадрата суммы), тот, скорее всего, даже не заметит проблем.
Пишем:
Как я додумался до этого равенства? Очень просто. Вспомнил, что в формуле квадрата суммы сидят сумма квадратов и удвоенное произведение:
И выразил нужную величину (сумму квадратов) через остальные — сумму (т.е. квадрат суммы) и произведение (удвоенное).
Вот и всё, практически. Осталось лишь подставить тройку вместо суммы и единицу вместо произведения корней, да и посчитать, что получится:
Ответ: 7
И все дела.) И корни не понадобились! Вообще.) Мощная штука — теорема Виета! Ну и формулы сокращённого умножения, само собой.)
Этот приём — выражение какой-то сложной конструкции через сумму и произведение корней — очень популярен в заданиях на теорему Виета! Я уж молчу про более серьёзные задания. Например, задачи с параметрами, там этот финт ушами используется на полную катушку.)
Например, задачи с параметрами, там этот финт ушами используется на полную катушку.)
Запоминаем:
В серьёзных заданиях на сумму и произведение корней пользуемся формулами сокращённого умножения и алгеброй 7-го класса! Здорово помогает.)
Как работать с неприведёнными уравнениями?
Как известно, самое сладкое — в конце трапезы. Обещанный десерт.)
Во всех примерах этого урока мы работали лишь с приведёнными квадратными уравнениями. Такими, у которых коэффициент при квадрате икса — единичка. А если уравнение не является приведённым? Т.е. а≠1? Что тогда? Про теорему Виета можно забыть?
Нет, забывать мы не будем. Мы поступим мудро и красиво. Раз уравнение не является приведённым, то мы его… сделаем! Как? Очень просто! Берём квадратное уравнение в общем виде:
и… делим обе части на «а»! Очищаем квадрат икса от коэффициента. Можно ли так делать? Конечно! Мы ведь с вами уже в курсе, что a никогда не бывает равно нулю (а≠0). Иначе уравнение будет не квадратным, а линейным. Вот и делим смело. Это совершенно безопасно. Естественно, все остальные слагаемые тоже придётся поделить на а, от этого никак не отвертишься.
Можно ли так делать? Конечно! Мы ведь с вами уже в курсе, что a никогда не бывает равно нулю (а≠0). Иначе уравнение будет не квадратным, а линейным. Вот и делим смело. Это совершенно безопасно. Естественно, все остальные слагаемые тоже придётся поделить на а, от этого никак не отвертишься.
Получим:
Вот и всё. Уравнение стало приведённым. Коэффициенты, правда, дробными стали, но тут уж ничего не поделать, да…) В этом новом уравнении в роли нового «b« выступает дробь b/a, а в роли нового свободного члена — дробь c/a. Можно записывать теорему Виета:
Вот так. Такая модифицированная запись теоремы Виета — более общая. Для любых квадратных уравнений годится — как приведённых (а=1), так и обычных (а≠1). С той лишь разницей, что при а=1 знаменатели исчезают — и теорема обретает свой привычный вид.
Имеет смысл запомнить эту общую форму записи: и для банальной проверки корней пригодится, и, опять же, для более солидных заданий на квадратные уравнения.
Например, надо решить уравнение:
Решаем, получаем корни:
Предположим, вам захотелось проверить, правильно ли вы нашли ваши иксы. Для этого, знамо дело, их надо подставить в исходное уравнение и посчитать результат. Но корни — дробные. Подставлять да считать долго и муторно…
Как проверить корни быстро и с минимумом вычислений? Не проблема! Записываем обобщённую теорему Виета для а=6:
И работаем. Складываем корни:
Так, по сумме всё проходит. Осталось перемножить:
И тут полный порядок! Значит, всё правильно.)
Очередной практический совет:
Найденные корни стараемся проверять! По сумме и произведению. Это здорово уменьшает количество ошибок при решении квадратных уравнений. Если уравнение не является приведённым, то для проверки пользуемся соответствующей модифицированной теоремой Виета.
Это здорово уменьшает количество ошибок при решении квадратных уравнений. Если уравнение не является приведённым, то для проверки пользуемся соответствующей модифицированной теоремой Виета.
Итак, мы с вами выяснили, что теорема Виета — штука простая. И очень полезная. И это не только трафаретное решение квадратных уравнений! В ВУЗе, при работе со всякими там пределами, интегралами, дифференциальными уравнениями и прочими прелестями высшей математики, вы ещё не раз вспомните добрым словом знаменитого французского математика с его теоремой.)
Ну что, порешаем?
1. Найдите подбором корни уравнений:
Ответы (в беспорядке):
2. Сумма катетов прямоугольного треугольника равна 23 см, а гипотенуза равна 17 см. Найдите больший катет треугольника.
3. Разность корней уравнения 2х2 — 5х + с = 0 равна 1,5. Найдите с.
Найдите с.
4. Дано уравнение: x2 — 6x + 4 = 0. Не решая уравнения, найдите сумму кубов его корней.
5. Известно, что х1 и х2 — корни уравнения х2-18х+11 = 0.
Найдите значение выражения:
Ответы (в беспорядке):
144; 15; -1; 1
Всё сошлось? Рад за вас! Значит, отныне теорема Виета — не ваша очередная головная боль, а новый надёжный друг и помощник при решении уравнений (и не только квадратных, между прочим!).
Задания 4 и 5 не идут? Корни иррациональные получаются? Это специально.) Да и не нужны они вам… Да, есть там одна загвоздочка. Но алгебра седьмого класса и действия с дробями вам помогут! И этот урок, само собой. И всё получится.)
«Какой смысл подробно изучать теорему Виета в школе?» — Яндекс Кью
Математика и математики
104472 участника сообщества
Я не ханжа и не из тех, кто спрашивает «зачем детям вся эта тригонометрия с логарифмами». Разумеется, математика в целом нужна, интересна и полезна. Но конкретно теорема Виета меня смущает. Нет, я совсем не против, чтобы школьники научились доказывать её при необходимости. Однако есть ли смысл запоминать теорему наизусть и тем более как-то использовать её?
Разумеется, математика в целом нужна, интересна и полезна. Но конкретно теорема Виета меня смущает. Нет, я совсем не против, чтобы школьники научились доказывать её при необходимости. Однако есть ли смысл запоминать теорему наизусть и тем более как-то использовать её?
Для чего вообще нужна теорема Виета? В меру моего понимания, с её помощью можно угадать корни квадратного уравнения в некоторых простых случаях. Но зачем эти корни угадывать (тратя время и рискуя в конце концов не угадать), если имеется однозначная формула, позволяющая получить оба корня? Конечно, эта формула не так проста для запоминания (должен ли школьник её запоминать — отдельный вопрос, но факт в том, что формула есть). Но она всегда гарантированно
Почему в большинстве? Мне приходилось в жизни решать множество квадратных уравнений (я преподаватель в университете), и ни разу не было случая, чтобы теорема Виета могла бы оказаться при этом полезной. Потому просто, что в реальной жизни корни попросту не целочислены (или вовсе представляют собой некие буквенные параметры). Соответственно саму теорему я обычно даже не помню и не вспоминаю о ней, хотя, разумеется, при необходимости (если бы она была) способен её вывести за несколько секунд в уме.
Потому просто, что в реальной жизни корни попросту не целочислены (или вовсе представляют собой некие буквенные параметры). Соответственно саму теорему я обычно даже не помню и не вспоминаю о ней, хотя, разумеется, при необходимости (если бы она была) способен её вывести за несколько секунд в уме.
Конечно, остаётся вариант «теорема полезна для проверки полученного решения». Но опять-таки, полученное решение проще проверить, пересчитав по исходной формуле, нежели запоминать ещё два дополнительных уравнения и проверять по одному из них.
Вопрос возник потому, что ребёнок в школе, наконец, дошёл до этой теоремы. Насколько будет педагогичным сказать ему: «Выучи, потому что от тебя этого требуют, и попробуй применять для тех искусственных примеров, что даёт учебник; после этого можешь спокойно забыть и пользоваться основной формулой»? 🙂
El Selenita · ·
5,0 K
Андрей Плахов
Математика
Кандидат физ. -мат. наук, делаю Яндекс, увлекаюсь… · 25 нояб 2021
-мат. наук, делаю Яндекс, увлекаюсь… · 25 нояб 2021
Самое полезное в ней не её применение, а её доказательство.
По-моему, для будущего технаря очень полезное упражнение умножить (x-a)*(x-b), раскрыть скобки и немного помедитировать над левой и правой частями: что это за a и b такие слева, почему в скобках знак «минус», а не «плюс», и чему соответствуют их комбинации справа. Без этого понимания квадратные уравнения просто какой-то изолированный и нечасто пригождающийся технический навык, вроде деления в столбик на листе бумаги, а если осознать эту операцию, потом гораздо проще оперировать более сложными многочленами и их корнями, если вдруг придется.
·
251
Надежда Шихова
подтверждает
25 нояб 2021
Действительно, теорема Виета — не только инструмент для решения задач, но еще и путь к более глубокому пониманию предмета.
Комментировать ответ…Комментировать…
Борис Державец
Data science
Openstack DevOps and IBM/Informix Certified DBA… · 25 нояб 2021
Теорема Виета в общем виде верна для уравнений с постоянными коэффициентами любой степени «n». Достаточно часто задачи ЕГЭ или Олимпиад начинаются с подбора целого делителя у свободного члена за которым следует деление по схеме… Читать далее
1 оценил·
110
Комментировать ответ…Комментировать…
Ирина Солдатенко
Математика
МГТУ им. Баумана, доцент, репетитор. · 28 нояб 2021
Я бы многое выкинула из школьного курса, но не теорему Виета!
В реальной школьной жизни она нужна постоянно, прежде всего для проверки полученных корней!
По моему опыту самые частые (и самые обидные) вычислительные ошибки на… Читать далее
Читать далее
·
Комментировать ответ…Комментировать…
Сергей Леонтьев
Математика
Астрономия, криптография · 26 нояб 2021
Смысл: математическое обоснование методов решения, как квадратных уравнений, так и уравнений более высокой степени. Конечно, можно зазубрить формулы: квадратного уравнения, Кардано и т.п., и тупо доказать их тупой подстановкой… Читать далее
3 оценили·
151
Комментировать ответ…Комментировать…
Владимир Горбацевич
Математика
математика нестандартный психоанализ · 26 нояб 2021
Теорема Виета хороша в школе, так как с помощью несложного рассуждения доказывается неожиданный (для новичка) результат. Нахождение же корней квадратного уравнения с ее помощью — это как бы «бесплатное приложение» к ней.
·
115
Oleg Kuznetsov
1 дек 2021
точно — то что была довольно активная попытка методичного и циничного вымывания из школьного курса самих основ анал… Читать дальше
Комментировать ответ…Комментировать…
Михаил Мулюков
Математика
Математик-теоретик, занимаюсь исследованиями в… · 26 нояб 2021
Теорема Виета широко используется для решения школьных задач, зависящих от параметра (предпоследняя задача из ЕГЭ). На практике при исследовании расположения корней многочленов высоких степеней бывает важно доказать… Читать далее
2 оценили·
128
Комментировать ответ…Комментировать…
Андрей Бахматов
Биология
Увлекаюсь естественными науками и математикой. .. · 25 нояб 2021
.. · 25 нояб 2021
В школе как таковые формулы Виета вообще не изучают, а изучают только использование одного из простых частных случаев, то же верно и в отношении дискриминанта. Формулы Виета очень важны, но в школьной программе просто не даются… Читать далее
1 оценил·
115
Комментировать ответ…Комментировать…
Вадим Романский
Физика
младший научный сотрудник ФТИ им. Иоффе · 25 нояб 2021 ·
astropolytech
Вы совершенно правы, что теорема Виета совершенно не нужна для нахождения корней уравнения. В реальных физических задачах вообще целых коэффициентов в принципе не бывает. Но само по себе такое угадывание — довольно неплохая… Читать далее
астрофизическое образование
Перейти на vk.com/astropolytech20 оценили·
1,4 K
Михаил Мулюков
26 нояб 2021
След, детерминант и все остальные матричные инварианты)
Комментировать ответ…Комментировать…
Дмитрий Иванов
Астрономия
По образованию физик и математик (МФТИ). … · 28 нояб 2021
… · 28 нояб 2021
Далась Вам именно теорема Виета? Она несложная и много времени не отнимает. Это не «Война и Мир», которую только прочитать кучу времени занимает
3 оценилиКомментировать ответ…Комментировать…
Сергей Перовский
Топ-автор
Научные заметки о жизни. https://zen.yandex.ru/id/… · 25 нояб 2021
Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням. Обратная задача нахождения полинома по его корням встречается в науке и технике… Читать далее
2 оценили·
134
Сергей Лыткин
подтверждает
30 нояб 2021
А ещё теорема Виета позволяет в простых случаях угадать корни квадратного уравнения без вычисления дискриминанта. .. Читать дальше
.. Читать дальше
Комментировать ответ…Комментировать…
Полиномы Виета-Пелла и Виета-Пелла-Лукаса | Достижения в непрерывных и дискретных моделях
В этом разделе приведены некоторые фундаментальные рекурсивные свойства полиномов Виета-Пелла и Виета-Пелла-Лукаса.
Характеристическое уравнение
Полиномы Виета-Пелла и Виета-Пелла-Лукаса имеют следующее характеристическое уравнение: −1,β=x−x2−1.
Также α и β удовлетворяют следующим уравнениям:
α+β=2x,αβ=1,α−β=Δ=2×2−1.
(1)
Форма Бине
С помощью соответствующей процедуры мы можем легко найти формы Бине как βн.
(3)
Производящая функция
Полиномы Виета-Пелла и Виета-Пелла-Лукаса могут быть определены следующими производящими функциями:
∑n=0∞tn(x)yn=y(1−2xy+y2 )−1,∑n=0∞sn(x)yn=(2−2xy)(1−2xy+y2)−1.
Отрицательный индекс
Мы также можем расширить определение tn(x) и sn(x) до отрицательного индекса
t−n(x)=−tn(x),s−n(x)=sn( Икс).
Формулы Симсона
tn+1(x)tn−1(x)−tn2(x)=−1,sn+1(x)sn−1(x)−sn2(x)=4(x2−1 ).Разместим первые десять коэффициентов tn(x) в таблице 1. Пусть T(n,j) обозначает элемент в строке n и столбце j , где j⩾0, n⩾1. Как видно из таблицы 1, очевидно, что
T(n,0)=2T(n−2,0)+T(n−1,0)
можно записать как коэффициенты полиномов Пелла в [7]. При этом
∑j=0⌊n−12⌋T(n,j)=n.
Например, для n=8 можно найти
∑j=03T(8,j)=T(8,0)+T(8,1)+T(8,2)+T(8,3 )=8.
Пусть Pn обозначает n -е число Пелля, поэтому мы имеем
∑j=1⌊n−12⌋|T(n,j)|=Pn.
Таблица 1 Первые десять коэффициентов числа tn(x)Полная таблица
2.1 Взаимосвязь tn(x) и sn(x)
Большинство приведенных ниже уравнений можно получить, используя форму Бине и удобные рутинные операции
tn+1(x)−tn−1(x)=sn(x)=2xtn(x)−2tn−1(x ),
(4)
sn+1(x)−sn−1(x)=4(x2−1)tn(x),tn(x)sn(x)=t2n(x),sn2( x)+4(x2−1)tn2(x)=2s2n(x),sn2(x)−4(x2−1)tn2(x)=4,tn+12(x)−tn2(x)=t2n +1(x),sn+12(x)−sn2(x)=4(x2−1)t2n+1(x),sn+12(x)+sn2(x)=2xs2n+1(x)+ 4,tn+12(x)−tn−12(x)=2xt2n(x),sn(x)sn+1(x)−4(x2−1)tn(x)tn+1(x)=4x ,sn(x)sn+1(x)+4(x2−1)tn(x)tn+1(x)=2s2n+1(x),s4n(x)−2=4(x2−1)t2n2 (x),tn+1(x)−xtn(x)=12sn(x),2sn+1(x)−2xsn(x)=4(x2−1)tn(x).
(5)
Предложение 1 sn(2×2−1)−sn2(x)=−2.
Доказательство Рассмотрим выражение sn(2×2−1). Тогда α , β , Δ заменяются на α∗, β∗, Δ∗ соответственно. Итак, α∗=α2, β∗=β2, ∆∗=2x∆ и с использованием формы Бине доказательство завершено. □
2.2 Связанные последовательности
Определение 1 k -я ассоциированная последовательность {tn(k)(x)} и {sn(k)(x)} {tn(x)} и {sn(x)} )} определяются соответственно (k≥1)
tn(k)(x)=tn+1(k−1)(x)−tn−1(k−1)(x),
(6)
sn(k)(x)=sn +1(k−1)(x)−sn−1(k−1)(x),
(7)
, где tn(0)(x)=tn(x) и sn(0)(x )=sn(x).
В настоящее время
tn(1)(x)=sn(x)(по (4)),sn(1)(x)=∆2tn(x)(по (5))
являются членами первые ассоциированные последовательности {tn(1)(x)} и {sn(1)(x)}. При многократном применении (6) и (7) получаются результаты
−2)(x)=∆2j−2sn(x).
Некоторые специальные значения tn(x) и sn(x)
{tn(−x)=(−1)n+1tn(x),tn(1)=n,tn(−1)=(−1 )n+1n,t2n(0)=0,t2n−1(0)=(−1)n+1,{sn(1)=2,sn(−1)=2(−1)n,s2n( 0)=2(−1)n,s2n−1(0)=0.
2.3 Формулы дифференцирования
dsn(x)dx=2ntn(x),dtn(x)dx=nsn(x)−2xtn(x)2(x2−1),d2sn(x)dx2=n(nsn( х)−2xtn(x)x2−1).
Поскольку производная функция sn(x) является многочленом, все производные должны существовать для всех действительных чисел. Таким образом, мы можем привести следующие формулы.
Предложение 2
d2sn(x)dx2|x=1=23(n4−n2),d2sn(x)dx2|x=−1=23(−1)n−1(n2−n4).
Доказательство Если мы возьмем предел на sn″(x)=n(nsn(x)−2xtn(x)x2−1), мы получим численное значение sn″ при x=1 и x=−1 .
sn″(1)=n2limx→1nsn(x)−2xtn(x)(x−1).
Поскольку sn(1)=2, tn(1)=n, применим правило Лопиталя:
sn″(1)=n2limx→1ddx(nsn(x)−2xtn(x))ddx(x−1 )=n2limx→1ddx(nsn(x)−2xtn(x))=n2limx→1(2n2tn(x)−2tn(x)−2xddxtn(x))=n2(2n2tn(1)−2tn(1)−2limx →1ddxtn(x))=n2(2n3−2n)−12limx→1ddx(2ntn(x))=n4−n2−12sn″(1).
Итак, доказательство для x=−1 аналогично. □
2.4 Некоторые формулы суммирования
В этом разделе мы имеем дело с матрицей
V=[2x−110].
По индукции имеем
Vm=[tm+1(x)−tm(x)tm(x)−tm−1(x)].
(8)
Итак, матрица V порождает полиномы Виета-Пелла и Виета-Пелла-Лукаса. Отсюда
[tm+1(x)tm(x)]=Vm[10]
(9)
и из (1.10) в [8] получаем
tm(x)=[10] Вм-1[10].
(10)
Известно, что
Vm+n=VmVn.
(11)
Из (8) и (11) элементарные формулы для tn(x) очевидны
tm+n+1(x)=tm+1(x)tn+1(x)− tm(x)tn(x),tm+n(x)=tm+1(x)tn(x)−tm(x)tn−1(x),tm+n−1(x)=tm(x )tn(x)−tm−1(x)tn−1(x).
Если использовать матричный метод суммирования из [8], то первое конечное суммирование получается следующим образом.
Предложение 3
- (я)
∑n=1mtn(x)=tm+1(x)−tm(x)−12(x−1),
- (ii)
∑n=1msn(x)=sm+1(x)−sm(x)+2−2×2(x−1).

Доказательство (i) Пусть матрица A ,
A=I+V+V2+⋯+Vn−2+Vn−1
представляет собой серию матриц. Тогда имеем
ВА=V+V2+⋯+Vn−1+Vn.
Следовательно,
(V−I)A=Vn−I,A=(V−I)−1(Vn−I)A=12(x−1)[tn+1(x)−tn(x )−1tn−1(x)−tn(x)+1tn(x)−tn−1(x)−1tn−2(x)−tn−1(x)+2x−1],∑n=1mtn( x)=[10]A[10](по (10))∑n=1mtn(x)=12(x−1)[tm+1(x)−tm(x)−1tm−1(x)− tm(x)+1][10]∑n=1mtn(x)=12(x−1)[tm+1(x)−tm(x)−1].
Итак, доказательство завершено.
- (ii)
∑n=1msn(x)=∑n=1m(αn+βn)(по (3))=α(1−αm1−α)+β(1−βm1−β)=(α+β)−2αβ −(αm+1+βm+1)+αβ(αm+βm)2−2x=2x−2−(αm+1+βm+1)+αm+βm2(1−x)(по (1))= sm+1(x)−sm(x)+2−2×2(x−1)(по (3)).
Это завершает доказательство. □
Теорема 1 Пусть V – квадратная матрица такая, что V2=2xV−I. Затем , для всех n∈Z+,
Затем , для всех n∈Z+,
Vn=tn(x)V−tn−1(x)I,
, где tn(x) есть n-й Pell111 — 900 многочлен и I является единичной матрицей .
Доказательство Доказательство очевидно по индукции. □
[Персонализированная медицина в области психического здоровья: прецизионная психиатрия]
Сохранить цитату в файл
Формат: Резюме (текст) PubMedPMIDAbstract (текст) CSV
Добавить в коллекции
- Создать новую коллекцию
- Добавить в существующую коллекцию
Назовите свою коллекцию:
Имя должно содержать менее 100 символов
Выберите коллекцию:
Не удалось загрузить вашу коллекцию из-за ошибки
Повторите попытку
Добавить в мою библиографию
- Моя библиография
Не удалось загрузить делегатов из-за ошибки
Повторите попытку
Ваш сохраненный поиск
Название сохраненного поиска:
Условия поиска:
Тестовые условия поиска
Электронное письмо: (изменить)
Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый рабочий день
Который день? ВоскресеньеПонедельникВторникСредаЧетвергПятницаСуббота
Формат отчета: SummarySummary (text)AbstractAbstract (text)PubMed
Отправить максимум:
1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.
5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.
Отправить, даже если нет новых результатов
Необязательный текст в электронном письме:
Создайте файл для внешнего программного обеспечения для управления цитированием
Редакция
. 2015 июль-сен;8(3):117-8.
doi: 10.1016/j.rpsm.2015.03.003. Эпаб 2015 8 мая.
[Статья в испанский]
Эдуард Виета 1
принадлежность
- 1 Instituto de Neurociencias, Hospital Clinic, Барселонский университет, Барселона, Испания; Институт биомедицинских исследований Августа Пи и Суньера (IDIBAPS), Барселона, Испания; Centro de Investigacion Biomédica en Red de Salud Mental (CIBERSAM), Барселона, Испания.
 Электронный адрес: [email protected].
Электронный адрес: [email protected].
- PMID: 25959401
- DOI: 10.1016/ж.рпсм.2015.03.003
От редакции
[Статья в испанский]
Эдуард Виета. Преподобный Псикиатр Салуд Мент. 2015 июль-сен.
. 2015 июль-сен;8(3):117-8.
doi: 10.1016/j.rpsm.2015.03.003. Эпаб 2015 8 мая.
Автор
Эдуард Виета 1
принадлежность
- 1 Instituto de Neurociencias, Hospital Clinic, Барселонский университет, Барселона, Испания; Институт биомедицинских исследований Августа Пи и Суньера (IDIBAPS), Барселона, Испания; Centro de Investigacion Biomédica en Red de Salud Mental (CIBERSAM), Барселона, Испания.
 Электронный адрес: [email protected].
Электронный адрес: [email protected].
- PMID: 25959401
- DOI: 10.1016/ж.рпсм.2015.03.003
Реферат отсутствует
Похожие статьи
Джошуа Гордон.
[Нет авторов в списке] [Нет авторов в списке] Nat Rev Drug Discov. 2017 31 июля; 16 (8): 523-524. doi: 10.1038/nrd.2017.134. Nat Rev Drug Discov. 2017. PMID: 28757625 Аннотация недоступна.
Быстрое и медленное мышление — в клинической психиатрии.
Паркер Г. Паркер Г.
 Acta Psychiatr Scand. 2018 фев; 137 (2): 85-87. doi: 10.1111/acps.12837. Epub 2017 23 ноября.
Acta Psychiatr Scand. 2018.
PMID: 29171023
Аннотация недоступна.
Acta Psychiatr Scand. 2018 фев; 137 (2): 85-87. doi: 10.1111/acps.12837. Epub 2017 23 ноября.
Acta Psychiatr Scand. 2018.
PMID: 29171023
Аннотация недоступна.Точность в психиатрии.
ван дер Стель Дж.К. ван дер Стель Дж. Acta Psychiatr Scand. 2015 г., октябрь; 132 (4): 310-1. doi: 10.1111/acps.12461. Epub 2015 3 июля. Acta Psychiatr Scand. 2015. PMID: 26137894 Аннотация недоступна.
Персонализированная медицина в психиатрии: проблемы и перспективы.
Озомаро У., Валестедт С., Немерофф С.Б. Озомаро У и др. БМС Мед. 2013 16 мая; 11:132. дои: 10.1186/1741-7015-11-132. БМС Мед. 2013. PMID: 23680237 Бесплатная статья ЧВК. Рассмотрение.
Подходы машинного обучения для клинической психологии и психиатрии.

Дуайер Д.Б., Фалкаи П., Куцулерис Н. Дуайер Д.Б. и др. Annu Rev Clin Psychol. 2018 7 мая; 14:91-118. doi: 10.1146/annurev-clinpsy-032816-045037. Epub 2018 Янв 29. Annu Rev Clin Psychol. 2018. PMID: 29401044 Рассмотрение.
Посмотреть все похожие статьи
Цитируется
МикроРНК, стволовые клетки при биполярном расстройстве и подход к терапии литием.
Кораддуцца Д., Гаррони Г., Конджарджу А., Бальзано Ф., Кручиани С., Седда С., Ниволи А., Майоли М. Кораддуцца Д. и соавт. Int J Mol Sci. 2022 10 сентября; 23(18):10489. дои: 10.3390/ijms231810489. Int J Mol Sci. 2022. PMID: 36142403 Бесплатная статья ЧВК. Рассмотрение.
Выход за рамки универсального обоснования глобального психического здоровья: перспективы парадигмы точной психологии.

Purgato M, Singh R, Acarturk C, Cuijpers P. Пургато М. и соавт. Эпидемиол Psychiatr Sci. 2021, 11 октября; 30:e63. дои: 10.1017/S2045796021000500. Эпидемиол Psychiatr Sci. 2021. PMID: 34632978 Бесплатная статья ЧВК.
Депрессия с точки зрения точного психического здоровья: использование персонализированных концепций для руководства персонализированным лечением.
Дейф Р., Салама М. Дейф Р. и др. Фронтовая психиатрия. 2021 11 мая; 12:650318. doi: 10.3389/fpsyt.2021.650318. Электронная коллекция 2021. Фронтовая психиатрия. 2021. PMID: 34045980 Бесплатная статья ЧВК. Рассмотрение.
Оценка мобильного приложения для повышения реляционной осведомленности и изменений во время когнитивно-аналитической терапии: серия случаев смешанных методов.

Келлетт С., Истон К., Купер М., Миллингс А., Симмондс-Бакли М., Парри Г. Келлетт С. и соавт. Ментальное здоровье JMIR. 2020, 18 декабря; 7(12):e19888. дои: 10.2196/19888. Ментальное здоровье JMIR. 2020. PMID: 33337342 Бесплатная статья ЧВК.
Исследование в социальных сетях о влиянии психиатрических препаратов.
Саха К., Шугар Б., Тороус Дж., Абрахао Б., Киджиман Э., Де Чоудхури М. Саха К. и др. Proc Int AAAI Conf Weblogs Soc Media. 2019 7 июня; 13: 440-451. Proc Int AAAI Conf Weblogs Soc Media. 2019. PMID: 32280562 Бесплатная статья ЧВК.
Просмотреть все статьи «Цитируется по»
Типы публикаций
термины MeSH
вещества
Полнотекстовые ссылки
Эдисионес Дойма, С.


 Электронный адрес:
Электронный адрес: 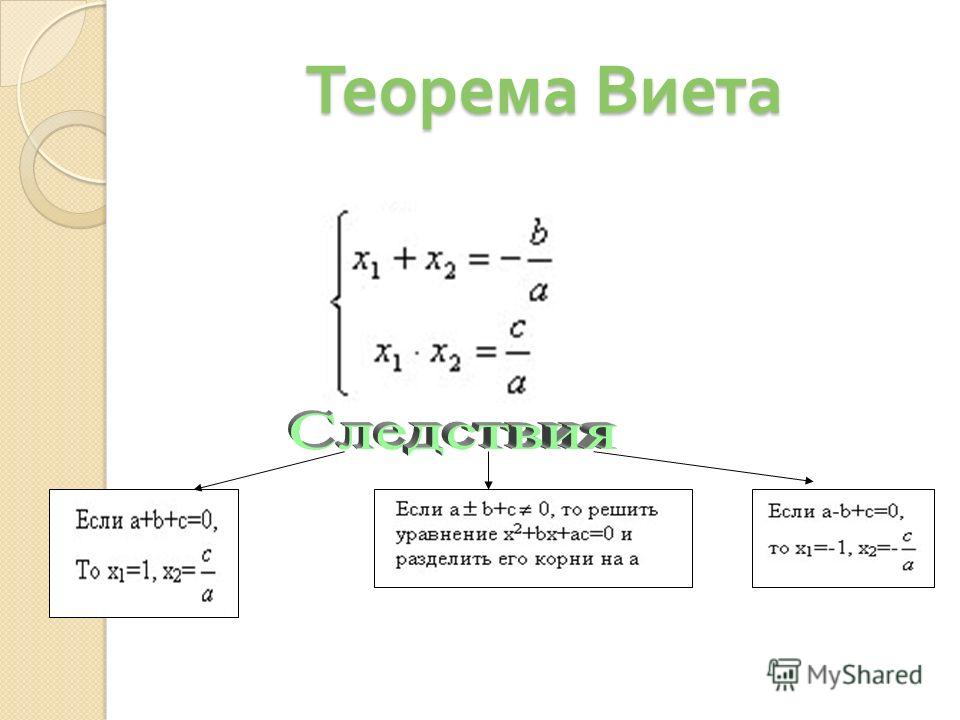 Электронный адрес:
Электронный адрес:  Acta Psychiatr Scand. 2018 фев; 137 (2): 85-87. doi: 10.1111/acps.12837. Epub 2017 23 ноября.
Acta Psychiatr Scand. 2018.
PMID: 29171023
Аннотация недоступна.
Acta Psychiatr Scand. 2018 фев; 137 (2): 85-87. doi: 10.1111/acps.12837. Epub 2017 23 ноября.
Acta Psychiatr Scand. 2018.
PMID: 29171023
Аннотация недоступна.

