Как решать примеры с отрицательной степенью: Уравнения с отрицательными степенями примеры решения. Степенные выражения (выражения со степенями) и их преобразование. Возведение числа в степень

1=2\)

 

Готов ответ.

Ответ: \(2\)

Возведение в степень в Python – способы, типы степеней, отбратные операции

upd:

30.01.2022

Александр Зайков

46.8K

Содержание:развернуть

Когда я был студентом, мой преподаватель по методам программирования любил повторять: «В математике все идеи простые». Чаще всего, фраза звучала в момент объяснения новой сложной темы, а потому вызывала определённые внутренние противоречия.

С возведением в степень всё не так — это действительно простая операция.

История

Возведение в степень — частный случай умножения, поэтому данную операцию изначально не рассматривали, как самостоятельную. Но уже в работах Диофанта Александрийского степени отведено особое место. или «галочка». Этот символ популярен и вне программирования.

Определение

В Python возведение в степень записывается при помощи двойной «звёздочки» — «**»

a = 2 ** 4 print(a) > 16

Вторая форма записи — встроенная функция pow():

# первый аргумент — основание, а второй — показатель b = pow(2, 4) print(b) > 16

Обратные операции

Извлечение корня

У возведения в степень две обратные операции. Первая — извлечение корня. Подробнее о корнях в Python вы можете почитать в нашей статье. Отметим лишь, что корень в питоне вычисляется с помощью той же функции pow():

# корень четвёртой степени из 16 root = pow(16, (1/4)) print(root) > 2.0

Либо с применением оператора «**»:

# корень кубический из 27 cub_root = 27 ** (1/3) print(cub_root) > 3.0

Для извлечения квадратного корня справедливы оба вышеуказанных способа, но существует и третий, специализированный. Для его применения требуется импортировать модуль

math:

import math # квадратный корень из 100 sqr_root = math. sqrt(100) print(sqr_root) > 10.0

Логарифмирование

Логарифмирование — вторая обратная операция.

Логарифмом числа «b» по основанию «a» зовётся такой показатель степени, в который следует возвести «a», чтобы получить «b».

Здесь x — логарифм. Пример из математики — найдем значение выражения:

Легче всего эта запись читается в формате вопроса: «В какую степень нужно возвести 2, чтобы получить 16?». Очевидно, в 4-ю. Следовательно,

В питоне операция нахождения логарифма также заложена в функционал модуля math:

import math # отыщем логарифм 100 по основанию 10 # 100 — основание логарифма, а 10 — аргумент log = math.log(100, 10) print(log) > 2.0

Степень

Целочисленная

В целочисленную степень можно возводить положительные и отрицательные int и float числа:

# int print(3 ** 9) > 19683 print(pow(-2, 10)) > 1024 # float print(3.14 ** 9) > 29673.367320587102 print(pow(-1. 1, 1001)) > -2.7169262098066285e+41

И функция pow() и оператор «**» умеют возводить комплексные числа:

# complex a = complex(2, 1) print(pow(a, 2)) > (3+4j) print(a ** 2) > (3+4j)

Показатель степени может быть положительным, отрицательным и нулевым:

# + print(12 ** 4) > 20736 # - print(100 ** -2) > 0.0001 # 0 print(1231 ** 0) > 1

Результат не определён, когда 0 возводят в отрицательную степень:

print(0 ** -4) > ZeroDivisionError: 0.0 cannot be raised to a negative power

Ошибка деления на ноль возникает из-за следующего свойства степени:

Рациональная

Возведение числа в рациональную степень напрямую связано с извлечением корня из этого числа отношением:

Если рациональный показатель отрицательный, а основание равно нулю, то Питон все ещё будет выдавать ошибку:

print(0 ** -(5/4)) > ZeroDivisionError: 0.0 cannot be raised to a negative power

В случае, когда основание меньше нуля, числитель показателя нечётный, а знаменатель, напротив, чётный, результат получается комплексным. Но это свойство рациональных степеней учитывается только в функции pow():

print(pow(-5, (5/4))) > (-5.286856317202822-5.286856317202821j) print(type(pow(-5, (5/4)))) > <class 'complex'>

В остальном возведение в рациональную степень работает, как и для целочисленной:

print(0 ** (3/2)) > 0.0 print(pow(1, (23/24))) > 1.0 print(10 ** (6/7)) > 7.196856730011519

Вещественная

В начале автор объявил, что возведение в степень — штука несложная. Так вот, для вещественных степеней это уже не совсем так. Идеи, заложенные в эту операцию, хоть и просты, но их много, и каждая из них достойна собственной статьи. Описать вкратце разложение в ряд Тейлора и численное интегрирование не получится. Это будет не справедливо, как по отношению к вам, так и к математике. Поэтому, выделим главное:

Python умеет возводить в вещественную степень даже вещественные числа (пусть и псевдо)

Сделать такое инструментами математики ой как непросто:

# возведём число Пи в степень e print(pow(math. pi, math.e)) > 22.45915771836104

Ноль в степени ноль

Дискуссии по поводу значения 0 в степени 0 продолжаются уже больше двух веков. Обычно значение нуля в нулевой степени принято считать неопределённым, но символическое соглашение о том, что «0 в степени 0 равно 1» помогает в записи формул и алгоритмов. Ровно поэтому так сделано и в Python:

print(pow(0, 0)) > 1 print(0 ** 0) > 1

Видео: Решение уравнений с положительными или отрицательными показателями переменных или простых членов

Стенограмма видео

В этом видео мы будем решать уравнения с положительными или отрицательными показателями переменных или простых членов. Итак, мы рассмотрим несколько примеров, подобных тому, который вы можете видеть здесь ниже, и просто рассмотрим, как их решить, и представим ваши ответы.

Тогда давайте начнем с простого. Найдите значение 𝑥, когда 𝑥 в квадрате равно шестнадцати. Таким образом, чтобы найти значение 𝑥, когда мы получили значение 𝑥 в квадрате, нам придется извлекать квадратные корни, потому что это противоположно возведению в квадрат.

Итак, мы снова используем обратные операции для отмены этих показателей степени. Итак, квадратный корень из 𝑥 в квадрате — это просто 𝑥, но квадратный корень из шестнадцати? Итак, четыре раза четыре равно шестнадцати, но минус четыре раза минус четыре тоже шестнадцать. Итак, есть два возможных значения.

И мы используем этот символ плюс или минус, чтобы обозначить тот факт, что ответ может быть как положительным, так и отрицательным. И когда мы выпишем ответ, мы фактически запишем их как два отдельных решения: ответ 𝑥 равно четырем или 𝑥 равно отрицательным четырем.

Дело в том, что когда показатель степени четный, у вас всегда будет положительный отрицательный результат. Таким образом, для четных степеней, если 𝑥 отрицательное, у вас будет четное количество отрицательных чисел, сокращающихся. Таким образом, значение 𝑥 может быть отрицательным, и вы получите положительный ответ, или значение 𝑥 может быть положительным, и вы все равно получите положительный ответ.

Номер два: 𝑥 в кубе равно восьми. Решите для 𝑥. Итак, мы снова воспользуемся обратной операцией, а наоборот, если вам нравится что-то кубировать, это укоренение чего-то в кубе. Итак, мы собираемся извлечь кубический корень из обеих сторон. Таким образом, кубический корень из 𝑥 в кубе равен кубическому корню из восьми. Ну, кубический корень из 𝑥 в кубе — это просто 𝑥, потому что 𝑥 умножить на 𝑥 умножить на 𝑥, что дает нам 𝑥 в кубе. А кубический корень из восьми равен двум, потому что дважды два раза два равно восьми. Теперь это не может быть минус два, потому что минус два раза минус два раза минус два — хорошо минус два раза минус два будет четыре, а четыре раза минус два будет минус восемь. Поэтому, когда у вас есть нечетный показатель, у вас не будет положительной отрицательной дилеммы. Так что на такие вопросы есть только один ответ. И в данном случае это 𝑥 равно двум.

Теперь третье решение: 𝑥. У нас получилось, что единица больше 𝑥 в квадрате равна единице больше двадцати пяти. Теперь на этот вопрос у меня больше 𝑥 в квадрате. Итак, единица над чем-то равна единице над двадцатью пятью равна единице над чем-то. Итак, если один над чем-то равен другому над чем-то другим, эти две вещи должны быть равны.

Итак, 𝑥 в квадрате должно быть равно двадцати пяти. Так что я просто возьму квадратный корень из обеих сторон. А квадратный корень из 𝑥 в квадрате — это просто 𝑥. Помните, что квадратный корень из двадцати пяти — это четная степень, поэтому нам придется иметь либо положительную, либо отрицательную версию. А пять — это квадратный корень.

Итак, когда мы запишем это в нашем ответе, 𝑥 равно пяти или 𝑥 равно минус пять. Или мы могли бы даже записать это как набор решений. Таким образом, используя нотацию множества, в этом множестве есть два элемента: отрицательная пятерка и пятерка.

Теперь давайте повторим этот вопрос. Но что, если бы я не заметил в начале этого маленького трюка, который гласил, что знаменатели должны быть равны, потому что числители уже равны. Что ж, я постараюсь убрать член 𝑥 из знаменателя. Таким образом, я бы умножил обе части моего уравнения на 𝑥 в квадрате, чтобы я мог сократить 𝑥 в квадрате слева — в левой части.

Но поскольку это дроби, я бы не стал просто умножать их на 𝑥 в квадрате. Я бы умножил его на дробную версию 𝑥 в квадрате, то есть просто 𝑥 в квадрате на единицу. Теперь в левой части у меня есть 𝑥 в квадрате числителя и 𝑥 в квадрате знаменателя, поэтому они оба сокращаются, и моя левая часть просто становится единицей на единицу, что равно единице.

А справа у меня 𝑥 в квадрате в числителе и двадцать пять, умноженное на единицу, что всего двадцать пять в знаменателе. Теперь мне нужно умножить обе части на двадцать пять, чтобы попытаться избавиться от этого числа в знаменателе в правой части. И снова записываю двадцать пять в форме дроби справа, чтобы я мог просто отменить эти два и оставить 𝑥 в квадрате справа.

Теперь я готов извлечь квадратный корень из обеих сторон. На самом деле я сейчас на том же месте, что и в самом начале другого вопроса, так что теперь я могу перейти к этому пункту здесь. Таким образом, обнаружение этой маленькой хитрости в начале и приравнивание знаменателей избавило от всей этой работы с правой частью.

Хорошо, тогда давайте перейдем к примеру номер четыре. Решите для 𝑥. 𝑥 минус пять все в степени четыре равно шестнадцати. Итак, я возьму корень четвертой степени из обеих частей, потому что корень четвертой степени — это обратная операция возведения чего-либо в степень числа четыре. А корень четвертой степени из 𝑥 минус пять в степени четыре — это просто 𝑥 минус пять. И именно поэтому мы, конечно же, сделали корень четвертой степени.

И корень четвертой степени из шестнадцати, ну, два раза два раза два раза два равно шестнадцати, поэтому корень четвертой степени равен двум. Но, конечно, помните, что это четный показатель. Так что минус два или минус два тоже подойдут. Отрицательное два раза отрицательное два равно четырем, отрицательное два раза отрицательное два равно четырем, а четыре раза четыре равно шестнадцати. Таким образом, есть два возможных ответа: положительный или отрицательный два.

В левой части у меня 𝑥 минус пять равно плюсу или минусу два. Поэтому, если я добавлю пять к обеим частям моего уравнения, я просто оставлю себя с 𝑥 в левой части. Итак, слева у меня 𝑥 минус пять плюс пять. Ну понятно, что минус пять прибавить пять становится ноль. Так что я просто остался с 𝑥. А справа у меня либо плюс два плюс пять, что равно семи, либо минус два плюс пять, что равно плюсу три. Итак, мы снова получили два возможных ответа.

И в зависимости от того, где вы живете и какую учебную программу вы изучаете, вы, вероятно, либо представите это в таком формате 𝑥 равно семи или 𝑥 равно трем, либо вы выпишете свой набор решений и скажете, что набор решений содержит третий и седьмой элементы.

Тогда давайте перейдем к пятому. Итак, единица на 𝑥 плюс два, все в степени три, равно ноль целых ноль единиц, и мы должны найти 𝑥. Что ж, я настоятельно рекомендую вместо того, чтобы работать с десятичными дробями, работать с дробью.

Теперь, если мы подумаем о разрядности этих десятичных разрядов: первый десятичный знак — десятый, второй десятичный — сотый, а третий десятичный — тысячный. Итак, это означает одну тысячную, то есть один больше тысячи. Поэтому я могу просто переписать это выражение для нашего уравнения как один на 𝑥 плюс два, все в кубе равно одному на тысячу.

Теперь я снова проделаю наш старый трюк. У нас единица над чем-то равна единице над чем-то. Так что эти две вещи должны быть равны. А как мы получили 𝑥 плюс два все в кубе равно тысяче? Поэтому мне нужно подумать об обратных операциях: что такое обратная операция от кубирования чего-либо? Это кубическое укоренение.

Таким образом, кубический корень из левой части равен кубическому корню из правой части. Что ж, кубический корень из чего-то в кубе — это как раз то, что нужно. Итак, в левой части у меня только что 𝑥 плюс два. Вот что делают обратные операции; они гасят друг друга. А справа я ищу кубический корень из тысячи, который равен десяти. Помните о нечетных степенях: вам не нужно беспокоиться о плюсе или минусе. Итак, 𝑥 плюс два равно десяти. Теперь все, что мне нужно сделать, это убрать два из каждой части моего уравнения, так что если два вычесть два в левой части, останется только 𝑥, а десять уберут два в правой части, останется восемь . Итак, мы получили один ответ: 𝑥 равно восьми. И наш набор решений будет выглядеть вот так, и у нас будет только один элемент, а их будет восемь.

Хорошо, следующий пример, 𝑥 плюс три все в степени минус три равно двадцати семи, и мы должны решить это для 𝑥. Итак, у нас есть нечетная сила, поэтому нам не нужно беспокоиться о положительном отрицательном. Но здесь отрицательная экспонента, минус три, поэтому нам нужно вспомнить, что наличие отрицательной экспоненты означает, что она больше единицы. Это будет один больше 𝑥 плюс три в степени три. Итак, мы только что вычислили отрицательную часть экспоненты. Мы вроде выяснили, что это значит. Это означает, что мы должны перевернуть эту дробь.

А теперь я поместил двадцать семь в дробную форму, двадцать семь на единицу. Теперь мы находимся не в той хорошей ситуации, в которой были раньше, когда у нас был один и тот же числитель, равный единице, поэтому мы могли просто сравнивать знаменатели. Итак, нам нужно умножить обе части нашего уравнения на 𝑥 плюс три в степени три. Мы только что сказали, что можем удалить эту переменную из знаменателя в левой части.

Теперь вы заметили, что я вернул число двадцать семь, чтобы скорректировать число двадцать семь, так как оно не должно быть дробью. Единственная причина, по которой я попробовал это как дробь, заключалась в том, чтобы посмотреть, можем ли мы сравнивать числители или сравнивать знаменатели. Итак, в правой части мы получили двадцать семь раз 𝑥 плюс три в кубе. И в левой части то, что у нас есть, — нам нужна дробная версия 𝑥 плюс три, все в степени три, чтобы затем мы могли их отменить, у меня есть 𝑥 плюс три, все в степени три. на дне. Разделите это само по себе, вы получите один, то же самое сверху, вы получите один. Итак, с левой стороны теперь у меня только один раз один на один раз один, и это всего лишь один.

Ну, теперь у меня двадцать семь раз 𝑥 плюс три в кубе. Итак, что я собираюсь сделать, так это на самом деле разделить обе части на двадцать семь, чтобы я мог просто изолировать 𝑥 плюс три в кубе сам по себе. Кубический член сам по себе, обратная операция будет кубическим корнем. Вот к чему мы и подошли. Итак, давайте сначала разделим обе части на двадцать семь.

А это значит, что мы можем исключить двадцать семь в правой части. А это значит, что у нас один больше двадцати семи равно 𝑥 плюс три в кубе. Итак, мы подошли к моменту, когда мы можем извлечь кубический корень. Итак, мы собираемся извлечь кубический корень из обеих сторон: кубический корень из единицы из двадцати семи в левой части и кубический корень из 𝑥 плюс три в кубе с правой стороны. Очевидно, что обратная операция просто оставит нас с 𝑥 плюс три в правой части.

Но чему равен кубический корень из единицы больше двадцати семи? Ну, это то же самое, что кубический корень из единицы на кубический корень из двадцати семи. Так что пока буду писать именно так. Итак, у меня кубический корень из единицы на кубический корень из двадцати семи равен 𝑥 плюс три. Ну, кубический корень из единицы равен единице, потому что один раз один раз один равно одному. А кубический корень из двадцати семи равен трем, потому что трижды трижды три равно девятикратно трем, то есть двадцать семь.

И мы почти у цели. Итак, чтобы изолировать 𝑥, мне просто нужно вычесть эту тройку с обеих сторон. А это значит, что в правой части у меня 𝑥 плюс три минус три, что равно 𝑥, потому что эти два сокращаются. В этом смысл вычитания трех с обеих сторон. Так что теперь мне нужно сделать одну треть минус три.

Итак, первый шаг — когда мы делаем вычитание дробей, мне нужно получить две дроби. Так что я собираюсь сделать одну треть минус три на один. И мне нужно найти дробь, эквивалентную трем на один, у которой знаменатель равен трем. Так что я собираюсь умножить это на три на три. Три на три — это всего лишь один. Таким образом, мы не меняем величину числа; мы просто хотим получить эквивалентную дробь для трех с тем же знаменателем, что и три.

И трижды три сверху — девять; один раз три на дне три. Итак, теперь у меня одна треть минус девять третей. Что ж, это приводит нас на ужасную территорию отрицательных дробей, и- но один минус девять будет минус восемь. Итак, у меня отрицательные восемь третей. И если я преобразую это в смешанное число, у меня получится 𝑥, равное минус двум и двум третям.

Так что это был более сложный пример. Но поскольку у нас здесь была странная сила, нам не нужно было беспокоиться о положительных или отрицательных вещах. Но у нас была отрицательная экспонента, а это означало, что нам пришлось перевернуть дробь. Затем мы обнаружили, что не можем воспользоваться этим удобным способом сравнения знаменателей, потому что единица больше чего-то равна двадцати семи больше единицы. Поэтому нам пришлось умножить обе стороны, как мы сделали здесь. А затем мы столкнулись с этой дополнительной проблемой: кубический корень из единицы из двадцати семи, но мы могли выразить это как кубический корень из единицы из двадцати семи, что позволило нам понять, что это был за ответ. относительно легко.

Итак, вернемся к нашему последнему примеру, у нас есть десять тысяч больше 𝑥 минус четыре, все в степени минус четыре равно единице, и мы должны найти 𝑥. Итак, у нас есть четная степень, четыре, что означает, что у нас будет вся ситуация с двумя возможными ответами: положительными и отрицательными. Но у нас также есть ситуация, когда это отрицательный показатель. Итак, у нас есть отрицательный показатель степени в нижней части дроби. Так что я просто переосмыслю это.

А 𝑥 минус четыре в степени минус четыре в-на знаменателе есть то же самое, что 𝑥 минус четыре в степени четыре в числителе. Этот отрицательный показатель степени означает, что мы должны перевернуть эту часть дроби. Так что это движение вверх к числителю. Ну, я пытаюсь получить 𝑥 самостоятельно. Так что я должен посмотреть, что я могу сделать с этим десятитысячным сроком здесь. Что ж, операция, обратная умножению на десять тысяч, — это деление на десять тысяч. Вот что я собираюсь сделать с обеими сторонами моего уравнения. Так что у нас это. Мы разделили обе стороны на десять тысяч. А в левой части теперь у меня десять тысяч в числителе, умноженное на что-то, и десять тысяч в знаменателе. Я могу их отменить. Итак, я только что получил 𝑥 минус четыре в степени четыре в левой части.

И это равно единице на десять тысяч, то есть что-то в степени четыре. Таким образом, операция, обратная степени четыре, — это извлечение корня четвертой степени. Итак, мы возьмем четвертый корень из обеих сторон. А корень четвертой степени из 𝑥 минус четыре в степени четыре — это просто 𝑥 минус четыре. Обратные операции, они компенсируют друг друга. А корень четвертой степени из единицы из десяти тысяч я перепишу как корень четвертой степени из единицы из корня четвертой из десяти тысяч.

Таким образом, корень четвертой степени из единицы равен единице, потому что один раз один раз один раз один равно единице. Итак, в числителе всего один, а в знаменателе корень четвертой степени из десяти тысяч равен десяти, потому что десять раз десять — это сто, десять раз — тысяча, десять раз — десять тысяч. Итак, наше уравнение стало таким: 𝑥 минус четыре равно одному больше десяти.

Но эй эй эй! Я слышу, ты говоришь, держись! Четвертый корень из единицы может быть отрицательным, потому что отрицательный, умноженный на отрицательный, один, умноженный на отрицательный, один, умноженный на отрицательный, тоже равен единице. Так что на самом деле это плюс или минус, и это тоже плюс или минус. Итак, у нас есть 𝑥 минус четыре плюс или минус одна десятая — это положительная или отрицательная одна десятая. Итак, теперь 𝑥 минус четыре равно положительной или отрицательной десятой. И мне нужно добавить четыре к обеим сторонам, чтобы я мог получить 𝑥 сам по себе с левой стороны.

Итак, в левой части весь смысл добавления четырех состоял в том, что я получил отрицательные четыре плюс четыре, что равняется нулю, так что у меня остается только 𝑥. А справа у меня есть два возможных значения. Итак, у меня либо положительный результат десятая плюс четыре, либо отрицательный результат десятая плюс четыре. Так что либо четыре и десятая, либо три и девять десятых, либо четыре целых один, либо три целых девять десятых. И тогда у нас есть два возможных ответа.

Итак, с чем мы имеем дело в последнем вопросе? Ну, у нас была отрицательная экспонента, что означало, что мы должны были перевернуть дробь в первую очередь. И у нас была равная сила, поэтому у нас был такой положительный или отрицательный вопрос, который мы чуть не упустили, когда решали вопрос. Так что вы должны быть очень осторожны с этим.

А это означало, что в итоге у нас было два возможных ответа. У нас также была проблема, когда у нас был четвертый корень из единицы из десяти тысяч, который мы разделили на четвертый корень из одного из четвертого корня из десяти тысяч.

Надеемся, что эти примеры помогут вам решать уравнения с положительными или отрицательными показателями переменных или простых членов.

Работа с нулевыми и отрицательными показателями: полное руководство

Работа с экспоненциальными выражениями — неизбежный этап ваших курсов алгебры, поскольку они используются в уравнениях и других приложениях.

• Что такое экспонента?
• Что такое нулевые и отрицательные показатели?
  • Нулевые экспоненты
  • Отрицательные экспоненты
• Нулевые и отрицательные экспоненты на примере
  • Решение с нулевыми экспонентами
    • Правило нулевого экспонента
    9 0090
• Решение с отрицательными показателями
  • Правило отрицательного показателя
• Что Является ли использование нулевых и отрицательных показателей?
  • Измерения и расчеты
  • Упрощение
• Формулы
  • Правило нулевой степени
  • Правило отрицательной степени
• Сводка

Что такое экспонент?

Показатель степени — это количество раз, которое базовое число будет умножено само на себя. Это может быть любое число, которое может быть классифицировано как отрицательная экспонента, нулевая экспонента или положительная экспонента.

Экспоненты, начинающиеся с 1, называются положительными экспонентами и являются наиболее распространенными — вы, вероятно, часто сталкивались с ними.

Что такое нулевые и отрицательные показатели?

Нулевые и отрицательные показатели являются особыми случаями показателей.

Например, :

2 ³  то же самое, что 2 x 2 x 2, повторное умножение приводит к окончательному ответу 8: 2 x 2 x 2 = (2 x 2) x 2 = 4 x 2 = 8.

Однако с нулевыми и отрицательными показателями так просто не получится.

Zero Exponents

Это показатель степени, который всегда и автоматически приравнивает любое базовое число к 1. Проще говоря, какое бы ни было базовое число, пока оно возведено в нулевую степень, оно всегда будет равно 1. Все не имеет значения, независимо от того, как большое значение числа или является ли оно положительным числом или отрицательным основанием.

Например:

Будь то 3 ⁰  или 300 000 000 ⁰ , ответ по-прежнему равен 1.

Отрицательные степени

с другой стороны, вы перемещаете позицию базового числа с помощью показатель степени, чтобы убрать отрицательный знак и сделать его положительным. Другими словами, вы отвечаете взаимностью на данное и делаете показатель степени положительным. Результат всегда будет дробью.

Например:

2 ^-4  = (1/2) x (1/2) x (1/2) x (1/2) = 1/16

или 2 ^-4  = 1/(24) = 1/(2 x 2 x 2 x 2) = 1/16

базовое число с показателями в нижней части дроби сделает показатель степени положительным. Другими словами, когда любое число больше 1 возводится в отрицательную степень, оно может быть положительным, если вы поместите его в знаменатель с 1 в числителе.

Другой пример:

10 ^-1  = 1/10 ¹

Нулевые и отрицательные показатели объясняются примерами

Описания и обзоры нулевых и отрицательных показателей были рассмотрены в предыдущем разделе.

Теперь мы рассмотрим и обсудим, как их решить.

Решение с нулевыми показателями

При работе с нулевыми показателями проще всего объяснить это с помощью правила отношения степеней. Вспомним ваши первые пять правил экспоненты:

 (x/y) ⁵  = (x ⁵ )/(y ⁵ ) или (x ² /г ³ ) ³  = x ⁶ /г ⁹

1. Правило произведения степеней или правило произведения. умножение двух оснований одного и того же числа может быть упрощено до одного и того же числа. Затем добавьте показатели степени основных чисел: 7 ²  x 7 ⁵  = 7 ²⁺⁵  = 7 ⁷
2. Правило отношения степеней или правило отношения —  деление двух оснований с одинаковым значением может быть упрощено до одного и того же основания. Затем вычтите его показатели: (13 ⁴ )/(13 ¹ ) = 13 ^4-1  = 13 ³
3. Степень Степени Правило  — при возведении степени в другую степень показатели степени умножаются, а общее основание сохраняется: (x ² ) ³ = x ^2×3  = x ⁶
4. Степень произведения Правило — когда основание в скобках xy возводится в степень, показатель степени распределяется на каждую часть основания: (xy) ⁴ = (х ⁴ ) х (у ⁴ )
5. Сила частного правила — работает так же, как мощность правила произведения; показатель степени распределяется как на делимое, так и на делитель:

Правило нулевой степени

Теперь, чтобы полностью объяснить, почему число, возведенное в нулевую степень, всегда равно 1, мы можем использовать правило отношения степеней. Согласно правилу частных, деление одних и тех же оснований приведет к одному и тому же основанию и показателю разности верхнего и нижнего показателей.

Например:  объяснение 7 ⁰  = 1:

7 ⁰ может состоять из 7 ²  деленное на 7 ² .

7 ² /7 ²  = ?

Следуя правилу частных, вычтите степени друг из друга. В этом случае показатели будут отменены, так как они одинакового значения: 2.

7 ² /7 ² = 7 ^(2-2) = 1 или

7 ^{( 2-2)}  = 7 ⁰  = 1

Кроме того, не имеет значения, насколько длинное уравнение. Любое уравнение, возведенное в ноль, пока оно заключено в круглые скобки, всегда будет равно 1.

Например:

(5x ⁴ y ⁵ ) ⁰ = (5 ⁰ x 90 149 0 y ⁰ ) = 1

Решение с отрицательными показателями

С отрицательными показателями работать на первый взгляд сложно, но на самом деле это не так.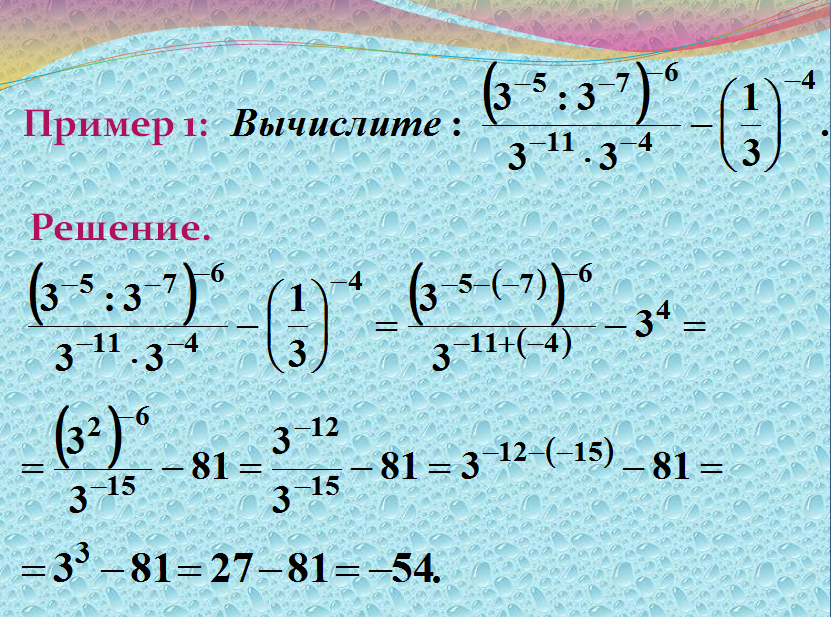 Помните, что результат всегда будет дробью, а процесс всегда будет взаимностью данного. Вспоминая, как сделать число обратным:

1. Сделайте из числа дробь или поставьте над единицей.
2. Переверните число в числителе в знаменатель и наоборот.
3. При изменении положения отрицательного числа в дроби оно становится положительным, даже если оно является показателем степени.

Правило отрицательного показателя степени

Помните, что: (x ^-2 )/(y ^-3 ) = y ³ /x ² 9000 5

Как?

(х ^-2 )/(у ^-3 ) = (1/(х ² ))/(1/(у ³ ))

= (1/(х ² )) х ((у ³ )/1 )

= y ³ /x ²

Таким образом, отрицательные показатели в знаменателе переходят в числитель, а отрицательные показатели в числителе переходят в знаменатель.

Применим это к примеру с отрицательным показателем:

Случай 1 , когда дано изначально не дробь.

х ^-3 = ? 93

Случай 2 , когда дан дробь с отрицательным показателем в знаменателе.

1 / х ^-4 = ? -> возвратно-поступательный,

1/ x ^-4 => x ⁴

Какая польза от нулевых и отрицательных показателей?

Экспоненты, как правило, имеют множество применений в реальной жизни. Два использования нулевого и отрицательного показателей степени:

Измерения и расчеты

Два показателя степени используются для представления длин. Отрицательная экспонента, в частности, используется для выражения атрибуции чего-либо и демонстрации того, насколько что-то мало.

Например, отрицательные показатели степени используются для представления различных размеров мелких существ, таких как летучие мыши. Зоологи используют отрицательные показатели для измерения частей тела.

Измерение может быть показано как 1,08x 10-4 см: это делается, когда имеется слишком много знаков после запятой из-за небольшого размера измерения; поэтому для удобства цифра сокращена с использованием отрицательных показателей.

Точно так же эти показатели степени можно использовать для весов. Более легкие веса обычно выражаются с отрицательными показателями для простоты и облегчения вычислений.

Другим примером является «Экспоненциальное затухание», используемое в графиках и представлениях. Отрицательные показатели степени приводят к меньшим значениям и, следовательно, показывают «распад» на графике по мере того, как данные падают или уменьшаются в соответствии с выражением.

Упрощение

Нулевые и отрицательные показатели степени обычно используются для упрощения чисел и значений для лучшего использования и облегчения ввода в реальных приложениях. Как и в приведенных выше примерах, они используются для упрощения значений различных измерений для удобства.

Расчеты в различных профессиях, особенно в различных областях науки, используют отрицательные показатели степени, так как большинство измерений, как правило, слишком малы, чтобы их можно было использовать в исходном виде, со слишком большим количеством десятичных знаков.

Отрицательные показатели используются для упрощения измерений и наглядно показывают, насколько они малы. Большие отрицательные показатели означают меньшие измерения.

Нулевые показатели работают так же, как они используются во многих математических уравнениях, чтобы представить, что независимо от того, насколько велико число, пока оно возведено в нулевую степень, оно равно значению 1. 9-2 = 1/a ²

(a x ) ^-2 = 1/(a x ) ² или 1/ a ² x ²

Вариант 2 :

1/( a ^-3 ) = a ^3/1 или просто a ³

1/(( a х) ^-4 ) = ( a x) ^4/1 или a ⁴ x ⁴

Резюме

Подводя итог, любое число, возведенное в нулевую степень, всегда будет равно 1. Напротив, любое число, возведенное в отрицательную степень, будет преобразовано в положительное, прежде чем приступить к решению окончательного значения.