Как решать со степенью примеры: Свойства степеней, действия со степенями

Содержание

О теореме Абеля-Руффини без групп и теории Галуа / Хабр

Историческая справка

Поиск решения алгебраических уравнений оказал колоссальное влияние на развитие математики. Формула решения общего кубического уравнения впервые была получена итальянскими математиками 16-го века. Это событие ставшее первопричиной рассмотрения комплексных чисел, считается одним из поворотных моментов в истории математики. Судьбы Джероламо Кардано, Никколо Тартальи, Сципиона дель Ферро и их поисков решения кубического уравнения заслуживают отдельного романа со своими интригами, скандалами и расследованиями. Столь яркие истории достаточно редки в математике.

Начиная с 19-го века поиск формул для решения уравнений произвольных степеней положил начало теории групп и абстрактной алгебре, которые преобразили практически все разделы современной математики. Думаю, многие, кто интересовался историей и развитием алгебры, знают, что формулы для решения общего алгебраического уравнения степени выше четвертой не существует. Как сообщается, первое доказательство этого факта было дано итальянским математиком Паоло Руффини в самом конце восемнадцатого века, оно составляло около 500 страниц и все же содержало некоторые пробелы. Хотя отдельные математики, как Огюстен Коши, и признавали данное доказательство, но ввиду столь большого объема и сложности изложения, оно так и не было принято математическим сообществом. Считается, что первое полное доказательство дано норвежским математиком Нильсом Абелем и содержалось в двух работах, изданных в 1824 и 1826 годах. С тех пор оно носит название теоремы Абеля или теоремы Абеля-Руффини.

Если вы попытаетесь изучить это доказательство в его современном изложении, то окажется, что оно практически полность опирается на Теорию Галуа. Эварист Галуа был французским математиком 19-го века и современником Нильса Абеля. Помимо занятий математикой он вел активную политическую жизнь из-за чего несколько раз попадал в тюрьму. В возрасте всего двадцати лет был застрелен на дуэли, поводом для которой послужила любовная интрига, хотя есть предположения, что дуэль была подстроена его политическими противниками. Об этой истории написано достаточно много, кроме того, имеется перевод на русский язык его мемуаров и писем. Последнее письмо его другу Огюсту Шевалье было написано в ночь накануне дуэли, в нем он наспех излагает свои последние идеи. Несмотря на столь короткую жизнь, Эварист Галуа считается одним из родоначальников современной алгебры. Хотел бы заметить, что в популярном изложении создается некий романтический образ Галуа, как подростка-гения, который в одиночку, с нуля создал теорию групп и преобразил всю алгебру. Несомненно его идеи сыграли огромную роль, но если почитать его сочинения, то мы увидим, что он хорошо знал и опирался на знаменитые работы Лагранжа, Эйлера, Гаусса, Абеля, Якоби. Зачатки теории групп и перестановок появляются еще в работах Жозефа Луи Лагранжа по теории алгебраических уравнений, а также Карла Фридриха Гаусса в его знаменитых «Арифметических исследованиях». К тому же, теория Галуа в современном изложении была оформлена многими последующими математиками — Дедекиндом, Кронекером, Гильбертом, Артином и другими.

Мотивация данной статьи

Чуть менее года назад меня сильно увлекла статья об истории решения кубического уравнения и последующих безуспешных поисков формулы уравнения 5-й степени, длившихся почти триста лет. Сразу хочу отметить, что специального математического образования у меня нет и поэтому, попробовав прочесть современную версию доказательства теоремы Абеля-Руффини, я естественно ничего не понял. В моем сознании термины группа, кольцо и поле никак не ассоциировались с алгебраическими структурами. Но желание разобраться было столь велико, что я принялся за изучение курса высшей алгебры.

На первых этапах абстрактная алгебра была наверное самым сложным из того, что мне приходилось изучать ранее. Объем новых терминов и определений просто зашкаливал: группы, факторгруппы, моноиды, поля, кольца, тела, модули, идеалы, ядра, векторные пространства, биекции, сюръекции, инъекции, изоморфизмы, автоморфизмы, гомоморфизмы, эндоморфизмы и тд. Спустя несколько месяцев упорных занятий, я начал понимать формальную часть, но, к сожалению, интуитивного понимания, которое и являлось моей изначальной целью, я так и не достиг.

Дело в том, что практически все современные доказательства неразрешимости уравнений 5-й степени в радикалах сводятся к следующему. Рассматривается некоторое неприводимое уравнение, например x⁵-10x+2, после чего методами мат анализа определяется, что оно имеет три действительных и два комплексно-сопряженных корня. После чего заключается, что группой Галуа данного уравнения есть группа S₅, которая не является разрешимой, и следовательно данное уравнение неразрешимо в радикалах. Доказательство теоремы Абеля-Руффини о неразрешимости общего уравнения также сводится к неразрешимости группы S_n. Для меня данные доказательства были слишком абстрактными и оторванными от конкретных уравнений. Когда я пытался представить их в терминах элементарных алгебраических операций, чтобы понять в чем заключается главная причина неразрешимости уравнений, у меня ничего не получалось. Возможно для тех, кто занимается этим достаточно долго, эти вещи могут казаться интуитивно понятными.

Немного иной подход описан в книге Алексеева «Теорема Абеля в задачах и решениях», основанной на лекциях Владимира Арнольда, но в изложенном там доказательстве помимо теории групп используются элементы комплексного анализа и Римановых поверхностей. Я также находил похожие статьи, использующие топологические аргументы в виде комбинаций петель и коммутаторов, но мне хотелось найти что-то чисто алгебраическое.

Параллельно изучая историю математики и понимая, что современная формулировка и доказательство сильно отличаются от того, как излагали свои идеи Лагранж, Руффини, Абель и Галуа, я решил прочесть первоисточники. К сожалению, на русский или английский по этой теме переведены лишь сочинения Галуа и одна из работ Абеля.

После некоторых поисков я наткнулся на статью 1845 года французского математика Пьера Лорана Ванцеля, в которой он переработал и сильно упростил доказательство Абеля-Руффини, о чем он пишет во введении. В этой работе, он так же упоминает мемуары Галуа и отмечает, что они будут опубликованы в скором времени. Для заметки — работы Галуа были опубликованы лишь в 1846 году Жозефом Лиувиллем, спустя почти 15 лет после смерти Галуа. Кстати, Пьер Лоран Ванцель, также был первым, кто доказал неразрешимость трисекции угла и удвоения куба с помощью циркуля и линейки — знаменитых задач стоявших еще со времен античности. Доказательства Ванцеля были изложены без использования абстрактной алгебры и теории Галуа, поскольку на тот момент они еще не были разработаны. Хотя работа и была доступна лишь на французском, которого я до этого практически не знал, но ввиду специфической темы, небольшого размера (всего 7 страниц) и наличия гугл переводчика, я справился достаточно быстро. По моему субъективному мнению, его доказательство теоремы Абеля-Руффини является наиболее простым для понимания.

Уже позже я нашел пример подобного доказательства основанного на работе Руффини в книге Чеботарёва “Основы Теории Галуа”. Далее я постараюсь кратко изложить принцип решения уравнений в радикалах и идею доказательства неразрешимости уравнения 5-й степени.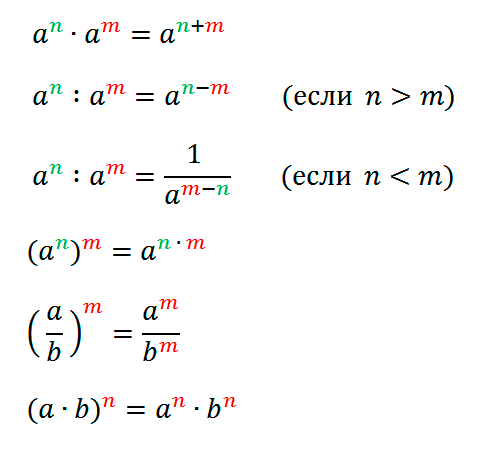

Решения уравнений в радикалах

Для дальнейшего понимания, потребуются минимальные пререквизиты:

Формулы Виета — напомню, что коэффициенты произвольного уравнения являются элементарными симметрическими функциями от его корней, то есть функциями, которые не меняют своего значения при любых перестановках корней. Примеры: x₁ + x₂ + x₃, x₁x₂x₃, x₁x₂ + x₁x₃ + x₂x₃.

Теорема о симметрических многочленах — каждую симметрическую функцию от корней, можно выразить с помощью элементарных симметрических функций (коэффициентов уравнения).

Первообразные корни n-й степени из единицы — комплексные величины не равные единице, но n-я степень которых, равна единице. Примеры: (-1)² = 1, (-1/2 + sqrt(-3)/2)³ = 1, i⁴ = 1 соответственно квадратный, кубический и биквадратный корни из единицы.

Основная теорема алгебры — гласит о том, что уравнение n-й степени с комплексными коэффициентами имеет ровно n комплексных корней с учетом кратности (корни могут быть одинаковые).

Первоначальная идея восходит к работе Жозефа Луи Лагранжа “Размышления о решении уравнений” 1770-1771 годов. Это достаточно объемное сочинение и я не нашел его перевода на русский или английский язык. Как указывается в разных источниках, в попытке найти формулу для уравнения 5-й степени, Лагранж проанализировал все имеющиеся к тому времени способы решения уравнений и выделил общий принцип, позволяющий решить уравнения 4-й и низших степеней. В этой же работе, изучая перестановки корней, он пришел к теореме, которая сейчас носит его имя. Принцип, открытый Лагранжем, заключался в том, чтобы найти выражения от корней заданного уравнения n-й степени, которые при всех возможных перестановках этих корней принимали n-1 значений, но в тоже время через них выражались первоначальные корни. На эти значения, можно составить уравнение n-1 степени и повторить операцию, тем самым сводя изначальное уравнение к цепочке уравнений меньших степеней, решив которые, можно получить корни первоначального уравнения. Рассмотрим один из примеров:

Пусть f(x) = x⁴ + ax³ + bx² + cx + d общее уравнение 4-й степени с произвольными коэффициентами a, b, c, d и x₁, x₂, x₃, x₄ его корни.

Напомним, что его коэффициенты — это элементарные симметрические функции от корней, в чем можно убедиться просто раскрыв скобки в выражении (x — x₁)(x -x₂)(x — x₃)(x — x₄):

x₁ + x₂ + x₃ + x₄ = -a

x₁x₂ + x₁x₃ + x₁x₄ + x₂x₃ + x₂x₄ + x₃x₄ = b

x₁x₂x₃ + x₁x₂x₄ + x₁x₃x₄ + x₂x₃x₄ = -c

x₁x₂x₃x₄ = d

Так как корни являются произвольными, то существует 4! = 24 различных вариантов их расположения, но можно составить выражение x₁x₂ + x₃x₄, которое принимает всего три разных значения при всех 24-х перестановках корней:

x₁x₂ + x₃x₄ = y₁

x₁x₃ + x₂x₄ = y₂

x₁x₄ + x₂x₃ = y₃

На эти три значения мы можем составить уже кубическое уравнение, корнями которого они и будут являться. Таким образом, мы сводим решение уравнения 4-й степени к уравнению 3-й степени. Для решения кубического уравнения мы можем воспользоваться резольвентой Лагранжа (y₁ + wy₂ + w²y₃)³, где w — это кубический корень из единицы. Данное выражение принимает всего два разных значения при всех возможных 3! = 6 перестановках. Оно будет сохранять значение при циклических перестановках и менять знак при любой транспозиции. Получим:

(y₁ + wy₂ + w²y₃)³ = z₁

(y₁ + w²y₂ + wy₃)³ = z₂

Теперь составим квадратное уравнение на z₁ и z₂:

(t — z₁)(t — z₂) = t² — t(z₁+z₂) + z₁z₂

z₁+z₂ и z₁z₂ — будут симметрическими функциями от корней нашего изначального уравнения f(x), следовательно, по теореме о симметрических многочленах, напрямую выражаться через коэффициенты a, b, c, d. Решив квадратное уравнение мы получим значения z₁, z₂. После чего, извлекая кубические корни из z₁, z₂, и складывая с коэффициентом b, сможем выразить y₁. Далее, c помощью y₁ и коэффициентов a, b, d, решив два квадратных уравнения, мы доберемся до корней x₁, x₂, x₃, x₄ изначального уравнения.

Данный пример показывает, что произвольное уравнение 4-й степени решается путем составления вспомогательных кубического и квадратных уравнений. Далее я приведу рассуждение, почему подобный прием невозможен для общего уравнения 5-й степени.

Неразрешимость уравнения 5-й степени

Итак, мы хотим показать, что ни один корень общего уравнения 5-й степени не может быть выражен через его коэффициенты путем решения цепочки вспомогательных двучленных уравнений низших степеней.

Пусть f(x) = x⁵ + ax⁴ + bx³ + cx² + xd + e общее уравнение 5-й степени с произвольными коэффициентами a, b, c, d, e и x₁, x₂, x₃, x₄, x₅его корни. Обозначим за y₁ первый радикал входящий в значение x₁ в порядке вычисления. Пусть y₁ⁿ = p, где p будет какой-то симметрической функцией от корней и, следовательно, напрямую выражаться через коэффициенты a, b, c, d, e. Заметим, что y₁ уже не будет симметрической, а лишь рациональной функцией g от корней — g(x₁, x₂, x₃, x₄, x₅). Следовательно, g должно менять значение при перестановке любых двух корней. Тогда эти значения будут являться корнями уравнения y₁ⁿ = p, которые имеют вид g, zg, z²g, z³g … z^n-1g, где z — первообразный корень n-й степени из единицы (zⁿ=1). Рассмотрим произвольную транспозицию, например (x₁, x₂), тогда

g(x₂, x₁, x₃, x₄, x₅) = zg(x₁, x₂, x₃, x₄, x₅)

если мы применим ее еще раз, то получим:

g(x₁, x₂, x₃, x₄, x₅) = zg(x₂, x₁, x₃, x₄, x₅)

что равносильно g(x₁, x₂, x₃, x₄, x₅) = z²g(x₁, x₂, x₃, x₄, x₅)

Из этого следует, что z² = 1, то есть z должен быть квадратным корнем из единицы (z = -1) и соответственно первый радикал y₁ будет квадратным. Поясним: так как корни являются произвольными, то g должно сохранять значение при любых четных перестановках корней и менять знак при нечетных. Теперь покажем, что значение функции g не будет меняться при циклической перестановке трех корней (x₁, x₂, x₃). Здесь стоит пояснить, что циклическая перестановка (x₁, x₂, x₃) четная и может быть представлена, как произведение транспозиций (x₁, x₂)(x₂, x₃). То есть, функция g не поменяет своего значения при данной перестановке. Еще заметим, что функция g не изменится при циклической перестановке пяти корней, так как она так же раскладывается в произведение четного количества транспозиций. Присоединяя радикал y₁ к выражениям от коэффициентов с помощью базовых арифметических операций, мы будем получать симметрические функции относительно всех циклов на трех и пяти корнях и вообще любых четных перестановок, но при перестановке содержащей нечетное количество транспозиций, y₁ будет менять знак. Дальнейшее присоединение квадратных радикалов не даст нам ничего нового. Теперь предположим, что мы пришли к радикалу, который меняет свое значение лишь при тройных циклах. Обозначим его y₂, тогда y₂ⁿ = q, где q — это рациональная функция от коэффициентов a, b, c, d, e и радикала y₁.

g(x₂, x₃, x₁, x₄, x₅) = zg(x₁, x₂, x₃, x₄, x₅)

g(x₃, x₁, x₂, x₄, x₅) = zg(x₂, x₃, x₁, x₄, x₅)

g(x₁, x₂, x₃, x₄, x₅) = zg(x₃, x₁, x₂, x₄, x₅)

что равносильно g(x₁, x₂, x₃, x₄, x₅) = z³g(x₁, x₂, x₃, x₄, x₅)

В данном случае z³ = 1, то есть z здесь будет кубическим корнем из единицы.

Теперь произведем циклическую перестановку 5-и корней

g(x₂, x₃, x₄, x₅, x₁) = zg(x₁, x₂, x₃, x₄, x₅)

g(x₃, x₄, x₅, x₁, x₂) = zg(x₂, x₃, x₄, x₅, x₁)

g(x₄, x₅, x₁, x₂, x₃) = zg(x₃, x₄, x₅, x₁, x₂)

g(x₅, x₁, x₂, x₃, x₄) = zg(x₄, x₅, x₁, x₂, x₃)

g(x₁, x₂, x₃, x₄, x₅) = zg(x₅, x₁, x₂, x₃, x₄)

Так как z должен быть кубическим корнем из единицы, как мы выяснили ранее, то единственным вариантом будет z = 1 и g должна быть инвариантна при любой из этих циклических перестановок. Но тогда она должна быть инвариантна и при циклической перестановке x₃,x₂,x₅,x₁,x₄ -> x₂,x₅,x₁,x₄,x₃. Отсюда, одной транспозицией мы можем получить, что

g(x₃, x₄, x₅, x₁, x₂) = g(x₂, x₃, x₁, x₄, x₅)

но, выше мы уже видели, что

g(x₁, x₂, x₃, x₄, x₅) = g(x₃, x₄, x₅, x₁, x₂)

а из этого следует

g(x₁, x₂, x₃, x₄, x₅) = g(x₂, x₃, x₁, x₄, x₅)

что приводит нас к противоречию, так как мы предполагали, что g меняет значение при циклической перестановке трех корней (x₁, x₂, x₃).

Еще одним вариантом, было бы показать что все четные перестановки на пяти корнях порождаются тройными циклами, то есть, если есть тройные циклы, то никаких выражений от корней, которые бы сохраняли набор значений при всех четных перестановках, не существует. Если теперь перевести это на теоретико-групповой язык, то получается, что группа общего уравнения пятой степени есть симметрическая группа S₅, в которой существует 5! = 120 различных перестановок пяти корней. Далее, путем присоединения квадратного корня из дискриминанта, мы можем понизить ее до знакопеременной группы четных перестановок A₅, которая содержит 120/2 = 60 перестановок. Но A₅ является простой группой, в которой нет никаких нетривиальных нормальных подгрупп, которым бы соответствовали выражения от корней сохраняющие значения при определенных перестановках, из чего следует, что присоединение любых дополнительных радикалов не приблизит нас к решению.

Заключение

Поводом для написания данной статьи послужило желание структурировать свои мысли по этой теме и представить идеи о неразрешимости уравнений в радикалах без привлечения абстрактной алгебры и теории Галуа. По моему мнению, в подавляющем большинстве современных изложений теряется связь между областью, в которой происходит доказательство и конкретными уравнениями. Если у кого-то есть замечания, дополнения или ссылки на подобные элементарные изложения, буду рад услышать.

Как решить задание 10 из ЕГЭ по математике

10 задание из ЕГЭ по математике — задача с прикладным содержанием. Выполнение связано с решением уравнений. Разбираемся, как сделать задачу из профиля и получить максимальный балл на экзамене.

Обращаем внимание

10 задачу из ЕГЭ по математике многие считают физической. Однако ее выполнение завязано на чистой математике. Единственный момент из физики — нужно понимать, что за процессы происходят, в чем особенность. Большинство величин не могут быть отрицательными. Ответ получился с минусом — нужно перепроверить.

В профильных заданиях нужно учитывать контекст. Представим, что вам досталась классическая задача на механику. Дано положительное ускорение, достаточно большая скорость… А пройденный путь оказывается с минусом. Это ошибка, нужно пересчитать. Не будете решать номер целиком, напишете неверное число — потеряете балл.

Решение уравнений

В 10 номере ЕГЭ по математике встречаются разные типы выражений. Если задание звучит как «определите наибольшее/наименьшее значение», составляйте неравенство. Важно правильно поставить знак. Если в задаче стоит вопрос «сколько?», то подойдет обычное уравнение. Чаще встречаются квадратные и линейные выражения.

Название	Пример	Принцип решения
Линейное уравнение	10 = 5x + 5	Проводим преобразования: умножаем, делим обе части на одно число; прибавляем, вычитаем одно и то же число; возводим в квадрат, извлекаем корни из обеих частей; переносим слагаемые из одной части в другую, меняя знак.
Квадратное уравнение	2t2 + 4t + 8 = 0 Общий вид: ax2 + bx + c = 0	Ищем дискриминант по формуле D = b2 — 4ac; Находим два корня по формуле ; Выбираем корень, подходящий по условию. Можно решить уравнение графически. Тогда корнями будут точки пересечения графика с осью Ох.
Линейное неравенство	10(v — 500) < 3000	Выполняем те же преобразования, что и для уравнения. Важно:
Квадратные неравенства	8t2 + t + 9 < 10 Общий вид: ax2 + bx + c < 0 Могут стоять знаки <, >, ≤, ≥, ≠	Преобразуем для приведения к общему виду. Решаем квадратное уравнение, находим корни. Подставляем корни в неравенство a(x — x1)(x — x2) > 0. Могут стоять знаки: <, >, ≤, ≥, ≠. Корни делят уравнение на интервалы. Находим их, рисуем на числовой прямой. Определяем знаки на каждом интервале. Выбираем те интервалы, которые соответствуют знаку неравенства. Отвечаем на поставленный вопрос.

Пример из ЕГЭ

Попробуем решить задание профильного уровня.

Задача. Радиоактивный элемент переживает распад, при котором его масса уменьшается по закону: , где

m₀ — начальная масса,

t — время, которое прошло от начала распада атома,

T — период полураспада.

Время полураспада составляет 10 минут. Начальная масса равна 40 мг. Определите, через какой промежуток масса уменьшится до 10 мг.

Решение. Суть задания — решение показательного уравнения. Нам нужно найти t. Поставляем известные величины:

Делим обе части на «10»:

Представляем «4» в виде степени с основанием «2»:

Правую часть записываем в виде степени с общим основанием:

Записываем единицу в виде степени с основанием «2»:

Приравниваем показатели степени и меняем местами правую и левую части:

Переносим «2» в правую часть и домножаем обе части на «-1»:

Находим t и записываем ответ:

t =20

Ответ: 20.

Мы разобрались, как решать 10 задание из профиля ЕГЭ по математике. У вас есть краткий план действий, осталось лишь практиковаться, выполняя номера с ФИПИ. Или можно записаться на курсы подготовки к ЕГЭ в центр «Уникум» при Российском университете дружбы народов. Преимущества курсов:

разные форматы обучения: очный, онлайн и дистанционный;
занятия проходят в главном здании РУДН. Поэтому можно сразу «окунуться» в студенческую жизнь.;
предоставляется скидка на первый год обучения в РУДН.

Содержание данной статьи носит ознакомительный характер. Для подготовки к сдаче ЕГЭ пользуйтесь дополнительными источниками информации!

Линейные уравнения с дробями — примеры и практические задания

Чтобы решить линейные уравнения с дробями, мы должны умножить все уравнение на наименьшее общее кратное, чтобы исключить дроби, а затем использовать обычный метод решения уравнений первой степени.

В этой статье мы рассмотрим несколько примеров с ответами, чтобы освоить эту тему, а также рассмотрим некоторые практические задачи и отработаем то, что узнали.

АЛГЕБРА

Актуально для …

Изучение линейных уравнений с дробями, примеры и практические задачи.

См. примеры

Содержание

АЛГЕБРА

Актуально для …

Изучение линейных уравнений с дробями, примеры и практические задачи.

См. примеры

Обобщение линейных уравнений с дробями

Напомним, что для уравнения первой степени все переменные в уравнении должны иметь максимальную степень 1. Например, уравнения $latex \frac{1}{3}x+2=6$ и $latex \frac{3}{2}x=\frac{1}{2}x+10$ представляют собой линейные уравнения с дробями. Мы можем решить линейные уравнения с дробями со следующими шагами:

Шаг 1: Удалите дроби: мы умножаем все уравнение на наименьшее общее кратное, чтобы удалить дроби.

Шаг 2: Упрощение: мы удаляем круглые скобки и другие знаки группировки и объединяем одинаковые термины.

Шаг 3: Решение для переменной: мы используем сложение и вычитание, чтобы переместить переменную только в одну часть уравнения.

Шаг 4: Решение: мы используем умножение и деление, чтобы полностью найти переменную.

Решенные примеры линейных уравнений с дробями

ПРИМЕР 1

Решите уравнение $latex \frac{x}{3}+4=6$.

Решение

Шаг 1: Удалите дроби: Умножаем все уравнение на 3:

$$\frac{x}{3}+4=6$$

$латекс x+4(3)=6(3)$

$латекс x+12=18$

Шаг 2: Упрощать: нам нечего упрощать.

Шаг 3: Найти переменную: вычесть 12 из обеих частей уравнения: Шаг 4: Решение: Мы уже получили ответ:

$латекс x=6$

ПРИМЕР 2

Найдите значение $latex x$ в уравнении $latex \frac{1}{2}x+4(x+2)=14-2x+20$.

Решение

1. Упростите:

Удалите скобки: $latex \frac{1}{2}x+4x+8=14-2x+20$.
Упростите дроби, умножив их на 2: $латекс x+8x+16=28-4x+40$.
Объедините похожие термины: $латекс 9x+16=68-4x$.

2. Изолируйте переменную: переместите 16 вправо и -4x влево:

$latex 9x+16-16=68-4x-16$

$latex 9x=52-4x$

$latex 9x+4x=52-4x+4x$

$latex 13x=52$

3. Примените различные операции, чтобы изолировать $latex x$: разделите обе части на 13:

$$\frac{13}{13}x=\frac{{52}}{13}$$

$$x=\frac{{52}}{13}=4$$

4. Проверьте свое решение: подставьте значение в исходное уравнение:

$$\frac{1}{2}(4)+4(4+2)=14-2(4)+20$$

$ латекс 2+16+8=14-8+20$

$латекс 26=26$

Верно

Ответ: $latex x=4$

ПРИМЕР 3

Найдите значение x в уравнении $latex \frac{x+1}{2}+2=4$.

Решение

Шаг 1: Удаляем дроби: Умножаем все уравнение на 2:

$$\frac{x+1}{2}+2=4$$

$latex x+1+2(2)=4(2)$

$латекс x+1+4=8$

Шаг 2: Упрощение: Объединяем подобные термины:

$latex x+1+4=8$

$latex x+5=8$

Шаг 3: Решение для переменной: вычитаем 5 из обеих частей:

$latex x+ 5-5=8-5$

$латекс x=3$

Шаг 4: Решение: мы уже получили ответ:

$латекс x=3$

ПРИМЕР 90
Найдите значение x в уравнении $latex \frac{2x+5}{3}+2x=7$.
Решение
Шаг 1: Удалите дроби: умножаем все уравнение на 3:
$$\frac{2x+5}{3}+2x=7$$
$latex 2x+5 +2x(3)=7(3)$
$латекс 2x+5+6x=21$
Шаг 2: Упрощение: Объединяем подобные термины:
$латекс 2x+5+6x =21$
$латекс 8x+5=21$
Шаг 3: Решение для переменной: Вычитаем 5 из обеих частей:
$latex 8x+5-5=21-5$
$latex 8x=16$
Шаг 4: Решение: делим обе части на 8: $
$ \frac
2{ }{8}=\frac{16}{8}$$
$latex x=2$
ПРИМЕР 5
Найдите значение $latex x$ в уравнении $latex \frac{1}{3} х+4+\фракция{1}{2}х=9$.
Решение
1. Упростите:
Скобки отсутствуют.
Упростите дроби: умножьте на 6: $латекс 2x+24+3x=54$.
Объедините одинаковые термины: $латекс 5x+24=54$.

2. Изолируйте переменную: переместите 24 вправо:
$latex 5x+24-24=54-24$
$latex 5x=30$
3. Примените различные операции, чтобы изолировать $latex x $: разделить обе части на 5:
$$\frac{5}{5}x=\frac{{30}}{5}$$
$$x=\frac{{30}}{5} =6$$
4. Проверьте свое решение: подставьте значение в исходное уравнение:
$$\frac{1}{3}(6)+4+\frac{1}{2}(6)= 9$$
$латекс 2+4+3=9$
$латекс 9=9$
Это правда
Ответ: $латекс x=6$.
ПРИМЕР 6
Найдите значение x в уравнении $latex \frac{3x-4}{4}+6=2x+10$.
Решение
Шаг 1: Удалите дроби: умножаем все уравнение на 4:
$$\frac{3x-4}{4}+6=2x+10$$
$$3x-4+6(4)=2x(4)+10(4)$$
$латекс 3x-4+24=8x+40$
Шаг 2: Упрощаем: мы объединяем, как термины:
$ lavex 3x-4+24 = 8x+40 $
$ Latex 3x+20 = 80+40 $
Шаг. 3: Решите для переменной: мы вычтем 20 и 8x из обеих частей уравнения:
$латекс 3x+20-20=8x+40-20$
$латекс 3x=8x+20$
$latex 3x-8x=8x+20-8x$
$latex -5x=20$
Шаг 4: Решение: делим обе части на -5:
$$\frac{-5x}{-5}=\frac{20}{-5}$$
$latex x=-4$
ПРИМЕР 7
Найдите значение $latex x$ в уравнение $$\frac{1}{2}x+2(x+1)=\frac{1}{5}x+4+x+11$$
Решение
1. Упростить:
Удалите скобки: $latex \frac{1}{2}x+2x+2=\frac{1}{5}x+4+x+11$.
Удалите дроби: умножьте на 10: $$5x+20x+20=2x+40+10x+110$$
Объедините похожие термины: $латекс 25x+20=12x+150$.
2. Изолируйте переменную: переместите 20 вправо, а 12x влево:
$латекс 25x+20-20=12x+150-20$
$латекс 25x=12x+130$
$латекс 25x-12x=12x-12x+130$

$латекс 13x=130$
$
$латекс 25x-12x=12x-12x+130$ 3. Примените операции, чтобы изолировать $латекс x$: разделите обе части на 13:
$$\frac{13}{13}x=\frac{{130}}{13}$$
$$x= \frac{{130}}{13}=10$$
4. Проверьте свое решение: подставьте значение в исходное уравнение:
$$\frac{1}{2}(10)+2(10+ 1)=\frac{1}{5}(10)+4+10+11$$
$латекс 5+2(11)=2+4+10+11$
$латекс 27=27$
Верно
Ответ: $латекс x=10$.
ПРИМЕР 8
Решите уравнение $latex \frac{t+5}{2}+5=\frac{t-6}{3}+10$ для t .
Решение
Шаг 1: Удалите дроби: умножаем все уравнение на 6:
$$\frac{t+5}{2}+5=\frac{t-6} {3}+10$$
$$3(t+5)+5(6)=2(t-6)+10(6)$$
$латекс 3(t+5)+30=2( т-6)+60$
Шаг 2: Упрощение: Раскрываем круглые скобки и объединяем одинаковые термины:
$latex 3(t+5)+30=2(t-6)+60$
$latex 3t+ 15+30=2t-12+60$
$латекс 3t+45=2t+48$

$латекс 3т+45-45=2т+48-45$
$латекс 3т=2т+3$
$латекс 3т-2т=2т+3-2т$
$латекс t=3$
Шаг 4: Решение: Мы уже получили ответ:
$latex t=3$
ПРИМЕР 9
Решить уравнение {5xlate1} $ +5=2(2x-2)+1$.
Решение
Шаг 1: Удалите дроби: умножаем все уравнение на 2:
$$\frac{5x-10}{2}+5=2(2x-2)+ 1$$
$$5x-10+5(2)=2(2)(2x-2)+1(2)$$
$латекс 5x-10+10=4(2x-2)+2 $
Шаг 2: Упрощение: мы удаляем круглые скобки и объединяем одинаковые термины:
$латекс 5x-10+10=4(2x-2)+2$
$латекс 5x-10+10 =8x-8+2$
$latex 5x=8x-6$
=8x-6-8x$
$latex -3x=-6$
Шаг 4: Решение: делим обе части на -3:
$$\frac{-3x}{-3}=\frac{-6}{-3}$$
$latex x=2$
ПРИМЕР 10
Найдите значение z из уравнения $latex \frac{2z+1}{3}+\frac{z-1}{2}=\frac{-3z-5}{2}-11$.
Решение
Шаг 1: Удалите дроби: умножим все уравнение на 6, чтобы исключить все дроби:
$$\frac{2z+1}{3}+\frac{z- 1}{2}=\frac{-3z-5}{2}-11$$
$$2(2z+1)+3(z-1)=3(-3z-5)-6(11) $$
$$2(2z+1)+3(z-1)=3(-3z-5)-66$$
Шаг 2: Упрощение: убираем круглые скобки и объединяем одинаковые термины:
$$2(2z+1)+3(z-1)=3(-3z-5)-66$$
$латекс 4z+2+3z-3=-9z-15-66$
$ латекс 7z-1=-9z-81$
Шаг 3: Решите для переменной: добавьте 1 и 9 z из обеих частей уравнения:
$latex1+1 7z-1 -9z-81+1$
$латекс 7z=-9z-80$
$latex 7z+9z=-9z-80+9z$
$latex 16z=-80$
Шаг 4: Решение: Делим обе части на 13 $\frac 9000 {16z}{16}=\frac{-80}{16}$$
$latex x=-5$
Линейные уравнения с дробями.
Практические задачи
Вы прошли тест!
Найдите значение x в $latex \frac{2x-2}{3}+\frac{3x}{2}=-5$.
Запишите ответ в поле ввода.
х=
См. также
Хотите узнать больше о решении уравнений? Взгляните на эти страницы:
20 примеров линейных уравнений
Линейные уравнения с двумя неизвестными Примеры
Упражнения на линейные уравнения
Предварительное исчисление по алгебре — Как вы решаете уравнения любой степени?
В области финансовой математики вы рассматриваете задачу о сложных процентных ставках (за $\mathbf{n}$
периодов начисления сложных процентов ), где $100x$ – процентная ставка или доходность, а $\mathbf{x} $ относительная норма начисления за период . Когда $n$ — количество периодов начисления сложных процентов в год, $\mathbf{nx}$ — номинальная годовая процентная ставка, а $\mathbf{f(x)}$ — безразмерная величина , сравнивающая с ростом по сравнению с $ \mathbf{n}$ периодов с ростом только за один период и применим, например, к ипотеке с фиксированной ставкой, когда $n=12$. В этом контексте $\mathbf{x \cdot f(x)}$ – это эквивалентная годовая ставка, также известная как годовая процентная ставка ( апр. 900 10), годовая эквивалентная ставка ( AER ), и другие различные комбинации $$ \text{годовой/-} \четверка \text{действующий/эквивалентный/-} \четверка \text{процент/процент/-} \четверка \text{скорость/доходность} $$ ( т. е. около 42 различных формулировок, если мы требуем хотя бы одно из слов «ежегодный», «действующий» или «эквивалентный» — чтобы было ясно, о чем мы говорим — но позволяем менять их порядок при использовании два ).
Обычно задача, которую вам дают, не имеет $x$ в знаменателе, что делает задачу легко решаемой с помощью логарифмов и соотношения будущих и настоящих значений. В большинстве финансовых калькуляторов есть способ решить эту проблему напрямую. Наверняка есть и хорошие веб-ресурсы. Когда-то можно было запрограммировать это на Javascript для использования в автономном режиме; у кого-то, наверное, уже есть. {\frac{2\pi ik}{n}}-1$ образует угол $\frac{2\pi ik}{n}$ с положительной действительной осью, поскольку он идет радиально от $- 1$. Формула на RHS говорит, что эти корни можно сгруппировать по знаменателю $\frac{k}{n}$ в низших членах.

Третья строка выполняет другую группировку в квадратичные множители, соответствующие парам комплексно-сопряженных корней, за исключением линейного множителя $x+2$ для корня в $-2$ в случае, если $n$ четно; этот последний необязательный бит выполняется с выражением $\left\lfloor\frac{n}2\right\rfloor -\левый\lэтаж\фракция{n-1}2\правый\rпол =\href{http://en.wikipedia.org/wiki/Floor_function#Mod_operator}{(n-1)- 2\левый\lэтаж\фрак{n-1}2\правый\rпол}$, что дает остаток от $n-1$ по модулю $2$, т. е. он равен $0$ или $1$ в зависимости от того, является ли $n$ нечетным или четным. Все коэффициенты здесь снова действительны, и все множители неприводимы над действительными полями. Интересным следствием этого, глядя на $f(0)$, является то, что $$ \ prod_ {k = 1} ^ {\ left \ lfloor \ frac {n-1} 2 \ right \ rfloor} \sin^2\tfrac{k\pi}{n} =\frac{n}{2^{n-1}}. $$ 9{nx}-1}{x}$ для $x>-1$. Обе стороны приближаются к $n$ как $x \rightarrow 0$. Неравенство действительно верно для всех $x>-1$ и является строгим для $x\ne0$. Это следует из наблюдения, что $\ln(1+x)$ является возрастающей и выпуклой с касательной $y=x$ в начале координат.
Определение $f(0)=n$ (или взятие биномиальной суммы степеней в качестве нашего определения) сделало бы $f$ непрерывной в $0$, расширив область определения до $(-1,\infty)$, поскольку $f(x )$ приближается к производной степенной функции степени $n$ при $x \rightarrow 0$. 9x-1$ как $n \rightarrow \infty$.
При $f(0)=0$ производная $f\,'(0)=\frac{n(n-1)}{2}$ существует и непрерывна.
$f\,'(x)=1$ для $n=2$.
Решение $y=f(x)$ относительно $x$ при заданном $y$ будет иметь одно решение для $y>n$ ($y\gen n$, если мы допускаем $x=0$) и никаких решений для $ у
No related posts.