Таблицы истинности, с формулами и примерами
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Главная Справочник Таблицы Таблицы истинности
Они могут принимать значения «истина» или «ложь» (1 или 0). Для функции, содержащей две переменные, наборов значений переменных всего четыре:
Значения логических функций определяются с помощью таблица истинности.
Таблицы истинности для основных двоичных логических функций
1. Конъюнкция (логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения.
Обозначение:
2. Дизъюнкция (логическое сложение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны.
Обозначение:
3. Импликация (логическое следствие) – это сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно, а следствие ложно.
Обозначение:
4. Эквиваленция – это сложное логическое высказывание, которое является истинным только при одинаковых значениях истинности простых выражений, входящих в него.
Обозначение:
5. Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.
Обозначение:
6. Штрих Шеффера – операция, отрицающая конъюнкцию, т.е. значение ложно тогда и только тогда, когда оба простых выражения истинны.
Обозначение:
7. Стрелка Пирса – операция, отрицающая конъюнкцию, т.е. значение истинно тогда и только тогда, когда оба простых выражения ложны.
Стрелка Пирса – операция, отрицающая конъюнкцию, т.е. значение истинно тогда и только тогда, когда оба простых выражения ложны.
Обозначение:
Порядок выполнения логических операций
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций:
- Инверсия
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквиваленция
- Штрих Шеффера
- Стрелка Пирса
Для последних двух операций приоритет не определен.
Замечание. Если необходимо изменить указанный порядок выполнения логических операций используются скобки.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Основы логики. Логические операции и таблицы истинности
Содержание:
- Глоссарий, определения логики
- Логические операции и таблицы истинности
- Порядок выполнения логических операций в сложном логическом выражении
На данной странице будут рассмотренны 5 логических операций:
конъюнкция,
дизъюнкция,
инверсия,
импликация и
эквивалентность,
которых Вам будет достаточно для решения сложных логических выражений.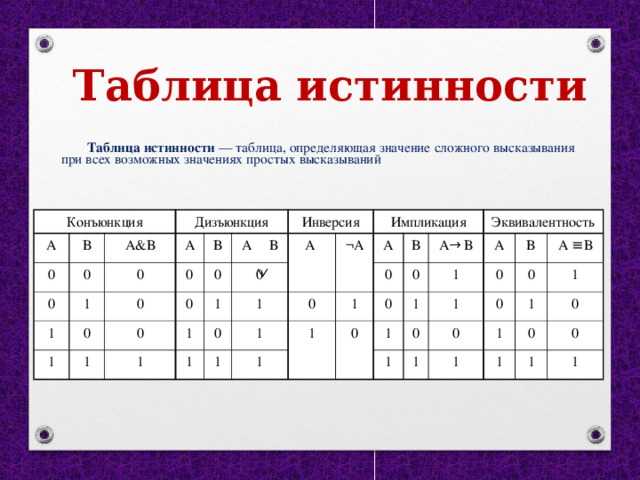
Глоссарий, определения логики
Высказывание — это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами,
обязательно входят переменные величины (объекты).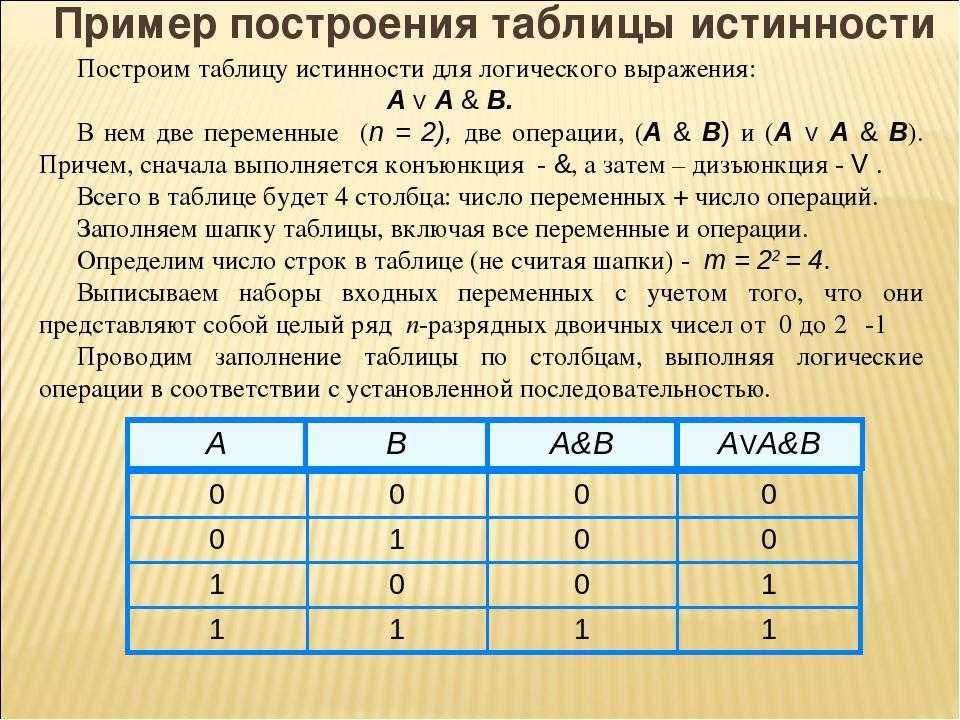
Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда
оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из
простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
| A | неА |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины
следует ложь.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Как решать задачи с таблицами истинности
Таблица истинности представляет собой список всех возможных комбинаций входных значений и результатов, к которым они приводят. Название происходит от того факта, что это математическая таблица, которая показывает все возможные результаты всех возможных фактов. В логических задачах, например в булевой алгебре и электронных схемах, обычно используются таблицы истинности.
Определение таблицы истинности Таблица истинности — это математическая таблица, которая помогает определить, является ли сложное утверждение истинным или ложным. В таблице истинности каждое утверждение обычно представляется буквой или переменной, например p, q или r. Каждое утверждение также имеет свой собственный столбец в таблице, в которой перечислены все возможные значения истинности. В этом уроке мы рассмотрим несколько примеров таблиц истинности и изучим основные правила их составления.
В таблице истинности каждое утверждение обычно представляется буквой или переменной, например p, q или r. Каждое утверждение также имеет свой собственный столбец в таблице, в которой перечислены все возможные значения истинности. В этом уроке мы рассмотрим несколько примеров таблиц истинности и изучим основные правила их составления.
Возможно, в повседневной жизни мы не рисуем таблицы истинности, но мы по-прежнему используем ту же логику, которая используется для составления таблиц истинности, чтобы выяснить, правда это или ложь. Скажем, кто-то говорит нам: «Если на улице идет дождь, футбольный матч не состоится». Мы можем использовать правила логического рассуждения, чтобы выяснить, является ли утверждение истинным или ложным, и, возможно, составить план Б. таблица — это способ увидеть все способы решения проблемы. Для дискретной математики вы должны знать, как использовать таблицы истинности. Здесь мы рассмотрим все ответы на простое уравнение p q.
Шаг 2: Изучите знаки
Первый шаг к получению таблицы истинности — выяснить, что означают знаки.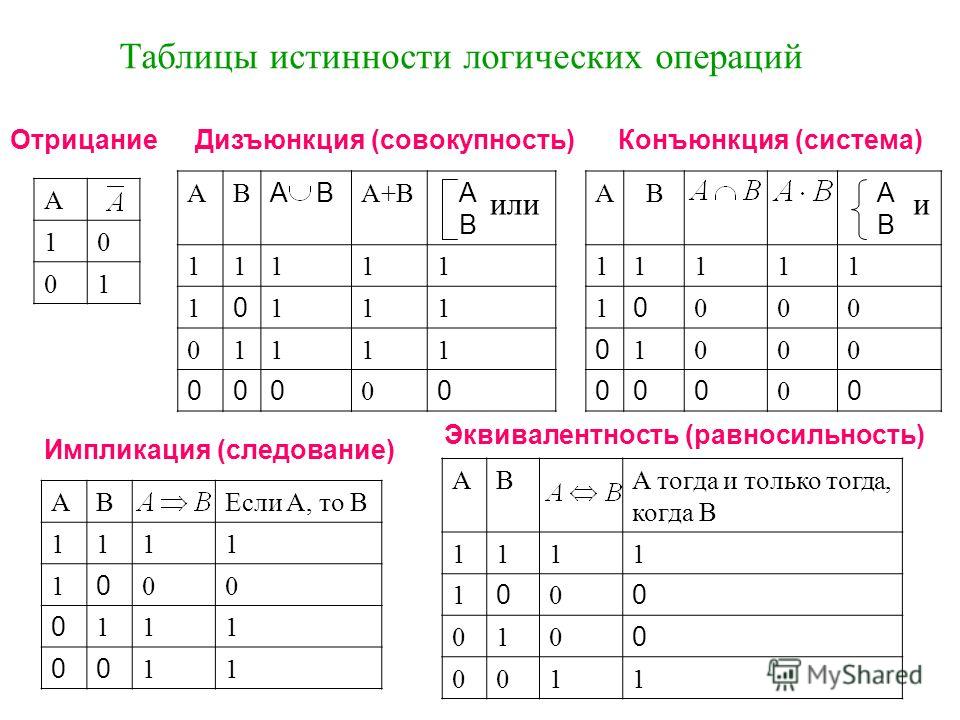 В этой конкретной задаче «» означает «не». «p» и «q» могут меняться. «» — это то же самое, что и слово «и». Это уравнение можно записать как «не p и q», что означает, что оно истинно, если p ложно, а q истинно.
В этой конкретной задаче «» означает «не». «p» и «q» могут меняться. «» — это то же самое, что и слово «и». Это уравнение можно записать как «не p и q», что означает, что оно истинно, если p ложно, а q истинно.
Шаг 3: Форматирование таблицы
Теперь давайте сделаем таблицу. Важно рассматривать каждую часть проблемы отдельно. Для этой задачи мы разобьем ее на p, p, q и p q. Изображение дает вам хорошее представление о том, как должен выглядеть ваш стол.
Шаг 4: Присвоение значений True и False
Поскольку переменных всего две, для каждой переменной есть только четыре возможных ответа. Для p мы помещаем T (истинно) в половину пробелов и F в другую половину (ложно).
Шаг 5: Отрицание
Поскольку p противоположно p, вы записываете знак, которого у p нет.
Шаг 6: Переменная «q»
Чтобы получить все возможные комбинации для q, вы переключаетесь между T и F. Поскольку уравнение касается только p, мы можем игнорировать столбец p при выяснении, верно ли оно .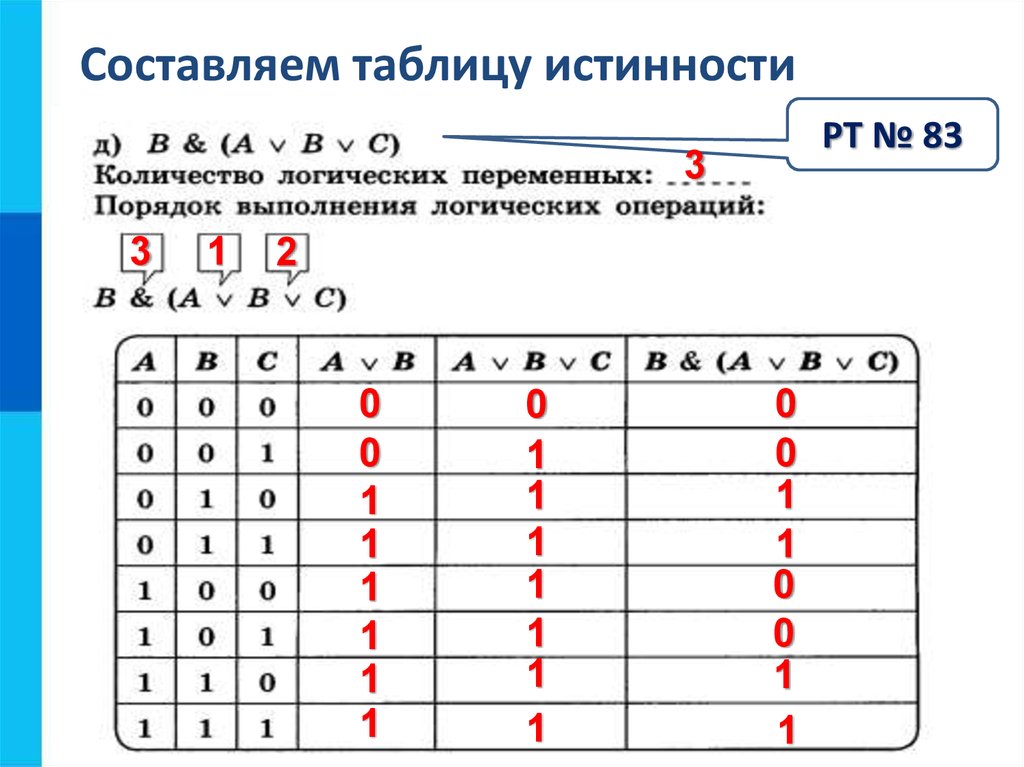 «» означает, что и p, и q должны быть истинными, чтобы уравнение было верным.
«» означает, что и p, и q должны быть истинными, чтобы уравнение было верным.
Шаг 7: Нахождение False в последнем столбце
Для первой строки p равно F, q равно T, поэтому, если p равно F, а q равно T, то p q равно F. Только если оба p и q T делает уравнение равным T.
Шаг 8: Найдите правильный ответ в последнем столбце
Это означает, что третья строка единственная с буквой T.
Шаг 9: Завершение таблицы
Проверьте еще раз, чтобы убедиться, что ваша таблица верна. Для этого вам нужно убедиться, что ваши знаки верны и что последний столбец сделан правильно. В последнем столбце вы можете увидеть результат всех различных способов объединения переменных.
Шаг 10: Готово
Теперь, когда вы знаете, как составить простую таблицу истинности, продолжайте делать это. Больше практики сделает вас лучше в их выполнении.
Примеры таблиц истинности Пример 1: Используйте конъюнкцию, чтобы найти логическую таблицу истинности для набора значений.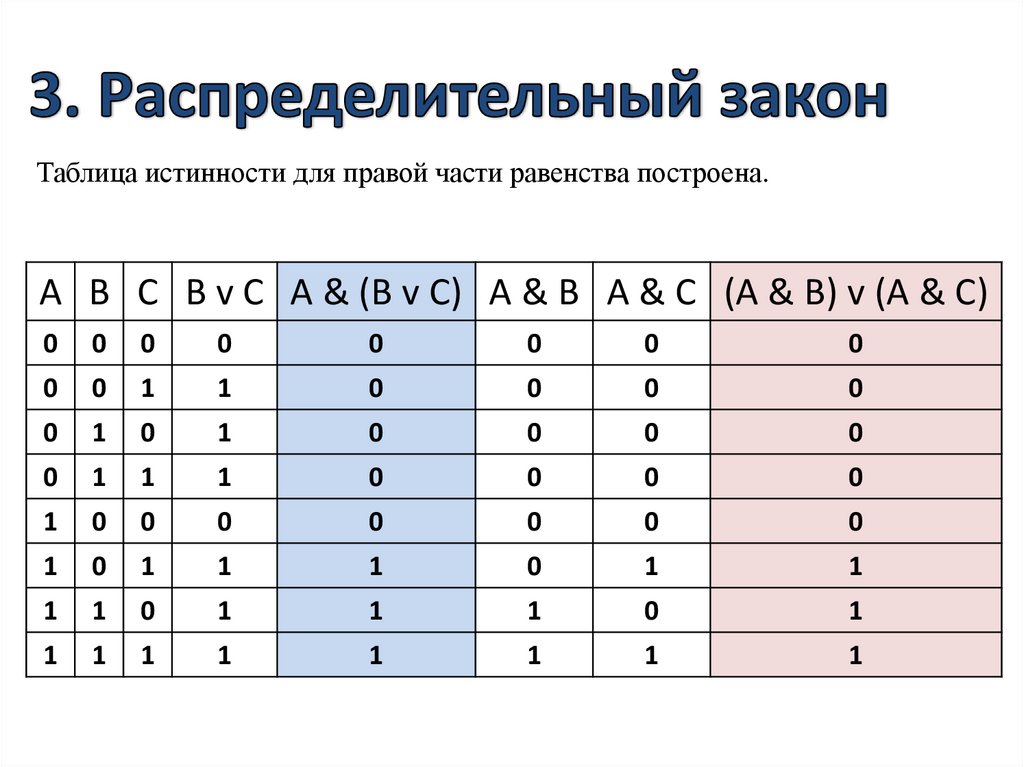
Если P равно F F T F T и Q равно F T T T F,
Решение:
P | Q | 210003|
Ф | Ф | Ф |
| 9 Ф 002 Т | Ф | |
Т | Т | Т |
Ф | Т | Ф |
Ф |
Пример 2: Составьте таблицу истинности для выражений ~P∨∼Q и ∼(P∧Q).
Решение:
P | Q | ~P | 2 91~P∨∼Q | (P∧Q) | ~(P∧Q) | |
T | T | F | Ф | Ф | Т | Ф |
2 Т | ||||||
Ф | Т | Т | Ф | Т | ||
Ф | Т | Т | Т | Ф | Т | |
Ф | Ф | Т | Пример 3 : Пусть S будет непустой частью R.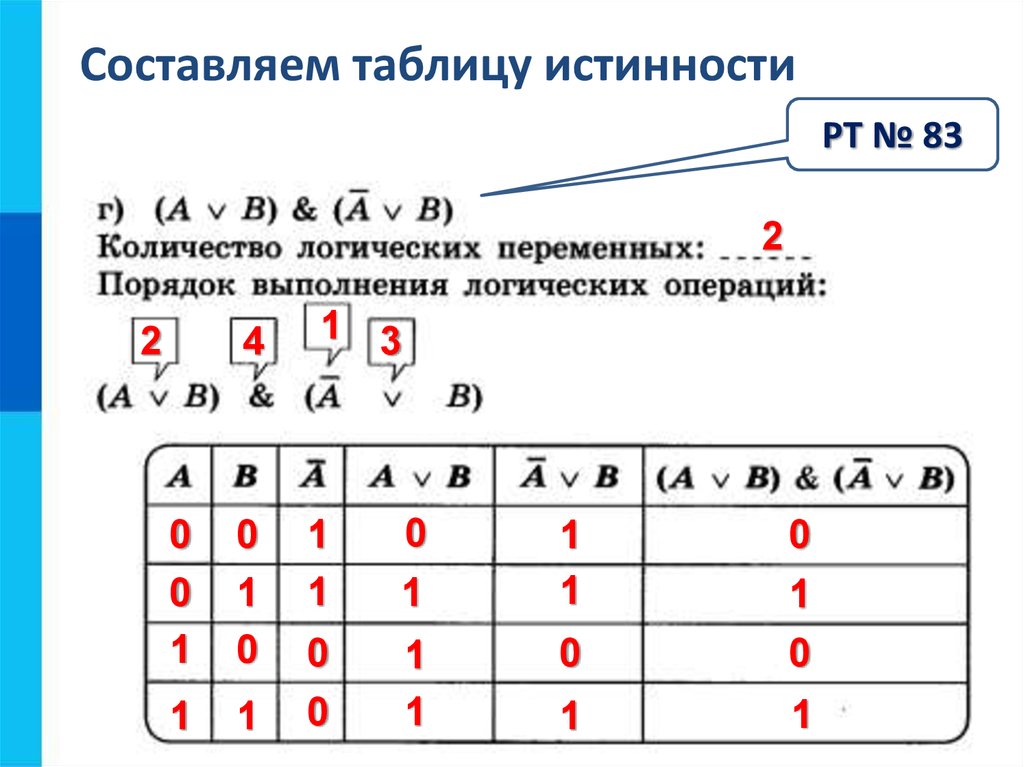 Подумайте о следующем предложении: P: В S есть рациональное число x, большее 0. Какое из приведенных ниже утверждений противоположно утверждению p? Подумайте о следующем предложении: P: В S есть рациональное число x, большее 0. Какое из приведенных ниже утверждений противоположно утверждению p?
Решение: P: Существует рациональное число x S, где x > 0. P: Каждое рациональное число x S удовлетворяет условию x 0. Заключениекоторый показывает логическое выражение функции логического вентиля. В таблице истинности логического вентиля перечислены все возможные входы вентиля или схемы и выходы, которые являются результатом этих входов (ов). Символическая логика с таблицами истинности. Мы рассмотрели основы символьной логики… | Бретт Берри | Математические приемыПример Мы рассмотрели основы символьной логики в последнем посте . Последнее сообщениеВведение в таблицы истинности и булеву алгебруТаблица истинности — это небольшой удобный логический прибор, который используется не только в математике, но также в информатике и…medium.com Генерация таблицы истинности для (A ∧ ~B) → (C ∨ D)Ключ к решению этой проблемы состоит в том, чтобы разбить ее на простейшие компоненты и решать по частям. . Шаги 1 и 2Шаг 1: У нас есть 4 переменные, поэтому нам нужно 4 столбца. Нам также понадобится 16 рядов, так как их по два варианта для каждого. Самый простой способ скомпоновать таблицу — использовать чередующийся шаблон T/F . В первой колонке заполните первую половину буквой T, а вторую половину буквой F. Затем чередуйте T/F через каждые 8÷2 или 4 во второй колонке. Продолжайте следовать шаблону, чередуя T/F каждые 2 в третьем столбце и каждый второй пробел в последнем столбце. Шаг 2: Нам нужно ~B вместо B, поэтому переверните все значения истинности в столбце B. Если вы используете карандаш, вы можете стереть столбец B и просто заменить его на ~B. Шаг 3: Далее нам нужно вычислить (A ∧ ~B) и (C ∨ D). Для этих вычислений мы добавим в нашу таблицу еще два столбца. Для логической конъюнкции, т. е. оператора И, нам нужно, чтобы и A, и ~B были истинными, чтобы получить истинный результат. Для ИЛИ нам нужно, чтобы только один из C или D был True, чтобы получить True. Используйте эти знания, чтобы заполнить последние два столбца. Шаг 3Шаг 4: Это последний шаг! Добавьте еще один столбец в конец для нашего окончательного вычисления: (A ∧ ~ B) → (C ∨ D). Мы знаем, что только в одном случае импликация (→) ложна, и это когда T → F. Поэтому проверьте столбцы (A ∧ ~B) и (C ∨ D) для этого случая. В нашей таблице есть только одна строка, где это происходит. |

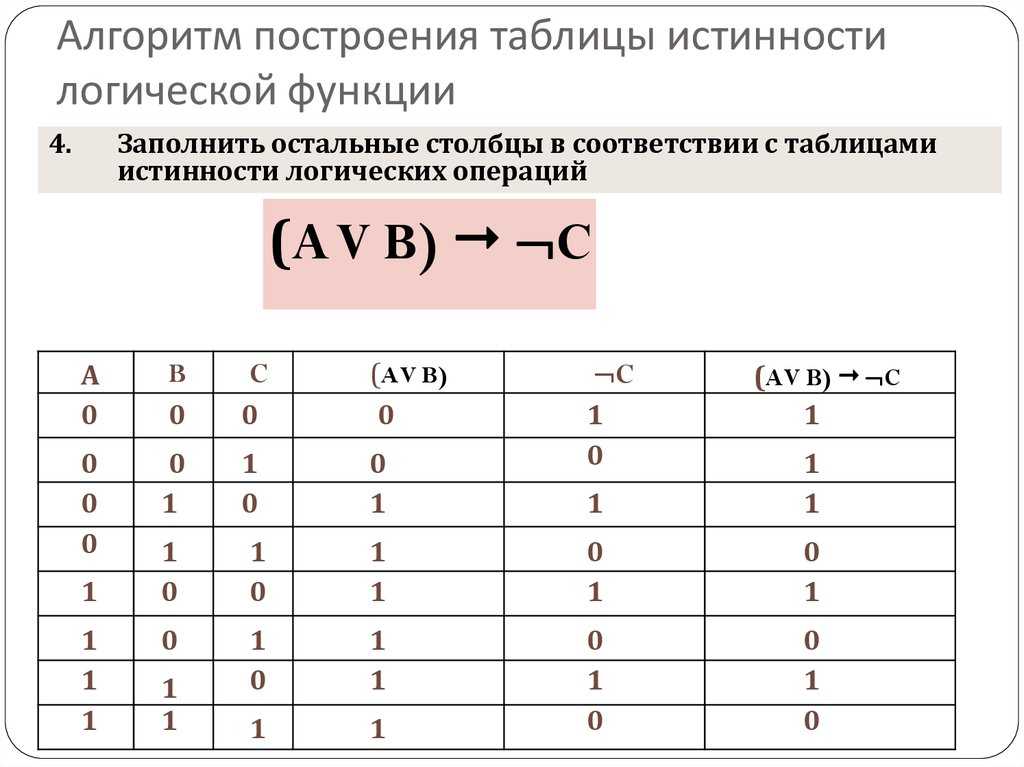 Теперь давайте воспользуемся этими навыками, решив оператор символьной логики.
Теперь давайте воспользуемся этими навыками, решив оператор символьной логики.  Это охватывает все возможные перестановки.
Это охватывает все возможные перестановки.