Как решать тригонометрические уравнения сложные: § 22. Примеры решения более сложных тригонометрических уравнений и их систем.

alexxlab / / Разное

Содержание

§ 22. Примеры решения более сложных тригонометрических уравнений и их систем.

   Иногда приходится решать тригонометрические уравнения, в которые входят только сумма или разность синуса и косинуса одного и того же аргумента и их произведение. В таком случае целесообразно эту сумму (или разность) обозначить новой переменной.

Задача 1. Решите уравнение 3 (sin x + cos x) = 2 sin 2х.

Комментарий

Если в заданном уравнении привести все тригонометрические функции к одному аргументу х, то получим уравнение (1) (см. решение), в которое входят только сумма синуса и косинуса одного и того же аргумента х и их произведение. Для решения этого уравнения введем новую переменную sin x + cos x = y. Чтобы получить произведение sin x cos x, достаточно возвести в квадрат обе части равенства замены и учесть, что sin2 x + cos2 x = 1. Выполняя обратную замену, удобно также учесть, что

Решение

   Данное уравнение равносильно уравнению

                                  3 (sin x + cos x) = 4 sin х cos x.

                                     (1)

Если обозначить sin x + cos x = у, то

Тогда  Подставляя эти значения в уравнение (1), получаем

Таким образом, sin x + cos x = 2 или sin x+cos x =

Тогда  или  Получаем  (корней нет, поскольку ) или  Отсюда  Тогда

Ответ:

   З а м е ч а н и е. При возведении обеих частей уравнения в квадрат можно получить посторонние корни (см. таблицу 7). Но возведение обеих частей равенства замены в квадрат является равносильным преобразованием. Действительно, в этом случае левая и правая части равенства имеют одинаковые знаки, и тогда a = b Если обе части равенства a = b положительны, то для положительных значений t функция y =возрастает и поэтому каждое свое значение принимает только при одном значении аргумента. Таким образом, при a > 0, b > 0 из равенства a = b следует равенство и, наоборот, из равенства следует равенство a = b, что и гарантирует равносильность выполненного преобразования для положительных a и b.

Аналогично для  используем то, что для не положительных значений t функция y =убывает и поэтому каждое свое значение принимает только при одном значении аргумента.

   Для решения некоторых тригонометрических уравнений могут применяться свойства функций (соответствующие общие подходы к решению были рассмотрены в § 3, пункт 3.2), в частности, оценка левой и правой частей уравнения.

Задача 2. Решите уравнение 

         Оценим область значений функции 

         Поскольку  то есть 

         Выясним, существуют ли такие значения х, при которых функция f (x) может принимать наибольшее значение 2. Если cos 6x будет меньше 1, то для того чтобы сумма равнялась 2, необходимо, чтобы значение было больше 1, что невозможно. Аналогично, если допустить, что меньше 1, то для того чтобы сумма равнялась 2, необходимо, чтобы значение cos 6x было больше 1, что невозможно. Таким образом, равенство в данном уравнении возможно тогда и только тогда, когда cos 6x и равны 1.

Поэтому данное уравнение равносильно системе

         Приравнивая правые части этих равенств, получаем

         Поскольку k и n — целые числа, то для получения всех решений последнего уравнения в целых числах (см. § 9) достаточно подставить в правую часть последнего равенства вместо п все остатки при делении на 5 и найти, для каких значений п по этой формуле k также будет целым числом. Только при n = 1 получаем целое k = 3. В случае, когда коэффициент 12 при переменной n в числителе дроби и знаменатель 5 — взаимно простые числа, повторение делимости нацело будет только через знаменатель, то есть через 5. Поэтому последнее уравнение имеет решения в целых числах только вида n = 1 + 5m,. Подставляя значение п в одно из решений системы, получаем х = π + 4πm. Эти значения и являются решениями последней системы, а следовательно, и решениями данного уравнения.

Ответ: х = π + 4πm,.

Задача 3. Решите уравнение 

Комментарий

         Преобразуем левую часть по формуле  и оценим область значений функций, стоящих в левой и правой частях уравнения. Решая полученную систему двух уравнений с одним неизвестным, можно несколько упростить выкладки и решить только одно уравнение системы, а для другого проверить, удовлетворяют ли ему полученные решения.

Решение

         Данное уравнение равносильно уравнению

(1)

        

 

Обозначим: . Поскольку 

         Левая часть уравнения (1) меньше или равна 2, а правая часть больше или равна 2. Равенство между ними возможно тогда и только тогда, когда левая и правая части уравнения равны 2, то есть данное уравнение равносильно системе

         Из первого уравнения системы имеем , откуда 

         Проверим, удовлетворяют ли найденные значения второму уравнению системы. Если , тогда sin 8x=0 и поэтому 

Ответ:

   Иногда для решения тригонометрических уравнений приходится применять тригонометрические формулы, которые приводят к сужению ОДЗ данного уравнения. Такие преобразования могут приводить к потере корней уравнения. Чтобы этого не случилось, можно пользоваться таким о р и е н т и р о м:

если для решения уравнений (или неравенств) приходится выполнять преобразования, сужающие ОДЗ исходного уравнения (или неравенства), то те значения, на которые сужается ОДЗ, необходимо рассматривать отдельно.

   В таблице 42 указаны тригонометрические формулы, которые могут приводить к сужению ОДЗ, и соответствующие значения переменной, которые приходится проверять при использовании этих формул.

Чтобы убедиться, что приведенные формулы приводят к сужению ОДЗ, достаточно сравнить области допустимых значений их левых и правых частей.

Например, рассмотрим формулу 

ОДЗ левой части: . Для нахождения ОДЗ правой части формулы учитываем, что знаменатель дроби не равен нулю:, таким образом, . То есть ОДЗ правой части задается системой ограничений  Сравнивая ОДЗ левой и правой частей рассмотренной формулы, видим, что ОДЗ правой части содержит дополнительное ограничение. Таким образом, при переходе по этой формуле от ее левой части к правой происходит сужение ОДЗ (отбрасываются именно те значения, которые указаны в таблице: Чтобы не потерять корни данного уравнения, при использовании формулы, значение , необходимо рассмотреть отдельно (конечно, только в том случае, когда оно входит в ОДЗ данного уравнения).

Приведем пример использования указанного о р и е н т и р а.

Задача 4. Решите уравнение

Комментарий

Если воспользоваться первыми двумя формулами таблицы 42, то мы приведем все тригонометрические выражения в этом уравнении и к одному аргументу, и к одной функции — tg x. Но при использовании указанных формул происходит сужение ОДЗ на значение ,  и вследствие этого можно потерять корни уравнения, если числа такого вида входят в ОДЗ исходного уравнения и являются его корнями. Чтобы этого не случилось, разобьем решение на две части.

  1. Подставляем те значения переменной, на которые сужается ОДЗ, в                уравнение (1).
    При вычислениях учитываем периодичность функций и формулы приведения.
  2. При (на ОДЗ уравнения (1)) использование формул и приводит к уравнению (2) (см. решение), которое равносильно заданному (на той части ОДЗ, где ), потому что эти формулы сохраняют верное равенство как при переходе от равенства (1) к равенству (2), так и при обратном переходе от равенства (2) к равенству (1). Замена переменной (и обратная замена) также приводит к уравнению, равносильному заданному (на указанной части ОДЗ исходного уравнения).

   Заметим, что ОДЗ уравнения (2) отличается от ОДЗ уравнения (1) только тем, что в нее не входят значения , которые входят в ОДЗ уравнения (1). Поскольку эти «плохие» значения мы учли в процессе решения, то ОДЗ уравнения (1) можно в явном виде не фиксировать (как в приведенном решении). В ответе записываем все корни, которые были получены в первой и второй частях решения.

Решение

  1. Если , то из данного уравнения получаем:

– верное равенство.

Таким образом, – корни уравнения (1).

  1. Если , получаем:

(2)

 

        Замена tg x = t приводит к уравнению  которое при  и  равносильно уравнению . Тогда 

Обратная замена даёт: tg x= -1 или , то есть:

   Некоторые тригонометрические уравнения удается решить, исполь­зуя такой ориентир, который условно можно назвать «ищи квадратный трехчлен», то есть:

попробуйте рассмотреть данное уравнение как квадратное относительно некоторой переменной (или относительно некоторой функции).

Решение показательных тригонометрических уравнений. Более сложные тригонометрические уравнения

Требует знания основных формул тригонометрии — сумму квадратов синуса и косинуса, выражение тангенса через синус и косинус и другие. Для тех, кто их забыл или не знает рекомендуем прочитать статью » «.

Итак, основные тригонометрические формулы мы знаем, пришло время использовать их на практике. Решение тригонометрических уравнений при правильном подходе – довольно увлекательное занятие, как, например, собрать кубик Рубика.

Исходя из самого названия видно, что тригонометрическое уравнение – это уравнение, в котором неизвестное находится под знаком тригонометрической функции.
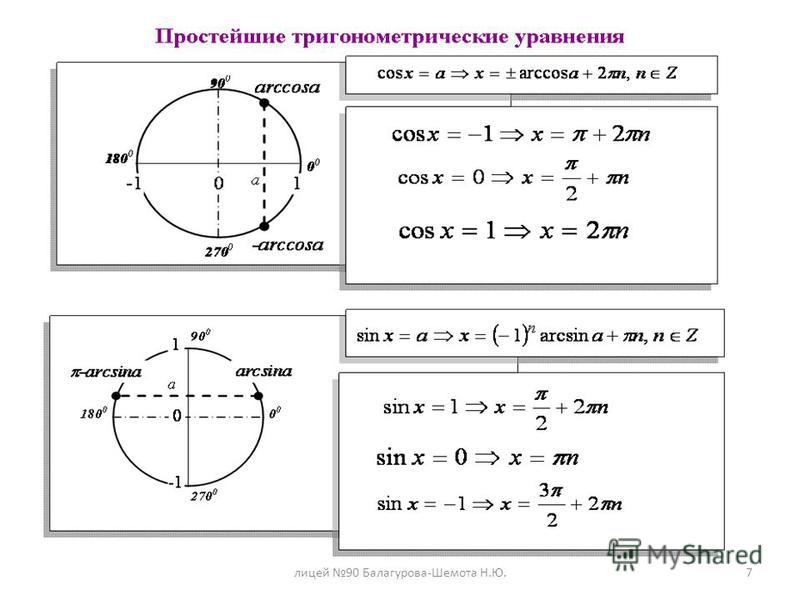
Существуют так называемые простейшие тригонометрические уравнения. Вот как они выглядят: sinх = а, cos x = a, tg x = a. Рассмотрим, как решить такие тригонометрические уравнения , для наглядности будем использовать уже знакомый тригонометрический круг.

sinх = а
cos x = a

tg x = a

cot x = a

Любое тригонометрическое уравнение решается в два этапа: приводим уравнение к простейшему виду и далее решаем его, как простейшее тригонометрическое уравнение.
Существует 7 основных методов, с помощью которых решаются тригонометрические уравнения.

  1. Метод замены переменной и подстановки

    2. Решить уравнение 2cos 2 (x + /6) – 3sin( /3 – x) +1 = 0

    Используя формулы приведения получим:

    2cos 2 (x + /6) – 3cos(x + /6) +1 = 0

    Заменим cos(x + /6) на y для упрощения и получаем обычное квадратное уравнение:

    2y 2 – 3y + 1 + 0

    Корни которого y 1 = 1, y 2 = 1/2

    Теперь идем в обратном порядке

    Подставляем найденные значения y и получаем два варианта ответа:

  2. Решение тригонометрических уравнений через разложение на множители

    3. Как решить уравнение sin x + cos x = 1 ?

    Перенесем все влево, чтобы справа остался 0:

    sin x + cos x – 1 = 0

    Воспользуемся вышерассмотренными тождествами для упрощения уравнения:

    sin x — 2 sin 2 (x/2) = 0

    Делаем разложение на множители:

    2sin(x/2) * cos(x/2) — 2 sin 2 (x/2) = 0

    2sin(x/2) * = 0

    Получаем два уравнения

  3. Приведение к однородному уравнению

    4. Уравнение является однородным относительно синуса и косинуса, если все его члены относительно синуса и косинуса одной и той же степени одного и того же угла. Для решения однородного уравнения, поступают следующим образом:

    а) переносят все его члены в левую часть;

    б) выносят все общие множители за скобки;

    в) приравнивают все множители и скобки к 0;

    г) в скобках получено однородное уравнение меньшей степени, его в свою очередь делят на синус или косинус в старшей степени;

    д) решают полученное уравнение относительно tg.

    Решить уравнение 3sin 2 x + 4 sin x cos x + 5 cos 2 x = 2

    Воспользуемся формулой sin 2 x + cos 2 x = 1 и избавимся от открытой двойки справа:

    3sin 2 x + 4 sin x cos x + 5 cos x = 2sin 2 x + 2cos 2 x

    sin 2 x + 4 sin x cos x + 3 cos 2 x = 0

    Делим на cos x:

    tg 2 x + 4 tg x + 3 = 0

    Заменяем tg x на y и получаем квадратное уравнение:

    y 2 + 4y +3 = 0, корни которого y 1 =1, y 2 = 3

    Отсюда находим два решения исходного уравнения:

    x 2 = arctg 3 + k

  4. Решение уравнений, через переход к половинному углу

    5. Решить уравнение 3sin x – 5cos x = 7

    Переходим к x/2:

    6sin(x/2) * cos(x/2) – 5cos 2 (x/2) + 5sin 2 (x/2) = 7sin 2 (x/2) + 7cos 2 (x/2)

    Пререносим все влево:

    2sin 2 (x/2) – 6sin(x/2) * cos(x/2) + 12cos 2 (x/2) = 0

    Делим на cos(x/2):

    tg 2 (x/2) – 3tg(x/2) + 6 = 0

  5. Введение вспомогательного угла

    6. Для рассмотрения возьмем уравнение вида: a sin x + b cos x = c ,

    где a, b, c – некоторые произвольные коэффициенты, а x – неизвестное.

    Обе части уравнения разделим на :

    Теперь коэффициенты уравнения согласно тригонометрическим формулам обладают свойствами sin и cos, а именно: их модуль не более 1 и сумма квадратов = 1. Обозначим их соответственно как cos и sin , где – это и есть так называемый вспомогательный угол. Тогда уравнение примет вид:

    cos * sin x + sin * cos x = С

    или sin(x + ) = C

    Решением этого простейшего тригонометрического уравнения будет

    х = (-1) k * arcsin С — + k, где

    Следует отметить, что обозначения cos и sin взаимозаменяемые.

    Решить уравнение sin 3x – cos 3x = 1

    В этом уравнении коэффициенты:

    а = , b = -1, поэтому делим обе части на = 2

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

  • Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

  • Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
  • Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
  • Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
  • Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

  • В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
  • В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Решение простейших тригонометрических уравнений.

Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.

Вспомним определения косинуса и синуса.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .

Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов (или 0 радиан) соответствует точка с координатами (1;0)

Используем эти определения для решения простейших тригонометрических уравнений.

1. Решим уравнение

Этому уравнению удовлетворяют все такие значения угла поворота , которые соответствуют точкам окружности, ордината которых равна .

Отметим на оси ординат точку с ординатой :


Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату . Эти точки соответствуют углам поворота на и радиан:


Если мы, выйдя из точки, соответствующей углу поворота на радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.

То есть первая серия решений исходного уравнения имеет вид:

, , — множество целых чисел (1)

Аналогично, вторая серия решений имеет вид:

, где , . (2)

Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .

Эти две серии решений можно объединить в одну запись:

Если мы в этой записи возьмем (то есть четное ), то мы получим первую серию решений.

Если мы в этой записи возьмем (то есть нечетное ), то мы получим вторую серию решений.

2. Теперь давайте решим уравнение

Так как — это абсцисса точки единичной окружности, полученной поворотом на угол , отметим на оси точку с абсциссой :


Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:


Запишем две серии решений:

,

,

(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть .

Объедим эти две серии в одну запись:

3. Решим уравнение

Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY

Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):


Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на и :


Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии радиан друг от друга, то мы можем записать решение таким образом:

4. Решим уравнение

Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .

Отметим на линии котангенсов точку с абсциссой -1:


Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:


Поскольку эти точки отстоят друг от друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:

В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.

Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение :





ОСОБЫЕ РЕШЕНИЯ:

Отметим на окружности точки, ордината которых равна 0:


Отметим на окружности единственную точку, ордината которой равна 1:


Отметим на окружности единственную точку, ордината которой равна -1:


Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:

Отметим на окружности точки, абсцисса которых равна 0:


5.
Отметим на окружности единственную точку, абсцисса которой равна 1:


Отметим на окружности единственную точку, абсцисса которой равна -1:


И чуть более сложные примеры:

1.

Синус равен единице, если аргумент равен

Аргумент у нашего синуса равен , поэтому получим:

Разделим обе части равенства на 3:

Ответ:

2.

Косинус равен нулю, если аргумент косинуса равен

Аргумент у нашего косинуса равен , поэтому получим:

Выразим , для этого сначала перенесем вправо с противоположным знаком:

Упростим правую часть:

Разделим обе части на -2:

Заметим, что перед слагаемым знак не меняется, поскольку k может принимать любые целые значения.

Ответ:

И в заключение посмотрите видеоурок «Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности»

На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать . 2+3t-4=0\). Корнями являются \(t_1=-4, \ t_2=1\). Сделаем обратную замену:

 

\(\left[\begin{gathered} \begin{aligned} &\mathrm{tg}\,x=1\\&\mathrm{tg}\,x=-4 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=\dfrac{\pi}4+\pi n\\[1ex]&x=-\mathrm{arctg}\,4+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)

 

\(\blacktriangleright\) Однородные тригонометрические уравнения первой степени: \[II.\quad {\Large{a\sin x+b\cos x=0}}, a\ne0, b\ne 0\]

Заметим, что в данном уравнении никогда не являются решениями те значения \(x\), при которых \(\cos x=0\) или \(\sin x=0\). Действительно, если \(\cos x=0\), то, подставив вместо косинуса ноль в уравнение, получим: \(a\sin x=0\), откуда следует, что и \(\sin x=0\). Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если \(\cos x=0\), то \(\sin x=\pm 1\).

 

Аналогично и \(\sin x=0\) не является решением такого уравнения.

 

Значит, данное уравнение можно делить на \(\cos x\) или на \(\sin x\). Разделим, например, на \(\cos x\):

 

\(a \ \dfrac{\sin x}{\cos x}+b \ \dfrac{\cos x}{\cos x}=0\), откуда имеем \(a\mathrm{tg}\, x+b=0 \Rightarrow \mathrm{tg}\, x=-\dfrac ba\)

 

Пример 6. Решить уравнение \(\sin x+\cos x=0\)

 

Разделим правую и левую части уравнения на \(\sin x\):

 

\(1+\mathrm{ctg}\, x=0 \Rightarrow \mathrm{ctg}\, x=-1 \Rightarrow x=-\dfrac{\pi}4+\pi n, n\in\mathbb{Z}\)

 

\(\blacktriangleright\) Неоднородные тригонометрические уравнения первой степени: \[II.\quad {\Large{a\sin x+b\cos x=c}}, a\ne0, b\ne 0, c\ne 0\]

Существует несколько способов решения подобных уравнений. Рассмотрим те из них, которые можно использовать для любого такого уравнения:

 

1 СПОСОБ: при помощи формул двойного угла для синуса и косинуса и основного тригонометрического тождества:   \({\large{\sin x=2\sin{\dfrac x2}\cos{\dfrac x2}, \qquad \cos x=\cos^2 {\dfrac x2}-\sin^2 {\dfrac x2},\qquad c=c\cdot \Big(\sin^2 {\dfrac x2}+\cos^2 {\dfrac x2}\Big)}}\)   данное уравнение сведется к уравнению \(I\):

 

Пример 7. 2}=2\):

 

\(\dfrac12\sin 2x-\dfrac{\sqrt3}2\cos 2x=-\dfrac12\)

 

Заметим, что числа \(\dfrac12\) и \(\dfrac{\sqrt3}2\) получились табличные. Можно, например, взять за \(\dfrac12=\cos \dfrac{\pi}3, \ \dfrac{\sqrt3}2=\sin \dfrac{\pi}3\). Тогда уравнение примет вид:

 

\(\sin 2x\cos \dfrac{\pi}3-\sin \dfrac{\pi}3\cos 2x=-\dfrac12 \Rightarrow \sin\left(2x-\dfrac{\pi}3\right)=-\dfrac12\)

 

Решениями данного уравнения являются:

 

\(\left[ \begin{gathered} \begin{aligned} &2x-\dfrac{\pi}3=-\dfrac{\pi}6+2\pi n\\[1.5ex] &2x-\dfrac{\pi}3=-\dfrac{5\pi}6+2\pi n \end{aligned} \end{gathered} \right. \Rightarrow \left[ \begin{gathered} \begin{aligned} &x=\dfrac{\pi}{12}+\pi n\\[1.5ex] &x=-\dfrac{\pi}4+\pi n \end{aligned} \end{gathered} \right. \ \ n\in\mathbb{Z}\)

 

Заметим, что при решении уравнения третьим способом мы добились “более красивого” ответа (хотя ответы, естественно, одинаковы), чем при решении первым или вторым способом (которые, по сути, приводят уравнение к одному и тому же виду). 2-3t-2=0\] Корнями данного уравнения являются \(t_1=2, t_2=-\dfrac12\).

 

По формулам вспомогательного аргумента \(\sin2x+\cos 2x=\sqrt2\sin\left(2x+\dfrac{\pi}4\right)\), следовательно, сделав обратную замену: \[\left[ \begin{gathered} \begin{aligned} &\sqrt2\sin\left(2x+\dfrac{\pi}4\right)=2\\[1ex] &\sqrt2\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac12 \end{aligned} \end{gathered} \right. \Rightarrow \left[ \begin{gathered} \begin{aligned} &\sin\left(2x+\dfrac{\pi}4\right)=\sqrt2\\[1ex] &\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac1{2\sqrt2} \end{aligned} \end{gathered} \right.\] Первое уравнение корней не имеет, т.к. область значений синуса находится в пределах от \(-1\) до \(1\). Значит: \(\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac1{2\sqrt2} \Rightarrow \left[ \begin{gathered} \begin{aligned} &2x+\dfrac{\pi}4=-\arcsin {\dfrac1{2\sqrt2}}+2\pi n\\[1ex] &2x+\dfrac{\pi}4=\pi+\arcsin {\dfrac1{2\sqrt2}}+2\pi n \end{aligned} \end{gathered} \right. \Rightarrow \)  
\(\Rightarrow \left[ \begin{gathered} \begin{aligned} &x=-\dfrac12\arcsin {\dfrac1{2\sqrt2}}-\dfrac{\pi}8+\pi n\\[1ex] &x=\dfrac{3\pi}8+\dfrac12\arcsin {\dfrac1{2\sqrt2}}+\pi n \end{aligned} \end{gathered} \right. 2=(\sin x\pm \cos x)(1\pm \sin 2x)\)   (по первой формуле)

 

Исследовательская работа по теме «Однородные тригонометрические уравнения» — презентация на Slide-Share.ru 🎓

1

Первый слайд презентации: Исследовательская работа по теме «Однородные тригонометрические уравнения»

Работу выполнили: Исмагилов Руслан, Фазылханова Алёна Руководитель: Лунёва С.В Муниципальное автономное образовательное учреждение «Средняя общеобразовательная школа №2» Секция : Математика Г. Чернушка, 2013

Изображение слайда

2

Слайд 2

Изображение слайда

3

Слайд 3: Актуальность:

При изучении тригонометрии, мы рассмотрели решения простых однородных уравнений первой и второй степени, но мы решили рассмотреть можно ли другие уравнения решать таким способом.

Изображение слайда

4

Слайд 4: Цель:

Исследовать решения более сложных тригонометрических уравнений с помощью метода однородных тригонометрических уравнений.

Изображение слайда

5

Слайд 5: Задачи:

Повторить понятие однородных тригонометрических уравнений; Отработать алгоритм решения однородных тригонометрических уравнений; Попробовать решить более сложные уравнения данным методом; Поделиться опытом с классом ; Рассмотреть другие методы решения тригонометрических уравнений и сделать выводы о рациональности метода.

Изображение слайда

6

Слайд 6: Поэтапная работа:

1 ЭТАП: найти материал по данной теме. Уравнение вида аsinx + bcosx = 0 называют однородным тригонометрическим уравнением первой степени. Уравнение вида  а sin mx +  b cos mx = 0  тоже называют однородным тригонометрическим уравнение первой степени и решатся деление обеих частей уравнения на косинус mх. Отличительные признаки однородных уравнений: а) все одночлены имеют одинаковую степень, б) свободный член равен нулю, в) в уравнении присутствуют степени с двумя различными основаниями. Уравнение вида asin ²x + bsinxcosx+c cos²x=0 – Однородное тригонометрическое уравнение 2 степени Решается делением на cos²x, если asin ²x не равен 0.

Изображение слайда

7

Слайд 7: 2 этап : решение уравнений

мы прорешали уравнения: 1) 4cos ² 2x + 16sin2x-11=0 11) 2) 12) 3) 13) 4)   sinx + √3 cosx = 0 14) 5) 15) 6) 7)   sin 2 x + 2sinx cosx – 3cos 2 x = 0 8) 9) 10)

Изображение слайда

8

Слайд 8

Оказалось, что только 1,2,3,4,7,11 удобно решать методом однородных тригонометрических уравнений. При этом, нужно проверить, не потеряли ли мы корни.

Изображение слайда

9

Слайд 9: 3 этап поделиться с классом

Мы напомнили на одном из элективов классу, как решаются однородные тригонометрические Прорешали некоторые уравнения: sinx + √3 cosx = 0 Разделив обе части уравнения почленно на cosx, получим: tgx +√ 3=0 tgx =-√ 3 x = arctg (-√ 3 ) +∏ n, n Є Z x = -∏/3 + П n, n Є Z Ответ: х= -П/3+П n, n Є Z

Изображение слайда

10

Слайд 10

Изображение слайда

11

Слайд 11: sin 2 x + 2sinx cosx – 3cos 2 x = 0

tgx = а, тогда получаем уравнение: а 2  + 2а – 3 = 0 D = 4 – 4 (–3) = 16 а 1  = 1 а 2  = –3 tgx =1 tgx =-3 X= ∏ /4+ ∏ n x=arctg(-3)+ П n, n Z х= — arctg3+ П n, n Z Ответ: x= П\4+П n, — arctg3+ П n, n Z

Изображение слайда

12

Слайд 12

Показали как презентацию свою работу классу Задали классу уравнения : A) Б) и работали в качестве консультантов Задали домашнее задание

Изображение слайда

13

Слайд 13: 4 этап

Мы посмотрели другие методы и решения тригонометрических уравнений : -понижение степени -решение уравнений с помощью универальной тригонометрической подстановки -метод оценок -метод разложения на множители -переход к половинному углу -введение дополнительного угла

Изображение слайда

14

Слайд 14: Однородное введение доп.

угла

Изображение слайда

15

Слайд 15: заключение

Этот метод не очень сложный, используется довольно часто, с его помощью можно решить многие тригонометрическое уравнение, но нужно быть очень внимательным, чтобы при делении на cosx не потерять корни.

Изображение слайда

16

Последний слайд презентации: Исследовательская работа по теме «Однородные тригонометрические уравнения»: Список литературы:

А.Г.Мордкович «Алгебра и начала математического анализа» Б.М.Ивлев, А.М.Абрамов «Задачи повышенной трудности по алгебре и началам математического анализа» В.К.Егерев, В.В.Зайцев «Сборник конкурсных задач по математике» http://tat15534059. narod.ru/p5aa1.html http://uztest.ru/abstracts/?idabstract=78

Изображение слайда

Решение тригонометрических уравнений — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Проект урока алгебры и начал анализа в 10 классе по теме:

МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЕЧЕРНЯЯ (СМЕННАЯ)
ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 9
ПРИ ИСПРАВИТЕЛЬНОЙ КОЛОНИИ
Проект урока алгебры и начал
анализа в 10 классе по теме:
«Решение
тригонометри
ческих
уравнений».
Учитель математики Васильева Е.В.
Ульяновск, 2011г.

2. Тип урока: 

Тип урока:
Урок изучения и
первичного закрепления
новых знаний

3. Цели урока:

Обучения:
повторить решение простейших тригонометрических
уравнений; научить решать более сложные
тригонометрические уравнения, выделить основные методы
решения.
Развития:
продолжить развитие культуры логического мышления,
памяти, формирование умения работать с проблемной
ситуацией, умений сравнивать, переносить знания в новую
ситуацию, формирование коммуникативной компетенции.
Воспитания:
воспитание активности, желания работать до конца,
содействовать побуждению интереса к математике,
формирование грамотной математической речи.

4. Оборудование

Мультимедиапроектор
Экран
Компьютер
Презентация
Листы-памятки
Листы с заданием
Карточки с дозированной помощью
Таблица «Простейшие тригонометрические уравнения»
Таблица значений углов
Эпиграф: Учиться можно только весело… Чтобы
переваривать
знания, надо поглощать их с аппетитом.
Анатоль Франс

5. Структура урока:

Организационный момент (ознакомление с темой
урока, постановка его целей). (1мин)
Актуализация опорных знаний и умений учащихся
(8 мин):
— самостоятельная работа (3 мин)
— проверка самостоятельной работы (1 мин)
— установите соответствие (3 мин)
— проверка (1 мин)
Изучение нового материала. (22 мин)
Первичный контроль (5 мин)
Самопроверка первичного контроля. (1 мин)
Исторические сведения (2 мин)
Рефлексия. (1 мин)
Учиться можно только
весело…
Чтобы переваривать
знания, надо поглощать
их с аппетитом.
Анатоль Франс
1844 — 1924

7. Тригонометрическими уравнениями обычно называют уравнения, в которых переменная содержится под знаками тригонометрических

I.Актуализация опорных знаний
Тригонометрическими уравнениями обычно
называют уравнения, в которых переменная
содержится под знаками тригонометрических
функций.
К их числу прежде всего относятся
простейшие тригонометрические уравнения, т. е.
уравнения вида sinx=a, cosx=a, tgx=a, где a действительное число.

8. Самостоятельная работа.

1. Каково будет решение
4. Каково будет решение
уравнения cos x = a при а > 1 уравнения sin x = a при а > 1
2. При каком значении а 5. При каком значении а
уравнение cos x = a имеет уравнение sin x = a имеет
решение?
решение?
3. Какой формулой
выражается это решение?
6. Какой формулой
выражается это решение?
7. Какой формулой
выражается решение
уравнения tg x = а?
8. Какой формулой
выражается решение
уравнения сtg x = а?
№
1.
2.
3.
4.
5.
Проверь!
Нет решения
а 1
х arccos a 2 n, n Z
Нет решения
а 1
6.
x 1 arcsin a k , k Z
7.
x arctg a n,
n Z
8.
x arcctg a k ,
k Z
n

10. Установите соответствие:

1
sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = — 1
cos x = 0
2
2 k , k Z
k , k Z
2 k , k Z
2
2
k , k Z
2 k , k Z
2 k , k Z
4
k , k Z

11.

Установите соответствие:1
sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = — 1
cos x = 0
2
2 k , k Z
k , k Z
2 k , k Z
2
2
k , k Z
2 k , k Z
2 k , k Z
4
k , k Z

12. Решение тригонометрических уравнений.

II. Изучение нового материала
Удачи!
sin 4x sin
– sin
2×1 = 0
x
=
cos x = 0
Решение
тригонометрических
уравнений.
Классификация тригонометрических уравнений
по методам решения.
1) Разложение на множители.
(sin x
1
2
)(cos x ) 0
3
5
3 cos 2 x 3 sin x cos x 0
2) Введение новой переменной.
2 sin 2 x 5 sin x 2 0
cos 2 x sin 2 x cos x 0
3) Уравнения сводимые к алгебраическим.
cos 2 x sin 2 x sin x 0,25
3 cos 2x 5 cos x 1
4) Введение вспомогательного аргумента.
sin x
3 cos x 2
2 cos x
2 sin x 1
5) Уравнения, решаемые с помощью формул
сложения.
sin x sin 3x 4 cos 3 x
cos 3x cos 5x sin 4x

14. Решим уравнения (фронтальное решение у доски)

1.Способом разложения на множители:
3 cos 2 x +
3 sin x cos x = 0
2.Способом введения новой переменной:
cos 2 x — sin2 x — cos x = 0
III. Первичный контроль знаний
№1 Решите уравнение, заполнив
пропуски
№2 Выполните замену и решите уравнение:
1
2
(sin x )(cos x ) 0
3
5
2 sin 2 x 5 sin x 2 0
Решение:
sin x
1
0
3
или cos x
sin x ? или
1
x ( 1) arcsin ? или
3
n
Ответ:
?
2
0
5
cos x ?
x arccos? 2 n
sin x y
Решение:
Пусть
, тогда
2? – 5? + 2 = 0
………………………………
……………………………….
………………………………
Ответ: ?

16. Проверь себя и оцени!

Пример 1
Метод разложения на множители
1
2
(sin x )(cos x ) 0
3
5
1
2
sin x или cos x
3
5
1
2
x ( 1) n arcsin n; x arccos( ) 2 n
3
5
Ответ:
1
2
x ( 1) n arcsin n; x arccos( ) 2 n
3
5
Критерии оценивания:
«2» — все задания выполнены неверно
«3» — верно выполнено 1 уравнение
«4» — верно выполнены 1 уравнение и замена во 2
уравнении
«5» — верно выполнено 1 уравнение и правильно решено
2 уравнение.
Пример 2
Метод введения новой переменной
2 sin 2 x 5 sin x 2 0
sin x y
2 y2 5y 2 0
D = b 2 — -4ac = 25 – 16 = 9
y1 2;
sin x 2
y2
1
2
(не имеет решений)
1
2
x ( 1) n
n
6
sin x
Ответ: x ( 1) n
6
n
«ВОЗНИКНОВЕНИЕ
ТРИГОНОМЕТРИИ».
• Тригонометрия математическая
дисциплина изучающая
зависимость между
сторонами и углами
треугольника.
• Тригонометрия — слово
греческое и в буквальном
переводе означает
измерение треугольников.
Возникновение тригонометрии связано с
землемерением, астрономией и строительным
делом.
Тригонометрия возникла из практических
нужд человека. С ее помощью можно
определить расстояние до недоступных
предметов и, вообще существенно упрощать
процесс геодезической съемки местности для
составления географических карт.
• Длительную историю имеет понятие синус.
Фактически различные отношения отрезков
треугольника и окружности встречаются уже в III
веке до н. э. в работах великих математиков
Древней Греции Евклида, Архимеда, Апполония
Пергского. В римский период эти отношения
достаточно систематично исследовались
Менелаем (I век н.э.), хотя и не приобрели
специального названия. Современный синус ,
например, изучался как полухорда, на которую
опирается центральный угол величиной , или как
хорда удвоенной дуги.
Слово косинус намного моложе. Косинус это
сокращение латинского выражения completely
sinus, т. е. “дополнительный синус”.
Тангенсы возникли в связи с решением
задачи об определении длины тени. Тангенс
(а также котангенс) введен в X веке арабским
математиком Абу-ль-Вафой, который
составил и первые таблицы для нахождения
тангенсов и котангенсов.
Рефлексия
•Что нового узнали сегодня на уроке?
•Как вы оцениваете свою работу на уроке?
•Научились ли решать тригонометрические
уравнения способами разложения на множители и
введением новой переменной?
•Какой способ больше понравился?
•Комментирование и выставление оценок.

English     Русский Правила

Простая физика — EASY-PHYSIC

В этой статье будут рассмотрены тригонометрические уравнения с корнями. Прежде чем приступить к решению, вспомним, когда появляется опасность потерять корни или приобрести посторонние. Итак:

При решении тригонометрических уравнений могут появиться посторонние корни, если:

1)      Уравнение содержит тангенс или котангенс;

2)      Обе части уравнения умножаются или делятся на выражение, содержащее неизвестное;

3)      Обе части уравнения возводятся в квадрат.

При решении тригонометрических уравнений могут быть потеряны корни, если:

1)      Обе части уравнения умножаются или делятся на выражение, содержащее неизвестное;

2)      Используются тригонометрические формулы, которые справедливы не при всех значениях неизвестного;

3)      При решении системы тригонометрических уравнений для обозначения целого числа в найденных значениях x и y используется только одна буква.

Теперь можно начать решение.

Задача 1. Решить уравнение:

Возводим обе части уравнения в квадрат:

Разложим формулу , и представим единицу как сумму квадрата синуса и квадрата косинуса:

Сгруппируем слагаемые:

Видим, что в первой скобке – квадрат суммы:

Приравниваем к нулю каждый множитель и решаем два получившихся уравнения:

Первое:

При возведении в квадрат:

Заметим, что по решению синус и косинус равны по модулю, но разные по знаку. В этом варианте решения в исходном уравнении слева под корнем окажется величина отрицательная, значит, это – посторонние корни, поэтому мы даже не будем их записывать. Приобрели мы посторонние корни в результате возведения уравнения  квадрат.

Второе:

Возводим в квадрат:

Снова уравнение распалось на два:

– это посторонний корень, который приведет к появлению в исходном уравнении корня из отрицательного числа в правой части.

или  — данный корень тоже содержит посторонние корни, которые также приобретены в результате возведения уравнения в квадрат. При синусе, равном нулю, косинус может быть равен как 1, так и (-1). Второе – недопустимо: в этом случае в правой части исходного уравнения – отрицательное число под корнем. Поэтому решение у уравнения всего одно: .

 

Задача 2. Решить уравнение:

Возводим обе части уравнения в квадрат:

Косинус двойного аргумента заменяем, также от синуса переходим к косинусу с помощью основного тригонометрического тождества:

Вводим замену:

 

Корни:

Обратная замена:

или

Решения:

Проверка показывает, что все корни удовлетворяют исходному уравнению.

 

Задача 3. Решить уравнение:

Чтобы избавиться от корня, возведем в квадрат:

Домножим на 2 для удобства:

Произведем перегруппировку:

или

Первое:

При возведении в квадрат:

Так как правая часть уравнения должна быть неотрицательной, и, кроме того, синус и косинус – разных знаков, то решение одно:

Второе:

Так как решения уравнения не являются решениями исходного уравнения, то деление на не приведет к потере корней, тогда разделим на :

Решением этого уравнения является угол, синус и косинус которого имеют разные знаки. При этом угол в четвертом квадранте нам не подойдет: у такого угла отрицательный синус и положительный косинус, а это противоречит исходному уравнению: приведет к отрицательному значению операции извлечения корня. Угол во втором квадранте нас устроит.

Ответ: ,

 

Задача 4. Решить уравнение:

Сразу делаем вывод, что полученный нами далее в ходе решения должен быть неположительным , иначе результат извлечения корня не будет положительным.

Возводим все уравнение в квадрат, чтобы избавиться от корня:

Раскрываем формулу двойного аргумента и заменяем синусы на косинусы:

Получили квадратное уравнение относительно косинусов:

или   — очевидно, что решение второго – пустое множество.

С учетом того, что синус должен быть отрицателен (или равен нулю), решение единственное:

Ответ: .

 

Задача 5. Решить уравнение:

Полученный в ходе решения косинус может быть или отрицательным числом, или нулем.

Возводим уравнение в квадрат:

Формулу тройного аргумента раскроем:

или – сумма коэффициентов уравнения равна 0, поэтому первый корень – 1, а второй – с/a – (-1/2)

Итак, имеем: , или , или

Решения первого уравнения:

Решения второго уравнения:

– не являются решениями исходного уравнения, так как косинус должен быть отрицателен.

Решения третьего:

Ответ: ,

 

Задача 6. Решить уравнение:

Замечаем, что синус должен быть неотрицательным числом, так как слева – корень.

Возводим в квадрат:

Раскроем формулу тройного аргумента:

Домножим на 3 для удобства:

Приравняем к нулю оба множителя:

или 

Решаем теперь второе, квадратное, уравнение:

Корни получаются такие: 2/3 и (-3/4) – последний корень не подходит по ОДЗ, так как результат извлечения корня не может быть отрицательным.

Второму корню будет соответствовать решение:

и , эти два решения можно объединить в одно и записать:

Ответ: , .

Решение сложных триггерных уравнений | Purplemath

Easy/Medium

Purplemath

Это можно сделать разными способами, но я думаю, что выберу самый простой. Разделив на косинус, я получу тангенс:

тангенс( х /2) = 1

(Почему это деление нормально? Ну, я не могу делить на ноль, поэтому это деление Это нормально, только если косинус не равен нулю. Но в исходном уравнении синус и косинус были равны, и они никогда не равны нулю в одном и том же месте. И тангенс никогда не равен единице, где косинус равен нулю. в этом случае не было проблемы с делением на ноль, но всегда не забывайте проверять себя, чтобы быть уверенным.)

Содержание продолжается ниже

MathHelp.com

Тангенс равен 1 для

x /2 = 45°, 225° в первом периоде. Но это упражнение требует ответа «в полной общности». Очевидно, я не могу перечислить все значения решения, потому что их бесконечно много. Поэтому мне придется использовать формулу.

Из того, что я знаю о графике касательной, я знаю, что касательная будет равна 1 при 45° через каждые 180°. Эти решения для

tan( x /2) находятся под углами 0° + 45°, 180° + 45°, 360° + 45° и так далее. Чтобы дать ответ «в полной общности», я буду использовать формулу:

x /2 = (180 × n )° + 45°, для всех целых чисел n

Теперь мне нужно найти само x . Я умножу на 2:

x = (360 n )° + 90°

В радианах приведенное выше решение будет

x /2 = π/4, 5π/4, 9π/4 и т. д.; и общее решение будет x = 2π n + π/2

. 1[tan( x ) — 1] = 0

[tan( x ) — 1][3tan 2 ( x ) — 1] = 0

= 1 x tan( 1  или tan 2 ( x ) = 1/3

тангенс ( x ) = 1 или тангенс ( x ) = ±1 / sqrt [3]

Решение первого уравнения в первый период:

x = 45°, 225°

, as:

x = 30°, 150°, 210°, 330°

Чтобы сделать решение «общим», мне нужно сформулировать вышеприведенные решения по формуле, чтобы учесть каждый период.

Первое решение на 45° больше, чем кратное 180°, поэтому (180 n )° + 45° должно подойти. Второе решение на 30° больше, чем кратное 180° и (из-за «плюс/минус») тоже 30° меньше, чем того же кратного, поэтому (180 n )° ± 30° охватит эту часть.

x = (180 n )° ± 30°, (180 n )° + 45° для всех целых чисел n

  • Решите на [0, 2π)

Что за черт. ..?!?

Когда ничего не похоже на то, что это сработает, иногда полезно представить все в терминах синуса и косинуса. Этот процесс, примененный к этому уравнению, дает мне:

Ненамного лучше… но первые два члена имеют общий множитель 2. Если я приведу последний член к общему знаменателю с третьим членом, что это мне даст?

Если я разложу 2 из первых двух членов и квадратный корень из 3 и косинус из вторых двух членов, я получу:

Теперь я могу взять общий множитель впереди:

Ух ты! Это действительно сработало! Хорошо, теперь мне нужно решить факторы. Первый фактор решает как:

Это уравнение верно при x = 60° и, в силу симметрии касательной, также при x = 180° + 60° = 240°. В радианах это

.

Второй множитель решается как:

Косинус принимает это значение при x = 30° и, в силу симметрии кривой косинуса, также при x = 360° — 30° = 330°. В радианах это

. Итак, мое решение:

Натуральный логарифм (ну, любой логарифм ) равен нулю, когда аргумент равен 1, поэтому это дает мне:

2 − sin 2 ( x ) = 1

1 − 5 sin 29000 ( x ) = 0

(1 − sin( x ))(1 + sin( x )) = 0

1 = sin( x ) или 1 = −sin ( )

Из того, что я знаю о синусоиде, мое решение:

x = 90°, 270°

По природе логарифмов эквивалентное показательное уравнение:

Синус принимает это значение при

, а также при . Тогда мое решение:

Предполагается, что для решения некоторых тригонометрических уравнений потребуется факторизация (особенно квадратичная), а также предполагается, что потребуется использовать тригонометрические тождества. Не бойтесь пробовать разные методы; иногда ваш первый порыв ни к чему не приводит, но вторая догадка может сработать. И обратите особое внимание на любые необычайно сложные примеры в вашем учебнике, так как они могут содержать подсказки о том, какие приемы вам понадобятся, особенно на следующем тесте.

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении тригонометрических уравнений. Попробуйте введенное упражнение или введите свое собственное упражнение. (Если вам не велят решать «в полном объеме», не забудьте включить интервал, как показано ниже.) Затем нажмите кнопку и для достижения наилучших результатов выберите «Решить за интервал», чтобы сравнить свой ответ с ответом Mathway.

Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.

Примечание. Решатель может предоставить только «точные» решения, а иногда и вообще любое решение, если вы находитесь в радианах. Используйте степени на свой страх и риск!

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления. ) 1

Как решить уравнение тригея, которое имеет несколько функций тригонометрии

: Мэри Джейн Стерлинг и

Обновлен: 03-26-2016

ТРИГОНЕТРИЯ Некоторые уравнения тригонометрии содержат более одной тригонометрической функции. Другие имеют смеси нескольких углов и одиночных углов с одной и той же переменной. Некоторые примеры таких уравнений включают 3cos
2 x = SIN 2 x , 2SEC x = TAN x + COT x , COS 2 x + COS x , COS 2 x + COS x , COS 2 x + COS x , COS 2 x + COS . потому что х = 1/2.

Чтобы привести эти уравнения в более удобную форму, чтобы вы могли использовать факторинг или другой метод для их решения, вы используете тождества для замены некоторых или всех терминов. Например, чтобы решить 3cos 2 x = sin 2 x для всех углов между 0 и 2π, примените тождество Пифагора.

  1. Replace the term sin 2 x with its equivalent from the Pythagorean identity, sin 2 x + cos 2 x = 1 or sin 2 x = 1 – cos 2 х .

    3cos 2 x = 1 – cos 2 x

  2. Добавить cos 2 x в каждую сторону и упростите путем деления.

  3. Извлеките квадратный корень из каждой стороны.

  4. Найдите значения x , удовлетворяющие уравнению.

В следующем примере вы начинаете с трех различных триггерных функций. Хорошая тактика состоит в том, чтобы заменить каждую функцию, используя тождество соотношения или взаимное тождество. Использование этих тождеств создает дроби, а дроби требуют общих знаменателей.

Между прочим, наличие дробей в уравнениях триггера хорошо , потому что произведения, полученные в результате умножения и создания эквивалентных дробей, обычно являются частями тождеств, которые затем можно подставить, чтобы сделать выражение намного проще. Решите 2sec x = tan x + cot x для всех возможных решений в градусах.

  1. Замените каждый термин его соответствующим обратным или пропорциональным тождеством.

  2. Перепишите дроби с общим знаменателем sin x cos x .

    Умножьте каждый член на дробь, равную 1, с синусом или косинусом как в числителе, так и в знаменателе.

  3. Сложите две дроби справа. Затем, используя тождество Пифагора, замените новый числитель на 1.

  4. Установите уравнение равным 0, вычитая правый член с каждой стороны.

  5. Теперь установите числитель равным 0.

    Если числитель равен 0, то вся дробь равна 0. Нельзя допускать, чтобы знаменатель был равен 0 — такого числа не существует.

  6. Найдите значения x , которые удовлетворяют исходному уравнению.

В следующем примере задействованы два разных угла. Один угол в два раза больше другого, поэтому вы используете тождество двойного угла, чтобы свести термины к функциям только одного угла. Хитрость заключается в том, чтобы выбрать правильную версию тождества косинуса двойного угла.

Решите cos 2 x + cos x + 1 = 0 для x между 0 и 2 p .

  1. Заменить cos 2 x на 2 cos 2 x – 1.

    2cos 2 x – 1 + cos x + 1 = 0

    Эта версия тождества косинуса и двойного угла предпочтительнее, потому что другая триггерная функция в уравнении уже содержит косинус.

  2. Упростите уравнение. Затем вычтите cos х .

  3. Установить каждый коэффициент равным 0.

  4. Найдите значения x , которые удовлетворяют исходному уравнению.

Последний пример может показаться обманчиво простым. Загвоздка в том, что вы должны заранее распознать двойную идентичность и быстро переключиться.

  1. Используйте тождество синуса двойного угла, чтобы создать замену для выражения слева.

    Начав с тождества и умножив каждую сторону на 1/2, вы получите

  2. Замените выражение слева от исходного уравнения его эквивалентом из тождества двойного угла.

  3. Умножьте каждую часть уравнения на 2.

  4. Перепишите выражение как обратную функцию.

    2 x = sin –1 (1)

  5. Определите, какие углы в пределах двух оборотов удовлетворяют выражению.

    2 х = грех –1 (1) = 90°, 450°

    Вы используете два поворота, потому что коэффициент x равен 2.

  6. Разделите каждое слагаемое на 2.

    Обратите внимание, что результирующие углы находятся в диапазоне от 0 до 360 градусов.

Вы можете обобщить метод двойного угла из приведенного выше примера для других выражений с несколькими углами.

Эту статью можно найти в категории:

  • Тригонометрия ,

9.

5 Решение тригонометрических уравнений — алгебра и тригонометрия

Цели обучения

В этом разделе вы:
  • Решение линейных тригонометрических уравнений относительно синуса и косинуса.
  • Решите уравнения с одной тригонометрической функцией.
  • Решите тригонометрические уравнения с помощью калькулятора.
  • Решение тригонометрических уравнений квадратной формы.
  • Решите тригонометрические уравнения, используя фундаментальные тождества.
  • Решите тригонометрические уравнения с несколькими углами.
  • Решите задачи на прямоугольный треугольник.

Рисунок 1 Египетские пирамиды стоят рядом с современным городом. (кредит: Oisin Mulvihill)

Фалес Милетский (около 625–547 гг. до н. э.) известен как основатель геометрии. Легенда гласит, что он рассчитал высоту Великой пирамиды в Гизе в Египте, используя теорию подобных треугольников , которую он разработал, измерив тень своего посоха. Основанная на пропорциях, эта теория находит применение в ряде областей, включая фрактальную геометрию, инженерию и архитектуру. Часто угол возвышения и угол наклона находят с помощью подобных треугольников.

В предыдущих разделах этой главы мы рассмотрели тригонометрические тождества. Тождества верны для всех значений в домене переменной. В этом разделе мы начинаем изучение тригонометрических уравнений для изучения реальных сценариев, таких как определение размеров пирамид.

Решение линейных тригонометрических уравнений с помощью синуса и косинуса

Тригонометрические уравнения — это, как следует из названия, уравнения, включающие тригонометрические функции. Во многом подобно решению полиномиальных уравнений или рациональных уравнений, только определенные значения переменной будут решениями, если решения вообще есть. Часто мы будем решать тригонометрическое уравнение на заданном интервале. Однако столь же часто нас будут просить найти все возможные решения, а поскольку тригонометрические функции являются периодическими, решения повторяются в каждом периоде. Другими словами, тригонометрические уравнения могут иметь бесконечное число решений. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предположим, что какое-либо решение является допустимым. Период как функции синуса, так и функции косинуса равен 2π,2π. Другими словами, через каждые 2π2π единиц y- значения повторяются. Если нам нужно найти все возможные решения, то мы должны добавить   2πk,  2πk, где   k    k   — целое число, к исходному решению. Вспомним правило, дающее формат для формулировки всех возможных решений функции с периодом 2π:2π:

sinθ=sin(θ±2kπ)sinθ=sin(θ±2kπ)

возможные решения для других тригонометрических функций. Решение тригонометрических уравнений требует тех же методов, что и решение алгебраических уравнений. Читаем уравнение слева направо, по горизонтали, как предложение. Мы ищем известные шаблоны, факторизуем, находим общие знаменатели и заменяем определенные выражения переменной, чтобы упростить процесс решения. Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.

Пример 1

Решение линейного тригонометрического уравнения с функцией косинуса

Найдите все возможные точные решения уравнения cosθ=12.cosθ=12.

Решение

Из единичного круга мы знаем, что

cosθ=12θ=π3,5π3cosθ=12θ=π3,5π3

Это решения в интервале [0,2π].[0,2π]. Все возможные решения задаются формулами

θ=π3±2kπ и θ=5π3±2kπθ=π3±2kπ и θ=5π3±2kπ

, где kk — целое число.

Пример 2

Решение линейного уравнения с функцией синуса

Найдите все возможные точные решения уравнения sint=12.sint=12.

Решение

Решение для всех возможных значений t означает, что решения включают углы вне периода 2π,2π. Из рисунка 2 видно, что решения имеют вид t=π6t=π6 и t=5π6.t=5π6. Но проблема заключается в том, чтобы указать все возможные значения, которые решают уравнение. Поэтому ответ

t=π6±2πk и t=5π6±2πkt=π6±2πk и t=5π6±2πk

, где kk — целое число.

Как

Дано тригонометрическое уравнение, решить с помощью алгебры .

  1. Ищите шаблон, который предполагает алгебраическое свойство, такое как разность квадратов или факторинговая возможность.
  2. Замените тригонометрическое выражение одной переменной, например xx или u.u.
  3. Решите уравнение так же, как решали бы алгебраическое уравнение.
  4. Замените тригонометрическое выражение на переменную в результирующих выражениях.
  5. Найдите угол.

Пример 3

Решение линейного тригонометрического уравнения

Точное решение уравнения: 2cosθ−3=−5,0≤θ<2π. 2cosθ−3=−5,0≤θ<2π.

Решение

Используйте алгебраические методы для решения уравнения.

2cosθ−3=−52cosθ=−2cosθ=−1θ=π2cosθ−3=−52cosθ=−2cosθ=−1θ=π

Попытайся #1

Точно решить следующее линейное уравнение на отрезке [0,2π):2sinx+1=0.[0,2π):2sinx+1=0.

Решение уравнений с одной тригонометрической функцией

Когда нам даны уравнения, включающие только одну из шести тригонометрических функций, их решения включают использование алгебраических методов и единичной окружности (см. рис. 2). Нам нужно сделать несколько соображений, когда уравнение включает тригонометрические функции, отличные от синуса и косинуса. Проблемы, связанные с обратными величинами основных тригонометрических функций, необходимо рассматривать с алгебраической точки зрения. Другими словами, мы напишем обратную функцию и найдем углы, используя эту функцию. Кроме того, уравнение, включающее функцию тангенса, немного отличается от уравнения, содержащего функцию синуса или косинуса. Во-первых, как мы знаем, период касательной равен   π,  π, а не  2π. 2π. Далее, областью определения тангенса являются все действительные числа, за исключением нечетных целых чисел, кратных π2,π2, если, конечно, проблема не накладывает свои ограничения на область определения.

Пример 4

Решение задачи с одной тригонометрической функцией

Точно решить задачу: 2sin2θ−1=0,0≤θ<2π.2sin2θ−1=0,0≤θ<2π.

Решение

Так как эту задачу нелегко решить, мы будем решать ее с помощью свойства квадратного корня. Во-первых, мы используем алгебру, чтобы изолировать sinθ.sinθ. Потом найдем углы.

2sin2θ−1=0 2sin2θ=1sin2θ=12sin2θ=±12sinθ=±12=±22θ=π4,3π4,5π4,7π42sin2θ−1=0 2sin2θ=1sin2θ=12sin2θ=±12sinθ=±12=±4,22 3π4,5π4,7π4

Пример 5

Решение тригонометрического уравнения с косекансом

Точно решить следующее уравнение: cscθ=−2,0≤θ<4π.cscθ=−2,0≤θ<4π.

Решение

Нам нужны все значения θθ, для которых cscθ=−2cscθ=−2 в интервале 0≤θ<4π.0≤θ<4π.

cscθ=−21sinθ=−2sinθ=−12θ=7π6,11π6,19π6,23π6cscθ=−21sinθ=−2sinθ=−12θ=7π6,11π6,19π6,23π6

Анализ

Поскольку sinθ=−12,sinθ=−12, обратите внимание, что все четыре решения находятся в третьем и четвертом квадрантах.

Пример 6

Решение уравнения с касательной

Точно решить уравнение: tan(θ−π2)=1,0≤θ<2π.tan(θ−π2)=1,0≤θ<2π.

Решение

Напомним, что функция тангенса имеет период π,π. На интервале [0,π),[0,π) и под углом π4,π4 тангенс имеет значение 1. Однако искомый угол равен (θ−π2).(θ−π2) . Таким образом, если tan(π4)=1,tan(π4)=1, то

θ−π2=π4θ=3π4±kπθ−π2=π4θ=3π4±kπ

На интервале [0,2π),[0 ,2π), имеем два решения:

θ=3π4 и θ=3π4+π=7π4θ=3π4 и θ=3π4+π=7π4

Попытайся #2

Найдите все решения для tanx=3. tanx=3.

Пример 7

Найти все решения уравнения с касательной

Найти все точные решения уравнения 2(tanx+3)=5+tanx,0≤x<2π.2(tanx+3)=5+tanx,0≤x <2π.

Решение

Мы можем решить это уравнение, используя только алгебру. Изолируйте выражение tanxtanx слева от знака равенства.

2(tanx)+2(3)=5+tanx2tanx+6=5+tanx 2tanx-tanx=5−6tanx=-12(tanx)+2(3)=5+tanx2tanx+6=5+tanx2tanx −tanx=5−6tanx=−1

На единичной окружности есть два угла, тангенс которых равен −1: θ=3π4−1: θ=3π4 и θ=7π4.θ=7π4.

Решение тригонометрических уравнений с помощью калькулятора

Не все функции можно решить точно, используя только единичный круг. Когда мы должны решить уравнение, включающее угол, отличный от одного из специальных углов, нам нужно будет использовать калькулятор. Убедитесь, что он установлен в правильном режиме, либо в градусах, либо в радианах, в зависимости от критериев данной задачи.

Пример 8

Использование калькулятора для решения тригонометрического уравнения с синусом

Используйте калькулятор для решения уравнения sinθ=0,8,sinθ=0,8, где   θ    θ  в радианах.

Решение

Убедитесь, что режим установлен в радианах. Чтобы найти θ, θ, используйте функцию обратного синуса. На большинстве калькуляторов вам потребуется нажать кнопку 2 ND , а затем кнопку SIN, чтобы вызвать функцию sin-1sin-1. На экране отображается sin-1(.sin-1(. Калькулятор готов к вводу в скобках. Для этой задачи мы вводим sin-1(0.8),sin-1(0.8) и нажимаем ENTER Таким образом, до четырех знаков после запятой,

SIN -1 (0,8) ≈0,9273SIN -1 (0,8) ≈0,9273

Решение составляет

θдоля 0,9273 ± 2πkθ≈0,9273 ± 2πk

Измерение угла в градусах равно

θ. 180°−53,1°≈126,9°θ≈53,1°θ≈180°−53,1°≈126,9°

Анализ

Обратите внимание, что калькулятор возвращает только угол в квадрантах I или IV для функции синуса, так как это диапазон обратного синуса. Другой угол получается с помощью π−θ.π−θ. Таким образом, дополнительное решение равно ≈2,2143±2πk≈2,2143±2πk

Пример 9

Использование калькулятора для решения тригонометрического уравнения с секущей

Используйте калькулятор для решения уравнения secθ=−4,secθ=−4, давая ответ в радианах.

Решение

Мы можем начать с алгебры.

secθ=−41cosθ=−4cosθ=−14secθ=−41cosθ=−4cosθ=−14

Убедитесь, что MODE указан в радианах. Теперь используйте функцию арккосинуса.

cos−1(−14)≈1,8235θ≈1,8235+2πkcos−1(−14)≈1,8235θ≈1,8235+2πk

Поскольку π2≈1,57π2≈1,57 и π≈3,14, π≈3,14, 1,8235 находится между этими двумя числами, таким образом, θ≈1,8235  θ≈1,8235  находится в квадранте II. Косинус также отрицателен в квадранте III. Обратите внимание, что калькулятор будет возвращать только угол в квадрантах I или II для функции косинуса, так как это диапазон арккосинуса. См. рис. 2.

Рис. 2

Итак, нам также нужно найти меру угла в третьем квадранте. В квадранте II опорный угол равен θ​’≈π−1,8235≈1,3181. θ​’≈π−1,8235≈1,3181. Другое решение в квадранте III равно θ​’≈π+1,3181≈4,459.7.θ​’≈π+1,3181≈4,4597.

Решения равны θ≈1,8235±2πkθ≈1,8235±2πk и θ≈4,4597±2πk.θ≈4,4597±2πk.

Попытайся #3

Решите cosθ=-0,2.cosθ=-0,2.

Решение тригонометрических уравнений в квадратичной форме

Решение квадратного уравнения может быть более сложным, но опять же, мы можем использовать алгебру, как и для любого квадратного уравнения. Посмотрите на схему уравнения. Есть ли в уравнении более одной тригонометрической функции или только одна? Какая тригонометрическая функция является квадратом? Если представлена ​​только одна функция и один из ее членов возведен в квадрат, подумайте о стандартной форме квадратного числа. Замените тригонометрическую функцию переменной, такой как xx или u.u. Если подстановка делает уравнение похожим на квадратное уравнение, то мы можем использовать те же методы решения квадратного уравнения для решения тригонометрических уравнений.

Пример 10

Решение тригонометрического уравнения в квадратной форме

Точно решить уравнение: cos2θ+3cosθ−1=0,0≤θ<2π.cos2θ+3cosθ−1=0,0≤θ<2π.

Решение

Начнем с подстановки и замены cos θθ на x.x. Нет необходимости использовать подстановку, но это может облегчить визуальное решение проблемы. Пусть cosθ=x.cosθ=x. У нас есть

x2+3x−1=0x2+3x−1=0

Уравнение нельзя разложить на множители, поэтому мы будем использовать квадратичную формулу x=−b±b2−4ac2a.x=−b±b2−4ac2a.

х=-3±(-3)2-4(1)(-1)2=-3±132x=-3±(-3)2-4(1)(-1)2=-3± 132

Замените xx на cosθ,cosθ и решите.

cosθ=-3±132θ=cos-1(-3+132)cosθ=-3±132θ=cos-1(-3+132)

Обратите внимание, что используется только знак +. Это связано с тем, что мы получаем ошибку, когда решаем θ=cos−1(−3−132)θ=cos−1(−3−132) на калькуляторе, поскольку область определения функции арккосинуса равна [−1,1 ].[−1,1]. Однако есть и второе решение:

θ=cos−1(−3+132)≈1,26θ=cos−1(−3+132)≈1,26

Эта крайняя сторона угла лежит в квадранте I. Поскольку косинус также положителен в квадранте IV, второе решение равно

θ=2π−cos−1(−3+132)≈ 5,02θ=2π−cos−1(−3+132)≈ 5,02

Пример 11

Решение тригонометрического уравнения в квадратной форме с помощью факторизации

Точно решить уравнение: 2sin2θ−5sinθ+3=0,0≤θ≤2π.2sin2θ−5sinθ+3=0,0≤θ≤2π.

Решение

С помощью группировки этот квадрат можно разложить на множители. Либо сделайте реальную замену, sinθ=u,sinθ=u, либо вообразите ее, помножив на множители: (2sinθ−3)(sinθ−1)=0

Теперь установите каждый коэффициент равным нулю.

2sinθ−3=02sinθ=3sinθ=32sinθ−1=0sinθ=12sinθ−3=02sinθ=3sinθ=32sinθ−1=0sinθ=1 диапазон функции синуса [−1,1].[−1,1]. Однако sinθ=1,sinθ=1, что дает решение θ=π2.θ=π2.

Анализ

Обязательно проверьте все решения в данной области, так как некоторые факторы не имеют решения.

Попытайся #4

Решение sin2θ=2cosθ+2,0≤θ≤2π. sin2θ=2cosθ+2,0≤θ≤2π. [Подсказка: сделайте замену, чтобы выразить уравнение только через косинус.]

Пример 12

Решение тригонометрического уравнения с помощью алгебры

Точное решение:

2sin2θ+sinθ=0;0≤θ<2π2sin2θ+sinθ=0;0≤θ<2π

Решение

Эта задача должна показаться знакомой, так как она похожа на квадратичную. Пусть sinθ=x.sinθ=x. Уравнение принимает вид 2×2+x=0,2×2+x=0. Начнем с факторизации:

2×2+x=0x(2x+1)=02×2+x=0x(2x+1)=0

Приравняем каждый множитель к нулю.

х=0(2х+1)=0х=-12х=0(2х+1)=0х=-12

Затем снова подставьте в уравнение исходное выражение sinθsinθ для x.x. Таким образом,

sinθ=0θ=0,πsinθ=−12θ=7π6,11π6sinθ=0θ=0,πsinθ=−12θ=7π6,11π6

Решения в области 0≤θ<2π0≤θ<2π равны θ= 0,π,7π6,11π6.θ=0,π,7π6,11π6.

Если мы предпочитаем не заменять, мы можем решить уравнение, следуя той же схеме разложения на множители и приравняв каждый множитель к нулю.

2sin2θ+sinθ=0sinθ(2sinθ+1)=0sinθ=0θ=0,π2sinθ+1=02sinθ=−1sinθ=−12θ=7π6,11π62sin2θ+sinθ=0sinθ(2sinθ+1)=0sinθ=0,=0θ=0,=0θ=0sinθ π2sinθ+1=02sinθ=−1sinθ=−12θ=7π6,11π6

Анализ

Мы можем видеть решения на графике на рисунке 3. На интервале 0≤θ<2π,0≤θ<2π график пересекает ось x- четыре раза, в отмеченных решениях. Обратите внимание, что тригонометрические уравнения в квадратной форме могут давать до четырех решений вместо ожидаемых двух, которые можно найти с помощью квадратных уравнений. В этом примере каждое решение (угол), соответствующее положительному значению синуса, даст два угла, которые дадут это значение.

Рисунок 3

Мы также можем проверить решения на единичной окружности на рис. 2.

Пример 13

Решение квадратного тригонометрического уравнения в форме

Точно решить квадратное уравнение в форме: 2sin2θ−3sinθ+1=0,0≤θ<2π.2sin2θ−3sinθ+1=0,0≤θ<2π.

Решение

Мы можем факторизовать, используя группировку. Значения решения θθ можно найти на единичной окружности.

(2sinθ−1)(sinθ−1)=0 2sinθ−1=0sinθ=12θ=π6,5π6sinθ=1θ=π2(2sinθ−1)(sinθ−1)=0 2sinθ−1=0sinθ=12θ=π6 ,5π6sinθ=1θ=π2

Попытайся #5

Решите квадратное уравнение 2cos2θ+cosθ=0,2cos2θ+cosθ=0.

Решение тригонометрических уравнений с использованием фундаментальных тождеств

Хотя алгебру можно использовать для решения ряда тригонометрических уравнений, мы также можем использовать фундаментальные тождества, поскольку они упрощают решение уравнений. Помните, что методы, которые мы используем для решения, отличаются от методов проверки личности. Здесь применяются основные правила алгебры, в отличие от переписывания одной стороны тождества, чтобы она соответствовала другой стороне. В следующем примере мы используем два тождества для упрощения уравнения.

Пример 14

Использование тождеств для решения уравнения

Использование тождеств для точного решения тригонометрического уравнения в интервале 0≤x<2π,0≤x<2π.

cosxcos(2x)+sinxsin(2x)=32cosxcos(2x)+sinxsin(2x)=32

Решение

Обратите внимание, что левая часть уравнения представляет собой формулу разности для косинуса.

cosxcos(2x)+sinxsin(2x)=32cos(x−2x)=32Формула разности для cosinecos(−x)=32Используй тождество отрицательного угла.cosx=32cosxcos(2x)+sinxsin(2x)=32cos(x− 2x)=32Формула разности для cosinecos(−x)=32Использование отрицательного угла Identity.cosx=32

Из единичного круга на рисунке 2 видно, что cosx=32cosx=32, когда x=π6,11π6.x=π6,11π6.

Пример 15

Решение уравнения с помощью формулы двойного угла

Точно решить уравнение с помощью формулы двойного угла: cos(2θ)=cosθ.cos(2θ)=cosθ.

Решение

У нас есть три варианта выражения для замены двойного угла косинуса. Поскольку проще решать одну тригонометрическую функцию за раз, мы выберем тождество двойного угла, включающее только косинус:

cos(2θ)=cosθ2cos2θ−1=cosθ2cos2θ−cosθ−1=0(2cosθ+1)(cosθ−1)=02cosθ+1=0cosθ=−12cosθ−1=0cosθ=1cos(2θ)=cosθ2cos2θ−1 =cosθ2cos2θ−cosθ−1=0(2cosθ+1)(cosθ−1)=02cosθ+1=0cosθ=−12cosθ−1=0cosθ=1

Итак, если cosθ=−12,cosθ=−12, то θ =2π3±2πkθ=2π3±2πk и θ=4π3±2πk;θ=4π3±2πk; если cosθ=1,cosθ=1, то θ=0±2πk.θ=0±2πk.

Пример 16

Решение уравнения с помощью тождества

Точно решить уравнение с использованием тождества: 3cosθ+3=2sin2θ,0≤θ<2π.3cosθ+3=2sin2θ,0≤θ<2π.

Решение

Если мы перепишем правую часть, мы можем записать уравнение в терминах косинуса: 1)(cosθ+1)=02cosθ+1=0cosθ=−12θ=2π3,4π3cosθ+1=0cosθ=−1θ=π3cosθ+3=2sin2θ3cosθ+3=2(1−cos2θ)3cosθ+3=2−2cos2θ2cos2θ+ 3cosθ+1=0(2cosθ+1)(cosθ+1)=02cosθ+1=0cosθ=−12θ=2π3,4π3cosθ+1=0cosθ=−1θ=π

Наши решения равны θ=2π3,4π3,π. θ=2π3,4π3,π.

Решение тригонометрических уравнений с несколькими углами

Иногда невозможно решить тригонометрическое уравнение с тождествами, имеющими кратные углы, например sin(2x)sin(2x) или cos(3x).cos(3x). Столкнувшись с этими уравнениями, вспомните, что y=sin(2x)y=sin(2x) — это горизонтальное сжатие в 2 раза функции y=sinx.y=sinx. На интервале 2π,2π мы можем изобразить два периода y=sin(2x),y=sin(2x), а не один цикл y=sinx.y=sinx. Это сжатие графика приводит нас к мысли, что 9 может быть в два раза больше.0526 x — перехваты или решения для sin(2x)=0sin(2x)=0 по сравнению с sinx=0.sinx=0. Эта информация поможет нам решить уравнение.

Пример 17

Решение тригонометрического уравнения с несколькими углами

Точно решить: cos(2x)=12cos(2x)=12 на [0,2π).[0,2π).

Решение

Мы видим, что это уравнение является стандартным уравнением с кратным углу. Если cos(α)=12,cos(α)=12, мы знаем, что αα находится в квадрантах I и IV. Хотя θ=cos-112θ=cos-112 даст решения только в квадрантах I и II, мы понимаем, что решения уравнения cosθ=12cosθ=12 будут в квадрантах I и IV.

Следовательно, возможные углы равны θ=π3θ=π3 и θ=5π3.θ=5π3. Итак, 2x=π32x=π3 или 2x=5π3,2x=5π3, значит, x=π6x=π6 или x=5π6.x=5π6. Имеет ли это смысл? Да, потому что cos(2(π6))=cos(π3)=12.cos(2(π6))=cos(π3)=12.

Возможны ли другие ответы? Вернемся к нашему первому шагу.

В квадранте I 2x=π3,2x=π3, так что x=π6x=π6, как уже отмечалось. Давайте снова вернемся по кругу:

2x=π3+2π=π3+6π3=7π32x=π3+2π=π3+6π3=7π3

, значит, x=7π6.x=7π6.

Еще одно вращение дает

2x=π3+4π=π3+12π3=13π32x=π3+4π=π3+12π3=13π3

x=13π6>2π,x=13π6>2π, поэтому это значение для xx больше, чем 2π,2π, так что это не решение на [0,2π).[0,2π).

В квадранте IV 2x=5π3,2x=5π3, значит, x=5π6x=5π6, как уже отмечалось. Давайте снова вращаемся по кругу:

2x=5π3+2π=5π3+6π3=11π32x=5π3+2π=5π3+6π3=11π3

, значит, x=11π6. x=11π6.

Еще одно вращение дает

2x=5π3+4π=5π3+12π3=17π32x=5π3+4π=5π3+12π3=17π3

x=17π6>2π,x=17π6>2π, так что это значение для xx больше, чем 2π,2π, поэтому это не решение на [0,2π).[0,2π).

Наши решения: x=π6,5π6,7π6, и 11π6x=π6,5π6,7π6, и 11π6. Обратите внимание, что всякий раз, когда мы решаем задачу в виде sin(nx)=c,sin(nx)=c, мы должны пройти единичный круг nn раз.

Решение задач на прямоугольный треугольник

Теперь мы можем использовать все изученные нами методы для решения задач, связанных со свойствами прямоугольных треугольников и теоремой Пифагора. Мы начинаем со знакомой теоремы Пифагора, a2+b2=c2,a2+b2=c2, и моделируем уравнение, соответствующее ситуации.

Пример 18

Использование теоремы Пифагора для моделирования уравнения

Использование теоремы Пифагора и свойств прямоугольных треугольников для моделирования уравнения, соответствующего задаче.

Необходимо заменить один из тросов, которыми колесо обозрения London Eye крепится к земле. Центр колеса обозрения находится на высоте 69,5 метров над землей, а второй якорь на земле — в 23 метрах от основания колеса обозрения. Приблизительно какой длины кабель и каков угол подъема (от земли до центра колеса обозрения)? См. рис. 4.

Рисунок 4

Решение

Используя предоставленную информацию, мы можем нарисовать прямоугольный треугольник. Длину кабеля можно найти по теореме Пифагора.

a2+b2=c2(23)2+(69,5)2≈53595359≈73,2 ma2+b2=c2(23)2+(69,5)2≈53595359≈73,2 м

Угол места θ,θ, образован вторым анкером на земле и кабелем, доходящим до центра колеса. Мы можем использовать функцию тангенса, чтобы найти его меру. Округлить до двух знаков после запятой.

tanθ=69,523tan−1(69,523)≈1,2522≈71,69°tanθ=69,523tan−1(69,523)≈1,2522≈71,69°

Угол возвышения приблизительно 71,7°, 71,7°, длина кабеля составляет 73,2 метра.

Пример 19

Использование теоремы Пифагора для моделирования абстрактной задачи

Правила техники безопасности OSHA требуют, чтобы основание лестницы располагалось на расстоянии 1 фута от стены на каждые 4 фута длины лестницы. Найдите угол, под которым лестница любой длины образует землю, и высоту, на которой лестница касается стены.

Решение

Для любой длины лестницы основание должно находиться на расстоянии от стены, равном одной четвертой длины лестницы. Эквивалентно, если основание лестницы находится на расстоянии « а» на расстоянии футов от стены, длина лестницы будет равна 4 а футов. См. рис. 5.

Рис. 5

Сторона, примыкающая к θθ, равна a , а гипотенуза равна 4a.4a. Таким образом,

cosθ=a4a=14cos−1(14)≈75,5°cosθ=a4a=14cos−1(14)≈75,5°

Возвышение лестницы образует с землей угол 75,5°75,5°. Высоту, на которой лестница касается стены, можно найти с помощью теоремы Пифагора:

a2+b2=(4a)2b2=(4a)2−a2b2=16a2−a2b2=15a2b=a15a2+b2=(4a)2b2=(4a)2−a2b2=16a2−a2b2=15a2b=a15

Таким образом , лестница касается стены на расстоянии a15a15 футов от земли.

9.5 Секционные упражнения

Вербальный

1.

Всегда ли будут решения уравнений тригонометрических функций? Если нет, опишите уравнение, которое не имеет решения. Объясните, почему да или почему нет.

2.

Всегда ли при решении тригонометрического уравнения, включающего более одной тригонометрической функции, мы пытаемся переписать уравнение, чтобы оно выражалось в терминах одной тригонометрической функции? Почему или почему нет?

3.

При решении линейных триггерных уравнений только с помощью синуса или косинуса, как мы узнаем, будут ли решения?

Алгебраический

Для следующих упражнений найдите все решения точно на интервале 0≤θ<2π.0≤θ<2π.

4.

2sinθ=−22sinθ=−2

5.

2sinθ=32sinθ=3

6.

2cosθ=12cosθ=1

7.

2cosθ=−22cosθ=−2

8.

тангенс θ=-1тангенс θ=-1

9.

тангенс=1тангенс=1

10.

котх+1=0котх+1=0

11.

4sin2x−2=04sin2x−2=0

12.

csc2x-4=0csc2x-4=0

Для следующих упражнений решите точно на [0,2π).[0,2π).

13.

2cosθ=22cosθ=2

14.

2cosθ=−12cosθ=−1

15.

2sinθ=−12sinθ=−1

16.

2sinθ=−32sinθ=−3

17.

2sin(3θ)=12sin(3θ)=1

18.

2sin(2θ)=32sin(2θ)=3

19.

2cos(3θ)=−22cos(3θ)=−2

20.

cos(2θ)=−32cos(2θ)=−32

21.

2sin(πθ)=12sin(πθ)=1

22.

2cos(π5θ)=32cos(π5θ)=3

Для следующих упражнений найдите все точные решения на [0,2π).[0,2π).

23.

сек(х)sin(x)−2sin(x)=0сек(x)sin(x)−2sin(x)=0

24.

tan(x)−2sin(x)tan(x)=0tan(x)−2sin(x)tan(x)=0

25.

2cos2t+cos(t)=12cos2t+cos(t)=1

26.

2tan2(t)=3сек(t)2tan2(t)=3сек(t)

27.

2sin(x)cos(x)−sin(x)+2cos(x)−1=02sin(x)cos(x)−sin(x)+2cos(x)−1=0

28.

cos2θ=12cos2θ=12

29.

сек2х=1сек2х=1

30.

tan2(x)=-1+2tan(-x)tan2(x)=-1+2tan(-x)

31.

8sin2(x)+6sin(x)+1=08sin2(x)+6sin(x)+1=0

32.

tan5(x)=tan(x)tan5(x)=tan(x)

Для следующих упражнений решите методами, показанными в этом разделе, точно на интервале [0,2π).[0,2π).

33.

sin(3x)cos(6x)−cos(3x)sin(6x)=−0,9sin(3x)cos(6x)−cos(3x)sin(6x)=−0,9

34.

sin(6x)cos(11x)−cos(6x)sin(11x)=−0,1sin(6x)cos(11x)−cos(6x)sin(11x)=−0,1

35.

cos(2x)cosx+sin(2x)sinx=1cos(2x)cosx+sin(2x)sinx=1

36.

6sin(2t)+9sint=06sin(2t)+9sint=0

37.

9cos(2θ)=9cos2θ−49cos(2θ)=9cos2θ−4

38.

sin(2t)=costsin(2t)=стоимость

39.

cos(2t)=sintcos(2t)=sint

40.

cos(6x)−cos(3x)=0cos(6x)−cos(3x)=0

Для следующих упражнений решите точно на интервале [0,2π).[0,2π). Используйте квадратичную формулу, если уравнения не учитывают.

41.

tan2x-3tanx=0tan2x-3tanx=0

42.

sin2x+sinx-2=0sin2x+sinx-2=0

43.

sin2x-2sinx-4=0sin2x-2sinx-4=0

44.

5cos2x+3cosx-1=05cos2x+3cosx-1=0

45.

3cos2x-2cosx-2=03cos2x-2cosx-2=0

46.

5sin2x+2sinx-1=05sin2x+2sinx-1=0

47.

tan2x+5tanx-1=0tan2x+5tanx-1=0

48.

cot2x=-cotxcot2x=-cotx

49.

−tan2x−tanx−2=0−tan2x−tanx−2=0

Для следующих упражнений найдите точные решения на интервале [0,2π). [0,2π). Ищите возможности использовать тригонометрические тождества.

50.

sin2x-cos2x-sinx=0sin2x-cos2x-sinx=0

51.

sin2x+cos2x=0sin2x+cos2x=0

52.

sin(2x)-sinx=0sin(2x)-sinx=0

53.

cos(2x)−cosx=0cos(2x)−cosx=0

54.

2tanx2-sec2x-sin2x=cos2x2tanx2-sec2x-sin2x=cos2x

55.

1-cos(2x)=1+cos(2x)1-cos(2x)=1+cos(2x)

56.

сек2х=7сек2х=7

57.

10sinxcosx=6cosx10sinxcosx=6cosx

58.

−3sint=15costsint−3sint=15costsint

59.

4cos2x−4=15cosx4cos2x−4=15cosx

60.

8sin2x+6sinx+1=08sin2x+6sinx+1=0

61.

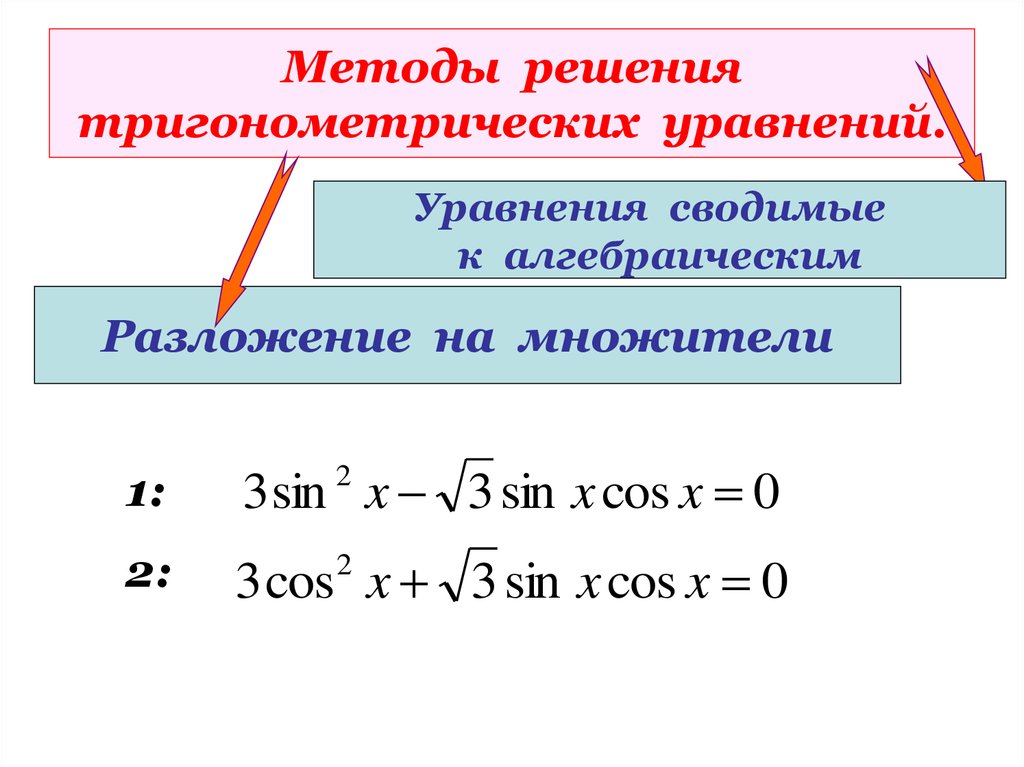
8cos2θ=3−2cosθ8cos2θ=3−2cosθ

62.

6cos2x+7sinx-8=06cos2x+7sinx-8=0

63.

12sin2t+затраты-6=012sin2t+затраты-6=0

64.

tanx=3sinxtanx=3sinx

65.

cos3t=costcos3t=стоимость

Графический

В следующих упражнениях алгебраически точно определите все решения тригонометрического уравнения, затем проверьте результаты, построив уравнение на графике и найдя нули.

66.

6sin2x−5sinx+1=06sin2x−5sinx+1=0

67.

8cos2x-2cosx-1=08cos2x-2cosx-1=0

68.

100tan2x+20tanx-3=0100tan2x+20tanx-3=0

69.

2cos2x-cosx+15=02cos2x-cosx+15=0

70.

20sin2x−27sinx+7=020sin2x−27sinx+7=0

71.

2tan2x+7tanx+6=02tan2x+7tanx+6=0

72.

130tan2x+69tanx-130=0130tan2x+69tanx-130=0

Технология

В следующих упражнениях используйте калькулятор, чтобы найти все решения до четырех знаков после запятой.

73.

sinx=0,27sinx=0,27

74.

sinx=-0,55sinx=-0,55

75.

tanx=-0,34tanx=-0,34

76.

cosx=0,71cosx=0,71

В следующих упражнениях решите уравнения алгебраически, а затем с помощью калькулятора найдите значения на интервале [0,2π).[0,2π). Округлите до четырех знаков после запятой.

77.

tan2x+3tanx-3=0tan2x+3tanx-3=0

78.

6tan2x+13tanx=-66tan2x+13tanx=-6

79.

tan2x-secx=1tan2x-secx=1

80.

sin2x-2cos2x=0sin2x-2cos2x=0

81.

2tan2x+9tanx-6=02tan2x+9tanx-6=0

82.

4sin2x+sin(2x)secx−3=04sin2x+sin(2x)secx−3=0

Удлинители

Для следующих упражнений найдите в точности все решения уравнений на отрезке [0,2π).[0,2π).

83.

csc2x-3cscx-4=0csc2x-3cscx-4=0

84.

sin2x-cos2x-1=0sin2x-cos2x-1=0

85.

sin2x(1-sin2x)+cos2x(1-sin2x)=0sin2x(1-sin2x)+cos2x(1-sin2x)=0

86.

3sec2x+2+sin2x-tan2x+cos2x=03sec2x+2+sin2x-tan2x+cos2x=0

87.

sin2x-1+2cos(2x)-cos2x=1sin2x-1+2cos(2x)-cos2x=1

88.

tan2x-1-sec3xcosx=0tan2x-1-sec3xcosx=0

89.

sin(2x)sec2x=0sin(2x)sec2x=0

90.

грех(2x)2csc2x=0sin(2x)2csc2x=0

91.

2cos2x-sin2x-cosx-5=02cos2x-sin2x-cosx-5=0

92.

1сек2х+2+sin2x+4cos2x=41сек2x+2+sin2x+4cos2x=4

Реальные приложения

93.

Бензина у самолета хватит только на то, чтобы долететь до города в 200 милях к северо-востоку от его текущего местоположения. Если пилот знает, что город находится в 25 милях к северу, сколько градусов к северу от востока должен лететь самолет?

94.

Если погрузочная рампа расположена рядом с грузовиком на высоте 4 фута, а длина рампы составляет 15 футов, какой угол образует рампа с землей?

95.

Если погрузочная рампа расположена рядом с грузовиком на высоте 2 фута, а длина рампы составляет 20 футов, какой угол образует рампа с землей?

96.

Женщина наблюдает за запущенной ракетой на высоте 11 миль. Если она стоит в 4 милях от стартовой площадки, под каким углом она смотрит вверх от горизонтали?

97.

Космонавт находится в запущенной ракете на высоте 15 миль. Если человек стоит в 2 милях от стартовой площадки, под каким углом она смотрит на него сверху вниз? (Подсказка: это называется углом депрессии.)

98.

Женщина стоит в 8 метрах от 10-метрового здания. Под каким углом она смотрит на крышу здания?

99.

Мужчина стоит в 10 метрах от 6-метрового здания. Кто-то наверху здания смотрит на него сверху вниз. Под каким углом на него смотрит человек?

100.

Здание высотой 20 футов имеет тень длиной 55 футов. Каков угол возвышения солнца?

101.

Здание высотой 90 футов имеет тень длиной 2 фута. Каков угол возвышения солнца?

102.

Прожектор на земле в 3 метрах от человека ростом 2 метра отбрасывает 6-метровую тень на стену в 6 метрах от человека. Под каким углом свет?

103.

Прожектор на земле в 3 футах от женщины ростом 5 футов отбрасывает тень высотой 15 футов на стену в 6 футах от женщины. Под каким углом свет?

Для следующих упражнений найдите алгебраическое решение следующей задачи со словами. Затем воспользуйтесь калькулятором, чтобы проверить результат. Округлите ответ до десятых долей градуса.

104.

Человек делает стойку на руках, касаясь ногами стены и руками на расстоянии 1,5 фута от стены. Какой угол составляют ноги человека со стеной, если его рост 6 футов?

105.

Человек делает стойку на руках, касаясь ногами стены и руками на расстоянии 3 футов от стены. Если рост человека 5 футов, какой угол составляют его ступни со стеной?

106.

23-футовая лестница расположена рядом с домом. Если лестница соскальзывает на расстоянии 7 футов от дома из-за недостаточного сцепления, какой угол должна составлять лестница с землей, чтобы избежать соскальзывания?

Объяснение урока: Решение тригонометрического уравнения

В этом объяснении мы научимся решать тригонометрическое уравнение с помощью факторизации или возведения в квадрат.

Определение:

Тригонометрическое уравнение – это уравнение, в котором используется любая из трех тригонометрических функций: синус, косинус или тангенс.

Прежде чем мы приступим к этим новым методам, мы уже должны быть знакомы с решением простых тригонометрических уравнений, таких как sin𝜃=𝑘, cos2𝜃=𝑘 и tan(𝜃−30)=𝑘, используя либо график, либо CAST-диаграмму. Мы также должны вспомнить некоторые ключевые свойства, относящиеся к функциям синуса, косинуса и тангенса:

  • sinsin𝜃 = (180–𝜃) ∘∘∘
  • Coscos𝜃 = (360– 𝜃) ∘∘∘
  • Tantan𝜃 = (180+𝜃) ∘∘∘

Перед решанием тригонометрического уравнения, это часто помогает. чтобы рассмотреть, сколько решений, как мы ожидаем, будет иметь уравнение, поскольку это может обеспечить средство проверки нашего ответа. Мы можем определить, сколько раз тригонометрическая функция равна определенному значению в заданном интервале, проведя горизонтальную линию через ее график в этом значении, а затем подсчитав, сколько раз эта линия пересекает график. Например, если мы хотим определить количество решений уравнения sin𝑥=0,5 в интервале 0≤𝑥≤360∘∘, мы проводим горизонтальную линию в точке 𝑦=0,5 через график 𝑦=𝑥sin и определяем, что эта линия дважды пересекает график на заданном интервале. Таким образом, мы можем заключить, что уравнение sin𝑥=0,5 имеет два решения в интервале 0≤𝑥≤360∘∘.

Давайте теперь рассмотрим более сложный пример такого типа задач. Нам также потребуется одно из ключевых тригонометрических тождеств, определяющее связь между тремя тригонометрическими функциями. Мы напомним это тождество ниже.

Определение: тождество касательной

Для всех значений 𝜃 tansincos𝜃≡𝜃𝜃.

Пример 1: Определение количества решений тригонометрического уравнения

Заполните пропуск: Если 0≤𝑥≤360∘∘, то количество решений уравнения 4𝑥=𝑥синтан равно .

Ответ

В этом уравнении участвуют два тригонометрических соотношения: синус и тангенс. Однако мы можем выразить функцию тангенса через функции синуса и косинуса, вспомнив тождество tansincos𝑥≡𝑥𝑥. Сделав эту замену в правой части уравнения, мы получим 4𝑥=𝑥𝑥4𝑥−𝑥𝑥=0.sinsincossinsincos

На этом этапе может возникнуть соблазн разделить уравнение на общий множитель sin𝑥. Однако это потенциально может привести к потере некоторых решений, если множитель, на который мы делим, равен 0. Мы знаем, что деление на 0 не определено, поэтому, если есть какой-либо риск того, что член, на который мы делим, равен 0 , вместо этого мы должны факторизовать уравнение по этому члену. Факторинг по sin𝑥 дает sincos𝑥4−1𝑥=0.

Теперь у нас есть произведение, равное 0. Произведение может равняться 0 только в том случае, если хотя бы один из множителей сам равен 0. Чтобы найти все возможные решения, мы устанавливаем каждый множитель равным 0 и решаем полученное уравнения. В этом вопросе мы на самом деле не стремимся полностью решить каждое уравнение, а скорее определить количество решений в указанном интервале.

Установив первый множитель равным 0, мы получим уравнение sin𝑥=0. Вспоминая график функции синуса, мы видим, что sin𝑥=0 трижды в интервале 0≤𝑥≤360∘∘.

Между прочим, эти значения 𝑥 равны 0∘, 180∘ и 360∘, но значения не требуются для этой задачи. Вот почему важно, чтобы мы учитывали, а не делили на общий фактор греха𝑥; если бы мы разделили, то потеряли бы эти три действительных решения уравнения.

Присвоение второму множителю значения 0 дает уравнение 4−1𝑥=0,cos, которое требует дальнейших манипуляций. Умножение на cos𝑥 дает 4𝑥−1=04𝑥=1𝑥=14.coscoscos

Вспоминая график функции косинуса и проводя горизонтальную линию через график в точке 𝑦=14, мы находим, что есть два значения 𝑥 в интервале 0 ≤𝑥≤360∘∘, для которого cos𝑥=14:

Хотя мы не можем прочитать точные значения 𝑥 из нашего графика, они явно не совпадают со значениями, для которых sin𝑥=0, и поэтому все наши решения уникальны.

Есть 5 решений уравнения 4𝑥=𝑥синтан в интервале 0≤𝑥≤360∘∘.

Теперь рассмотрим подробный пример того, как мы можем найти все решения более сложного тригонометрического уравнения с помощью факторизации.

Пример 2. Поиск решений тригонометрического уравнения в заданном диапазоне с помощью факторинга

Найдите множество значений, удовлетворяющих тантан𝜃+𝜃=0, где 0≤𝜃180∘∘.

Ответ

При осмотре мы можем сразу определить, что это квадратное уравнение с загаром𝜃. В качестве альтернативы нам может оказаться полезным рассмотреть замену 𝑥=𝜃tan. Параллельно рассмотрим отработку как с этой заменой, так и без нее. LettanthenconsidertheequationtantanfactoringbygivesfactoringsbytangivestantantingTeachFactorequaltOweHavesetTygeAceFactorequaltOweHaveOrtanReversingThesubstitution, weobtaintanortan𝑥 = 𝜃.𝑥+𝑥 = 0.0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0,0 1=0.𝜃=0𝜃+1=0.

Итак, мы видим, что приходим к той же паре уравнений. Выбор того, делать ли формальную замену, является личным, и этот шаг можно пропустить, поскольку знакомство с этими типами проблем увеличивается. Теперь нам нужно решить два уравнения.

Наше первое уравнение tan𝜃=0. Вспоминая график функции тангенса, мы видим, что единственным решением этого уравнения в интервале 0≤𝜃180∘∘ является 𝜃=0∘. Мы также должны признать, что tan0=0∘, не рисуя график, так как это один из ключевых углов, для которого мы должны запомнить значения трех тригонометрических отношений. Обратите внимание, что хотя tan180=0∘, 180∘ не является решением, поскольку интервал содержит только значения 𝜃, которые строго меньше 180∘.

Второе уравнение можно преобразовать в tan𝜃=−1. Применяя функцию арктангенса, мы получаем 𝜃=(−1)=−45.tan∘

Это значение или главный аргумент находится за пределами требуемого интервала для 𝜃. Вспоминая периодичность функции тангенса, мы находим второе решение уравнения, добавляя 180 ∘: . Добавление любых дополнительных значений, кратных 180∘, выведет нас за верхнюю границу интервала, поэтому мы нашли все решения.

Набор значений, удовлетворяющих тантан𝜃+𝜃=0, где 0≤𝜃180∘∘, равен {0,135}∘.

Обратите внимание, что в предыдущем примере было важно, чтобы мы учитывали tan𝜃, а не делили на него. Если бы мы разделили на tan𝜃, то потеряли бы одно из решений исходного уравнения. Это связано с тем, что tan𝜃 может равняться 0 в интервале, в котором мы искали решения, а деление на 0 не определено. Действительно, tan𝜃=0 было одним из уравнений, которые нам впоследствии пришлось решать.

Мы всегда должны внимательно следить за интервалом, в котором мы ищем решения. Обычно интервал составляет 0≤𝜃≤360∘∘, но, как мы видели в предыдущем примере, это не всегда так. Дополнительные значения вполне могут быть допустимыми решениями уравнения, но если они выходят за указанный интервал, то они неверны в контексте задачи.

Теперь рассмотрим несколько более сложную задачу, связанную с другой тригонометрической функцией.

Пример 3. Поиск решений тригонометрического уравнения в заданном диапазоне с помощью факторинга

Найдите множество значений, удовлетворяющих условию 2√2𝜃+2𝜃=0coscos, учитывая, что 0≤𝜃≤360∘∘.

Ответ

Это уравнение включает единственную тригонометрическую функцию, функцию косинуса, но оно включает член порядка 2 и поэтому является квадратным уравнением. Поскольку у него нет постоянного члена (или постоянный член равен 0), его можно решить, разложив на множители по 2𝜃cos: 2𝜃√2𝜃+1=0.coscos

Следовательно, либо 2𝜃=0cos, либо √2𝜃+1=0cos.

В первом уравнении мы делим на 2, чтобы получить cos𝜃=0. Рассматривая график функции косинуса, видим, что в искомом интервале есть два решения этого уравнения: 𝜃=90∘ и 𝜃=270∘.

Решение второго уравнения немного сложнее. Перестановка дает √2𝜃=−1𝜃=−1√2.coscos

Умножив числитель и знаменатель частного в правой части на √2, это можно переписать как cos𝜃=−√22.

Напомним, что cos45=√22∘. Однако мы ищем такие значения 𝜃, что cos𝜃=−√22. Используя диаграмму CAST, мы видим, что cos𝜃 отрицателен во втором и третьем квадрантах, а с помощью симметрии мы находим, что cos𝜃=−√22, когда 𝜃=180−45∘∘ и 𝜃=180+45∘∘.

Это дает еще два решения: 135∘ и 225∘.

Набор значений, для которых 2√2𝜃+2𝜃=0coscos в интервале 0≤𝜃≤360∘∘ равен {90 135 225 270}∘∘∘∘.

Предыдущие два примера состояли из решения квадратных уравнений только с одной тригонометрической функцией. Теперь рассмотрим пример, в котором мы встречаемся с уравнением, включающим две тригонометрические функции.

Пример 4. Решение тригонометрического уравнения, содержащего синус и косинус, путем факторизации

Найдите множество значений, удовлетворяющих условию 3𝜃−2𝜃𝜃=0sinsincos, где 0≤𝜃≤360∘∘. Дайте ответ с точностью до минуты.

Ответ

Начнем с факторизации по общему множителю sin𝜃: sinsincos𝜃(3𝜃−2𝜃)=0.

Поскольку теперь у нас есть произведение, равное 0, мы можем решить, установив каждый множитель равным 0, а затем решив полученные уравнения. Установка первого фактора равным 0 дает уравнение sin𝜃=0.

Вспоминая график функции синуса, находим, что в искомом интервале есть три значения 𝜃: 0∘, 180∘ и 360∘.

Установка скобок, равных 0, дает уравнение 3𝜃−2𝜃=0sincos, которое можно преобразовать в sincos𝜃=23𝜃.

Чтобы выразить это уравнение только через одну тригонометрическую функцию, мы можем разделить на cos𝜃. Деление на тригонометрический член может быть рискованным, так как мы должны гарантировать, что не потеряем никаких решений, что может произойти, если член, на который мы делим, равен 0. Однако, если бы cos𝜃 был равен 0, это привело бы к sin𝜃=0 , и поскольку нет значений 𝜃, для которых синус и косинус равны нулю, мы знаем, что cos𝜃 не равен 0 ни для одного из наших решений. Следовательно, мы можем быть уверены, что деление на cos𝜃 не приведет к потере каких-либо решений, и мы получим sincos𝜃𝜃=23.

Вспоминая тождество tansincos𝜃≡𝜃𝜃, теперь мы можем выразить уравнение через одну тригонометрическую функцию: tan𝜃=23.

Нахождение главного значения 𝜃 с точностью до минуты дает 𝜃=23=33,690…≈3341′.tan∘∘

Чтобы найти любые другие значения в требуемом интервале, рассмотрим CAST диаграмма:

Значения тангенса𝜃 также положительны в третьем квадранте, поэтому мы находим второе значение, добавляя 180∘ к нашему основному значению: 𝜃=180+3341′=21341′.∘∘∘

Мы могли бы также найти это второе значение, вспомнив о периодичности функции тангенса, что снова потребовало бы от нас добавления 180∘. В требуемом интервале больше нет значений, поэтому мы нашли все возможные решения.

Набор значений, удовлетворяющих данному уравнению с точностью до минуты, равен {0,3341′,180,21341′}∘∘∘∘.

Другой подход, который мы можем использовать для решения некоторых конкретных типов тригонометрических уравнений, заключается в возведении в квадрат обеих частей уравнения. В некоторых случаях это может создать выражения вида sincos𝜃+𝜃, которые можно упростить, вспомнив тождество Пифагора.

Определение: тождество Пифагора

Для всех значений 𝜃 sincos𝜃+𝜃≡1.

Возведение в квадрат обеих частей уравнения может быть рискованным, если мы не проявим большую осторожность. Например, рассмотрим простое уравнение 𝑥=3. Возведение обеих сторон в квадрат дает 𝑥=9, а затем решение этого уравнения путем нахождения квадратного корня дает 𝑥=±√9=±3.

Поскольку возведение в квадрат и нахождение квадратного корня не являются взаимно однозначными операциями, мы «создали» дополнительное решение этого уравнения, 𝑥=−3. Это известно как постороннее решение и неверно, учитывая, что нашей отправной точкой было единственное значение 𝑥=3. Если нам нужно решить тригонометрическое уравнение возведением в квадрат, мы должны впоследствии проверить все наши решения в исходном уравнении, чтобы убедиться, что мы не получили никаких посторонних значений.

Пример 5. Нахождение решений тригонометрического уравнения в заданном диапазоне путем возведения в квадрат и распознавания посторонних решений

Сначала возведя в квадрат обе части или иначе, решите уравнение 4𝜃−4𝜃=√3sincos, где 0𝜃≤360∘∘. Будьте осторожны, чтобы удалить любые посторонние растворы. Дайте ответ с точностью до двух знаков после запятой.

Ответ

В вопросе говорится, что мы подходим к этой проблеме, сначала возводя в квадрат обе части уравнения. Делая это, а затем упрощая, мы получаем (4𝜃−4𝜃)=√316𝜃−32𝜃𝜃+16𝜃=3.0003

Затем мы вспоминаем пифагореанскую идентичность Sincos𝜃+𝜃 зор, что позволяет нам дальнейшее упрощение: 16𝜃+𝜃 -32𝜃𝜃 = 316–32𝜃𝜃 = 3–32𝜃𝜃 = −13𝜃𝜃 = 1332. Sincossossossossossincoss

Это уравнение основано на функциях синуса и косинуса. Объединив это с нашим исходным уравнением, мы теперь имеем два уравнения с двумя переменными sin𝜃 и cos𝜃, и поэтому эту систему уравнений можно решать одновременно. Чтобы получить уравнение только с одной функцией, мы сначала переформулируем исходное уравнение, чтобы выразить sin𝜃 через cos𝜃:0003

Теперь мы можем подставить это выражение для sin𝜃 во второе уравнение: √3+4𝜃4𝜃=1332.coscos

имеем √34𝜃+𝜃=13328√3𝜃+32𝜃=1332𝜃+8√3𝜃−13=0.coscoscoscoscos

Теперь у нас есть квадратное уравнение относительно cos𝜃, которое мы можем решить, применяя квадратную формулу. Коэффициент cos𝜃 равен 32, коэффициент cos𝜃 равен 8√3, а постоянный член равен −13. Подстановка этих значений в квадратичную формулу дает cos𝜃=−8√3±8√3−(4×32×−13)2×32.

Упрощая, мы приходим к cos𝜃=−8√3±√185664, который мы можем еще упростить, упростив радикал √1856 и затем сократив коэффициент 8: cos𝜃=−8√3±8√2964=−√3 ±√298.

Теперь нам нужно решить два уравнения. Сначала извлечем положительный корень: 360−62,829…=297,170…≈297,17.

Мы называем это «возможным» решением, поскольку позже мы должны проверить все наши значения в исходном уравнении, чтобы определить, не являются ли они посторонними.

Извлекая отрицательный корень, мы имеем coscos𝜃=−√3−√298𝜃=−√3−√298=152,829…≈152,83,

Опять же, используя симметрию функции косинуса, наше второе возможное решение составляет 𝜃=360−152,829…=207,170…≈207,17.

Мы нашли четыре возможных решения данного уравнения, набор значений {62,83,152,83,207,17,297,17}∘∘∘∘.

Наконец, мы должны проверить справедливость каждого из этих «решений» в исходном уравнении. Подставляем каждое значение по очереди в левую часть уравнения и определяем, равно ли полученное значение √3(1,732…).

Для нашего первого значения 62,83∘: 462,83−462,83=1,732…,sincos∘∘, поэтому 62,83∘ является допустимым решением.

Для второго значения 152,83∘: 4152,83−4152,83=5,385…,sincos∘∘ и поэтому 152,83∘ на самом деле является посторонним решением. Точно так же мы обнаруживаем, что наше третье значение 207,17∘ является допустимым решением, а четвертое значение 297,17∘ — нет.

Следовательно, есть два решения уравнения 4𝜃−4𝜃=√3sincos в заданном интервале, которые с точностью до двух знаков после запятой равны 𝜃=62,83∘ и 𝜃=207,17∘.

В предыдущем примере подчеркивается важность проверки всех наших «решений» в исходном уравнении, если метод, который мы использовали для его решения, включал возведение в квадрат. Если бы мы пропустили этот шаг, мы бы предложили четыре, а не два значения для 𝜃, два из которых были бы недействительными.

Мы видели различные методы решения более сложных тригонометрических уравнений, включая разложение на множители, возведение в квадрат и использование тригонометрических тождеств. В некоторых случаях можно будет применить более одного метода, поэтому выбранный нами метод будет зависеть от типа и сложности данного уравнения.

Давайте закончим, повторив некоторые ключевые моменты.

Ключевые моменты

  • Некоторые тригонометрические уравнения можно решить с помощью факторизации. Чрезвычайно важно, чтобы любые общие множители были факторизованы, а не разделены, чтобы избежать потенциальной потери решений, если эти множители равны 0.
  • Некоторые тригонометрические уравнения можно решить, возведя в квадрат обе части. Всякий раз, когда используется этот подход, необходимо соблюдать осторожность, чтобы не создавать каких-либо посторонних решений.
  • Два ключевых тригонометрических тождества tansincos𝜃≡𝜃𝜃 и sincos𝜃+𝜃≡1 могут быть полезны для упрощения тригонометрических уравнений.
  • Графики тригонометрических функций, их свойства и диаграмма CAST могут быть использованы для определения дополнительных решений после определения главного значения.

Тригонометрические уравнения – объяснение и примеры

Тригонометрические уравнения – это уравнения, в которых используются тригонометрические функции и неизвестные углы.

Эти уравнения часто требуют использования тригонометрических тождеств для решения неизвестной переменной. Поскольку тригонометрические функции являются периодическими, существует решение между $0$ и $2\pi$, если решение существует, но в этом случае будет существовать бесконечно много других решений. Возможно также, что уравнение не имеет решения.

Поскольку тригонометрические уравнения предполагают решение неизвестных переменных, они полезны во всех конкретных приложениях тригонометрии, включая науку и технику.

Прежде чем читать этот раздел, обязательно ознакомьтесь с тем, как решать линейные и квадратные уравнения, обратные триггерные функции и триггерные тождества.

В этом разделе рассматриваются:

  • Что такое тригонометрическое уравнение?
  • Как решить тригонометрическое уравнение
  • Тригонометрические уравнения с более чем одной функцией тригея
  • Основные тригонометрические уравнения

    • ТРИГОНЕМЕТРИЧЕСКИЕ Уравнения

    ТРИГОНЕМЕТРИЧЕСКИЕ Уравнения

    TRIGONOMETIRCENTICE

    TRIGONOMETRICE

    .

    Тригонометрическое уравнение — это уравнение, включающее тригонометрические функции и неизвестные углы. Эти неизвестные углы будут переменными в уравнениях.

    Поскольку тригонометрические функции являются периодическими, они имеют бесконечно много решений, если существует решение с действительным знаком. Обычно за решение уравнения принимают решение на интервале от $0$ до $2\pi$ радиан, если не указано иное. Это называется основным решением.

    Однако иногда требуется общее решение. Это решение, которое включает в себя все возможные углы, которые могут работать в уравнении. Такое решение будет включать переменную «n», где «n» — целое число.

    Простой пример тригонометрического уравнения: $sinx=0$. Поскольку синус равен $0$ при $0$ радианах и $\pi$ радианах, главным решением является $0$ или $\pi$. Общее решение: $0+n\pi$, где $n$ — целое число.

    Однако в большинстве случаев тригонометрические уравнения требуют больше работы, чем простое использование обратных триггерных функций. Это потому, что они обычно немного сложнее. Как правило, использование тригонометрических тождеств для перезаписи уравнения с использованием только одного типа тригонометрической функции является лучшим способом решения тригонометрических уравнений.

    Как решить тригонометрическое уравнение

    Решение тригонометрических уравнений работает почти так же, как решение полиномиальных уравнений, когда задействована только одна тригонометрическая функция. То есть триггерные функции следует рассматривать как переменные в некоторой степени, даже если они являются функциями переменной.

    Если наивысшая степень тригонометрического уравнения равна $1$, получить все тригонометрические функции с одной стороны уравнения, а все остальные — с другой. Затем используйте обратные триггерные функции в обеих частях уравнения, чтобы отменить триггерную функцию. Это создаст общее полиномиальное уравнение, которое можно решить, используя обратный порядок операций.

    Если наибольшая степень тригонометрических функций больше $1$, ее можно решить так же, как полиномы со степенью больше $1$. Их легче всего решить, если их можно разложить на множители как квадратичные. Факторинг также с группировкой работает, когда мощность больше $2$.

    Однако, если существует более одной триггерной функции, необходимо сначала переписать уравнение, чтобы была только одна функция. Это делается с помощью тригонометрических тождеств. После этого эти шаги можно использовать для упрощения и решения.

    Тригонометрические уравнения с более чем одной тригонометрической функцией

    Иногда тригонометрические уравнения включают более одной тригонометрической функции. В этом случае нет смысла применять обратную триггерную функцию к обеим частям уравнения, поскольку это не отменит все триггерные функции. В этом случае используйте тригонометрические тождества, чтобы сделать все триггерные функции одинаковыми.

    Если добавляется или вычитается триггерная функция (такая как $sinx+siny$), используйте тождества сложения/вычитания, чтобы объединить ее в одну функцию.

    Конечная цель решения тригонометрических функций состоит в том, чтобы получить одну тригонометрическую функцию первой степени с одной стороны уравнения и числа с другой стороны. Это означает, что левая часть может быть отменена с помощью обратной триггерной функции, что делает возможным нахождение переменной, если решение существует.

    Основные тригонометрические уравнения

    Основные тригонометрические уравнения имеют форму $funx=a$, где $fun$ обозначает любую из шести тригонометрических функций: синуса, косинуса, тангенса, косеканса, секанса и котангенса, а $a$ число.

    Это базовые тригонометрические уравнения, поскольку для их решения не требуется никакой перестановки. Чтобы отменить тригонометрическую функцию, примените обратные тригонометрические функции к обеим сторонам. Следовательно, решением этого уравнения является $x=arcfun(a)$, где $arcfun$ — соответствующая обратная тригонометрическая функция.

    При решении уравнения вида $fun(f(x))=a$ начните, как и раньше, с применения обратной тригонометрической функции к обеим частям. Это дает $f(x)=arcfun(a)$. Затем найдите $x$, используя алгебраические методы.

    Если функция триггера представляет собой синус, косинус, секанс или косеканс, общее решение будет $arcfun(a)+2n\pi$ для любого целого числа $n$. Если тригонометрическая функция является касательной или кокасательной, общим решением является $arcfun(a)+n\pi$ для любого целого числа $n$.

    Важно знать, как решать эти основные уравнения, потому что конечной целью решения общего тригонометрического уравнения является приведение уравнения к форме $fun(x)=a$ или $fun(f(x))=a$.

    Тригонометрические уравнения без решения

    Не все тригонометрические уравнения имеют решение.

    Некоторые тригонометрические уравнения не имеют решений. Это связано с тем, что обратная триггерная функция не всегда определена для всех значений. Например, синус и косинус угла должны быть между $-1$ и $1$. Косеканс и секанс не могут лежать в интервале $(-1, 1)$.

    Таким образом, уравнения типа $cosx=5$ и $cscx=0$ не имеют решения в действительных числах. Существуют решения с участием мнимых (комплексных) чисел, но они выходят за рамки этой статьи.

    Обратите внимание, что, хотя тангенс и котангенс определены для всех вещественных значений, все же можно получить уравнение, в котором $tanx=c$ для комплексного, не действительного числа $c$. Такая функция также не имела бы вещественного решения.

    Примеры

    В этом разделе рассматриваются распространенные задачи, связанные с тригонометрическими уравнениями, и их пошаговые решения.

    Пример 1

    Найдите главное и общее решения основного тригонометрического уравнения $cosx=-1$.

    Решение

    Это уравнение уже имеет вид $funx=a$. Поэтому для решения примените обратную тригонометрическую функцию — в данном случае функцию арккосинуса — к обеим частям уравнения.

    $arccos(cosx)=arccos(-1)$.

    Упрощая, это:

    $x=\pi$ радиан.

    Это главное решение или решение на интервале $(0, 2\pi)$. Однако, поскольку периодичность косинуса $2\pi$, общее решение равно $\pi+2n\pi$ радианам для любого целого числа $n$. 92x} = \pm \sqrt{1}$.

    Помните, что есть положительный и отрицательный квадратный корень, потому что $1\time1=1$ и $-1 \times -1=1$.

    Следовательно, упрощая, это:

    $sinx=1$ или $sinx=-1$.

    Чтобы решить это, возьмите арксинус обеих частей двух уравнений. Это дает:

    $x=\frac{\pi}{2}$ радиан или $x=\frac{3\pi}{2}$ радиан.

    Это основное решение. Поскольку синус периодичен в $2\pi$, общее решение равно $\frac{\pi}{2}+2n\pi$ радиан или $\frac{3\pi}{2}+2n\pi$ радиан для любого целого числа $n$. Это можно упростить как $\frac{\pi}{2}+n\pi$ радиан для любого целого числа $n$. 92+2x+1-\frac{2\pi}{3}=0$.

    Поскольку третье слагаемое не простое, для решения используйте квадратичную формулу.

    $x = \frac{-2 \pm \sqrt{4-4(1-\frac{2\pi}{3})}}{2}$ радиан.

    Это упрощается до $x=1-\sqrt{\frac{2\pi}{3}}$ радиан или $x = \sqrt{\frac{2\pi}{3}}-1$ радиан, или приблизительно $-2,45$ радиан или $0,45$ радиан.

    Поскольку тангенс является $\pi$-периодическим, общими решениями являются $x=1-\sqrt{\frac{2\pi}{3}}+n\pi$ радиан или $x = \sqrt{\frac{ 2\pi}{3}}-1+n\pi$ радиан для любого целого числа $n$.

    Пример 4

    Найдите решение тригонометрического уравнения $sin(x-1)+sin(x+1)+1=0$.

    Решение

    Начните с составления уравнения так, чтобы в левой части были только триггерные функции, а в правой — только числа. Для этого просто нужно вычесть 1 доллар с обеих сторон.

    $sin(x-1)+sin(x+1) = -1$.

    Это уравнение, однако, не имеет формы $funx=a$. Существуют две различные функции синуса. Используйте формулу суммы, чтобы помочь.

    $sin(x-1)+sin(x+1) = 2sin(\frac{x+1+x-1}{2})cos(\frac{x+1-(x-1)}{ 2})$.

    Это упрощает:

    $2sin(x)cos(1)$.

    В этом случае $cos(1)$ — это просто число. Его можно рассматривать как константу. Следовательно, тригонометрическое уравнение можно переписать так:

    $2sin(x)cos(1) = -1$ 

    Или

    $sin(x) = \frac{-1}{2cos(1)}$.

    Возьмите арксинус обеих сторон, чтобы получить точный ответ:

    $x = arcsin(\frac{-1}{2cos(1)})$.

    В десятичном приближении это составляет $-1,18$ радиан. Таким образом, общее решение равно $-1,18+2n\pi$ для любого целого числа $n$. 92(2x) = \frac{2-\sqrt{2}}{2}$.

    Затем извлеките квадратный корень из обеих сторон, чтобы получить:

    $cos(2x) = \sqrt{\frac{2-\sqrt{2}}{2}}$.

    Теперь уравнение имеет вид $fun(f(x))=a$. Поэтому возьмите арккосинус обеих сторон. Это:

    $2x = arccos(\sqrt{\frac{2-\sqrt{2}}{2}}$.

    Наконец, разделите обе части на $2$, чтобы найти $x$.

    $x = \frac{arccos(\sqrt{\frac{2-\sqrt{2}}{2}}}{2}$ радиан.

    Хотя правая часть этого уравнения выглядит сложной, это просто константа. значения в калькулятор показывает, что он имеет десятичную аппроксимацию 0,50 радиан.

    Это основное решение. Поскольку косинус периодичен в $2\pi$, общее решение равно $\frac{arccos(\sqrt{\frac{2-\sqrt{2}}{2}}}{2} + 2n\pi$ радиан для любого целого числа , $n$

    Пример 6

    Найдите решение уравнения $tan(x)+cot(x) = \frac{1}{2}$

    Решение

    И снова это уравнение содержит два различные типы тригонометрических функций.Использование тригонометрических тождеств для того, чтобы иметь только один тип функции, упростит уравнение.92x}{cosxsinx} = \frac{1}{2}$.

    Тождество Пифагора показывает, что числитель равен $1$. Таким образом, все уравнение упрощается до установки равных знаменателей.

    $cosxsinx=2$.

    Похоже на тождество $2cosxsinx=sin(2x)$. Поэтому умножьте обе части уравнения на $2$.

    $2cosxsinx=4$

    $sin(2x)=4$.

    Но синус любого угла должен быть между $-1$ и $1$. Следовательно, не существует угла $2x$, такого что $sin(2x)=4$. Таким образом, у этого уравнения нет решения.

    Тригонометрические уравнения: формулы, тождества, решения, примеры

    • Автор Gnanambigai GS
    • Последнее изменение 19-07-2022
    • Автор Гнанамбигай GS
    • Последнее изменение 19-07-2022

    Тригонометрические уравнения : Тригонометрия — это раздел математики, который занимается изучением длин сторон и углов, входящих в прямоугольные треугольники. Он широко используется в геодезии и навигации. Обычно используются шесть тригонометрических функций. Это синус, косинус, тангенс, котангенс, секанс и косеканс. Уравнения, в которые входят тригонометрические функции переменной, называются тригонометрическими уравнениями.

    Применение тригонометрии в нашей повседневной жизни

    Тригонометрические функции

    Шесть тригонометрических функций определяются следующим образом:

    (i) Синус: \(\sin \,\theta = \frac{{{\text{противоположный}}}}{{{\text{гипотенуза}}}}\)
    (ii) Косинус: \(\cos \,\theta = \frac{{{\text{adjacent}}}}{{{\text{гипотенуза}}}}\)
    (iii) Тангенс: \(\tan \, \theta = \frac{{{\text{напротив}}}}{{{\text{смежно}}}}\)
    (iv) Котангенс: \(\cot \,\theta = \frac{{{\text{adjacent}}}}{{{\text{противоположный}}}}\)
    (v) Секанс: \(\sec \,\theta = \frac{{hypotenuse}}{{adjacent}}\)
    (vi) Косеканс: \({\rm{cosec}}\,\theta = \frac{{{ \rm{гипотенуза}}}}{{{\rm{противоположное}}}}\)

    Тригонометрические тождества

    Тригонометрические уравнения, которые справедливы для всех значений переменных, называются тригонометрическими тождествами.
    Перечислены различные типы тригонометрических тождеств и примеры для каждого из них.

    1. Пифагорейские тождества
    i. \(\тета + \тета = 1\)
    ii. \(1 + \тета = \тета\)

    2. Тождества суммы и разности
    i. \(\sin \;\left( {u \pm v} \right)\; = \sin \;u\;\cos \;v\; + \cos \;u\;\sin \;v\)
    ii. \(\tan \;\left( {u \pm v} \right)\; = \frac{{\tan \;u\;\; \pm \;\tan \;v\;}}{{1 \; \mp \;\tan \;u\;\tan \;v\;}}\)

    3. Суммирование идентификаторов продуктов
    i. \(\sin \,u\,\cos \;\,v + \cos \,u\,\sin \,v\; = \sin \left( {u \pm v} \right)\)
    ii. \(\cos \,u\; — \;\cos \,v\; = \; — 2\left( {\frac {{u + v}}{2}} \right)\;\;\sin \;\влево ({\ гидроразрыва {{и\; — \;v}}{2}} \вправо)\)

    4. Произведение суммирования тождеств
    i. \(\ sin \, u \, \ cos \, v \; = \; \ frac {1} {2} \ left [ {\ sin \; \ left ( {u + v} \ right) + \ sin \ ;\left( {u – v} \right)} \right]\)
    ii. \(\ cos \,u\,\cos \,u\; = \frac{1}{2}\left[ {\cos \;\left( {u\; — v} \right)\; + \ cos \left( {u + v} \right)} \right]\)

    5. Взаимные тождества
    i. \(\tan \,\theta = \frac{1}{{\cot \,\theta}}\)
    ii. \(\cos\,\operatorname{co} \,\theta = \frac{1}{{\sec \,\theta}}\)

    6. Частные тождества
    i. \(\cot \,\theta = \frac{{\cos \,\theta}}{{\sin \,\theta}}\)
    ii. \(\tan \,\theta = \frac{{\sin \,\theta}}{{\cos \,\theta}}\)

    7. Четно-нечетные тождества
    i. \(\sin\left( { – x} \right)\; = \; – \sin \,x\)
    ii. \(\cos \left( { – x} \right)\; = \cos \,x\)

    8. Тождества с двойным углом
    i. \(\tan \,2\theta = \frac{{2\tan \,\theta }}{{1 – \theta }}\)
    ii. \(\sin\,2u = 2\sin\,u\;\cos\,u\)

    9. Полуугольные тождества
    i. \(u = \frac{{1 + \cos \,2u}}{2}\)
    ii. \(u = \frac{{1 – \cos \,2u}}{2}\)

    10. Кофункциональные тождества
    i. \(\sec \;\left( {\frac{\pi }{2} – x} \right) = x\)
    ii. \ (\ кроватка \; \ влево ( {\ гидроразрыва {\ pi} {2} — x} \ right) = \ tan \, x \)

    Как решать тригонометрические уравнения?

    Простые уравнения типа \(\cos\,\cos\,x = 1\) могут решаться численно путем приближения. Сложные уравнения нуждаются в более аналитическом подходе. Чтобы решить сложные тригонометрические уравнения, выполните пять шагов.

    Шаг 1: Перепишите уравнение в терминах одной функции одного угла.
    Шаг 2: Найдите значения в тригонометрической функции.
    Шаг 3: Перечислите различные возможные решения для угла. Решите для угла.
    Шаг 4: Найдите переменную, если необходимо.
    Шаг 5: Примените любые ограничения, если они доступны.

    Давайте изучим \(5\) шагов, используя два примера задач.
    Пример 1: Решите уравнение: \(x – x + \sin \,x = 0\).
    Пример 2: Решите: \(3\left( {\frac{B}{2}} \right) – 1 = 0\).

    Шаг 1: изменение одной функции одного угла
    Подобно алгебраическим выражениям, состоящим из переменных, тригонометрическое уравнение состоит из функций и углов. Чтобы решить уравнение, первым шагом является преобразование членов как одной функции одного угла. Это означает, что все члены уравнения должны иметь один и тот же угол и одну и ту же функцию. Для этого преобразования можно использовать любое из тригонометрических тождеств.

    Пример 1: Решите уравнение: \(x – x +\sin \,x = 0\).
    Здесь обратите внимание, что существует два типа функций: синус и косинус. Цель первого шага состоит в том, чтобы преобразовать уравнение в одну функцию одного угла. Вспоминая тригонометрические тождества, мы можем записать \(x\) через \(x\). Следовательно, мы получим
    \(x – \left( {x – 1} \right) + \sin \,x\; = 0\)
    \(x – \left( {x + 1} \right) + \sin \,x\; = 0\)
    Заметьте, что уравнение теперь записано в терминах одной функции одного угла. Это может быть дополнительно упрощено в следующих шагах.

    Пример 2: Решить: \(3\left( {\frac {B}{2}} \right) – 1 = 0\)
    Шаг 1: Это не обязательно, так как уравнение приведено в члены одной функции одного угла.

    Шаг 2: Найдите значения тригонометрической функции
    В конце шага \(1\) уравнение будет иметь только один тип функции с одним типом угла. На этом шаге найдите значение этой функции путем упрощения, аналогичного алгебраическому упрощению. Используйте алгебраические тождества везде, где это необходимо.

    Пример 1: Продолжая предыдущий шаг, мы можем еще больше упростить поиск значения тригонометрической функции.
    \(х – х + 1 + \sin \,x = 0\)
    \(1 + \sin \,x = 0\)
    \( \sin \,x = -1\)

    Пример 2: Поскольку шаг \(1\) не относится к этому тригонометрическому уравнению, продолжаем с шагом \(2\).
    Шаг 2: Найдем тригонометрическую функцию.
    \(\ влево ( {\ гидроразрыва {B} {2}} \ справа) = \ гидроразрыва {1} {3} \)
    \ (\ загар \; \ влево ( {\ гидроразрыва {B} {2}} \справа) = \pm \sqrt {\frac{1}{3}} \)
    Примечание. Не забудьте добавить знак \(\pm \) при использовании квадратных корней во время упрощения.

    Шаг 3: Нахождение угла
    После нахождения функции, переходим к нахождению угла.
    я. Если углы кратны \(\frac{\pi }{6}\) или \(\frac{\pi }{4}\), их относительно легче решить.
    ii. Если углы кратны половинным углам, то для оценки используются тождества половинных углов.
    Тригонометрические функции являются периодическими. Это означает, что их значения повторяются в цикле. Следовательно, для любого тригонометрического уравнения существует либо ноль, либо бесконечно много решений.
    Например, рассмотрим уравнение \(\tan\,\theta = 1\).
    Здесь показан график для различных значений \(y = \tan \,x\).

    Решения уравнения \(\tan \,\theta = 1\) идентифицируются по графику как:
    \(\theta = \ldots – \frac{{7\pi }}{4},\; – \frac{{3\pi }}{4},\frac{\pi }{4},\frac{{5\pi }}{4},. .. \)
    Цикл здесь равен \(\frac{{ 5\pi }}{4}\;- \;\frac{\pi }{4} = \frac{{4\pi }}{4} = \pi \)
    Следовательно, общее решение для этой функции можно быть определена как \(\theta = \frac{\pi }{4} + n\pi \), где \(n\) — целое число.
    Аналогичным образом найдите углы в данном уравнении, перечислив возможные решения.

    Пример 1: Продолжая шаг \(2\), мы должны найти \(x\).
    \(\sin \,x = – 1\)
    Используя общее решение тригонометрических уравнений, мы знаем, что общее решение равно
    \(x = \left( {4n – 1} \right)\frac{\ pi }{2}\)
    Обратите внимание, что не все вычисления будут такими простыми.

    Пример 2: Продолжая шаг \(2\), теперь мы находим углы.
    Пусть \(\frac{B}{2} = \theta \). Имеем
    \(\tan \,\theta = \pm \sqrt {\frac{1}{3}} \)
    То есть \(\tan\,\theta \; = \sqrt {\frac{ 1}{3}} \) или \(\tan \,\;\theta =\, — \sqrt {\frac{1}{3}} \)
    \(\theta = \frac{\pi }{ 6}\) или \(\theta = \frac{5\pi }{6}\)
    Общее решение можно записать в виде \(\theta = \frac{\pi }{6} + n\pi \ ) или \(\theta = \frac{{5\pi}}{6} + n\pi \)
    Но, \(\theta = \frac{B}{2}\), следовательно, общее решение: \(\frac{B}{2} = \frac{\pi }{6} + n\pi \) или \(\frac{B}{2} = \frac{{5\pi}}{6} + п\пи\)

    Шаг 4: Решение для переменной
    Эффективное решение для угла представляет собой \(2-\)шаговый процесс, если в углы входит переменная. В случае двойного угла или половинного угла убедитесь, что периодичность добавляется к конкретному углу, а не к половинным или двойным значениям. Важно работать с углом, а не с переменной в функции угла.

    Пример 2: Продолжая, мы имеем общее решение из шага \(3\) как:
    \(\ frac {B} {2} = \ frac {\ pi} {6} + n \ pi \) или \ (\ frac {B} {2} = \ frac {5 \ pi} {6} + n \пи\)

    Шаг 4: Теперь найдем переменную.
    Умножив на \(2\) с обеих сторон, мы получим
    \(B = \left( {\frac{\pi }{6} + n\pi } \right) \times 2\) или \(B = \left ( {\ frac {5 \ pi} {6} + n \ pi} \ right) \ times 2 \)
    \ (B = \ frac {\ pi} {3} + 2n \ pi \) или \ (B = \frac{5\pi }{3} + 2n\pi \)
    Обратите внимание, что угол \(\theta\) или \(\frac {B}{2}\) имеет период \(\ pi\), а переменная \(B\) имеет период \(2\pi\).

    Шаг 5: Применение любого ограничения Доступно
    Последний шаг решения тригонометрического уравнения включает в себя применение любого заданного ограничения. Наиболее распространенным ограничением является предоставляемый интервал. Он предоставляется либо в виде обозначения, либо в виде неравенства.
    Например:
    Обозначение интервала: \(( – \pi ,\;2\pi )\)
    Неравенство: \( – \pi \le \theta < 2\pi \)
    Помните об открытых или закрытых интервалах или слабое и строгое неравенства, в зависимости от того, что применяется, если они снабжены интервалами.
    При отсутствии ограничений шаг \(4\) является последним. Набор решений будет содержать все действительные решения, полученные на предыдущем шаге.

    Пример 2: Используя общее решение из шага \(4\), мы имеем:
    \(B = \frac{\pi }{3} + 2n\pi \) или \(B = \frac{5 \pi }{3} + 2n\pi \)
    Допустим, неравенство равно \(0 \le B < \pi \)

    Шаг 5: Примените ограничение.
    я. Для \(n = \,- 1\),
    \(B = \frac{\pi }{3} + 2\left( { – 1} \right)\pi \) или \(B = \frac{ 5 \pi }{3} + 2\влево( { – 1} \вправо)\pi \)
    \(B = \frac{\pi }{3} – 2\pi \) или \(B = \frac{5\pi }{3} – 2\pi \)
    \(B =\, – \ frac{{5\pi }}{3}\) или \(B = \,- \frac{{\pi }}{3}\)
    ii. Для \(n = 0\),
    \(B = \frac{\pi} {3} + 2\left({0} \right)\pi \) или \(B = \frac{5 \pi} {3} + 2\left( { 0} \right)\pi \)
    \(B = \frac{{\pi}}{3}\) или \(B = \frac{{5\pi}} {3}\)
    Обратите внимание, что существует только одно решение, лежащее в заданном интервале.
    \(\следовательно \) Решение: \(B = \frac {\pi}{3}\)
    Это называется главным решением тригонометрического уравнения.

    Общее решение против основного решения

    Решение тригонометрических уравнений может привести к двум типам решений – основному и общему.
    Для тригонометрических уравнений, содержащих тригонометрические функции от переменной \(x\), где \(x\) лежит в интервале \([0,\,2\pi]\), называется главным решением.
    Если решение тригонометрического уравнения находится в терминах \(n\), где \(n\) — целое число, оно называется общим решением.

    Выводы и доказательства теорем 9n}y,\;n \in Z\)


    Доказательство:
    Дано: \(\sin\,x = \sin\,y\)
    Перестановка, \(\sin\,x – \sin\, y = 0\)
    \( \Rightarrow 2\cos \;\frac{{x + y}}{2}\;\sin \;\frac{{x — y}}{2} = 0\)
    \(\следовательно \,\cos\;\frac{{x + y}}{2} = 0\) или \(\sin \;\frac{{x — y}}{2} = 0\)
    \( \Rightarrow \frac{{x + y}}{2} = \left( {2n + 1} \right)\frac{\pi }{2}\) или \(\frac{{x — y} }{2} = n\pi \), где \(n = Z\)
    Упрощая, получаем,
    \(x = \left( {2n + 1} \right)\pi – y\) или \( х = 2п\пи + у\) 9n}y,\;n \in Z\).

    Теорема 2: Для любых действительных чисел \(x\) и \(y\), \(\cos \,x = \cos \,y\; \Rightarrow x = 2n\pi \pm y,\, \;n \in Z\).
    Доказательство:
    Дано: \(\cos \,x = \cos \,y\)
    Перестановка, \(\cos \,x — \cos \,y = 0\)
    \( \Rightarrow — 2 \sin \;\frac{{x + y}}{2}\;\sin \;\frac{{x — y}}{2} = 0\)
    \(\следовательно \,\sin \;\ frac{{x + y}}{2} = 0\) или \(\sin \;\frac{{x — y}}{2} = 0\)
    \( \Rightarrow \frac{{x + y }}{2} = n\pi \) или \( \frac{{x – y}}{2} = n\pi \), где \(n = Z\)
    Упрощая, получаем,
    \(x = 2n\pi – y\) или \(x = 2n\pi + y\)
    Объединяя, получаем, \(x = 2n\pi \pm y,\,n \в З\)

    Теорема 3: Если \(x\) и \(y\) не являются нечетными кратными \(\frac {\pi}{2}\), то докажите, что \(\tan \,x = \tan \,y\; \Стрелка вправо x = n\pi + y,\,n \in Z\).
    Доказательство:
    Дано: \(\tan \,x = \tan \,y\)
    Перестановка, \(\tan \,x – \tan \,y = 0\)
    \( \Rightarrow \frac {{\ sin \, x \; \ cos \, y \; — \ cos \, x \, \ sin \, y}} {{\ cos \, x \; \ cos \, y}} = 0 \ )
    \(\sin \,x\;\cos \,y – \cos \,x\;\sin \,y = 0\)
    Это можно записать как
    \(\sin \,(x – y ) = 0\)
    \(\следовательно, x – y = n\pi\)
    \( \Стрелка вправо x = n\pi + y,\,n \in Z\).

    Тригонометрические уравнения и их общие решения

    Ниже приведен список общих тригонометрических уравнений и их общих решений, где \(n\) — целое число.

    Тригонометрическое уравнение Общее решение 9n}\alpha \)
    \(\cos\,\theta = \cos\,\alpha \) \(\theta = 2n\pi \pm \alpha \)
    \(\ tan \,\theta = \tan \,\alpha \) \(\theta = n\pi + \alpha \)
    \(\sin \,\theta = 0\) \(\ тета = n\pi \)
    \(\cos \,\theta = 0\) \(\theta = \left( {2n + 1} \right)\frac{\pi} {2} \)
    \(\tan \,\theta = 0\) \(\theta = n \pi\)
    \(\sin \,\theta = 1\) \(\theta = \left( {4n + 1} \right)\frac{\pi }{2}\)
    \( \cos\,\theta = 1\) \(\theta = 2 n \pi\)
    \(\sin \,\theta = – 1\) \(\theta = \left( {4n – 1} \right)\frac{\pi }{2}\)
    \(\cos \,\theta = – 1\) \(\theta = \left( {2n + 1 } \right) {\pi }\)
    \(\theta = \alpha \) \(\theta = n\pi \pm \alpha \) 92}} }}\)

    Теперь научимся решать тригонометрические уравнения, используя опорные углы и тригонометрические тождества.

    Решенные задачи: тригонометрические уравнения

    Q.1. Каковы решения \(\sin \;\left( {x\; – \;\frac{\pi }{3}} \right) =\,- \frac{1}{2}\) в \(x-\) интервал \([0,\,2\pi]\)?
    Ответ:     Возьмите \(x\; – \;\frac{\pi }{3} = y\)
    \(\следовательно \,\sin \,y\; = \,- \frac{1} {2}\)
    \( \Rightarrow y = \,- \frac{\pi }{6},\,\frac{{7\pi }}{6}\) (в интервале \(\left[ {0,\,2\pi } \right] – \frac{\pi }{3} \le \left( {x – \frac{\pi }{3}} \right) \le \frac{{5 \пи}}{3}\)) 9{\rm{o}}}.\)
    Ответ:     Используя, \(\alpha = 1 – \alpha\),
    Получаем, \(\alpha = \,-\cos \;\alpha + \ влево( {1 — \alpha } \right)\)
    \(\alpha \; + \alpha \; + \cos \,\alpha \; — 1 = 0\)
    \(2 \alpha \; + \ cos \,\alpha \; – 1 = 0\)
    Факторинг,
    \((2 \cos \,\alpha \; – 1)(\cos\,\alpha \; + 1) = 0\)
    Отсюда ,
    \((2 \cos \,\alpha \; — 1) = 0\) и \((\cos \,\alpha \; + 1) = 0\)
    \(2 \cos \,\alpha = 1\) и \(\cos\,\alpha = \,- 1\)
    \(\cos \,\alpha = \frac {1}{2}\) 9\круг\).

    Q.4. Найдите общее решение уравнения \(\cos \;2x\; – 2\tan \;x\; + 2 = 0\)
    Ответ:     Используя \(\cos \;2x\; = \frac{ {1 – x\;}}{{1 + x}}\), получаем,
    \(\frac{{1 – x\;}}{{1 + x\;}} – 2\tan \, x\; + 2 = 0\)
    \(1 – x\; – 2\tan \,x\;\left( {1 + x\;} \right) + 2\left( {1 + x\; } \right) = 0\)
    \(1 — x\; — 2\tan \,x\; — 2x\; + 2 + 2x\; = 0\)
    \( — 2x\; + x\; – 2\tan \,x\; + 3 = 0\)
    \(2x\; – x\; + 2\tan \,x\; – 3 = 0\)
    Разлагая на множители, получаем
    \(\left( {\tan \,x\; — 1} \right)\left( {2x\; + \tan \,x\; + 3} \right) = 0\)
    Здесь
    \(\left( {2x\; + \tan \,x\; + 3} \right)\) имеет мнимые корни.
    Следовательно, \(\left( {\tan \,x\; – 1} \right) = 0\)
    \( \Стрелка вправо \tan \,x = 1\)
    \(x = \frac{\pi {4} + п\пи \).

    Q.5. Найдите все решения для \(\left({\frac{E}{2}} \right) — \;\left({\frac{E}{2}} \right) = 1\).
    Ответ:     Замена \(\left({\frac{E}{2}} \right) = 1\; — \left({\frac{E}{2}} \right)\) 9\цирк\).

    Резюме

    Итак, мы знаем, что такое тригонометрические уравнения, как можно вывести некоторые первичные тригонометрические уравнения с помощью тригонометрических функций и тригонометрические тождества. Существует два типа решений тригонометрических уравнений – общее решение и основное решение. В то время как общее решение записывается через n, где n — целое число, главное решение представляет собой тригонометрическую функцию от переменной \(x\), где \(x\) лежит в интервале \([0,\,2 \Пи]\).

    Научившись находить решение тригонометрических уравнений за пять шагов, мы также решили несколько примеров, используя полученные знания.

    Изучите важные формулы тригонометрии

    Часто задаваемые вопросы (FAQ)

    Q.1. Что такое тригонометрические уравнения?
    Ответ:     Уравнения, в которые входят тригонометрические функции переменной, называются тригонометрическими уравнениями.

    Q. 2. В чем польза тригонометрических уравнений?
    Ответ:     Хотя тригонометрия может не иметь прямого применения в сценариях реальной жизни, она используется в различных областях. Тригонометрия применяется в медицине, геодезии, архитектуре, звуковом дизайне, спутниковой навигации и астрономии.

    Q.3. Как решать тригонометрические уравнения?
    Ответ:     Чтобы аналитически решить тригонометрическое уравнение, выполните следующие действия.
    Шаг 1: Перепишите уравнение в терминах одной функции одного угла.
    Шаг 2: Найдите значения в тригонометрической функции.
    Шаг 3: Перечислите различные возможные решения для угла. Решите для угла.
    Шаг 4: Найдите переменную, если необходимо.
    Шаг 5: Примените любые ограничения, если они доступны.

    Q.4. Являются ли тригонометрические уравнения линейными?
    Ans:     Линейное уравнение имеет вид \(ax + bx = c\).

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *