Квадратные неравенства — tutomath.ru репетитор по математике
Чтобы решить квадратные неравенства вспомним, что такое квадратичная функция?
Квадратичная функция – это функция записанная формулой : y=ax2+bx+c, где x – независимая переменная, a, b и c – некоторые числа, при этом a≠0.
Графиком квадратичной функции является парабола.
В зависимости от значения a ветви графика направлены вверх или вниз:
- если a>0, то ветви параболы направлены вверх;
- если a<0, то ветви параболы направлены вниз;
- точки пересечения параболы с осью x, называются нулями функции и являются корнями квадратного уравнения: ax2+bx+c=0
Квадратные неравенства имеют вид.
ax2+bx+c>0
ax2+bx+c<0
ax2+bx+c≥0
ax2+bx+c≤0
Чтобы начать решать квадратные неравенства, необходимо знать как решаются квадратные уравнения?
А также для графического метода решения неравенства, необходимо знать алгоритм построения квадратичной функции или параболы?
Как решать квадратные неравенства?
Решение квадратных неравенств рассмотрим на примерах. Для начала разберем случаи, когда у квадратного уравнения дискриминант меньше нуля (нет корней).
Для начала разберем случаи, когда у квадратного уравнения дискриминант меньше нуля (нет корней).
Пример:
3x2+2x+20>0
Приравняем к 0
3x2+2x+20=0
D=22—4•3•20=—236
Дискриминант меньше нуля —236, следовательно у уравнения нет корней, а это значит, что весь график параболы находится выше оси х, потому что а=3>0 (ветви параболы смотрят вверх)
Можно проверить себя взяв любое число с числовой прямой, например число 1. Подставить число 1 вместо переменой х в неравенство 3x2+2x+20>0.
3•12+2•1+20>0
25>0
Получили верное неравенство 25>0, следовательно так как у нас нет корней уравнения нам подойдут все точки числовой прямой.
Ответ: x∈(-∞; +∞)
Пример:
Рассмотрим этот же пример со знаком неравенства меньше 0
3x2+2x+20<0
Приравняем к 0
3x2+2x+20=0
D=22—4•3•20=—236
Дискриминант меньше нуля —236, следовательно у уравнения нет корней, значит парабола не пересекает ось x. Весь график параболы находится выше оси х, потому что а=3>0.
Весь график параболы находится выше оси х, потому что а=3>0.
А знак уравнения меньше <0. Так как ниже оси x у нас нет параболы, следовательно нет решения у данного неравенства.
Можно проверить себя взяв любое число с числовой прямой, например число 1. Подставить число 1 вместо переменой х в неравенство 3x2+2x+20<0.
3•12+2•1+20<0
25<0
Получили неверное неравенство 25<0, следовательно у неравенства нет решения или пустое множество ø.
Ответ: x∈ ø
Пример:
Рассмотрим следующий пример.
x2+x-2<0
Приравняем к 0
x2+x-2=0
D=12—4•1•(—2)=9
x1=(-1+3)⁚2=1
x2=(-1-3)⁚2=-2
Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.
Знак уравнения меньше <0. Нам в ответ необходимо записать часть параболы, которая находится ниже оси x.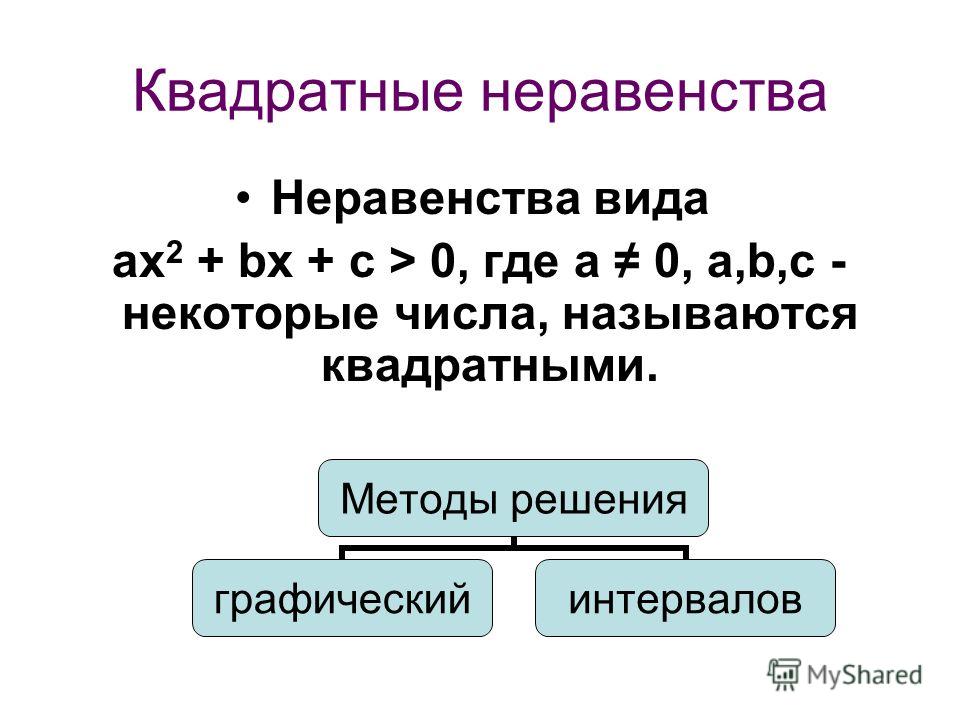 Визуально графически можно оценить по картинке, нам подходит интервал (-2;1).
Визуально графически можно оценить по картинке, нам подходит интервал (-2;1).
Также можно решить методом интервалов. Ось x делится на три участка. Первый участок (-∞;-2). На этом участке можно взять любое число меньше -2, например возьмем число -3 и подставим в неравенство x2+x-2<0 вместо переменой x.
(-3)2+(-3)-2<0
4<0
Получили неверное неравенство 4<0, следовательно у неравенства нет решения на участке (-∞; 2).
Второй участок (-2; 1). На этом участке можно взять число 0.
(0)2+(0)-2<0
-2<0
Получили верное неравенство -2<0, следовательно этот участок (-2; 1) подходит нам для ответа.
Третий участок (1; +∞). На этом участке можно взять число 2.
(2)2+(2)-2<0
4<0
Получили неверное неравенство 4<0, следовательно у неравенства нет решения на участке (1; +∞).
Ответ: x∈(-2; 1)
Пример:
Рассмотрим этот же пример с другим знаком неравенства.
x2+x-2>0
x2+x-2=0
D=12—4•1•(—2)=9
x1=(-1+3)⁚2=1
x2=(-1-3)⁚2=-2
Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.
Знак уравнения больше >0. Нам в ответ необходимо записать часть параболы, которая находится выше оси x. Визуально графически можно оценить по картинке, нам подходят интервалы (-∞;-2) и (1;+∞).
Также можно решить методом интервалов. Ось x делится на три участка.
Первый участок (-∞;-2). На этом участке можно взять любое число меньше -2, например возьмем число -3 и подставим в неравенство x2+x-2<0 вместо переменой x.
(-3)2+(-3)-2>0
4>0
Получили верное неравенство 4>0, следовательно этот интервал (-∞; 2) подходит.
Второй участок (-2; 1). На этом участке можно взять число 0.
(0)2+(0)-2>0
-2>0
Получили неверное неравенство -2>0, следовательно этот интервал (-2; 1) не подходит.
Третий участок (1; +∞). На этом участке возьмем число 2.
(2)2+(2)-2>0
4>0
Получили верное неравенство 4>0, следовательно этот интервал (1; +∞) подходит.
Ответ: x∈(-∞; 2)⋃(1; +∞)
Как решать квадратные неравенства методом интервалов
В данной публикации мы рассмотрим, что такое квадратное неравенство, и как оно решается методом интервалов в зависимости от количества корней. Также разберем практические примеры по этой теме.
- Определение квадратного неравенства
- Решение квадратных неравенств
- С двумя корнями
- С одним корнем
- Без корней
Определение квадратного неравенства
Если старшая степень неизвестной переменной (чаще всего это x) равняется двум, то неравенство называется квадратным.
Например:
- x2 – 3x + 4 > 0
- 2x2 + 7x – 5 < 0
- x2 + 12x + 2 ≥ 0
- 3x2 – 4 ≤ 0
Решение квадратных неравенств
С двумя корнями
Квадратные уравнения решаются с помощью так называемого метода интервалов, принцип которого заключается в следующем:
1.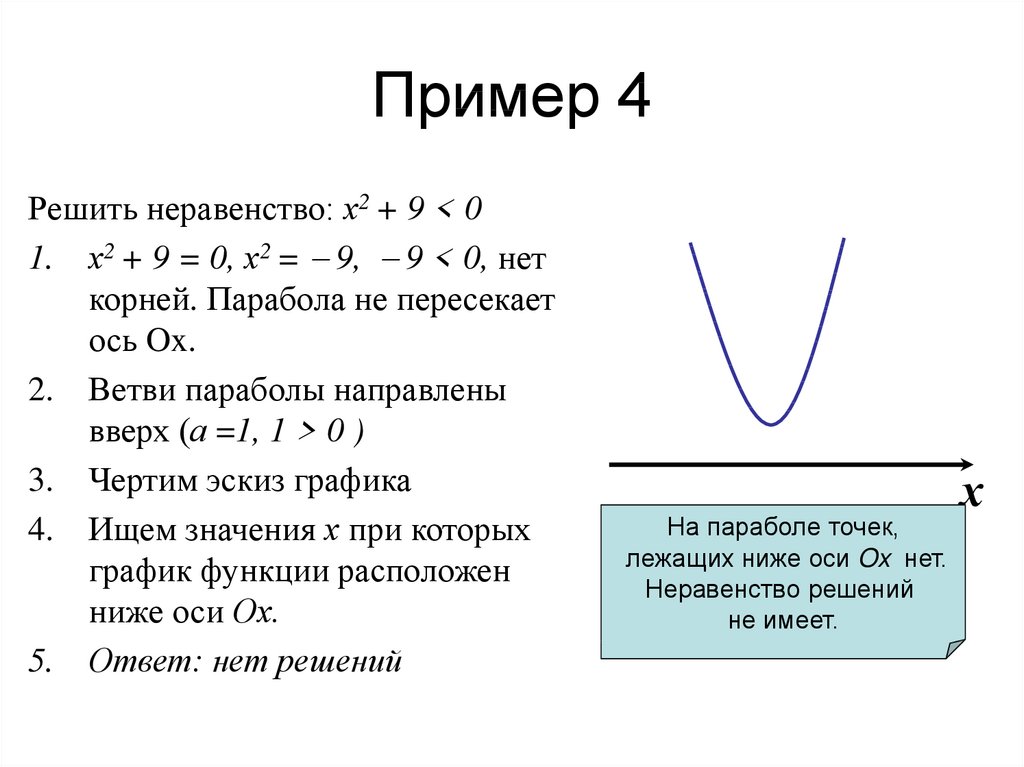 Все элементы неравенства собираем в левой части, в правой должен остаться только ноль. Помним, что при переносе элемента из одной части в другую его знак меняется на противоположный.
Все элементы неравенства собираем в левой части, в правой должен остаться только ноль. Помним, что при переносе элемента из одной части в другую его знак меняется на противоположный.
2. Если перед неизвестной переменной во второй степени стоит отрицательный коэффициент, умножаем все элементы неравенства на число -1, изменив знак сравнения на противоположный.
3. Заменив знак сравнения на “равно” решаем полученное квадратное уравнение.
4. Найденные корни отмечаем на числовой оси.
При этом, если знак сравнения строгий (“больше” или “меньше”), то отметкой обычно является незакрашенный внутри кружок, если нестрогий (“больше или равно”, “меньше или равно”) – закрашенный.
5. Рисуем интервалы, и справа-налево присваиваем им знаки “плюс” и “минус” (начинаем с “+”, затем чередуем).
6. Если в неравенстве стоят знаки “>“ или “≥“, нам нужны положительные интервалы, если “<“ или “≤“ – отрицательные.
Пример 1
Решим квадратное неравенство x2 + 4x > -3.
Решение:
1. Т.к. правая часть должны быть нулевой, перенесем число -3 в левую, заменив его знак на “плюс”:
x2 + 4x + 3 > 0
2. Теперь найдем корни квадратного уравнения x2 + 4x + 3 = 0.
Мы подробно рассматривали данный вопрос в отдельной публикации, поэтому здесь отдельно на этом останавливаться не будем.
Итак, корни заданного уравнения: x1 = -1, x2 = -3. Отмечаем их на числовой оси (незакрашенные кружки, т.к. неравенство является строгим).
Рисуем интервалы, отметив знаками “плюс” и “минус”.
Нам нужные только положительные области, т.к. в неравенстве стоит знак “больше”.
Таким образом, решение неравенства следующее:
x > -1 и x < -3.
Примечание: если бы в рассматриваемом нами неравенстве стояли другие знаки, область решения была бы следующей:
- знак “<“, тогда -3 < x < -1
- знак “≥”, тогда x ≥ -1 и x ≤ -3
- знак “≤”, тогда -3 ≤ x ≤ -1
С одним корнем
Квадратные уравнения не всегда имеют два корня, иногда он может быть один.
Пример 2
Давайте решим x2 – 4x + 4 < 0.
Решение:
Корень у соответствующего квадратного уравнения всего один: x1 = x2 = 2, т.е. его значение повторяется дважды.
Отмечаем точку в виде незаполненного кружка на числовой оси и рисуем два исходящих от нее интервала.
Теперь нужно присвоить знаки интервалам, и здесь эта процедура отличается от описанного выше (когда у уравнения два корня): если значение корня в уравнении повторяется четное количество раз, то при смене интервалов знак не меняется. Проставляем их, также, справа-налево, начав с “плюса”.
В нашем случае значение повторяется два раза, т.е. получаем:
Нам нужны только отрицательные интервалы, а их здесь нет. К тому же, неравенство строгое. Следовательно, решений у него нет.
Примечание: если бы этом неравенстве стояли другие знаки, область решения была бы следующей:
- знак “>”, тогда x > 2 и x < 2
- знак “≥”, тогда x ≥ 2 и x ≤ 2, т.
 е. все действительные числа.
е. все действительные числа. - знак “≤”, единственное решение – это x = 2
Без корней
В некоторых случаях квадратные уравнения могут и вовсе не иметь действительных корней.
В этом случае у соответствующее неравенства, также, не будет действительных решений. Это и будет ответом.
Пример 3
x2 + 3x + 5 > 0
Решение:
Уравнение не имеет корней, следовательно, у неравенства нет действительных решений.
Решение квадратных неравенств
Чтобы решить квадратное неравенство, выполните следующие действия:
Решите неравенство, как уравнение.
Вещественные решения уравнения становятся граничными точками для решения неравенства.
Сделайте граничные точки сплошными кругами, если исходное неравенство включает равенство; в противном случае сделайте граничные точки незамкнутыми кругами.
Выберите точки из каждой области, созданной граничными точками.
 Замените эти «контрольные точки» в исходном неравенстве.
Замените эти «контрольные точки» в исходном неравенстве. Если контрольная точка удовлетворяет исходному неравенству, то область, содержащая эту контрольную точку, является частью решения.
Представьте решение в графической форме и в виде набора решений.
Пример 1
Решить ( x – 3)( х + 2) > 0,
Решите ( x – 3)( x + 2) = 0. По свойству нулевого произведения,
Сделайте граничные точки. Здесь граничные точки — открытые кружки, поскольку исходное неравенство не включает равенство (см. рис. 1).
Выберите точки из разных созданных регионов (см. рис. 2).
Проверить, удовлетворяют ли контрольные точки исходному неравенству.
С х = –3 удовлетворяет исходному неравенству, область х < –2 является частью решения. Поскольку x = 0 не удовлетворяет исходному неравенству, область –2 < x < 3 не является частью решения. Поскольку x = 4 удовлетворяет исходному неравенству, область x > 3 является частью решения.
Поскольку x = 4 удовлетворяет исходному неравенству, область x > 3 является частью решения.
Представьте решение в графической форме и в виде набора решений. Графическая форма показана на рисунке 3.
Форма набора решений: { x | x < –2 или x > 3}.
Рис. 1. Граничные точки.
Рис. 2. Созданы три области.
Рисунок 3. Решение примера
Пример 2
Решить 9 x 2 – 2 ≤ –3 x .
По факторингу,
Отметьте граничные точки сплошными кружками, как показано на рис. 4, поскольку исходное неравенство включает равенство.
Выберите точки из созданных областей (см. рис. 5).
Проверить, удовлетворяют ли контрольные точки исходному неравенству.
Поскольку x = –1 не удовлетворяет исходному неравенству, область не является частью решения. Поскольку x = 0 удовлетворяет исходному неравенству, область является частью решения.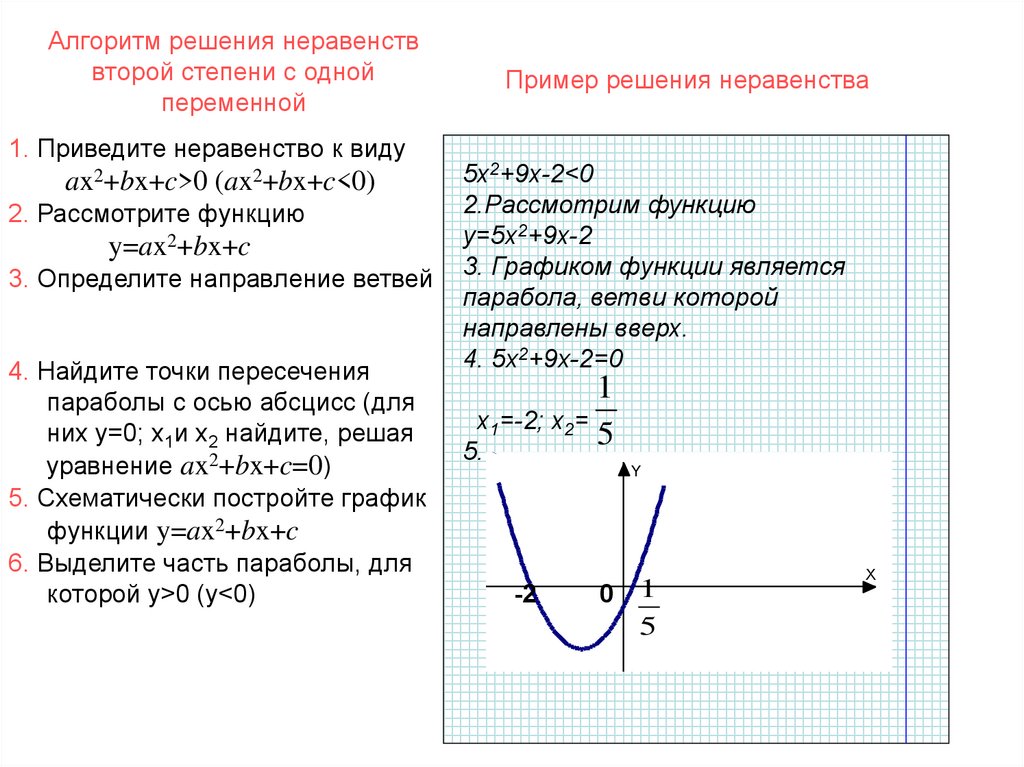 Поскольку x = 1 не удовлетворяет исходному неравенству, область составляет , а не часть решения.
Поскольку x = 1 не удовлетворяет исходному неравенству, область составляет , а не часть решения.
Представьте решение в графической форме и в виде набора решений. Графическая форма показана на рисунке 6.
Форма набораРисунок 4. Сплошные точки означают включение.
Рисунок 5. Области для тестирования для примера
Рис. 6. Решение примера.
Пример 3
Решить 4 t 2 – 9 < –4 t .
Так как это квадратичное число нелегко разложить на множители, для его решения используется квадратичная формула.
Уменьшить путем деления общего множителя 4.
Так как примерно 3.2,
Отметьте граничные точки незакрашенными кружками, как показано на рис. 7, поскольку исходное неравенство не включает равенство.
Выберите точки из разных созданных регионов (см. рис. 8).
Проверить, удовлетворяют ли контрольные точки исходному неравенству.
Поскольку t = 3 не удовлетворяет исходному неравенству, область не является частью решения. Поскольку
Представьте решение в графической форме и в виде набора решений. Графическая форма показана на рисунке 9.
Форма набора решений
Рисунок 7. Открытые точки означают исключение.
Рис. 8. Области для тестирования для примера.
Рис. 9. Решение примера.
Пример 4
Решить
Так как это квадратное число не может быть факторизовано с помощью рациональных чисел, для его решения будет использоваться формула квадратного уравнения.
Это воображаемые ответы, и их нельзя отобразить на прямой числовой прямой. Следовательно, неравенство х 2 + 2 х + 5 < 0 не имеет действительных решений.
Решение и графическое изображение квадратных неравенств: шаги и примеры
Ранее мы научились строить графические изображения квадратных уравнений, чтобы найти их корни. Графически визуализируя эти квадратные уравнения, мы смогли определить поведение кривой для данного квадратного уравнения. В этом уроке мы стремимся построить графики квадратных неравенств так же, как мы делали это для квадратных уравнений.
Квадратные неравенства
Прежде чем мы начнем, давайте определим квадратное неравенство.
A Квадратное неравенство — это полином второй степени, в котором вместо знака равенства используется знак неравенства.
Существует четыре типа квадратных неравенств (с двумя переменными), которые мы обсудим в этой теме, а именно
квадратное неравенство с одной переменной имеет только одно неизвестное в квадратном выражении и может быть представлено на одной оси или числовая линия — обычно это ось x.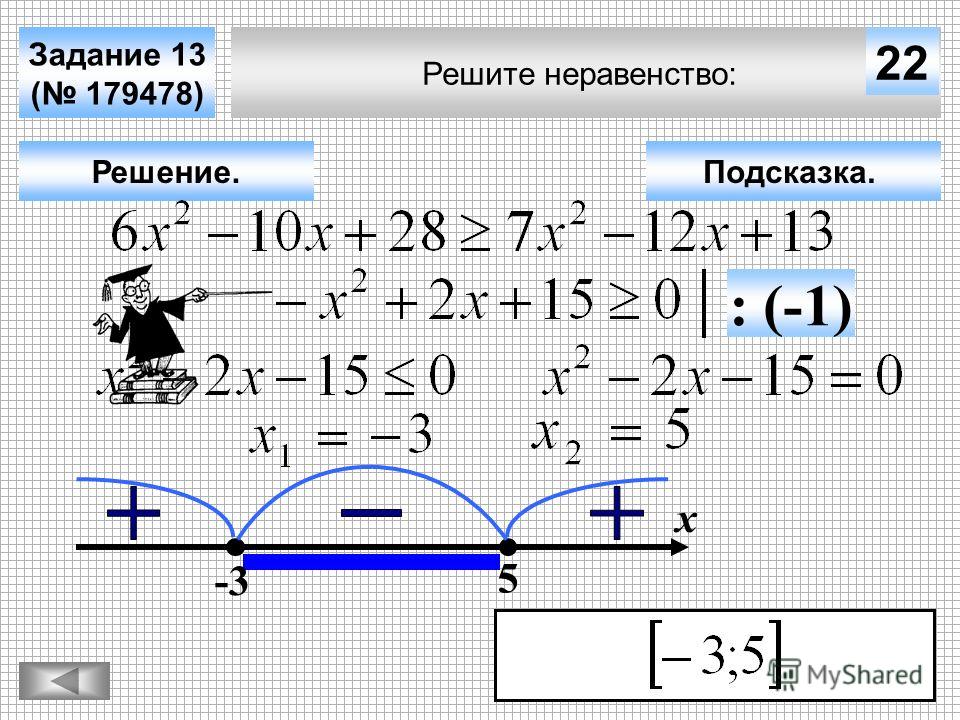 График квадратного неравенства с двумя переменными составляют все упорядоченные пары (x, y), являющиеся решениями данного квадратного неравенства.
График квадратного неравенства с двумя переменными составляют все упорядоченные пары (x, y), являющиеся решениями данного квадратного неравенства.
Квадратное неравенство с двумя переменными описывает область на декартовой плоскости с параболой (кривой) в качестве границы. Здесь мы рассматриваем как ось x, так и ось y.
Стандартные формы квадратных неравенств (с одной переменной):
Решение квадратных неравенств с одной переменной
Решение квадратных неравенств с одной переменной в основном аналогично решению квадратных уравнений. Единственное отличие здесь состоит в том, что нас интересует нахождение интервала действительных чисел, для которого выполняется неравенство, а не приравнивание заданного выражения к нулю.
В этом разделе мы будем использовать основные методы факторизации для решения таких квадратных неравенств. Шаги для этой техники объясняются ниже.
Шаг 1: Запишите квадратное неравенство в общем виде, т. е. с ax 2 + bx + c, где a ≠ 0, в одной части неравенства;
е. с ax 2 + bx + c, где a ≠ 0, в одной части неравенства;
Шаг 2: Полностью факторизовать квадратное выражение неравенства;
Шаг 3: Определите корни неравенства с помощью соответствующего уравнения;
Шаг 4: Определите поведение квадратного неравенства:
Если неравенство имеет вид когда тогда, ;
Если неравенство имеет вид когда то .
Шаг 5: Выразите решение в виде неравенства или в виде интервала
Случаи а) и б) следуют аналогично для неравенств < и > соответственно.
Графики квадратных неравенств с одной переменной
Для вычисления квадратных неравенств с одной переменной можно также воспользоваться графиком заданного многочлена. В таблице ниже описано графическое представление для каждого случая неравенства, которое может иметь квадратное выражение.
The shaded region in the plots below represents the correct solution to the given quadratic inequality
Case | a > 0 | a < 0 |
1 | AX 2 + BX + C <0 | |
Метод:
| Inequality graph Case 1 (a), Aishah Amri — StudySmarter Originals Solution: x 1 < x < x 2 | Inequality graph Case 1 ( b), Aishah Amri — StudySmarter Originals Решение: x |
2 | ||
2 | 5 | |
2 | 5 | |
2 9031 | 5 | |
2 | 5 | |
| 9000 2 | ||
Метод:
| График неравенства Случай 2 (a), Айша Амри — StudySmarter Оригиналы Решение: x ≤ x 1 или x ≥ x 2 | 33333333333333333333 гг. 333333333333333333333 гг. 1 ≤ x ≤ x 2 |
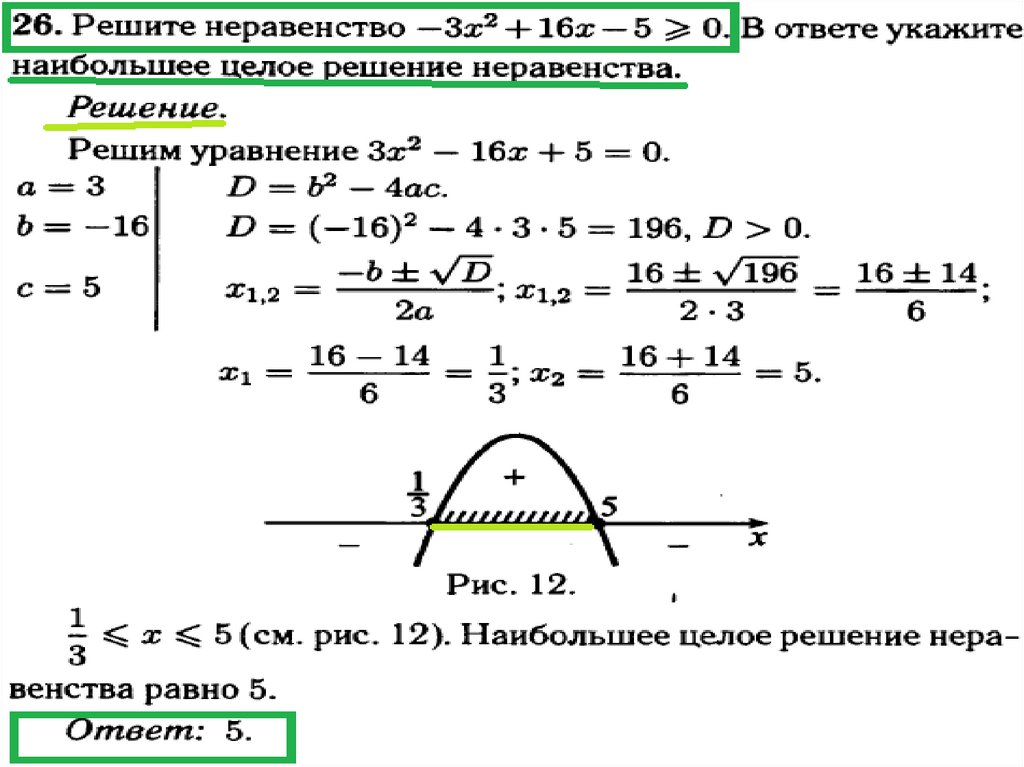
Решите неравенство .
Решение
Шаг 1: Подставляя –6 в левую часть неравенства, получаем
Факторизация этого квадратного неравенства дает
Шаг 2: Теперь нам нужно найти корни неравенства. Нашим первым побуждением здесь может быть использование свойства нулевого продукта. Однако обратите внимание, что свойство нулевого продукта используется для уравнений, а не для неравенств. Вместо этого нам нужно решить для точек пересечения по оси x, переключив неравенство в уравнение, а затем скорректировав знак неравенства для рассматриваемой ситуации с точки зрения найденных точек пересечения по оси x. Это показано ниже.
Вместо этого нам нужно решить для точек пересечения по оси x, переключив неравенство в уравнение, а затем скорректировав знак неравенства для рассматриваемой ситуации с точки зрения найденных точек пересечения по оси x. Это показано ниже.
Шаг 3: Из таблицы мы находим, что это неравенство удовлетворяет случаю 2 с a > 0. Поскольку y положителен, мы должны выбрать значения x, при которых кривая находится выше оси x.
Шаг 4: Теперь, записав решение в интервальной записи, получим
График показан ниже.
Пример 1, Айша Амри — StudySmarter Originals
Решите неравенство .
Решение
Шаг 1: Подставляя 19x и –6 в левую часть неравенства, получаем
Факторизация этого квадратного неравенства дает будем рассматривать наше неравенство выше как уравнение, чтобы определить его корни, как показано ниже.
Шаг 3: Снова обратившись к нашей таблице, мы видим, что это неравенство удовлетворяет случаю 1 с a > 0. Поскольку y отрицательно, мы должны выбрать значения x, при которых кривая находится ниже оси x .
Поскольку y отрицательно, мы должны выбрать значения x, при которых кривая находится ниже оси x .
Шаг 4: Таким образом, записав решение в соответствующей ему интервальной записи, мы получим
График показан ниже.
Пример 2, Айша Амри — StudySmarter Originals
Графики квадратных неравенств с двумя переменными
Графики квадратных неравенств (с двумя переменными) основаны на тех же принципах, что и линейные неравенства. Ниже приведен подробный метод решения таких проблем.
Шаг 1: Нарисуйте квадратичную функцию y = ax 2 + bx + c. Определите характер параболы на основе данного неравенства.
Нарисуйте пунктирную параболу для неравенств с < или >, чтобы описать, что точки на параболе не являются решениями.
Нарисуйте сплошную параболу для неравенств с ≤ или ≥, чтобы описать, что точки на параболе являются решениями.

Гленко МакГроу-Хилл, Алгебра 2 (2008)
Шаг 2: Возьмите точку (x 1 , y 1 ) внутри параболы. Проверьте, является ли эта точка решением неравенства.
Glencoe McGraw-Hill, Algebra 2 (2008)
Шаг 3: Закрасьте правильную область, удовлетворяющую неравенству.
Если (x 1 , y 1 ) является решением, заштрихуйте область внутри параболы.
Если (х 1 , у 1 ) не является решением, заштрихуйте область вне параболы.
Glencoe McGraw-Hill, Algebra 2 (2008)
Ниже приведены несколько рабочих примеров, демонстрирующих эту технику.
Нарисуйте квадратное неравенство.
Решение
Шаг 1: Начнем с построения полинома
Коэффициент при x 2 отрицательный, поэтому кривая открывается вниз. Факторизуя это выражение, получаем
Приравнивая это к нулю, мы имеем корни в .
Так как неравенство >, наша кривая должна быть пунктирной линией. График показан ниже.
Пример 3 (1), Айша Амри — StudySmarter Originals
Шаг 2: Теперь проверим точку внутри параболы, скажем (1, 2). Подставляя x = 1 и y = 2 в наше квадратное неравенство, мы находим, что
Шаг 3: 2 не больше 6, поэтому неравенство неверно. Таким образом, (1, 2) не является решением неравенства, и поэтому мы должны заштриховать область вне параболы, как показано ниже.
Пример 3 (2), Айша Амри — StudySmarter Originals
Теперь, если мы рассмотрим квадратное неравенство с одной переменной, мы получим
Следовательно, y отрицательно, и мы должны выбрать значения x, для которых кривая находится ниже оси x. Окончательный график показан ниже.
Пример 3 (3), Айша Амри — StudySmarter Originals
Использование квадратичной формулы для решения квадратных неравенств неравенства.
Нарисуйте квадратное неравенство.
Решение
Шаг 1: Как и прежде, мы попытаемся сначала построить график многочлена .
Коэффициент при x 2 положительный, поэтому кривая размыкается. Обратите внимание, что мы не можем факторизовать это выражение, используя стандартные методы факторинга. Следовательно, мы будем применять квадратную формулу для определения корней.
Учитывая, что
вычисляем
Таким образом, получаем два иррациональных корня
Поскольку неравенство ≤, наша кривая должна быть сплошной линией. График показан ниже.
Пример 4 (1), Айша Амри — StudySmarter Originals
Шаг 2: Давайте теперь проверим точку внутри параболы, скажем, (1, –1). Подставляя x = 1 и y = –1 в наше неравенство, мы находим, что
Шаг 3: –1 не меньше или равно –4, поэтому неравенство не выполняется. Таким образом, (1, –1) не является решением неравенства, и поэтому мы должны заштриховать область вне параболы, как показано ниже.
Таким образом, (1, –1) не является решением неравенства, и поэтому мы должны заштриховать область вне параболы, как показано ниже.
Пример 4 (2), Айша Амри — StudySmarter Originals
Теперь, если мы рассмотрим квадратное неравенство с одной переменной, мы получим
Следовательно, y положительно, и мы должны выбрать значения x, для которых кривая выше оси x. Окончательный график показан ниже.
Пример 4 (3), Айша Амри — StudySmarter Originals
Примеры из реальной жизни с использованием квадратичных неравенств
Квадратичные неравенства могут помочь в моделировании определенных типов реальных сценариев, таких как финансы, движение и архитектура. Вот пример, который показывает, как мы можем применять квадратные неравенства в таких случаях.
Высота мяча, брошенного между двумя людьми, может быть смоделирована функцией
,
, где высота h задается в метрах, а время x в секундах. В какой момент полета мяч находится на расстоянии 6 м от земли?
Решение
Высота шара описывается функцией h.
Мы хотим найти значения x, для которых h(x) ≤ 6.
Построив график функции y = –7x 2 + 15x – 4, мы получим рисунок ниже.
Пример 5 (1), Айша Амри — StudySmarter Originals
Корни можно найти с помощью квадратичной формулы, поскольку выражение –7x 2 + 15x – 4 нельзя разложить на множители с помощью стандартных методов факторинга. При этом мы получили следующие два корня с точностью до двух знаков после запятой: x ≈ 0,31 и x ≈ 1,83.
Теперь, учитывая неравенство, область, для которой выполняется выражение, показана ниже.
Пример 5 (2), Айша Амри — StudySmarter Originals
Обратите внимание, что график лежит ниже оси x, когда x < 0,31 или x > 1,83. Отсюда делаем вывод, что мяч находится в пределах 6 метров от земли первые 0,31 секунды своего полета и снова через 1,83 секунды, пока мяч не коснется земли через 2,14 секунды.
Графики и решения квадратных неравенств — ключевые выводы
- График квадратного неравенства состоит из всех упорядоченных пар (x, y), являющихся решениями данного квадратного неравенства.

- Решение квадратных неравенств с одной переменной
- Запишите квадратное неравенство в общем виде: ax 2 + bx + c, где a ≠ 0
- Полностью факторизуем квадратное выражение неравенства
- I 9024 неравенства
- Выразите решение в виде неравенства или интервального обозначения
- Определите поведение квадратного неравенства
- Для неравенств < или > парабола представляет собой пунктирную линию. Это показывает, что точки на параболе не являются решениями.
- Для неравенств ≤ или ≥ парабола сплошная. Это показывает, что точки на параболе являются решениями.
- График квадратичных неравенств с двумя переменными
- Нарисовать квадратичную функцию y = ax 2 + bx + c. Определите характер параболы на основе данного неравенства.
- Возьмем точку (x 1 , y 1 ) внутри параболы. Проверьте, является ли эта точка решением неравенства.


 е. все действительные числа.
е. все действительные числа. Замените эти «контрольные точки» в исходном неравенстве.
Замените эти «контрольные точки» в исходном неравенстве. 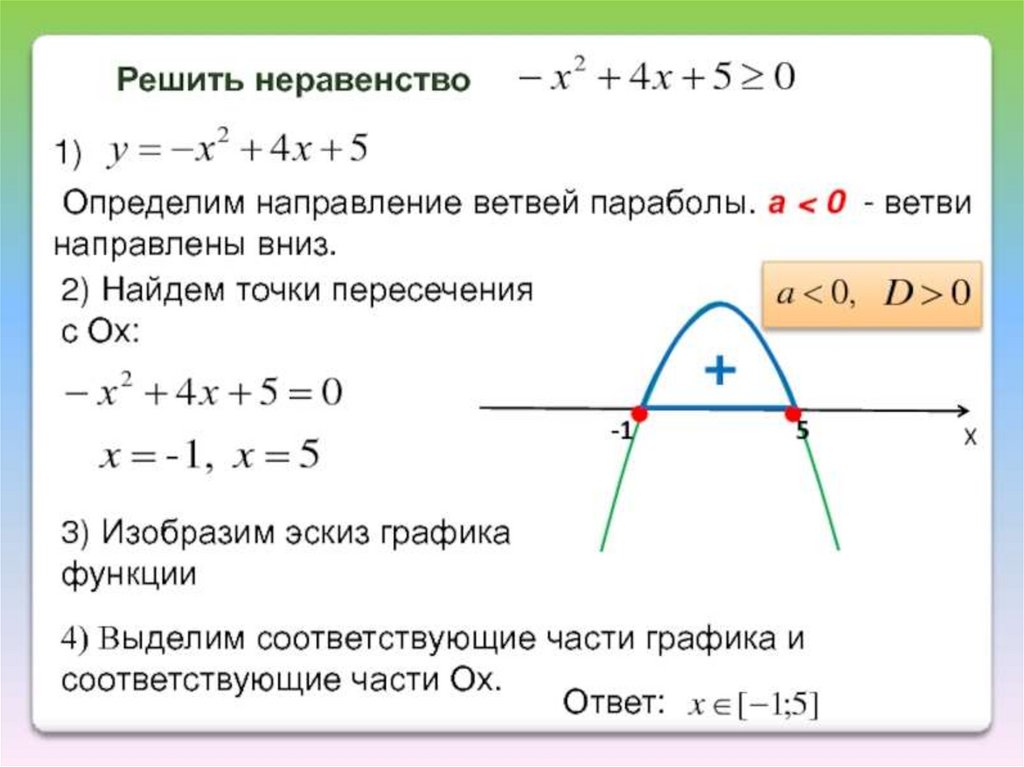 SIELECT SIELECT SIELECT SIFECT SIFEGE SIFEAR SIFEA SIFEA SIFEA DY. -значения, для которых график лежит ниже оси x
SIELECT SIELECT SIELECT SIFECT SIFEGE SIFEAR SIFEA SIFEA SIFEA DY. -значения, для которых график лежит ниже оси x , включите x-перехваты в решение. Это обозначено закрытыми кружками (как видно на графике)
, включите x-перехваты в решение. Это обозначено закрытыми кружками (как видно на графике)

