Как решить функции: § Функция y = kx и её график. Решение задач.

Содержание

Функции в программировании. Урок 11 курса «Python. Введение в программирование»

Функция в программировании представляет собой обособленный участок кода, который можно вызывать, обратившись к нему по имени, которым он был назван. При вызове происходит выполнение команд тела функции.

Функции можно сравнить с небольшими программками, которые сами по себе, то есть автономно, не исполняются, а встраиваются в обычную программу. Нередко их так и называют – подпрограммы. Других ключевых отличий функций от программ нет. Функции также при необходимости могут получать и возвращать данные. Только обычно они их получают не с ввода (клавиатуры, файла и др.), а из вызывающей программы. Сюда же они возвращают результат своей работы.

Существует множество встроенных в язык программирования функций. С некоторыми такими в Python мы уже сталкивались. Это print(), input(), int(), float(), str(), type(). Код их тела нам не виден, он где-то «спрятан внутри языка». Нам же предоставляется только интерфейс – имя функции.

С другой стороны, программист всегда может определять свои функции. Их называют пользовательскими. В данном случае под «пользователем» понимают программиста, а не того, кто пользует программу. Разберемся, зачем нам эти функции, и как их создавать.

Предположим, надо три раза подряд запрашивать на ввод пару чисел и складывать их. С этой целью можно использовать цикл:

i = 0
while i < 3:
    a = int(input())
    b = int(input())
    print(a+b)
    i += 1

Однако, что если перед каждым запросом чисел, надо выводить надпись, зачем они нужны, и каждый раз эта надпись разная. Мы не можем прервать цикл, а затем вернуться к тому же циклу обратно. Придется отказаться от него, и тогда получится длинный код, содержащий в разных местах одинаковые участки:

print("Сколько бананов и ананасов для обезьян?")
a = int(input())
b = int(input())
print("Всего", a+b, "шт.
  ")
 
print("Сколько жуков и червей для ежей?")
a = int(input())
b = int(input())
print("Всего", a+b, "шт.")
 
print("Сколько рыб и моллюсков для выдр?")
a = int(input())
b = int(input())
print("Всего", a+b, "шт.")

Пример исполнения программы:

Сколько бананов и ананасов для обезьян?
15
5
Всего 20 шт.
Сколько жуков и червей для ежей?
50
12
Всего 62 шт.
Сколько рыб и моллюсков для выдр?
16
8
Всего 24 шт.

Внедрение функций позволяет решить проблему дублирования кода в разных местах программы. Благодаря им можно исполнять один и тот же участок кода не сразу, а только тогда, когда он понадобится.

Определение функции. Оператор def

В языке программирования Python функции определяются с помощью оператора def. Рассмотрим код:

def count_food():
    a = int(input())
    b = int(input())
    print("Всего", a+b, "шт.")

Это пример определения функции. Как и другие сложные инструкции вроде условного оператора и циклов функция состоит из заголовка и тела.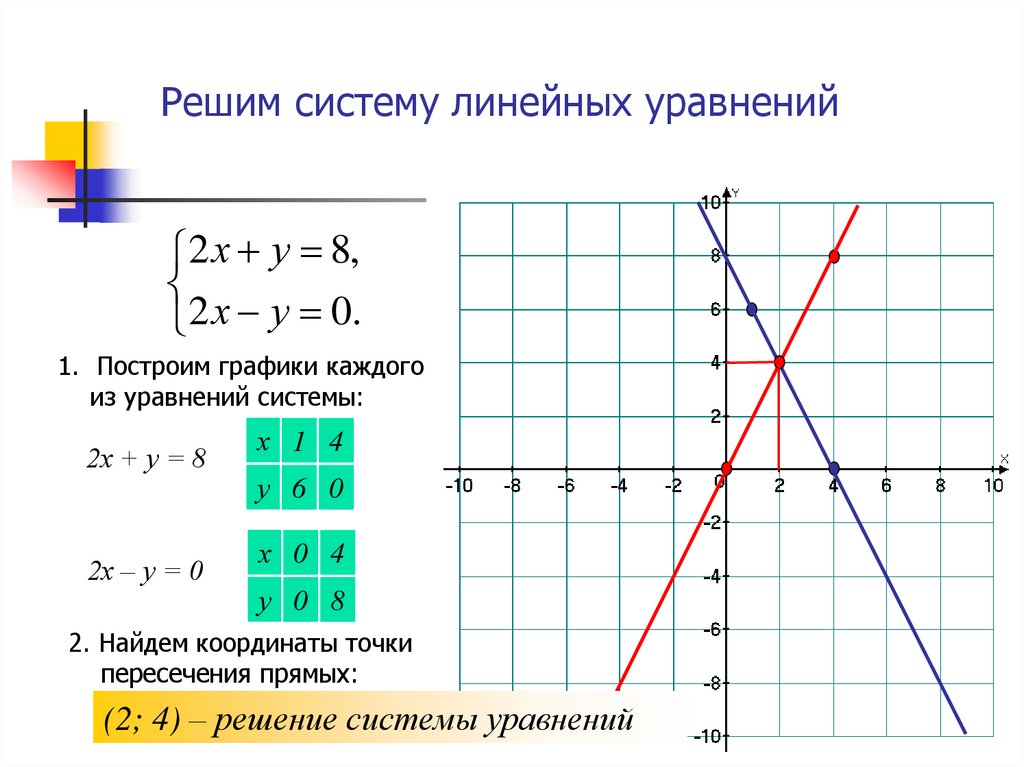 Заголовок оканчивается двоеточием и переходом на новую строку. Тело имеет отступ.

Ключевое слово def сообщает интерпретатору, что перед ним определение функции. За def следует имя функции. Оно может быть любым, также как и всякий идентификатор, например, переменная. В программировании весьма желательно давать всему осмысленные имена. Так в данном случае функция названа «посчитать_еду» в переводе на русский.

После имени функции ставятся скобки. В приведенном примере они пустые. Это значит, что функция не принимает никакие данные из вызывающей ее программы. Однако она могла бы их принимать, и тогда в скобках были бы указаны так называемые параметры.

После двоеточия следует тело, содержащее инструкции, которые выполняются при вызове функции. Следует различать определение функции и ее вызов. В программном коде они не рядом и не вместе. Можно определить функцию, но ни разу ее не вызвать. Нельзя вызвать функцию, которая не была определена.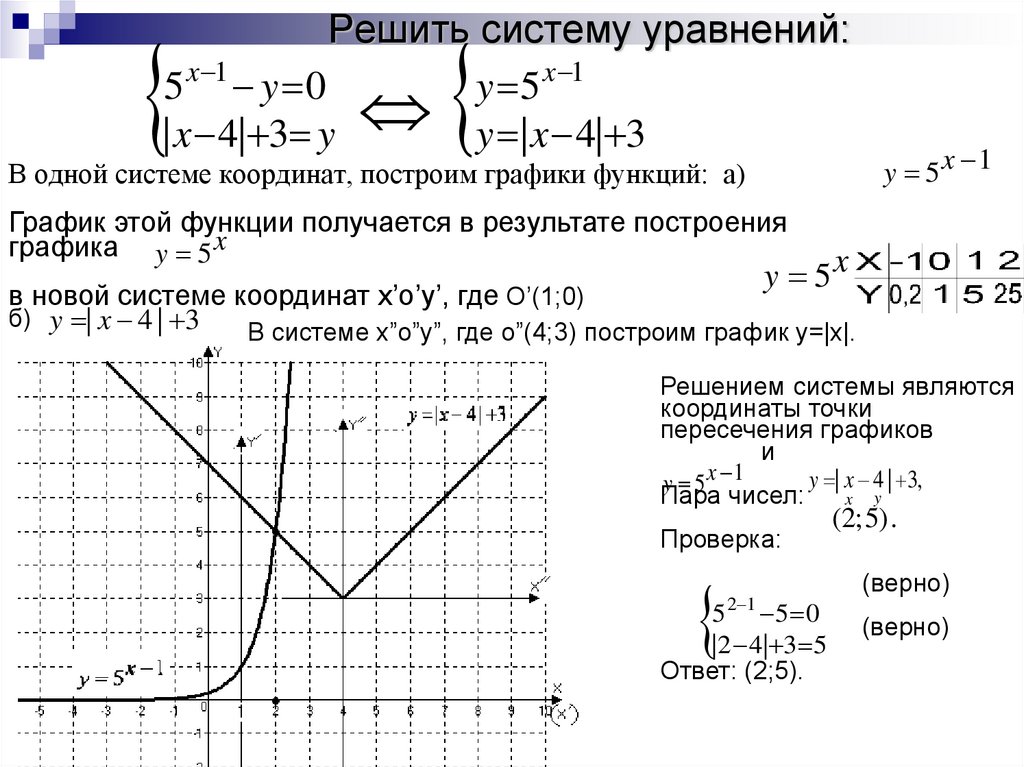

Определив функцию, но ни разу не вызвав ее, вы никогда не выполните ее тела.

Вызов функции

Рассмотрим полную версию программы с функцией:

def count_food():
    a = int(input())
    b = int(input())
    print("Всего", a+b, "шт.")
 
print("Сколько бананов и ананасов для обезьян?")
count_food()
 
print("Сколько жуков и червей для ежей?")
count_food()
 
print("Сколько рыб и моллюсков для выдр?")
count_food()

После вывода на экран каждого информационного сообщения осуществляется вызов функции, который выглядит просто как упоминание ее имени со скобками. Поскольку в функцию мы ничего не передаем скобки опять же пустые. В приведенном коде функция вызывается три раза.

Когда функция вызывается, поток выполнения программы переходит к ее определению и начинает исполнять ее тело. После того, как тело функции исполнено, поток выполнения возвращается в основной код в то место, где функция вызывалась. Далее исполняется следующее за вызовом выражение.

В языке Python определение функции должно предшествовать ее вызовам. Это связано с тем, что интерпретатор читает код строка за строкой и о том, что находится ниже по течению, ему еще неизвестно. Поэтому если вызов функции предшествует ее определению, то возникает ошибка (выбрасывается исключение NameError):

print("Сколько бананов и ананасов для обезьян?")
count_food()
 
print("Сколько жуков и червей для ежей?")
count_food()
 
print("Сколько рыб и моллюсков для выдр?")
count_food()
 
def count_food():
    a = int(input())
    b = int(input())
    print("Всего", a+b, "шт.")

Результат:

Сколько бананов и ананасов для обезьян?
Traceback (most recent call last):
  File "test.py", line 2, in <module>
    count_food()
NameError: name 'count_food' is not defined

Для многих компилируемых языков это не обязательное условие. Там можно определять и вызывать функцию в произвольных местах программы. Однако для удобочитаемости кода программисты даже в этом случае предпочитают соблюдать определенные правила.

Функции придают программе структуру

Польза функций не только в возможности многократного вызова одного и того же кода из разных мест программы. Не менее важно, что благодаря им программа обретает истинную структуру. Функции как бы разделяют ее на обособленные части, каждая из которых выполняет свою конкретную задачу.

Пусть надо написать программу, вычисляющую площади разных фигур. Пользователь указывает, площадь какой фигуры он хочет вычислить. После этого вводит исходные данные. Например, длину и ширину в случае прямоугольника. Чтобы разделить поток выполнения на несколько ветвей, следует использовать оператор

if-elif-else:

figure = input("1-прямоугольник, 
2-треугольник, 3-круг: ")
 
if figure == '1':
  a = float(input("Ширина: "))
  b = float(input("Высота: "))
  print("Площадь: %.2f" % (a*b))
elif figure == '2':
  a = float(input("Основание: "))
  h = float(input("Высота: "))
  print("Площадь: %.2f" % (0.5 * a * h))
elif figure == '3':
  r = float(input("Радиус: "))
  print("Площадь: %. 2f" % (3.14 * r**2))
else:
  print("Ошибка ввода")

Здесь нет никаких функций, и все прекрасно. Но напишем вариант с функциями:

def rectangle():
    a = float(input("Ширина: "))
    b = float(input("Высота: "))
    print("Площадь: %.2f" % (a*b))
 
def triangle():
    a = float(input("Основание: "))
    h = float(input("Высота: "))
    print("Площадь: %.2f" % (0.5 * a * h))
 
def circle():
    r = float(input("Радиус: "))
    print("Площадь: %.2f" % (3.14 * r**2))
 
figure = input("1-прямоугольник, 
2-треугольник, 3-круг: ")
if figure == '1':
  rectangle()
elif figure == '2':
  triangle()
elif figure == '3':
  circle()
else:
  print("Ошибка ввода")

Он кажется сложнее, а каждая из трех функций вызывается всего один раз. Однако из общей логики программы как бы убраны и обособлены инструкции для нахождения площадей. Программа теперь состоит из отдельных «кирпичиков Лего». В основной ветке мы можем комбинировать их как угодно. Она играет роль управляющего механизма.

Если нам когда-нибудь захочется вычислять площадь треугольника по формуле Герона, а не через высоту, то не придется искать код во всей программе (представьте, что она состоит из тысяч строк кода как реальные программы). Мы пойдем к месту определения функций и изменим тело одной из них.

Если понадобиться использовать эти функции в какой-нибудь другой программе, то мы сможем импортировать их туда, сославшись на данный файл с кодом (как это делается в Python, будет рассмотрено позже).

Практическая работа

В программировании можно из одной функции вызывать другую. Для иллюстрации этой возможности напишите программу по следующему описанию.

Основная ветка программы, не считая заголовков функций, состоит из одной строки кода. Это вызов функции test(). В ней запрашивается на ввод целое число. Если оно положительное, то вызывается функция positive(), тело которой содержит команду вывода на экран слова «Положительное».

Если число отрицательное, то вызывается функция negative(), ее тело содержит выражение вывода на экран слова «Отрицательное».

Понятно, что вызов test() должен следовать после определения функций. Однако имеет ли значение порядок определения самих функций? То есть должны ли определения positive() и negative() предшествовать test() или могут следовать после него? Проверьте вашу гипотезу, поменяв объявления функций местами. Попробуйте объяснить результат.

Примеры решения и дополнительные уроки в pdf-версии и android-приложении курса

Способы задания функции: аналитический, табличный и графический

Аналитический способ
Табличный способ
Графический способ

Основной признак функциональной зависимости между двумя переменными величинами — это наличие соответствия между значениями этих величин: каждому допустимому значению одной переменной соответствует строго определённое значение другой.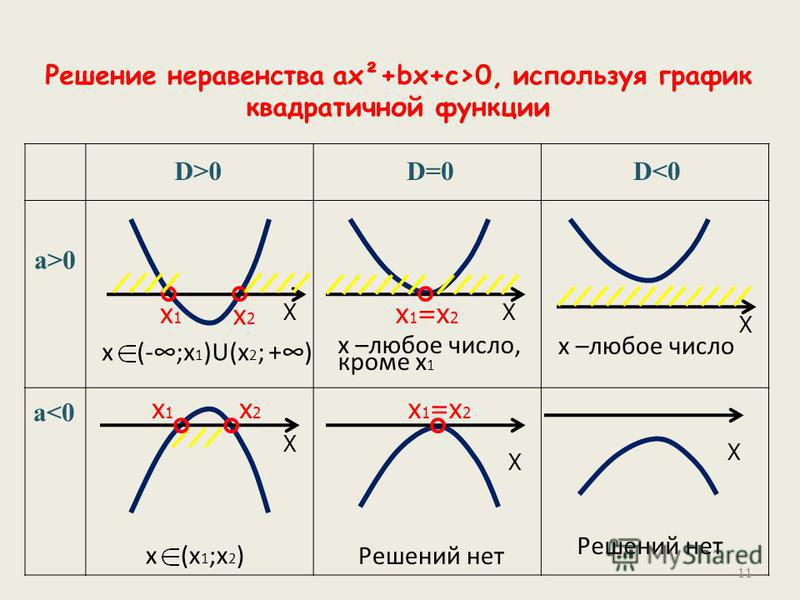

Функция считается заданной, как только установлено соответствие между двумя переменными. Это соответствие может быть установлено различными способами. Рассмотрим подробнее три из них: аналитический, табличный и графический.

Аналитический способ

Аналитический способ — это способ задания функции с помощью формулы.

Например, формула y = x — 2 показывает, как с помощью значения аргумента x вычислить соответствующее ему значение функции y.

Табличный способ

Табличный способ — это способ задания функции с помощью таблицы со значениями.

Например, если измерять температуру воздуха каждый час в течении суток, то каждому часу (t) будет соответствовать определённая температура (T). Такое соответствие можно записать в виде таблицы:

t (ч)	0	1	2	3	4	5	6	7	8	9	10	11
T (°)	14	14	14,5	14,5	15	15	16	16	16	16,5	16,5	17

t (ч)	12	13	14	15	16	17	18	19	20	21	22	23
T (°)	18	20	22	24	24,5	24,5	24	23	21	20	18	16

Следовательно, T функция от t — T(t), определённая с помощью множества целых чисел от 0 до 24 и заданная таблицей. Соответствие между величинами двух переменных задаётся в данном случае не формулой, а таблицей.

Графический способ

Графический способ — это способ задания функции с помощью графика. В этом случае аргумент является абсциссой точки, а значение функции, соответствующее данному аргументу, ординатой.

Графики позволяют быстро находить значение функции по значению аргумента и наоборот — значение аргумента по значению функции. Например, рассмотрим уже готовый график функции:

Чтобы узнать, какое значение функции будет соответствовать аргументу x = 1, надо провести из соответствующей точки оси абсцисс (оси x) перпендикуляр на график. Ордината точки пересечения перпендикуляра с графиком (точки M) и будет соответствующим значением функции. Поэтому, так как точка M имеет координаты (1; 2), то запись этих значений в виде функции будет выглядеть так: y(1) = 2.

Как решать кусочные функции?

Кусочная функция — это функция, график которой имеет несколько кривых. В этом посте блога вы узнаете больше о кусочной функции.

Кусочная функция имеет разные определения в зависимости от количества входных данных, т. е. кусочная функция ведет себя по-разному для разных входных данных.

Пошаговое руководство по кусочной функции

Кусочная функция — это функция \(f(x)\), которая имеет разные определения в разных интервалах \(x\). График кусочной функции имеет разные части, соответствующие каждому из ее определений. Функция абсолютного значения — очень хороший пример кусочной функции. Давайте разберемся, почему он так называется. Мы знаем, что функция абсолютного значения \(f(x)=| x |\) определяется следующим образом: \(\begin{cases}x, \
if\ x≥0\ \\ -x, \
if\ x<0\end{cases}\), Нам нужно прочитать эту кусочную функцию как:

\(f(x)\) равно \(x\), когда \(x\) больше или равно \(0\) и
\(f(x)\) равно \(-x\), когда \(x\) меньше чем \(0\)

Тогда диаграмма \(f(x)\) состоит из двух частей, одна из которых соответствует \(x\) (когда \(x\) находится в интервале \([0, ∞) \)) и другой, соответствующий \(-x\) (когда \(x\) находится в интервале \((-∞, 0)\)).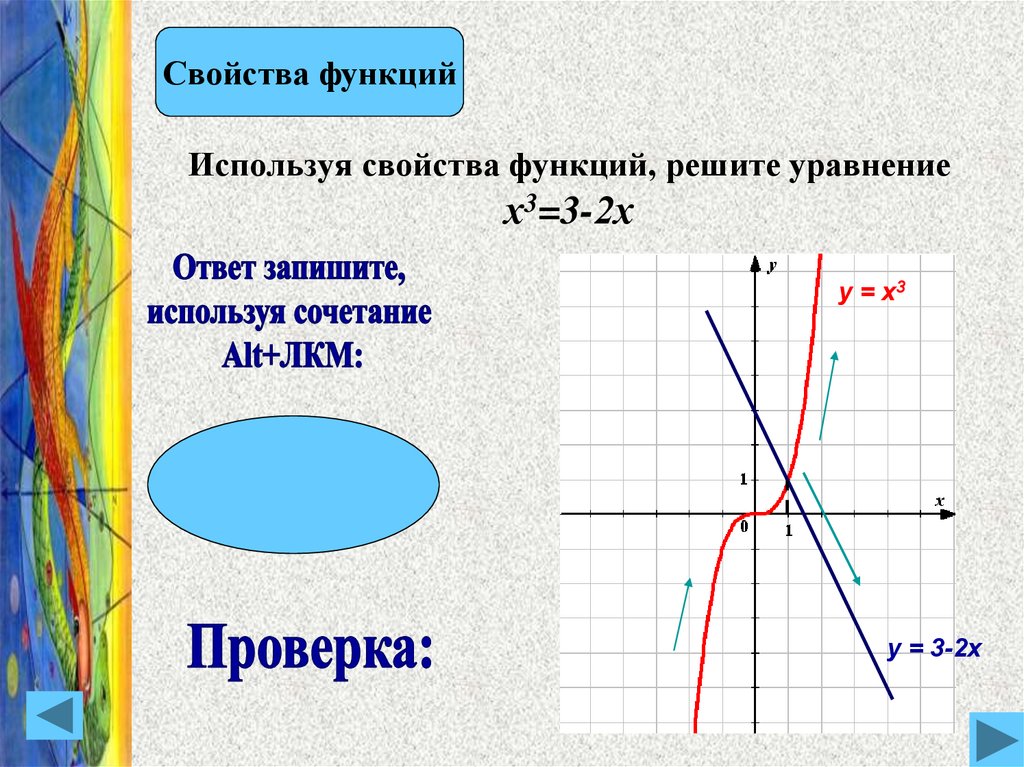

График кусочной функции 92+ bx+c\) представляет собой квадратичную функцию (которая дает параболу) и т.д. Чтобы у нас было представление о том, какой формы получится часть функции.
Шаг 2: Запишите интервалы, показанные в определении функции, вместе с их определениями.
Шаг 3: Создайте таблицу из двух столбцов, помеченных \(x\) и \(y\), соответствующих каждому интервалу. Вставьте конечные точки интервала в обязательном порядке. Если конечная точка удаляется из интервала, обратите внимание, что мы получаем открытую точку, соответствующую этой точке на графике.
Шаг 4: В каждой таблице добавьте больше чисел (случайных чисел) в столбец \(x\), который лежит в соответствующем интервале, чтобы получить идеальную форму графика. Если кусок представляет собой прямую линию, значений \(2\) достаточно для \(x\). Если кусок не является прямой линией, возьмите \(3\) или больше вместо \(x\).
Шаг 5: Подставьте каждое значение \(x\) из каждой таблицы в определение функции, чтобы получить соответствующие значения \(y\).
Шаг 6: Теперь просто нарисуйте все точки из таблицы (учитывая незаполненные точки) на листе графика и соедините их кривыми.
Область и диапазон кусочной функции
Чтобы найти область определения кусочной функции, мы можем только взглянуть на определение данной функции. Возьмите объединение всех интервалов с \(x\), и это даст нам домен.
Чтобы найти диапазон кусочной функции, проще всего построить ее и посмотреть на ось \(y\). Посмотрите, какие \(y\)-значения покрываются графиком.
Оценка кусочной функции
92, x<0 \\ -2\sqrt{x}, x>0\\5, x=0\end{case}\)
Решение:
Здесь \(x= 3\) и оно удовлетворяет условию \(x>0\). Таким образом, соответствующая функция равна \(f(x) = -2\sqrt{x}\). Подставьте \(x= 3\) в это определение:
\(f(3)=-2\sqrt{3}\)
Кусочно-непрерывная функция
Кусочно-непрерывная функция, как следует из ее названия, является непрерывной функция, а это значит, что в ее графике есть разные части, но тем не менее мы сможем нарисовать график, не отрывая карандаша. 92, 0≤x<2\end{case}\)
решение:
Создадим таблицы для каждого из заданных интервалов, используя соответствующие определения функции.
Давайте просто нарисуем их и соединим кривыми. Нам не нужно продолжать какие-либо кривые здесь, потому что ни один из интервалов не имеет пределов как \(∞\) или \(-∞\).
Обратите внимание, что в \((0, 0)\) первой таблицы должна была быть открытая точка. Но она стала частью функции второй таблицы и поэтому в \((0, 0)\ не должно быть открытой точки), а функция в \((0, 0)\) непрерывна. 92, x>0\end{case}}\)
\(\color{blue}{\begin{cases}x+1, x<0 \\ −x+1, 0≤x≤2\ \x-1, x>2\end{case}}\)
Как найти и решить составную функцию?
Составные функции можно рассматривать как «функции внутри функций». Например, предположим, что
f(x) = x ³
г(х) = х + 5
определено для всех действительных чисел.
(Примечание: составные функции могут иметь другое обозначение, например (f ○ g)(x))
Q1) Решите уравнение fg(x) = 27
Во-первых, мы должны найти составную функцию fg(x) через x, прежде чем решать ее. Для этого мы можем разбить функцию следующим образом:
fg(x) = f[g(x)] = f(x+5)
Как видите, мы разбили fg(x) на функцию от g внутри — функцию от f. Теперь мы можем заменить «x» в f(x) = x ³ на «x+5»:
. fg(x) = f(x+5) = (x+5) ³
Теперь мы можем использовать приведенную выше функцию для перестановки и решения для fg(x) = 27.
fg(x) = (x+5) ³ = 27
х+5 = ³ √(27)
= 3
х = 3 — 5
A1) x = -2
Также возможно сформировать составную функцию, применяя одну и ту же функцию дважды. Например, если мы применим функцию f к f( x ), у нас есть ff( x ) или f ² ( x ).
f ² ( x ) = f[f(x)]
= f(x ³ )
= (х ³ ) ³
= х ⁹
При расчете составных функций следует отметить, что fg(x) вряд ли будет таким же, как gf(x) . Например, используя f(x) и g(x) из нашего примера выше, мы можем вычислить gf(x) ниже:
gf(x) = g[f(x)]
= г(х ³ )
= х ³ + 5
Этот результат полностью отличается от нашего результата fg(x) = (x+5) ³
Еще один момент, который следует учитывать при решении составных функций, — это массив значений, для которых выполняется функция, то есть домен и диапазон функции. Эти значения определяют, будет ли составная функция решать для определенного значения, поэтому важно найти домен и диапазон. Теперь мы будем использовать другой пример из приведенного выше, чтобы продемонстрировать этот момент.
Пусть f(x) = x ² + 3
г(х) = 2х + 1
Q2) Найдите fg(x) и объясните, почему fg(x) = 1 не имеет реального решения.
Как и в Q1) мы должны найти функцию fg(x), прежде чем решать ее:
fg(x) = f[g(x)]
= f(2x+1)
= (2x+1) ² + 3
Если мы будем следовать тому же методу, что и раньше, мы обнаружим, что fg(x) = 1 не имеет реального решения:
фг(х) = (2х+1) ² + 3 = 1
(2x+1) ² = -2
Следующим шагом, который мы обычно делаем, является извлечение квадратного корня из числа в правой части уравнения, но мы не можем извлекать квадратный корень из отрицательного числа, не давая комплексного решения, поэтому fg(x) не имеет действительного решения.
No related posts.