Как решить кубическое уравнение: Решение кубических уравнений онлайн

{2}+b y+a=0}\]

В этом уравнении переменные a и b – это коэффициенты.

Первым делом при решении таких уравнений в математике выполняется группировка:

ay3+by2+by+a=a(y³+1)+b(y²+y)=a(y+1)(y²-y+1)+by(y+1)=(y+1)(ay²+y(b-a)+a)

В полученном выражении корень равен y=-1. Исходя из этого, чтобы получить корень квадратного трехчлена ay²+y(b-a)+a, потребуется найти дискриминант.

Определение

Дискриминант – произведение квадратов разностей корней в различных вариаций.

Решение кубических уравнений в составе которых рациональные корни

Предположим, что y=0. В этом случае он будет корнем уравнения, которое выглядит следующим образом:

ay³+by²+cy+d=0

При условии, что в уравнении свободные члены, d=0. Преобразуем уравнение и получим:

ay3+by2+cy=0

Решение кубических уравнений такого вида предполагает вынесение y за скобку. В итоге получается уравнение вида:

y(ay²+by+c)=0

Рассмотрим на конкретном примере, как решить кубическое уравнение с подробным решением:

5y³+2y²+4y=0

Решение:

Первым делом стоит упростить уравнение.

5y³+2y²+4y=0

Получим уравнение вида:

y(5y²+2y+4)=0

y=0, так как является корнем выражения.

Следующий шаг – поиск корней квадратного трехчлена 5y²+2y+4, который мы получили после упрощения. Для поиска приравняем к нулю и будем использовать дискриминант.

В ходе решения кубического уравнения с дискриминантом получим:

D=2²-2*5*4=-38

Так как в ответе мы получили отрицательное значение, корней у данного трехчлена нет, значит x=0.

Если в уравнениях вида ay³+by²+cy+d=0 коэффициентами являются целые числовые значения, то при решении таких уравнений и нахождении его значения мы может получить иррациональные корни.

В случае, когда a не равно 0, при умножении на a² каждой составляющей уравнения происходит замещение переменных, и получается: x=ay

ay³+by²+cy+d=0

Каждую составляющую выражения умножаем на a²:

a³*y³+b*a²*y²+c*a*a*y+d*a²=0

Учитывая, что решение кубических уравнений с подробным решением предполагает замещение переменных x=ay, то:

x²+b*x²+c*a*x+d*a²

Полученное уравнение является кубическим. В таких уравнениях корни могут быть разными – и целыми, и рациональными. Чтобы привести такое уравнение к тождественному равенству, потребуется подставить делители в полученное равенство. В этом случае полученный x₁ будет корнем, и в то же время корнем начального уравнения:

x₁=y₁/a

Чтобы найти значение корней квадратного трехчлена, потребуется многочлен ay3+by2+cy+d разделить на y-y_1.

Рассмотрим решение кубических уравнений такого вида на примере.

Пример:

Решить уравнение \[x 3-3 x 2-13 x+15=0\].

Решение:

Ищем первый корень перебором чисел: \[0, \pm1, \pm2, \pm3, \pm5, \pm15\] и подстановкой в уравнение. В результате находим, что 1 является корнем. Тогда делим левую часть этого уравнения на двухчлен x-1 и получаем:

Теперь, решая квадратное уравнение: \[x 2-2 x-15=0\], находим оставшиеся два корня: x1=-3 и x2=5.

Ответ: 1; -3; 5.

Такой способ решения кубических уравнений используется для преобразования и решения возвратных уравнений.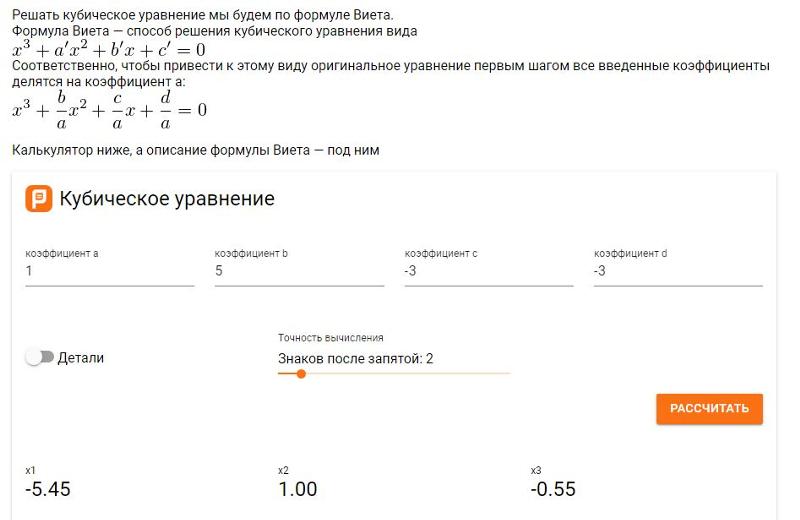 Из приведенного примера видно, что корнем является -1, значит, левую часть можно разделить на x+1. После того, как эти действия выполнены, можно находить корни квадратного трехчлена. Если рациональные корни отсутствуют, необходимо находить иные методы решения и разложения многочлена на множители.

Решение кубического уравнения с помощью формулы Кардано

Есть еще один способ — формула Кардано для решения кубических уравнений.

Если взять уравнение вида B₀y³+B₁y²+B₂y+B₃=0, то A₁=B₁/B₀, A₂=B₂/B₀, A₃=B₃/B₀.

Z=-A²₁/3+A₂

P=2A³₁/27-A₁A₂/3+A₃.

Выведенные значение Z и P подставим в формулу Кардано.

X=³√-P/2+√P²/4+Z³/27+³√-P/2-+√P2/4+Z3/27

В итоге подбор кубических корней должен соответствовать значению –Z/3. {3}=-27\]

Так \[\Delta\] каноническое уравнение имеет 3 действительных корня. Поскольку \[q=0 \Rightarrow
\varphi=\frac{\pi}{2}=>\]

\[y_{1}=2 \sqrt{-\frac{p}{3}} * \cos \left(\frac{\varphi}{3}\right)=2 \sqrt{-\frac{-9}{3}} * \cos
\left(\frac{\frac{\pi}{2}}{3}\right)=2 \sqrt{3} * \cos \left(\frac{\pi}{6}\right)=2 \sqrt{3} *
\frac{\sqrt{3}}{2}=3,\\y_{2}=2 \sqrt{-\frac{p}{3}} * \cos \left(\frac{\varphi}{3}+\frac{2 \pi}{3}\right)=2
\sqrt{3} * \cos \left(\frac{\frac{\pi}{2}}{3}+\frac{2 \pi}{3}\right)=2 \sqrt{3} * \cos \left(\frac{5
\pi}{6}\right)=-2 \sqrt{3} * \frac{\sqrt{3}}{2}=-3,\\y_{3}=2 \sqrt{-\frac{p}{3}} * \cos
\left(\frac{\varphi}{3}+\frac{4 \pi}{3}\right)=2 \sqrt{3} * \cos \left(\frac{\frac{\pi}{2}}{3}+\frac{4
\pi}{3}\right)=2 \sqrt{3} * \cos \left(\frac{3 \pi}{2}\right)=0.\]

В данном случае для корней начального уравнения мы получим:

x₁=y₁-2=3-2=1;

x₂=y₂-2=-3-2=-5;

x₃=y₃-2=0-2=-2.

Получаем ответы: 1, -5, -2.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Общее решение кубического уравнения, если известен один из корней

За исходное уравнение возьмем следующее:

y³+ay²+by+c=0

Предположим, что a,b,c являются действительными цифровыми значениями. Известный корень пометим, как y₁. В таком случае, если произвести деление начального уравнения y³+ay²+by+c=0 на y-y₁ получим квадратное уравнение. При решении такого уравнения удастся найти еще два корня – y₂ и y₃.

Чтобы доказать это, преобразуем кубический многочлен следующим образом:

y₃+ay₂+by+c=(y-y₁)(y-y₂)(y-y₃)

При решении таких уравнений часто допускаются ошибки. Их решение – это сложное, многократное преобразование, которое требует точного знания формул и математических законов. Чтобы избежать ошибок и погрешностей, потребуется применить не только практические навыки, но и теоретические знания. Для решения кубических уравнений можно использовать специальный онлайн калькулятор. Принцип его действия основан на формуле Кардано. В том случае, если один или несколько коэффициентов такого уравнения равны нулю, или между ними присутствует определенная зависимость, решение будет более простым.

Чтобы научиться решать подобные уравнения, необходимо рассматривать примеры и тренироваться на их решении разными способами.

Как решить кубическое уравнение на научном калькуляторе? – Обзоры Вики

Как посчитать куб на калькуляторе? Если вы не хотите сначала конвертировать единицы измерения в дюймы, ничего страшного, ниже приведены формулы для других единиц измерения.

1. длина (дюймы) × ширина (дюймы) × высота (дюймы) = кубические дюймы (дюйм³)
2. длина (фут) × ширина (фут) × высота (фут) × 1728 = кубические дюймы (дюйм³)
3. длина (ярды) × ширина (ярды) × высота (ярды) × 46656 = кубические дюймы (дюйм³)

Как найти кубический многочлен?

Формула кубического полинома имеет общий вид ax³ + бх² + сх + д а формула решения кубического уравнения есть ax³ + бх² + сх + d = 0.

Как решить кубическое уравнение за 82 мс калькулятор?

Какая формула объема? В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.

Как решить квадратное уравнение на Casio FX 82es Plus?

Как решить квадратное уравнение на Casio FX 83gt Plus?

Каковы корни кубического уравнения?

Три корня x3 + ax + b равны действительные числа 2R, -R + / 3I и -R — / 3I. Эти четыре шага вместе составляют кубическую формулу. Он использует комплексные числа (D и z) для создания действительных чисел (2R, -R + / 3I и -R — / 3I), которые являются корнями кубического многочлена x3 + ax + b.

Как найти кубическое уравнение с 4 точками? общее кубическое уравнение у=ax3+bx2+cx+d. Подставьте координаты точек для x и y, и вы получите систему из четырех уравнений с четырьмя переменными, а именно a, b, c и d. Надеюсь, это поможет!

Как решить кубическое уравнение с 4 точками?

Как решить кубическое уравнение

Опубликовано 19 ноября 2022 г. от John

Процесс решения кубического уравнения кажется последовательностью таинственных трюков. Я хотел бы попытаться сделать шаги менее загадочными.

Вдавленное кубическое уравнение

В предыдущем посте было показано, как свести общее кубическое уравнение к одному в форме

, которое называется «вдавленным кубическим». Короче говоря, вы делите на старший коэффициент, а затем выполняете простую замену переменных, которая удаляет квадратичный член.

Что теперь? В этом посте будет представлен мотивированный, но совершенно неисторический подход к удалению линейного члена cx .

Результат

Предположим, мы не знаем, как решать кубические уравнения. Что мы знаем, как решить? Квадратные уравнения. Поэтому возникает естественный вопрос: как найти квадратное уравнение, имеющее те же корни, что и наше кубическое уравнение? Ну, а как вообще можно сказать, имеют ли два многочлена общий корень? Результаты.

Здесь мы полностью нарушаем исторический порядок. Тарталья открыл общее решение вдавленных кубических уравнений в 16 веке [1], а Сильвестр ввел результант в 19 веке.век. Результаты были отличной идеей, но не кроликом из шляпы. Нет ничего удивительного в том, что какой-то определитель может сказать вам, имеют ли два многочлена общий делитель, поскольку это аналогично двум наборам векторов, имеющих перекрывающиеся интервалы. Я нашел идею использования результантов в этом контексте в [2].

Преобразование Чирнхауса

В 1683 году Чирнхаус опубликовал преобразование, которое в современной терминологии означает нахождение многочлена T ( x 92 + a x + 2 c/3 + y, x]

Это дает нам

, которое представляет собой кубическое уравнение относительно y . Если бы коэффициент y был равен нулю, то мы могли бы решить кубическое уравнение для y , просто взяв кубический корень. Но мы можем сделать это, выбрав и , то есть мы выбираем и для решения квадратного уравнения

. Итак, мы решаем это уравнение для и , подставляем любой корень для и в выражение для результат, затем решить для и . Затем мы берем это значение y и находим, где полином Чирнхауса равен нулю, решая квадратное уравнение

. общий корень. Таким образом, один из корней приведенного выше уравнения является корнем нашего исходного кубического уравнения.

Footnotes

[1] В этом сообщении блога мы сначала привели общий квадратичный алгоритм к депрессивной форме, а затем решили депрессивную форму. Это не исторический порядок. Тарталья нашел общее решение депрессивного кубического уравнения, но не смог решить уравнения, содержащие квадратичный член.

[2] Виктор Адамчик и Дэвид Джеффри. Полиномиальные преобразования Чирнхауса, Бринга и Джеррарда. Бюллетень ACM SIGSAM, том 37, № 3, сентябрь 2003 г.

Категории: Математика

Добавить в закладки постоянную ссылку

Решение квадратных, кубических, четвертых уравнений и уравнений более высокого порядка; examples

Опубликовано 14 января 2014 г. автором dougaj4

В предыдущем посте была представлена ​​электронная таблица с функциями для решения уравнений кубической и четвертой степени, которая была дополнена еще одной функцией, решающей многочлены более высокого порядка. Функции на самом деле очень просты в использовании, но документация в электронных таблицах довольно краткая, а большое количество представленных опций может отталкивать.

Чтобы сделать эти функции более доступными, в этом посте представлен пример использования кубической функции и некоторые примечания об альтернативах и использовании других функций. Эти примеры были добавлены отдельным файлом в загружаемый файл: Polynomial.zip. Как обычно, загружаемые файлы содержат полный код с открытым исходным кодом. Тем, кто интересуется включенными функциями Python, см.: Python для пользователей VBA — 5; Использование встроенных функций numpy.

Задача, которую нужно решить, если у нас есть кубическое полиномиальное уравнение формы: 92 + cX + d = 0,
путем вычитания Y с обеих сторон; то есть: d = e – Y.

Введите коэффициенты от a до d в один столбец или строку:

Введите кубическую функцию с диапазоном значений коэффициента в качестве аргумента.

Это вернет одно из трех решений кубического уравнения. Чтобы отобразить все три решения, а также количество реальных решений, введите в качестве функции массива:
— выберите ячейку, содержащую функцию, и три ячейки ниже.
— нажмите клавишу F2 (Редактировать)
— нажмите Ctrl-Shift-Enter
Четыре требуемых значения будут отображаться, как показано ниже:

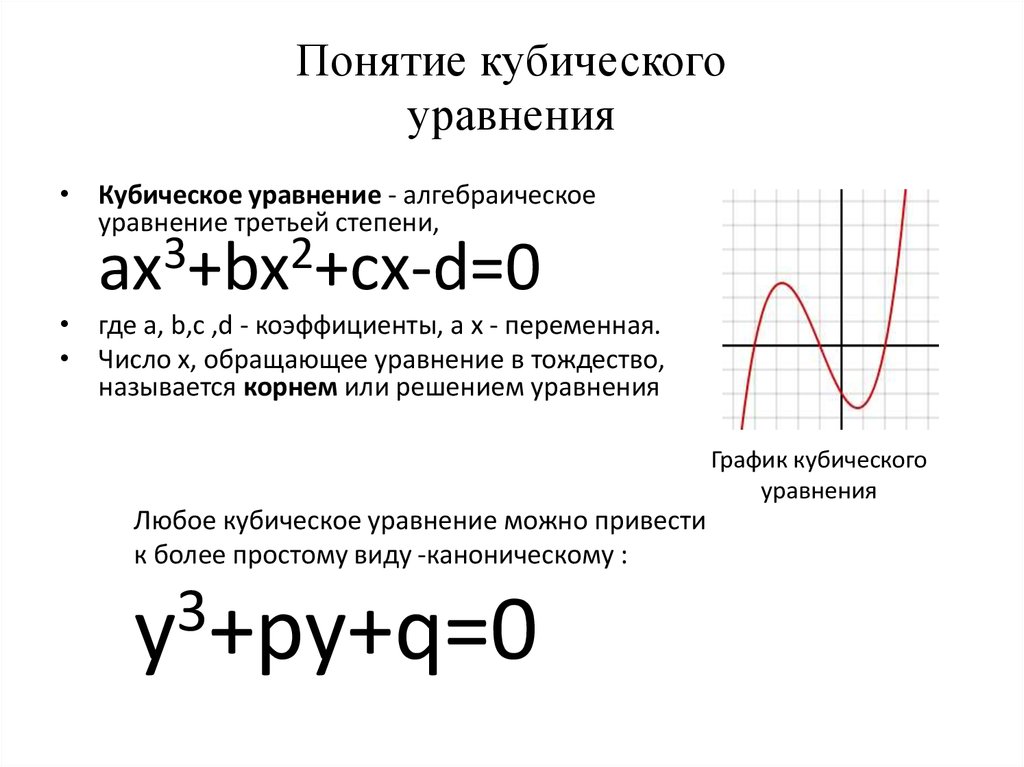
Это график решения кубической функции. Видно, что три решения представляют собой значения X, при которых функция равна нулю.

Некоторые кубические уравнения, такие как на графике ниже, имеют только одно «действительное» решение и два «комплексных» решения, т. е. решения с «действительной» и «мнимой» частями.

Если требуются сложные решения, следует использовать функцию CubicC. Эта функция используется так же, как Cubic, за исключением того, что выходной диапазон составляет два столбца; для действительной и мнимой частей решения:

Если требуется отобразить одно решение, отличное от первого, это можно сделать с помощью необязательных аргументов Out1 и Out2, как показано ниже.

No related posts.