Как решить квадратное уравнение: Квадратные уравнения — урок. Алгебра, 8 класс.

Как решать квадратное уравнение | Подготовка к ЕГЭ по математике

Загляни сюда, – вдруг узнаешь себя!

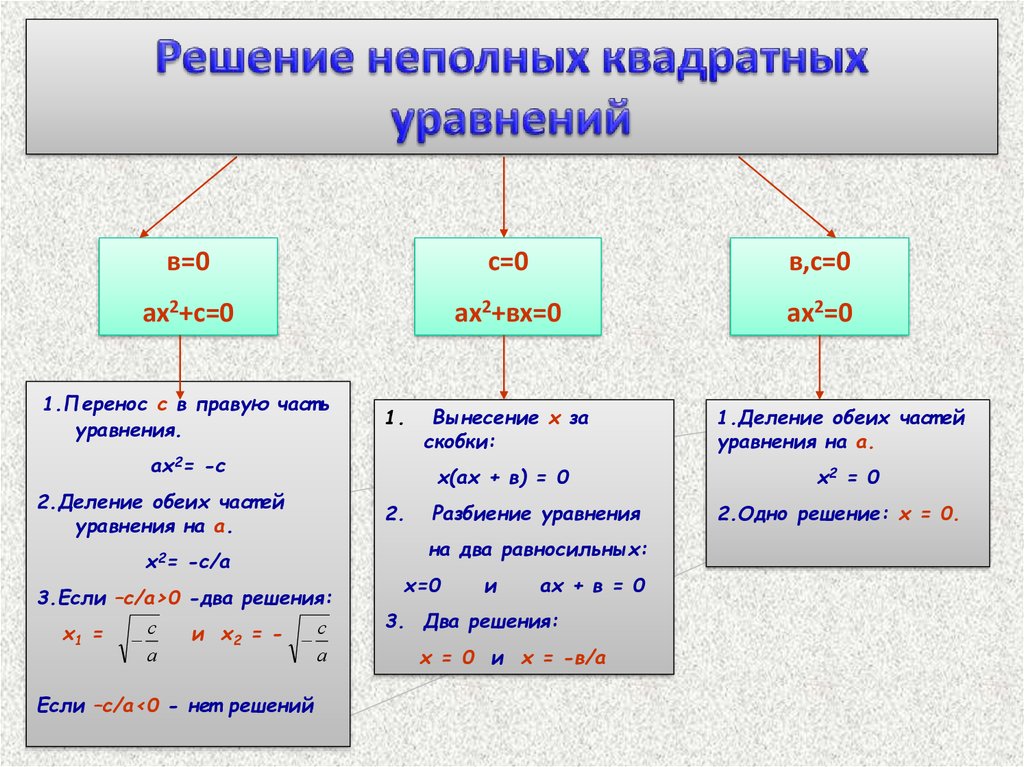
Надеюсь, вы внимательно изучили таблицу, приведенную выше. Если все еще есть вопросы, – давайте разбираться.

Во первых, почему рассматриваются только случаи при ? Просто потому, что при у нас уже будет не квадратное уравнение, а линейное.

Формулу дискриминанта знают практически все, но почему же тогда возникают все же сложности с решением уравнений?

Начнем с того, что иногда происходит путаница с коэффициентами , и . Ни в коем случае мы не считаем, что – это тот коэффициент, что стоит на первом месте! Но – тот, что при . Давайте договоримся, что будем приводить всякое квадратное уравнение к стандартному виду, ставя на первое место слагаемое, содержащее , на последнее – свободный от член (если таковой имеется). Например, уравнение будем переписывать так .

Далее, некоторых может сбить с толку минусовой коэффициент при старшем члене (то есть ). В этом случае советую домножать обе части уравнения на -1. Например, встречая уравнение , переписывать его в таком виде , и только потом высчитывать дискриминант, находить корни.

И, наконец, замечу, находятся и такие товарищи, которые, встречая, например, уравнение , спешат выносить за скобку, путая это уравнение с неполным. Нет, это обычное полное квадратное уравнение, которое после переноса влево примет вид , – решаем мы его через дискриминант.

Поэтому, давайте договоримся всякое уравнение приводить к такому виду, чтобы справа стоял только ноль и ничего больше.

Плавно перешли к неполным квадратным уравнениям. Если мы будем придерживаться последного совета, то мы не сможем спутать неполное уравнение с полным уж это точно. Справа будет два слагаемых (вырожденный случай – одно), а не три как у полного уравнения. Можно, конечно, и такие уравнения решать через дискриминант,но проще поступить иначе.

У нас в случае неполного уравнения будет всегда получаться либо уравнение с двумя , либо с одним . Что делать, в случае, если у нас оба слагаемых содержат (например, )? Ну, конечно, выносить его за скобку (), в этом случае будем всегда получать, что произведение двух множителей равно . Когда такое возможно? Конечно, когда один из множителей равен нулю (либо , либо ). В этом случае у нас всегда один из корней будет нулевым.

Во втором же случае, неполное уравнение будет содержать лишь одно слагаемое с (например, или ). Если свободный член отрицательный (как в первом случае, ), то мы всегда сможем разложить левую часть на множители по формуле разность квадратов  ( для уравнения имеем , далее ). Если же свободный член положителен, то уравнение не имеет корней (действительно, в уравнении первое слагаемое должно бы быть равным -3, чтобы в сумме с 3 дать 0, но такое невозможно).

В общем, каждое отдельно взятое квадратное уравнение мы решам одним из трех способов, – выбор не велик.

Заметим, также, что в случае полного квадратного уравнения в зависимости от того, какой дискриминант мы получаем, – на выходе разное количество корней. Если , то будем иметь два корня, если , то имеем один корень (или два совпавших), наконец, если , то корней нет.

Смотрите также статью «Что делать, если дискриминант громоздкий?»

Решить квадратное уравнение / Даны катеты прямоугольного треугольника. Найти площадь, периметр и гипотенузу треугольника / Пользователь вводит сумму вклада в банк и годовой процент. Найти сумму вклада через 5 лет. · GitHub

	import UIKit
	// 1. Решить квадратное уравнение
	let a:Float = 1
	let b:Float = 2
	let c:Float = 3
	var x1:Float
	var x2:Float
	var d:Float
	var discriminant:Float
	d = b * b — (4 * a * c)
	if(d >= 0){
	discriminant = sqrt(d)
	x1 = (-b + discriminant) / (2 * a)
	x2 = (-b — (discriminant)) / (2 * a)
	print(x1, x2)
	}else if(d < 0){
	d = ((4 * a * c) — pow(b,2)) / (2 * a)
	print(d)
	}
	// 2. Даны катеты прямоугольного треугольника. Найти площадь, периметр и гипотенузу треугольника.
	var v:Double = 6
	var n:Double = 8
	var m:Double = 10
	var p:Double
	p = v + n + m
	m = sqrt(pow(v,2) + pow(n,2))
	print(«Периметр треугольника равен \(p)»)
	print(«гипотенуза треугольника равна \(m)»)
	// 3. Пользователь вводит сумму вклада в банк и годовой процент. Найти сумму вклада через 5 лет.
	var deposit:Float = 1000
	var percent:Float = 15
	percent = percent / 100
	var result1 = deposit + (deposit * percent)
	var result2 = result1 + (result1 * percent)
	var result3 = result2 + (result2 * percent)
	var result4 = result3 + (result3 * percent)
	var result5 = result4 + (result4 * percent)
	var counter = 1
	var time = [result1, result2,result3, result4, result5]
	for i in time{
	print(«Чрезе \(counter) год/лет сумма вклада будет равна \(i)»)
	counter += 1
	}

Как решать квадратные уравнения (4 метода) – JDM Educational

Квадратные уравнения часто встречаются в математике и физике, и очень важно знать, как их решать. К счастью, есть несколько способов сделать это.

Итак, как решать квадратные уравнения? Вы можете решать квадратные уравнения с помощью графика, разложения на множители, составления квадрата и квадратной формулы. Графики дают хорошее визуальное представление, но трудно найти значения x на графике без уравнения. Если разложение на множители затруднено, помогает квадратичная формула (сокращение для завершения квадрата).

Конечно, квадратная формула будет работать для любого выбранного вами квадратного уравнения. Однако в некоторых случаях может быть проще использовать фактор, чтобы избежать радикалов и дробей в квадратичной формуле.

В этой статье мы поговорим о четырех методах, которые можно использовать для решения квадратного уравнения, и приведем несколько примеров для каждого из них. Мы также более подробно рассмотрим, как эти методы связаны друг с другом.

Начнем.

Как решать квадратные уравнения

Вот четыре метода, которые вы можете использовать для решения квадратного уравнения:

• График — это хороший визуальный метод, если у вас есть форма вершины параболы или если у вас есть параболоподобная кривая из набора данных. . Если построить график квадратичной функции f(x) = ax ² + bx + c, можно узнать, где она пересекает ось x. Единственным недостатком является то, что может быть трудно найти точные значения x. Также график не будет пересекать ось абсцисс, если решения комплексные (в случае отрицательного дискриминанта).
• Факторинг — этот метод полезен в некоторых случаях, чтобы избежать работы по построению графика, составлению квадрата или использованию формулы квадрата. Однако некоторые квадратичные уравнения трудно разложить на множители, и в этих случаях более полезной будет квадратичная формула.
• Завершить квадрат — этот метод долгий, но он работает. Квадратичная формула является упрощением для этого метода. Мы также используем метод заполнения квадрата, чтобы привести некоторые уравнения окружности в правильную форму.
• Квадратная формула – этот метод работает всегда. Он получен с использованием предыдущего метода (заполнить квадрат) на общем квадратном в стандартной форме: ax ² + bx + c = 0. Единственным недостатком является то, что вычисления могут стать утомительными, поскольку они включают умножение, сложение, радикалы и деление (дроби).

Вот как эти методы связаны друг с другом:

• Когда метод завершения квадрата используется для общего квадратного уравнения в стандартной форме, ось ² + bx + c = 0, в результате получаем квадратичную формулу.
• Когда мы используем формулу квадратного уравнения для квадратного уравнения, мы получаем два решения уравнения: r и s. Эти решения могут быть различными и вещественными (положительный дискриминант), двойным вещественным (нулевой дискриминант) или комплексно-сопряженными (отрицательный дискриминант).
• Если мы используем коэффициент «а» вместе с решениями r и s, мы можем записать факторизованную форму квадратного уравнения как a(x – r)(x – s) = 0,
• Если мы возьмем среднее двух решений r и s, мы сможем найти x-координату вершины параболы (то есть ось симметрии). Если r и s действительны, у нас также есть точки пересечения параболы по оси x, что упрощает построение графика.

Давайте рассмотрим несколько примеров каждого метода, начиная с построения графиков.

Когда у квадратного уравнения нет решения…

Пожалуйста, включите JavaScript

Когда у квадратного уравнения нет решения?

Как решать квадратные уравнения с помощью графика

Чтобы решить квадратное уравнение с помощью графика, все, что нам действительно нужно сделать, это выяснить, где находятся нули (точки, в которых график пересекает ось x).

Пример: решение квадратного уравнения с помощью графика

Рассмотрим следующую параболу (график квадратного уравнения):

Иногда мы можем найти решения квадратного уравнения с помощью графика и нахождения точек пересечения (нулей).

Из графика видно, что парабола пересекает ось x (линию y = 0) в точках x = 2 и x = 6. В этот момент мы знаем, что решения уравнения равны x = 2 и x = 6.

Однако мы можем найти и квадратное уравнение. Во-первых, квадратичная факторизованная форма выглядит следующим образом:

• y = a(x – r)(x – s)
• y = a(x – 2)(x – 6)   [r = 2 и s = 6 — два решения квадратного уравнения]

Теперь нам просто нужно найти значение a. Для этого мы можем использовать вершину параболы.

Мы знаем, что ее координата x будет средним значением нулей x = 2 и x = 6. Это дает нам координату x x = 4 для вершины.

Снова взглянув на график, мы видим, что вершина действительно находится в точке x = 4 со значением y = -12. Мы будем использовать это значение в квадрате, чтобы найти a:

• y = a(x – 2)(x – 6)
• -12 = a(4 – 2)(4 – 6)
• -12 = a(2)(-2)
• -12 = -4a
• 3 = a

Таким образом, значение a равно 3, а квадратичная форма

3 равна

13:

у = а(х – 2)(х – 6)  

y = 3(x – 2)(x – 6)   [подставить a = 3]

y = 3(x ² – 8x + 12) [ФОЛЬГА] 90x5y

² – 24x + 36) [распределите 3 через круглые скобки]

Теперь мы знаем решения квадратного уравнения, а также стандартную и факторизованную формы.

Как решать квадратные уравнения с помощью разложения на множители

Во многих случаях проще разложить квадратное уравнение на множители, чем построить график, дополнить квадрат или использовать квадратную формулу.

Тем не менее, нужно немного попрактиковаться, чтобы научиться правильно определять, когда вы можете легко разложить квадратное число. Давайте посмотрим на некоторые примеры.

Пример 1. Решение квадратного уравнения с помощью факторизации

Рассмотрим следующее квадратное уравнение:

• x ² – 16 = 0

Мы видим, что левая часть представляет собой разность квадратов: 2 – 4 ² . Помните, что формула для факторизации разности квадратов:

• A ² – B ² = (A + B)(A – B)

Используя эту формулу здесь с A = x и B = 4, мы получаем:

• A
• 2 – B ² = (A + B)(A – B)
• x ² – 4 ² = (x + 4)(x – 4)

999 – 16 = (x + 4)(x – 4)

Теперь мы можем переписать исходное квадратное уравнение как:

• x ² — 16 = 0
• (x + 4) (x — 4) = 0

Свойство нулевого продукта сообщает нам, что либо

• x + 4 = 0

или

• 1966

или

• 19199 = 0

или

• 199. x – 4 = 0

Это означает, что x = 4 и x = -4 являются решениями квадратного уравнения. Вы можете увидеть это на графике ниже.

График квадратного уравнения y = x ² – 16. Он имеет нули при x = 4 и x = -4, которые являются решениями соответствующего квадратного уравнения.

Пример 2. Решение квадратного уравнения с помощью факторинга

Иногда нам нужно вынести на множители GCF (наибольший общий множитель), прежде чем мы сможем использовать другой метод факторинга.

Рассмотрим следующее квадратное уравнение:

• 4x ² – 36 = 0

. 4(x ² – 9) = 0

Мы видим, что левая часть выражения в скобках представляет собой разность квадратов: x ² – 3 ² .

Используя формулу разности квадратов из примера 1 с A = x и B = 3, получаем:

• A ² – B ² = (A + B)(A – B)
• x ² – 3 ² = (x + 3)(x – 3)
• x ² – 9 = (x + 3)(x – 3)

90 Теперь мы можем переписать исходное квадратное уравнение как:

• 4x ² – 36 = 0
• 4(x ² – 9) = 0
• 4(x + 3)(x – 3) = 0

Свойство нулевого произведения говорит нам, что либо

=
0

или

• x – 3 = 0

Это означает, что x = 3 и x = -3 являются решениями квадратного уравнения. Вы можете увидеть это на графике ниже.

График квадратного уравнения y = 4x ² – 36. Он имеет нули при x = 3 и x = -3, которые являются решениями соответствующего квадратного уравнения.

Пример 3. Решение квадратного уравнения с помощью факторизации

Рассмотрим следующее квадратное уравнение:

• 5x ² – 10x = 0

Мы можем вынести из обоих членов GCF, равный 5x, :

• 5x(x – 2) = 0

The zero product property tells us that either

• x = 0

or

• x – 2 = 0

Это означает, что x = 0 и x = 2 являются решениями квадратного уравнения. Вы можете увидеть это на графике ниже.

График квадратичного y = 5x ² – 10x. Он имеет нули при x = 0 и x = 2, которые являются решениями соответствующего квадратного уравнения.

Пример 4. Решение квадратного уравнения с помощью разложения на множители

Рассмотрим следующее квадратное уравнение:

• x ² – 10x + 25 = 0

Мы можем видеть, что постоянный член2 = полный квадрат 5 ² . Мы также видим, что линейный коэффициент равен -10, что равно -2*5.

Это говорит нам о том, что у нас есть идеальный квадратный трехчлен. The formula for factoring a perfect square trinomial is:

• x ² – 2Ax + A ² = (x – A) ²

or

• x ² – 2Ax + A ² = (x – A)(x – A)

Используя здесь трехчленную формулу полного квадрата с A = 5, мы получаем:

• x ² – 2Ax + A ² = (х – А)(х – А)
• х ² – 2(5)х + 5 ² = (х – 5)(х – 5)
• х

  2 2 – 10x + 25 = (x – 5)(x – 5)

Теперь мы можем переписать исходное квадратное уравнение в следующем виде: 5)(x – 5) = 0

Свойство нулевого произведения говорит нам, что

• x – 5 = 0

Это означает, что x = 5 является двойным корнем или повторным решением квадратного уравнения . Вы можете увидеть это на графике ниже.

График квадратного уравнения y = x ² – 10x + 25. Он имеет ноль при x = 5 (двойной корень), который является решением соответствующего квадратного уравнения.

Пример 5. Решение квадратного уравнения с помощью факторизации

Рассмотрим следующее квадратное уравнение:

• x ² – 7x + 6 = 0

Мы можем видеть, что постоянный член может иметь только 1 множитель *6 или 6 = (-1)*(-6). Поскольку нам нужен отрицательный линейный член, мы выбираем отрицательные факторы.

Поскольку -1 + -6 = -7, мы нашли правильную пару значений для использования: -1 и -6. Применяя их, мы получаем:

• x ² – 7x + 6 = 0
• (x – 1)(x – 6) = 0

2 Свойство нулевого произведения говорит нам, что либо 0, либо

x – 1 = 0

или

• x – 6 = 0

Это означает, что x = 1 и x = 6 являются решениями квадратного уравнения. Вы можете увидеть это на графике ниже.

График квадратного уравнения y = x ² – 7x + 6. Он имеет нули при x = 1 и x = 6, которые являются решениями соответствующего квадратного уравнения.

Как решать квадратные уравнения, заполняя квадрат

Заполняя квадрат — это еще один метод, который мы можем использовать для решения квадратного уравнения. Этот метод используется для получения квадратичной формулы, и он может быть полезен для преобразования уравнений окружности в форму, которую мы можем легко построить.

Пример 1. Решение квадратного уравнения путем заполнения квадрата

Рассмотрим следующее квадратное уравнение:

• x ² – 6x + 2 = 0

Мы не можем факторизовать, как мы делали ранее, но мы можем заполнить квадрат для решения.

Во-первых, мы преобразуем уравнение так, чтобы оно имело форму x ² + Bx = C. Здесь это означает, что мы вычитаем 2 из обеих частей, чтобы получить:

• x ² – 6x = -2

Помните, что если у нас есть x ² + Bx = C, то мы берем половину B, возводим ее в квадрат, а затем прибавляем эту сумму к обеим частям уравнения (то есть добавляем B ² /4 на обе стороны).

Здесь B = -6, поэтому мы добавляем B ² / 4 = (-6) ² / 4 = 36 / 4 = 9 к обеим частям уравнения:

• x ² – 6x + 9 = -2 + 9
• x ² – 6x + 9 = 7

Теперь у нас есть правильный квадратный трехчлен с левой стороны, с A = 3. Это делит как:

• (x – 3) ² = 7

Теперь мы можем извлечь квадратный корень из обеих частей, чтобы получить:

• √(x – 3) ² = √7
• x – 3 = √7

Два решения: x = 3 + √3 –7 и √3 –7. Вы можете увидеть это на графике ниже.

График квадратного уравнения y = x ² – 6x + 2. Он имеет нули при x = 3 + √7 и x = 3 – √7, которые являются решениями соответствующего квадратного уравнения.

Пример 2. Решение квадратного уравнения путем заполнения квадрата

Рассмотрим следующее квадратное уравнение:

• x ² – 4x + 40 = 0

Мы не можем факторизовать, как раньше, но мы можем заполнить квадрат для решения.

Во-первых, мы преобразуем уравнение так, чтобы оно имело вид x ² + Bx = C. Здесь это означает, что мы вычитаем 40 с обеих сторон, чтобы получить:

• x ² – 4x = -40

Опять же, если у нас есть x ² + Bx = C, то мы берем половину B, возводим ее в квадрат, а затем прибавляем эту сумму к обеим частям уравнения (то есть добавляем B ² /4 на обе стороны).

Здесь B = -4, поэтому мы добавляем B ² / 4 = (-4) ² / 4 = 16 / 4 = 4 к обеим частям уравнения:

• x ² – 4x + 4 = -40 + 4
• x ² – 4x + 4 = -36

Теперь у нас есть правильный квадратный трехчлен с левой стороны, с A = 2. Это делит как:

• (x – 2) ² = -36

Теперь мы можем извлечь квадратный корень из обеих частей, чтобы получить:

• √(x – 2) ² = √(-36)
• x – 2 = i√6

, где i = √-1.

Два решения: x = 2 + i√6 и x = 2 – i√6. Вы можете увидеть график этого квадратичного уравнения ниже (поскольку корни комплексные, они не отображаются на графике).

График квадратного уравнения y = x ² – 4x + 40. Он имеет нули при x = 2 + i√6 и x = 2 – i√6, которые являются решениями соответствующего квадратного уравнения (эти решения сложные, поэтому на графике они не отображаются).

Как решать квадратные уравнения с помощью квадратной формулы

Квадратная формула — это гарантированный метод решения любой квадратной формулы. Как бы ни было сложно разложить на множители, квадратичная формула всегда даст нам решение.

Однако при использовании формулы нам приходится иметь дело с радикалами и дробями. Помните, что для квадратного уравнения в стандартной форме:

• ax ² + bx + c = 0

квадратная формула определяется как:

Квадратная формула дает нам общее решение для любого квадратного уравнения в стандартной форме.

Давайте рассмотрим несколько примеров его использования.

Пример 1. Решение квадратного уравнения по квадратной формуле

Рассмотрим следующее квадратное уравнение: GCF 2 и деление на 2 с обеих сторон, чтобы получить:

• 2x ² — 16x + 30 = 0
• 2 (x ² — 8x + 15) = 0
• x ² — 8x + 15 = 0

999922 2 . с меньшими коэффициентами для работы, что немного облегчает нашу работу с квадратичной формулой.

Это квадратное уравнение имеет a = 1, b = -8 и c = 15. Подстановка этих значений в квадратную формулу дает нам:

• x = [-b +/- √(b ² – 4ac )] / 2а
• х = [-(-8) +/- √((-8) ² – 4(1)(15))] / 2(1)
• х = [8 +/- √(64 – 60)] / 2
• x = [8 +/- √4] / 2
• x = [8 +/- 2] / 2
• x = 10 / 2 или 6 / 2
• x = 5 или x = 3

Это означает, что x = 3 и x = 5 являются решениями квадратного уравнения. Вы можете увидеть это на графике ниже.

График квадратичного y = 2x ² – 16x + 30. Имеет нули при x = 3 и x = 5, которые являются решениями соответствующего квадратного уравнения.

Пример 2. Решение квадратного уравнения по квадратной формуле

Рассмотрим следующее квадратное уравнение: и c = 12. Подстановка этих значений в квадратичную формулу дает нам:

• x = [-b +/- √(b ² – 4ac)] / 2a
• x = [-(6) +/- √((6) ² – 4(3)(11))] / 2(3)
• x = [6 +/- √(36 – 132)] / 6
• x = [6 +/- √(-96)] / 6
• x = [6 +/- 4i√(6)] / 6
• x = (6 + 4i√6) / 6 или x = (6 – 4i√6) / 6 или
• x = 1 + (2i√6) / 3) или x = 1 – (2i√6/3)

Это означает, что x = 1 + (2i√6)/3) и x = 1 – (2i√6)/3) являются решениями квадратного уравнения. Вы можете увидеть график ниже (поскольку решения сложные, они не отображаются на графике).

График квадратичного уравнения y = 2x ² – 16x + 30. Он имеет нули при x = 1 + (2i√6) / 3) и x = 1 – (2i√6) / 3), которые являются решения соответствующего квадратного уравнения (эти решения комплексные, поэтому на графике не отображаются).

Заключение

Теперь вы знаете о 4 методах решения квадратных уравнений. Вы также знаете, когда может быть проще использовать каждый из них и как методы связаны друг с другом.

Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.

Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!

Подпишитесь на наш канал на YouTube!

~Джонатон

Квадратная формула: обзор, объяснение и примеры

Прелесть квадратной формулы в том, что она всегда подходит для решения квадратных уравнений.

Точно так же, как мы знаем, что завтра утром взойдет солнце, мы знаем, что квадратичная формула даст решения (действительные и мнимые) наших квадратных уравнений. Если вы ищете немного больше красоты (и гораздо меньше стирания) при решении квадратичных уравнений, продолжайте читать, чтобы просмотреть квадратную формулу, понять вывод квадратной формулы и увидеть примеры того, как использовать квадратичную формулу! 92 равен a, коэффициент перед x равен b, а коэффициент без переменной равен c.

Вы можете узнать больше о стандартной форме и других формах квадратных уравнений в нашей обзорной статье о формах квадратных уравнений.

Начните заниматься алгеброй 1 на Альберте прямо сейчас!

История квадратной формулы

Ранняя история

Решение квадратных уравнений не является современным достижением. На самом деле древние вавилоняне составляли квадрат для решения квадратных уравнений задолго до того, как появилось слово «алгебра», согласно Хакворту и Хауленду в тексте «Введение в математику колледжа: история действительных чисел».

Представьте, что вы решаете квадратные уравнения на счетах вместо того, чтобы доставать калькулятор. Согласно Mathnasium, не только вавилоняне, но и китайцы решали квадратные уравнения, дополняя квадрат с помощью этих инструментов.

В 700 году нашей эры Брахмагупта, математик из Индии, разработал общее решение квадратного уравнения, но только в 1100 году нашей эры известное нам сегодня решение было разработано другим математиком из Индии по имени Бхаскара. заявил Матназиум.

Хакворт и Хауленд сообщили нам, что до тех пор, пока не существовала индуистская математика, математика, разработанная в Индии, числа не выглядели так, как мы их знаем, с системой счисления с основанием 10. Другими словами, одновременно с этими разработками в области решения квадратных уравнений в математике произошло много других разработок. Знаменитые древние математики, такие как Пифагор, не понимали существования таких чисел, как \sqrt{2} или \pi. На самом деле, как сообщил нам Mathnasium, распознавание Бхаскарой двух решений квадратного корня из числа помогло ему решать квадратные уравнения. Britannica сообщает нам, что Бхаскара также смог аппроксимировать значение \pi как 3,141666.

Более поздняя история

Мухаммад Аль-Хорезми, «отец алгебры»

В период между Брахмагуптой и Бхаскарой арабский математик Аль-Хорезми также решал квадратные уравнения, согласно Mathnasium. Он написал текст под названием «Аль-джабр валь мукабала», из которого, согласно Хакворту и Хауленду, мы получили слово «алгебра». Хакворт и Хауленд также сообщили нам, что в своем тексте Аль-Хорезми объясняет с помощью конкретных шагов, как решать уравнения, в том числе квадратные уравнения. В эпоху Возрождения, примерно в 1545 году нашей эры, Джироламо Кардано основывался на работах Аль-Хорезми, как утверждает Матназиум, включая воображаемые решения. В то время как работы Кардано включают мнимые числа, Аль-Хорезми не включал даже отрицательных решений, согласно Хэкворку и Хауленду. 92 — 4ac}}{2a}

Потребовалось немного работы, но теперь у нас есть проверенное квадратичная формула будет работать во всех случаях!

Если вы хотите увидеть этот процесс в наглядной форме, ниже представлено короткое видео от YouTuber patrickJMT, показывающее, как вывести формулу квадрата:

Вернуться к оглавлению

Когда использовать формулу квадрата

Иногда, пытаясь решить квадратное уравнение с помощью факторизации, мы натыкаемся на препятствие. Не каждое квадратное уравнение факторизуемо.

Хорошая новость о квадратичной формуле заключается в том, что вы всегда можете ее использовать! Не существует квадратных уравнений, для которых квадратная формула не дает решения. Даже в тех случаях, когда нет реальных решений, квадратичная формула все равно дает решения! Ознакомьтесь с нашим разделом ниже о дискриминанте, чтобы узнать больше о том, как квадратичная формула всегда дает подходящие решения.

Однако, когда квадратное уравнение факторизуемо, факторинг часто является более эффективным методом решения уравнений. На самом деле вы можете определить, является ли квадратное уравнение факторизуемым, используя нечто, называемое дискриминантом (для получения дополнительной информации об этом перейдите к нашему разделу ниже о дискриминантах и ​​факторинге).

Квадратные уравнения также можно решать, дополняя квадрат — метод, который мы использовали выше для получения квадратной формулы.

Вы никогда не ошибетесь с квадратной формулой, но есть и другие способы решения квадратных уравнений!

Вернуться к оглавлению

Примеры квадратичных формул с ответами (шаг за шагом)

Реальные решения

Попробуем сами! Решим квадратное уравнение:

92} — 4\цвет{красный}{(7)}\цвет{зеленый}{(9)}}}{2\цвет{красный}{(7)}}

\dfrac{1 \pm \sqrt{1-252}}{14}

\dfrac{1 \pm \sqrt{-251}}{14}

Поскольку у нас есть квадратный корень из отрицательного числа, у нас есть два воображаемых решения. Мы должны переписать \sqrt{-251}, используя мнимые числа. Затем мы запишем наше решение в форме комплексного числа a+bi.

\dfrac{1 \pm \sqrt{-251}}{14}

\dfrac{1 \pm i\sqrt{251}}{14}

\dfrac{1}{14} \pm \dfrac{i \sqrt{251}}{14} 92-x+9 равно

\dfrac{1}{14} + \dfrac{i \sqrt{251}}{14} и \dfrac{1}{14} — \dfrac{i \sqrt{251}} {14}.

Вернуться к оглавлению

Бесплатный рабочий лист с квадратичными формулами

Учителя математики: вы ищете простой в использовании рабочий лист с квадратными формулами, который включает краткие заметки и некоторые основные практические задачи?

Предварительный просмотр рабочего листа квадратичной формулы:

Нажмите, чтобы загрузить бесплатный рабочий лист квадратичной формулы 92 — 4ac}}{2a}

• Если дискриминант положительный , это означает, что мы извлекаем квадратный корень из положительного числа. У нас будет положительное и отрицательное реальное решение. Это уравнение будет иметь два действительных решения или точки пересечения.

• Если дискриминант равен нулю , мы берем квадратный корень из нуля, который равен нулю. Добавление нуля и вычитание нуля дают одно и то же значение, поэтому уравнение будет иметь только одну точку пересечения по оси x.

• Наконец, если дискриминант отрицательный , мы извлекаем квадратный корень из отрицательного числа. У этого уравнения не будет действительных решений, а только два мнимых решения, потому что i=\sqrt{-1}.

В этой таблице показано, как использовать дискриминант для определения количества и типа решений в квадратном уравнении:

918867 Положительное 918630874

Дискриминант	Число решений уравнения
Два реальных решения
Отрицательный	Два воображаемых решения
Zero	One Real Solution

777777. Возврат на Table To Table To Table To Table To Table To Table To Table To Table To Table To Table To Tabletors Altent Oftors Altestors

.

БЫСТРЫЙ СОВЕТ: Дискриминанты и факторинг 

Вы также можете использовать дискриминант, чтобы определить, являются ли уравнения факторизуемыми. Если a, b и c являются целыми значениями, когда дискриминант представляет собой полный квадрат, квадратное уравнение факторизуемо. 92}-4\цвет{красный}{(1)}\цвет{зеленый}{(9)}

36-36

0

Мы знаем, что 0=0. Дискриминант со значением , равным 0,, говорит нам, что уравнение имеет только одну точку пересечения по оси x . Мы можем увидеть, как функция попала в x, построив график этого квадратного уравнения.

Больше визуалов? Посмотрите отличное видео, объясняющее, как найти дискриминант квадратного числа:

Вернуться к оглавлению

5 лучших песен с квадратичными формулами

Что может быть лучше, чем слушать раздражающую песню, чтобы запомнить формулу? Да, есть несколько приятных песен, но песня, которая будет играть в вашей голове, даже когда вы захотите, чтобы она остановилась, лучше всего поможет вам запомнить формулу. Вот несколько отличных вариантов для вас!

1. С более чем тремя миллионами просмотров нам пришлось начать с полностью оригинальной песни с квадратичной формулой.
2. Вот еще одна оригинальная версия песни о квадратичной формуле — предупреждение: она может застрять у вас в голове.
3. Вот отличный кавер на песню One Direction с использованием квадратичной формулы.
4. Хотя этот рэп может и не заставит формулу застрять у вас в голове, в нем рассматриваются три метода решения квадратных уравнений!
5. Чтобы завершить наш список, еще одна обложка. Припев в этой версии — действительно приятный способ пропеть квадратичную формулу (начинается с 1:00).

Практика с квадратичной формулой

Для практических вопросов, посвященных квадратичной формуле, изучите практический курс Albert’s Algebra 1! Все вопросы Альберта включают объяснения решений и способы избежать распространенных ошибок. Учителя математики: прочитайте наше подробное руководство о том, как преподавать квадратные уравнения, включая стратегии, примеры из жизни и необходимые навыки учащихся.