Как решить транспортную задачу в excel: Решение транспортной задачи в Excel с примером и описанием

Решение транспортных задач в MS Excel 2013 ⋆ ДПА и ЗНО онлайн

Одной из самых распространенных проблем во всех областях экономики является транспортировка груза или товара с минимальными материальными и временными затратами. Так как огромное количество возможных вариантов перевозок затрудняет получение самого экономичного плана эмпирическим или экспертным путем, то появилась необходимость разработки специальной теории, позволяющей быстро решать подобные задачи с помощью алгоритмизации. Применение математических методов в планировании перевозок дает большой экономический эффект. Такие транспортные задачи очень просто можно решать при помощи MS Excel.

Транспортная задача

Для строительства четырех объектов используется кирпич, изготавливаемый на трех заводах. Транспортные издержки задаются матрицей $$C:$$
$$C=\begin{pmatrix} 2 & 6 & 3 & 5\\ 9 & 4 & 2 & 7\\ 3 & 2 & 5 & 4 \end{pmatrix}$$
Ежедневно каждый из заводов может изготовить 100, 400 и 200 условных единиц кирпича (так называемые мощности поставщиков). Потребности в кирпиче на каждом из строящихся объектов ежедневно составляют 250, 300, 100 и 200 условных единиц (спрос потребителей). Т.к. суммарная мощность поставщиков не совпадает с суммарным спросом потребителей:
$$100+400+200=700\neq 850=250+300+100+200,$$
то имеем дело с открытой транспортной задачей. Т.к. спрос превышает предложение, то для обеспечения баланса необходимо ввести условного поставщика с мощностью в 150 у.е. и нулевыми транспортными издержками. В противном случае нужно было бы ввести условного потребителя. Для транспортных задач закрытого типа (есть баланс) ничего вводить не нужно.
Транспортная задача заключается в распределении груза для каждой пары «поставщик – потребитель» таким образом, чтобы спрос был удовлетворен и суммарные транспортные издержки были бы минимальными.
Введем исходные данные транспортной задачи в MS Excel.

Рабочий лист EXCEL с введенными исходными данными

Далее обращаемся к надстройке Поиск решения.

Подключение надстройки Поиск решения в Excel 2013

Файл – Параметры – Надстройки – в выпадающем списке выбрать Надстройки Excel и нажать на кнопку Перейти… – поставить галочку напротив Поиск решения и нажать OK.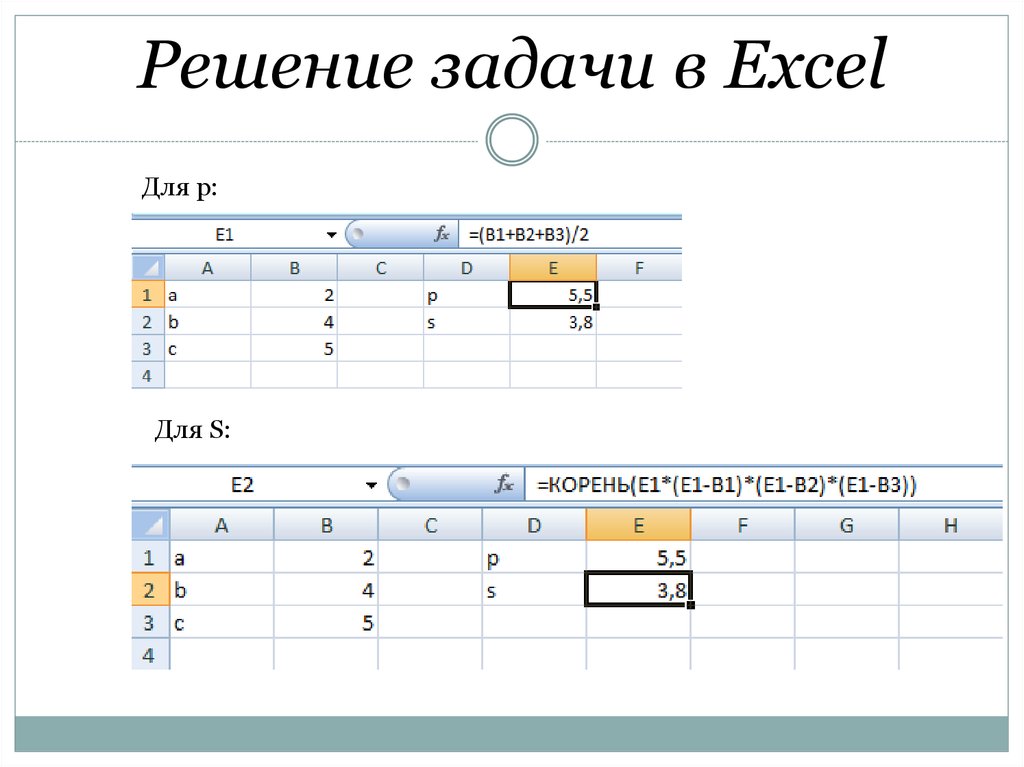

Вызов надстройки Поиск решения

Данные – Анализ – Поиск решения

Заполняем диалоговое окно Параметры поиска решения

Диалоговое окно Параметры поиска решения

Оптимизировать целевую функцию: $B$17 (суммарные транспортные издержки)

До: Минимуму (суммарные транспортные издержки должны быть минимальными)

Изменяя ячейки переменных: $C$13:$F$16 (распределение грузов)

В соответствии с ограничениями (нажимаем добавить):

• Соответствующие предложения поставщиков из 1 и 2 таблиц равны между собой

• Соответствующий спрос потребителей из 1 и 2 таблиц равны между собой

• Распределенные грузы должны быть целыми и неотрицательными

Выберите метод решения: (Поиск решения нелинейных задач методом ОПГ, Поиск решения лин. задач симплекс-методом, Эволюционный поиск решения). Выбираем Поиск решения лин. задач симплекс-методомВ итоге получится следующее:

В диалоговом окне Параметры поиска решения нажимаем на кнопку Найти решение, отмечаем сохранить найденное решение, нажимаем ОК и получаем оптимальное распределение грузов (диапазоне ячеек C13:F16) с минимальными суммарными транспортными издержками (ячейка B17).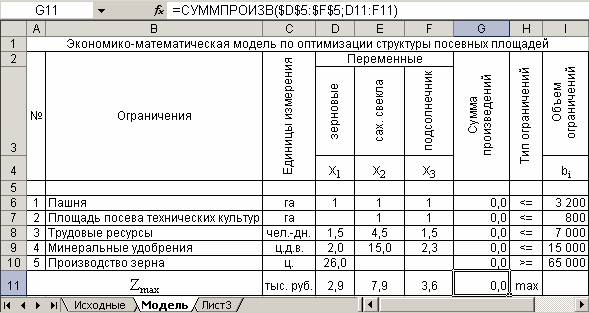

Оптимальное решение

Поделиться

Больше материалов

Материалы по теме

Решение транспортной задачи открытого типа с помощью Поиска решений Excel

Решение транспортной задачи открытого типа с помощью Поиска решений Excel

Приветствую всех, кого

нужда

судьба завела на наш сайт) В этой статье рассмотрим решение транспортной задачи открытого типа с помощью инструмента оптимизации «Поиск решений» Microsoft Excel. Данный материал идет в продолжение нашего предыдущего поста: «Решение транспортной задачи закрытого типа». Поэтому, настоятельно рекомендую вам обновить его в памяти.

Итак, рассмотренная ранее транспортная задача закрытого типа характеризовалась тем, что суммарные запасы груза и суммарная потребность в нем равнялись друг другу, рис. 1.

Рис. 1. Транспортная задача закрытого типа

*Увеличить любой рисунок можно кликнув на нем мышкой

Здесь совокупные запасы в пяти пунктах отправления рассчитаны в ячейке В9 как сумма ячеек F2:F6 и равняются 610 тонн.

Соответственно, совокупная потребность в грузе рассчитана в ячейке В11 как сумма ячеек В7:Е7 и также равняется 610 тонн.

Транспортную задачу такого типа мы решать уже умеем.

Если же, совокупные запасы превышают потребность в них, или наоборот, совокупная потребность превышает имеющиеся запасы груза в пунктах отправления, тогда такая задача называется транспортной задачей открытого типа.

Решение транспортной задачи открытого типа сводится к ее преобразованию к задаче закрытого типа путем добавления еще одного фиктивного пункта назначения или фиктивного пункта отправки. Получив таким образом задачу закрытого типа, решаем ее Поиском решений, как мы уже умеем это делать.

На рис. 2 показан случай, когда совокупные запасы равны 680 тонн и превышают суммарную потребность в них, равную 610 тонн.

Рис. 2. Транспортная задача открытого типа: совокупные запасы превышают суммарную потребность в них

В данном примере в Пункте отправления 4 запасы груза увеличились с 90 тонн до 160 тонн. За счет этого совокупные запасы стали превышать потребность в них на 70 тонн.

Чтобы сбалансировать спрос и предложение, вводим в данном случае еще один, фиктивный пункт назначения с потребностью в 70 тонн. При этом, матрица стоимости перевозок для данного фиктивного пункта назначения заполняется нулями, ячейки F2:F6, рис. 3.

Рис. 3. Преобразование транспортной задачи открытого типа к закрытому путем введения фиктивного пункта назначения

А такую задачу мы решать уже умеем! Кто забыл, смотрим видеоурок по ссылке.

И еще один пример. На рис. 4 показан случай, когда совокупные запасы равны 610 тонн и уступают совокупному спросу в объеме 700 тонн.

Рис. 4. Транспортная задача открытого типа: совокупные запасы уступают суммарной потребности в них

В этом примере в Пункте назначения 3 спрос на груз вырос с 220 тонн до 310 тонн. За счет этого, совокупная потребность теперь превышает имеющиеся запасы груза на 90 тонн. Аналогично, чтобы сбалансировать спрос и предложение, вводим в данном случае еще один, фиктивный пункт отправления с запасами в 90 тонн.

При этом, матрица стоимости перевозок для данного фиктивного пункта отправления заполняется нулями, ячейки В7:Е7 рис. 5.

Рис. 5. Преобразование транспортной задачи открытого типа к закрытому путем введения фиктивного пункта отправления

И снова мы получили транспортную задачу закрытого типа, которую можно решать Поиском решений.

Подробно весь процесс решения данных примеров показан в нашем видеоуроке.

Если вам понравился мой видеоурок, жду лайков, подписки и комментариев. Критические отзывы также приветствуются! Спасибо за внимание.

Как сообщалось на нашем сайте ранее, с помощью инструмента оптимизации «Поиск решений» Microsoft Excel можно решать и другие типы задач линейного программирования, например, задачу о распределении ресурсов.

Популярные сообщения из этого блога

Куда пропал редактор формул Microsoft Equation?

Работая в Microsoft Word , мне часто приходится набирать формулы. На протяжении многих лет, для этих целей я использовал встроенный в Word редактор формул Microsoft Equation . И даже, когда Microsoft добавил в свой Office новый инструмент » Формулы «, я все равно, по привычке, продолжал использовать Microsoft Equation . Для работы я использую два разных ноутбука с абсолютно одинаковым софтом. Microsoft Office 2010 у меня устанавливался на обоих компьютерах с одного дистрибутива. Каково же было мое удивление, когда однажды, открыв созданный ранее документ Word на втором ноутбуке, я не смог войти в режим редактирования формулы! То есть, документ открылся без проблем и все набранные ранее формулы отобразились корректно. Но когда мне понадобилось одну из них отредактировать, то оказалось, что Word этого сделать не может по причине отсутствия Microsoft Equation .

Читать дальше… »

Что делать, если копируемый из Интернета текст не выравнивается по ширине

Каждый когда-либо сталкивался с ситуацией, когда скопированный из Интернета и вставленный в Word текст не удается выровнять по ширине: по левому краю выравнивает, по правому — тоже, а вот по ширине — ни в какую. Еще хуже обстоят дела, если вы захотите увеличить размер шрифта: выравнивание текста окончательно откажется работать. Разбираемся в причинах и ищем способ, как это исправить.

Читать дальше… »

Скопированный в Word текст выходит за границы страницы

Скопировав текст в Word с Интернет-сайта или другого текстового документа, часто приходится сталкиваться с ситуацией, когда он выходит за границы страницы. Ситуация осложняется тем, что маркер » Отступ справа » на горизонтальной линейке, с помощью которого можно было бы все исправить, отсутствует. Как быть? Выход есть и он очень простой. Для этого необходимо выполнить несколько действий.

Читать дальше… »

Решение транспортных задач с помощью Excel — онлайн-вебинар

Факультет

Мохаммед Булам

Группа ДИСЛОГА

Халид Идрисси

Группа JESA

Варианты покупки

Добавить в список желаний

Почему Лорман?

Более 36 лет и 1,4 миллиона клиентов обеспечивают непрерывное обучение. Мы стремимся предоставить вам обучение мирового класса, чтобы помочь вам добиться успеха в бизнесе и как профессионал.

Повестка дня

Варианты покупки

Добавить в список желаний

Почему Лорман?

Более 36 лет и 1,4 миллиона клиентов обеспечивают непрерывное обучение. Мы стремимся предоставить вам обучение мирового класса, чтобы помочь вам добиться успеха в бизнесе и как профессионал.

Кредиты

Варианты покупки

Добавить в список желаний

Почему Лорман?

Более 36 лет и 1,4 миллиона клиентов обеспечивают непрерывное обучение. Мы стремимся предоставить вам обучение мирового класса, чтобы помочь вам добиться успеха в бизнесе и как профессионал.

Факультет

Мохаммед Булам

DISLOG Group

• Специалист по планированию спроса в Dislog Group, лидере в области транспорта, логистики, цепочки поставок и хранения
• Опыт управления цепочками поставок, планирования поставок, планирования и прогнозирования спроса, управления запасами, исследования операций, многокритериального анализа и программирования на Python, R и VBA
• Обучение участников многих соревнований по цепочке поставок, которые проводились в регионе MENA
• Предоставление технической поддержки и рекомендаций для студентов, плохо знакомых с программным обеспечением моделирования цепочки поставок SCM Globe
• Победитель в номинации «Самые ценные сообщения о цепочке поставок» в 2021 году в категории технологий
• Автор сообщений в блоге SCM Globe Как решать транспортные проблемы с помощью Excel Solver и управлять транспортом, решая задачу маршрутизации транспортных средств
• Степень инженера-технолога
• Можно связаться по адресу [email protected] или +212 619360303

Халид Идрисси

Группа JESA

• Экспедитор проектов строительства и инфраструктуры, Группа JESA
• Обеспечивает надлежащую поставку экономичных и высококачественных материалов и оборудования, необходимых для выполнения этапов проекта
• Инженер по цепочкам поставок и управлению производством Высшей школы горного дела в Рабате
• Можно связаться по адресу [email protected] или +212 6 65 93 42 23

Варианты покупки

Добавить в список желаний

Почему Лорман?

Более 36 лет и 1,4 миллиона клиентов обеспечивают непрерывное обучение. Мы стремимся предоставить вам обучение мирового класса, чтобы помочь вам добиться успеха в бизнесе и как профессионал.

Все ваши тренировки здесь, в Лормане.

Оплатите один раз и получите полный год неограниченного обучения в любом формате, в любое время!

• Курсы по запросу
• Живые вебинары
• Загрузки MP3
• Учебные пособия
• Исполнительные отчеты
• Белые книги и статьи

Дополнительные преимущества:

• Кредитный трекер штата
• All-Access Pass Course Консьерж

Вопросы? Позвоните по телефону 877-296-2169, чтобы поговорить с реальным человеком.

Зарегистрируйтесь сегодня
с этим курсом

Доступ ко всем учебным продуктам на один год

699 долларов США в год

Неограниченное обучение Lorman

С All-Access Pass вы не угадаете, что вам понадобится для вашего годового бюджета на обучение. $699 покроет все ваши потребности в обучении в течение всего года!

Простая регистрация

После того, как вы купите пропуск All-Access Pass, вы всегда будете на расстоянии одного клика от посещения любого учебного курса Lorman.

Инвестируйте в себя

Вы не добились своего профессионального успеха только благодаря удаче; потребовалось много тяжелой работы и тренировок. Инвестируйте в себя с All-Access Pass.

Решение проблем транспортировки или распределения с помощью Excel Solver

В этой статье мы обсудим 2 кейса для , решающих проблемы транспортировки или распределения с помощью Excel Solver . Хорошо известно, что компании производят продукцию в разных местах и ​​отгружают ее клиентам в разные места. Менеджеры по сбыту должны распределять и отгружать товары наиболее эффективным и рентабельным способом. Такого рода задачи называются транспортными задачами . Сегодня мы обсудим 2 случая. Используя эти случаи, вы можете легко использовать Solver для задач транспортировки или распределения в Excel.

---

Скачать практическую рабочую тетрадь

2 подходящих случая решения проблем с транспортировкой или распределением с помощью Excel Solver

Пример 1. Минимизация общей стоимости доставки при соблюдении требований

Случай 2: максимизация прибыли после налогообложения при ограниченной производственной мощности

Заключение

Загрузить рабочую тетрадь

Вы можете скачать учебную тетрадь отсюда.

---

2 Подходящие случаи решения задач транспортировки или распределения с помощью Excel Solver

Сегодня мы обсудим два случая решения задач транспортировки или распределения с помощью Excel Solver . В случае Case 1 мы постараемся минимизировать общую стоимость доставки при соблюдении требований. А в Случай 2 мы максимизируем прибыль после уплаты налогов при ограниченных производственных мощностях. Вы можете увидеть краткий обзор Case 1 ниже.

---

Пример 1. Минимизация общей стоимости доставки при соблюдении требований

В первом случае мы постараемся минимизировать общую стоимость доставки при соблюдении всех требований, используя Решатель в Excel. Для этого нам нужно сначала понять проблему. Предположим, что северная, центральная и южная Калифорния потребляют по 100 миллиардов галлонов воды каждый день. Кроме того, предположим, что в северной и центральной Калифорнии имеется 120 миллиардов галлонов воды, тогда как в южной Калифорнии доступно 60 миллиардов галлонов воды. Стоимость доставки 1 миллиарда галлонов воды между тремя регионами выглядит следующим образом:

Нам нужно найти самый дешевый способ доставки того количества воды, которое необходимо каждому региону.

В данном случае наша цель — вычислить общую стоимость доставки и минимизировать ее. Общая стоимость может быть выражена следующим образом:

(Количество миллиардов галлонов воды, отправленных с севера на север)*(Стоимость одного миллиарда галлонов воды, отправленной с севера на север) + (Количество миллиардов галлонов воды, отправленных с севера на север)*(Стоимость за миллиард галлонов подачи воды из северного региона в центральный) + (Количество миллиардов галлонов воды, отправленного из северного региона в южный)*(Стоимость одного миллиарда галлонов воды, отправленного из северного региона в южный) + …… + (Количество миллиардов галлонов воды, отправленного из южного в центральный)*(Стоимость за миллиард галлонов воды, перекачиваемой с юга в центр) + (Количество миллиардов галлонов воды, перекачиваемой с юга в южную)*(Стоимость за миллиард галлонов, перекачиваемой с юга в южную)

Если мы переведем приведенную выше модель в формулу Excel, это не только будет стоить нам много времени, но и подвергнет нас высокому риску совершить ошибку. Итак, давайте выполним шаги, чтобы увидеть, как мы можем реализовать более простую формулу и использовать Solver , чтобы найти минимальную стоимость доставки.

ШАГИ:

• В первую очередь нам необходимо создать набор данных для ввода отгрузок по каждой точке снабжения в каждый регион.
• Здесь диапазон C10:E12 изображает это. Это « путем изменения ячеек », которые мы будем использовать в инструменте Solver .

• Во-вторых, нам нужно назначить ячейки для Цель и Ограничения .
• В нашем случае Cell G5 — это ячейка Objective , которая будет содержать минимальную стоимость доставки.
• Аналогично, диапазон C15:D17 представляет Ограничение 1 и диапазон G10:I12 обозначает Ограничение 2 .
• Ограничение 1 говорит, что Спрос на воду в каждом регионе должен быть равен или больше 100 галлонов. После минимизации получим Получено количества воды в диапазоне C12:C14 .
• С другой стороны, Ограничение 2 означает, что в северной и центральной Калифорнии объем воды равен или меньше 120 галлонов, тогда как в южной Калифорнии объем воды равен или меньше 60 галлона воды. После минимизации мы получим количество галлонов воды в диапазоне G10:G12 , которое должно быть SENT .

• На следующем этапе нам нужно ввести приведенную ниже формулу в ячейку G5 , чтобы получить общую стоимость доставки :
.

=СУММПРОИЗВ(C5:E7,C10:E12)

В этой формуле мы использовали функцию СУММПРОИЗВ . Чтобы найти общую стоимость, мы помещаем стоимость доставки 1 миллиардов галлонов воды между этими тремя регионами в ячейку в диапазоне C5:E7 . А отгрузки по каждой точке снабжения в каждый регион заносились в ячейку диапазон C10:E12 . Эти два диапазона имеют одинаковые размеры, поэтому для вычисления общей стоимости здесь можно использовать функцию СУММПРОИЗВ .

• На данный момент мы определили нашу цель и « Путем изменения ячеек ».
• Теперь нам нужно применить уравнения для ограничений.
• Поскольку Ограничение 2 указывает, что количество воды, отправляемой из каждого региона, должно быть меньше или равно галлонам доступной воды, мы можем использовать приведенную ниже формулу в ячейке G10 для расчета общего количества галлонов воды, отправленной из Северной Калифорнии . :

=СУММ(C10:E10)

• Перетащите ручку заполнения вниз до Ячейка G12 , чтобы получить количество воды, отправленной из Центральной и Южной Калифорнии .

Здесь мы использовали функцию СУММ , чтобы найти результат диапазона C10:E10 .

• С другой стороны, Ограничение 1 заключается в том, что количество воды, получаемой каждым регионом, должно быть равно или больше 100 миллиардов галлонов воды.
• Это ограничение было помещено в диапазон C15:E17 и приведенная ниже формула используется для подсчета суммы Получено в ячейке C15 :

=СУММ(10 канадских долларов:12 канадских долларов)

• Теперь перетащите маркер заполнения вправо до ячейки E15 , чтобы скопировать формулу.

• После вставки формул перейдите на вкладку Данные и выберите Решатель в разделе Анализ . Он откроет Параметры решателя поле.

• Заполните диалоговое окно, как показано на рисунке ниже.
• Общая стоимость доставки вычисляется путем сложения условий изменения ячейки * константы в ячейке G5 . Итак, « Установить цель » — это G5 .
• После этого выберите Min и введите диапазон C10:E12 в поле « By Changeable Variable Cells ».
• Два явных ограничения создаются путем сравнения сумм изменяющихся ячеек с константой. Мы вставили ограничения, используя Добавить опцию .
• Как видите, и наша цель, и ограничения могут быть представлены линейной зависимостью. Поэтому наша модель является линейной моделью, и был выбран двигатель Simplex LP .
• Очевидно, что отгрузки должны быть положительными, и именно поэтому мы установили флажок Сделать неограниченные переменные неотрицательными .
• После этого выберите параметр РЕШИТЬ .

• Снова нажмите OK в поле Solver Results .

• Наконец, вы автоматически найдете требования и общую стоимость доставки.

Минимальная стоимость выполнения требований составляет $ 1 580 000 и мы можем достичь этого, применяя следующий график:

• Мы можем отправить 100 миллиардов галлонов воды из Северный в Северный и 4 миллиарда 9009 вода от С севера на юг .
• Также мы можем перекачивать 100 миллиарда галлонов воды из Центрального в Центральный и 20 миллиардов галлонов воды из Центрального в Южный.
• Southern сохраняет всю доступную воду для собственного использования.

---

Пример 2. Максимизация прибыли после налогообложения при ограниченной производственной мощности

Во втором случае мы минимизируем прибыль после налогообложения при ограниченной производственной мощности с помощью 9Надстройка 0093 Solver .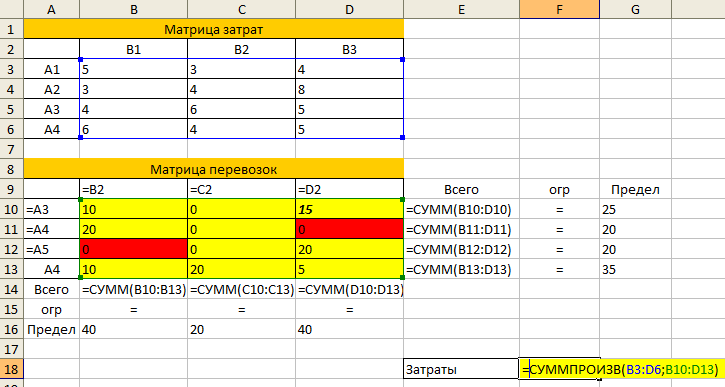 Чтобы проиллюстрировать пример, мы будем использовать следующую задачу:

Компания производит и продает наркотики в нескольких местах. Решение о том, где производить товары для каждого места продаж, может оказать огромное влияние на прибыльность. Предположим, что нам нужно производить лекарства на шести заводах и продавать их покупателям в шести районах . « налог ставка » и « переменная продукция стоимость » зависят от места производства. « продажная цена ”каждого препарата зависит от места продажи. Также каждый из шести заводов может выпускать до 6 млн единиц в год. Вы можете увидеть годовой спрос на продукты в каждой области в обзоре проблем ниже. Стоимость доставки единицы товара зависит от завода и региона. Вы можете найти подробности в обзоре ниже.

Нам нужно найти максимальную прибыль после налогообложения при ограниченной производственной мощности.

Давайте выполним следующие шаги, чтобы увидеть, как мы максимизируем прибыль, используя Инструмент Solver в Excel.

ШАГИ:

• Во-первых, нам нужно создать набор данных для вычислений.
• Поскольку налоговая ставка , переменные производственные затраты и продажная цена относятся к месту производства или продажи, мы можем упростить задачу, вычислив прибыль для каждого завода, а затем сложив их вместе.
• Вы можете увидеть переупорядоченный набор данных со столбцом Прибыль . Здесь мы посчитаем прибыль для каждого завода.

• Во-вторых, вставьте ячейки для « Путем изменения ячеек переменных » в диапазоне C14:h29 . Эти ячейки будут содержать количество перетаскиваний, отправленных с заводов в зоны .
• Также одно ограничение указывает, что мощность заводов меньше, чем 6 миллионов единиц. Мы вставляем это ограничение в диапазон J4:L19 .

• Опять же, второе ограничение обозначает количество Получено и Требовано шт. Он находится в диапазоне C21:h33 , как показано на рисунке ниже.

• Теперь, чтобы вычислить прибыль после уплаты налогов , введите приведенную ниже формулу в ячейку K5 :

=(СУММПРОИЗВ(C14:h24,$C$11:$H$11)-J14*I5-СУММПРОИЗВ(C14:h24,C5:H5))*J5

• Нажмите Введите и перетащите Ручку заполнения вниз до Ячейка K10 .
• Затем в ячейке K11 введите приведенную ниже формулу:

=СУММ(К5:К10)

• После этого введите приведенную ниже формулу в Cell J14 , чтобы подсчитать количество наркотиков, отправленных с заводов в места:

=СУММ(C14:h24)

• Нажмите Введите и перетащите ручку заполнения вниз в ячейку J19 .

• Чтобы найти количество Получено лекарств, введите приведенную ниже формулу в ячейку C21 :

=СУММ(С14:С19)

• Нажмите Введите и перетащите Ручку заполнения вправо к ячейке h31 .

• На следующем шаге перейдите на вкладку Data и выберите Solver из Analyze 9раздел 0094. Откроется окно Solver Parameters .

• В поле Solver Parameters заполните диалоговое окно, как показано на рисунке ниже.
• Здесь мы вычислили Общая прибыль путем сложения прибыли каждого завода. Итак, « Set Objective » — это K11 .
• После этого выберите Макс. и введите диапазон C14:h29 в поле « By Changeable Variable Cells ».
• Теперь вставьте ограничения, используя параметр Добавить .
• Первое ограничение заключается в том, что в каждое место должны поступать лекарства, равные или превышающие потребности. Мы можем описать это, используя « $C$21:$H$21 >= $C$23:$H$23 ».
• Другим ограничением является то, что производимые лекарства не могут превышать мощности. Вы можете написать это, используя « $J$14:$J$19 <= $L$14:$L$19 ».
• Как видите, и наша цель, и ограничения могут иметь линейную зависимость. Следовательно, наша модель является линейной моделью, и нам нужно выбрать Двигатель Simplex LP .
• Очевидно, что отгрузки должны быть положительными, и именно поэтому мы установили флажок Сделать неограниченные переменные неотрицательными .
• После этого выберите параметр РЕШИТЬ .

• Снова нажмите OK , чтобы продолжить.

  No related posts.