Как считать площадь прямоугольника с разными сторонами: Формула площади прямоугольника определение запись. Как вычислить площадь прямоугольника с разными сторонами

Содержание

Калькулятор расчета площади прямоугольника

Калькулятор расчета площади прямоугольника
Как рассчитать площадь прямоугольника
Площадь прямоугольника. Видео-урок.

Полезный калькулятор для школьников и взрослых позволяет быстро вычислить площадь прямоугольника по двум его сторонам. Подобный расчет мы часто производим не только в рамках школьного курса геометрии, но и в повседневной жизни. Например, если нужно посчитать площадь комнаты при ремонте квартиры, для расчета необходимого количества материалов.

Удобная навигация по статье:

1 Калькулятор расчета площади прямоугольника
- 1.1 Как рассчитать площадь прямоугольника
- 1.2 Площадь прямоугольника. Видео-урок.

Как рассчитать площадь прямоугольника

Прямоугольником принято называть геометрическую плоскую фигуру, которая имеет параллельно расположенные противоположные стороны при углах в 90 градусов. В качестве длины этой геометрической фигуры выступает величина, которая имеет большую сторону. При этом, за ширину принимается величина меньшей стороны. Для правильного вычисления площади прямоугольника Вам необходимо знать определённые параметры, которыми обладает данная фигура. В их числе:

диагональ;
ширина;
так называемый угол наклона к одной из сторон диагонали;
длина.

Таким образом, произвести расчёт площади прямоугольника можно различными способами. Всё зависит от количества информации о фигуре, а именно, какие величины нам точно известны.

Как вычислить площадь прямоугольника, имея линейные параметры его сторон?

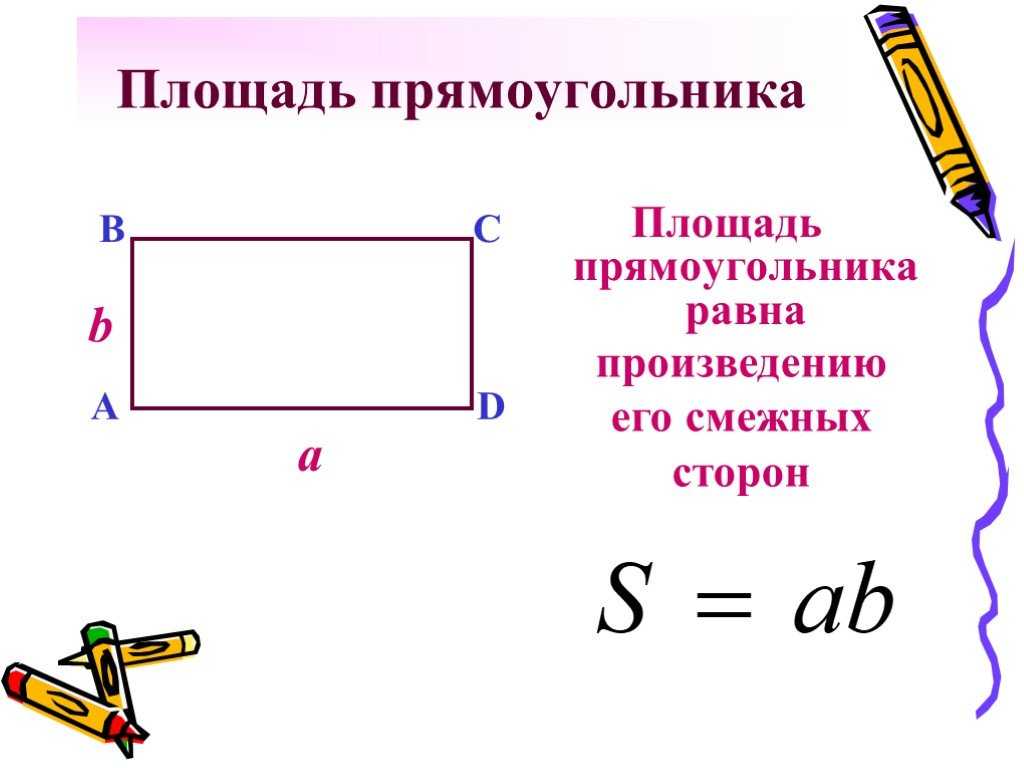
Давайте в качестве обозначения длины прямоугольника будем использовать букву «а», для его ширины – букву «b», а площадь геометрической фигуры обозначим буквой «S». Согласно этому, наша формула будет выглядеть следующим образом: S = a x b.

Зная линейные параметры прямоугольника, можно легко определить его периметр последующей формуле: P = 2(a + b), где в качестве обозначения периметра мы используем букву «P».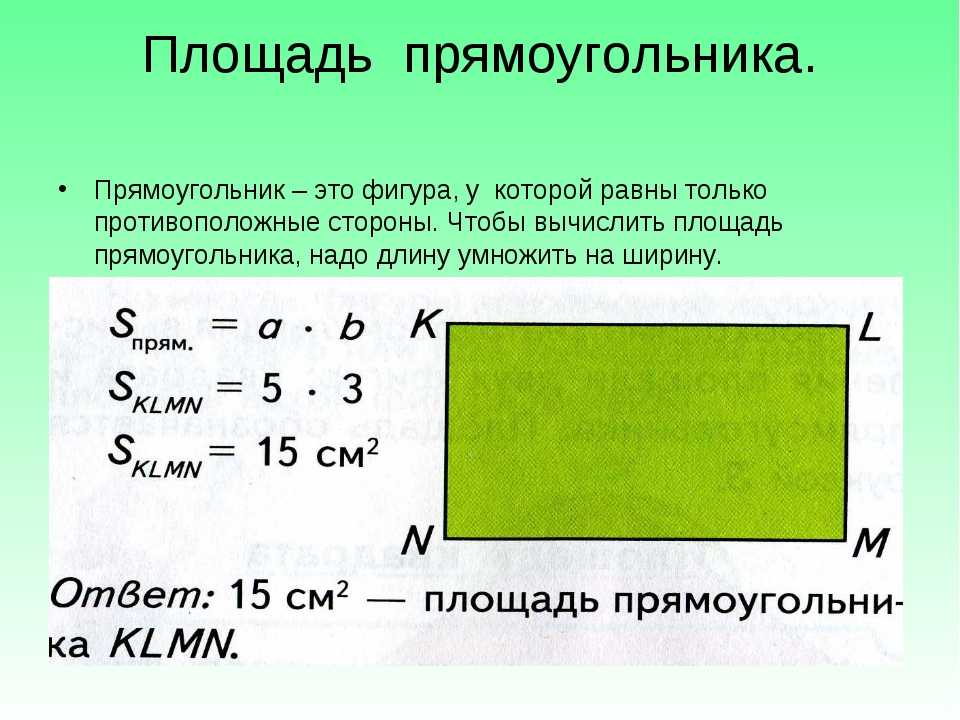

Как можно вычислить площадь прямоугольника, зная величину одну из его сторон и диагональ?

Как нам известно, диагональ делит любой прямоугольник на два так называемых прямоугольных треугольника. Давайте присвоим диагонали индекс «с», а длину стороны обозначим буквой «а». Теперь необходимо произвести следующий порядок действий:

для начала необходимо найти длину неизвестной стороны. Для этого мы используем формулу Пифагора: b = V c2 – a2.
После этого, нам следует определить площадь нашей основной геометрической фигуры (прямоугольника) как площадь треугольника, умноженную на два: Sтр = ½ (а х в).
Согласно вышеописанной схеме расчёта площадь прямоугольника в данном случае будет равна: S = 2 x Sтр = а х в.

В том случае, если нам известны периметр прямоугольника, а также длина одной из его сторон, то площадь этой геометрической фигуры можно вычислить, определив длину второй стороны (b = (P – 2xa), по такой формуле: S = a x b.

Если же нам известны размер диагонали прямоугольника, а также угол между стороной и самой диагональю, то площадь можно вычислить при помощи следующих тригонометрических функций: Sтр = ½ х с2 х sinФ х cosФ.

При этом, общая площадь в данном случае будет составлять S = 2 x Sтр.

Площадь прямоугольника. Видео-урок.

Площадь прямоугольника. Онлайн калькулятор

0
AC		+/-	÷
7	8	9	×
4	5	6	—
1	2	3	+
0	00	,	=

При помощи данного калькулятора вы можете легко найти площадь прямоугольника (через две стороны, периметр и любую сторону, диагональ и любую сторону, диагональ и синус острого угла между диагоналями, радиус описанной окружности и любую сторону, через диаметр описанной окружности и любую сторону) и получите подробное решение

Укажите известную величину прямоугольника
Две стороныПериметр и любая сторонаДиагональ и любая сторонаДиагональ и синус острого угла между диагоналямиРадиус описанной окружности и любая сторонаДиаметр описанной окружности и любая сторона

Сторона a

Сторона b

Как вычислить площадь прямоугольника

Прямоугольник — это четырехугольник, все углы которого прямые

Площадь прямоугольника равна

S = a · b =

Pa — 2a²

Pb — 2b²

a√d² — a²

b√d² — b²

d² · sin α

a√4R² — a²

b√4R² — b²

a√D² — a²

b√D² — b²

, где

а — сторона прямоугольника
b — сторона прямоугольника
P — периметр прямоугольника
d — диагональ прямоугольника
sin α — синус острого угла между диагоналями
R — радиус описанной окружности прямоугольника
D — диаметр описанной окружности прямоугольника

Вам могут также быть полезны следующие сервисы

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка.

Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление.

Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона.

Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора.

Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Вычисление площади любого четырехугольника

Вычисление площади любого четырехугольника Открыть/закрыть навигацию

Домашняя страница
Строительство
- Размер лестницы
- Расчет уклона, уклона, наклона
Геометрия
- Цилиндр
- Треугольник
- Уклон, уклон, наклон
- Параллелограмм
- Четырехугольник
- Эволюционная спираль
Математика
- Правило трех

Карта сайта > Геометрия > Четырехугольник

Каждый четырехугольник представляет собой многоугольник с четырьмя сторонами любой длины, соединенными друг с другом в углах. Метод расчета четырехугольников — триангуляция, для которой требуется знать длины одной из двух диагоналей.

По этой формуле можно найти площадь любого четырехугольника, будь то параллелограмм, ромб, трапеция – короче говоря, каждая 4-сторонняя поверхность кроме скрещенного четырехугольника.

Расчет четырехугольника

Примечание: в этой форме используется метод расчета триангуляции.

Четырехугольник

* Соблюдайте порядок сторон и используйте диагональ «ab», как показано на рисунке, иначе вы можете получить неверный результат.

Четырехсторонние данные:

Единицы:

миллиметрсантиметрсантиметрдециметрметрдекаметргектометркилометрдюймфутярдмиля

Сторона и :

Сторона b :

диагональ аб :

Боковой c :

Сторона d :

Десятичные разряды:

012345678910

Единицы измерения углов:

Градусы Радианы Градианы

Четырехсторонние результаты:

Поверхность:	0,87 м ²
Периметр:	4,00 м
Четырехугольные углы :
(альфа) α :	60,00°
(бета) β :	120,00°
(гама) γ :	60,00°
(дельта) δ :	120,00°

Углы четырехугольника

Начиная с этого момента, на этой странице будут отображаться значения 4 углов. Вы можете выбрать между градусами, радианами или градианами.

Расчет производится следующим образом: найти сумму квадратов двух соседних сторон угла, которую затем вычесть из квадрата противоположной диагонали. Затем разделите результат этого «сложения/вычитания» на произведение двух соседних сторон, умноженное на два. Наконец, вы вычисляете арккосинус приведенного выше результата. Какая подвязка! Теперь для тех, кто в этом нуждается, вы можете найти аспирин, тайленол или другое лекарство от головной боли в ближайшей аптеке…

Четырехугольники дома

Знание расчета любого четырехугольника полезно для точного определения площади предметов домашнего обихода, особенно в старых домах. Часто встречаются комнаты, в которых стены не перпендикулярны друг другу, что делает их не просто прямоугольниками, а различными типами четырехугольников.

Тем не менее, вычислить площадь поверхности земли очень сложно, если поверхность считается прямоугольником, что почти никогда не бывает. Зная его четыре стороны, одну из двух диагоналей и используя формулу на этой странице, вы получите точные результаты.

Используя инструмент масштабирования в Google Earth и заполнив эту формулу, легко найти (по крайней мере, очень точно) интересующую вас область географических местоположений.

Скрещенные четырехугольники

Четырехугольник может быть выпуклым (обычный случай), вогнутым (образующим углубление) или скрещенным. В этом последнем случае он создает два треугольника. Чтобы вычислить его характеристики, проще всего вычислить характеристики двух треугольников, составляющих скрещенный четырехугольник.

Список страниц расчетов

Конструкция
- Размер лестницы
- Расчет уклона, уклона, наклона
Геометрия
- Цилиндр
- Треугольник
- Уклон, уклон, наклон
- Параллелограмм
- Четырехугольник
- Эволюционная спираль
Математика
- Правило трех

Как найти площадь с 4 разными сторонами? – Reviews Wiki

Используйте следующее уравнение: Площадь = сторона × сторона или A = s . Пример: если одна сторона квадрата имеет длину 4 фута (t = 4), то площадь этого квадрата равна t ² , или 4 x 4 = 16 квадратных футов.
…
Параллелограммы включают:

Квадраты: Четыре стороны, все одинаковой длины. …
Прямоугольники: четыре стороны; противоположные стороны имеют одинаковую длину. 92.

Что такое четырехугольник с неравными сторонами? Разносторонний четырехугольник — это четырехсторонний многоугольник, у которого нет конгруэнтных сторон.

Во-вторых Как найти площадь с неравными сторонами? Как использовать калькулятор неправильной площади?

Шаг 1: Измерьте все стороны площади в одной единице (футы, метры, дюймы или любые другие).
Шаг 2: Введите длину горизонтальных сторон в поля «Длина 1» и «Длина 2». И ширину вертикальных сторон в поля «Ширина 1» и «Ширина 2». …
Шаг 3: Нажмите кнопку расчета. …
Наша формула: Площадь = b × h.

Что такое неправильный четырехугольник?

Другими словами, неправильный четырехугольник — это четырехугольник, у которого не все стороны равны по длине . … Обратите внимание, что не все стороны имеют одинаковую длину. Противоположные стороны имеют одинаковую длину, но не все они равны. Следовательно, это неправильный четырехугольник.

Затем Какая фигура имеет 4 стороны разной длины? Четырёхугольники — это многоугольники с четырьмя сторонами (отсюда и начало «квадрат», что означает «четыре»). Многоугольник с неравными сторонами называется неправильным, поэтому фигура, которую вы описываете, является неправильным четырехугольником. Стороны этой фигуры равны 1, 2, 3 и 4 соответственно, поэтому это неправильный четырехугольник.

Как найти диагональ неправильного четырехугольника? Нахождение диагонали неправильного четырехугольника

Домашнее задание. В неправильном четырехугольнике ABCD длины всех сторон равны AB=a BC=b CD=c DA=d, а длина диагонали AC равна x. …
Домашнее задание Уравнения. Формула косинуса c ² = a ² + b ² – 2abcosθ
Попытка решения. Я действительно понятия не имею, как начать.

Сколько существует различных четырехугольников?

Существует 5 типов четырехугольников – Прямоугольник, Квадрат, Параллелограмм, Трапеция или Трапеция и Ромб.

Все ли правильные четырехугольники? Некоторые примеры четырехугольников: прямоугольник, квадрат, ромб, параллелограмм, трапеция и т. д. Правильный четырехугольник должно иметь 4 равные стороны, 4 равных угла и его диагонали должны делиться друг на друга пополам . Квадрат — единственный четырехугольник, удовлетворяющий всем этим условиям.

Что такое четырехугольник с четырьмя сторонами?

Четырехугольник — это четырехугольник с четырьмя углами. Существует много видов четырехугольников. Пять наиболее распространенных типов — это параллелограмм, прямоугольник, квадрат, трапеция и ромб . Наведите курсор мыши на цифры справа, чтобы узнать больше.

Какие четырехугольники имеют 4 стороны одинаковой длины? Ромб представляет собой четырехугольник с 4 равными сторонами. Фигура с четырьмя сторонами одинаковой длины. Фигура имеет два набора параллельных сторон и не имеет прямых углов.

Какая фигура имеет 4 вершины и 4 стороны?

Четырехугольник — это многоугольник, у которого ровно четыре стороны. (Это также означает, что четырехугольник имеет ровно четыре вершины и ровно четыре угла.)

Как найти четвертую сторону параллелограмма?

Мы знаем, что противоположные стороны параллелограмма равны друг другу. Итак, АВ=CD и ВС=AD. х=9 и у=4. Следовательно, четвертая вершина равна (9,4) .

Чем отличаются четырехугольники? Четырехугольник — это многоугольник с четырьмя сторонами . … Когда мы начинаем сравнивать и сопоставлять четырехугольники, мы обнаруживаем, что некоторые из этих особых характеристик одинаковы, а другие совершенно разные. Например, у квадрата и прямоугольника разные длины сторон, но у обоих по четыре 9углы 0 градусов.

Сколько сторон в четырехугольнике?

Quadrilateral
Edges and vertices	4
Schläfli symbol	{4} (for square)
Area	various methods; см. ниже
Внутренний угол (градусы)	90° (для квадрата и прямоугольника)

Какие 8 четырехугольников? Четырехугольники можно определить как типы многоугольников, которые имеют четыре стороны, четыре вершины и четыре угла вместе с парой диагоналей.
…
Выпуклые четырехугольники

Трапеция.
Воздушный змей.
Параллелограмм.
Прямоугольник.
Ромб.
Квадрат.

Какие из этих фигур имеют более 4 сторон?

Геометрическая форма « Pentagon » имеет более 4-х сторон. Пятиугольник — это геометрическая фигура, имеющая пять сторон и пять ребер. Пятиугольник представляет собой 5-сторонний многоугольник замкнутой формы.

Что имеет четыре стороны и не имеет четырех сторон? (четверка означает четыре, боковая сторона означает сторону). Четырехугольник имеет четыре стороны, он двумерный (плоская форма), замкнутый (линии соединяются) и имеет прямые стороны.
…
Трапеция (Великобритания: Трапеция)

	Трапеция	Трапеция
In the US:	a pair of parallel sides	NO parallel sides
In the UK:	NO parallel sides	a pair of parallel sides

What are the 4 types четырехугольников?

Какие существуют типы четырехугольников? Существует 5 типов четырехугольников — прямоугольник, квадрат, параллелограмм, трапеция или трапеция и ромб.

У треугольников четыре стороны? Вопрос: СКОЛЬКО СТРАН У ТРЕУГОЛЬНИКА? Треугольник имеет три стороны по (3). Треугольник — это многоугольник, который содержит три стороны, три внутренних угла и три вершины. … Треугольник — это примитивная форма геометрии (многоугольник), которая в своей простейшей форме может иметь только три стороны.

Как называется четырехугольник, у которого 4 равных угла, но разные длины сторон?

Наиболее конкретное имя для этого типа четырехугольника ромб . Это также разновидность параллелограмма.

Как называется фигура, имеющая 4 стороны? Определение: Четырехугольник — это многоугольник с 4 сторонами. Диагональ четырехугольника — это отрезок, концы которого лежат в противоположных вершинах четырехугольника.

Как называется четырехугольник с 4 равными сторонами и без прямых углов?

Сначала начнем с Ромб . Итак, ромб — это параллелограмм, у которого все стороны равны, а диагонали перпендикулярны друг другу.