Сложение и вычитание положительных и отрицательных чисел. Записи с меткой «сложение отрицательных чисел»
В рамках этого материала мы затронем такую важную тему, как сложение отрицательных чисел. В первом параграфе мы расскажем основное правило для этого действия, а во втором – разберем конкретные примеры решения подобных задач.
Yandex.RTB R-A-339285-1
Основное правило сложения натуральных чисел
Перед тем, как вывести правило, вспомним, что мы вообще знаем о положительных и отрицательных числах. Ранее мы условились, что отрицательные числа нужно воспринимать как долг, убыток. Модуль отрицательного числа выражает точные размеры этого убытка. Тогда сложение отрицательных чисел можно представить как сложение двух убытков.
Воспользовавшись этим рассуждением, сформулируем основное правило сложения отрицательных чисел.
Определение 1
Для того чтобы выполнить сложение отрицательных чисел , нужно сложить значения их модулей и поставить минус перед полученным результатом. В буквенном виде формула выглядит как (− a) + (− b) = − (a + b) .
В буквенном виде формула выглядит как (− a) + (− b) = − (a + b) .
Исходя из этого правила, можно сделать вывод, что сложение отрицательных чисел аналогично сложению положительных, только в итоге у нас обязательно должно получиться отрицательное число, ведь перед суммой модулей надо ставить знак минус.
Какие можно привести доказательства этого правила? Для этого нам потребуется вспомнить основные свойства действий с действительными числами (или с целыми, или с рациональными –они одинаковы для всех этих типов чисел). Для доказательства нам нужно всего лишь продемонстрировать, что разность левой и правой части равенства (− a) + (− b) = − (a + b) будет равна 0 .
Вычесть одно число из другого – это то же самое, что и прибавить к нему такое же противоположное число. Следовательно, (− a) + (− b) − (− (a + b)) = (− a) + (− b) + (a + b) . Вспомним, что числовые выражения со сложением обладают двумя основными свойствами – сочетательным и переместительным. Тогда мы можем сделать вывод, что (− a) + (− b) + (a + b) = (− a + a) + (− b + b) .
Во втором параграфе мы возьмем конкретные задачи, где нужно складывать отрицательные числа, и попробуем применить в них изученное правило.
Пример 1
Найдите сумму двух отрицательных чисел — 304 и — 18 007 .
Решение
Выполним действия пошагово. Сначала нам надо найти модули складываемых чисел: — 304 = 304 , — 180007 = 180007 . Далее нам нужно выполнить действие сложения, для чего мы используем метод подсчета столбиком:
Все, что нам осталось, – это поставить минус перед результатом и получить — 18 311 .
Ответ: — — 18 311 .
От того, какие у нас числа, зависит, к чему мы можем свести действие сложения: к нахождению суммы натуральных чисел, к сложению обыкновенных или десятичных дробей. Разберем задачу с такими числами.
Пример N
Найдите сумму двух отрицательных чисел — 2 5 и − 4 , (12) .
Решение
Находим модули искомых чисел и получаем 2 5 и 4 , (12) . У нас получились две разные дроби. Сведем задачу к сложению двух обыкновенных дробей, для чего представим периодическую дробь в виде обыкновенной:
4 , (12) = 4 + (0 , 12 + 0 , 0012 + . . .) = 4 + 0 , 12 1 — 0 , 01 = 4 + 0 , 12 0 , 99 = 4 + 12 99 = 4 + 4 33 = 136 33
В итоге мы получили дробь, которую будет легко сложить с первым исходным слагаемым (если вы забыли, как правильно складывать дроби с разными знаменателями, повторите соответствующий материал).
2 5 + 136 33 = 2 · 33 5 · 33 + 136 · 5 33 · 5 = 66 165 + 680 165 = 764 165 = 4 86 105
В итоге мы получили смешанное число, перед которым нам осталось только поставить минус. На этом расчеты завершены.
Ответ: — 4 86 105 .
Действительные отрицательные числа складываются аналогичным образом. Результат такого действия принято записывать числовым выражением. Его значение можно и не вычислять или ограничиться примерными расчетами. Так, к примеру, если нам надо найти сумму — 3 + (− 5) , то ответ мы записываем как — 3 − 5 . Сложению действительных чисел мы посвятили отдельный материал, в котором можно найти и другие примеры.
Его значение можно и не вычислять или ограничиться примерными расчетами. Так, к примеру, если нам надо найти сумму — 3 + (− 5) , то ответ мы записываем как — 3 − 5 . Сложению действительных чисел мы посвятили отдельный материал, в котором можно найти и другие примеры.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Правило сложения отрицательных чисел
Если вспомнить урок математики и тему «Сложение и вычитание чисел с разными знаками», то для сложения двух отрицательных чисел необходимо:
- выполнить сложение их модулей;
- дописать к полученной сумме знак «–».
Согласно правилу сложения можно записать:
$(−a)+(−b)=−(a+b)$.
Пример 1
Сложить отрицательные числа $−185$ и $−23 \ 789.$
Решение .
Воспользуемся правилом сложения отрицательных чисел.
Найдем модули данных чисел:
$|-23 \ 789|=23 \ 789$.
Выполним сложение полученных чисел:
$185+23 \ 789=23 \ 974$.
Поставим знак $«–»$ перед найденным числом и получим $−23 \ 974$.
Краткая запись решения: $(−185)+(−23 \ 789)=−(185+23 \ 789)=−23 \ 974$.
Ответ : $−23 \ 974$.
При сложении отрицательных рациональных чисел их необходимо преобразовать к виду натуральных чисел, обыкновенных или десятичных дробей.
Пример 2
Сложить отрицательные числа $-\frac{1}{4}$ и $−7,15$.
Решение.
Согласно правилу сложения отрицательных чисел, сначала необходимо найти сумму модулей:
$|-\frac{1}{4}|=\frac{1}{4}$;
Полученные значения удобно свести к десятичным дробям и выполнить их сложение:
$\frac{1}{4}=0,25$;
$0,25+7,15=7,40$.
Поставим перед полученным значением знак $«–»$ и получим $–7,4$.
Краткая запись решения:
$(-\frac{1}{4})+(−7,15)=−(\frac{1}{4}+7,15)=–(0,25+7,15)=−7,4$.
Для сложения положительного и отрицательного числа необходимо:
- вычислить модули чисел;
выполнить сравнение полученных чисел:
- если они равны, то исходные числа являются противоположными и их сумма равна нулю;
- если они не равны, то нужно запомнить знак числа, у которого модуль больше;
из большего модуля вычесть меньший;

Сложение чисел с противоположными знаками сводится к вычитанию из большего положительного числа меньшего отрицательного числа.
Правило сложения чисел с противоположными знаками выполняется для целых, рациональных и действительных чисел.
Пример 3
Сложить числа $4$ и $−8$.
Решение.
Требуется выполнить сложение чисел с противоположными знаками. Воспользуемся соответствующим правилом сложения.
Найдем модули данных чисел:
Модуль числа $−8$ больше модуля числа $4$, т.е. запомним знак $«–»$.
Поставим знак $«–»$, который запоминали, перед полученным числом, и получим $−4.$
Краткая запись решения:
$4+(–8) = –(8–4) = –4$.
Ответ : $4+(−8)=−4$.
Для сложения рациональных чисел с противоположными знаками их удобно представить в виде обыкновенных или десятичных дробей.
Вычитание чисел с разными и отрицательными знаками
Правило вычитания отрицательных чисел:
Для вычитания из числа $a$ отрицательного числа $b$ необходимо к уменьшаемому $a$ добавить число $−b$, которое является противоположным вычитаемому $b$.
Согласно правилу вычитания можно записать:
$a−b=a+(−b)$.
Данное правило справедливо для целых, рациональных и действительных чисел. Правило можно использовать при вычитании отрицательного числа из положительного числа, из отрицательного числа и из нуля.
Пример 4
Вычесть из отрицательного числа $−28$ отрицательное число $−5$.
Решение.
Противоположное число для числа $–5$ – это число $5$.
Согласно правилу вычитания отрицательных чисел получим:
$(−28)−(−5)=(−28)+5$.
Выполним сложение чисел с противоположными знаками:
$(−28)+5=−(28−5)=−23$.
Ответ : $(−28)−(−5)=−23$.
При вычитании отрицательных дробных чисел необходимо выполнить преобразование чисел к виду обыкновенных дробей, смешанных чисел или десятичных дробей.
Сложение и вычитание чисел с разными знаками
Правило вычитания чисел с противоположными знаками совпадает с правилом вычитания отрицательных чисел.
Пример 5
Вычесть положительное число $7$ из отрицательного числа $−11$.
Решение.
Противоположное число для числа $7$ – это число $–7$.
Согласно правилу вычитания чисел с противоположными знаками получим:
$(−11)−7=(–11)+(−7)$.
Выполним сложение отрицательных чисел:
$(−11)+(–7)=−(11+7)=−18$.
Краткая запись решения: $(−28)−(−5)=(−28)+5=−(28−5)=−23$.
Ответ : $(−11)−7=−18$.
При вычитании дробных чисел с разными знаками необходимо выполнить преобразование чисел к виду обыкновенных или десятичных дробей.
Сложение отрицательных чисел.
Сумма отрицательных чисел есть число отрицательное. Модуль суммы равен сумме модулей слагаемых .
Давайте разберемся, почему же сумма отрицательных чисел будет тоже отрицательным числом. Поможет нам в этом координатная прямая, на которой мы выполним сложение чисел -3 и -5. Отметим на координатной прямой точку, соответствующее числу -3.
К числу -3 нам нужно прибавить число -5. Куда мы пойдем от точки, соответствующей числу -3? Правильно, влево! На 5 единичных отрезков. Отмечаем точку и пишем число ей соответствующее. Это число -8.
Отмечаем точку и пишем число ей соответствующее. Это число -8.
Итак, при выполнении сложения отрицательных чисел с помощью координатной прямой мы все время находимся слева от начала отсчета, поэтому, понятно, что результат сложения отрицательных чисел есть число тоже отрицательное.
Примечание. Мы складывали числа -3 и -5, т.е. находили значение выражения -3+(-5). Обычно при сложении рациональных чисел просто записывают эти числа с их знаками, как бы перечисляют все числа, которые нужно сложить. Такую запись называют алгебраической суммой. Применяют (в нашем примере) запись: -3-5=-8.
Пример. Найти сумму отрицательных чисел: -23-42-54. (Согласитесь, что эта запись короче и удобнее вот такой: -23+(-42)+(-54))?
Решаем по правилу сложения отрицательных чисел: складываем модули слагаемых: 23+42+54=119. Результат будет со знаком «минус».
Записывают обычно так: -23-42-54=-119.
Сложение чисел с разными знаками.
Сумма двух чисел с разными знаками имеет знак слагаемого с большим модулем.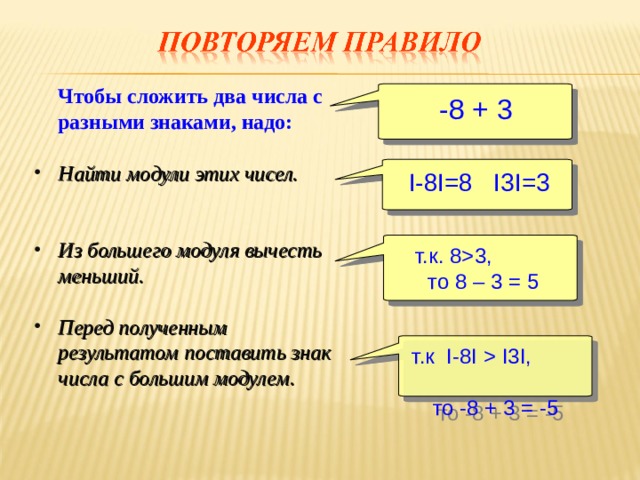 Чтобы найти модуль суммы, нужно из большего модуля вычесть меньший .
Чтобы найти модуль суммы, нужно из большего модуля вычесть меньший .
Выполним сложение чисел с разными знаками с помощью координатной прямой.
1) -4+6. Требуется к числу -4 прибавить число 6. Отметим число -4 точкой на координатной прямой. Число 6 — положительное, значит от точки с координатой -4 нам нужно идти вправо на 6 единичных отрезков. Мы оказались справа от начала отсчета (от нуля) на 2 единичных отрезка.
Результат суммы чисел -4 и 6 — это положительное число 2:
— 4+6=2. Как можно было получить число 2? Из 6 вычесть 4, т.е. из большего модуля вычесть меньший. У результата тот же знак, что и у слагаемого с большим модулем.
2) Вычислим: -7+3 с помощью координатной прямой. Отмечаем точку, соответствующую числу -7. Идем вправо на 3 единичных отрезка и получаем точку с координатой -4. Мы были и остались слева от начала отсчета: ответ — отрицательное число.
— 7+3=-4. Этот результат мы могли получить так: из большего модуля вычли меньший, т. е. 7-3=4. В результате поставили знак слагаемого, имеющего больший модуль: |-7|>|3|.
е. 7-3=4. В результате поставили знак слагаемого, имеющего больший модуль: |-7|>|3|.
Примеры. Вычислить: а) -4+5-9+2-6-3; б) -10-20+15-25.
Отрицательные числа — это числа со знаком минус (−), например −1, −2, −3. Читается как: минус один, минус два, минус три.
Примером применения отрицательных чисел является термометр, показывающий температуру тела, воздуха, почвы или воды. В зимнее время, когда на улице очень холодно, температура бывает отрицательной (или как говорят в народе «минусовой»).
Например, −10 градусов холода:
Обычные же числа, которые мы рассматривали ранее, такие как 1, 2, 3 называют положительными. Положительные числа — это числа со знаком плюс (+).
При записи положительных чисел знак + не записывают, поэтому мы и видим привычные для нас числа 1, 2, 3. Но следует иметь ввиду, что эти положительные числа выглядят так: +1, +2, +3.
Содержание урока
Это прямая линия, на которой располагаются все числа: и отрицательные и положительные. Выглядит следующим образом:
Выглядит следующим образом:
Здесь показаны числа от −5 до 5. На самом деле координатная прямая бесконечна. На рисунке представлен лишь её небольшой фрагмент.
Числа на координатной прямой отмечают в виде точек. На рисунке жирная чёрная точка является началом отсчёта. Начало отсчёта начинается с нуля. Слева от начала отсчёта отмечают отрицательные числа, а справа — положительные.
Координатная прямая продолжается бесконечно по обе стороны. Бесконечность в математике обозначается символом ∞. Отрицательное направление будет обозначаться символом −∞, а положительное символом +∞. Тогда можно сказать, что на координатной прямой располагаются все числа от минус бесконечности до плюс бесконечности:
Каждая точка на координатной прямой имеет своё имя и координату. Имя — это любая латинская буква. Координата — это число, которое показывает положение точки на этой прямой. Проще говоря, координата это то самое число, которое мы хотим отметить на координатной прямой.
Например, точка А(2) читается как «точка А с координатой 2» и будет обозначаться на координатной прямой следующим образом:
Здесь A — это имя точки, 2 — координата точки A.
Пример 2. Точка B(4) читается как «точка B с координатой 4»
Здесь B — это имя точки, 4 — координата точки B.
Пример 3. Точка M(−3) читается как «точка M с координатой минус три» и будет обозначаться на координатной прямой так:
Здесь M — это имя точки, −3 — координата точки M.
Точки можно обозначать любыми буквами. Но общепринято обозначать их большими латинскими буквами. Более того, начало отчёта, которое по другому называют началом координат принято обозначать большой латинской буквой O
Легко заметить, что отрицательные числа лежат левее относительно начала отсчёта, а положительные числа правее.
Существуют такие словосочетания, как «чем левее, тем меньше» и «чем правее, тем больше» . Наверное, вы уже догадались о чём идёт речь. При каждом шаге влево, число будет уменьшаться в меньшую сторону. И при каждом шаге вправо число будет увеличиваться. Стрелка, направленная вправо, указывает на положительное направление отсчёта.
Наверное, вы уже догадались о чём идёт речь. При каждом шаге влево, число будет уменьшаться в меньшую сторону. И при каждом шаге вправо число будет увеличиваться. Стрелка, направленная вправо, указывает на положительное направление отсчёта.
Сравнение отрицательных и положительных чисел
Правило 1. Любое отрицательное число меньше любого положительного числа.
Например, сравним два числа: −5 и 3. Минус пять меньше , чем три, несмотря на то, что пятёрка бросается в глаза в первую очередь, как цифра большая, чем три.
Связано это с тем, что −5 является отрицательным числом, а 3 — положительным. На координатной прямой можно увидеть, где располагаются числа −5 и 3
Видно, что −5 лежит левее, а 3 правее. А мы говорили, что «чем левее, тем меньше» . И правило говорит, что любое отрицательное число меньше любого положительного числа. Отсюда следует, что
−5
«Минус пять меньше, чем три»
Правило 2. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой.
Например, сравним числа −4 и −1. Минус четыре меньше , чем минус единица.
Связано это опять же с тем, что на координатной прямой −4 располагается левее, чем −1
Видно, что −4 лежит левее, а −1 правее. А мы говорили, что «чем левее, тем меньше» . И правило говорит, что из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Отсюда следует, что
Минус четыре меньше, чем минус единица
Правило 3. Ноль больше любого отрицательного числа.
Например, сравним 0 и −3. Ноль больше , чем минус три. Связано это с тем, что на координатной прямой 0 располагается правее, чем −3
Видно, что 0 лежит правее, а −3 левее. А мы говорили, что «чем правее, тем больше» . И правило говорит, что ноль больше любого отрицательного числа. Отсюда следует, что
Ноль больше, чем минус три
Правило 4. Ноль меньше любого положительного числа.
Например, сравним 0 и 4. Ноль меньше , чем 4. Это в принципе ясно и так. Но мы попробуем увидеть это воочию, опять же на координатной прямой:
Ноль меньше , чем 4. Это в принципе ясно и так. Но мы попробуем увидеть это воочию, опять же на координатной прямой:
Видно, что на координатной прямой 0 располагается левее, а 4 правее. А мы говорили, что «чем левее, тем меньше» . И правило говорит, что ноль меньше любого положительного числа. Отсюда следует, что
Ноль меньше, чем четыре
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Теперь давайте разберемся с умножением и делением .
Предположим, нам нужно умножить +3 на -4. Как это сделать?
Давайте рассмотрим такой случай. Три человека залезли в долги, и у каждого по 4 доллара долга. Чему равен общий долг? Для того чтобы его найти, надо сложить все три долга: 4 доллара + 4 доллара + 4 доллара = 12 долларов. Мы с вами решили, что сложение трех чисел 4 обозначается как 3×4. Поскольку в данном случае мы говорим о долге, перед 4 стоит знак «-». Мы знаем, что общий долг равен 12 долларам, так что теперь наша задача имеет вид 3х(-4)=-12.
Мы получим тот же результат, если по условию задачи каждый из четырех человек имеет долг по 3 доллара. Другими словами, (+4)х(-3)=-12. А поскольку порядок сомножителей значения не имеет, получаем (-4)х(+3)=-12 и (+4)х(-3)=-12.
Давайте обобщим результаты. При перемножении одного положительного и одного отрицательного числа результат всегда будет отрицательным числом . Численная величина ответа будет той же самой, как и в случае положительных чисел. Произведение (+4)х(+3)=+12. Присутствие знака «-» влияет только на знак, но не влияет на численную величину.
А как перемножить два отрицательных числа?
К сожалению, на эту тему очень трудно придумать подходящий пример из жизни. Легко себе представить долг в сумме 3 или 4 доллара, но совершенно невозможно вообразить -4 или -3 человека, которые залезли в долги.
Пожалуй, мы пойдем другим путем. В умножении при изменении знака одного из множителей меняется знак произведения. Если мы меняем знаки у обоих множителей, мы должны дважды сменить знак произведения , сначала с положительного на отрицательный, а затем наоборот, с отрицательного на положительный, то есть у произведения будет первоначальный знак.
Следовательно, вполне логично, хотя немного странно, что (-3)х(-4)=+12.
Положение знака при умножении изменяется таким образом:
- положительное число х положительное число = положительное число;
- отрицательное число х положительное число = отрицательное число;
- положительное число х отрицательное число = отрицательное число;
- отрицательное число х отрицательное число = положительное число.
Иначе говоря, перемножая два числа с одинаковыми знаками, мы получаем положительное число . Перемножая два числа с разными знаками, мы получаем отрицательное число .
Такое же правило справедливо и для действия противоположного умножению – для .
Вы легко можете в этом убедиться, проведя обратные операции умножения . Если в каждом из примеров, приведенных выше, вы умножите частное на делитель, то получите делимое, и убедитесь, что оно имеет тот же самый знак, например (-3)х(-4)=(+12).
Поскольку скоро зима, то пора уже подумать о том, в что переобуть своего железного коня, что бы не скользить по льду и чувствовать себя уверено на зимних дорогах. Можно, например, взять шины йокогама на сайте: mvo.ru или какие-то другие, главное, что бы качественный, больше информации и цены вы можете узнать на сайте Mvo.ru.
Можно, например, взять шины йокогама на сайте: mvo.ru или какие-то другие, главное, что бы качественный, больше информации и цены вы можете узнать на сайте Mvo.ru.
6 класс. Математика. Сложение чисел с разными знаками — Сложение чисел с разными знаками
Комментарии преподавателяНайдем значение выражения:
Сначала к 5 прибавляем 7 – это будет 12, и из 12 вычитаем 10 – это будет 2:
Однако известно, что сложение и вычитание – это равноправные операции и их можно выполнять в любом порядке. Поэтому можно начать считать с вычитания:
Что же такое ? Увеличение числа на 7, а потом уменьшение на 10 в итоге означает уменьшение на 3. Поэтому считаем равным :
Далее к пяти прибавляем , то есть вычитаем 3:
Число не обозначает никакого реального количества. Такие числа называются отрицательными, они вводятся для упрощения механизма вычисления.
Следовательно, чтобы вычесть из меньшего числа большее, необходимо вычесть из большего числа меньшее, но в ответе поставит знак «–».
Пример
Найти значение выражения:
Можно сделать все действия подряд:
Однако из первого числа легче вычесть третье, а потом прибавить второе число:
Существует еще один способ пояснения, что такое отрицательное число.
Для каждого натурального числа, например 5, введем новое число, которое обозначим (–5), и определим, что оно обладает следующим свойством: сумма числа (–5) и 5 равна 0.
Число (–5) будем называть отрицательным, а числа (–5) и 5 – противоположными. Таким образом, мы получили бесконечное количество новых чисел, например:
(–1) – противоположное для числа 1;
(–10) – противоположное числу 10;
(–259) – противоположное числу 259;
(–1 000 000) – противоположное числу 1 000 000;
Вычтем из меньшего числа большее:
Прибавим к данному выражению 5:
Получили ноль.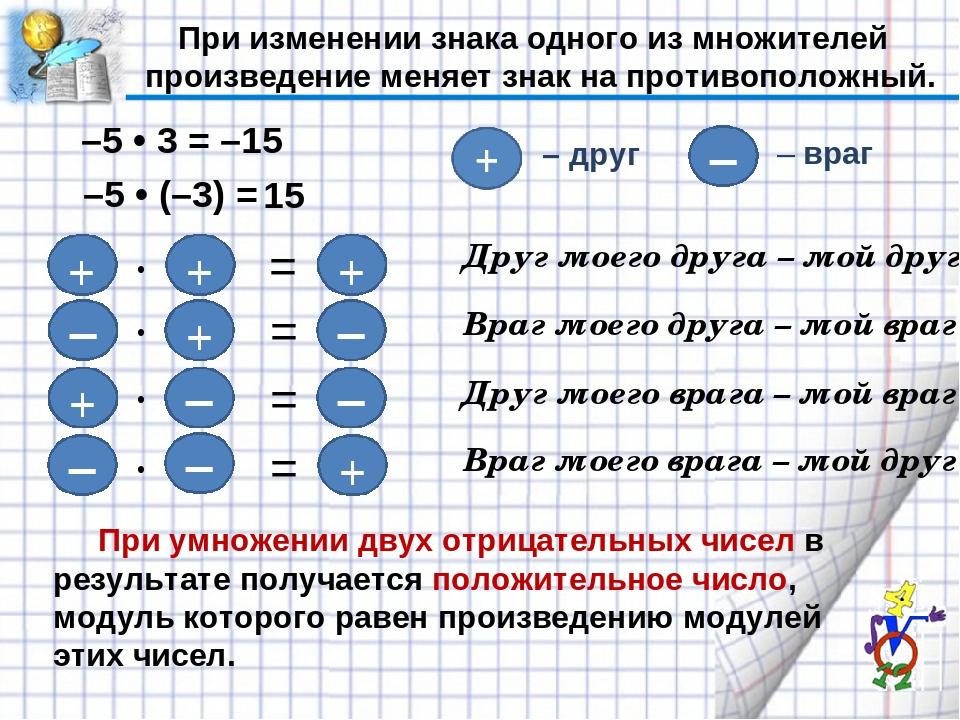 Однако, согласно свойству: число, которое в сумме с пятью дает ноль, обозначается минус пять (–5):
Однако, согласно свойству: число, которое в сумме с пятью дает ноль, обозначается минус пять (–5):
Следовательно, выражение можно обозначить как (–5):
У каждого положительного числа существует «число-близнец», которое отличается только тем, что перед ним стоит знак «–». Такие числа называются противоположными (см. Рис. 1).
Рис. 1. Примеры противоположных чисел
Свойства противоположных чисел1. Сумма противоположных чисел равна нулю.
2. Если из нуля вычесть положительное число, то результатом будет противоположное отрицательное число.
1. Сложение отрицательных чисел
Для сложения отрицательных чисел необходимо сложить противоположные положительные числа и в ответе поставить знак «–».
2. Сложение чисел с разными знаками
Прибавление отрицательного числа можно считать как вычитание положительного.
Складывать числа можно проще, если использовать понятие модуля. У положительного числа модуль равен самому числу, а у отрицательного – противоположному положительному. То есть модули противоположных чисел равны.
1. Правило сложения отрицательных чисел
Чтобы сложить два отрицательных числа, нужно сложить их модули и поставить знак минус.
2. Правило сложения противоположных чисел
Чтобы сложить отрицательное и положительное число, нужно из большего модуля вычесть меньший модуль и поставить знак числа с большим модулем.
Решите примеры:
1.
Два данных числа отрицательные, следовательно, складываем их модули и ставим знак минус:
2.
Два числа с разными знаками, следовательно, из модуля числа 25 (больший модуль) вычитаем модуль числа 13 и ставим знак минус (знак числа с большим модулем):
3.
Два числа с разными знаками, следовательно, из модуля числа 25 (больший модуль) вычитаем модуль числа 13 и ставим знак плюс (знак числа с большим модулем):
У положительных и отрицательных чисел исторически разная роль.
Натуральные числа были введены для счета предметов, положительные дроби – для счета нецелых количеств, частей. Отрицательные же числа вводились не для счета каких-либо количеств, а как инструмент для упрощения расчетов. Однако они оказались настолько удобными, что им нашлось применение в быту.
Отрицательные величины в жизни используют только для сравнения. Например:
1. Отрицательная температура по Цельсию является отрицательной только по сравнению с нулем, который выбрал автор шкалы Андерс Цельсий. Есть другие шкалы, и та же самая температура уже может быть в них положительной.
2. Если в гостинице оборудовали подвал и туда пустили лифт, то, чтобы оставить привычную нумерацию этажей, может появиться минус первый этаж (см. Рис. 2). Этот минус первый означает всего лишь на этаж ниже уровня земли.
Рис. 2). Этот минус первый означает всего лишь на этаж ниже уровня земли.
Рис. 2. Минус первый и минус второй этажи
источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/tema/slozhenie-chisel-s-raznymi-znakami
источник видео — http://www.youtube.com/watch?v=bWLuAIf8B7I
источник видео — http://www.youtube.com/watch?v=-lGJFW3W54U
источник презентации — http://prezentacii.com/matematike/13647-slozhenie-chisel-s-raznymi-znakami-6-klass.html
Как сложить положительные и отрицательные целые числа?
Целые числа представляют собой комбинацию целых чисел с отрицательными числами. Таким образом, числа -3, -2, -1, 0, 1, 2, 3 называются целыми.
- Натуральные числа 1, 2, 3 называются целыми положительными числами.
- Отрицательные числа -3, -2, -1 называются отрицательными целыми числами.
- Число 0 также является целым числом, но оно не является ни положительным, ни отрицательным целым числом.

Представление целых чисел в числовой строке
- Нарисуйте линию и обозначьте точку на ней как ноль.
- Выберите единицу длины. Начните отмечать точки на линии с интервалом в единицу длины по обе стороны от 0 (нуля).
- Справа от нуля пометьте точки как 1, 2, 3, … и точки слева от нуля как -1, -2, -3, …
- Наконец, добавьте стрелки с обеих сторон линии, чтобы показать, что линия бесконечно продолжается в обоих направлениях.
- Чтобы добавить положительное число, нам нужно переместиться вправо от числовой строки.
- Чтобы добавить отрицательное число, нам нужно переместиться влево от числовой строки.
Примеры задач
Вопрос 1: Найдите (-4) + 2.
Решение:
Начните с -4 на числовой прямой.
Переместитесь на 2 единицы вправо. Доходим до -2.
Следовательно, (-4) + 2 = -2
Вопрос 2: Найдите 4 + (-2).
Решение:
Начните с 4 на числовой прямой. Переместиться на 2 единицы влево. Доходим до +2.
Следовательно, 4 + (-2) = 2
Вопрос 3: Найдите (-2) + (-1).
Решение:
Сложение положительных и отрицательных чисел без числовой строкиНачните с -2 на числовой прямой. Переместиться на 1 единицу влево. Доходим до -3.
Следовательно, (-2) + (-1) = -3
Использование числовой строки для сложения больших чисел — очень утомительная задача. Есть лучшая альтернатива, у нас есть следующие правила сложения целых чисел.
1. Чтобы сложить два положительных числа – сложите их как натуральные числа.
2.
Чтобы сложить два отрицательных числа – сложите их абсолютные значения и, наконец, присвойте сумме отрицательный знак. Во время тренировки не обращайте внимания на знаки, найдите сумму чисел и присвойте полученной сумме знак минус.
3. Чтобы сложить положительное и отрицательное число – из большего числа вычесть меньшее и поставить знак того числа, которое больше. Пример 1. Вычисление (+130) + (+200) складывать их просто как натуральные числа.
Следовательно, (+130) + (+200) = 130 + 200 = 330.
Сложение двух отрицательных чисел
Пример 2. Вычисление (-130) + (-200)
Решение:
Как мы видим, оба числа здесь отрицательные. сложить их просто как натуральные числа, а затем присвоить сумме отрицательный знак.
Следовательно, (-130) + (-200) = -(130 + 200) = -330.
Сложение одного положительного и одного отрицательного числа
Пример 3: Вычисление (-130) + (+200)
Решение:
Как мы видим здесь, одно число положительное, а другое отрицательное, поэтому нам нужно вычесть меньшее число из большего числа и указать знак большего числа, т.
е. вычесть 130 из 200 и подписать окончательную сумму как положительный.
Следовательно, (-130) + (+200) = 200 – 130 = +70.
Сложение и вычитание положительных и отрицательных целых чисел
Сложение и вычитание положительных и отрицательных целых чисел
- 2 набора по 10-20 визуально и тактильно разных жетонов. Некоторые наборы MathBuilders, такие как Unit 1, имеют текстурированные формы. Другие альтернативы:
- 20 пенни и 20 четвертаков
- 20 валетов и 20 шариков
- 20 маленьких фетровых кругов и 20 монет
- 2 квадрантные рабочие доски.
- Для визуалов: большой кусок дубовой бирки или картона размером не менее 14 x 8 дюймов, разделенный на 2 области размером 7 x 8 дюймов толстой сплошной линией.
- Для тактичных учеников поднос для работы и игр с разделителем на 2 части (APH). Листы для печенья и доски на липучке также работают и будут удерживать магнитные жетоны или жетоны на липучке на месте.
 Разделите густым клеем, ершиками, карандашом…
Разделите густым клеем, ершиками, карандашом…
- Используя двухквадрантную рабочую доску, попросите учащихся установить «ноль», спросив их, сколько жетонов находится на доске. Объясните, что правый квадрант — это положительный квадрант, как и на числовой прямой. Слева отрицательный, как и на числовой прямой. Установите, какие токены будут «положительными», а какие «отрицательными». Объясните, что только положительные жетоны могут располагаться в правом или положительном квадранте, а отрицательные должны располагаться в левом или отрицательном квадранте.
- Объясните, что добавление означает размещение жетонов на доске. Предложите учащимся поместить разное количество положительных жетонов с правой стороны. После каждого размещения спрашивайте у них «ценность» их доски. Например, «Поместите 7 положительных жетонов (+7) на доску. Какова ценность вашей доски?»
- Попросите учеников добавить 5 положительных жетонов к 7 жетонам на их доске. Спросите их о стоимости их доски.
 (+7) + (+5) =
(+7) + (+5) = - Объясните, что вычитание означает «снятие» с доски. Попросите учащихся убрать различное количество положительных жетонов. После каждого вычитания спрашивайте у них стоимость их доски.
- Попросите учащихся разместить на доске 7 положительных жетонов. Попросите их убрать или вычесть 5 из них. Попросите их вычесть еще 2. Какова ценность их доски? (+7) – (+5) – (+2) =
- Попросите учащихся положить на доску 5 положительных жетонов. Пусть они уберут 7 положительных жетонов.
- (+5) – (+7) = Обсудите, что происходит. Как вы можете представить значение? Введите отрицательный токен. Учащимся понадобятся 2 отрицательных жетона на левой или отрицательной стороне доски, чтобы представить значение «-2».
- Потренируйтесь вычитать до отрицательного результата. Убедитесь, что они записали математическое выражение и результат для каждого примера. Считыватели Брайля могут объединиться с другим учеником. Считыватель Брайля может записывать каждую задачу с помощью планшета и стилуса на каталожной карточке, в то время как учащийся со зрением записывает ту же задачу на обратной стороне карточки.



 Переместитесь на 2 единицы вправо. Доходим до -2.
Переместитесь на 2 единицы вправо. Доходим до -2. Чтобы сложить два отрицательных числа – сложите их абсолютные значения и, наконец, присвойте сумме отрицательный знак. Во время тренировки не обращайте внимания на знаки, найдите сумму чисел и присвойте полученной сумме знак минус.
Чтобы сложить два отрицательных числа – сложите их абсолютные значения и, наконец, присвойте сумме отрицательный знак. Во время тренировки не обращайте внимания на знаки, найдите сумму чисел и присвойте полученной сумме знак минус.  е. вычесть 130 из 200 и подписать окончательную сумму как положительный.
е. вычесть 130 из 200 и подписать окончательную сумму как положительный. Разделите густым клеем, ершиками, карандашом…
Разделите густым клеем, ершиками, карандашом…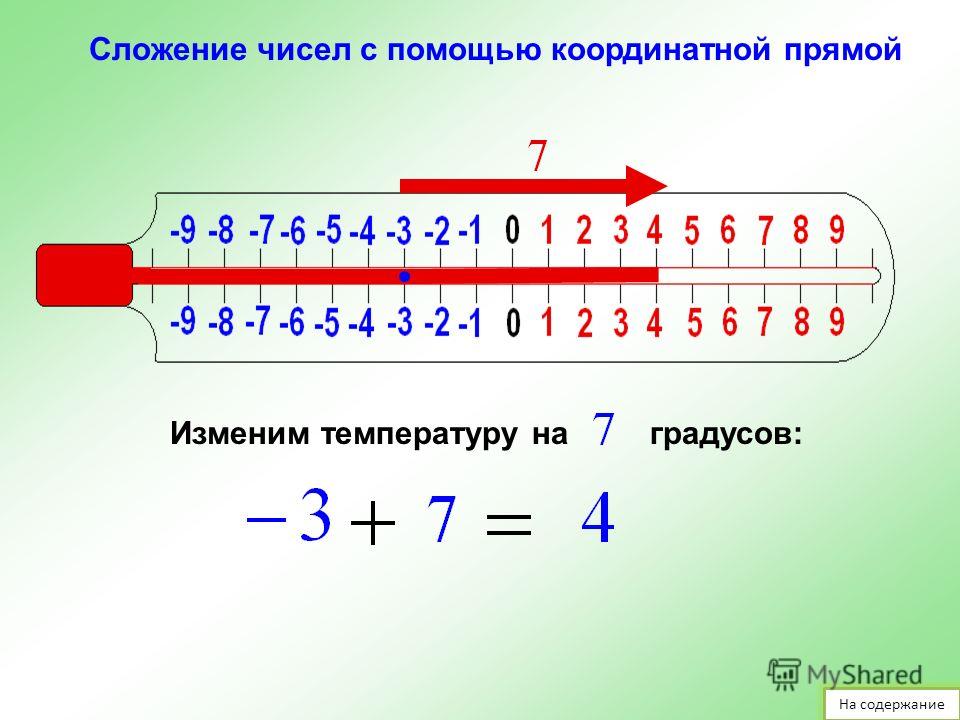 (+7) + (+5) =
(+7) + (+5) =