Как смешанную дробь превратить в обыкновенную: Представление смешанного числа в виде неправильной дроби и наоборот — урок. Математика, 5 класс.

Смешанное число / Обыкновенные дроби / Справочник по математике 5-9 класс

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Обыкновенные дроби
5. Смешанное число

Пусть у нас есть 7 яблок:

Нам необходимо разделить их поровну между тремя детьми. Как это возможно сделать?

1 способ:

Можно каждое яблоко разделить на три доли, то есть мы получим по  яблока, и дать всем детям долю от каждого яблока. Тогда каждый ребенок получит семь таких долей, значит, один ребенок получит  яблока:

2 способ:

Так как у нас семь яблок, то мы можем каждому ребенку дать по два целых яблока, а седьмое поделить между ними поровну, то есть по яблока каждому:

В этом случае каждый ребенок получит по яблока.

Такую сумму, как  , принято записывать так: . Число читают: «две целых одна третья». Число называют смешанным числом.

В нем  число 2 называют целой частью, а число — его дробной частью, при этом дробная часть смешанного числа — это всегда правильная дробь.

Вернемся к задаче, которую мы рассматривали. В обоих случаях дети получили одинаковые части яблок, то есть мы можем сказать, что: .

Данное равенство показывает, что неправильную дробь можно записать в виде смешанного числа . Говорят, что из неправильной дроби выделена целая часть. При этом из любой неправильной дроби, числитель которой нацело не делится на знаменатель, можно выделить целую часть, то есть записать ее в виде смешанного числа. При этом, если числитель делится нацело на знаменатель, то эта дробь равна натуральному числу.

Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

Пример 1: Выделим целую часть из неправильной дроби .

Для этого разделим 157 на 9 с остатком, имеем: 157: 9 = 17 (ост. 4)

То есть получили, что неполное частное равно 17, а остаток — 4. Значит, .

Мы выделили целую часть неправильной дроби, или по-другому, представили неправильную дробь в виде смешанного числа. На практике часто приходится выполнять обратное, то есть смешанное число представлять в виде неправильной дроби.

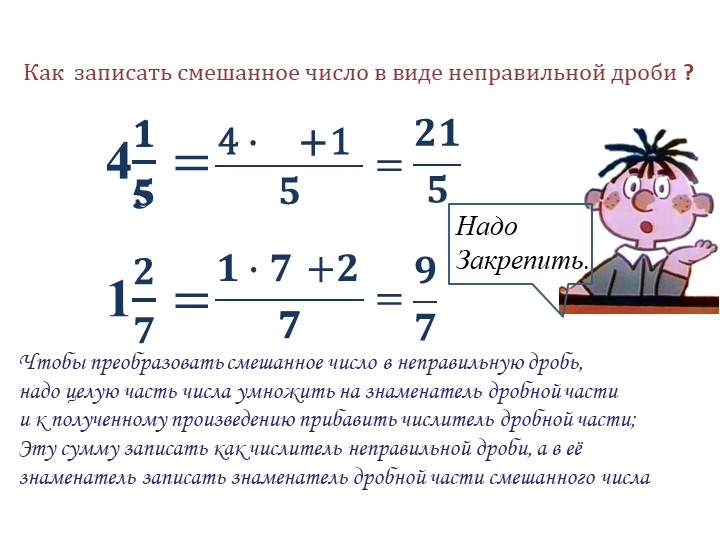
Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.

Пример 2: Преобразуем в смешанную дробь число :

.

Стоит отметить, что переместительное и сочетательное свойство сложения натуральных чисел выполняются и для смешанных чисел. На их основе мы можем записать:

Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

Пример 3:  Найдем сумму чисел и :

Обратите внимание

, что число не является смешанным, так как дробь является неправильной.

Со смешанными числами можно также проводить операцию вычитания. При этом, если дробная часть уменьшаемого больше или равна дробной части вычитаемого, то можно воспользоваться следующим правилом.

Чтобы найти разность двух смешанных чисел, надо из целой и дробной частей уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

Пример 4: Найдем разность чисел и :

В случае, если дробная часть уменьшаемого меньше дробной части вычитаемого, данное правило использовать нельзя, но уменьшаемое можно преобразовать так, чтобы данное правило было применимо.

Пример 5: Найдем разность чисел и :

Мы видим, что дробная часть уменьшаемого меньше дробной части вычитаемого, выполним преобразование уменьшаемого:

Тогда имеем:

Советуем посмотреть:

Доли. Обыкновенные дроби

Сравнение дробей

Делители и кратные

Признаки делимости на 10, на 5 и на 2

Четные и нечетные числа

Признаки делимости на 9 и на 3

Простые и составные числа

Разложение на простые множители

Наибольший общий делитель

Наименьшее общее кратное

Деление и дроби

Сложение и вычитание дробей с одинаковыми знаменателями

Сложение и вычитание смешанных чисел

Основное свойство дроби

Решето Эратосфена

Приведение дробей к общему знаменателю

Сравнение, сложение и вычитание дробей с разными знаменателями

Умножение обыкновенных дробей

Деление обыкновенных дробей

Обыкновенные дроби

Правило встречается в следующих упражнениях:

5 класс

Задание 1085, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1092, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1129, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1152, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1167, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 769, Мерзляк, Полонский, Якир, Учебник

Номер 786, Мерзляк, Полонский, Якир, Учебник

Номер 807, Мерзляк, Полонский, Якир, Учебник

Номер 1139, Мерзляк, Полонский, Якир, Учебник

Номер 7, Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 345, Мерзляк, Полонский, Якир, Учебник

Номер 1116, Мерзляк, Полонский, Якир, Учебник

Номер 1, Мерзляк, Полонский, Якир, Учебник

Задание 524, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 551, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 577, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 644, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 678, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1307, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 8, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

7 класс

Номер 3, Мерзляк, Полонский, Якир, Учебник

Номер 47, Мерзляк, Полонский, Якир, Учебник

Номер 125, Мерзляк, Полонский, Якир, Учебник

Номер 197, Мерзляк, Полонский, Якир, Учебник

Номер 238, Мерзляк, Полонский, Якир, Учебник

Номер 355, Мерзляк, Полонский, Якир, Учебник

Номер 573, Мерзляк, Полонский, Якир, Учебник

Номер 580, Мерзляк, Полонский, Якир, Учебник

Номер 1146, Мерзляк, Полонский, Якир, Учебник

Номер 1215, Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 47, Мерзляк, Полонский, Якир, Учебник

Номер 207, Мерзляк, Полонский, Якир, Учебник

Номер 212, Мерзляк, Полонский, Якир, Учебник

Номер 225, Мерзляк, Полонский, Якир, Учебник

Номер 254, Мерзляк, Полонский, Якир, Учебник

Номер 277, Мерзляк, Полонский, Якир, Учебник

Номер 305, Мерзляк, Полонский, Якир, Учебник

Номер 3, Мерзляк, Полонский, Якир, Учебник

Номер 380, Мерзляк, Полонский, Якир, Учебник

Номер 397, Мерзляк, Полонский, Якир, Учебник

---

Mathway | Популярные задачи

1	Множитель	x^2-4
2	Множитель	4x^2+20x+16
3	График	y=-x^2
4	Вычислить	2+2
5	Множитель	x^2-25
6	Множитель	x^2+5x+6
7	Множитель	x^2-9
8	Множитель	x^3-8
9	Вычислить	квадратный корень из 12
10	Вычислить	квадратный корень из 20
11	Вычислить	квадратный корень из 50
12	Множитель	x^2-16
13	Вычислить	квадратный корень из 75
14	Множитель	x^2-1
15	Множитель	x^3+8
16	Вычислить	-2^2
17	Вычислить	квадратный корень из (-3)^4
18	Вычислить	квадратный корень из 45
19	Вычислить	квадратный корень из 32
20	Вычислить	квадратный корень из 18
21	Множитель	x^4-16
22	Вычислить	квадратный корень из 48
23	Вычислить	квадратный корень из 72
24	Вычислить	квадратный корень из (-2)^4
25	Множитель	x^3-27
26	Вычислить	-3^2
27	Множитель	x^4-1
28	Множитель	x^2+x-6
29	Множитель	x^3+27
30	Множитель	x^2-5x+6
31	Вычислить	квадратный корень из 24
32	Множитель	x^2-36
33	Множитель	x^2-4x+4
34	Вычислить	-4^2
35	Множитель	x^2-x-6
36	Множитель	x^4-81
37	Множитель	x^3-64
38	Вычислить	4^3
39	Множитель	x^3-1
40	График	y=x^2
41	Вычислить	2^3
42	Вычислить	(-12+ квадратный корень из -18)/60
43	Множитель	x^2-6x+9
44	Множитель	x^2-64
45	График	y=2x
46	Множитель	x^3+64
47	Вычислить	(-8+ квадратный корень из -12)/40
48	Множитель	x^2-8x+16
49	Вычислить	3^4
50	Вычислить	-5^2
51	Множитель	x^2-49
52	Вычислить	(-20+ квадратный корень из -75)/40
53	Множитель	x^2+6x+9
54	Множитель	4x^2-25
55	Вычислить	квадратный корень из 28
56	Множитель	x^2-81
57	Вычислить	2^5
58	Вычислить	-8^2
59	Вычислить	2^4
60	Множитель	4x^2-9
61	Вычислить	(-20+ квадратный корень из -50)/60
62	Вычислить	(-8+ квадратный корень из -20)/24
63	Множитель	x^2+4x+4
64	Множитель	x^2-10x+25
65	Вычислить	квадратный корень из -16
66	Множитель	x^2-2x+1
67	Вычислить	-7^2
68	График	f(x)=2^x
69	Вычислить	2^-2
70	Вычислить	квадратный корень из 27
71	Вычислить	квадратный корень из 80
72	Множитель	x^3+125
73	Вычислить	-9^2
74	Множитель	2x^2-5x-3
75	Вычислить	квадратный корень из 40
76	Множитель	x^2+2x+1
77	Множитель	x^2+8x+16
78	График	y=3x
79	Множитель	x^2+10x+25
80	Вычислить	3^3
81	Вычислить	5^-2
82	График	f(x)=x^2
83	Вычислить	квадратный корень из 54
84	Вычислить	(-12+ квадратный корень из -45)/24
85	Множитель	x^2+x-2
86	Вычислить	(-3)^3
87	Множитель	x^2-12x+36
88	Множитель	x^2+4
89	Вычислить	квадратный корень из (-8)^2
90	Множитель	x^2+7x+12
91	Вычислить	квадратный корень из -25
92	Множитель	x^2-x-20
93	Вычислить	5^3
94	Множитель	x^2+8x+15
95	Множитель	x^2+7x+10
96	Множитель	2x^2+5x-3
97	Вычислить квадратный корень	квадратный корень из 116
98	Множитель	x^2-x-12
99	Множитель	x^2-x-2
100	Вычислить	2^2

Смешанные числа и неправильные дроби

Обновлено 8 мая 2019 г. | Инфопожалуйста Персонал

Смешанное число представляет собой комбинацию целого числа и дроби. Например, если у вас есть два целых яблока и одна половина яблока, вы можете описать это как 2 + ¹ /2 яблок или 2 ¹ /2 яблок.

Запись смешанных чисел в виде дробей

Это смешанное число также можно представить в виде дроби. Каждое целое яблоко содержит две половинки яблока. Ваши два целых яблока также являются четырьмя половинками яблок. Четыре половинки яблока плюс одна половинка — это пять половинок яблок. Итак, у вас есть ⁵ /2 яблок.

Другими словами: превратить смешанное число в дробь, умножить целое число на знаменатель (нижняя часть) и прибавить результат к числителю (верхняя часть).

2 ¹ /2 = ?
Умножить целое число на знаменатель.
Целое число равно 2.
Знаменатель равен 2.
2 x 2 = 4.
Добавьте результат к числителю:
Числитель равен 1.
4 + 1 = 5
Числитель равен 5. В знаменателе останется 2
2 ¹ /2 = ⁵ /2

Другой пример

Давайте попробуем другой пример:

5 ² /3 = ?
Умножить целое число на знаменатель.
Целое число равно 5.
Знаменатель равен 3.
5 x 3 = 15.
Добавьте результат к числителю:
В числителе 2.
15 + 2 = 17
В числителе 17. В знаменателе остается 3.
5 ² /3 = ¹⁷ /3

Правильные и неправильные дроби

Дробь, в которой числитель меньше знаменателя, например ¹ /3 или ² /5, называется правильной дробью. Дробь, в которой числитель больше или равен знаменателю, например ⁵ /2, ¹⁷ /3 или ⁶ /6, называется девяткой.0005 неправильная дробь. (Иными словами, дробь со значением меньше 1 — правильная дробь. Дробь со значением больше или равное 1 — неправильная дробь. )

Как мы показали выше, смешанные числа можно записать в виде неправильных дробей. Точно так же неправильные дроби можно записать в виде смешанных чисел.

Запись неправильных дробей в виде смешанных чисел

Чтобы записать неправильную дробь в виде смешанного числа, разделите числитель (верхняя часть) на знаменатель (нижняя часть). Частное — это целое число, а остаток — это числитель.

Как бы вы представили ¹⁷ /4 в виде смешанного числа?
Разделить числитель на знаменатель:
17 ÷ 4 = 4 с остатком 1
Частное 4 — это целое число. Остаток, 1, является числителем. В знаменателе остается 4.
¹⁷ /4 = 4 ¹ /4

Еще два примера

Давайте попробуем еще пару примеров:

¹⁴ /9 = ?
Разделить числитель на знаменатель:
14 ÷ 9 = 1, с остатком 5
Частное 1 — это целое число. Остаток, 5, является числителем. В знаменателе остается 9.
¹⁴ /9 = 1 ⁵ /9

Если остатка нет, просто возьмите частное как целое число:

²⁰ /5 = ?
Разделить числитель на знаменатель:
20 ÷ 5 = 4
Частное 4 — это целое число. Нет остатка.
²⁰ /5 = 4

 

Наименьшие общие кратные

Факторы и дроби

Умножение дробей и смешанных чисел

.com/ipa/0/9/3/3/4/5/A0933459.html

Источники +

Наши общие источники

• Приведение дробей к наименьшим терминам

• Ядерные и химические аварии

• Факты переработки

• Текущие события на этой неделе: апрель 2023

• 70 цитат из книг о любви

• Иностранные языки: испанский

• Статуя Свободы: факты, история и профиль

правильных дробей | Неправильные дроби

ПРАВИЛЬНАЯ Дробь

Примеров: `2/3` , `3/4` , `1/4` , `5/8` Нажмите, чтобы увидеть больше примеров

НЕПРАВИЛЬНАЯ Дробь

Примеры: `128/5`, `29/15`, `35/12` Нажмите, чтобы увидеть больше примеров

СМЕШАННАЯ ФРАКЦИЯ

Примеры: `4 1/3`, `5 82/210`, `6 9/20` Нажмите, чтобы увидеть больше примеров

Действия по преобразованию неправильной дроби в смешанное число

Дробь, у которой числитель меньше знаменателя, называется правильной дробью, означает дробь, меньшую 1.

Пример 1:

Пример 2:

Пример 3:

Пример 4:

Пример 5:

---

Дробь, в которой числитель больше или равен знаменателю, называется правильной дробью, означает дробь, которая больше или равна 1.

Пример 1:

Пример 2:

Пример 3:

---

Смешанное число — это дробь, включающая в себя как целое число, так и правильную дробь.

Пример 1:

Пример 2

Пример 3:

---

  Шаги по преобразованию

Неправильная дробь в смешанном числе

•   Разделите числитель на знаменатель.

  Например: Преобразование «5/4» в смешанное число

  	`1`
  `4`	`5`
  	`4`
  	`1`

•   Используйте частное как целое число.

  в нашем примере частное равно 1.

•   Используйте остаток как числитель правильной дроби.

  в нашем примере остаток равен 1.

•   Знаменатель останется прежним.

  в нашем примере знаменатель равен 4.

  Следовательно, искомое смешанное число равно `1 1/4`

Смешанное число в неправильную дробь

  Умножьте целое число на знаменатель.

Например: Преобразование «2 1/4» в неправильную дробь

В нашем примере целое число равно 2 , а знаменатель равен 4

, следовательно, 2 x 4 = 8

5 9 прибавим к произведению числитель правильной дроби.