Составить интервальный вариационный ряд (используя формулу Стерджесса)
Составить интервальный вариационный ряд (используя формулу Стерджесса).
2. Начертить гистограмму.
3. Найти средние характеристики:
а) среднюю выборочную ;
б) моду ;
в) медиану .
4. Найти характеристики вариации:
а) размах вариации ;
б) дисперсию D;
в) среднее квадратическое отклонение ;
г) коэффициент вариации V;
д) ошибку выборочного среднего .
5. Сделать вывод.
Исходные данные:
Метание гранаты 500г (мужчины 29-34 года)
17,4 18,7 13,8 19,5 18,7 14,3 18,8 15,9 18,6 17,2
13,4 22,2 15,7 16,3 17,5 19,8 15,8 19,9 14,8 20,2
19,9 18,3 18,9 18,7 21,0 17,1 20,0 16,6 19,4 17,8
16,9
Решение:
1.Проведем группировку исходных данных. Количество интервалов подсчитаем по формуле Стерджесса. k = 1+3,322∙lg n k = 1+3,322∙lg 31 = 5,95 6
Минимальное значение min xi = 13,4, максимальное max xi = 22,2.
Размах вариации: 22,2 – 13,4 = 8,8.
Величина отдельного интервала: .
Начало первого интервала а1 = хmin – h/2 = 13,4 – 0,8 = 12,6. В этом случае серединой первого интервала как раз станет минимальное значение выборки, число 13,4. Тогда а1 =12,6, а2 = 12,6 + h = 12,6 + 1,6 = 14,2, а3 = 14,2 + 1,6 = 15,8, и так далее. Получим такие интервалы: 12,6–14,2, 14,2–15,8, 15,8–17,4, 17,4–19,0, 19,0–20,6, 20,6–22,2. Проверяем, чтобы максимальное значение 22,2 попало в последний интервал. Это условие выполнено, интервалы построены верно.
Подсчитаем частоту n i по каждому интервалу. Получим интервальный вариационный ряд:
интервал 12,6–14,2 14,2–15,8 15,8–17,4 17,4–19 19–20,6 20,6–22,2
2 3 8 9 7 2
Проверим: сумма частот должна быть равна объему выборки:
2+3+8+9+7+2=31 – верно.
2. Построим гистограмму
Гистограмма частот – это ступенчатая фигура, которая состоит из прямоугольников, которые строятся на данных интервалах и имеют высоту :
3. Найти средние характеристики:
а) среднюю выборочную ;
б) моду ;
в) медиану .
Перейдем к дискретному ряду распределения, выбрав в качестве вариант xi
середины интервалов.
Интервал Середина
12,6 14,2 13,4
14,2 15,8 15,0
15,8 17,4 16,6
17,4 19,0 18,2
19,0 20,6 19,8
20,6 22,2 21,4
Данная работа не уникальна. Ее можно использовать, как базу для подготовки к вашему проекту.
а) средняя выборочная:
б) Мода Мо интервального статистического распределения выборки :
Мо =
Здесь модальный интервал : 17,4–19,0 (интервал с самой большой частотой), тогда начало модального интервала = 17,9; длина интервала h = 1,6 ;
частота модального интервала =9; частота домодального интервала =8; частота послемодального интервала =7; тогда
Мо =
в) Медиана Ме интервального статистического распределения выборки определяется по формуле: , где х0 – начало медианного интервала , то есть интервала (17,4–19,0), в котором находится серединный элемент (16-й), k – длина медианного интервала, n – объем выборки, – сумма частот интервалов, которые предшествуют медианному, nі – частота медианного интервала.
То есть здесь Ме = .
4. Найти характеристики вариации:
а) размах вариации ;
б) дисперсию D;
в) среднее квадратическое отклонение ;
г) коэффициент вариации V;
д) ошибку выборочного среднего .
а) Размах вариации: 22,2 – 13,4 = 8,8.
Для облегчения дальнейших расчетов составим расчетную таблицу:
№
1 13,4 2 26,8 -4,34 37,59
2 15 3 45 -2,74 22,45
3 16,6 8 132,8 -1,14 10,31
4 18,2 9 163,8 0,46 1,94
5 19,8 7 138,6 2,06 29,84
6 21,4 2 42,8 3,66 26,86
Сумма 31 549,8
128,99
б) Вычислим выборочную дисперсию:
.
в) Выборочное стандартное отклонение – это корень квадратный из выборочной дисперсии:
= .
г) ) коэффициент вариации
д) ошибка выборочного среднего 0,366.
5. Выводы:
Средний результат по метанию гранаты 500 г для мужчин 29-34 лет составляет 17,74 м, среднее квадратическое отклонение составляет 2,04 м, коэффициент вариации меньше 20%, что говорит об относительной однородности совокупности. Наиболее распространенным является результат 17,93 м. При этом половина участников показала результат меньше 17,84 м, а вторая половина – больше 17,84 м.
Наиболее распространенным является результат 17,93 м. При этом половина участников показала результат меньше 17,84 м, а вторая половина – больше 17,84 м.
Часть II. Проверка статистических гипотез
|
|
Математика — это язык, на котором написана книга природы.
РЕШЕНИЕ ЗАДАЧ, КОНТРОЛЬНЫХ РАБОТ ПО ВЫСШЕЙ МАТЕМАТИКЕ                                                                                                         Галилео Галилей | |||||||||||||||||||||||||||||||
|
Главная Оплата Примеры Учебники |
|
|||||||||||||||||||||||||||||||
 ru ru |
||||||||||||||||||||||||||||||||
Tables
Таблица помогает нам организовать и проанализировать набор значений данных. В этом разделе мы рассмотрим таблицы частот и стемплоты (т.е. стеблево-листовые участки).Таблицы частот
Таблица частот представляет собой табличное представление набора данных в порядке возрастания с соответствующими им частотами. Это — это простое устройство для подсчета частоты появления значения данных.
Примечание:
Слово «частота» означает «как часто».
Пример 7
За выполнение задания 25 учащихся получили следующие баллы:
4 7 5 9 8 6 7 7 8 5 6 9 8
5 8 7 4 7 3 6 8 9 7 6 9
Представьте эту информацию в таблице частот и найдите моду.
Решение:
Таблица частот выглядит следующим образом:
Наиболее часто встречается 7.
Интервалы классов
Данные группируются в интервала класса , если таблица частот становится слишком большой, чтобы помочь нам организовать, интерпретировать и проанализировать данные. частота интервала класса — это количество значений данных, попадающих в диапазон, заданный интервалом.
Размер интервала класса часто выбирается как 5, 10, 15 или 20 и т. д. Каждый интервал класса начинается со значения, кратного размеру.
Например, если размер интервала класса равен 5, то класс
интервалы должны начинаться с 0, 5, 10, 15, 20 и т. д. Интервалы классов будут
затем 0-4, 5-9, 10-14 и т. д.
д.
Таблицы частот с интервалами классов
Таблица частот для набора данных, содержащего большое количество данных значений строится следующим образом:
- Определите диапазон данных набора данных.
- Определите ширину интервалов классов.
Пример 8
Школьная медсестра взвесила 30 учеников 10 класса. Их вес (в кг) были записаны следующим образом:
50 52 53 54 55 65 60 70 48 63
74 40 46 59 68 44 47 56 49 58
63 66 68 61 57 58 62 52 56 58
а. Представьте эту информацию в таблице частот.
Представьте эту информацию в таблице частот.
б. Прокомментируйте режим таблицы.
Решение:
а.
Есть 7 интервалов занятий. Это разумно для приведенных данных.
Таблица частот выглядит следующим образом:
б.
Мы замечаем, что модальный интервал класса составляет 55-59. То есть большая часть школьники весят от 55 до 59килограммы.
Стемплом (график ствола и листьев) — это устройство, используемое для группировки
небольшой набор данных (примерно до 50 значений данных). Набор данных расположен в
в порядке возрастания, сохраняя при этом все исходные значения данных. Это позволяет
нам найти первый
квартиль, медиана и третий квартиль легко. stemplot полезен для получения информации о центре, распространении, форме
и выбросы распределения.
stemplot полезен для получения информации о центре, распространении, форме
и выбросы распределения.
Создание шаблона
В stemplot каждое значение данных считается состоящим из двух частей: основы и листа . Первые цифры значения данных образуют основу, а конечная цифра (цифры) становится листом.
Далее следуют три примера stemplot:
- Значения данных 65, 70 и 74 записываются, как показано ниже:
- Значения данных 349, 366 и 480 записываются, как показано ниже:
- Значения данных 35.8, 36.2 и 36.9 записываются, как показано ниже:
Примечание:
Чтобы построить участок, мы:
- введите стебли слева от вертикальной разделительной линии и лист справа от вертикальной разделительной линии для каждого значения данных
- запишите каждое значение данных, как указано в наборе данных, чтобы построить
неупорядоченный шаблон.

- Затем мы создаем упорядоченный шаблон из неупорядоченной версии с помощью расположение листьев в порядке возрастания.
Пример 9
Подготовьте шаблон для следующего набора оценок, которые являются отметками
получено 16 студентами:
Решение:
Схема для значений оценки в диапазоне от 21 до 74 выглядит следующим образом:
Этот шаблон не заказан.
Упорядоченный ствол получается путем расположения листьев по порядку, как показано ниже.
Примечание:
Для каждого значения данных стебель представляет собой разряд десятков, а лист — разряд единиц.
Пример 10
Следующие данные представляют количество пробежек за подачу игрока. забил за сезон.
забил за сезон.
Построить упорядоченный шаблон для отображения данных.
Решение:
Дается упорядоченный шаблон для оценок в диапазоне от 4 до 127. ниже. Стебли 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 образованы десятками цифры; тогда как основы 10, 11 и 12 образованы сотнями и десятки цифр. Листья формируются единичными цифрами значений.
Замечаем, что баллы 4, 116 и 127 отделены от основного тело данных. Итак, 4, 116 и 127 равно 9.0002 выбросы . Stemplot для данные, состоящие из выбросов, могут быть отображены следующим образом:
Примечание:
Значение 4 указано в верхней части таблицы как выброс, а
значения 116 и 127 указаны под таблицей как выбросы.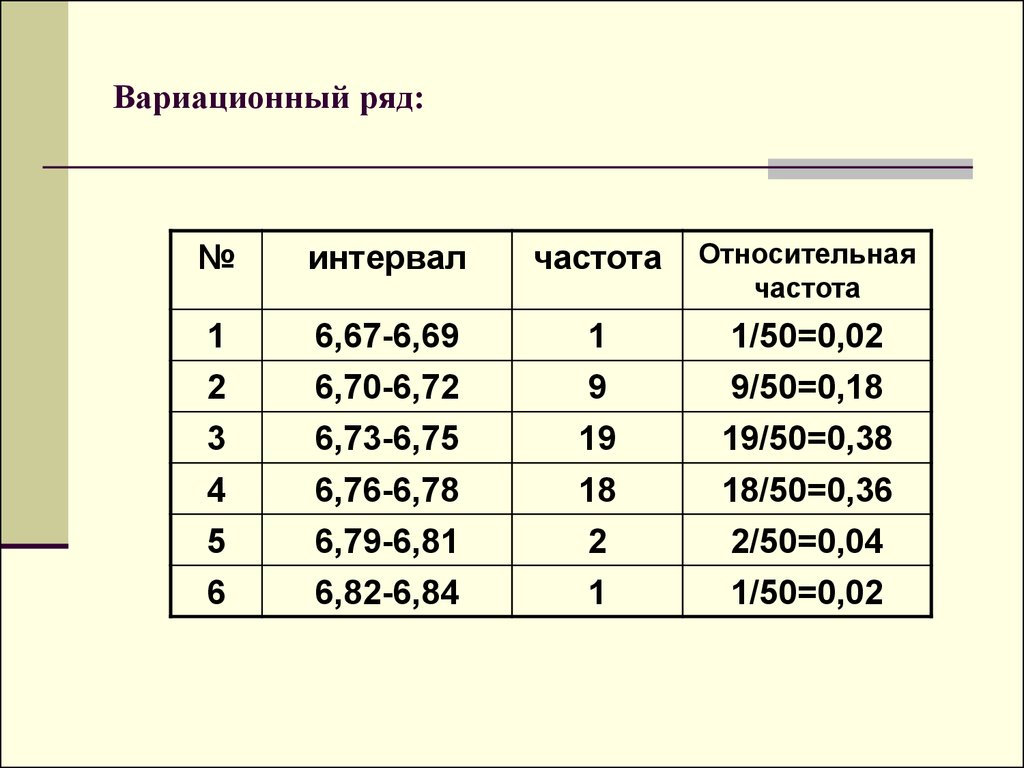
Основные термины
таблицы, таблицы частот, класс интервалы, стеблевые диаграммы, стебель-и-лист участки, стебель, лист
исчисление — Создание степенного ряда с интервалом сходимости с заданным интервалом
Заданный вопрос
Изменено 4 года, 6 месяцев назад
Просмотрено 2к раз
$\begingroup$
Итак, я знаю, что для определения интервала для степенного ряда мы будем использовать такие вещи, как тест отношения, а затем некоторые другие тесты для определения конечных точек, но как вы поступите в обратном порядке?
Если бы у нас был такой интервал, как (a,b], [a,b], [a,b) или (a,b), как бы вы создали степенной ряд с таким интервалом?
Наблюдение, о котором я подумал, так как общее выражение для степенного ряда содержит $(x-c)$, где ряд сосредоточен вокруг $c$, мы хотели бы, чтобы $c$ = $(a+b)/ 2$
Есть ли систематический способ сделать это?
- исчисление
- последовательности-и-ряды
- сходимость-расхождение
- силовая серия
$\endgroup$
$\begingroup$
Абсолютно, и вы хорошо начали.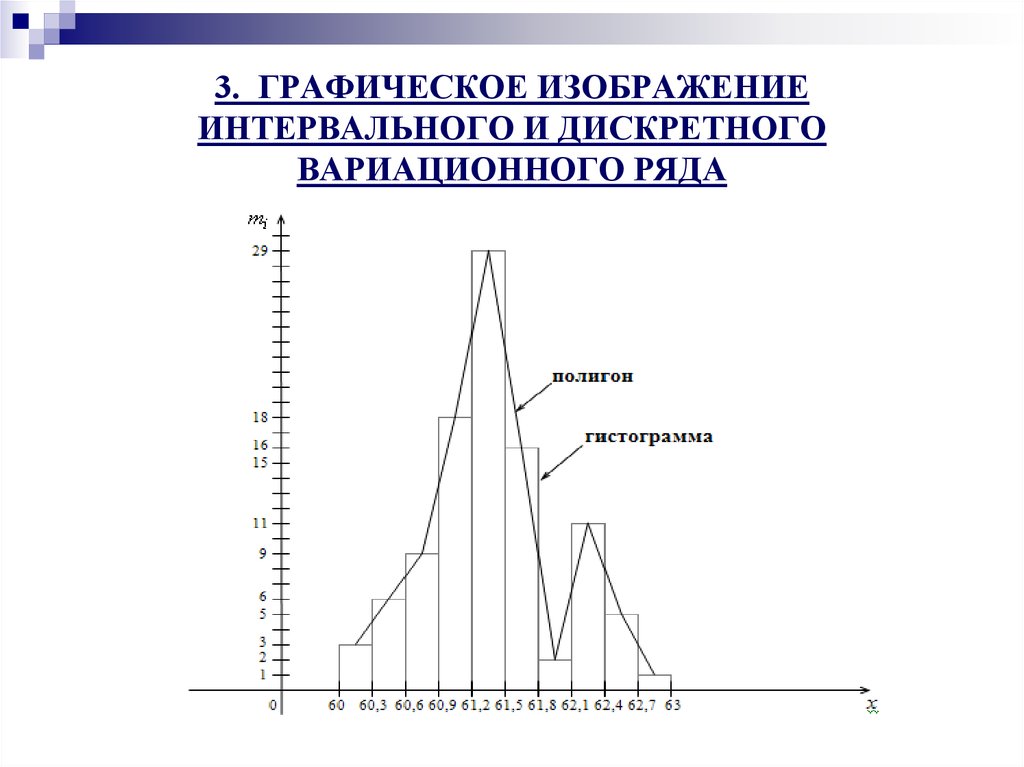


 Гистограмма – столбиковая диаграмма. Основание столбика – ширина
интервала. Высота столбика равна частоте.
Гистограмма – столбиковая диаграмма. Основание столбика – ширина
интервала. Высота столбика равна частоте. Абсцисса и будет модой. Мо ≈ 27,5. Значит, наиболее часто
встречаемый возраст в данной совокупности 27-28 лет.
Абсцисса и будет модой. Мо ≈ 27,5. Значит, наиболее часто
встречаемый возраст в данной совокупности 27-28 лет.