Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
10.20
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
Сколько существует различных натуральных чисел N, таких что остаток от деления числа 2017 на N равен 217?
На доске 25×2525×25 стоят фишки.
Ряд (строку или столбец) назовем если в нем не более двух фишек. Оказалось, что каждая фишка стоит в почти пустой
В левой верхней клетке квадрата 4×4 написано число 40 и стоит фишка. Мистер Фокс двигает фишку: если он подвинул её вправо, то новое число, которое
Решено
Стас загадал трехзначное число N, а Коля его угадывает. Коля уже знает, что: -число 458 содержит одну цифру числа N, причем на правильном месте; —
Решено
Определи скалярное произведение данных векторов, если длина ребра куба равна 2 ед. изм 1. A1D1⋅BC 2. D1B1⋅BD 3. AD⋅AC 4.DA⋅B1D1
Пользуйтесь нашим приложением
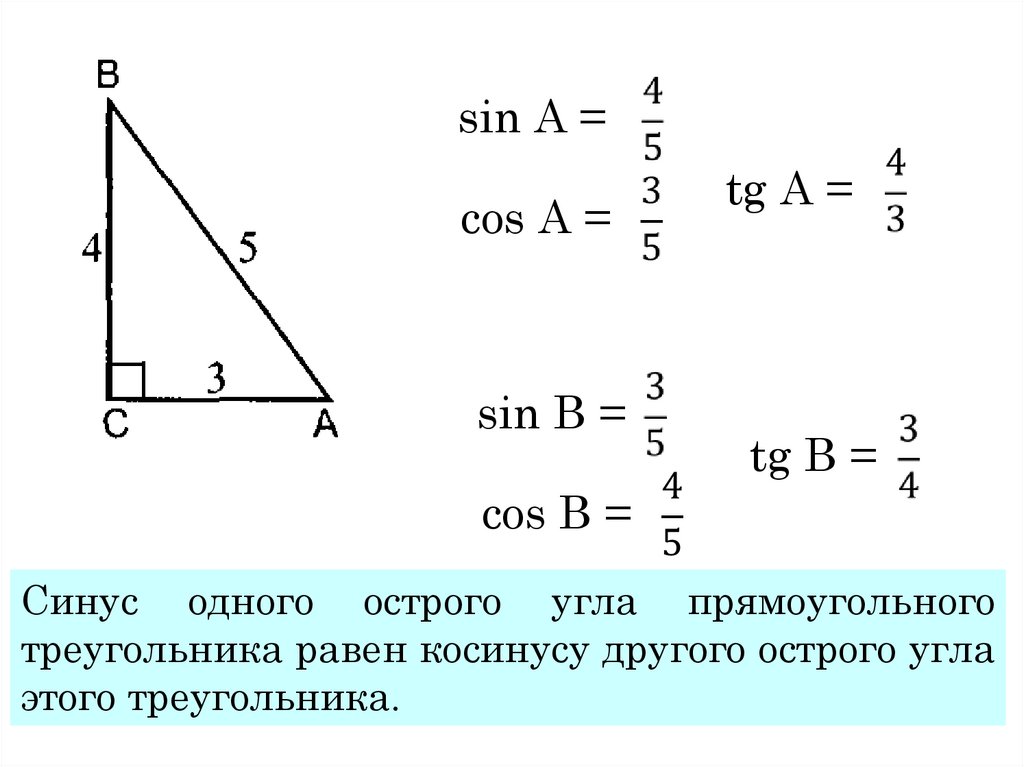
Задачи на синус, косинус, тангенс, котангенс за 10 класс пл алгебре
Дата публикации: .
Задачи c ответами и рекомендациями по решению к учебнику Мордковича А.
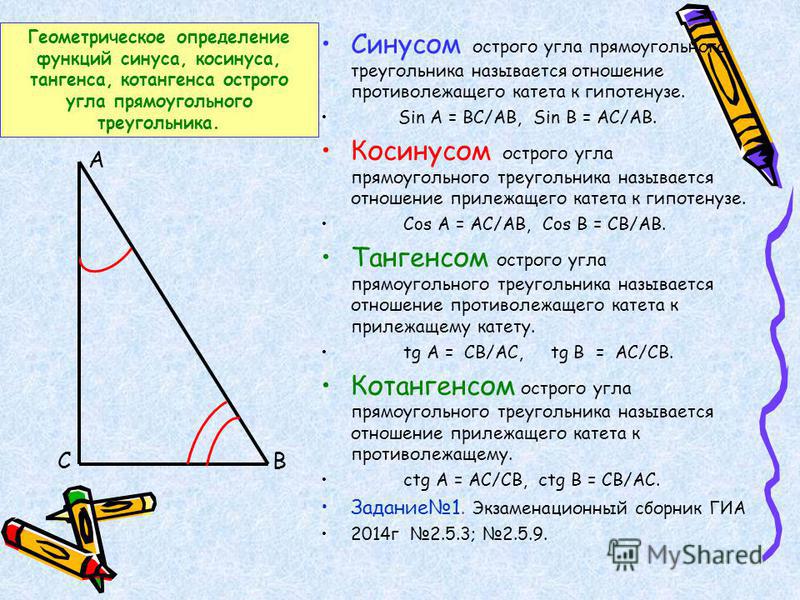{-1}(t)$.5. 1.
Решение.
$sin(3*360+30)+\sqrt{3}cos(3*360-30)-ctg(180*3+45)=sin(30)+\sqrt{}3cos(30)-ctg(45)=0,5+1,5-1=1$.
6. $sin(t)=-\frac{\sqrt{5}}{3}$; $tg(t)=\frac{\sqrt{5}}{2}$; $ctg(t)=\frac{2}{\sqrt{5}}$.
Рекомендация. Воспользуйтесь основным тригонометрическим тождеством и определите, в какой четверти находится угол?
7. Нет решений.
Решение.
Для решения задачи необходимо сравнить число $\frac{1}{\sqrt{5}-\sqrt{7}}$ с единицей и минус единицей, если это число больше единицы или меньше минус единицы, то решение не существует. Если от минус одного до одного, то решение существует.
8.
a) $\frac{\sqrt{3}}{2}$.
б) $-\frac{\sqrt{2}}{2}$.
в) $\frac{-1}{\sqrt{3}}$.
г) 0.
9.
а) $\frac{3π}{2}+2πn$; n∈Z.
б) $±\frac{2π}{3}+2πn$; n∈Z.
10. $-2cos(t)$.
12. -1.
13. $cos(t)=\frac{\sqrt{7}}{4}$; $tg(t)=\frac{3}{\sqrt{7}}$; $ctg(t)=\frac{\sqrt{7}}{3}$.
14. Нет.
обыкновенных дифференциальных уравнений. В чем разница между косинусом Фурье и рядом синусов, помимо периодической функции?
спросил
Изменено 4 года, 4 месяца назад
Просмотрено 2к раз
$\begingroup$
Я знаю, что для ряда косинусов Фурье у вас есть четное расширение f(x), а для ряда синусов есть нечетное расширение, первое требует a_o , a_n и косинуса в качестве периодической функции, а последнее содержит b_n с синусом в качестве периодической функции.
Однако нельзя ли какую-либо функцию перевести в эквивалент синуса или косинуса? Зачем изучать оба метода? Есть ли какая-то внутренняя разница, которую я не узнаю? Во всяком случае, разве вы не должны всегда просто вычислять ряд синусов для каждого f (x), поскольку вам нужно вычислить только один коэффициент ( б_н )?
Это действительно сбивает с толку, и я не могу найти в Интернете никаких статей, описывающих очевидные различия или преимущества/недостатки любого метода.
Спасибо!
- обыкновенные дифференциальные уравнения
- ряды Фурье
$\endgroup$
2
$\begingroup$
Косинусный ряд фиксирует четную часть функции
$$f_{e}(x) = \dfrac{f(x)+f(-x)}{2}$$
Синусоидальный ряд фиксирует нечетную часть функции
$$f_{o }(x) = \dfrac{f(x)-f(-x)}{2}$$
И можно встретить функции, для которых никогда не может быть чисто четной или чисто нечетной функции, независимо от того, как функция смещается, напр.
$$f(x) = cos(x) + sin(x)$$
Таким образом, вам нужны оба для обработки любой возможной функции, с которой вы можете столкнуться.
$\endgroup$
$\begingroup$
Однако нельзя ли какую-либо функцию преобразовать в ее синусоидальный или косинусный эквивалент?
№
Напомним, что линейная комбинация четных функций четна, а линейная комбинация любых нечетных функций нечетна. Это означает, что ни один из классов не является достаточным для представления функций, которые не являются ни четными, ни нечетными.
Теперь то, что есть верно, так это то, что любая функция может быть записана как сумма четных и нечетная функция, так что вы можете разложить четные части через косинус, нечетные части через синус , и сложим их, чтобы получить ряд Фурье.
$\endgroup$
12
Рассмотрим функцию, изображенную здесь:
Эта функция не является ни нечетной, ни четной.
Более того, вы не можете перевести его, чтобы сделать его нечетным или сделать его четным.
Как правило, вам нужны как косинус, так и синус, а не только одно или другое. Четные и нечетные функции являются исключительными случаями.
$\endgroup$
1
Тригонометрия Обзор (SINE, COSINE, TANGENT) THESCIENCEGIANT
THESCIENTGIANT
381 Последователи
также включены в
Poneygiant Physlab тела (предметы) и системы тел (группы предметов) без оглядки на причину этого движения. Другими словами, КАК? а не ПОЧЕМУ?Учителя используют процедуру построения модели стратегического обучения (SIM) для преобразования
7
Продукция
$ 12.22price $ 12,22 $ 13,502 Цена $ 13,50. Рамка сравнения понятий противопоставляет синус, косинус и тангенс, поэтому учащиеся могут попробовать тригонометрию, чтобы найти равнодействующую прямоугольного треугольника.
Учащиеся практикуются в определении компонентов, поиске отсутствующей стороны и нахождении измерения угла. Например, помочь физикам лучше понять значения движения и направления в двух измерениях для векторов скорости.Процедура сравнения понятий используется для сравнения и противопоставления ключевых понятий. В частности, учащиеся используют похожие и отличные характеристики и категории, общие и не общие для двух или более понятий, чтобы лучше понять общую концепцию. Учащиеся, обучавшиеся с использованием методики Content Enhancement, получили более высокие общие результаты тестов, чем учащиеся, обучавшиеся с использованием метода «лекция-обсуждение».
Лично я использую Сравнение понятий, чтобы выяснить, что я хочу сказать и как я хочу это сказать. Это удерживает мое время «Мудреца на сцене» ограниченным тем, что умещается на 2-3 страницах (около 45 минут направленного обсуждения в классе).
Этот продукт включает в себя как завершенное сравнение концепций, так и пустое руководство для учащихся, за исключением уже заполненных словарного запаса, вопросов о строительных лесах и графических изображений.
форму, чтобы T могли настроить обсуждение в соответствии с потребностями своих S.Эта программа улучшения содержания протестирована в классе, чтобы помочь учащимся в изучении следующих научных стандартов штата Флорида «Солнечное сияние следующего поколения»:
☀ SC.912.P.12.1 Различать скалярные и векторные величины и определять, какие из них следует использовать для описания события.
☀ SC.912.P.12.2 Анализ движения объекта с точки зрения его положения, скорости и ускорения (относительно системы отсчета) как функции времени.
Сопутствующие товары
• Вопрос Исследование: Сколько 1+1= при сложении векторов? ЧАСТЬ 1
• Исследование вопроса: Сколько 1+1= в сложении векторов? ЧАСТЬ 2
• Исследование вопроса: как использовать векторные компоненты для анализа движения снаряда
#StayGiant и следите за моими новыми ресурсами и новостями STEM. Найдите зеленую звезду ★ в верхней части любой страницы моего магазина и нажмите «СЛЕДУЙТЕ».
Или подпишитесь на @TheScienceGiant в Твиттере. Встаньте на плечи великанов, и вместе мы увидим дальше, вдохновим студентов и просветим пытливые умы! CCSSHSN-VM.A.1
Распознавать векторные величины как имеющие как величину, так и направление. Представляйте векторные величины в виде направленных отрезков и используйте соответствующие символы для векторов и их величин (например, 𝙫, |𝙫|, ||𝙫||, 𝘷).
CCSSHSF-TF.C.9
Докажите формулы сложения и вычитания для синуса, косинуса и тангенса и используйте их для решения задач.
CCSSHSG-SRT.C.8
Использование тригонометрических соотношений и теоремы Пифагора для решения прямоугольных треугольников в прикладных задачах.
CCSSHSG-SRT.D.10
Докажите законы синусов и косинусов и используйте их для решения задач.
CCSSHSG-SRT.11
Понимание и применение закона синусов и закона косинусов для нахождения неизвестных измерений в прямоугольных и непрямоугольных треугольниках (например, геодезические задачи, равнодействующие силы).
Учащиеся практикуются в определении компонентов, поиске отсутствующей стороны и нахождении измерения угла. Например, помочь физикам лучше понять значения движения и направления в двух измерениях для векторов скорости.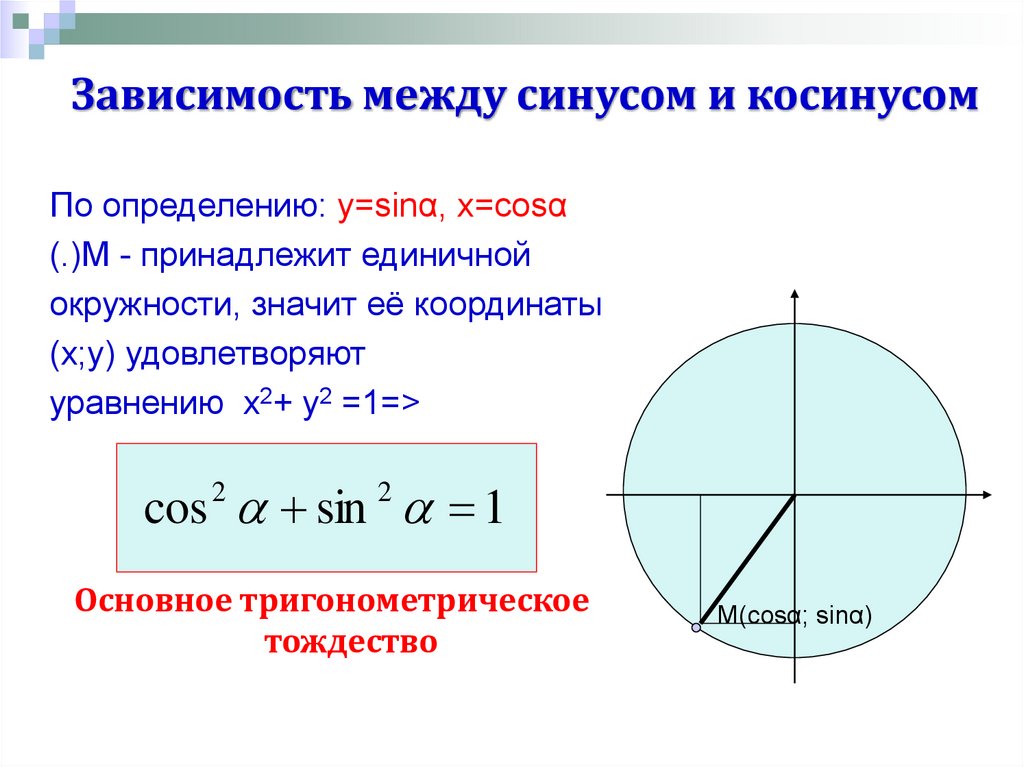
форму, чтобы T могли настроить обсуждение в соответствии с потребностями своих S.
Или подпишитесь на @TheScienceGiant в Твиттере. Встаньте на плечи великанов, и вместе мы увидим дальше, вдохновим студентов и просветим пытливые умы! 