Как строить гиперболу по точкам: описание процесса пошагово, алгоритм по уравнению, точкам и фокусам

график — Python matplotlib Построение гиперболы

Добрый день! Хочу при помощи matplotlib построить, например, гиперболу. Есть следующий код:

import matplotlib.pyplot as plt
import pylab, math
xmin = -200
xmax = 200
dx = 0.1
xlist = [float(x) for x in range(xmin,xmax)]
ylist = [float(1/x) for x in range(xmin,xmax)]
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.grid(True)
plt.title('График функции ')
pylab.plot(xlist,ylist)
pylab.savefig('123.png')

Пример работы на картинке Как видно, между двумя ветвями функции есть отрезок. Я знаю, что это связанно с тем, что есть значение крайних точек ветвей, а плот их соединяет. Но это мне не нужно, мне нужно получить нормальный график. Если бы этот график был всегда гиперболой, было бы нормально. Но этим графиком может быть любой график с разрывом.

Как избежать этого отрезка? Видел способы, но там использовались дополнительные пакеты(numpy), я не хочу тянуть их в этот код []

• python
• график
• matplotlib

1

Для начала повторюсь, что matplotlib уже внутри себя использует numpy, так что избежать его не выйдет. Тем не менее, вот первая версия без numpy в основном коде:

import matplotlib.pyplot as plt
import decimal
# Это замена np.arange
def arange(start, stop, step):
    while start < stop:
        yield start
        start += decimal.Decimal(step)
hyperbola = lambda x: 1 / x
def asymptote_checker(argument, function):
    try:
        function(argument)
        return True
    except ZeroDivisionError:
        return False
xmin = -20
xmax = 20
dx = 0.1
xlist = [round(x, 4) for x in arange(xmin, xmax, dx)]
ylist = [hyperbola(x) if asymptote_checker(x, hyperbola) else float('nan') for x in xlist]
plt.
  plot(xlist, ylist)
plt.show()

С numpy выйдет покороче:

import matplotlib.pyplot as plt
import decimal
import numpy as np
xmin = -20
xmax = 20
dx = 0.1
xlist = np.around(np.arange(xmin, xmax, dx), decimals=4)
ylist = 1 / xlist
plt.plot(xlist, ylist)
plt.show()

Пара общих важных моментов для обеих версий: числа в xlist вместо нуля могут внезапно превратиться в мусор типа 7.0485345e-13 или типа того, что выльется в огромное значение по оси Oy. Второй момент — matplotlib игнорирует (и не соединяет точки) числа типа +inf, -inf, NaN — их можно пометить руками, доверить это numpy или использовать numpy masked array.

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

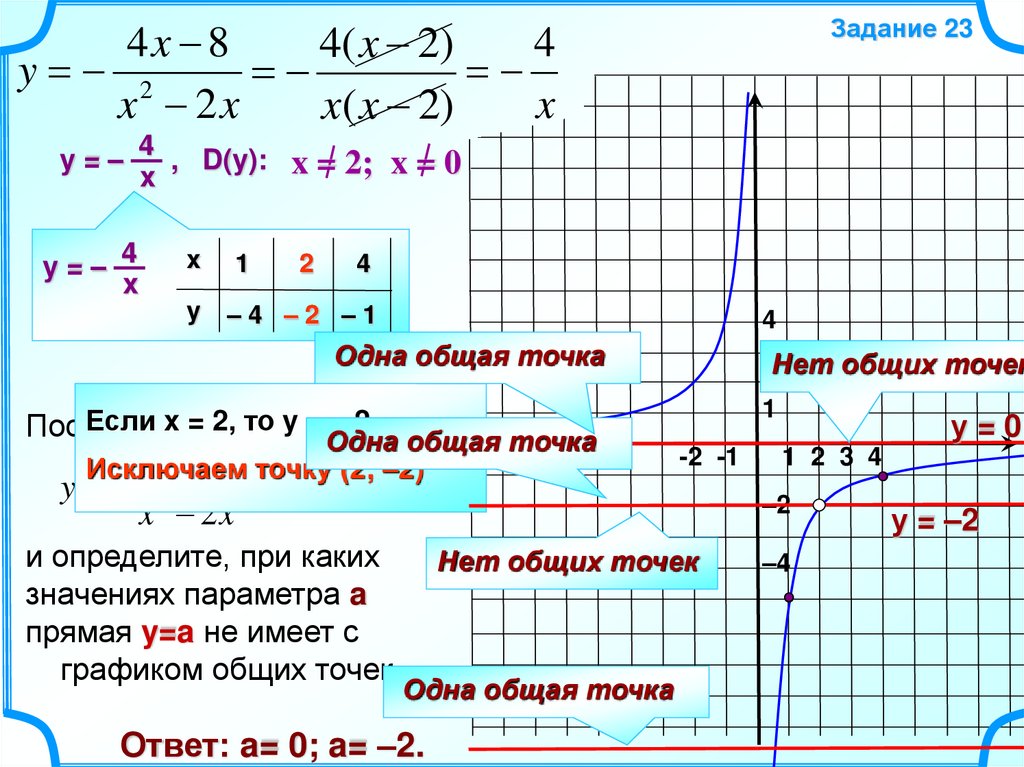
область определения функции, правила построения, примеры задач

Понятие гиперболы

Определение 1

Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (фокусов) — величина постоянная и меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы:

где a, b — положительные действительные числа.

Более простое определение:

Определение 2

Гипербола — это график функции обратной пропорциональности, которая задается следующей формулой:

y=k/x, где:

• x — независимая переменная;
• y — функция;
• k — коэффициент пропорциональности. При этом k≠0. При k>0 график расположен в 1 и 3 четвертях координатной плоскости (функция убывает), при k<0 — во 2 и 4 четвертях(функция возрастает).

Форма гиперболы

График гиперболы выглядит следующим образом:

1. Зеленые кривые называются ветвями гиперболы. Расположение ветвей гиперболы зависит от знака k.
2. Оси абсцисс (OX) и ординат (OY) являются асимптотами графика. Асимптота — прямая, к которой стремится график, но не пересекает ее.
3. Ось симметрии (синяя прямая) выражается уравнением: y=x (при k>0) или y=-x (при k<0).

Описание гиперболы

Основные свойства:

1. Две симметричные ветви относительно начала координат. Поэтому функция нечетная.
2. Две асимптоты.
3. Область значений принимает любое число, кроме нуля.
4. Область определения принимает любое число, кроме нуля.
5. Не имеет наибольших или наименьших значений.

Основные формулы

Как мы уже выяснили, сама функция задается уравнением:

y=k/x

Но также для построения необходимо знать, как расположены асимптоты.

В стандартном случае это оси абсцисс и ординат. Но асимптоты могут быть и смещены. Тогда функция будет задаваться уравнением вида:

y=k/(x-a)+b, где:

• x=a — вертикальная асимптота графика (при a≠0) вместо оси ординат. Если перед a стоит «минус», то смещение вправо. Если перед a стоит «плюс», то смещение влево;
• y=b — горизонтальная асимптота графика (при b≠0) вместо оси абсцисс. Если перед b стоит «минус», то смещение вниз. Если перед b стоит «плюс», то смещение вверх.

Построение гиперболы

Алгоритм построения гиперболы по точкам:

1. Строим систему координат.
2. Решить, в каких четвертях будет располагаться график (в зависимости от знака коэффициента k).
3. Определяемся со смещением асимптот.
4. Составляем таблицу значений. Берем (как минимум) три положительных и три отрицательных значения x, подставляем в уравнение, вычисляем y.
5. Наносим точки на координатную плоскость.
6. Соединяем точки, получаем график.

Примеры решения задач

Пример 

Построить гиперболу по заданному уравнению:

y=-2/(x-3)+4

График будет располагаться во 2 и 4 координатных четвертях, так как k<0.

График будет смещен на 3 единицы вправо и на 4 единицы вверх.

Найдем значения функции, составим таблицу значений:

Начертим график:

Написание уравнения гиперболы

Home > Математика > Исчисление >Написание уравнения гиперболы

Запомните два шаблона для гипербол:

Мы можем написать уравнение гиперболы, выполнив следующие шаги:

1. Определите центральную точку (h, k)
2. Определите a и c
3. Используйте формулу c ² = a ² + b ² , чтобы найти b (или b ² )
. 4. Вставьте h, k, a и b в правильный шаблон.
5. Упрощение

Иногда вам дадут график, а иногда вам просто сообщат некоторую информацию.

Давайте попробуем несколько.

1. Найдите уравнение гиперболы, вершины которой находятся в точках (-1, -1) и (-1, 7), а фокусы находятся в точках (-1, 8) и (-1, -2).

Для начала построим график имеющейся у нас информации:

Мы можем сказать, что это вертикальная гипербола. Давайте найдем нашу центральную точку и отметим ее. Если мы хотим, мы можем также нарисовать грубую гиперболу, просто чтобы ее было легче визуализировать:

Центральная точка (-1, 3). Чтобы найти a, мы будем считать от центра до любой вершины. a = 4. Чтобы найти c, мы будем считать от центра к любому из фокусов.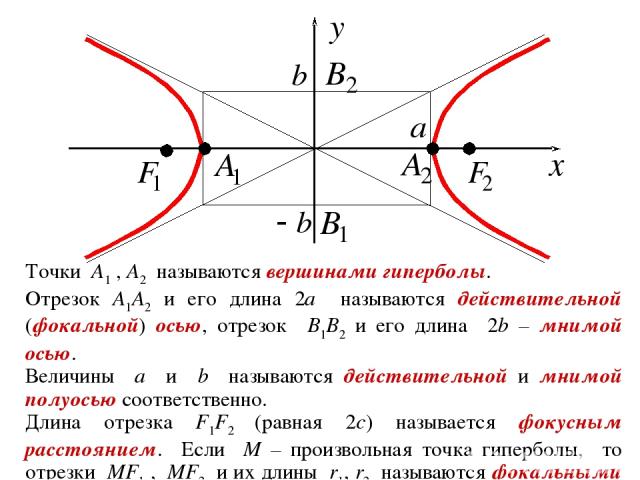 c = 5

Воспользуемся формулой c ² = a ² + b ² , чтобы найти b. Для этого мы подставим a = 4 и c = 5, а затем найдем b.

в ² = а ² + б ²
5 ² = 4 ² + б ²
25 = 16 + б ²
9 = b ² Нам нужно извлечь квадратный корень.
б = 3

У нас есть вся наша информация: h = -1, k = 3, a = 4, b = 3. Поскольку это вертикальная гипербола, мы выберем эту формулу и подставим в нашу информацию.

И упростить:

2. Найдите уравнение этой гиперболы:

Мы можем сказать, что это горизонтальная гипербола. Далее найдем нашу центральную точку и отметим ее.k

Центральная точка (1, 2). Чтобы найти a, мы будем считать от центра до любой вершины. a = 2. Чтобы найти c, мы будем считать от центра к любому из фокусов.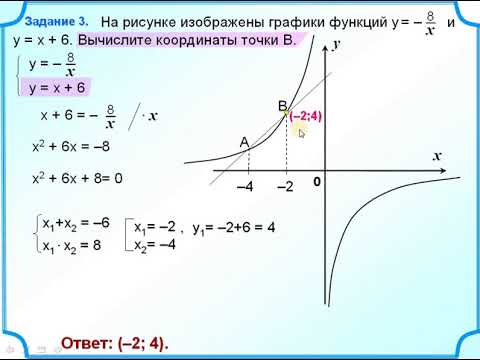 c = 6

Мы будем использовать формулу c ² = a ² + b ² , чтобы найти b. Для этого мы подставим a = 2 и c = 6, а затем найдем b.

в ² = а ² + б ²
6 ² = 2 ² + б ²
36 = 4 + б ²
32 = б ²

Чтобы найти b, нам нужно было бы извлечь квадратный корень, но это не выйдет равномерно. Это нормально, потому что для шаблона требуется b ² , поэтому мы можем просто заменить b ² на 32 .

У нас есть вся наша информация: h = 1, k = 2, a = 2, b ² = 32 . Поскольку это горизонтальная гипербола, мы выберем эту формулу и подставим в нашу информацию.

И упростить:

Практика: Найдите уравнение каждой параболы:

1) Вершины: (2, 1) и (2, -5) Фокусы: (2, 3) и (2, -7)
2) Вершины: (0, 1) и (6, 1) Фокусы: (-1, 1) и (7, 1)
3) Вершины: (1, 0) и (3, 0) Фокусы: (-1, 0) и (5, 0)

Ответы:

Ссылки по теме: Математика Дроби Факторы

Определение, примеры, уравнение и формула

Гипербола — это тип конического сечения, состоящего из двух кривых, которые напоминают параболы (хотя и не являются таковыми). Эти пары кривых, также называемые ответвлениями, могут открываться вверх и вниз или влево и вправо. Кроме того, каждая кривая содержит вершину.

В этой статье мы стремимся рассмотреть свойства гипербол и тождественных уравнений, описывающих такие конические сечения. Ознакомившись с этими понятиями, мы можем в конечном итоге построить график гипербол с заданной парой координат.

Гипербола представляет собой множество H всех точек P на плоскости, где абсолютная величина разности расстояний между двумя фиксированными точками, называемыми фокусами, F ₁ и F ₂ , постоянна, k, то есть

H={P:||PF1|–|PF2||=k,k∈ℝ}.

Далее мы рассмотрим компоненты этого графика в следующем разделе.

Для наглядности посмотрите на график ниже.

Обратите внимание, что в отличие от других типов конических сечений гиперболы состоят из двух ветвей, а не из одной.

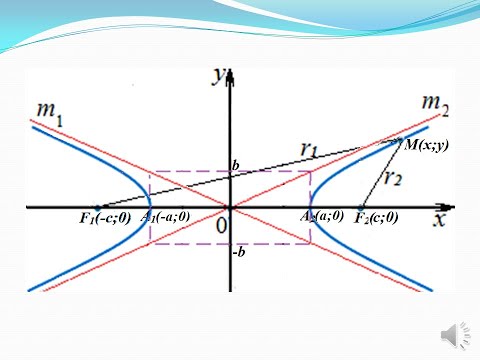
Геометрические компоненты гиперболы

С геометрической точки зрения, гипербола получается, когда плоскость пересекается параллельно оси конуса с двойной вершиной.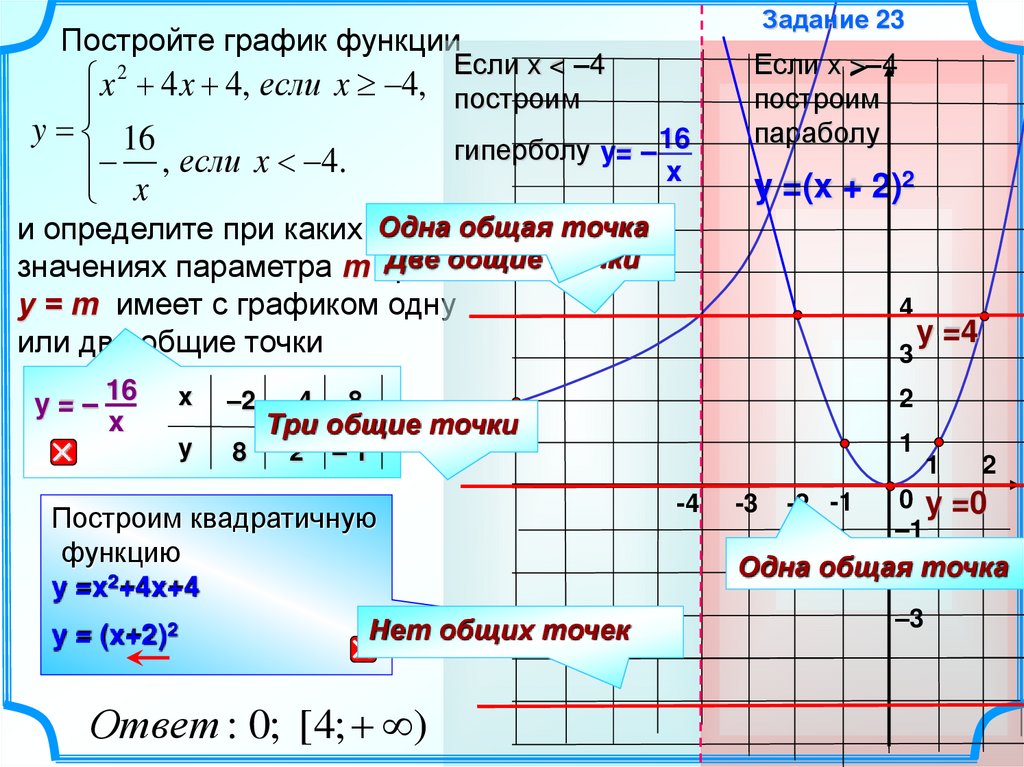

Давайте более подробно рассмотрим графическое представление гиперболы. Здесь мы вводим более важные компоненты, составляющие гиперболу.

1. Каждая гипербола имеет две оси симметрии: поперечную и сопряженную

2. Сопряженная ось (ось Y) представляет собой линию, перпендикулярную поперечной оси и содержащую ко-вершины.

3. Поперечная ось (ось x) — это линия, проходящая через центр гиперболы. Фокусы (фокус F ₁ и фокус F ₂₎ лежат на поперечной линии. Вершины — это точки пересечения обеих ветвей гиперболы с поперечной линией. И фокусы, и вершины симметричны относительно сопряженной оси, что означает, что они будут иметь одну и ту же координату x, но с противоположными знаками.

4. Центр — это середина поперечной оси и сопряженной оси. Здесь пересекаются две линии.

5. Каждая гипербола имеет две асимптоты (красные пунктирные линии), проходящие через центр. По мере удаления гиперболы от центра ветви приближаются к этим асимптотам. По определению, ветви гиперболы никогда не пересекаются с ее асимптотами.

6. Центральный прямоугольник (оранжевые пунктирные линии) центрирован в начале координат. Стороны проходят через каждую вершину и ковершину.

Полезно определить это при построении графика гиперболы и ее асимптот. Чтобы нарисовать асимптоты гиперболы, все, что нам нужно сделать, это продолжить диагонали центрального прямоугольника.

Уравнения гиперболы

Теперь выведем уравнение гиперболы с центром в начале координат.

Пусть P = (x, y), а фокусы гиперболы с центром в начале координат равны F ₁ = (–c, 0) и F ₂ = (c, 0)

Из На графике выше (a, 0) является вершиной гиперболы, поэтому расстояние от (−c, 0) до (a, 0) равно a − (−c) = a + c. Точно так же расстояние от (c, 0) до (a, 0) равно c − a.

Сумма расстояний от фокусов до вершины равна (a + c) − (c − a) = 2a. Пусть P(x, y) — точка на гиперболе, которую мы хотим исследовать.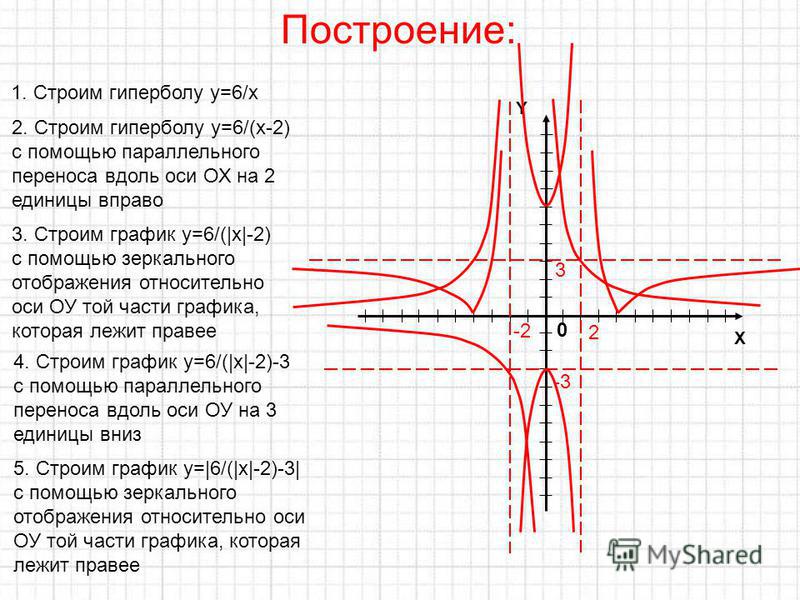 Отсюда мы можем определить d ₁ и d ₂ как:

d ₁ = расстояние от (c, 0) до (x, y)

0) до (x, y)

По определению, гипербола — это множество всех точек, в которых разность расстояний между (x, y) и фокусами постоянна. Таким образом, д ₂ — d ₁ постоянна для любой точки (x, y) гиперболы. Мы знаем, что разница этих расстояний равна 2а для вершины (а, 0). Итак, д ₂ – д ₁ = 2а.

Чтобы найти уравнение гиперболы, воспользуемся формулой расстояния и решим наше выражение алгебраически.

Формула расстояния

Напомним, что формула расстояния для двух точек (x ₁ , y ₁ ) и (x ₂ , y ₂ ) определяется как

d=(x2-x1)2+(y ₂ -y ₁ )2

По формуле расстояния между (-c, 0) и (c, 0)

d2-d1=(x-(-c))2+(y-0)2-(x-c)2+(y-0)2=2a⇒(x+c)2+y2-(x-c )2+y2=2a⇒(x+c)2+y2=2a+(x-c)2+y2

Возводя в квадрат обе стороны, получаем

⇒(x+c)2+y2=2a+(x-c)2+y22 ⇒x2+2cx+c2+y2=4a2+4a(x-c)2+y2+(x-c)2+y2

Разложение двучленов и сокращение подобных членов,

⇒x2+2cx+c2+y2=4a2+4a(x-c )2+y2+x2-2cx+c2+y2⇒4cx-4a2=4a(x-c)2+y2

Теперь разделив обе стороны на 4 и возведя обе стороны в квадрат,

⇒cx-a2=a(x-c)2+y2⇒cx-a22=a(x-c)2+y22

Расширяя это и отменяя подобные члены, снова получаем,

⇒c2x2-2a2cx+a4=a2(x2-2cx+c2+y2)⇒c2x2-2a2cx+a4=a2x2-2a2cx+a2c2+a2y2⇒c2x2-a2x2-a2y2=a2c2-a4

9 Это упрощает до 9 ⇒x2(c2-a2)-a2y2=a2(c2-a2)

Расстояние между фокусами равно 2c, где c ² = a ² + b ² . Таким образом, мы можем положить b ² = c ² — а ² . При этом мы получаем

⇒x2b2-a2y2=a2b2

Теперь разделив обе части на a ² b ² , уравнение для гиперболы примет вид

⇒x2a2-y2b2=1

, что и требовалось! Ниже приведен рабочий пример, демонстрирующий использование формулы расстояния в отношении гипербол.

Определите уравнение гиперболы, представленное на графике ниже.

Решение

Гипербола ниже имеет фокусы в точках (0 , –5) и (0, 5), а вершины расположены в точках (0, –4) и (0, 4). Расстояние между этими двумя координатами равно 8 единицам.

Таким образом, разница между расстоянием от любой точки (x, y) гиперболы до фокусов составляет 8 или –8 единиц, в зависимости от порядка вычитания.

Используя формулу расстояния, мы получаем уравнение гиперболы следующим образом.

Let,

d ₁ = расстояние от (0, 5) до (x, y)

d ₂ = расстояние от (0, –5) до (x, y)

d2-d1 =±8⇒(y-5)2+x2-(y+5)2+x2=±8⇒(y-5)2+x2=±8+(y+5)2+x2⇒(y-5 )2+x2=±8+(y+5)2+x22⇒y2-10y+25+x2=64+16(y+5)2+x2+(y+5)2+x2⇒y2-10y+25 +x2=64±16(y+5)2+x2+y2+10y+25+x2⇒-20y-64=±16(y+5)2+x2⇒5y+16=±4(y+5) 2+x2⇒5y+162=16(y+5)2+x22⇒25y2+160y+256=16(y2+10y+25+x2)⇒25y2+160y+256=16y2+160y+400+16×2⇒9y2-16×2=144

Разделив выражение на 9×16, мы получим

⇒y216+x29=1

Свойства гипербол

Теперь перейдем к свойствам гипербол.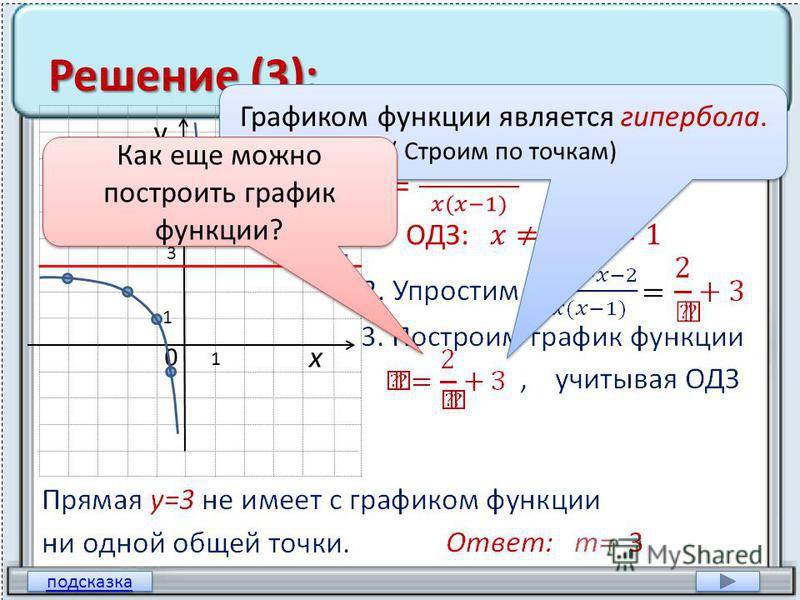 Здесь следует рассмотреть два случая:

Случай 1: Гипербола с центром в начале координат (0, 0)

Свойство	Центр (0,0)
Стандартная форма уравнения =1	y2a2-x2b2=1
General Plot
Opening	Opens left and right	Opens up and down
Direction of Transverse Axis	Horizontal	Vertical
Foci	( в, 0), (-в, 0)	(0, в), (0, -в)
Вершины	(а, 0), (-а, 0)	(0, а ), (0, -a)
Длина поперечной оси	2a units	2a units
Length of Conjugate Axis	2b unites	2b units
Equation of Asymptotes	y=±bax	y=±abx

Case 2 : Гипербола с центром в точке (h, k)

Свойство	Центр (h,k)
Стандартная форма уравнения -(x-h)2b2=1
Общий участок
Вершины	(ч + а, к), (ч — а, к), (к — а, к)	)
Фокусы	(h + c, k), (h — c, k)	(h, k + c), (h, k — c)
Уравнение асимптот	y =k±ba(x-h)	y=k±ab(x-h)

Расположение фокусов и вершин заданной гиперболы

Определение фокусов и вершин гиперболы y249-x232=1.

Решение

Уравнение имеет вид

y2a2-x2b2=1

Таким образом, поперечная ось лежит на оси y. Центр находится в начале координат, поэтому точки пересечения по оси Y являются вершинами графа. Таким образом, мы можем найти вершины, установив x = 0 и найдя y, как показано ниже.

y249-(0)232=1⇒y249=1⇒y2=49⇒y=±49=±7

Фокусы расположены в точках (0,±c) и по соотношению между a, b и c установлено раньше получаем

c2=a2+b2⇒c=±a2+b2=±49+32=±81=±9

Таким образом, вершины равны (0, –7) и (0, 7), а фокусы равны (0, –9) и (0, 9). График показан ниже.

Определите фокусы и вершины гиперболы (y-2)29-(x-3)225=1.

Решение

Уравнение имеет вид

(y-k)2a2-(x-h)2b2=1

Таким образом, поперечная ось лежит на оси y. Здесь h = 3 и k = 2, поэтому центр находится в точке (3, 2). Чтобы найти вершины, воспользуемся приведенной ниже формулой.

(h,k±a)⇒(3,2±9)=(3,2±3)

Фокусы расположены в (0,±c) и, используя как и ранее c2=a2+b2, получаем

c=±9+25=±34≈±5,83(исправить до двух знаков после запятой)

Таким образом, вершины равны (3, –1) и (3, 5), а фокусы равны (0, –5,83) и (0, 5.83). График показан ниже.

Уравнение для асимптот можно найти по формуле, приведенной в таблице. Попробуйте эти примеры! Всегда полезно сначала нарисовать асимптоты, прежде чем рисовать две ветви гиперболы.

Нахождение уравнения гиперболы для заданных фокусов и вершин

Выразите следующую гиперболу в стандартной форме для заданных фокусов и вершин.

Вершины:(±6,0)Фокусы:(±210,0)

Решение

Обратите внимание, что вершины и фокусы находятся на оси x. Следовательно, уравнение гиперболы примет вид

x2a2-y2b2=1

Поскольку вершины равны (±6,0), то

a=6⇒a2=36

Учитывая, что фокусы равны (±210 ,0), то

c=210⇒c2=40

Решая b ² , мы получаем

b2=c2-a2=40-36⇒b2=4

Теперь, когда мы нашли ^{2 0} 1 и b 1 44 и 34 , мы можем подставить это в стандартную форму как

x236-y24=1

График показан ниже.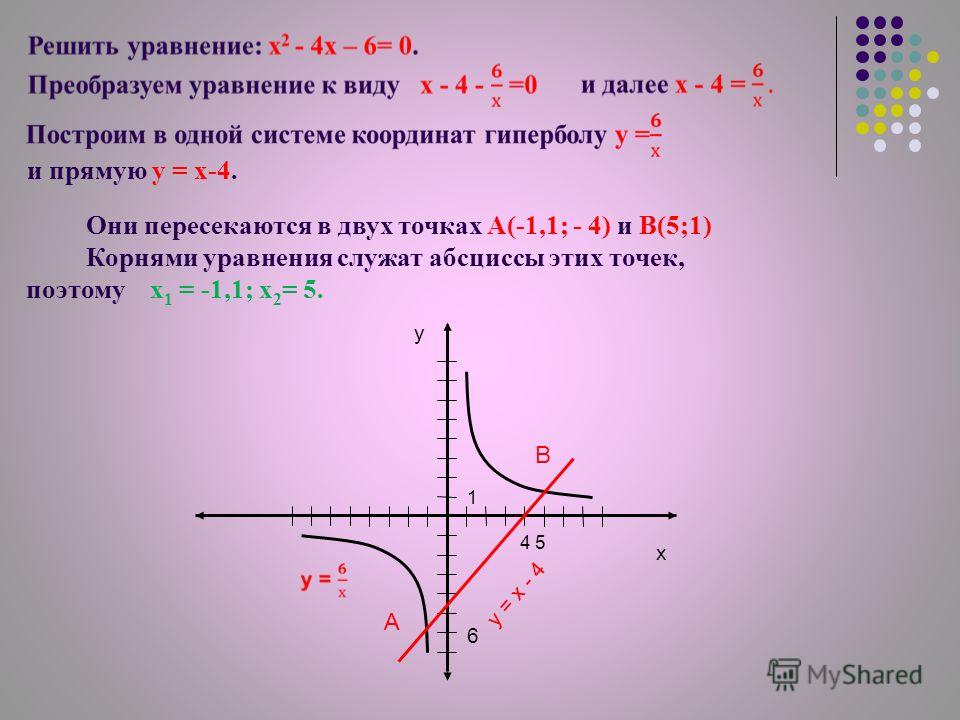

Выразите следующую гиперболу в стандартной форме, учитывая следующие фокусы и вершины.

Вершины:(1,-2)и(1,8)Фокусы:(1,-10)и(1,16)

Решение

Вершины и фокусы имеют одинаковые координаты x, поэтому поперечная ось параллельна оси y. Таким образом, уравнение гиперболы примет вид

(y-k)2a2-(x-h)2b2=1

Сначала мы должны определить центр, используя формулу средней точки. Центр лежит между вершинами (1, –2) и (1, 8), поэтому

(h,k)=1+12,-2+82=(1,3)

Длина поперечной оси , 2а, ограничен вершинами. Чтобы найти ² , мы должны оценить расстояние между y-координатами вершин.

2a=-2-8=-10=10⇒a=5⇒a2=25

Координаты очагов

(h,k±c)⇒(h,k-c)=(1,-10 )and(h,k+c)=(1,16)

Используя k + 3 = 16 и подставляя k = 3, мы получаем

c=13⇒c2=169

Таким образом, мы можем найти для b ² на

b2=c2-a2⇒b2=169-25=144

Наконец, подставляя эти значения в стандартный вид, получаем

(y-3)225-(x-1)2144=1

График показан ниже.

Графические гиперболы

В этом заключительном разделе мы построим графики гипербол, используя понятия, введенные в этом уроке.

График уравнения в стандартной форме

Вернемся к нашим предыдущим примерам для этого сегмента,

График гиперболы x236-y24=1

Решение

форма.

x2a2-y2b2=1

Это означает, что у нас есть пара кривых, открывающихся слева и справа. Вершины (±6,0) и фокусы (±210,0). Центр гиперболы — это начало координат (0, 0). Здесь,

a2=36⇒a=6andb2=4⇒b=2

Уравнение асимптот:

y=±bax=±26x=±13x

Всегда рисуйте асимптоты при графическом построении гипербол. Таким образом, мы можем точно нарисовать кривые, связанные с уравнением.

График x236-y24=1 показан ниже.

График уравнения не в стандартной форме

В этом разделе может быть полезно вспомнить метод заполнения квадратов для решения таких задач.

Нарисуйте гиперболу ниже.

9×2-25y2-36x-50y-214=0

Решение

Чтобы решить это выражение, мы должны попытаться преобразовать его в стандартную форму гиперболы. Делаем это, заполнив квадрат следующим образом.

9×2-36x-25y2-50y=2149(x2-4x+A)-25(y2+2y+B)=214+9(A)-25(B)

Нам нужно идентифицировать A и B. В при этом получаем

9(x2-4x+4)-25(y2+2y+1)=214+9(4)-25(1)⇒9(x-2)2-25(y+1 )2=225

Разделив обе части на 225, получим уравнение

⇒(x-2)225-(y+1)29=1

Центр равен (2, –1). У нас также есть значения h=2,k=-1,a=5,b=3andc=34. Таким образом, мы получаем следующие значения для вершин, фокусов и асимптот.

Вершины

(h±a,k)=(2±5,-1)⇒(-3,-1)и(7,-1)

Фокусы

(h±c,k) =(2±34,-1)⇒(2-34,-1)и(2-34,-1)

Асимптоты

y=k±ba(x-h)=-1±35(x-2 )⇒y+1=-35(x-2)andy+1=35(x-2)

График (x-2)225-(y+1)29=1 показан ниже.

Эксцентриситет гиперболы

Эксцентриситет конического сечения описывает, насколько тесно кривая связана с окружностью. Эксцентриситет описывается переменной e.

Эксцентриситет окружности равен нулю, e = 0.

Эксцентриситет гиперболы всегда больше 1, e > 1 . Формула для нахождения эксцентриситета гиперболы приведена ниже.

Формула: эксцентриситет гиперболы

e=a2+b2a

Чем больше эксцентриситет, тем меньше искривление конического сечения.

Найти эксцентриситет гиперболы x225-y29=1

Решение

Здесь a ² = 25 и b ² = 9. Таким образом, эксцентриситет a 0003 гиперболы определяется формулой

25=5⇒e=25+95⇒e=345≈1,17(исправить до двух знаков после запятой)

Гиперболы — ключевые выводы

• Чтобы найти вершины и фокусы, заданные уравнением гиперболы в стандартной форме, мы предпринимаем следующие шаги:
  1. Identify the location of the transverse axis

     Iftheequationisoftheformx2a2-y2b2=1⇒transverseaxisliesonthex-axisandtheverticesare(±a,0)andthefociare(±c,0)

     Iftheequationisoftheformy2a2-x2b2=1⇒transverseaxisliesonthey -ось и вершины равны (0,±a) и фокусы равны (0,±c) стандартную форму с учетом вершин и фокусов гиперболы с центром в (0,0), мы используем следующий метод: Определите местоположение поперечной оси Iftheverticesare (± A, 0) и TheFociare (± C, 0) ⇒ TransvereaExisliesonTHEX-AXISISISISISISOFTheforeFtheformx2a2B2 = 1000. 9000.9000.9000.9000.9000.9000.9000.9000.9000.9000.9000.9000.9000.9000.9000.9000.9000.9000.9000.9000.9000.9010.9010.9010. 0101010.9010.9010.9010.9010.9010 (± A, 0). и Thefociare (0, ± c) ⇒ TransverseaxiSliesonthey-OxisisandTheequationisoftheformy2a2-x2b2 = 1 Решение для B 2 с использованием B 2 a = ulpe для b 2 .2 Подставьте a 2 и b 2 в стандартную форму, установленную на шаге 1 . Чтобы записать уравнение в стандартной форме с учетом вершин и фокусов гиперболы с центром в точке (h,k), мы применяем методика ниже: Решите, параллельна ли поперечная ось оси x или оси y 9015- (X-H) 2B2 = 10003 — (x-H) 2B2 = 1 — (x-H) 2B2 = 10003— (x-H) 2B2 = 1 — (x-H) 9015 9015 9015 9015 9. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Если их координаты вершин и фокусов совпадают ⇒ поперечная ось лежит на оси x и уравнение имеет форму (x-h)2a2-(y-k)2b2=1 92b20003 Ifthex-CoordinatesofTheverticesAndFociarethesamethythy TranserseaxiSiliesonthey-Assisisandtheequationisoftheform (y-k) 2A2- (x-H) 2B2 = 10003