График линейного уравнения с двумя переменными
Категория: Математика.
Цели.
Образовательная:
1. Знать определение графика уравнения с двумя переменными;
2. Знать, что является графиком линейного уравнения с двумя переменными;
3. Уметь строить график линейного уравнения с двумя переменными.
Развивающая: учить анализировать, сравнивать, обобщать определять и объяснять понятия, т.е. умение мыслить.
Воспитательная: развивать нравственные отношения у школьников с окружающим миром (качество честности, трудолюбие).
Оборудование:
рабочая карта;
кроссворд;
карта-таблица;
карточки для дополнительного уровневого задания;
таблица “Уравнения с двумя переменными и их графики”;
таблица “Расположение графиков линейного уравнения с двумя переменными относительно осей координат”.
Ход урока
1. Запись домашней работы: (учитель проговаривает)
п.
41, повторить п.п.15-16.
№1046, №1049, для желающих № 1152 — график с параметром.
2. Проверка домашнего задания. (До урока на перемене)
Выразить одну переменную через другую (а, б)
№1034(б), №1140 (а)
На доске “Проверь себя” (До урока на перемене учащиеся проверяют домашнее задание, сверяя с решением на доске.) – решение уравнений, критерии оценок.
(Выразить одну переменную через другую (а, б))
а) 6х — у = 12;
у = 6х — 12.
б) 10х + 7у = 0;
10х = -7у;
х = -0,7у.
№1034(б).
6х + 2у =7;
2у = 7 — 6х;
у = (7 — 6х) / 2;
у = 3,5 – 3х;
Точки: (0; 3,5), (1; 0,5), (2;-2,5).
№1140 (а).
ах – 2у = 1, х=5, у = 7, а = ?
5а — 14 = 1;
5а = 15;
а=3.
Критерий:
Все решено правильно и самостоятельно — “5”;
Все решено правильно, но с помощью — “4”;
Решено с помощью и с ошибкой — “3”.
№ 1140 — оценивается по тем же критериям, только “5” и “4”.
После записи домашней работы предлагаю выставить оценки согласно критериям каждому за свою домашнюю работу (самооценка) в рабочую карту (предварительно подписав карт). Рабочая карта отражена на рисунке 4.
3. Совместная постановка цели урока.
Читаем тему урока на доске.
— Ребята, как вы думаете, что должны знать и чему научиться на этом уроке?
[1. Знать определение графика уравнения с двумя переменными.]
[2. Что является графиком линейного уравнения с двумя переменными.]
[3. Уметь строить график линейного уравнения с двумя переменными.]
А что бы этого достичь, нужно анализировать, сравнивать, объяснять понятия. Работая в классе, необходимо с уважением относиться к окружающим и быть предельно честным.
Для успешной работы повторим теоретический материал, разгадывая кроссворд. Кроссворды находятся в каждой группе (на работу 3 минуты).
Рисунок 1.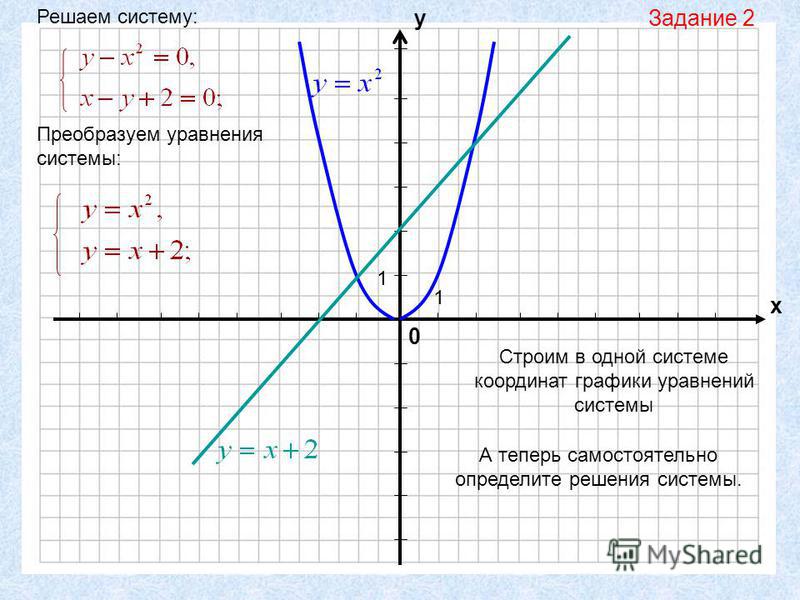
Кроссворд.
Вопросы к кроссворду:
1. Что является графиком линейной функции?
2. Один из способов задания функции.
3. Пара чисел, изображающаяся в координатной плоскости.
4. Независимая переменная.
5. Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
6. Зависимость между переменными, при которой каждому значению независимой переменной соответствует единственной значение зависимой переменной.
7. Какими называются уравнения с двумя переменными имеющие одни и те же решения, или не имеющие решений?
Чья группа угадает быстрее, получает жетон. Всего дается три жетона, т.е. первым трем группам.
Для тех, кто закончил работу, на доске задание (устно):
1. Назвать коэффициенты в уравнениях;
2. Выразить у через х из уравнений:
3х – у = 2;
у = 3х — 2.
5х + 2у = 7;
у = 3,5 — 2,5х.
х + 2у = 4;
у = 2 — 0,5х.
2х – у = 11;
у = 2х — 11.
3. Как назвать эти равенства:
х2+у2=20;
ху=12;
|х|+ |у| = 10.
Внимание на доску, проверим кроссворд. (Ответы на кроссворд и критерий оценки работы на доске:)
1. Прямая.
2. Формула.
3. Точка.
4. Аргумент.
5. График.
6. Функция.
7. Равносильными.
Критерий: Быстро и правильно — два “+”, отметить на жетоне номер группы;
Правильно — один “+”.
— Поднимите руку, кто получил два “+”, один “+”. Кто не угадал, повторить определения.
Переходим к проверке (решению) устного упражнения:
1. Проговариваем коэффициенты;
2. Выражаем у через х из уравнений;
3. Называем эти равенства — уравнениями с двумя переменными.
— Что является решением уравнения с двумя переменными? (Пара значений переменных — х и у)
— Сколько решений имеет уравнение с двумя переменными? (Много)
— Как изображается пара значений переменных на координатной плоскости? (Точкой)
— Сколько таких точек можно изобразить? (Много)
— Что является координатами каждой из этих точек? (Абсцисса — значение х, ордината — значение у)
— Что образуют все эти точки на координатной плоскости? (График)
— Так что называется графиком уравнения с двумя переменными? (Множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения)
— Откройте учебник, п.
Рисунок 2. Уравнения с двумя переменными и их графики.
— Что вы видите на таблице? (Уравнения с двумя переменными и их графики).
— Есть ли среди них линейные уравнения с двумя переменными? (Нет)
— Графики этих уравнение вы будите изучать в старших классах. А мы с вами должны узнать, что является графиком линейного уравнения с двумя переменными.
4. Изучение нового материала.
— Открыли тетради, записали тему урока. Дайте определение линейной функции и запишем:
у = kх + b,
где х и у — переменные, k, b — некоторые числа.
— Дайте определение линейного уравнения с двумя переменными и запишем:
ах + bу = с,
где х и у — переменные, 
— Сравните, что общего в этих видах математической записи (входят две переменные х и у, числа).
— Как по-другому называются числа? (Коэффициенты).
— Чем отличаются? (Количеством чисел 2 и 3; в первом — выражена зависимость — функция, во втором — не выражена — уравнение).
— А можно ли в линейном уравнении с двумя переменными выразить зависимость одной переменной от другой? (Да).
— Давайте выразим зависимость переменной у от переменной х в линейном уравнении с двумя переменными:
ах+by = с,
где х и у — переменные, а, b, с — некоторые числа.
— Выражаем в общем виде: bу = с — ах.
— Что сейчас мы должны обязательно оговорить? (Что коэффициент при переменной у не равен нулю):
у = (с – ах) / b, при условии b 0.
у = (с / b) – (а / b)х.
— Запишем в стандартном виде:
у = – (а / b)х + (с / b).
— Таким образом, мы получили вид линейной функции у = kx + b, только по-другому записаны числа.
— Что является графиком линейной функции? (Прямая).
— Что необходимо, что бы построить прямую? (Построить две точки).
— А почему две точки? (Согласно аксиоме).
— Так что же является графиком линейного уравнения с двумя переменными, если коэффициент при у не равен нулю (т.е. b 0)? (Прямая).
— Что является координатами каждой из точек? (Пара значений переменных х и у, которые являются решением данного уравнения).
— Запишем уравнение 2х — у = 3. Коэффициент при переменной у не равен нулю. Запишите одно решение (спрашиваю троих и записываю три решения).
— Как проверить, что каждая пара значений переменных
— Как нашли это решение? (Х — произвольное значение, у — находим).
— Какую фигуру будет изображать пара чисел, являющаяся решением линейного уравнения на координатной плоскости? (Точку).
— Сколько пар решений нужно, чтобы построить график? (Две пары).
— Мы рассмотрели с вами общий случай построения графика линейного уравнения с двумя переменными. Кроме общего случая существуют частные случаи построения графиков, когда хотя бы один из коэффициентов равен нулю.
Постановка проблемного вопроса.
— А что же является графиком линейного уравнения с двумя переменными, если хотя бы один из коэффициентов равен нулю?
— Для ответа на этот вопрос предлагается работа по группам. Возьмите карты-таблицы “Что является графиком уравнения ax + by = с, если хотя бы один из коэффициентов равен нулю?”. Подпишите их. Карта-таблица представлена на рисунке 3.— Смотрим таблицу. В первом столбце записаны
уравнения. Второй столбец вы должны заполнить,
записывая коэффициенты линейных уравнений.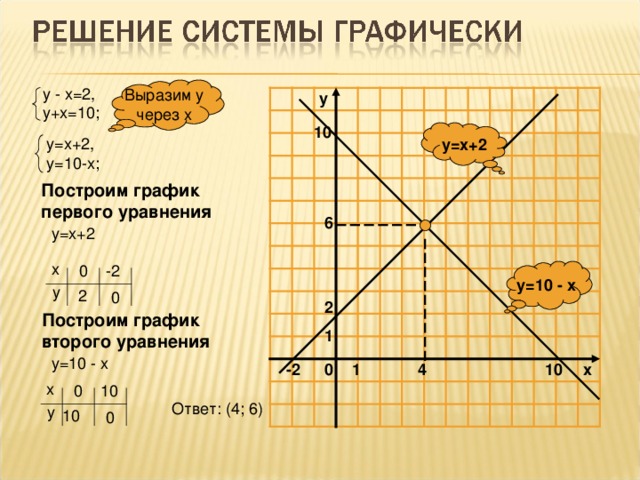
Потом записываете пары решений для каждого из
уравнений. Затем в соответствии с координатной
плоскостью строите графики. И в последнем
столбце записываете, что является графиком.
Таблица заполняется по строкам. (При этой работе
вызываю по одному ученику для заполнения
карты-таблицы на доске после некоторого времени,
когда большинство заполнят).
— Если группа заканчивает работу раньше других, то на доске задание, которое выполняется устно.
По окончании работы заслушиваю двух человек. Обобщаем, что же является графиком линейного уравнения, если хотя бы один из коэффициентов равен нулю? (Прямая).
Рисунок 3. Карта-таблица “Что является графиком уравнения ax + by = с, если хотя бы один из коэффициентов равен нулю?”.
Внимание на доску! (На доске таблица с графиками линейных уравнений).
— Какого случая у нас нет? (а 0, b 0, с = 0). Что является графиком? (Прямая пропорциональность).
— А теперь найдите в тексте учебника п.
41
определение графика линейного уравнения с двумя
переменными и зачитайте его.
— Повторим, что является графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов не равен нулю? (Прямая).
— А можно ли по виду линейного уравнения с двумя переменными определить, что является графиком данного уравнения? (Можно).
На доске записаны линейные уравнения с двумя переменными:
1) 4х — 3у = 5;
2) -7х = 14;
3) 0х + 0у = 0;
4) 0х = — 6;
5) 2у — 6 = 0;
6) 0у = 10.
— Назвать уравнения, графиком которых является прямая, плоскость, нет графика. (Прямая — 1, 2, 5; плоскость — 3; нет графика — 4, 6).
— И еще раз, что же является графиком линейного уравнения с двумя переменными, если хотя бы один из коэффициентов отличен от нуля.
— А сейчас за работу с картой-таблицей
консультант проставит каждому оценки в рабочую
карту. Критерий оценки — как для домашнего
задания. Поднимите руку, кто справился на “5”,
кто на “4”.
5. Закрепление материала.
— Самостоятельная работа на доске (проверка у консультанта, консультант проверяет у группы).
Постройте график уравнения:
а) 2х — у = 6;
б) х + 6у = 0;
в) 1,2х = — 4,8;
г) 1,5у = 6.
Критерий оценки (на доске):
правильно решены все — “5”;
правильно решены 4-5 — “4”;
правильно решены 3 — “3”.
— Поднимите руку, кто справился на “5”, кто на “4”, кто на “3”.
Тому, кто закончит раньше, даются уровневые карточки.
6. Рефлексия.
На рабочей карте (рисунок 4) имеются незаконченные предложения. Пожалуйста, закончите их.
На уроке мне было легко при…
На уроке я испытывал(а) трудности при…
Рисунок 4. Рабочая карта.
Рабочие карты сдать консультанту для итоговой оценки. Консультанты сдадут мне.
Урок окончен! До свидания!
26.05.2014
Курс высшей математики, Т.
1 Курс высшей математики, Т.1
ОглавлениеПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ 1. Величина и ее измерение. 2. Число. 3. Величины постоянные и переменные.  4. Промежуток. 5. Понятие о функции. 6. Аналитический способ задания функциональной зависимости. 7. Неявные функции. 8. Табличный способ. 9. Графический способ изображения чисел. 10. Координаты. 11. График и уравнение кривой. 12. Линейная функция. 13. Приращение. Основное свойство линейной функции. 14. График равномерного движения. 15. Эмпирические формулы. 16. Парабола второй степени. 17. Парабола третьей степени. 18. Закон обратной пропорциональности. 19. Степенная функция. 20. Обратные функции. 21. Многозначность функции. 22. Показательная и логарифмическая функции. 23. Тригонометрические функции. 24. Обратные тригонометрические, или круговые, функции. § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 25. Упорядоченное переменное. 26. Величины бесконечно малые. 27. Предел переменной величины. 28. Основные теоремы. 29. Величины бесконечно большие. 30. Монотонные переменные. 31.  Признак Коши существования предела.32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью. 33. Примеры. 34. Непрерывность функции. 35. Свойства непрерывных функций. 36. Сравнение бесконечно малых и бесконечно больших величин. 37. Примеры. 38. Число е. 39. Недоказанные предложения. 40. Вещественные числа. 41. Действия над вещественными числами. 42. Точные границы числовых множеств. Признаки существования предела. 43. Свойства непрерывных функций. 44. Непрерывность элементарных функций. ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ 45. Понятие о производной. 46. Геометрическое значение производной. 47. Производные простейших функций. 48. Производные сложных и обратных функций. 49. Таблица производных и примеры. 50. Понятие о дифференциале. 51. Некоторые дифференциальные уравнения. 52. Оценка погрешностей. § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 53.  Производные высших порядков.54. Механическое значение второй производной. 55. Дифференциалы высших порядков. 56. Разности функций. § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ 57. Признаки возрастания и убывания функций. 58. Максимумы и минимумы функций. 59. Построение графиков. 60. Наибольшее и наименьшее значения функций. 61. Теорема Ферма. 62. Теорема Ролля. 63. Формула Лагранжа. 64. Формула Коши. 65. Раскрытие неопределенностей. 66. Различные виды неопределенностей. § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 68. Частные производные и полный дифференциал функции двух независимых переменных. 69. Производные сложных и неявных функций. § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ 70. Дифференциал дуги. 71. Выпуклость, вогнутость и кривизна. 72. Асимптоты. 73. Построение графиков. 74. Параметрическое задание кривой. 75. Уравнение Ван-дер-Ваальса. 76. Особые точки кривых. 77.  Элементы кривой.78. Цепная линия. 79. Циклоида. 80. Эпициклоиды и гипоциклоиды. 81. Развертка круга. 82. Кривые в полярных координатах. 83. Спирали. 85. Овалы Кассини и лемниската. ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ 86. Понятие о неопределенном интеграле. 87. Определенный интеграл как предел суммы. 88. Связь определенного и неопределенного интегралов. 89. Свойства неопределенного интеграла. 90. Таблица простейших интегралов. 91. Правило интегрирования по частям. 92. Правило замены переменных. Примеры. 93. Примеры дифференциальных уравнений первого порядка. § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 94. Основные свойства определенного интеграла. 95. Теорема о среднем. 96. Существование первообразной функции. 97. Разрыв подынтегральной функции. 98. Бесконечные пределы. 99. Замена переменной под знаком определенного интеграла. 100. Интегрирование по частям. § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 101.  Вычисление площадей.102. Площадь сектора. 103. Длина дуги. 104. Вычисление объемов тел по их поперечным сечениям. 105. Объем тела вращения. 106. Поверхность тела вращения. 107. Определение центров тяжести. Теоремы Гульдина. 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций. 109. Формула касательных и формула Понселе. 110. Формула Симпсона. 111. Вычисление определенного интеграла с переменным верхним пределом. 112. Графические способы. 113. Площади быстро колеблющихся кривых. § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 115. Разбиение промежутка на части и образование различных сумм. 116. Интегрируемые функции. 117. Свойства интегрируемых функций. ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 118. Понятие о бесконечном ряде. 119. Основные свойства бесконечных рядов. 120. Ряды с положительными членами. Признаки сходимости. 121. Признаки Коши и Даламбера.  122. Интегральный признак сходимости Коши. 123. Знакопеременные ряды. 124. Абсолютно сходящиеся ряды. 125. Общий признак сходимости. § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 126. Формула Тейлора. 127. Различные виды формулы Тейлора. 128. Ряды Тейлора и Маклорена. 129. Разложение exp(x). 130. Разложение sin x и cos x. 131. Бином Ньютона. 132. Разложение log(1+x). 133. Разложение arctg x. 134. Приближенные формулы. 135. Максимумы, минимумы и точки перегиба. 136. Раскрытие неопределенностей. § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 137. Свойства абсолютно сходящихся рядов. 138. Умножение абсолютно сходящихся рядов. 139. Признак Куммера. 140. Признак Гаусса. 141. Гипергеометрический ряд. 142. Двойные ряды. 143. Ряды с переменными членами. Равномерно сходящиеся ряды. 144. Равномерно сходящиеся последовательности функций. 145. Свойства равномерно сходящихся последовательностей. 146. Свойства равномерно сходящихся рядов.  147. Признаки равномерной сходимости. 148. Степенные ряды. Радиус сходимости. 149. Вторая теорема Абеля. 150. Дифференцирование и интегрирование степенного ряда. ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 152. О предельном переходе. 153. Частные производные и полный дифференциал первого порядка. 154. Однородные функции. 155. Частные производные высших порядков. 156. Дифференциалы высших порядков. 157. Неявные функции. 158. Пример. 159. Существование неявных функций. 160. Кривые в пространстве и поверхности. § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных. 162. Необходимые условия максимума и минимума функции. 163. Исследование максимума и минимума функции двух независимых переменных. 164. Примеры. 165. Дополнительные замечания о нахождении максимумов и минимумов функции.  166. Наибольшее и наименьшее значения функции. 167. Относительные максимумы и минимумы. 168. Дополнительные замечания. 169. Примеры. ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ 170. Комплексные числа. 171. Сложение и вычитание комплексных чисел. 172. Умножение комплексных чисел. 173. Деление комплексных чисел. 174. Возвышение в степень. 175. Извлечение корня. 176. Показательная функция. 177. Тригонометрические и гиперболические функции. 178. Цепная линия. 179. Логарифмирование. 180. Синусоидальные величины и векторные диаграммы. 181. Примеры. 182. Кривые в комплексной форме. 183. Представление гармонического колебания в комплексной форме. § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ 185. Разложение многочлена на множители. 186. Кратные корни. 187. Правило Горнера. 188. Общий наибольший делитель. 189. Вещественные многочлены. 190. Зависимость между корнями уравнения и его коэффициентами.  191. Уравнение третьей степени. 192. Решение кубического уравнения в тригонометрической форме. 193. Способ итерации. 194. Способ Ньютона. 195. Способ простого интерполирования. § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ 196. Разложение рациональной дроби на простейшие. 197. Интегрирование рациональной дроби. 198. Интеграл от выражений, содержащих радикалы. 199. Интегралы вида… 200. Интегралы вида… 201. Интегралы вида… |
Построение графика линейного уравнения по точкам
Сделать 6 минут чтения
Построение графика линейного уравнения по точкам
Существует несколько методов, которые можно использовать для построения графика линейного уравнения. Метод, который мы использовали для построения графика \(3x+2y=6\), называется построением точек или методом построения точек.
Пример. Как построить уравнение по точкам
Построить график уравнения \(y=2x+1\) по точкам.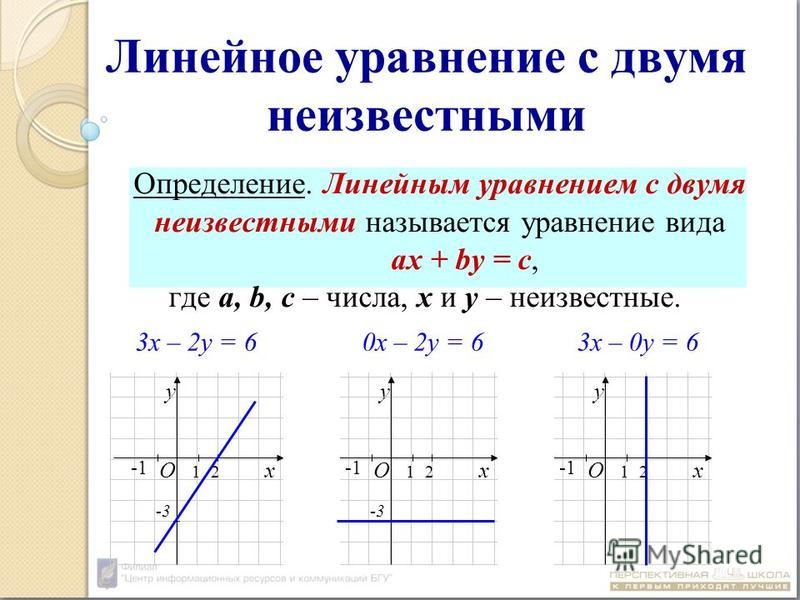
Решение
Шаги, которые необходимо предпринять для построения графика линейного уравнения с помощью точек, приведены ниже.
Построить график линейного уравнения по точкам.
- Найдите три точки, координаты которых являются решениями уравнения. Организуйте их в виде таблицы.
- Нанесите точки в прямоугольной системе координат. Убедитесь, что точки совпадают. Если их нет, внимательно проверьте свою работу.
- Проведите линию через три точки. Расширьте линию, чтобы заполнить сетку, и поставьте стрелки на обоих концах линии.
Это правда, что для определения линии требуется всего две точки, но использование трех точек является хорошей привычкой. Если вы нанесете только две точки, и одна из них неверна, вы все равно сможете нарисовать линию, но она не будет представлять решения уравнения. Это будет неправильная линия.
Если вы используете три точки, а одна неверная, точки не совпадут.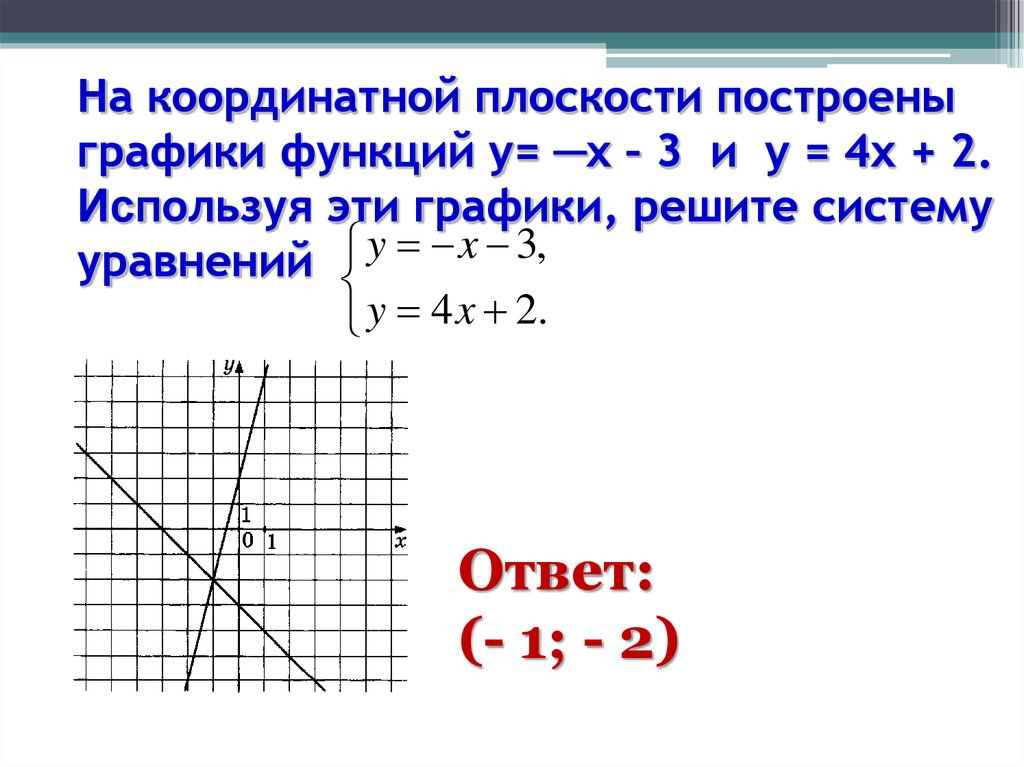
Это говорит о том, что что-то не так, и вам нужно проверить свою работу. Посмотрите на разницу между частью (a) и частью (b) на рисунке ниже.
Давайте сделаем еще один пример. На этот раз мы покажем последние два шага на одной сетке.
Пример
Нарисуйте уравнение \(y=-3x\).
Решение
Найдите три точки, являющиеся решениями уравнения. Здесь, опять же, проще выбрать значения для \(x\). Вы понимаете, почему?
Перечислим точки в таблице ниже.
| \(y=-3x\) | ||
| \(x\) | \(y\) | \(\left(x,y\right) \) |
| 0 | 0 | \(\влево(0,0\вправо)\) |
| 1 | \(-1,-3\) | \90 \справа)\) |
| \(-2\) | 6 | \(\слева(-2,6\справа)\) |
Нанесите точки, убедитесь, что они совпадают, и нарисуйте линию.
Когда уравнение включает дробь в качестве коэффициента при \(x\), мы все равно можем заменить \(x\) любыми числами. Но математика упрощается, если мы делаем «хороший» выбор значений \(x\). Таким образом, мы избежим дробных ответов, которые трудно точно изобразить в виде графика.
Пример
Нарисуйте уравнение \(y=\frac{1}{2}x+3\).
Решение
Найдите три точки, являющиеся решениями уравнения. Поскольку это уравнение имеет дробь \(\frac{1}{2}\) в качестве коэффициента \(x,\), мы будем тщательно выбирать значения \(x\). Мы будем использовать ноль в качестве одного варианта и числа, кратные 2, для других вариантов. Почему числа, кратные 2, являются хорошим выбором для значений \(x\)?
Точки показаны в таблице ниже.
Under the first column are the numbers 0, 2, and 4. Under the second column are the numbers 3, 4, and 5. Under the third column are the ordered pairs (0, 3), (2, 4), and (4, 5).»>9
\ (y \) \ (y \) \. \влево(х,у\вправо)\)
Нанесите точки, убедитесь, что они совпадают, и нарисуйте линию.
Пока что все уравнения, которые мы построили, имели \(y\), выраженные через \(x\). Теперь мы нарисуем уравнение с \(x\) и \(y\) на одной стороне. Давайте посмотрим, что происходит в уравнении \(2x+y=3\). Если \(y=0\), каково значение \(x\)?
Эта точка имеет дробную часть для координаты x , и, хотя мы можем изобразить эту точку на графике, трудно изобразить точные дроби. Помните, что в примере \(y=\frac{1}{2}x+3\) мы тщательно выбирали значения для \(x\), чтобы вообще не отображать дроби. Если мы решим уравнение \(2x+y=3\) относительно \(y\), будет легче найти три решения уравнения.
\(\begin{array}{ccc}\hfill 2x+y& =\hfill & 3\hfill \\ \hfill y& =\hfill & -2x+3\hfill \end{array}\)
Решения для \(x=0\), \(x=1\) и \(x=-1\) показаны в таблице ниже. График показан на рисунке ниже.
The first column header is x, the second is y and the third is (x, y). Under the first column are the numbers 0, 1, and negative 1. Under the second column are the numbers 3, 1, and 5. Under the third column are the ordered pairs (0, 3), (1, 1), and (negative 1, 5).»>Можете ли вы найти точку \(\left(\frac{3}{2},0\right)\) , который мы нашли, поставив \(y=0\) на строку?
Пример
Нарисуйте уравнение \(3x+y=-1\).
Решение
\(\begin{array}{cccccc}\text{Найдите три точки, являющиеся решениями уравнения.}\hfill & & & \hfill 3x+y& =\hfill & -1\hfill \\ \ text{Сначала решите уравнение для}\phantom{\rule{0.2em}{0ex}}y.\hfill & & & \hfill y& =\hfill & -3x-1\hfill \end{массив}\)
Пусть \(x\) будет 0, 1 и \(-1\), чтобы найти 3 точки. Упорядоченные пары показаны в таблице ниже. Нанесите точки, убедитесь, что они совпадают, и нарисуйте линию. См. рисунок ниже.
| \(3x+y=-1\) | ||
| \(x\) | \(y\) | \(\left(x,y\ справа)\) |
| 0 | \(-1\) | \(\слева(0,-1\справа)\) |
| 1 | \(-4\) | \(\левый(1,-4\правый)\) |
| \(-1\) | 2 | \(\левый(-1,2\правый) )\) |
Если вы можете выбрать любые три точки для построения линии, как вы узнаете, соответствует ли ваш график графику, показанному в ответах в книге? Если точки, в которых графики пересекают оси x и y , совпадают, графики совпадают!
Уравнение в приведенном выше примере было записано в стандартной форме, где \(x\) и \(y\) стоят на одной стороне.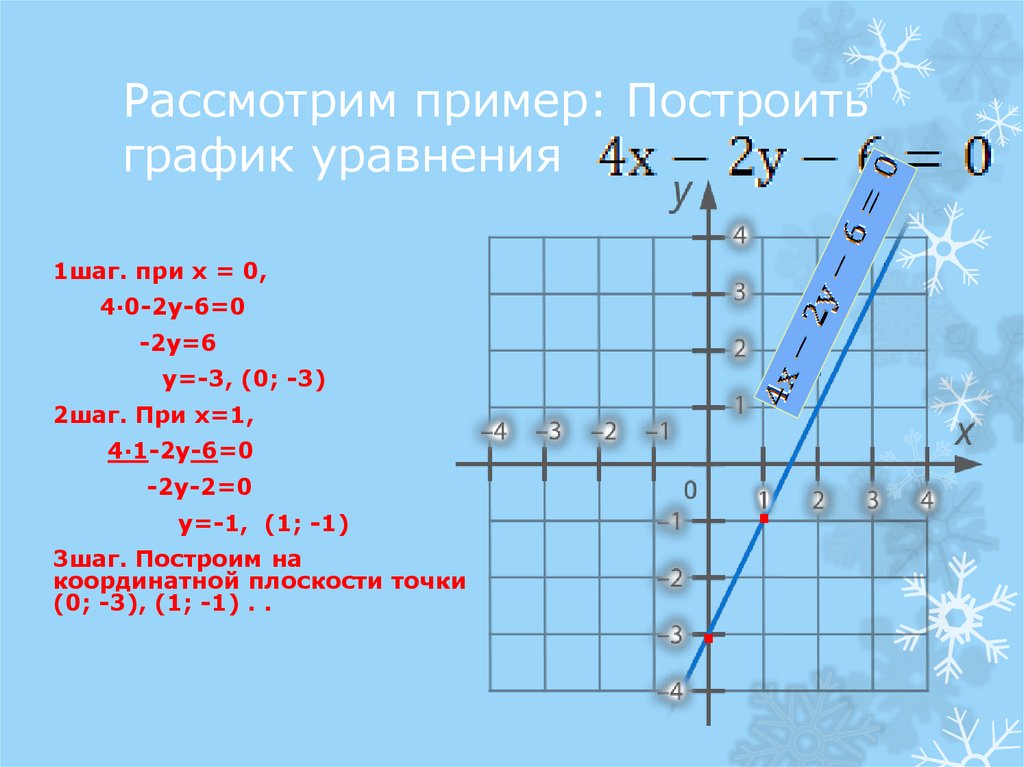
Мы решили это уравнение для \(y\) всего за один шаг. Но для других уравнений в стандартной форме решить относительно \(y\) не так просто, поэтому мы оставим их в стандартной форме. Мы все еще можем найти первую точку для построения, полагая \(x=0\) и находя \(y\). Мы можем построить вторую точку, полагая \(y=0\) и затем находя \(x\). Затем мы нанесем третью точку, используя другое значение для \(x\) или \(y\).
Пример
Нарисуйте уравнение \(2x-3y=6\).
Решение
\(\begin{array}{cccccc}\begin{array}{c}\text{Найдите три точки, являющиеся решениями}\hfill \\ \text{уравнения.}\hfill \end{ array}\hfill & & & \hfill 2x-3y& =\hfill & 6\hfill \\ \text{Сначала пусть}\phantom{\rule{0.2em}{0ex}}x=0.\hfill & & & \ hfill 2\left(0\right)-3y& =\hfill & 6\hfill \\ \text{Решить}\phantom{\rule{0.2em}{0ex}}y.\hfill & & & \hfill -3y& =\hfill & 6\hfill \\ & & & \hfill y& =\hfill & -2\hfill \\ \\ \\ \text{Теперь пусть}\phantom{\rule{0.2em}{0ex}}y= 0.\hfill & & & \hfill 2x-3\left(0\right)& =\hfill & 6\hfill \\ \text{Найти}\phantom{\rule{0.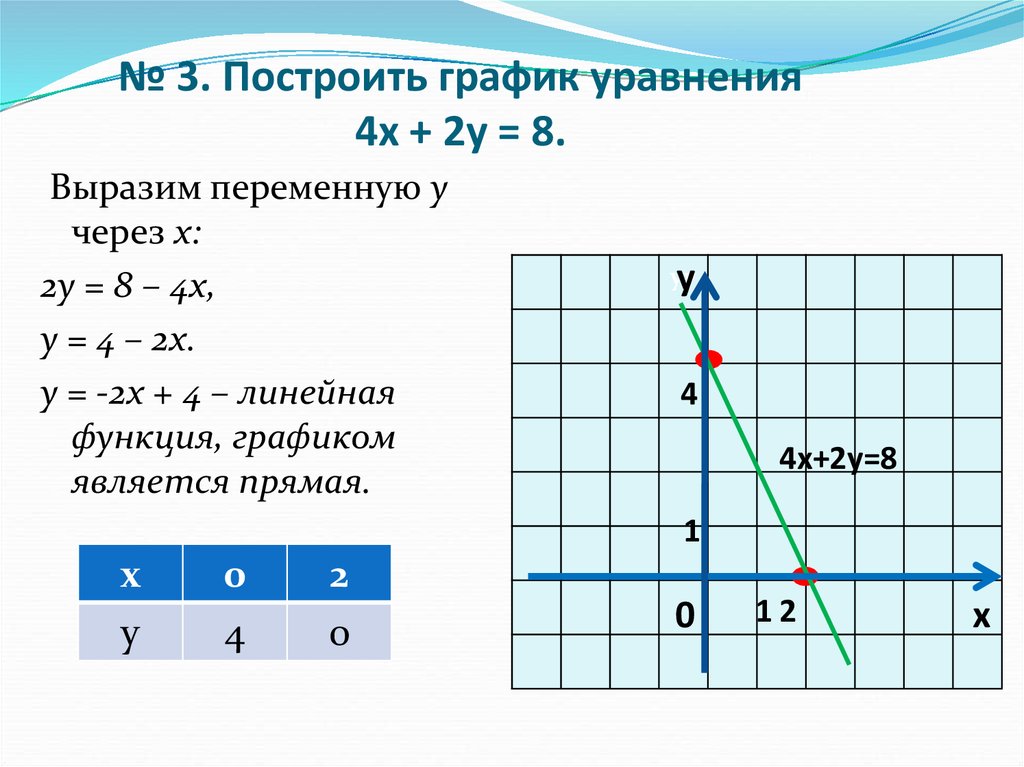
2em}{0ex}}x. \hfill & & & \hfill 2x& =\hfill & 6\hfill \\ & & & \hfill x& =\hfill & 3\hfill \\ \begin{array}{c}\text{Нам нужна третья точка. Помните , мы можем}\hfill \\ \text{выбрать любое значение для}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}\text{or}\phantom {\rule{0.2em}{0ex}}y.\phantom{\rule{0.2em}{0ex}}\text{Мы позволим}\phantom{\rule{0.2em}{0ex}}x=6 .\hfill \end{массив}\hfill & & & \hfill 2\le ft(6\right)-3y& =\hfill & 6\hfill \\ \text{Решить}\phantom{\rule{0.2em}{0ex}}y.\hfill & & & \hfill 12-3y& =\ hfill & 6\hfill \\ & & & \hfill -3y& =\hfill & -6\hfill \\ & & & \hfill y& =\hfill & 2\hfill \end{массив}\)
Мы перечисляем упорядоченные пары в таблице ниже. Нанесите точки, убедитесь, что они совпадают, и нарисуйте линию. См. рисунок ниже.
Under the first column are the numbers 0, 3, and 6. Under the second column are the numbers negative 2, 0, and 2. Under the third column are the ordered pairs (0, negative 2), (3, 0), and (6, 2).»>\(a_{b}\)
\(\sqrt{a}\)
\(\sqrt[b]{a}\)
\(\frac{a}{ б}\)
\(\cfrac{a}{b}\)
\(+\)
\(-\)
\(\times\)
\(\div\)
\(\pm\)
\(\cdot\)
\(\amalg\)
\(\ast\)
\(\barwedge\)
\(\bigcirc\)
\( \bigodot\)
\(\bigoplus\)
\(\bigotimes\)
\(\bigsqcup\)
\(\bigstar\)
\(\bigtriangledown\)
\(\bigtriangleup\)
\(\blacklozenge\)
\(\blacksquare\)
\(\blacktriangle\)
2 \(\
3) \(\bullet\)
\(\cap\)
\(\cup\)
\(\circ\)
\(\circledcirc\)
\(\dagger\)
\( \ddagger\)
\(\diamond\)
\(\dotplus\)
\(\lozenge\)
\(\mp\)
\(\ominus\)
\(\oplus \)
\(\oslash\)
\(\otimes\)
\(\setminus\)
\(\sqcap\)
\(\sqcup\)
\(\square\)
\(\star\)
\(\triangle\)
\(\triangledown\)
\(\triangleleft\)
\(\Cap\)
\(\Cup\)
\( \upplus\)
\(\vee\)
\(\veebar\)
\(\клин\)
\(\wr\)
\(\следовательно\)
\(\left ( a \right )\)
\(\left \| a \right \|\)
\(\влево [ a \вправо ]\)
\(\влево \{ a \вправо \}\)
\(\влево \lceil a \вправо \rceil\)
\(\влево \ lfloor a \right \rfloor\)
\(\left ( a \right )\)
\(\vert a \vert\)
\(\leftarrow\)
\(\leftharpoondown\)
\(\leftharpoonup\)
\(\leftrightarrow\)
\(\leftrightharpoons\)
\(\mapsto\)
\(\rightarrow\)
\(\rightharpoondown\)
\( \правый гарпунвверх\)
\(\rightleftharpoons\)
\(\to\)
\(\Leftarrow\)
\(\Leftrightarrow\)
\(\Rightarrow\)
\(\overset{a}{ \leftarrow}\)
\(\overset{a}{\rightarrow}\)
\(\приблизительно \)
\(\asymp\)
\(\cong \)
\(\dashv \)
\(\doteq \)
\(= \)
\(\equiv \)
\(\frown \)
\(\geq \)
\(\geqslant \)
\(\гг\)
\(\gt \)
\(| \)
\(\leq \)
\(\leqslant \)
\(\ll \)
\(\lt \)
\( \models\)
\(\neq \)
\(\ngeqslant \)
\(\ngtr \)
\(\nleqslant \)
\(\nless \)
\(\not \equiv \)
\(\overset{\underset{\mathrm{def}}{}}{=} \)
\(\parallel \)
\(\perp \)
\(\prec \)
\(\preceq \)
\(\сим\)
\(\simeq\)
\(\smile\)
\(\succ\)
\(\succeq\)
\(\vdash\)
\(\in\)
\ (\ni \)
\(\notin \)
\(\nsubseteq \)
\(\nsupseteq \)
\(\sqsubset \)
\(\sqsubseteq \)
\(\ sqsupset \)
\(\sqsupseteq \)
\(\subset \)
\(\subseteq \)
\(\subseteqq \)
\(\supset \)
\\(\supseteq )
\(\supseteqq \)
\(\emptyset\)
\(\mathbb{N}\)
\(\mathbb{Z}\)
\(\mathbb{Q}\)
\(\mathbb{R}\)
\(\mathbb{C}\)
\(\alpha\)
\(\beta\)
\(\gamma\)
\(\delta \)
\(\эпсилон\)
\(\дзета\)
\(\эта\)
\(\тета\)
\(\йота\)
\(\каппа\)
\(\lambda\)
\(\mu\)
\(\nu\)
\(\xi\)
\(\pi\)
\(\rho\)
\(\sigma\)
\(\tau\)
\(\upsilon\)
\(\phi\)
\(\chi\)
\(\psi\)
\(\omega\)
\(\Gamma\)
\(\Delta\)
\(\Theta\)
\( \Lambda\)
\(\Xi\)
\(\Pi\)
\(\Sigma\)
\(\Upsilon\)
\(\Phi\)
\(\Psi \)
\(\Омега\)
\((а)\)
\([а]\) 94(1/120)
Итак, мое уравнение, которое я хочу построить, выглядит следующим образом:
sol = f[x] /.NDsolve[{f[x] + 2f'[x]/x +f''[x] == 0, f[0.1] == ряд[0.1], f'[0.1] == ряд[0.1]}, е, {х, 0,1, 4}]
NDsolve[{f[x] + 2f'[x]/x +f''[x] == 0, f[0.1] == ряд[0.1], f'[0.1] == ряд[0.1]}, е, {х, 0,1, 4}]
Когда я делаю:
Plot[sol, {x, 0.1, 4}]
У меня просто пустая ось и нет графика, поэтому я действительно не знаю, почему это не работает и как это исправить. Есть идеи?
- построение графиков
- дифференциальные уравнения
- разложение в ряд
$\endgroup$
1
$\begingroup$
Ваше упрощенное уравнение можно решить аналитически:
sol =
DРешить[
{f''[x] + 2 f'[x]/x + f[x] == 0,
f[1/10] == серия[1/10],
f'[1/10] == серия[1/10]
},
ф, х
]
Использование расширения вашей серии вводит параметр x0 . Поскольку вы не указываете для него значения, я решил показать результаты для $x_0=1,2,3$ ниже. Обратите также внимание на то, что числовые значения содержат небольшие мнимые компоненты, возникающие из-за числовых неточностей; вы можете избавиться от тех, у кого Чоп .