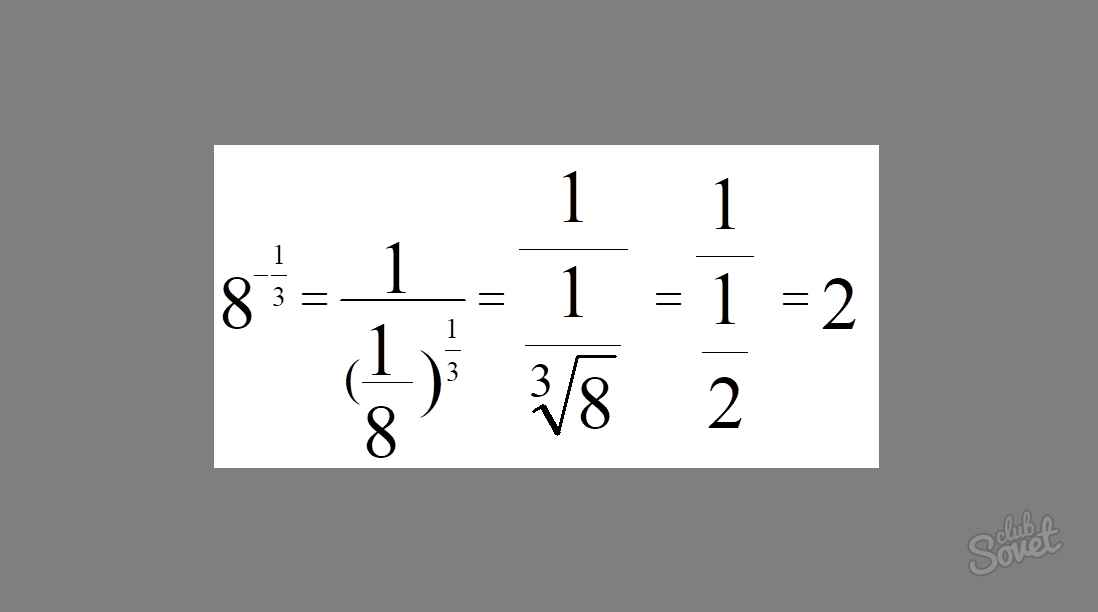Как умножать на отрицательную степень: Степень с отрицательным показателем — урок. Алгебра, 8 класс.

Как убрать отрицательную степень?

Как убрать отрицательную степень?

Чтобы возвести число в отрицательную степень нужно:

1. «перевернуть» число. Записать его в виде дроби с единицой наверху (в числителе) и с исходным числом в степени внизу;
2. заменить отрицательную степень на положительную;
3. возвести число в положительную степень.

Что значит возвести в отрицательную степень?

Определение. Если n — целое число, то речь идет о степени с целым отрицательным показателем и равенство верно для любого a, отличного от нуля (т. е. … Другими словами, чтобы возвести дробь в отрицательную степень, надо эту дробь «перевернуть»(числитель и знаменатель поменять местами) и изменить знак в показателе степени.

Что значит в минус первой степени?

Число в минус первой степени и данное число являются взаимно обратными числами. …

Что значит 2 в минус первой степени?

К примеру, 4 в минус 2 степени — это 1/42, 2 в минус 3 степени — это 1/23, 3 в минус 1 степени — это 1/3, 10 в минус первой степени — это 1/10 (0,1). 2 степени.

Сколько будет 10 в минус шестой степени?

10 в 6 степени = 1000000 10 в минус 9 степени = 0, 6 * 10 в 18 степени = 6 и ещё 18 нулей.

Что означает 10 в минус 3 степени?

Нет, 0001. 10 в 3 степени — 1000, а в минус 3 степени. Ваш ответ, это одна сотая = минус 2 степени..

Сколько будет 10 в минус 11 степени?

10 в 11 = 000, 10 в минус 11= 0,

Сколько будет 10 в 8 степени?

10 в 8 степени Решение: Возведение в степень это операция перемножения числа на само себя заданное количество раз. Десять в восьмой степени равно

Сколько будет 10 в минус 12 степени?

Приставки для дольных единиц

Десятичный множитель	Приставка	Обозначение
	русская	русское
10−9	нано	н
10−12	пико	п
10−15	фемто	ф

Сколько будет 10 в 12 степени?

Именные названия степеней тысячи

Название		Значение
Русское	Латинское	Короткая шкала
триллион (трлн)	trillion	1012
триллиард	trilliard	—
квадриллион	quadrillion	1015

Сколько будет два в седьмой степени?

2 в 7 степени Решение: Возведение в степень это операция перемножения числа на само себя заданное количество раз. Два в седьмой степени равно 128.

Как извлечь корень из числа в степени?

Теорема 1. Чтобы извлечь корень из степени положительного числа, показатель которой делится нацело на показатель корня, достаточно показатель подкоренного выражения разделить на показатель корня, оставив основание степени прежним. Действительно, Если п — нечетное число, то формула (2) верна и для а

Как находить корень из числа?

Как найти квадратный корень из десятичной дроби

1. забыть про запятую в исходной десятичной дроби и представить её в виде целого числа;
2. вычислить для целого числа квадратный корень;
3. полученное целое число заменить на десятичную дробь (поставить запятую исходя из правила умножения десятичных дробей).

Какие значения принимает арифметический корень четной степени?

Как мы знаем, корень чётной степени имеет два значения: положительное и отрицательное. … Арифметическим корнем n–й степени из неотрицательного числа a называется неотрицательное число, n–я степень которого равна a .

Как умножать корни с разными показателями?

Чтобы умножить корни с разными показателями, предварительно их нужно привести к общему показателю, а затем умножить как корни с одинаковыми показателями. Пусть, например, надо умножить n√a на m√b . Используя теорему 3 § 80, можно написать: √a = nm√a m ; m√b = mn√bn .

Как умножить корни с разными Подкоренными выражениями?

Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом: Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.

Можно ли сокращать корни в дроби?

Умножьте числитель и знаменатель на квадратный корень, от которого необходимо избавиться. Если в числителе и знаменателе присутствуют числа, которые можно и нужно сократить. Упрощайте такие выражения, как и любую дробь.

Можно ли умножать корни друг на друга?

Метод умножения корней без множителей Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т. е. со степенью 2, и его можно умножать на другие корни со степенью 2.

Как корень умножить на корень?

Извлеките квадратный корень из полного квадрата, а результат умножьте на множитель, стоящий перед знаком корня. Другой множитель оставьте под знаком корня. Так вы упростите подкоренное выражение.

Как целое число умножить на корень?

Умножьте множители. Множитель — число , стоящее перед знаком корня . Умножьте числа под знаком корня . После того как вы перемножили множители, перемножьте числа под знаком корня .

Как число умножить на дробь?

Итак, чтобы умножить натуральное число на дробь, можно числитель дроби умножить на это натуральное число, а знаменатель оставить тот же. Например: Вычислим произведение четырёх пятых и трёх. Умножение можно заменить сложением, то есть три раза сложить дробь четыре пятых.

Как складывать и вычитать корни?

У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня….( 45 ) + 4 5 :

1. Упрощаем √(45) . …
2. Выносим 3 из-под корня (√9=3):√45=3√5 ( 9 = 3 ) : 45 = 3 5 ;
3. Складываем множители у корней: 3√5+4√5=7√5 3 5 + 4 5 = 7 5 .

Как умножать числа в корне?

Умножение корней с множителями Умножьте множители. Множитель — число, стоящее перед знаком корня. Если его нет, то множитель равен 1.

Каковы примеры правила отрицательного экспонента? – Обзоры Вики

Число, возведенное в отрицательную степень, равно единице над числом, возведенным в положительную противоположную степень. 2.

Отсюда, как вы решаете для отрицательного показателя степени? Как решать отрицательные степени. Переверните основание и экспоненту в обратную, затем решить знаменатель. Разделите числитель на знаменатель, чтобы найти последний десятичный знак.

Дополнительно Что означает отрицательный показатель степени? Как объясняется на странице, отрицательная экспонента просто означает «мультипликативная инверсия основания, возведенная в положительную противоположность степени».

Что означают отрицательные показатели объясните примерами и правилом? Отрицательный показатель просто означает что основание находится не на той стороне дробной линии, поэтому вам нужно перевернуть основание на другую сторону. Например, «x^–2»(Произносится как« ecks to the minus two ») просто означает« x², но внизу, как в разрыве 1 x 2 {1} {x ^ 2} x21 “.

Что такое 10 в отрицательной степени?

Что означает отрицательный показатель степени в научной записи? Отрицательная экспонента показывает, что десятичная точка сдвинута на указанное количество разрядов влево. В экспоненциальной системе обозначений числовой термин обозначает количество значащих цифр в числе. … Другой пример: 0.00053 = 5.3 x 10^–4 Это число состоит из 2 значащих цифр.

Что означает отрицательная мощность в физике? Мощность — величина со знаком; отрицательная сила просто представляет мощность, текущая в направлении, противоположном положительной мощности. … Это увеличивает потенциальную энергию электрических зарядов, поэтому электрическая энергия перетекает из компонента в цепь.

Существует ли такая вещь, как отрицательный показатель?

Положительная экспонента говорит нам, сколько раз умножать базовое число, а отрицательная экспонента говорит нам, сколько раз нужно разделить базовое число. Мы можем переписать отрицательные показатели, такие как x⁻ⁿ, как 1 / xⁿ. Например, 2⁻⁴ = 1 / (2⁴) = 1/16.

Также Что такое 10 отрицательная 2-я степень? Ответ: число 10 в степени минус 2 равно 0.01.

Сколько 5 в отрицательной степени 2?

Ответ: 5 в степени отрицательного 2 равно 0.04.

Сколько 10 в отрицательной степени 7? Ответ: 10 в степени отрицательной 7 равно 0.0000001.

Как записать отрицательный показатель в стандартной форме?

Чтобы изменить число, записанное в экспоненциальной системе счисления с отрицательной степенью 10, на стандартную форму, переместите десятичную точку влево. Показатель степени показывает количество мест, на которое следует переместить десятичную запятую. Не забывайте при необходимости добавлять нули в качестве заполнителей.

Как сделать отрицательную экспоненту на научном калькуляторе?

Могут ли показатели быть отрицательными? Отрицательный показатель определяется как мультипликативная инверсия основания, возведенная в степень, противоположную данной степени. Проще говоря, мы записываем обратную величину числа, а затем решаем ее как положительные показатели. Например, (2/3)^–2 можно записать как (3/2)².

Отрицательная энергия поглощается или доставляется?

Суммарная мощность, подаваемая в цепь, равна полной потребляемой мощности. Учитывая, что передаваемая мощность является отрицательное количество а потребляемая мощность является положительной величиной, закон сохранения энергии подразумевает, что суммарная мощность всех элементов в цепи равна нулю.

Что произойдет, если мощность отрицательна? Отрицательный показатель помогает чтобы показать, что основание находится на стороне знаменателя дробной линии. 3. Не так уж плохо, верно?

Может ли у многочлена быть отрицательный показатель?

Многочлен не может иметь переменную в знаменателе или отрицательный показатель степени., так как мономы должны иметь только целые показатели степени. Полиномы обычно записывают так, чтобы степени одной переменной располагались в порядке убывания.

Чему равно 10 с показателем степени минус 2? Ответ: число 10 в степени минус 2 равно 0.01.

Может ли мощность ватт быть отрицательной?

Ватт — это значение «перемещения» (или, точнее, мощности), производимого всеми этими прыжками, поэтому оно также становится относительной величиной. Так да, у вас могут быть отрицательные ватты, хотя это используется меньше.

Чему равно 10 в отрицательной степени числа 3? Ответ: 10 в степени минус 3 равно 0.001.

Сколько 2 в отрицательной степени 2?

Что означает число 10 в отрицательной 5-й степени? 10^–5 = = 0. 00001.

Какая дробь равна 6 в степени отрицательной 2?

Что такое 5 в отрицательной степени?

Отрицательные показатели означают, что вместо умножения что многие из основных чисел вместе, вы делите. Например, 52=25, но 5−2=152=125. Вы можете использовать свойство произведения полномочий, чтобы показать это. Мы знаем, что 52=25, и мы знаем, что 50=1.

Объяснение урока: Упрощение мономов: отрицательные показатели

В этом объяснении мы узнаем, как упрощать одночлены с отрицательными показателями.

Начнем с того, что вспомним, что мы знаем о положительных показателях. Для выражения 2, это означает 2×2×2×2.

Здесь показатель степени 4 сообщает нам, сколько раз 2 умножается на сам. Равным образом, если мы рассмотрим выражение 𝑥, если 𝑛 является положительным целым числом, 𝑛 говорит нам, сколько раз 𝑥 умножается сам на себя. Что тогда произойдет, если у нас будет отрицательный показатель степени, такой как 2?

Как умножить число само на себя -3 раза? Это, конечно, не разумный способ введение отрицательных показателей. Начнем с введения шаблона уменьшающих степеней числа 2: 2=16,2=8,2=4,2=2,2=1.

Глядя на этот шаблон, похоже, что каждое уменьшение показателя степени 2 на единицу приводит к число в правой части делится на 2. Если бы мы продолжили этот шаблон, было бы разумно предположить, что показатель степени −1 (т. е. 2) будет равно 1÷2, т.е. 12. Точно так же показатель степени −2 будет 12÷2, что равно 14. Мы могли бы продолжить список следующим образом: 2=16,2=8,2=4,2=2,2=1,2=12,2=14,2=18,2=116. 

Верно ли наше предположение? Давайте посмотрим, можем ли мы обосновать это, используя правило отношения для экспоненты. Напомним, что 𝑥𝑥=𝑥.

Если мы рассмотрим выражение 22,

, используя правило частных показателей степени, мы можем упростить его до 2=2.



Точно так же мы можем переписать выражение как 2×2×22×2×2×2×2×2

, расширив показатели степени. Затем мы можем разделить верх и низ на 2 три раза, что дает нам 2×2×22×2×2×2×2×2.

Это упрощается до 12,

, что может быть оценено как 18.

Если мы вернемся к нашему списку показателей степени 2, мы увидим, что наше предположение, по крайней мере значение 2 действительно верно. Мы могли бы использовать очень похожий подход чтобы показать, что весь наш список степеней двойки был правильным. Один момент, на который следует обратить внимание в приведенном выше конструкция — это то, что мы показали 2=12.

Это можно обобщить для любого ненулевого 𝑥, возведённого в минус экспонента.

Ключевая информация: Отрицательные показатели степени

Для любого ненулевого 𝑥 мы имеем 𝑥=1𝑥.

Это, по сути, частный случай частного правила показателей. Напомним еще раз, что 𝑥𝑥=𝑥.



В приведенном выше обобщении 𝑎=0 и 𝑏=𝑘. У нас есть, следовательно, что 1𝑥.

Прежде чем рассматривать несколько примеров, сформулируем все часто используемые правила показателей в сочетании с тем, что мы только что узнали об отрицательных показателях. У нас есть продукт правило, частное правило, правило мощности и свойство нулевого показателя.

Ключевая информация: Правила экспоненты

1. Правило произведения экспонент: 𝑥×𝑥=𝑥
2. Частное правило экспонент: 𝑥)=𝑥
3. Нулевые показатели: 𝑥=1

Пример 1. Вычисление числа, возведенного в отрицательную степень

Вычислить 14.

Ответ

Напомним, что для любого отличного от нуля 𝑥 имеем 𝑥=1𝑥.

Используя это, мы можем переписать выражение так, чтобы оно было 14=114.

Теперь мы можем вычислить 14, что равно 196, чтобы найти что исходное выражение равно 1196.

Пример 2.

Вычисление выражений, содержащих отрицательные показатели

Вычислить 22.

Ответ

Напомним, что для любого отличного от нуля 𝑥 мы имеем 𝑥𝑥=𝑥,

и что 𝑥=1𝑥.

Используя наше правило возведения в степень, мы можем записать выражение степени следует: 22=2=2.

Используя правило отрицательного показателя степени, мы можем переписать это как 2=12.

Теперь мы можем вычислить выражение. Используя тот факт, что 2=64, мы имеем окончательное решение 12=164.

Пример 3. Распознавание эквивалентных выражений, содержащих отрицательные показатели

Какое из следующих утверждений эквивалентно 3?

1. 27
2. −9
3. −19
4. 127
5. 19

Ответ

Здесь у нас есть число, возведенное в степень −3. Распространенная ошибка будет быть оценить это до -9, который является произведением двух чисел. Этот, однако не правильно. Нам нужно вспомнить правило отрицательного показателя степени: для любой ненулевой 𝑥 мы имеем 𝑥=1𝑥.

Мы можем использовать это, чтобы переписать наше выражение: 3=13.

Это, однако, не то же самое, что любой из вариантов. Нам нужно оценить знаменатель выражения: 13=127.

Наш ответ, следовательно, D.

Все правила, которые мы использовали для предыдущих примеров, могут быть применены к обоим числовые и алгебраические выражения. Теперь перейдем к рассмотрению некоторых алгебраических Примеры.

Пример 4. Вычисление алгебраических выражений, содержащих отрицательные показатели

Упростить 5𝑥6𝑥.

Ответ

Чтобы ответить на этот вопрос, давайте сначала вспомним правило степени степени: (𝑥)=𝑥.

Если мы распределим мощность по каждому члену и применим правило мощности степени, мы получаем 5𝑥6𝑥.××

Упрощая каждый член, мы получаем 25𝑥36𝑥. 

2×5 два члена:

Затем мы можем изменить порядок двух членов: 25×5 36×𝑥×𝑥.

Теперь вы можете видеть, что мы можем перемножить два числа и использовать правило произведения показателей для упрощения членов 𝑥. Это дает нам 900𝑥.

Упрощая, получаем, что наш ответ 900𝑥.

Это наш ответ. Однако стоит отметить, что мы можем представить это в другом форма, которая была бы одинаково действительна. Если вспомнить правило отрицательных показателей, которое утверждает, что для любого ненулевого 𝑥, 𝑥=1𝑥,

мы можем переписать 𝑥 как 1𝑥. Этот означает, что наше решение может быть записано как 900×1𝑥,

, что совпадает с 900𝑥.

. Мы закончим рассмотрением последнего примера, в котором сочетаются правила с несколькими экспонентами.

Пример 5. Объединение правил экспоненты для упрощения выражений, содержащих отрицательные экспоненты

Ответ

Начнем с того, что вспомним правила произведения и степени показателей:

• Правило произведения показателей степени: 𝑥×𝑥=𝑥
• Правило степени степени степени: (𝑥)=𝑥

Сначала используя правило степени, мы можем переписать верхнюю часть рациональное выражение следующим образом:

Упрощая, получаем экспоненты, мы перепишем верх и низ нашего выражение, которое дает нам : 𝑥÷𝑥=𝑥.



Используя это, мы можем переписать выражение следующим образом: 𝑥.()

Будьте очень осторожны с отрицаниями и помните, что вычитание отрицательного числа — это то же самое добавляя, мы можем упростить выражение, чтобы дать нам 𝑥.

Это наш ответ, но стоит отметить, что его можно переписать, используя правило для отрицательные показатели. Помните, что для любого ненулевого 𝑥 мы имеем это 𝑥=1𝑥.

Это означает, что мы можем переписать наш ответ как 1𝑥.

Ключевые моменты

• Отрицательные показатели степени определяются следующим образом: для любого ненулевого 𝑥 мы имеем, что 𝑥=1𝑥.
• При работе с отрицательными показателями нам может понадобиться использовать следующие правила:
  • Правило произведения показателей: 𝑥×𝑥=𝑥.
  • Частное правило показателей: =𝑥.
  • Степенное правило показателей: (𝑥)=𝑥.
  • Нулевые показатели: для любого ненулевого 𝑥, 𝑥=1. 

Начальный учебник по алгебре 29

Beginning Algebra
Tutorial 29: Negative Exponents and Scientific Notation

---

WTAMU > Virtual Math Lab > Beginning Algebra

 

Learning Objectives

---

После завершения этого руководства вы сможете:

1. Упрощение экспоненциальных выражений с отрицательными показателями.
2. Запишите число в экспоненциальном представлении.
3. Запишите число в стандартной записи, без степеней.

Введение

---

Этот учебник начинается с учебника 26: Показатели остановлены. Это завершает правила показатели с отрицательными показателями. Также мы пройдемся по научным обозначение. Нравиться так это или нет, но лучший способ овладеть этими показателями — это проработать экспонента проблемы. Так что, я думаю, нам лучше перейти к этому.

 

 

Учебник

---

Отрицательные показатели степени
   или 

Будьте осторожны с негативом экспоненты. искушение состоит в том, чтобы отрицать основу, что было бы неправильно делать. С показателями еще один способ написать умножение и отрицание в степени, чтобы писать это как положительная экспонента, мы делаем мультипликативную обратную, которая должна возьмем обратное основание.

Пример 1:   Упростить .

*Переписать с поз. эксп. к принимая рецепт. базы

*Используйте по умолчанию. экспонентов оценить

Пример 2: Упрощение.

*Переписать с поз. эксп. к принимая рецепт. базы

*Используйте по умолчанию. экспонентов оценить

Упрощение экспоненты Выражение

При упрощении экспоненциального выражения так и напиши каждое основание записывается один раз с одним ПОЛОЖИТЕЛЬНЫМ показателем .

Другими словами, напишите это в наиболее сжатой форме, которую вы может убедиться что все ваши показатели положительны.

Много раз вам приходится использовать более одного правила получить работу сделанный. Пока вы правильно используете правило, вы должны будь умницей.

Обзор правил экспонента

За исключением правила отрицательного показателя степени, примеры следующее правила можно найти в Уроке 26: Экспоненты .

Правило продукта: 

Степенное правило для экспонент: 

Power of a Product: 

Power of a Quotient: 

Quotient Rule for Exponents: 

Zero Exponent: 
Negative Exponent: 

Пример 3:    Упрощение. Напишите ответ с положительный экспоненты.

*Когда мульт. как основания вы добавляете свои показатели

*Переписать с поз. эксп. взяв рецип. базы

Пример 4:   Упрощение. Используйте положительные показатели, чтобы писать ответ.

*Поднять каждое основание до -3
*Множ. ваши показатели

*Переписать с поз. эксп. взяв рецип. основания

 

Пример 5:   Упрощение.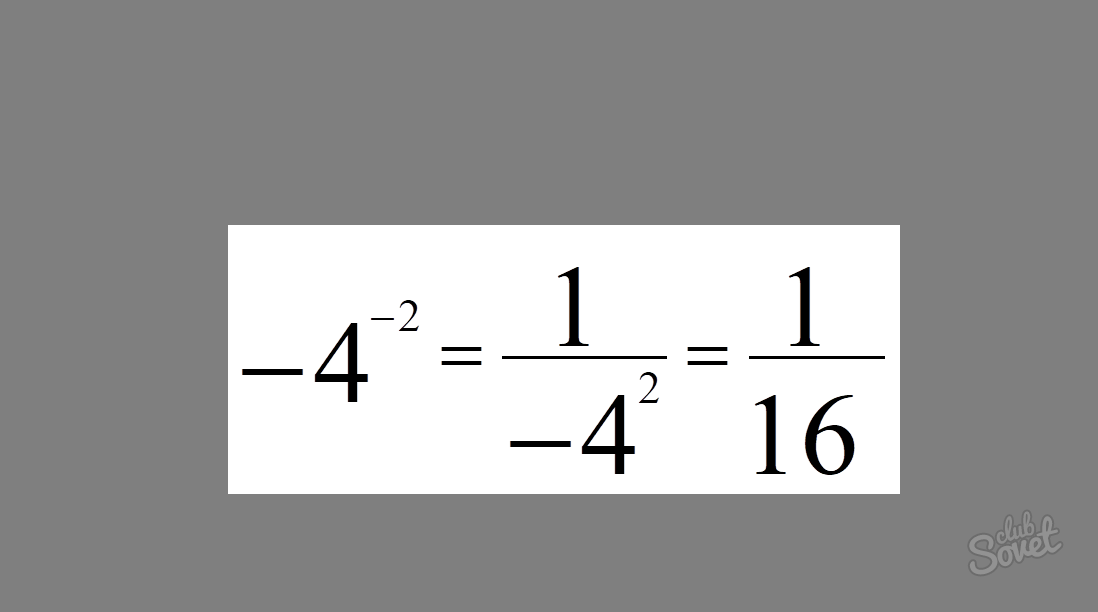 Используйте положительные показатели, чтобы писать ответ.

*Поднять каждое основание до -1
*Multi. ваши показатели

*Переписать с поз. эксп. взяв рецип. основания

 

Пример 6:    Упрощение. Напишите ответ с положительный экспоненты.

*Когда мульт. как основания вы добавляете свои показатели

*Когда разд. как основания, вы вычитаете свои показатели

*Переписать с поз. эксп. взяв рецип. базы

Будьте осторожны при вводе последней строки. Обратите внимание, что ты не видишь показатель степени, записанный цифрой 5. Это означает, что экспонента на 5 понимается как 1. Поскольку у него нет отрицательный показатель степени, мы НЕ берем обратное число 5. Единственное основание, которое имеет отрицательный показатель a , поэтому a — единственная база, для которой мы берем обратную.

Научное обозначение

Положительное число записывается в научная нотация если оно записано в виде:

где 1 < a < 10 и р есть целая степень числа 10.

Написание числа в научном Обозначение

Шаг 1. Переместите десятичную точку так что у вас есть число от 1 до 10.

Другими словами, вы поставите десятичную дробь после первый не нулевое число.

Шаг 2:   Подсчитайте число десятичных разрядов перенесено на Шаг 1.

Если десятичная точка была смещена влево, счетчик положительный.

Если десятичная точка сдвинута вправо, счет отрицательный.

Шаг 3.    Напишите как произведение числа (найдено на шаге 1) и 10 в степени счета (найдено на Шаг 2).

Пример 7:    Напишите число научным обозначение: 483 000 000.

Шаг 1. Переместить десятичная точка чтобы у вас было число от 1 до 10.

*Десятичная точка стоит в конце номер

*Переместите десятичную дробь, чтобы создать число между 1 и 10

Шаг 2:   Подсчет номер десятичных разрядов, перемещенных на шаге 1.

Сколько знаков после запятой мы переместили?
Мы начали с конца числа 483000000 и переместили его между 4 и 8. Это выглядит как ход на 8 мест.

В каком направлении он двигался?
Похоже, мы переместили его влево.

Итак, наш счет +8.

Шаг 3:   Напишите как продукт числа (найденного на шаге 1) и 10, возведенных в числовую степень (найдено на шаге 2).

Обратите внимание, что число, с которого мы начали, больше. чем тот мы умножаем на в научной нотации. Когда это в случае мы получим положительный показатель степени

Пример 8:    Напишите число научным обозначение: . 00054.

Шаг 1. Переместить десятичная точка чтобы у вас было число от 1 до 10.

*Десятичная запятая стоит в начале номер

*Переместите десятичную дробь, чтобы создать число между 1 и 10

Шаг 2:   Подсчет номер десятичных разрядов, перемещенных на шаге 1.

Сколько знаков после запятой мы переместили?
Мы начали с начала числа .00054, переместив его между 5 и 4. Это выглядит как ход на 4 позиции.

В каком направлении он двигался?
Похоже, мы сдвинули его вправо.

Итак, наш счет — 4.

Шаг 3:   Напишите как продукт числа (найденного на шаге 1) и 10, возведенных в числовую степень (найдено на шаге 2).

Обратите внимание, что число, с которого мы начали, меньше. чем тот мы умножаем на в научной нотации. Когда это в случае мы получим отрицательную экспоненту.

Напишите научный номер в Стандартная форма

По сути, вы просто умножаете первое число на сила 10.

Всякий раз, когда вы умножаете на степень 10, по сути что ты делаешь перемещает ваш десятичный разряд.

Если степень числа 10 положительна, вы перемещаете десятичную дробь место, что много единиц вправо.

Если степень числа 10 отрицательна, вы перемещаете десятичную дробь. место, что много единицы влево.

Убедитесь, что вы добавили все необходимые нули

Пример 9:  Запишите число в стандартной записи, без экспоненты.

*Переместить десятичную цифру 6 вправо

Пример 10:  Запишите число в стандартной записи, без экспоненты.

*Переместить десятичную цифру 5 влево

 

Практические задачи

---

Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти виды проблем. Математика работает так же, как что-либо иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться это. Даже лучшие спортсмены и музыканты получали помощь на этом пути и много практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.

Чтобы получить максимальную отдачу от этого, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответ/обсуждение для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.

 

Практика Задачи 1a — 1b: Упростите, используйте положительные показатели, чтобы напишите каждый ответ.

 

1а.
(ответ/обсуждение к 1а)

1б.
(ответ/обсуждение к 1б)

 

Практика Задача 2а: Запишите число научным обозначение.

 

2а. .00000146
(ответ/обсуждение к 2а)

 

Практика Задача 3а: Запишите число в стандартном обозначение, без показателей.

 

3а.
(ответ/обсуждение к 3а)

 

 

Нужна дополнительная помощь по этим темам?

---

Следующие веб-страницы что может помочь вы в темах, которые были затронуты на этой странице: 

Эта веб-страница помогает с правилом отношения для показателей степени.