Умножение вектора на число. Применение векторов к решению задач 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема 25.
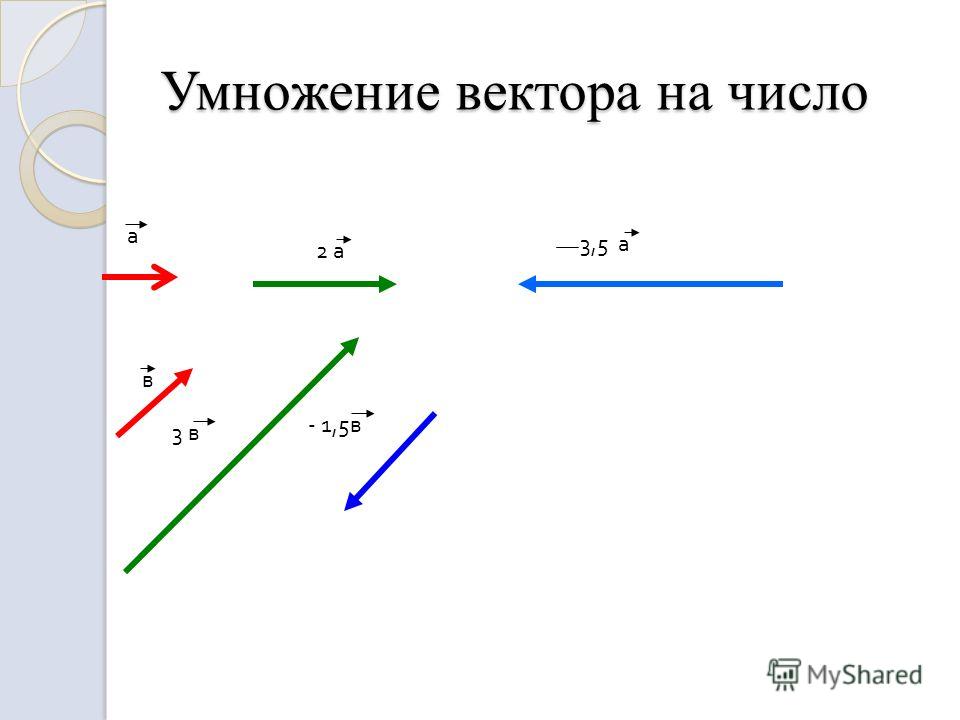
Умножение вектора на число.
На прошлом занятии мы научились складывать и вычитать векторы. Сегодня введем еще одно действие – умножение вектора на число.
Представим себе, что один автомобиль движется прямолинейно с постоянной скоростью, второй автомобиль движется в том же направлении со скоростью, вдвое большей, а третий автомобиль движется им навстречу, т.е. в противоположном направлении, и величина его скорости такая же, как у второго автомобиля. Если мы изобразим скорость первого автомобиля вектором v⃗, то естественно изобразить скорость второго автомобиля вектором, у которого направление вектора такое же, как у вектора v⃗, а длина в два раза больше, и обозначить этот вектор 2v⃗. Скорость третьего автомобиля изобразится вектором, противоположным вектору 2v⃗, то есть вектором -2v⃗. Естественно считать, что вектор 2v⃗ получается умножением вектора v⃗ на число 2, а вектор -2v⃗ получается умножением вектора v⃗ на число -2. Этот пример подсказывает, каким образом следует ввести умножение вектора на число.
Естественно считать, что вектор 2v⃗ получается умножением вектора v⃗ на число 2, а вектор -2v⃗ получается умножением вектора v⃗ на число -2. Этот пример подсказывает, каким образом следует ввести умножение вектора на число.
Произведением ненулевого вектора a⃗ на число k называется такой вектор b⃗, длина которого равна k⋅a⃗, причем векторы a⃗ и b⃗ сонаправлены при k≥0 и противоположно направлены при k<0.
Произведением нулевого вектора на любое число считается нулевой вектор.
Произведение вектора a⃗ на число k обозначается так: ka⃗.
Из определения произведения вектора на число непосредственно следует, что
- произведение любого вектора на число ноль есть нулевой вектор;
- для любого числа k и любого вектора a⃗ векторы a⃗ и ka⃗ коллинеарны.
Умножение вектора на число обладает следующими основными свойствами:
Для любых чисел k, l и любых векторов a⃗, b⃗ справедливы равенства:
10. (kl)a⃗=k(la⃗) (сочетательный закон).
(kl)a⃗=k(la⃗) (сочетательный закон).
20. (k+l)a⃗=ka⃗+la⃗ (первый распределительный закон).
30. k(a⃗+b⃗)=ka⃗+kb⃗ (второй распределительный закон).
Замечание
Рассмотренные нами свойства действий над векторами позволяют в выражениях, содержащий суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например, выражение
p⃗=2(a⃗ –;b⃗)+(c⃗+a⃗)–3(b⃗–c⃗+a⃗)
можно преобразовать так:
p⃗=2a ⃗–2b ⃗+c ⃗+a ⃗–3b ⃗+3c ⃗–3a ⃗=-5b ⃗+4c ⃗
Векторы могут использоваться для решения геометрических задач и доказательства теорем.
Рассмотрим задачу.
Точка С — середина отрезка AB, а O — произвольная точка плоскости. Доказать, что OC⃗=12OA⃗+OB⃗
По правилу треугольника
OC⃗=OA⃗+АС⃗, с другой стороны
OC⃗=OB⃗+BC⃗.
Складывая эти равенства, получим:
2OC⃗=OA⃗+OB⃗+AC⃗+BC⃗.
Так как точка C — середина отрезка AB, то AC⃗ + BC⃗ = 0⃗.
Таким образом, 2OC⃗=OA⃗+OB⃗, значит
OC⃗=12OA⃗+OB⃗.
ч.т.д.
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство
Пусть MN — средняя линия трапеции ABCD.
Докажем, что
MN//AD и MN=AD+BC2.
По правилу многоугольника
MN⃗=MB⃗+BC⃗+CN⃗ и
MN⃗=MA⃗+AD⃗+DN⃗. Сложим эти равенства и получим:
2MN⃗=(MB⃗+MA⃗)+(BC⃗+AD⃗)+(CN⃗+DN⃗).
Но M и N— середины сторон AB и CD, поэтому
MB⃗+MA⃗=0⃗ и CN⃗+DN⃗=0⃗.
Следовательно, 2MN⃗=AD⃗+BC⃗, откуда
MN⃗=12AD⃗+BC⃗Так как векторы AD⃗ и BC⃗ сонаправлены, то векторы MN⃗ и AD⃗ также сонаправлены, а длина вектора (AD⃗+BC⃗) равна AD + BC.
Отсюда следует, что
MN //AD
Умножение вектора на число » Аналитическая геометрия f(x)dx.Ru
п.9. Умножение вектора на число.
Определение. Произведением вектора на действительное число называется вектор , удовлетворяющий следующим двум условиям:
1) ;
2) , если и , если ;
и обозначается .
Теорема. (Свойства умножения вектора на число.)
1. Свойство ассоциативности: верно
равенство .
2. Свойство дистрибутивности умножения относительно
сложения чисел: верно равенство
.
3. Свойство дистрибутивности умножения относительно
сложения векторов: верно равенство
.
4. верно равенство .
Доказательство. Свойство 4 вытекает из определения умножения вектора на число. Докажем свойство 1.
Умножение вектора на число можно интерпретировать как гомотетию какой-нибудь плоскости Р, в которой лежит данный вектор, с центром гомотетии в начале вектора и коэффициентом .
Такая гомотетия плоскости Р оставляет точку А на месте, , а конец вектора – точку В переводит (отображает) в точку С, , причем
и точка С лежит на луче АВ, если и на
противоположном луче, если . См. рис. 10 и 11.
А В С
рис. 10.
С А В
рис.11.
Теперь свойство 1 следует из того что композиция гомотетий (т.е. последовательное их выполнение) есть гомотетия, причем и верно равенство: .
Пусть .
D А В С
|
рис. 12.
Тогда , и , т.е. .
Таким образом, и ,
следовательно, , ч.т.д.
Доказательство свойства 2 оставляем читателю в качестве самостоятельного упражнения. Заметим, что если оба числа и имеют одинаковый знак, то свойство 2 очевидно. Осталось рассмотреть случай разных знаков чисел и .
И, наконец, свойство 3 очевидно из следующего
рисунка, построенного для случая :
рис. 13.
Заметим, что такая картинка возникает, если мы применим к плоскости, в которой лежат оба вектора, отложенные от одной точки О, преобразование гомотетии с центром гомотетии в точке О и коэффициентом .
Теорема доказана.
Теорема. Множество всех векторов как направленных отрезков в пространстве точек S является векторным пространством над полем действительных чисел.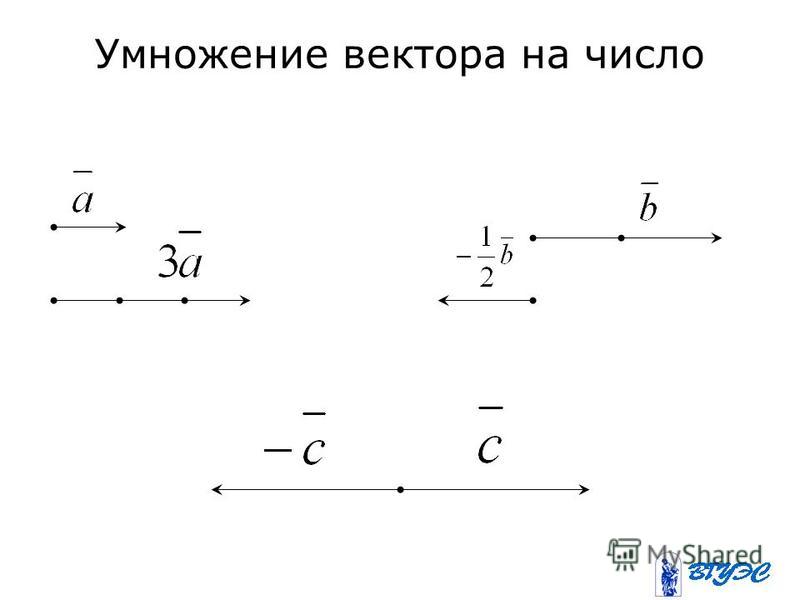
Доказательство следует из свойств сложения векторов и их умножения на действительные числа.
Определение. Векторное пространство над полем действительных чисел называется вещественным векторным пространством.
Пусть L произвольная прямая в пространстве S. Тогда ясно, что , т.е. множество векторов коллинеарных прямой L является подмножеством всех векторов .
Далее, сумма любых двух векторов коллинеарных прямой L также является вектором коллинеарным прямой L:
. В этом случае говорят, что множество векторов замкнуто относительно сложения векторов. Аналогично, , т.е. множество замкнуто относительно операции умножения вектора на действительное число. Отсюда сразу же следует, что для векторов из множества справедливы все свойства сложения и умножения на действительные числа, т.е. справедливы все аксиомы вещественного векторного пространства.
Таким образом, множество также является вещественным векторным пространством.
Говорят, что векторное пространство является векторным подпространством векторного пространства .
Аналогично и для множества всех векторов лежащих на некоторой плоскости Р или на параллельной ей плоскости. Множества также является векторным пространством и векторным подпространством векторного пространства .
Если прямая L лежит в плоскости Р или параллельна ей, то и – подпространство векторного пространства и одновременно векторного пространства .
Векторное пространство мы будем называть пространством векторов на прямой L, а –пространством векторов на плоскости Р.
п.10. Необходимое и достаточное условие коллинеарности двух векторов.
Определение. Пусть и два произвольных вектора. Если верно равенство , где , то говорят, что вектор линейно выражается через вектор .
Теорема. (О коллинеарности двух векторов.)
Для того, чтобы два вектора были коллинеарными необходимо и достаточно, чтобы либо один из них был нулевым, либо один из них линейно выражался через другой.
Другими словами, .
Доказательство. Если , то по определению.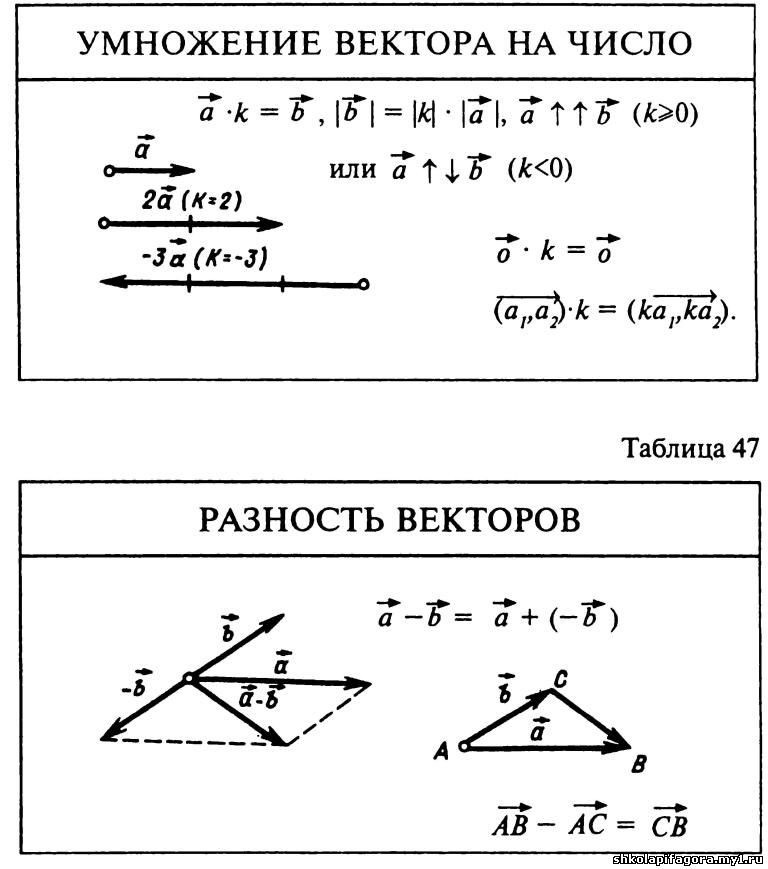 Пусть и . Тогда из определения умножения вектора на число следует, что либо , либо , в зависимости от знака числа , т.е. , ч.т.д.
Пусть и . Тогда из определения умножения вектора на число следует, что либо , либо , в зависимости от знака числа , т.е. , ч.т.д.
Пусть теперь и и . (Если или , то доказывать нечего.) Рассмотрим два возможных случая.
а) Пусть . Т.к. , то .
Обозначим буквой отношение длин этих векторов: . Отсюда следует равенство и, применяя определение умножения вектора на число, получаем, что .
б) Пусть . Положим по определению . Отсюда следует равенство и, применяя определение умножения вектора на число, получаем, что .
Теорема доказана.
Понимание умножения векторов на действительные числа
Умножение векторов является важным инструментом во многих областях физики, включая расстояния, энергии, силы, проделанную работу, электрические или магнитные поля и многие другие приложения.
Умножение любого вектора на вещественное число называется скалярным умножением. Это умножение изменяет величину вектора, но не меняет его направление. Однако, если умноженная величина отрицательна, этого не будет, и направление будет обратным. Второй закон движения Ньютона и проделанная работа — два самых известных примера применения скалярного умножения векторов в физике.
Второй закон движения Ньютона и проделанная работа — два самых известных примера применения скалярного умножения векторов в физике.
Когда мы умножаем вектор на действительное число, величина вектора изменяется, однако это не влияет на направление вектора.
Например, |p·Ā| = р|А| если р>0.
Если p<0, то изменяются и величина, и направление вектора.
Умножение векторовУмножение векторов применяется в различных областях физики, таких как расстояние, энергия, сила, проделанная работа, электрическое или магнитное поле и многое другое. Векторы можно умножать двумя способами: скалярным умножением и векторным умножением. Мы обсудим скалярное умножение, то есть умножение вектора на действительное число.
Скалярное умножение Умножение любого вектора на вещественное число называется скалярным умножением. Всякий раз, когда мы умножаем скалярную величину на любую векторную величину, величина вектора изменяется. Однако изменение его направления зависит от скалярной величины, на которую мы его умножаем. Если скалярная величина положительна, направление остается прежним, а если скалярная величина отрицательна, направление становится противоположным исходному направлению. Кроме того, если мы умножим вектор на ноль, он станет нулевым вектором (нулевым вектором).
Однако изменение его направления зависит от скалярной величины, на которую мы его умножаем. Если скалярная величина положительна, направление остается прежним, а если скалярная величина отрицательна, направление становится противоположным исходному направлению. Кроме того, если мы умножим вектор на ноль, он станет нулевым вектором (нулевым вектором).
Скалярное произведение двух векторов — это скалярное произведение их компонентов. Скалярное произведение двух векторов можно использовать для преобразования вектора в скаляр, представляющий его значение. Другими словами, скалярное произведение двух векторов — это скалярное значение, представляющее сумму элементов каждого вектора.
Скалярная формула произведения = A•B= |A| |Б| Cosθ
Свойства скалярного умножения- a·b — скалярная величина
- Если скалярное произведение двух векторов равно нулю, это означает, что они перпендикулярны друг другу. Это потому, что
А•В = |А| |Б| Cosθ = 0
Cosθ = 0 означает θ=90°
- Если скалярное произведение двух величин равно произведению их величин, это означает, что два вектора параллельны.
 Это потому, что Cosθ = 1 означает θ=0°
Это потому, что Cosθ = 1 означает θ=0° - Точно так же, если скалярное произведение двух векторов равно отрицательному результату произведения их величин, это означает, что они антипараллельны. Это связано с тем, что при Cos θ = -1 значение θ будет равно 180°.
- При решении скалярных произведений
i·i = j·j = k·k = 1 и i·j = i·k = j·k = 0 по тем же причинам, что и упомянутые выше.
- Cosθ = a.b/ |a||b|
- Точечные произведения (скалярные произведения) коммутативны по своей природе, т. е. a·b = b·a
- Они также следуют дистрибутивному свойству a·(b+c) = a·b + a·c
Второй закон движения Ньютона — лучший пример умножения векторов на действительное число. Он утверждает, что сила прямо пропорциональна ускорению движения. Когда мы обращаемся к пропорциональности, мы умножаем уравнение на массу постоянного значения. Уравнение получается
F = ma
Здесь и сила, и ускорение являются векторными величинами, тогда как m является скалярной величиной.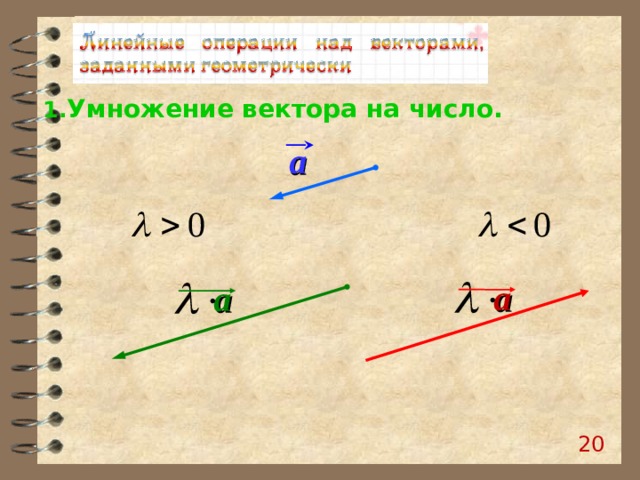 Сила получается умножением векторной величины на действительное число. Мы можем видеть, что это умножение ускорения только меняет его величину, чтобы дать величину силы, но не меняет направление силы. Сила приложена в направлении самого ускорения. Масса (m) всегда положительная величина. Следовательно, она не может быть меньше нуля, и, следовательно, направление силы не изменится.
Сила получается умножением векторной величины на действительное число. Мы можем видеть, что это умножение ускорения только меняет его величину, чтобы дать величину силы, но не меняет направление силы. Сила приложена в направлении самого ускорения. Масса (m) всегда положительная величина. Следовательно, она не может быть меньше нуля, и, следовательно, направление силы не изменится.
Векторы можно перемножать двумя способами: скалярным умножением и векторным умножением. Умножение векторов имеет приложения в различных областях физики, таких как расстояние, энергии, силы, проделанная работа, электрическое или магнитное поле и многие другие. Всякий раз, когда мы умножаем скалярную величину на любую векторную величину, изменяется величина вектора. Если скалярная величина положительна, направление остается прежним, а если скалярная величина отрицательна, направление становится противоположным исходному направлению. Второй закон движения Ньютона утверждает, что сила прямо пропорциональна ускорению движения, и, таким образом, является хорошим примером скалярного умножения.
NumPy | Умножение векторов
Сохранить статью
- Последнее обновление: 05 мая, 2020
Улучшить статью
Сохранить статью
Векторное умножение бывает трех типов:
- Скалярное произведение
- Скалярное произведение
- Перекрестное произведение
Скалярное умножение:
Скалярное умножение может быть представлено путем умножения элементов в векторе на все скалярные величины.
Code: Python code explaining Scalar Multiplication
V = NP. 4 , 1 ]) 3333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333. plt.ticklabel_format(style = 'sci' , axis = 'both' , |
Output :
w = [20 5]
Dot Product multiplication:
Code: Python code to explain Dot Product Multiplication
|
Here, точечный продукт также можно получить с помощью оператора ‘@’.
d = v@s
Вывод:
4
Кросс-произведение:
Код: код Python, объясняющий кросс-произведение
|

 Это потому, что Cosθ = 1 означает θ=0°
Это потому, что Cosθ = 1 означает θ=0°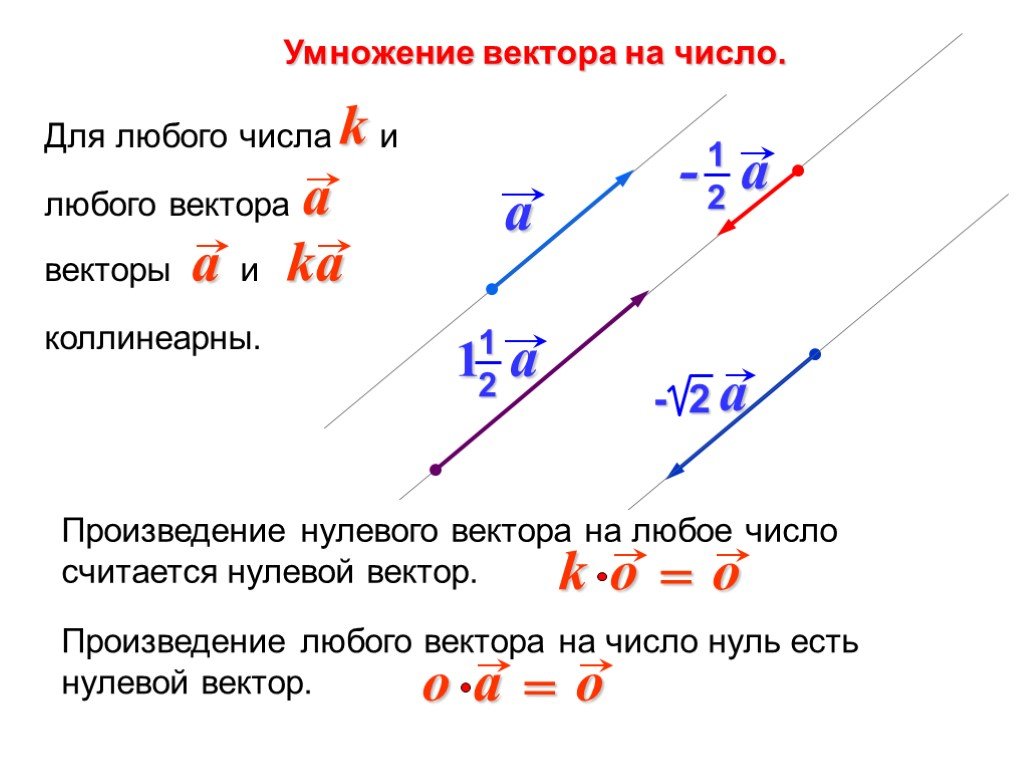 Array ([
Array ([ quiver(
quiver(  array([
array([ 