Сокращение дроби 22/11 — Calculatio
Калькулятор сокращения дробей
Сократить дробь
/
Как сократить дробь 22/11?
Ответ: Сокращенная дробь 22/11 это 2/1
Дробь 2/1 является сокращенной формой для дроби 22/11.
В нашем случае, числитель дроби [22] больше знаменателя [11] и знаменатель является делителем числителя. Следовательно, мы можем упростить дробь до целого числа:
Сокращение дроби 22/11 используя НОД
Первый способ сокращения дроби 22/11 — это нахождение Наибольшего Общего Делителя (НОД) для числителя [22] и знаменателя [11] нашей дроби.
НОД для 22 и 11 это 11
После того, как мы нашли НОД, необходимо разделить числитель [22] и знаменатель [11] нашей дроби на НОД [11].
22 ÷ 11
/
11 ÷ 11
=
Сокращение дроби 22/11 используя простые множители
Еще один способ, чтобы сократить дробь 22/11 — это нахождение Простых Множителей для числителя [22] и знаменателя [11].
Теперь мы можем записать новую дробь, состоящую из простых множителей и сократить общие множители в числителе и знаменателе:
2 × 11
/
11
=
Сокращение дроби 22/11 используя деление на минимальное возможное число
Для того, чтобы сократить нашу дробь, мы можем начать делить числитель [22] и знаменатель [11] дроби на минимально возможное число (2,3,4,5… и т.д.), и делать этого до того, пока не станет невозможным разделить без остатка.
22 ÷ 11
/
11 ÷ 11
=
Поделитесь текущим расчетом
Печать
https://calculat.io/ru/number/fraction-simplified/22—11
<a href=»https://calculat.io/ru/number/fraction-simplified/22—11″>Сокращение дроби 22/11 — Calculatio</a>
Калькулятор сокращения дробей
Данный калькулятор поможет сократить дробь.
Например, он может помочь узнать как сократить дробь 22/11? Введите дробь (числитель и знаменатель) (например ’22/11′) и нажмите кнопку ‘Сократить’.
Сократить дробь (например 22/11) – означает разделить ее числитель и знаменатель на одно и то же число (не равное нулю). В результате получается равная (эквивалентная) дробь, но с меньшими числителем и знаменателем, у которых нет общих делителей, кроме 1 (единицы).
Калькулятор сокращения дробей
Сократить дробь
/
Таблица сокращения дробей
FAQ
Как сократить дробь 22/11?
Сокращенная дробь 22/11 это 2/1
Смотрите также
Как сократить дробь | Алгебра
Как сократить алгебраическую (рациональную) дробь, числитель и знаменатель которой содержат выражения, которые отличаются только знаками?
Например, как сократить дробь
Для начала вспомним, как от выражения (a-b) перейти к выражению (b-a). Для этого нужно вынести «минус» за скобки (при этом все знаки слагаемых в скобках изменятся на противоположные):
В дроби вынести «минус» за скобки можно или в числителе, или в знаменателе.
По свойству алгебраических дробей, знак «минус» можно вынести перед дробью:
В данном примере числитель и знаменатель дроби сокращаем на (a-b):
Рассмотрим другие примеры сокращения алгебраических дробей такого вида.
Сокращать можно только множители!
В числителе и знаменателе дроби — многочлены. Чтобы сократить дробь, надо разложить многочлены на множители. В числителе есть общий множитель 2b, в знаменателе — a. Вынесем их за скобки:
Выражения, стоящие в скобках в числителе и в знаменателе, отличаются только знаками. Вынесем знак «минус» перед дробью, например, из знаменателя (при этом все знаки слагаемых, стоящих в скобках, изменятся на противоположные):
После чего сокращаем дробь на общий делитель (2a-b).
В числителе выносим общий множитель 2 за скобки, знаменатель раскладываем по формуле разности квадратов:
Вынесем «минус» перед дробью, например, из числителя:
Сокращаем дробь на (m-7).
В числителе — 4 слагаемых. Группируем первое слагаемое со вторым, третье — с четвертым. В знаменателе выносим общий множитель 6 за скобки:
В числителе выносим общие множители за скобки: из первых скобок — y, из вторых — -2, затем — (x-3):
Сокращаем дробь на (x-3):
Если после сокращения перед дробью остался «минус», а в числителе или знаменателе есть разность, «минус» надо внести в разность (при этом знаки слагаемых изменятся на противоположные). Вносим «-» в числитель, -(y-2)=2-y:
Соответственно,
То есть, чтобы сменить знаки слагаемых в квадрате разности, «минус» за скобки (и перед дробью) выносить не нужно. Это верно не только для квадрата разности, но и для любой другой четной степени:
В случае возведения разности в нечетную степень при смене знаков слагаемых знак «минус» за скобки выносить нужно:
Примеры.
В числителе — полный квадрат разности, в знаменателе — разность квадратов. Раскладываем на множители:
Удобнее изменить знаки слагаемых вверху, поскольку при этом не нужно изменять знак перед дробью:
Сокращаем дробь на (10y-9x):
Вынесем знак «минус» перед дробью, например, из знаменателя:
Сокращаем на (b-4)³:
Сокращение дробей в алгебре — важная составляющая часть сложения, вычитания, умножения и деления алгебраических дробей. Упрощать рациональные выражения приходится при решении уравнений, неравенств, задач и т.д.
Далее мы будем рассматривать действия над алгебраическими дробями.
Рубрика: Алгебраические дроби | КомментарииУпрощение дробей до меньших слагаемых — 3-й класс математики
Дроби показывают части целого.
Эквивалент дроби — это дроби с одинаковым значением , даже если их числители и знаменатели разные.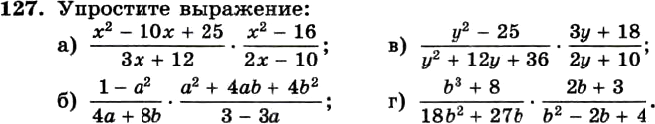
3/6 эквивалентно 1/2 .
Некоторые эквивалентные дроби проще других.
Дробь является простейшей формой , когда числитель и знаменатель не могут делиться ни на одно число, кроме 1.
Можем ли мы упростить 3 / 6 ?
Да, 3 и 6 кратны 3. Это означает, что они имеют общий делитель .
Совет : Факторы идут парами. Это два числа, которые вы можете перемножить, чтобы получить произведение.
Вы также можете думать о множителях как о числах, которые могут делить большее число без остатка.
К упрости дробь, найди любые общих множителей между числителем и знаменателем и разделить их от обоих.
Совет: Мы можем разделить и числитель, и знаменатель на 3, не меняя значение дроби.
Вот как мы можем доказать, что с уравнениями:
3/6 =
3/6 ÷ 1 =
3/6 ÷ (3/3) =
(3 ÷ (3/3) =
(3 3 ) / (6 ÷ 3 ) =
1/2
Можем ли мы еще упростить 1/2?
Нет, нет другого числа, кроме 1, на которое можно разделить и числитель, и знаменатель.
Итак, 1/2 — это простейшая форма из 3/6! 🎉
Совет: Можно также сказать, что 1/2 — это « самый низкий срок» из 3/6. Это язык, которым часто пользуются математики.
Действия по упрощению дробей до их наименьшего члена
Дробь в своем простейшем виде 9Форма 0005, или наименьший член, , если числитель и знаменатель нельзя разделить на общее число, отличное от 1.
Итак, как упростить дробь до наименьшего члена? 🤔
1️⃣ Сначала перечислите множители числителя и знаменателя.
2️⃣ Затем делят на любые общие множители обоих.
Попробуем на примере:
Упростим дробь 18 / 48 .
На какое число можно разделить оба 18 и 48?
Мы можем разделить оба числа на 2. Оба числа четные.
Совет: Это не меняет значение дроби, потому что мы делим на (2 / 2), то есть делим на 1, что не меняет число.
Получаем 9/24. Это более простая дробь , эквивалентная 18/48.
Но это еще не самая простая форма.
На какое число можно разделить 9 и 24 по?
Да, и 9, и 24 делятся на 3.
Далее разделим 9 и 24 на 3:
Теперь у нас есть 3 эквивалентные дроби:
18/48 = 9/24 = 3/6 8
Простая форма пока равна 3/8. Можно ли разделить 3 и 8 на какой-либо другой множитель?
Больше нет.
Итак, самый низкий термин из 18 / 48 равен 3 / 8. 060 Это простейших из этой дроби. На какое число можно разделить 135 и 180? 5 может быть хорошим выбором, так как числитель заканчивается на 5, а знаменатель на 0. Давайте разделим числитель и знаменатель на 5: Хорошо. 27/36 это больше просто , чем 135/180. Можно ли разделить числа 27 и 36 на какой-нибудь общий делитель? Да, 27 и 36 делятся на 9. Можем ли мы упростить 3/4? Это самое простое, что мы можем сделать. 🤗 SO, Простейшая Форма из 135 / 180 IS 3 / 4. 4 до Продолжайте делить, пока не найдете общих или общих множителей для деления. последняя дробь , которую вы получите, является наименьшим слагаемым . Помните, что вам нужно разделить и числитель и знаменатель на тот же номер . Теперь потренируйтесь самостоятельно упрощать дроби. Это полезный навык. Упрощение дробей включает в себя приведение дроби к простейшей форме. У дроби в простейшей форме числитель и знаменатель не имеют общих делителей, кроме 1. Например, . Все это эквивалентные дроби, но только в простейшей форме. Мы можем упростить все другие эквивалентные дроби и найти, что простейшая форма этих дробей будет . Существует два основных метода упрощения дробей. В одном используются простые числа, а в другом — наибольший общий делитель (НОД) числителя и знаменателя. Этот метод может быть немного проще в выполнении, чем метод GCF, но он может быть гораздо менее эффективным. Чтобы использовать этот метод, Причина, по которой мы используем простые числа, заключается в том, что поскольку мы начинаем делить от младших простых чисел к старшим, нам не нужно проверять кратные простые числа, такие как 2, 2 × 2 = 4, 4 × 2 = 8, и поэтому на. Если мы выполним шаги, описанные выше, и разделим на 2 до тех пор, пока не сможем больше, нам не нужно проверять, можем ли мы разделить на 4, потому что никогда не будет случая, когда мы полностью разделили на 2 и все еще можем разделить на 4 или 8 и т. д. Это верно для всех не простых чисел. Примеры 1. Упростить Поскольку четные числа делятся на 2, мы попробуем использовать 2 в качестве первого простого числа: мы могли бы еще дважды разделить 8 на 2, настолько, насколько мы можем упростить эту дробь. Давайте посмотрим на другой пример. 2. Упростить : В приведенном выше примере 2 мы могли бы сразу разделить числитель и знаменатель на 18, так как 2 × 3 × 3 = 18. Упрощение дробей Последний пример
Упрощение дроби 135 / 180 .
✅ Давайте рассмотрим
Как упростить фракции
.0006 дробь
наименьшее член , разделить числитель и знаменатель на любые общие делители .
Упрощение дробей
Как упростить дроби с помощью простых чисел
Начни с низкого на высокий