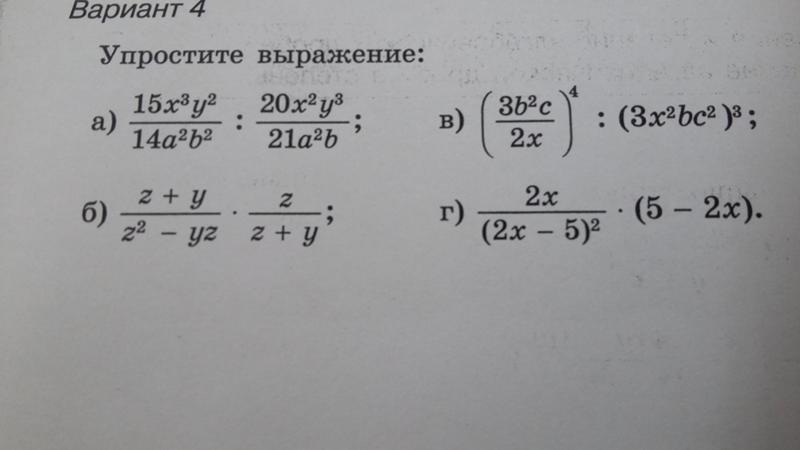Как упростить выражение 7 класс алгебра со степенями: Степенные выражения (выражения со степенями) и их преобразование

Степенные выражения (выражения со степенями) и их преобразование

Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.

Что представляют собой степенные выражения?

В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.

Определение 1

Степенное выражение – это выражение, которое содержит степени.

Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.

Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 32, 75+1, (2+1)5, (−0,1)4, 2233, 3·a2−a+a2, x3−1, (a2)3. А также степени с нулевым показателем: 50, (a+1)0, 3+52−3,20. И степени с целыми отрицательными степенями: (0,5)2+(0,5)-22.

Чуть сложнее работать со степенью, имеющей рациональный  и иррациональный показатели: 26414-3·3·312, 23,5·2-22-1,5, 1a14·a12-2·a-16·b12, xπ·x1-π, 233+5.

В качестве показателя может выступать переменная 3x-54-7·3x-58 или логарифм x2·lgx−5·xlgx.

С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.

Основные виды преобразований степенных выражений

В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.

Пример 1

Вычислите значение степенного выражения 23·(42−12).

Решение

Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 23·(42−12)=23·(16−12)=23·4.

Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32. Вот наш ответ.

Ответ: 23·(42−12)=32.

Пример 2

Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7.

Решение

Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.

Ответ: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.

Пример 3

Представьте выражение со степенями 9-b3·π-12 в виде произведения.

Решение

Представим число 9 как степень 32 и применим формулу сокращенного умножения:

9-b3·π-12=32-b3·π-12==3-b3·π-13+b3·π-1

Ответ: 9-b3·π-12=3-b3·π-13+b3·π-1.

А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений. 

Работа с основанием и показателем степени

Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, (2+0,3·7)5−3,7 и (a·(a+1)−a2)2·(x+1). Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.

Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.

Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2+0,3·7)5−3,7 можно выполнить действия для перехода к степени 4,11,3. Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a·(a+1)−a2)2·(x+1) и получить степенное выражение более простого вида a2·(x+1).

Использование свойств степеней

Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а

r и s — произвольные действительные числа:

Определение 2

• ar·as=ar+s;
• ar:as=ar−s;
• (a·b)r=ar·br;
• (a:b)r=ar:br;
• (ar)s=ar·s.

В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство am·an=am+n, где m и n – натуральные числа, то оно будет верно для любых значений a, как положительных, так и отрицательных, а также для a=0.

Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.

При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».

Пример 4

Представьте выражение a2,5·(a2)−3:a−5,5 в виде степени с основанием a.

Решение

Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a2)−3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:

a2,5·a−6:a−5,5= a2,5−6:a−5,5=a−3,5:a−5,5= a−3,5−(−5,5)=a2.

Ответ: a2,5·(a2)−3:a−5,5=a2.

Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.

Пример 5

Найти значение степенного выражения 313·713·2123.

Решение

Если мы применим равенство (a·b)r=ar·br, справа налево, то получим произведение вида 3·713·2123 и дальше 2113·2123. Сложим показатели при умножении степеней с одинаковыми основаниями: 2113·2123=2113+23=211=21.

Есть еще один способ провести преобразования:

313·713·2123=313·713·(3·7)23=313·713·323·723==313·323·713·723=313+23·713+23=31·71=21

Ответ: 313·713·2123=31·71=21

 

Пример 6

Дано степенное выражение a1,5−a0,5−6, введите новую переменную t=a0,5.

Решение

Представим степень a1,5 как a0,5·3 . Используем свойство степени в степени

(ar)s=ar·s справа налево и получим (a0,5)3: a1,5−a0,5−6=(a0,5)3−a0,5−6. В полученное выражение можно без проблем вводить новую переменную t=a0,5: получаем t3−t−6.

Ответ: t3−t−6.

Преобразование дробей, содержащих степени

Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.

Пример 7

Упростить степенное выражение 3·523·513-5-231+2·x2-3-3·x2.

Решение

Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:

3·523·513-5-231+2·x2-3-3·x2=3·523·513-3·523·5-23-2-x2==3·523+13-3·523+-23-2-x2=3·51-3·50-2-x2

Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12-2-x2=-122+x2

Ответ:  3·523·513-5-231+2·x2-3-3·x2=-122+x2

Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.

Пример 8

 

Приведите дроби к новому знаменателю: а) a+1a0,7 к знаменателю a, б) 1×23-2·x13·y16+4·y13 к знаменателю x+8·y12.

Решение

а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a0,7·a0,3=a0,7+0,3=a, следовательно, в качестве дополнительного множителя мы возьмем

a0,3. Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a0,3 не обращается в нуль.

Выполним умножение числителя и знаменателя дроби на a0,3:

a+1a0,7=a+1·a0,3a0,7·a0,3=a+1·a0,3a

б) Обратим внимание на знаменатель:

x23-2·x13·y16+4·y13==x132-x13·2·y16+2·y162

Умножим это выражение на x13+2·y16, получим сумму кубов x13 и 2·y16, т. е. x+8·y12. Это наш новый знаменатель, к которому нам надо привести исходную дробь.
 

Так мы нашли дополнительный множитель x13+2·y16. На области допустимых значений переменных x и y выражение x13+2·y16 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1×23-2·x13·y16+4·y13==x13+2·y16x13+2·y16x23-2·x13·y16+4·y13==x13+2·y16x133+2·y163=x13+2·y16x+8·y12

Ответ: а) a+1a0,7=a+1·a0,3a , б) 1×23-2·x13·y16+4·y13=x13+2·y16x+8·y12.  

Пример 9

Сократите дробь: а) 30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53, б) a14-b14a12-b12.

Решение

а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15. Также мы можем произвести сокращение на x0,5+1 и на x+2·x113-53.

Получаем:

30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1)

б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:

a14-b14a12-b12=a14-b14a142-b122==a14-b14a14+b14·a14-b14=1a14+b14

Ответ:  а)30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1), б) a14-b14a12-b12=1a14+b14.

К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.

Пример 10

Выполните действия x12+1×12-1-x12-1×12+1·1×12.

Решение

Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:

x12-1·x12+1

Вычтем числители:

x12+1×12-1-x12-1×12+1·1×12==x12+1·x12+1×12-1·x12+1-x12-1·x12-1×12+1·x12-1·1×12==x12+12-x12-12×12-1·x12+1·1×12==x122+2·x12+1-x122-2·x12+1×12-1·x12+1·1×12==4·x12x12-1·x12+1·1×12

Теперь умножаем дроби:

4·x12x12-1·x12+1·1×12==4·x12x12-1·x12+1·x12

Произведем сокращение на степень x12, получим 4×12-1·x12+1.

Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4×12-1·x12+1=4×122-12=4x-1.

Ответ: x12+1×12-1-x12-1×12+1·1×12=4x-1

Пример 11

Упростите степенное выражение x34·x2,7+12x-58·x2,7+13.
Решение

Мы можем произвести сокращение дроби на (x2,7+1)2. Получаем дробь x34x-58·x2,7+1.

Продолжим преобразования степеней икса x34x-58·1×2,7+1. Теперь можно использовать свойство деления степеней с одинаковыми основаниями:  x34x-58·1×2,7+1=x34—58·1×2,7+1=x118·1×2,7+1.

Переходим от последнего произведения к дроби x138x2,7+1.

Ответ: x34·x2,7+12x-58·x2,7+13=x138x2,7+1.

Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x+1)-0,23·x-1 можно заменить  на x3·(x+1)0,2.

Преобразование выражений с корнями и степенями

В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.

Пример 12

Представьте выражение x19·x·x36 в виде степени.

Решение

Область допустимых значений переменной x определяется двумя неравенствами  x≥0  и x·x3≥0 ,  которые задают множество [0, +∞).

На этом множестве мы имеем право перейти от корней к степеням: 

x19·x·x36=x19·x·x1316

Используя свойства степеней, упростим полученное степенное выражение.

x19·x·x1316=x19·x16·x1316=x19·x16·x1·13·6==x19·x16·x118=x19+16+118=x13

Ответ: x19·x·x36=x13.

Преобразование степеней с переменными в показателе

Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 52·x+1−3·5x·7x−14·72·x−1=0.

Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:

52·x·51−3·5x·7x−14·72·x·7−1=0, 5·52·x−3·5x·7x−2·72·x=0.

Теперь поделим обе части равенства на 72·x. Это выражение на ОДЗ переменной x принимает только положительные значения:

5·5-3·5x·7x-2·72·x72·x=072·x,5·52·x72·x-3·5x·7×72·x-2·72·x72·x=0,5·52·x72·x-3·5x·7x7x·7x-2·72·x72·x=0

Сократим дроби со степенями, получим: 5·52·x72·x-3·5x7x-2=0.

Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5·572·x-3·57x-2=0 , которое равносильно 5·57×2-3·57x-2=0.

Введем новую переменную t=57x, что сводит решение исходного показательного уравнения к решению квадратного уравнения 5·t2−3·t−2=0.

Преобразование выражений со степенями и логарифмами

Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 141-5·log23 или log3279+5(1-log35)·log53. Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Степенные выражения (выражения со степенями) и их преобразование

Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.

Что представляют собой степенные выражения?

В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.

Определение 1

Степенное выражение – это выражение, которое содержит степени.

Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.

Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 32, 75+1, (2+1)5, (−0,1)4, 2233, 3·a2−a+a2, x3−1, (a2)3. А также степени с нулевым показателем: 50, (a+1)0, 3+52−3,20. И степени с целыми отрицательными степенями: (0,5)2+(0,5)-22.

Чуть сложнее работать со степенью, имеющей рациональный  и иррациональный показатели: 26414-3·3·312, 23,5·2-22-1,5, 1a14·a12-2·a-16·b12, xπ·x1-π, 233+5.

В качестве показателя может выступать переменная 3x-54-7·3x-58 или логарифм x2·lgx−5·xlgx.

С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.

Основные виды преобразований степенных выражений

В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.

Пример 1

Вычислите значение степенного выражения 23·(42−12).

Решение

Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 23·(42−12)=23·(16−12)=23·4.

Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32. Вот наш ответ.

Ответ: 23·(42−12)=32.

Пример 2

Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7.

Решение

Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.

Ответ: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.

Пример 3

Представьте выражение со степенями 9-b3·π-12 в виде произведения.

Решение

Представим число 9 как степень 32 и применим формулу сокращенного умножения:

9-b3·π-12=32-b3·π-12==3-b3·π-13+b3·π-1

Ответ: 9-b3·π-12=3-b3·π-13+b3·π-1.

А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений. 

Работа с основанием и показателем степени

Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, (2+0,3·7)5−3,7 и (a·(a+1)−a2)2·(x+1). Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.

Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.

Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2+0,3·7)5−3,7 можно выполнить действия для перехода к степени 4,11,3. Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a·(a+1)−a2)2·(x+1) и получить степенное выражение более простого вида a2·(x+1).

Использование свойств степеней

Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:

Определение 2

• ar·as=ar+s;
• ar:as=ar−s;
• (a·b)r=ar·br;
• (a:b)r=ar:br;
• (ar)s=ar·s.

В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство am·an=am+n, где m и n – натуральные числа, то оно будет верно для любых значений a, как положительных, так и отрицательных, а также для a=0.

Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.

При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».

Пример 4

Представьте выражение a2,5·(a2)−3:a−5,5 в виде степени с основанием a.

Решение

Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a2)−3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:

a2,5·a−6:a−5,5= a2,5−6:a−5,5=a−3,5:a−5,5= a−3,5−(−5,5)=a2.

Ответ: a2,5·(a2)−3:a−5,5=a2.

Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.

Пример 5

Найти значение степенного выражения 313·713·2123.

Решение

Если мы применим равенство (a·b)r=ar·br, справа налево, то получим произведение вида 3·713·2123 и дальше 2113·2123. Сложим показатели при умножении степеней с одинаковыми основаниями: 2113·2123=2113+23=211=21.

Есть еще один способ провести преобразования:

313·713·2123=313·713·(3·7)23=313·713·323·723==313·323·713·723=313+23·713+23=31·71=21

Ответ: 313·713·2123=31·71=21

 

Пример 6

Дано степенное выражение a1,5−a0,5−6, введите новую переменную t=a0,5.

Решение

Представим степень a1,5 как a0,5·3 . Используем свойство степени в степени (ar)s=ar·s справа налево и получим (a0,5)3: a1,5−a0,5−6=(a0,5)3−a0,5−6. В полученное выражение можно без проблем вводить новую переменную t=a0,5: получаем t3−t−6.

Ответ: t3−t−6.

Преобразование дробей, содержащих степени

Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.

Пример 7

Упростить степенное выражение 3·523·513-5-231+2·x2-3-3·x2.

Решение

Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:

3·523·513-5-231+2·x2-3-3·x2=3·523·513-3·523·5-23-2-x2==3·523+13-3·523+-23-2-x2=3·51-3·50-2-x2

Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12-2-x2=-122+x2

Ответ:  3·523·513-5-231+2·x2-3-3·x2=-122+x2

Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.

Пример 8

 

Приведите дроби к новому знаменателю: а) a+1a0,7 к знаменателю a, б) 1×23-2·x13·y16+4·y13 к знаменателю x+8·y12.

Решение

а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a0,7·a0,3=a0,7+0,3=a, следовательно, в качестве дополнительного множителя мы возьмем a0,3. Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a0,3 не обращается в нуль.

Выполним умножение числителя и знаменателя дроби на a0,3:

a+1a0,7=a+1·a0,3a0,7·a0,3=a+1·a0,3a

б) Обратим внимание на знаменатель:

x23-2·x13·y16+4·y13==x132-x13·2·y16+2·y162

Умножим это выражение на x13+2·y16, получим сумму кубов x13 и 2·y16, т. е. x+8·y12. Это наш новый знаменатель, к которому нам надо привести исходную дробь.
 

Так мы нашли дополнительный множитель x13+2·y16. На области допустимых значений переменных x и y выражение x13+2·y16 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1×23-2·x13·y16+4·y13==x13+2·y16x13+2·y16x23-2·x13·y16+4·y13==x13+2·y16x133+2·y163=x13+2·y16x+8·y12

Ответ: а) a+1a0,7=a+1·a0,3a , б) 1×23-2·x13·y16+4·y13=x13+2·y16x+8·y12.  

Пример 9

Сократите дробь: а) 30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53, б) a14-b14a12-b12.

Решение

а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15. Также мы можем произвести сокращение на x0,5+1 и на x+2·x113-53.

Получаем:

30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1)

б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:

a14-b14a12-b12=a14-b14a142-b122==a14-b14a14+b14·a14-b14=1a14+b14

Ответ:  а)30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1), б) a14-b14a12-b12=1a14+b14.

К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.

Пример 10

Выполните действия x12+1×12-1-x12-1×12+1·1×12.

Решение

Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:

x12-1·x12+1

Вычтем числители:

x12+1×12-1-x12-1×12+1·1×12==x12+1·x12+1×12-1·x12+1-x12-1·x12-1×12+1·x12-1·1×12==x12+12-x12-12×12-1·x12+1·1×12==x122+2·x12+1-x122-2·x12+1×12-1·x12+1·1×12==4·x12x12-1·x12+1·1×12

Теперь умножаем дроби:

4·x12x12-1·x12+1·1×12==4·x12x12-1·x12+1·x12

Произведем сокращение на степень x12, получим 4×12-1·x12+1.

Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4×12-1·x12+1=4×122-12=4x-1.

Ответ: x12+1×12-1-x12-1×12+1·1×12=4x-1

Пример 11

Упростите степенное выражение x34·x2,7+12x-58·x2,7+13.
Решение

Мы можем произвести сокращение дроби на (x2,7+1)2. Получаем дробь x34x-58·x2,7+1.

Продолжим преобразования степеней икса x34x-58·1×2,7+1. Теперь можно использовать свойство деления степеней с одинаковыми основаниями:  x34x-58·1×2,7+1=x34—58·1×2,7+1=x118·1×2,7+1.

Переходим от последнего произведения к дроби x138x2,7+1.

Ответ: x34·x2,7+12x-58·x2,7+13=x138x2,7+1.

Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x+1)-0,23·x-1 можно заменить  на x3·(x+1)0,2.

Преобразование выражений с корнями и степенями

В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.

Пример 12

Представьте выражение x19·x·x36 в виде степени.

Решение

Область допустимых значений переменной x определяется двумя неравенствами  x≥0  и x·x3≥0 ,  которые задают множество [0, +∞).

На этом множестве мы имеем право перейти от корней к степеням: 

x19·x·x36=x19·x·x1316

Используя свойства степеней, упростим полученное степенное выражение.

x19·x·x1316=x19·x16·x1316=x19·x16·x1·13·6==x19·x16·x118=x19+16+118=x13

Ответ: x19·x·x36=x13.

Преобразование степеней с переменными в показателе

Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 52·x+1−3·5x·7x−14·72·x−1=0.

Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:

52·x·51−3·5x·7x−14·72·x·7−1=0, 5·52·x−3·5x·7x−2·72·x=0.

Теперь поделим обе части равенства на 72·x. Это выражение на ОДЗ переменной x принимает только положительные значения:

5·5-3·5x·7x-2·72·x72·x=072·x,5·52·x72·x-3·5x·7×72·x-2·72·x72·x=0,5·52·x72·x-3·5x·7x7x·7x-2·72·x72·x=0

Сократим дроби со степенями, получим: 5·52·x72·x-3·5x7x-2=0.

Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5·572·x-3·57x-2=0 , которое равносильно 5·57×2-3·57x-2=0.

Введем новую переменную t=57x, что сводит решение исходного показательного уравнения к решению квадратного уравнения 5·t2−3·t−2=0.

Преобразование выражений со степенями и логарифмами

Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 141-5·log23 или log3279+5(1-log35)·log53. Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Объяснение урока: Упрощение алгебраических выражений: Отрицательные и дробные показатели

В этом объяснении мы узнаем, как использовать правила отрицательных и дробных индексов для решения алгебраических задач.

Чтобы помочь вам понять правила отрицательных и дробных индексов, мы сначала вспомним правила умножения и деления показателей степени.

Правила возведения в степень: умножение и деление

Правила умножения и деления в степени следующие.

• Умножение степеней с одинаковым основанием: 𝑎×𝑎=𝑎, где 𝑚 и 𝑛 могут принимать любые значения в реальной области.
• Деление показателей с одинаковым основанием: 𝑎÷𝑎=𝑎, где 𝑎≠0 и где 𝑚 и 𝑛 могут принимать любые значения в реальной области.

Поскольку 𝑚 и 𝑛 могут принимать любые значения в реальном домене, эти правила применяются для отрицательные и дробные индексы. Сначала рассмотрим, что происходит, когда мы изменить эти правила так, чтобы мы получили отрицательную экспоненту.

Используя закон деления для показателей степени, 𝑎÷𝑎=𝑎, где 𝑎≠0, мы можем видеть, что когда 𝑚𝑛, это приведет к отрицательному индексу.

Далее, если положить 𝑚=0, то можно увидеть 𝑎÷𝑎=𝑎,𝑎≠0. где

Напомним, что 𝑎=1 при 𝑎≠0, поэтому получаем следующую формулу: 1÷𝑎=𝑎,𝑎≠0.где

Или, записав в виде дроби, получим следующее: 1𝑎=𝑎,𝑎≠0.где

Это приводит нас к следующему правилу показателей степени для отрицательных индексов.

Правила экспоненты: отрицательные индексы

Правило показателей степени для отрицательных индексов выглядит следующим образом: 𝑎=1𝑎, где 𝑎≠0 и 𝑛 могут принимать любые значения в реальном домене.

При записи алгебраических выражений с показателями степени принято упростите ответы так, чтобы показатель степени был положительным. В случае 𝑥, мы бы переписали это как 1𝑥 при даче окончательного ответа. Обратите внимание, что это может не всегда быть так, но это полезно рассмотреть.

В следующем примере мы применим правило экспонент для отрицательные индексы.

Пример 1. Переписывание алгебраических выражений с использованием законов экспонент с отрицательными экспонентами

Какое из следующих чисел равно −109𝑥𝑦?

1. −910𝑥𝑦
2. −109𝑥𝑦
3. −109𝑥𝑦
4. −10𝑥𝑦9

Ответ

Чтобы переписать выражение −109𝑥𝑦, мы должны использовать закон показателей для отрицательных показателей, который гласит, что 𝑎=1𝑎,𝑎≠0. где

Поскольку и 𝑥, и 𝑦 имеют отрицательные показатели, то мы применим правило для обеих переменных.

Вместо 𝑥 можно заменить 𝑛=2 и 𝑎=𝑥, что дает нам 𝑥=1𝑥.

Вместо 𝑦 можно заменить 𝑛=7 и 𝑎=𝑦, что дает нам 𝑦=1𝑦.

Теперь мы переписали обе переменные с положительными показателями, мы можем затем поместите их обратно в исходное выражение, дав нам −109𝑥𝑦=−109×1𝑥×1𝑦=−10×1×19×𝑥×𝑦=−109𝑥𝑦.

Следовательно, ответом является вариант C, −109𝑥𝑦.

В следующем примере мы будем использовать правило экспонент для отрицательных индексов, а также правило деления индексов.

Пример 2. Сопоставление двух выражений с использованием законов экспонент с отрицательными экспонентами

Верно или неверно: упрощенная форма 𝑥𝑥 равно 1𝑥.

Ответ

Чтобы упростить 𝑥𝑥, мы начнем с использования правила деления для показателей: 𝑎÷𝑎=𝑎,𝑎≠0. где

𝑚=−4 и 𝑛=−2, мы все еще можем применить это правило. Это также помогает перепишите здесь дробь как деление. Тем самым мы получаем 𝑥𝑥=𝑥÷𝑥=𝑥=𝑥.()

Далее, так как индекс все еще отрицательный, то используем закон степени для отрицательных показателей, в котором говорится, что 𝑎=1𝑎,𝑎≠0.где

Подставив в закон 𝑛=2 и 𝑎=𝑥, получим 𝑥=1𝑥.

Следовательно, 𝑥𝑥=1𝑥, значит, ответ верен.

Возвращаясь к предыдущему примеру, можно увидеть и другие способы упрощения. 𝑥𝑥, чтобы получить 1𝑥.

Другой подход заключается в использовании закона показателей сначала для отрицательных индексов, в котором говорится, что 𝑎=1𝑎,𝑎≠0,где

Затем мы заменяем 𝑛=4 и 𝑎=𝑥 на член в числителе и 𝑛=2 и 𝑎=𝑥 для члена в знаменателе. Это дает нам 𝑥𝑥=.

Затем мы можем использовать наше понимание дробей, чтобы записать это как =1𝑥÷1𝑥=1𝑥×𝑥=𝑥𝑥.

Затем мы используем правило деления показателей, которое гласит, что 𝑎÷𝑎=𝑎,𝑎≠0.где

При 𝑎=𝑥, 𝑚=2 и 𝑛=4 получаем 𝑥𝑥=𝑥÷𝑥=𝑥=𝑥=1𝑥.

Это показывает, что мы можем применять правила в другом порядке и получать одинаковые эквивалентное выражение.

В следующем примере мы упростим алгебраическое выражение, используя законы показателей, в том числе степенной закон, закон деления и закон для отрицательные индексы. Давайте сначала вспомним степенные законы.

Правила экспонентов: дальнейшие законы о электроэнергии

Правила экспонентов для полномочий экспонентов составляют

• (𝑎) = 𝑎,
• (𝑎𝑏) = 𝑎𝑏,
• 𝑎𝑏 = 𝑎𝑏, 𝑏≠0,

, где 𝑚 и 𝑛 могут принимать любые значения в реальной области.

Пример 3. Упрощение рациональных алгебраических выражений с использованием законов экспонент с отрицательными экспонентами

Ответ

Чтобы упростить это алгебраическое выражение, рассмотрим, какие законы обязательный. Поскольку есть дроби, возведенные в степень, мы можем сначала использовать степенной закон, который гласит, что 𝑎𝑏=𝑎𝑏, где 𝑏≠0 и 𝑚 могут принимать любые действительные значения.

При применении этого закона к первой части выражения, 𝑚𝑛, получаем 𝑚𝑛=𝑚(𝑛).

Мы можем еще больше упростить знаменатель, используя закон показателей для полномочия, в котором говорится: (𝑎)=𝑎, где 𝑚 и 𝑛 могут принимать любые действительные значения.

Итак, получаем 𝑚(𝑛)=𝑚𝑛=𝑚𝑛.×

Аналогично можно применить закон для степеней дробей ко второй части выражения 2𝑚𝑛, что дает нас. 2𝑚𝑛=2𝑚(𝑛).

Как и в первой части выражения, можно упростить знаменатель используя закон показателей для степеней, но для числителя мы используем закон о мощностях произведений, который гласит, что (𝑎𝑏)=𝑎𝑏, где 𝑚 может принимать любые действительные значения.

Итак, получаем 2𝑚(𝑛)=2×𝑚𝑛=2×𝑚𝑛=2×𝑚𝑛. ×

При объединении двух частей выражения 𝑚𝑛=𝑚𝑛2𝑚𝑛=2×𝑚𝑛,и мы получили 𝑚𝑛2𝑚𝑛 = 𝑚𝑛 × 2𝑚𝑛 = 𝑚 × 2𝑚𝑛 × 𝑛.

Далее мы используем правило умножения для показателей, в котором говорится, что 𝑎×𝑎=𝑎, где 𝑎, 𝑚 и 𝑛 — любое действительное значение.

Затем мы можем упростить числитель и знаменатель, так как некоторые из компоненты имеют одно основание: 𝑚×2𝑚𝑛×𝑛=2×𝑚×𝑚𝑛×𝑛=2𝑚𝑛=2𝑚𝑛.0003

Наконец, мы используем правило для отрицательных степеней, чтобы упростить 2. Это правило гласит, что 𝑎=1𝑎, где 𝑎≠0 и 𝑛 может быть любым вещественным числом.

Итак, мы имеем 2𝑚𝑛 = 2 × 𝑚𝑛 = 12 × 𝑚𝑛 = 18 × 𝑚𝑛 = 𝑚8𝑛.

Следовательно, 𝑚𝑛2𝑚𝑛 = 𝑚8𝑛 .

До сих пор мы встречали отрицательные индексы. Далее рассмотрим дробные индексы.

Рассмотрим выражение 𝑥.

Мы знаем, что √𝑥=𝑥,𝑥≥0для и аналогично √𝑥=𝑥,𝑥≥0.для

Предположим, что существует такой индекс 𝑚, что 𝑥=𝑥.

По степенному закону для показателей мы знаем, что 𝑥=𝑥.

Мы также знаем, что 𝑥=𝑥.

Следовательно, 𝑥=𝑥.

Итак, приравнивая индексы, получаем 2𝑚=1,𝑚=12.

Итак, 𝑥=𝑥,𝑥≥0.для

Поскольку √𝑥=𝑥, то мы можем сделать вывод, что 𝑥=√𝑥,𝑥≥0.для

Следовательно, мы видим, что любое число 𝑎≥0, возведённое в мощность половины равна к квадратному корню из 𝑎. Другими словами, 𝑎=√𝑎,𝑎≥0.для

Затем мы можем выполнить те же шаги для общего 𝑛-го корня в уравнении 𝑎=√𝑎.

Мы знаем, что для любого положительного целого числа 𝑛: √𝑥=𝑥,𝑥≥0,для и аналогично √𝑥=𝑥,𝑥≥0.для

Предположим, что существует индекс 𝑚 такой, что (𝑥)=𝑥𝑥≥0,для

По степенному закону для показателей мы знаем, что (𝑥)=𝑥. 

Мы также знаем, что 𝑥=𝑥.

Следовательно, 𝑥=𝑥.

Итак, приравнивая индексы, получаем 𝑚𝑛=1,𝑚=1𝑛.

Итак, (𝑥)=𝑥,𝑥≥0.для

Так как √𝑥=𝑥, то мы можем сделать вывод, что (𝑥)=√𝑥,𝑥≥0.для

Следовательно, мы видим, что любое число 𝑎≥0, возведенное в степень 1𝑛 равно 𝑛-му корню из 𝑎. Другими словами, 𝑎=√𝑎, для любого натурального числа 𝑛 и 𝑎≥0.

Выведя общий корень 𝑛-й степени, мы можем затем использовать закон показателей для полномочия найти закон для √𝑎.

Мы знаем, что закон показателей степени (𝑎)=𝑎, где 𝑎≥0, а 𝑚 и 𝑛 могут принимать любые значения в реальной области.

Итак, используя 𝑎=√𝑎, мы можем написать √𝑎=𝑎=𝑎=𝑎,× где 𝑎≥0, 𝑛 — натуральное число, а 𝑚 — реальное значение.

Выведенные нами законы резюмируются в следующем определении.

Определение: Закон показателей для дробных показателей

Правило показателей для дробных показателей следующее:

• 𝑎=√𝑎, для любого значения 𝑎≥0 и любое натуральное число 𝑛,
• 𝑎=√𝑎=√𝑎, для любого значения 𝑎≥0 и любое натуральное число 𝑛.

Обратите внимание, что в приведенных выше законах 𝑎 может быть отрицательным, но это выходит за рамки этот объяснитель, поскольку он обращается к свойствам комплексных чисел. Далее, разные результаты получены для отрицательных значений 𝑎 в зависимости от порядка операций корней и степеней, если индекс не упрощен. Поэтому рекомендуется чтобы полностью упростить дробный индекс перед оценкой.

В следующем примере мы рассмотрим упрощение как с дробными, так и с отрицательными числами. индексы.

Пример 4: Упрощение выражения с дробными и отрицательными индексами

Упростите выражение 𝑥𝑦.

Ответ

Для упрощения начнем со степенного закона для дробей, который говорится, что 𝑎𝑏=𝑎𝑏, где 𝑏≠0, а 𝑎 и 𝑚 могут принимать любые действительные значения.

Итак, имеем 𝑥𝑦=𝑥𝑦.××

Итак, мы получаем 𝑥𝑦=𝑥𝑦.××

Далее воспользуемся законом экспонент для отрицательных индексов, который утверждает, что 𝑎=1𝑎,𝑎≠0,где

Это дает нам 𝑥𝑦=𝑥=𝑥÷1𝑦=𝑥×𝑦1=𝑥𝑦. 

Следовательно, 𝑥𝑦=𝑥𝑦.

В следующем примере мы упростим выражения с отрицательными дробными индексами.

Пример 5. Упрощение выражений с отрицательными дробными индексами

Упростить выражение 𝑡𝑣𝑡𝑣.

Ответ

Для упрощения начнем со степенного закона для дробей, который говорится, что 𝑎𝑏=𝑎𝑏, где 𝑏≠0, а 𝑎 и 𝑚 могут принимать любые действительные значения.

Итак, имеем 𝑡𝑣𝑡𝑣 = 𝑡𝑣𝑡𝑣.

Далее мы применяем закон о мощности для продуктов к продуктам числитель и знаменатель, в котором говорится, что (𝑎𝑏)=𝑎𝑏, где 𝑎, 𝑏 и 𝑚 могут принимать любые действительные значения.

Для числителя это дает нам 𝑡𝑣=𝑡×𝑣=𝑡×𝑣=𝑡×𝑣=𝑡×𝑣. ××()×()

А для знаменателя имеем 𝑡𝑣=𝑡×𝑣=𝑡×𝑣=𝑡×𝑣=𝑡×𝑣. ×()×()

Подставляя обратно в исходное выражение, получаем 𝑡𝑣𝑡𝑣 = 𝑡 × 𝑣𝑡 × 𝑣. 

Далее мы используем правило деления для экспонентов , в котором говорится, что 𝑎÷𝑎=𝑎,𝑎≠0.где

Для упрощения и во избежание ошибки перепишем выражение поэтому подобные термины сгруппированы вместе.

Итак,

Упрощая часть выражения с помощью 𝑡 𝑡𝑡=𝑡÷𝑡=𝑡=𝑡=𝑡=𝑡, 

Аналогично, упрощение части выражения с 𝑣-термами дает нам 𝑣𝑣=𝑣÷𝑣=𝑣=𝑣=𝑣=𝑣.() 9000 обе части вернемся к выражению, получим 𝑡𝑡×𝑣𝑣=𝑡×𝑣=𝑡𝑣.

Следовательно, 𝑡𝑣𝑡𝑣=𝑡𝑣.

В этом объяснителе мы узнали об отрицательных и дробных индексах, и как применять различные законы показателей, чтобы упростить алгебраические выражения.

Ключевые моменты

• Применяются законы умножения, деления и степени индексов а также для дробных и отрицательных индексов: ,
• (𝑎𝑏)=𝑎𝑏,
• 𝑎𝑏=𝑎𝑏, 𝑏≠0.

Закон показателей для отрицательных индексов 1𝑎=𝑎,𝑎≠0.где

Законы показателей степени для дробных индексов:

• 𝑎=√𝑎, для любого значения 𝑎 и любое натуральное число 𝑛,
• 𝑎=√𝑎=√𝑎, для 𝑎≥0 и любое натуральное число 𝑛.

Wolfram|Alpha Examples: Common Core Math: выражения и уравнения

Wolfram|Alpha Examples: Common Core Math: выражения и уравнения

Ого! Wolfram|Alpha не работает без JavaScript.

Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.

Примеры для

С шестого по восьмой класс учащиеся применяют и расширяют прежнее понимание арифметики для работы с алгебраическими выражениями, в которых переменные обозначают неизвестные или изменяющиеся числа. Учащиеся развивают беглость в написании выражений и управлении ими, а также в решении уравнений и неравенств, в том числе с показателями степени и радикалами. Учащиеся представляют и анализируют отношения между зависимыми и независимыми переменными и изучают пропорциональные отношения и линейные уравнения.

Стандарты Common Core

Получить информацию об Стандартах Common Core.

Поиск конкретного стандарта:

CCSS.Math.Content.6.EE.A.Общий базовый стандарт 17-го класса EE.B.4

Поиск всех стандартов в предметной области:

выражений и уравнений общие базовые стандарты 7-й класс

Манипулировать выражения и решать уравнения и неравенства, в том числе с отрицательными числами.

Упрощение выражений (CCSS.Math.Content.7.EE.A.1):

расширенная форма 3.2 (x — 5) — 8x + 4 (2.7 + x) объединять одинаковые члены 1/2x + 2 — 3/4x + 3/2

Факторные выражения (CCSS.Math.Content.7.EE.A.1):

коэффициент 6x + 18

Решить уравнение (CCSS.Math.

Content.7.EE.B.4a): решить 0,5 (x + 3) = -15решить 46,4 = 4x + 11,2

Решить неравенство (CCSS.Math.Content.7.EE.B.4b):

решить 8 — x > 2,2Больше примеров6 класс

Запись, оценка и обработка выражений и решение уравнений и неравенства.

Напишите выражение для представления словесного описания (CCSS.Math.Content.6.EE.A.2a):

вычтите x из 10

Вычислите выражение (CCSS.Math.Content.6.EE.A.2c) :

, ​​если х = 4, сколько будет 3х + 50?

Напишите эквивалентные выражения (CCSS.Math.Content.6.EE.A.3):

распределите 9 (y + 2) на коэффициент 28x + 18

Решите уравнение (CCSS.Math.Content.6.EE.B.7 ):

решить x + 1/2 = 3/4

Проверить решения уравнений и неравенств (CCSS.Math.Content.6.EE.B.5):

равно 5 решению 1/2x + 2 > 3/ 4?Еще примеры 8 класс

Работа с выражениями, в том числе с показателями степени; решать уравнения и системы уравнений; и использовать научное обозначение. 9-4 в виде десятичного числа

Выполнение вычислений в экспоненциальном представлении (CCSS.