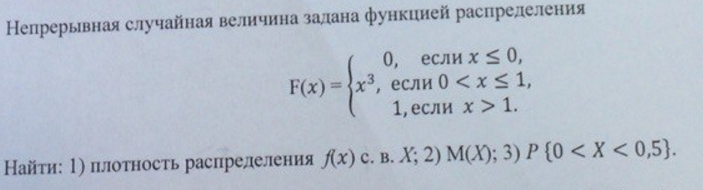Как узнать задает ли указанное правило функцию y f x: Вопросы»Задает ли указанное правило функцию y=F(x), если|Поступи в ВУЗ

Содержание

Задание 1.2. Контрольная работа 1. Вариант 3. Алгебра. 10 класс. Глизбург В. И. ГДЗ – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Помогите плиз ответить на вопросы к заданию
Задает ли указанное правило функцию у = f(x):

В случае положительного ответа:
а)   найдите область определения функции;
б)   вычислите значения функции в точках -6, -3, 0, 4;
в)   постройте график функции;
г)   найдите промежутки монотонности функции.

ответы

Держи

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

ЕГЭ

9 класс

11 класс

Химия

похожие вопросы 5

Помогите вычислить координаты точек. Работа № 36. Вариант 1. № 5. ГДЗ Алгебра 9 класс Кузнецова.

Вычислите координаты точек пересечения графика функции у = Зх2 — 15х с осью х.

ГДЗАлгебра9 классКузнецова Л. В.

Чему равна масса кабачка и тыквы вместе? ГДЗ 3 класс математика Моро Часть 1 Порядок выполнения действий стр 47 задание 3

Доброго дня, вот засела с братом за домашку, подскажите нам!
Масса кабачка 2 кг, а масса тыквы в 6 раз больше. Чему равна масса (Подробнее…)

ГДЗ3 классМатематикаМоро М. И.

Задание 1.1. Контрольная работа 1. Вариант 2. Алгебра. 10 класс. Глизбург В. И. ГДЗ

Как решить функцию?
Задает ли указанное правило функцию у = f(x):
(Подробнее…)

ГДЗАлгебраГлизбург В.И.10 класс

3. После того, как от ленты отрезали 11/5 м, осталось 4/7 ее первоначальной длины. Найдите… 6 класс А.П. Ершова Математика. С-13 Вариант А 1

3.
После того, как от ленты отрезали 11/5 м, осталось 4/7 ее первоначальной длины. Найдите длину оставшейся части ленты.

ГДЗМатематикаЕршова А.П.6 класс

Задание 6. Контрольная работа 1. Вариант 2. Алгебра. 10 класс. Глизбург В. И. ГДЗ

Товарищи хелп, горит контрольная, как ответить? (Подробнее…)

ГДЗАлгебраГлизбург В.И.10 класс

Контрольная работа для 10 класс №1

Контрольная работа № 1

Вариант 1

Задает ли указанное правило функцию:

В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках 0, 1, 3, – 1;

в) постройте график функции;

г) найдите промежутки монотонности функции.

Исследуйте функцию на четность.

На числовой окружности взяты точки Найдите все числа t , которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертеж.

Задайте аналитически и постройте график функции , у которой

______________________________________________________________

5. Найдите функцию, обратную функции . Постройте

на одном чертеже графики указанных двух взаимно обратных функций.

_______________________________________

Известно, что функция убывает на R. Решите неравенство

Контрольная работа № 1

Вариант 2

1. Задает ли указанное правило функцию:

В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках 0, 4;

в) постройте график функции;

г) найдите промежутки монотонности функции.

2. Исследуйте функцию на четность.

3. На числовой окружности взяты точки Найдите все числа t , которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертеж.

4. Задайте аналитически и постройте график функции , у которой

______________________________________________________________

5. Найдите функцию, обратную функции . Постройте

на одном чертеже графики указанных двух взаимно обратных функций.

_______________________________________

6.Известно, что функция возрастает на R. Решите неравенство

Контрольная работа № 1

Вариант 3

Задает ли указанное правило функцию:

В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках -1, 0, 2, 5;

в) постройте график функции;

г) найдите промежутки монотонности функции.

Исследуйте функцию на четность.

На числовой окружности взяты точки . Найдите все числа t , которым на данной окружности соответствуют точки, принадлежащие дуге KL. Сделайте чертеж.

Задайте аналитически и постройте график функции , у которой

______________________________________________________________

5. Найдите функцию, обратную функции . Постройте

на одном чертеже графики указанных двух взаимно обратных функций.

___________________________________

6.Известно, что функция убывает на R. Решите неравенство

Контрольная работа № 1

Вариант 4

1. Задает ли указанное правило функцию:

В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках 0, 4;

в) постройте график функции;

г) найдите промежутки монотонности функции.

2. Исследуйте функцию на четность.

На числовой окружности взяты точки . Найдите все числа t , которым на данной окружности соответствуют точки, принадлежащие дуге РВ. Сделайте чертеж.

Задайте аналитически и постройте график функции , у которой

______________________________________________________________

5. Найдите функцию, обратную функции . Постройте

на одном чертеже графики указанных двух взаимно обратных функций.

_______________________________________

6.Известно, что функция возрастает на R. Решите неравенство

5.2: Определение функций — Mathematics LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 25160

Харрис Квонг
Государственный университет Нью-Йорка во Фредонии через OpenSUNY

Определение: Функция

Пусть $A$ и $B$ — непустые множества. Функция

от $A$ до $B$ является правилом, которое присваивает каждому элементу из $A$ уникальный элемент из $B$. Мы называем $A$ доменом и $B$ кодовым доменом функции. Если функция называется $f$, мы пишем $f :A \to B$. Для данного $x\in A$ связанный с ним элемент в $B$ называется его изображение под $f$. Другими словами, функция – это отношение от $A$ к $B$ с условием, что для каждого элемента в домене существует уникальный образ в домене (на самом деле это два условия: существование образ и уникальность образа). Мы обозначаем его $f(x)$, что произносится как «$f$ of $x$».

Функцию иногда называют картой или отображением . Поэтому мы иногда говорим $f$ отображает $x$ в его образ $f(x)$.

Пример $\PageIndex{1}\label{eg:defnfcn-01}$

Функция $f:\{a,b,c\} $ в $\{1,3,5, 9\}$ определяется по правилу \[f(a)=1, \qquad f(b)=5, \qquad\mbox{and}\qquad f(c) = 9. \] четко определенная функция. Правило присваивания можно свести в таблицу: \[\begin{array}{|c||c|c|c|} \hline x & a & b & c \\ \hline f(x)& 1 & 5 & 9 \\ \hline \end{array}\] Мы также можем изобразить правило присваивания с помощью стрелочная диаграмма , как показано на рис. 6.2.

Два ключевых требования к функции:

каждый элемент в домене имеет изображение под $f$, и
изображение уникально.

Вы можете помнить, что каждый элемент в $A$ имеет только одного «партнера» в $B$.

Пример $\PageIndex{2}\label{eg:defnfcn-02}$

На рис. 6.3 показаны два примера не-функций. В изображении слева один из элементов домена не имеет связанного с ним изображения; таким образом, отсутствует существование изображения. На рисунке справа одному из элементов в домене назначено два изображения; таким образом, отсутствует уникальность изображения. Оба не являются функциями.

практическое упражнение $\PageIndex{1}\label{he:defnfcn-01}$

Выполните эти правила \[\begin{array}{|c||c|c|c|} \hline x & a & b & c \\ \hline f(x)& 5 & 3 & 3 \\ \hline \end{array} \hskip0. 75in \begin{array}{|c||c|c|} \hline x & b & c \\ \hline g(x)& 9 & 5 \\ \hline \end{массив} \hskip0.75in \begin{массив}{|c||c|c|c|c|} \ hline x & a & b & b & c \\ \hline h(x)& 1 & 5 & 3 & 9 \\ \hline \end{array}\] производят функции из $\{a,b,c\ }$ в $\{1,3,5,9\}$? Объяснять.

практическое упражнение $\PageIndex{2}\label{he:defnfcn-02}$

Соответствует ли определение \[r(x) = \cases{ x & если сегодня понедельник, \cr 2x & если сегодня не понедельник \cr}\] создать функцию от $\mathbb{R}$ до $\mathbb{R}$? Объяснять.

практическое упражнение $\PageIndex{3}\label{he:defnfcn-03}$

Соответствует ли определение \[s(x) = \cases{ 5 & if $x<2$, \cr 7 & если $x>3$, \cr}\] производят функцию от $\mathbb{R}$ до $\mathbb{R}$? Объяснять.

Пример $\PageIndex{3}\label{eg:defnfcn-03}$

Функция $f:{[0,\infty)}\to{\mathbb{R}}$ определяется как \[f(x) = \sqrt{x}.\] Также функция ${g}:{[2,\infty)}\to{\mathbb{R}}$ определяется как \[g( x) = \sqrt{x-2}. \] Можете ли вы объяснить, почему областью $g$ является $[2,\infty)$?

Пример $\PageIndex{4}\label{eg:defnfcn-04}$

Пусть $A$ обозначает множество студентов, изучающих дискретную математику, а $G=\{A,B,C, D,F\}$, а $\ell(x)$ — итоговая оценка учащегося $x$ по дискретной математике. Каждый учащийся должен получить итоговую оценку, а преподаватель должен сообщить об одной и только одной итоговой оценке для каждого учащегося. $\ell:A \to G.$ Это именно то, что мы называем функцией.

Пример $\PageIndex{5}\label{eg:defnfcn-05}$

Функция ${n}:{\mathscr{P}(\{a,b,c,d\})} \to{\mathbb{Z}}$ определяется как $n(S)=|S|$. Он оценивает мощность подмножества $\{a,b,c,d\}$. Например, \[n\big(\{a,c\}\big) = n\big(\{b,d\}\big) = 2.\] Обратите внимание, что $n(\emptyset)=0 $.

практическое упражнение $\PageIndex{4}\label{he:defnfcn-04}$

Рассмотрим пример 5.2.5. Какие другие подмножества $S$ множества $\{a,b,c,d\}$ также дают $n(S)=2$? Какое самое маленькое и какое самое большое изображение может создать функция $n$?

Пример $\PageIndex{6}\label{eg:defnfcn-06}$

Рассмотрим функцию \({f}:{\mathbb{Z}_7}\to{\mathbb{Z}_5}\ ).

Домен и кодовый домен:

\[\mathbb{Z}_7 = \{0,1,2,3,4,5,6\}, \qquad\mbox{and}\qquad \mathbb{Z} _5 = \{0,1,2,3,4\},\]

соответственно. Отличаются не только их элементы, но и бинарные операции. В домене $\mathbb{Z}_7$ арифметика выполняется по модулю 7, но арифметика в домене $\mathbb{Z}_5$ выполняется по модулю 5. Поэтому нам нужно быть осторожными при описании правило присваивания, если речь идет о вычислении. Можно сказать, например,

\[f(x) = z, \quad\mbox{где } z \equiv 3x \pmod{5}.\]

Следовательно, начиная с любого элемента $x$ в $\mathbb{Z }_7$, мы рассматриваем $x$ как обычное целое число, умножаем на 3 и уменьшаем ответ по модулю 5, чтобы получить изображение $f(x)$. Для краткости мы будем писать

\[f(x) \equiv 3x \pmod{5}.\]

Мы суммируем изображения в следующей таблице:

\[\begin{array}{|c|| *{7}{c|}} \hline n & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline f(n) & 0 & 3 & 1 & 4 & 2 & 0 & 3 \\ \hline \end{массив}\]

Обратите внимание, что изображения начинают повторяться после $f(4)=2$.

практическое упражнение $\PageIndex{5}\label{he:defnfcn-05}$

Табулируйте изображения ${g}:{\mathbb{Z}_{10}}\to{\ mathbb{Z}_5}$, определяемый \[g(x) \equiv 3x \pmod{5}.\]

Определение: функция как набор упорядоченных пар $A\times B$ такой, что $y=f(x)$.

Функция по определению представляет собой набор из заказанных пар, с некоторыми ограничениями.

Пример $\PageIndex{7}\label{eg:defnfcn-07}$

Функция $f$ в примере 5.26 может быть записана как набор упорядоченных пар \[\{(0,0) , (1,3), (2,1), (3,4), (4,2), (5,0), (6,3)\}.\] Если настаивать, мы могли бы отобразить график функции, использующей $xy$-плоскость, напоминающую обычную декартову плоскость. Имейте в виду: элементы $x$ и $y$ происходят из $A$ и $B$ соответственно. Мы можем «построить» график для $f$ в примере 5.26, как показано ниже.

Помимо использования графического представления, мы также можем использовать $(0,1)$-матрицу. $(0,1)$-матрица — это матрица, элементами которой являются 0 и 1. В качестве функции $f$ используется матрица $7\times5$, строки и столбцы которой соответствуют элементов $A$ и $B$ соответственно, и поставить единицу в $(i,j)$-ю запись, если $j=f(i)$, и ноль в противном случае. Результирующая матрица равна

\[\begin{array}{cc} & \begin{array}{ccccc} 0 & 1 & 2 & 3 & 4 \end{array} \\ \begin{array}{c} 0 \\ 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \end{массив} & \left(\begin{массив}{ccccc} 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \ \ 0 & 0 & 0 & 1 & 0 \end{массив}\right) \end{массив}\]

Мы называем это матрицей инцидентности для функции $f$.

практическое упражнение $\PageIndex{6}\label{he:defnfcn-06}$

«Постройте» график $g$ в практическом упражнении 5.2.5

Резюме и обзор

Функция $f$ из набора $A$ в набор $B$ (называемый соответственно доменом и кодоменом) — это правило, описывающее, как значение в codomain $B$ назначается элементу из домена $A$.
Но это не просто правило; скорее, правило должно присваивать каждому элементу $x$ в домене уникальное значение в домене кодов.
Это уникальное значение называется образом $x$ относительно функции $f$ и обозначается $f(x)$.
Мы используем обозначение ${f}:{A}\to{B}$, чтобы указать, что имя функции — $f$, домен — $A$ и кодовый домен — \ (Б\).
Функция ${f}:{A}\to{B}$ представляет собой набор всех упорядоченных пар $(x,y)$ из $A\times B$, таких что $y= f(x)$.
График функции не может быть кривой, как в случае реальной функции. Это может быть просто набор точек.
Мы также можем отображать изображения функции в виде таблицы или представлять функцию с помощью матрицы инцидентности.

Упражнения

упражнение $\PageIndex{1}\label{ex:defnfcn-01}$

Какое подмножество $A$ из $\mathbb{R}$ вы бы использовали, чтобы сделать $ {f}:{A}\to{\mathbb{R}}$ определено функцией $f(x) = \sqrt{3x-7}$?

Ответить: $\big[\frac{7}{3},\infty\big)$

упражнение $\PageIndex{2}\label{ex:defnfcn-02}$

Какое подмножество $A$ из $\mathbb{R}$ вы бы использовали для создания

$ {g}:{A}\to{\mathbb{R}}$, где $g(x) = \sqrt{(x-3)(x-7)}$
${h}:{A}\to{\mathbb{R}}$, где $h(x) = \frac{x+2}{\sqrt{(x-2)(5-x )}}$

функции?

упражнение $\PageIndex{3}\label{ex:defnfcn-03}$

Какие из этих данных поддерживают функцию от $\{1,2,3,4\}$ до $\{1,2,3,4\}$? Объяснять.

\[\begin{array}{|c||c|c|c|} \hline x & 1 & 2 & 3 \\ \hline f(x) & 3 & 4 & 2 \\ \hline \end {массив} \hskip0.4in \begin{массив}{|c||c|c|c|c|} \hline x & 1 & 2 & 3 & 4 \\ \hline g(x) & 2 & 4 & 3 и 2 \\ \hline \end{массив} \hskip0.4in \begin{array}{|c||c|c|c|c|c|} \hline x & 1 & 2 & 3 & 3 & 4 \\ \hline h(x) & 2 & 4 & 3 & 2 & 3 \\ \hline \end{массив}\]

Ответить: Только $g$ является функцией. Изображение $f(4)$ не определено, и есть два значения для $h(3)$. Следовательно, и $f$, и $h$ не являются корректно определенными функциями.

упражнение $\PageIndex{4}\label{ex:defnfcn-04}$

(a) Используйте диаграммы со стрелками, чтобы показать три различные функции из $\{1,2,3,4\}$ в $\{1,2,3,4\}$.
(b) Сколько различных функций от $\{1,2,3,4\}$ до $\{1,2,3,4\}$ возможно? 92=9\).

${t}:{\mathbb{R}}\to{\mathbb{R}}$, где $|x-t(x)|=4$.

упражнение $\PageIndex{7}\label{ex:defnfcn-07}$

Используйте диаграммы со стрелками, чтобы показать две разные функции от $\{a,b,c,d\}$ до $ \{1,2,3,4,5,6\}$.

Ответ: ответы будут разными

упражнение $\PageIndex{8}\label{ex:defnfcn-08}$

Пусть $T$ будет вашим семейным древом, которое включает вашу биологическую мать, вашу бабушку по материнской линии, вашу прабабушку по материнской линии и так далее, и все их потомки женского пола. Определите, что из следующего определяет функцию от $T$ до $T$.

${h_1}:{T}\to{T}$, где $h_1(x)$ — мать $x$.
${h_2}:{T}\to{T}$, где $h_2(x)$ — сестра $x$.
${h_3}:{T}\to{T}$, где $h_3(x)$ — тетя $x$.
${h_4}:{T}\to{T}$, где $h_4(x)$ — старшая дочь бабушки $x$ по материнской линии.

упражнение $\PageIndex{9}\label{ex:defnfcn-09}$

Для каждой из следующих функций определите образ данного $x$.

${k_1}:{\mathbb{N}-\{1\}}\to{\mathbb{N}}$, $k_1(x)=\mbox{наименьший простой делитель}x $, $х=217$.
${k_2}:{\mathbb{Z}_{11}}\to{\mathbb{Z}_{11}}$, $k_2(x)\equiv3x$ (mod 11), \ (х=6\).
${k_3}:{\mathbb{Z}_{15}}\to{\mathbb{Z}_{15}}$, $k_3(x)\equiv3x$ (mod 15), \ (х=6\).

Ответить: (а) 7 (б) 7 (в) 3

упражнение $\PageIndex{10}\label{ex:defnfcn-10}$

Для каждой из следующих функций определите образы заданных $x$-значений.

${\ell_1}:{\mathbb{Z}}\to{\mathbb{Z}}$, $\ell_1(x)=x\bmod7$, $x=250$ , $х=0$ и $х=-16$.

Примечание : Напомним, что без круглых скобок обозначение «мод» означает бинарную операцию мод.

${\ell_2}:{\mathbb{Z}}\to{\mathbb{Z}}$, $\ell_2(x)=\gcd(x,24)$, $x= 100$, $х=0$ и $х=-21$.

Эта страница под названием 5.2: Определение функций распространяется по лицензии CC BY-NC-SA, ее автором, ремиксом и/или куратором является Харрис Квонг (OpenSUNY) .

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Харрис Квонг
Лицензия
CC BY-NC-SA
Показать страницу TOC
да
Теги
1. стрелочная схема
2. кодовый домен
3. домен
4. карта
5. сопоставление

Раздел 4.

3 Обзор Раздел 4.3 Обзор

Расширенные функции

Индивидуальные функции | На Функции | Индивидуальные соответствия | Обратные функции

Индивидуальные функции

Пусть f : A B, функция из множества A в множество B. f называется однозначной функцией или инжекция тогда и только тогда, когда для всех элементов a ₁ и ₂ в,

Эквивалентно

И наоборот, функция f : A B не являются взаимно однозначными функциональными элементами a ₁ и ₂ в A такие, что f (a ₁ ) = f (a ₂ ) и ₁ а ₂ .

В терминах стрелочных диаграмм функция один к одному принимает различные точки домена в разные точки содомена. Функция не является однозначной функционируют, если хотя бы две точки области перенесены в одну и ту же точку содомен. Рассмотрим следующие диаграммы:


Один к одному функция	Функция А это не один к одному

Однозначные функции на бесконечных множествах

Чтобы доказать, что функция взаимно однозначна, метод прямого обычно используется доказательство. Рассмотрим пример:

Пример : Определить f : R R по правилу

Докажите, что f взаимно однозначно.

Доказательство: предположим, что x ₁ и x ₂ — действительные числа такие, что ф (х ₁) = ф (х ₂). (Нам нужно показать x ₁ = х ₂. )

5x ₁ — 2 = 5x ₂ — 2

Прибавление 2 к обеим сторонам дает

5x ₁ = 5x ₂

Деление на 5 с обеих сторон дает

х ₁ = х ₂

Мы доказали, что f взаимно однозначно.

С другой стороны, чтобы доказать функцию, которая не является однозначной, счетчик надо подавать пример.

Пример : Определить ч : Р Р определяется по правилу h (n) = 2n ² . Докажите, что ч есть не один к одному, приводя встречный пример.

Счетчик пример:

Пусть n ₁ = 3 и n ₂ = -3. Затем

h (n ₁ ) = ч (3) = 2 * 3 ² = 18 и

ч (н ₂ ) = ч (-3) = 2 * (-3) ² = 18

Следовательно ч (n ₁) = ч (n ₂), но n ₁ n ₂, и поэтому h не является взаимно однозначным.

Практические упражнения

Функции

Пусть f : AB быть функцией из множества A в множество B. f вызывается или сюръективен тогда и только тогда, когда все элементы в B могут найти некоторые элементы в A со свойством y = f (x), где y B и х А.

И наоборот, функция f : A B не на у в B такое, что x А, е (х) у.

В представлениях стрелочных диаграмм функция включена, если каждый элемент co-domain имеет стрелку, указывающую на него из какого-либо элемента домена. Функция не включен, если на какой-либо элемент домена не указывает стрелка. Рассмотреть возможность следующие схемы:


Функция включения	Функция А это не на

Доказательство или опровержение функций На

Пример : Определить f : R Р по правилу f (x) = 5x — 2 для всех x R . Докажите, что f лежит на.

Доказательство: Пусть y R . (Нам нужно показать, что х в R такое, что ф (х) = у.)

Если такое действительное число x существует, то 5x -2 = y и х = (у + 2)/5. x — действительное число, так как суммы и частные (кроме деления на 0) действительных чисел являются действительными числами. Отсюда следует, что

Пример : Определить г : Z З по правилу g (n) = 2n — 1 для всех n Z . Докажите, что g не является прямым, приведя контрпример.

Пример счетчика:

Домен g — это Z по определению г и 0 Z . Однако г (n) 0 для любого целого числа n.

Если г (n) = 0, то

2n -1 = 0

2n = 1 на добавление 1 с обеих сторон

n = 1/2 на деление 2 с обеих сторон

Но 1/2 не является целым числом. Следовательно, нет целых n для g (n) = 0, поэтому g не совпадает.

Практические упражнения

Один к одному Соответствия SRC=»images/unction>

ф : А Б может быть как один к одному, так и одновременно. Это означает, что при любом элемента a в A существует единственный соответствующий элемент b = f(a) в B. Также для любого IMG SRC=»images/I>b в B существует элемент a в A такой, что f (a) = b, поскольку f находится на и существует только один такой b, как f один к одному. В этом случае функция f устанавливает сопряжение между элементами из A и элементов B, который соединяет каждый элемент A ровно с одним элементом из B и каждый элемент B ровно с одним элементом из A. Это спаривание называется однозначное соответствие или биекция . При изображении стрелочными диаграммами это показано ниже:

Функция, являющаяся взаимно-однозначным соответствием

Обратные функции

Если есть функция f которой соответствует onIMG SRC=»images//I> из множества A в множество B, то существует функция из B в A, которая «отменяет» действие f .

Задание 1.2. Контрольная работа 1. Вариант 3. Алгебра. 10 класс. Глизбург В. И. ГДЗ – Рамблер/класс

Контрольная работа для 10 класс №1

5.2: Определение функций — Mathematics LibreTexts

Определение: Функция

Резюме и обзор

Упражнения

Раздел 4.

Добавить комментарий Отменить ответ