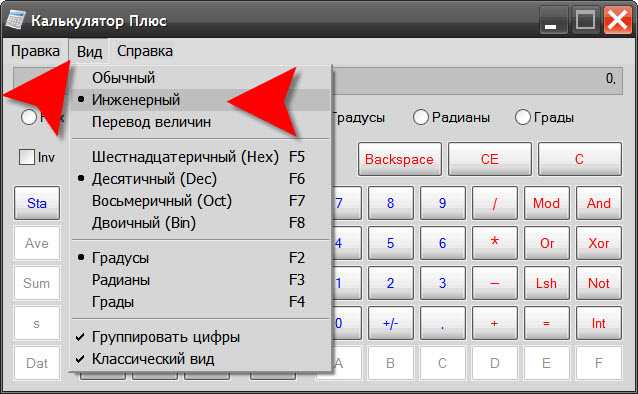
Онлайн-калькулятор Semestr Math. Основные возможности
Оформление результатов в формате Word
По умолчанию все вычисления оформляются в файле формата MS Word. Однако следует учесть, что такая возможность имеется только для браузеров, поддерживающих javascript. Если javascript отключены, необходимо включить их (в настройках браузера). В остальных случаях всегда доступен просмотр решения в формате html (т.е. непосредственно в браузере).Решение в Word не доступно чаще всего в этих случаях:
- В браузере установлен блокиратор AdBlock (AdFender, AdMuncher, Adguard). Если установлены антивирусы Kaspersky, DrWeb или Avast), то необходимо временно отключить этот фильтр или добавить сайт в список исключений (Подробнее).
- Если Вы ранее пользовались калькулятором, то необходимо очистить кэш вашего браузера и перезагрузить страницу.
- Загрузились не все javascript на предыдущем шаге. Необходимо вернуться на предыдущий шаг, обновить страницу и дождаться загрузки всех скриптов javascript.

Работа с формулами WORD
Для редактирования формул в MS Word 2003 используйте Shift+F9 или двойной щелчок мышью для запуска редактора формул Equation 3.0.
Частые вопросы и ответы
- Использовал ваш метод ветвей и границ, но рисунки не подгружаются.
Если количество рисунков на странице решения больше 15, то многие из них сразу не будут отображены. Для их отображение нажмите на правую кнопку мыши и выполните команду Перезагрузить изображение. - Картинки в калькуляторе Графический метод все равно не отображаются.
Проверьте формат входных данных. Например, положительные числа записываются без знака +. Правильно: 3,6,11. Неправильно: +3,+5. - Не получается решить задачу методом ветвей и границ с тремя переменными
На данный момент сервис учитывает только две переменные. (1/5)-1
(1/5)-1
- Не могу скачать решение в Word
Файл в Word необходимо скачать в течение 20 минут после получения решения. - В полученном решении формата Word в тексте встречаются слова Ошибка.
Возможно в двух случаях.
1. Это особенности отображения формул при большом размере шрифта. Необходимо выделить формулу Ошибка и выбрать меньший размер шрифта. Если формула находится в таблице, можно увеличить ширину столбца.
2. Зависит от региональных настроек интерфейса программы MS Word. А именно, какой символ используется в качестве разделителя списков. Подробнее.
Автозаполнение данных в браузере
Чтобы не заполнять ранее введенные данные, нажмите кнопку Или можно нажать кнопку Назад в меню браузера.
Или можно нажать кнопку Назад в меню браузера.
Использование Microsoft Excel в качестве калькулятора
Знакомство с Excel
Справка и обучение по Excel
Знакомство с Excel
Знакомство с Excel
Использование Microsoft Excel в качестве калькулятора
-
Создание книги
Статья -
Вставка и удаление листов
Статья -
Как перемещать и копировать листы или их данные в Excel
Статья -
Печать листа или книги
Статья -
Использование Microsoft Excel в качестве калькулятора
Статья -
Автоматическое заполнение ячеек листа данными
Статья -
Создание раскрывающегося списка
Статья
Далее: Строки и столбцы
Вместо калькулятора используйте для математических расчетов Microsoft Excel!
Вы можете ввести простые формулы для с суммы, деления, умножения и вычитания двух или более числных значений.
 Кроме того, с помощью функции «Автоумма» можно быстро свести ряд значений, не вводя их в формулу вручную. Создав формулу, вы можете скопировать ее в смежные ячейки, не создав одну и ту же формулу раз за разом.
Кроме того, с помощью функции «Автоумма» можно быстро свести ряд значений, не вводя их в формулу вручную. Создав формулу, вы можете скопировать ее в смежные ячейки, не создав одну и ту же формулу раз за разом.Вычитание в Excel
Умножение в Excel
Деление в Excel
Простые формулы
Все записи формул начинаются со знака равенства (=). Чтобы создать простую формулу, просто введите знак равенства, а следом вычисляемые числовые значения и соответствующие математические операторы: знак плюс ( +) для сложения, знак минус (—) для вычитания, звездочку (*) для умножения и наклонную черту (/) для деления. Затем нажмите клавишу ВВОД, и Excel тут же вычислит и отобразит результат формулы.
Например, если в ячейке C5 ввести формулу =12,99+16,99 и нажать клавишу ВВОД, Excel вычислит результат и отобразит 29,98 в этой ячейке.

Формула, введенная в ячейке, будет отображаться в строке формул всякий раз, как вы выберете ячейку.
Важно: Хотя существует функция СУММ, функция ВЫЧЕСТЬ не существует. Вместо этого используйте в формуле оператор минус (-). Например, =8-3+2-4+12. Вы также можете использовать знак «минус» для преобразования числа в его отрицательное значение в функции СУММ. Например, в формуле =СУММ(12;5;-3;8;-4) функция СУММ используется для сложить 12, 5, вычесть 3, сложить 8 и вычесть 4 в этом порядке.
Использование автосуммирования
Формулу СУММ проще всего добавить на лист с помощью функции автосуммирования. Выберите пустую ячейку непосредственно над или под диапазоном, который нужно суммировать, а затем откройте на ленте вкладку Главная или Формула и выберите Автосумма > Сумма. Функция автосуммирования автоматически определяет диапазон для суммирования и создает формулу.
 Она также работает и по горизонтали, если вы выберете ячейку справа или слева от суммируемого диапазона.
Она также работает и по горизонтали, если вы выберете ячейку справа или слева от суммируемого диапазона.Примечание: Функция автосуммирования не работает с несмежными диапазонами.
Автосуммирование по вертикали
На рисунке выше показано, что функция автосуммирования автоматически определила ячейки B2: B5 в качестве диапазона для суммирования. Вам нужно только нажать клавишу ВВОД для подтверждения. Если вам нужно добавить или исключить несколько ячеек, удерживая нажатой клавишу SHIFT, нажимайте соответствующую клавишу со стрелкой, пока не выделите нужный диапазон. Затем нажмите клавишу ВВОД для завершения задачи.
Руководство по функции Intellisense: СУММ(число1;[число2];.
 ..) Плавающий тег под функцией — это руководство Intellisense. Если щелкнуть имя функции или СУММ, изменится синяя гиперссылка на раздел справки для этой функции. Если щелкнуть отдельные элементы функции, их представительные части в формуле будут выделены. В этом случае будет выделен только B2:B5, поскольку в этой формуле есть только одна ссылка на число. Тег Intellisense будет отображаться для любой функции.
..) Плавающий тег под функцией — это руководство Intellisense. Если щелкнуть имя функции или СУММ, изменится синяя гиперссылка на раздел справки для этой функции. Если щелкнуть отдельные элементы функции, их представительные части в формуле будут выделены. В этом случае будет выделен только B2:B5, поскольку в этой формуле есть только одна ссылка на число. Тег Intellisense будет отображаться для любой функции.Автосуммирование по горизонтали
Дополнительные сведения см. в статье о функции СУММ.
Избегание переписывания одной формулы
После создания формулы ее можно просто копировать в другие ячейки, а не создавать ту же формулу. Вы можете скопировать формулу или использовать маркер заполнения для копирования формулы в смежные ячейки.
Например, когда вы копируете формулу из ячейки B6 в ячейку C6, в ней автоматически изменяются ссылки на ячейки в столбце C.

При копировании формулы проверьте правильность ссылок на ячейки. Ссылки на ячейки могут меняться, если они являются относительными. Дополнительные сведения см. в статье Копирование и вставка формулы в другую ячейку или на другой лист.
Что использовать в формуле для имитации клавиш калькулятора?
Клавиша калькулятора
Метод Excel
Описание, пример
Результат
+ (клавиша плюс)
+ (плюс)
Используйте в формуле для сложения чисел.
 Пример: =4+6+2
Пример: =4+6+212
— (клавиша минус)
— (минус)
Используйте в формуле для вычитания чисел или обозначения отрицательного числа.
Пример: =18-12
Пример: =24*-5 (24 умножить на отрицательное число 5)
6-120
x (клавиша умножения)
* (звездочка)
Используйте в формуле для умножения чисел.
 Пример: =8*3
Пример: =8*324
÷ (клавиша деления)
/ (косая черта)
Используйте в формуле для деления одного числа на другое. Пример: =45/5
9
% (клавиша процента)
% (процент)
Используйте в формуле со знаком * для умножения на процент.
 Пример: =15%*20
Пример: =15%*203
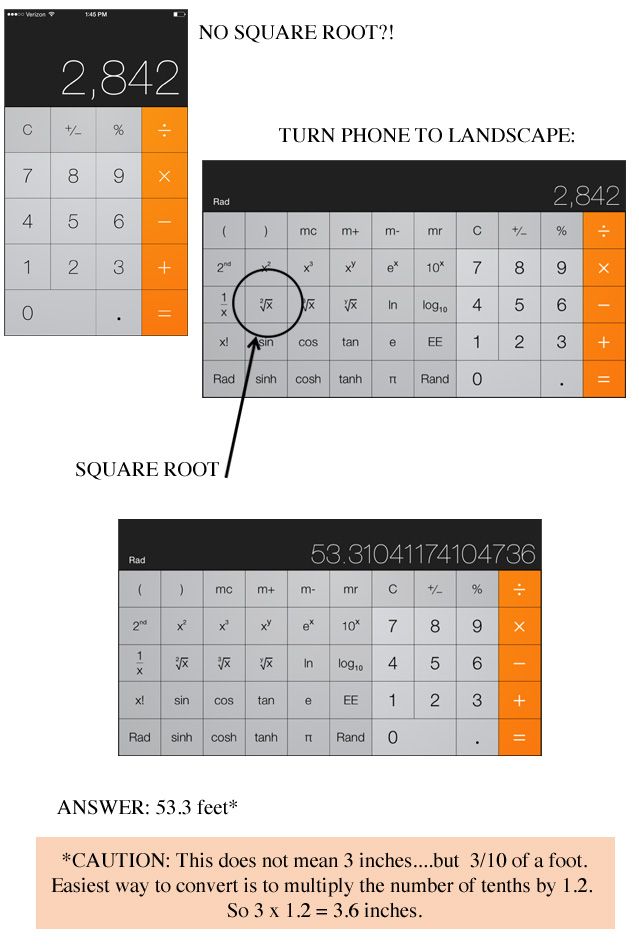
√ (квадратный корень)
SQRT (функция)
Используйте функцию SQRT в формуле, чтобы найти квадратный корень числа. Пример: =SQRT(64)
8
1/x (обратная величина)
=1/n
Используйте в формуле выражение =1/n, где n — число, на которое нужно разделить 1.

Пример: =1/8
0,125
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Калькулятор цифрового корня
Начнем с самого интересного применения цифрового корня:
- фокус !
Во-первых, вам нужен такой же занудный друг, как и вы. Попросите их мысленно выбрать число от 1 до 10. Теперь попросите их умножить его на 9 и найти сумму цифр кратного. Теперь притворитесь, что читаете их мысли, и скажите им, что они получили 9 в качестве ответа. Вы можете проделать этот трюк и с гораздо большими числами, однако вашему другу может потребоваться немного больше времени, чтобы вычислить цифровой корень из больших чисел, не зная этого трюка.
 Обратитесь к Свойству 1, упомянутому ниже, для получения дополнительных разъяснений по этому вопросу.
Обратитесь к Свойству 1, упомянутому ниже, для получения дополнительных разъяснений по этому вопросу.А теперь время откровений! Например, ваш друг выбрал 5. Умножив 5 на 9, он получит 45. «4+5=9», что не должно быть слишком сложно вычислить. Вы можете усложнять фокус, добавляя дополнительную драму, например, попросив друга перетасовать цифры.
- Цифровые корни можно использовать как примитивный способ проверки точности арифметических операций, таких как вычитание, умножение и сложение.
Давайте посмотрим, как мы можем использовать цифровой корень для проверки правильность умножения . Чтобы проверить правильность умножения или нет, перед выполнением умножения вычислите цифровой корень чисел в обеих частях уравнения. Затем умножьте цифровые корни и вычислите цифровой корень произведения. Цифровой корень в обеих частях уравнения должен быть равен, чтобы умножение было правильным. Давайте рассмотрим пример:
456*376= 398765.
Давайте сначала посмотрим на левую часть уравнения и найдем сумму цифр в этой части. Цифровой корень из
456это6. Цифровой корень376равен7. Перемножив6и7, мы получим42. Цифровой корень42равен6. Теперь цифровой корень правой части выглядит как2. Поскольку цифровые корни, полученные по обе стороны от знака равенства, различны, это умножение неверно.Аналогичным образом давайте посмотрим, как мы можем использовать цифровой корень для проверки правильности задачи на вычитание . Например, рассмотрим
340-172=168. Цифровой корень340равен7. Цифровой корень172равен1. Вычитая эти два, мы получаем6. Теперь давайте проверим цифровой корень правой стороны. Цифровой корень168равен6, так что это вычитание верно.
- Цифровые корни также могут помочь обнаружить ошибки округления в последовательности Фибоначчи .
При вычислении последовательности Фибоначчи для очень больших чисел вычислительные программы могут округлить и, следовательно, привести к ошибке при создании следующего числа в последовательности. Цифровой корень последовательности Фибоначчи имеет 24-значный цикл (1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9)., 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9), что означает, что последовательность цифрового корня повторяется каждые 24 числа. Если есть какое-то изменение в ожидаемой последовательности цифровых корней, это может быть связано с ошибкой округления. Вы можете использовать наш калькулятор Фибоначчи, чтобы легко сгенерировать последовательность Фибоначчи!
- Мы также можем использовать метод цифровой суммы для корректности квадратного корня .
Здесь, просто взглянув на цифровой корень полного квадрата, мы можем догадаться, правильный он или нет.
 Цифровым корнем полного квадрата будет одна из четырех цифр 1, 4, 7, 9.только. Следовательно, если мы найдем любую другую цифру в качестве цифровой суммы, число точно не будет идеальным квадратом.
Цифровым корнем полного квадрата будет одна из четырех цифр 1, 4, 7, 9.только. Следовательно, если мы найдем любую другую цифру в качестве цифровой суммы, число точно не будет идеальным квадратом.Калькулятор квадратного корня — ТАБЛИЦА ОЦЕНОК Z
Калькулятор квадратного корня
Быстро вычисляйте квадратный корень с помощью нашего простого в использовании онлайн-калькулятора квадратного корня. Получите мгновенные результаты и сэкономьте время с помощью нашего эффективного инструмента.
Калькулятор квадратного корняВведите число:
Как использовать наш калькулятор квадратного корня
- Введите число, для которого вы хотите вычислить квадратный корень, в поле ввода с надписью «Введите число».
- Нажмите кнопку «Рассчитать», чтобы увидеть квадратный корень из введенного числа.
- Значение квадратного корня будет отображаться в сообщении под кнопкой «Рассчитать» с пометкой «Результат».
- Если вы хотите вычислить квадратный корень для другого числа, просто введите новое число и снова нажмите «Вычислить».

Вот оно! Этот калькулятор может вычислять только квадратные корни. Если вам нужно вычислить другие типы корней, такие как кубический корень, корень четвертой степени, корень пятой степени и т. д., воспользуйтесь нашим калькулятором корней.Руководство по квадратным корням: все, что вам нужно знать
Квадратные корни могут быть сложной темой для многих людей, но при правильном понимании и инструментах любой может освоить эту концепцию. В этом посте мы рассмотрим различные аспекты квадратных корней, в том числе способы их вычисления вручную, формулы, используемые в калькуляторах квадратных корней, и способы нахождения квадратного корня из полных квадратов. Мы также рассмотрим иррациональные числа, отрицательные квадратные корни и способы нахождения квадратных корней с помощью деления в длину. Помните, что если вам нужно выполнить быстрый расчет, вы всегда можете воспользоваться нашим бесплатным калькулятором квадратного корня выше.

Как вычислить квадратный корень
Прежде чем мы углубимся в различные методы вычисления квадратного корня, давайте сначала определим, что такое квадратный корень. Квадратный корень — это число, которое при умножении само на себя дает исходное значение. Например, квадратный корень из 81 равен 9, потому что 9, умноженное само на себя, равно 81.
Символ квадратного корня представлен символом √ и используется для обозначения квадратного корня числа. Например, √25 равно 5.
Чтобы вычислить квадратный корень вручную, можно использовать несколько различных методов. Одним из наиболее распространенных является алгоритм квадратного корня, который включает в себя деление числа, из которого вы хотите найти квадратный корень, на серию меньших чисел. Например, чтобы найти квадратный корень из 64, вы должны начать с деления его на 2, что дает вам 32. Затем вы делите 64 на 32, что дает вам 2. Отсюда вы продолжаете процесс, пока не достигнете желаемого уровень точности.
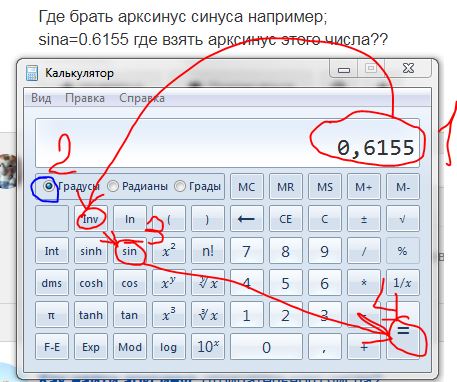
Может ли квадратный корень быть отрицательным
Отрицательные числа являются важным аспектом математики и играют важную роль в квадратных корнях. Отрицательный квадратный корень — это квадратный корень, который меньше нуля. Например, квадратный корень из -81 равен -9.
Для вычисления отрицательных квадратных корней можно использовать те же методы, что и для положительных квадратных корней. Однако нужно иметь в виду, что результат будет отрицательным.Вычисление квадратного корня вручную
Вычисление квадратного корня вручную может быть утомительным процессом, но это важный навык. Чтобы вычислить квадратный корень вручную, вы можете использовать метод, называемый делением в длину. Этот метод включает в себя разбиение числа, из которого вы хотите найти квадратный корень, на более мелкие части, а затем деление его на ряд меньших чисел, пока вы не достигнете желаемого уровня точности.
Например, чтобы найти квадратный корень из 100, сначала нужно разбить его на две цифры (10 и 0). Затем вы разделите 10 на 2, что даст вам 5. Затем вы добавите следующую цифру (0) и получите 50. Затем вы разделите 50 на 20, что даст вам 2,5. Вы продолжаете этот процесс, пока не достигнете желаемого уровня точности. Конечно, всегда достаточно просто ввести числа в онлайн-калькулятор квадратного корня выше и нажать «Рассчитать».
Затем вы разделите 10 на 2, что даст вам 5. Затем вы добавите следующую цифру (0) и получите 50. Затем вы разделите 50 на 20, что даст вам 2,5. Вы продолжаете этот процесс, пока не достигнете желаемого уровня точности. Конечно, всегда достаточно просто ввести числа в онлайн-калькулятор квадратного корня выше и нажать «Рассчитать».Почему квадратный корень из 2 иррационален
Число, которое нельзя представить в виде простой дроби, называется иррациональным числом. Квадратный корень из 2 — это пример иррационального числа, и он особенно интересен, потому что это одно из простейших иррациональных чисел.
Чтобы доказать, что квадратный корень из 2 иррационален, можно использовать доказательство от противного. Предположим, что квадратный корень из 2 можно выразить в виде дроби, а затем показать, что это приводит к противоречию. Доказательство относительно простое и включает в себя демонстрацию того, что если квадратный корень из 2 можно выразить в виде дроби, то эту дробь можно сократить до еще меньшей дроби, что противоречит исходному предположению.
Калькулятор квадратного корня Формула
Калькулятор квадратного корня — полезный инструмент для быстрого вычисления квадратного корня. Эти калькуляторы используют формулу для вычисления квадратных корней, основанную на алгоритме извлечения квадратного корня. Формула выглядит следующим образом:
x(n+1) = (x(n) + a/x(n))/2
, где x(n) — n-я оценка квадратного корня, а a — число, из которого вы хотите найти квадратный корень.
Чтобы использовать калькулятор квадратного корня, все, что вам нужно сделать, это ввести число, из которого вы хотите найти квадратный корень, и калькулятор предоставит вам результат.Идеальный квадрат
Число считается идеальным квадратом, если оно является произведением целого числа на само себя. Например, 49 — это идеальный квадрат, поскольку он равен 7, умноженному на 7. Найти квадратный корень из полного квадрата несложно; вам просто нужно взять квадратный корень из целого числа. Например, квадратный корень из 49 равен 7.

Идеальная таблица квадратных корней
Число Идеальный квадрат Идеальный квадратный корень 0 0 0 1 1 1 90179 6 4 2 3 9 3 4 16 4 5 25 5 6 9016 6 9 01667 6 7 2 7 49 7 8 64 8 9 81 9 10 906 10160 167 Квадратный корень из рациональных и иррациональных чисел
Рациональное число — это число, которое можно представить в виде простой дроби, а иррациональное число — это число, которое нельзя представить в виде простой дроби. Чтобы вычислить квадратный корень из рационального числа, вы можете использовать алгоритм квадратного корня или калькулятор квадратного корня.

Для вычисления квадратного корня из иррационального числа можно использовать те же методы, что и для рациональных чисел. Однако результатом будет само иррациональное число.Как найти квадратный корень с помощью длинного деления
Как мы упоминали ранее, длинное деление — это один из способов нахождения квадратного корня вручную. Чтобы использовать этот метод, вам нужно разбить число, из которого вы хотите найти квадратный корень, на более мелкие части, а затем разделить его на серию меньших чисел.
Чтобы найти квадратный корень числа с помощью деления в большую сторону, вы начинаете с группировки цифр числа в пары, начиная с самой правой цифры. Затем вы найдете наибольшее целое число, квадрат которого меньше или равен первой паре цифр. Это целое число становится первой цифрой квадратного корня. Вы вычитаете квадрат этого целого числа из первой пары цифр и опускаете следующую пару цифр. Затем вы повторяете процесс, пока не получите желаемый уровень точности.
- Использовал ваш метод ветвей и границ, но рисунки не подгружаются.


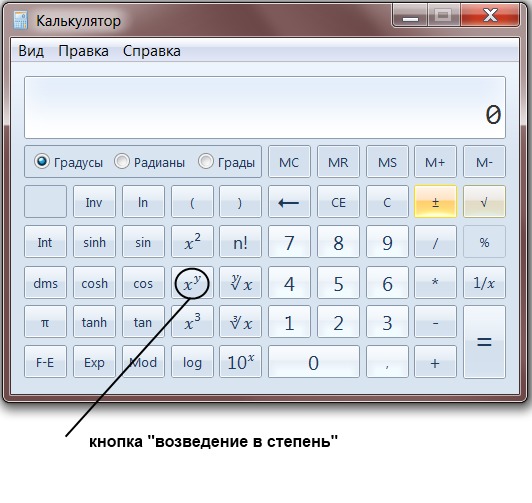 (1/5)-1
(1/5)-1
 Или можно нажать кнопку Назад в меню браузера.
Или можно нажать кнопку Назад в меню браузера.
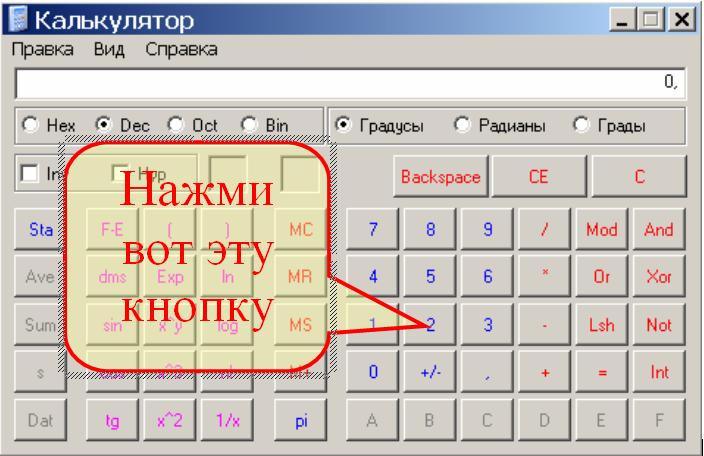 Кроме того, с помощью функции «Автоумма» можно быстро свести ряд значений, не вводя их в формулу вручную. Создав формулу, вы можете скопировать ее в смежные ячейки, не создав одну и ту же формулу раз за разом.
Кроме того, с помощью функции «Автоумма» можно быстро свести ряд значений, не вводя их в формулу вручную. Создав формулу, вы можете скопировать ее в смежные ячейки, не создав одну и ту же формулу раз за разом.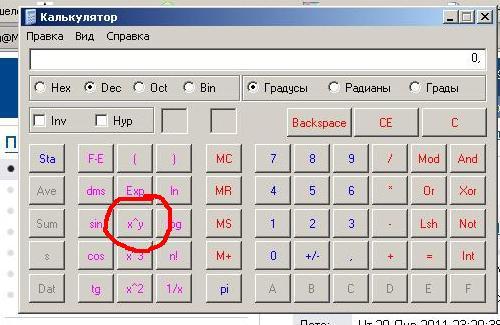
 Она также работает и по горизонтали, если вы выберете ячейку справа или слева от суммируемого диапазона.
Она также работает и по горизонтали, если вы выберете ячейку справа или слева от суммируемого диапазона. ..) Плавающий тег под функцией — это руководство Intellisense. Если щелкнуть имя функции или СУММ, изменится синяя гиперссылка на раздел справки для этой функции. Если щелкнуть отдельные элементы функции, их представительные части в формуле будут выделены. В этом случае будет выделен только B2:B5, поскольку в этой формуле есть только одна ссылка на число. Тег Intellisense будет отображаться для любой функции.
..) Плавающий тег под функцией — это руководство Intellisense. Если щелкнуть имя функции или СУММ, изменится синяя гиперссылка на раздел справки для этой функции. Если щелкнуть отдельные элементы функции, их представительные части в формуле будут выделены. В этом случае будет выделен только B2:B5, поскольку в этой формуле есть только одна ссылка на число. Тег Intellisense будет отображаться для любой функции.
 Пример: =4+6+2
Пример: =4+6+2 Пример: =8*3
Пример: =8*3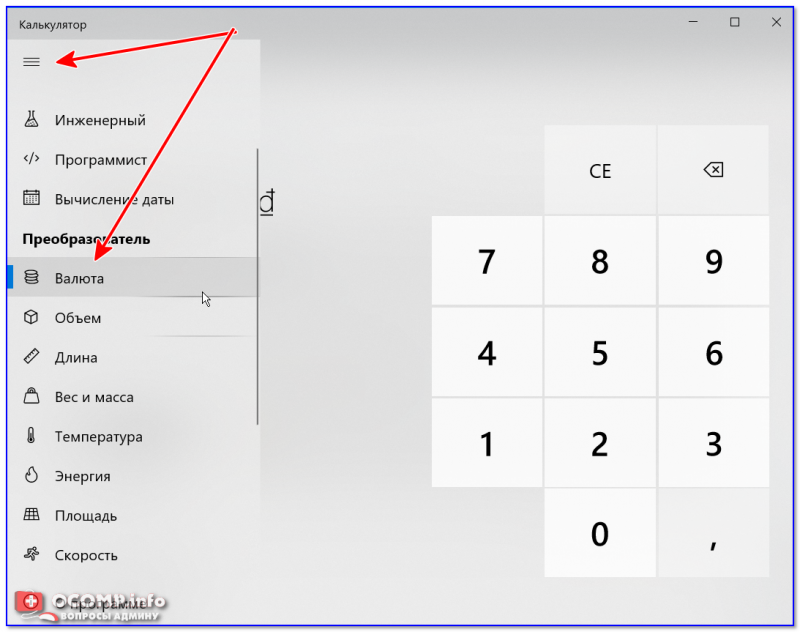 Пример: =15%*20
Пример: =15%*20
 Обратитесь к Свойству 1, упомянутому ниже, для получения дополнительных разъяснений по этому вопросу.
Обратитесь к Свойству 1, упомянутому ниже, для получения дополнительных разъяснений по этому вопросу.
 Цифровым корнем полного квадрата будет одна из четырех цифр 1, 4, 7, 9.только. Следовательно, если мы найдем любую другую цифру в качестве цифровой суммы, число точно не будет идеальным квадратом.
Цифровым корнем полного квадрата будет одна из четырех цифр 1, 4, 7, 9.только. Следовательно, если мы найдем любую другую цифру в качестве цифровой суммы, число точно не будет идеальным квадратом.
 Затем вы разделите 10 на 2, что даст вам 5. Затем вы добавите следующую цифру (0) и получите 50. Затем вы разделите 50 на 20, что даст вам 2,5. Вы продолжаете этот процесс, пока не достигнете желаемого уровня точности. Конечно, всегда достаточно просто ввести числа в онлайн-калькулятор квадратного корня выше и нажать «Рассчитать».
Затем вы разделите 10 на 2, что даст вам 5. Затем вы добавите следующую цифру (0) и получите 50. Затем вы разделите 50 на 20, что даст вам 2,5. Вы продолжаете этот процесс, пока не достигнете желаемого уровня точности. Конечно, всегда достаточно просто ввести числа в онлайн-калькулятор квадратного корня выше и нажать «Рассчитать».