6.1. Вычисление предела дробно-рациональной функции
6.1.1. Вычисление предела дробно — рациональной функции при
Пусть и – многочлены соответственно степеней и .
Выражение при может не представлять собой неопределённости или быть отношением двух бесконечно малых. При вычислении могут представляться следующие случаи.
А. Выражение не представляет собой неопределённости, если — не является корнем знаменателя, то есть . В этом случае используют теорему об арифметических действиях над функциями, имеющими предел в точке:
Б. Не представляет никакого труда вычисление предела и в случае, если – корень знаменателя, но не является корнем числителя, то есть , . В этом случае отношение При является бесконечно большой функцией, поэтому .
В. Если же является и корнем числителя и корнем знаменателя: , , то выражение При представляет собой неопределённость типа . В этом случае в числителе и в знаменателе можно выделить общий множитель наибольшей степени и сократить на него.
Пример 1. Вычислить .
Решение. Число не является корнем знаменателя: (случай А), поэтому
.
Пример 2. Вычислить
Решение. Здесь ситуация такая же: число 2 не является корнем знаменателя (хотя и является корнем числителя).
Пример 3. Вычислить
Решение. В данном случае число является корнем знаменателя, но не является корнем числителя (случай Б)
Пример 4. Вычислить
Решение. В этом случае является корнем и числителя, и знаменателя, а значит выражение представляет собой неопределённость . В знаменателе следует выделить множетель . Возможно этот множитель будет входить в некоторой степени (если корни кратные). В числителе выделить такой множитель несложно:
Для того чтобы выделить такой множитель в знаменателе удобно разделить знаменатель на “в столбик”.
Такое деление возможно без остатка по следствию из теоремы Безу. Действительно:
Теперь знаменатель можно представить как произведение:
Окончательно:
6.1.2 Вычисление предела дробно – рациональной функции при
Пусть при дробно-рациональная функция представляет собой неопределённость типа . Тогда при вычислении полезно учитывать, что при
Поэтому
Пример 6.
;
Пример 7.
;
Пример 8.
.
Если многочлены в числителе и знаменателе не представлены в стандартном виде, нужно внимательно отнестись к определению старшей степени. Например, выражение является многочленом третьей, а не четвёртой степени.
| < Предыдущая | Следующая > |
|---|
Предел дробно-рациональной функции
Дробно-рациональной функцией называется
частное двух многочленов
,
где,.
Интерес представляют два типа задач:
1. Вычислить . Неопределенность типа.
2. Вычислить , где– корень многочленови[2, 21]. Неопределенность типа.
При вычислении могут возникнуть три различные ситуации.
Пример 2.6. Вычислить.
Решение. Так как числитель и знаменатель дроби – бесконечно большие функции, то имеем дело с неопределенностью.
== [в числителе и знаменателе вынесем за скобки наивысшую степень] =
==[воспользуемся формулами (2.1)–(2.4)]= =.
Пример 2.7. Вычислить.
Решение. Выполним те же преобразования, что и в примере 2.6 и воспользуемся правилом 4:
===.
Пример 2.8. Вычислить.
Решение. ==== –1.
Обобщим результаты, полученные в
примерах 2.
2 – 2.8:
(2.7)
Пример 2.9. Вычислить.
Решение. Сначала раскроем скобки и приведем подобные слагаемые в числителе, а затем, сравнив степени многочленов, стоящих в числителе и знаменателе, по формуле (2.7) вычислим предел:
===
=.
Обратите внимание, что в ходе преобразования числителя третьи степени неизвестного сокращаются, а значит, числитель есть многочлен второй, а не третьей степени. Если этого не заметить и сразу воспользоваться формулой (2.7), то получится неверный ответ !
При вычислении , где– корень многочленовитакже возникают три различные ситуации.
Пример 2.10. Вычислить.
Решение. Найдем значения
числителя и знаменателя в точке 1: .Значит, многочленыи– бесконечно малые функции при.
Мы имеем дело с неопределенностью.
Число 1 является корнем обоих многочленов,
следовательно, они делятся на линейный
многочлен,
который и порождает неопределенность.
Разделим числитель и знаменатель дроби
на«уголком» [2, 19]:
Разложим числитель и знаменатель на множители и сократим на :
.
Проверим, уничтожило ли данное преобразование неопределенность. Вычислив значения многочленов ив точке 1, видим, что неопределенность сохранилась. Снова разложим числитель и знаменатель полученной дроби на множители и сократим общий множитель. Как только неопределенность уходит, можно воспользоваться формулами о пределе частного и суммы функций:
.
Напомним, что число называется корнем многочлена кратности, если многочлен делиться нацело на, но уже не делится нацело на. Если, то говорят, что кореньпростой.
В примере 2.10 число
является корнем многочленовикратности 2.
Пример 2.11. Вычислить.
Решение. Проверкой убеждаемся, чтоявляется корнем обоих многочленов, и раскладываем числитель и знаменатель на множители. Сокращение общего множителясразу уничтожает неопределенность:
=.
Число является простым корнем числителя и корнем знаменателя кратности 2.
Пример 2.12. Вычислить.
Решение.Рассуждаем так же, как и в предыдущих задачах:
.
Число является корнем числителя кратности 2 и простым корнем знаменателя.
Обобщим результаты, полученные в примерах 2.10 – 2.12: пусть число является корнем многочленакратностии корнем многочленакратности, тогда
Пример 2.13. Вычислить.
Решение.
Так как(пример 2.5), то исходный предел будет
зависеть от того, куда стремится
переменная.
Пусть сначала.
Тогда по правилусразу находим:
.
Если же , то имеет место неопределенность. Умножим и разделим выражение, стоящее под знаком предела, на сопряженное к нему. Затем в числителе полученной дроби воспользуемся формулой разности квадратов, полагая в ней:
.
Числитель и знаменатель последней дроби – бесконечно большие функции, таким образом, переходим от неопределенности к неопределенности, которая раскрывается вынесением из числителя и из знаменателя переменной в наивысшей степени:
==
.
Ответ:
Пример 2.14. Вычислить.
Решение. В данном случае предел числителя и предел знаменателя равны нулю. Домножим числитель и знаменатель на сопряженные выражения:
.
Пример 2.15. Вычислить.
Решение. Прием умножения на сопряженное выражение не пригоден для вычисления этого предела. С целью уничтожения иррациональности в числителе воспользуемся формулой. Положим:,. Чтобы получить в числителе разность кубов, надо его умножить на выражение. Умножив числитель и знаменатель на эту величину, получим:
.
2+n}-n$Задавать вопрос
спросил
Изменено 5 лет, 2 месяца назад
Просмотрено 13 тысяч раз
$\begingroup$
Существует ли для этого общая стратегия? Например я работаю на пределе 92 + n} — n$$
И на самом деле верхнюю границу $1/2$ можно было бы найти тем же методом.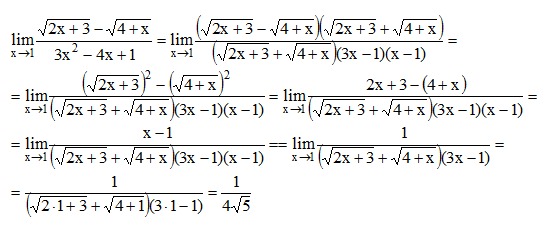
$\endgroup$
1
2.5: Пределы, включающие радикальные функции
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1116
Существует множество задач, связанных с извлечением корня n-й степени из переменного выражения, поэтому естественно, что иногда может возникнуть необходимость найти
Пределы с радикальными функциями
При оценке предела, включающего радикальную функцию , используйте прямую замену, чтобы увидеть, можно ли вычислить предел, когда это возможно.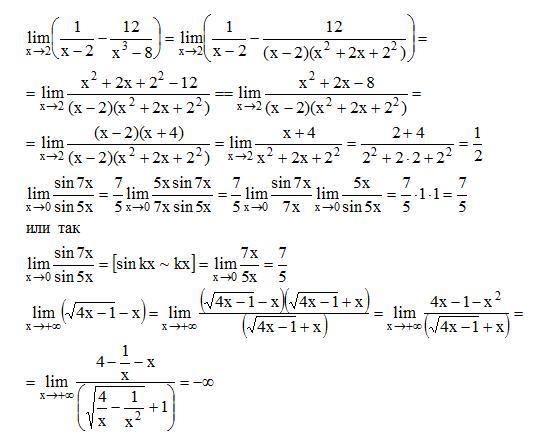
Если нет, необходимо изучить другие методы оценки предела.
Возьмем следующую функцию
Следовательно,
можно было бы определить путем прямого вычисления f(x) при x=9, т. е. путем прямой подстановки.
Теперь найдите
В обоих приведенных выше случаях для оценки пределов можно использовать прямую замену, и нет необходимости в альтернативных методах.
Взглянем на функцию
Сначала заметим, что мы должны исключить x=− 5 / 7 при любом вычислении. Использование прямой замены для нахождения предела приводит к неопределенной форме ∞ / ∞ . Чтобы преобразовать подкоренное выражение в лучшую форму, используйте тот факт, что значение x стремится ко все большим и большим положительным значениям. Это позволяет:
Следовательно,
Теперь найдите
Решение для оценки предела в отрицательной бесконечности похоже на описанный выше подход, за исключением того, что x всегда отрицательно.
Следовательно.
До сих пор вы могли найти предел рациональных функций, используя методы, показанные ранее. Однако бывают случаи, когда это невозможно. Возьмем функцию
Найдите
Использование прямой подстановки для нахождения предела приводит к неопределенной форме 00. Чтобы вычислить предел, нам нужно преобразовать выражение, чтобы удалить неопределенную форму. Это достигается с помощью соотношения разности квадратов действительных чисел: x 2 −y 2 = (x+y)(x−y).
Затем мы перепишем и упростим исходную функцию следующим образом:
Используем факторизацию разности квадратов, чтобы удалить 0 из знаменателя.
Отсюда
Теперь найдем конечное поведение той же функции, т.е. найдем
При увеличении x до больших положительных значений функция принимает неопределенный вид ∞ / ∞ . Приведенное выше преобразование также можно использовать для оценки предела (подход 1), а также метод, используемый при оценке рациональных функций (подход 2).
Отсюда
Наконец, найдите
Решение этой проблемы состоит в том, что предел не существует, поскольку область определения h(x) не включает x<0.
Примеры
Пример 1
Ранее вас спрашивали, можно ли использовать методы вычисления пределов, включающие многочлены и рациональные функции, для нахождения пределов радикальных функций. Некоторые методы работают для радикальных функций. Использование прямой замены является распространенным методом. Преобразование неопределенных или неопределенных форм путем нахождения и исключения общих множителей в числителе и знаменателе или факторизации и упрощения высших степеней переменных представляют собой распространенные подходы.
Одно из заслуживающих внимания различий между полиномиальными и радикальными функциями заключается в том, что область определения полиномов может включать все действительные значения независимой переменной, но область определения радикальных функций, например, x√, ограничена.
Пример 2
Найти
Использование прямой подстановки для нахождения предела функции приводит к неопределенной форме 0 / 0 . Чтобы преобразовать подкоренное выражение в лучшую форму, сделайте следующее:
… Рационализировать числитель: умножить на сопряженное число
Следовательно,
Обзор
Найдите каждый из следующих пределов, если они существуют.
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 2.6.
Словарь
| Срок | Определение |
|---|---|
| предел | Предел — это значение, к которому приближается выход функции, когда вход функции приближается к заданному значению. |
| радикальная функция | Радикальные функции — это функции, содержащие корни n-й степени переменных выражений. |