Как выглядит периметр: Как найти периметр прямоугольника, формула ⬅️

Вычислить периметр правильного шестиугольника онлайн

Правильный шестиугольник — это выпуклая многоугольная фигура с шестью сторонами одинаковой длины и углами равной величины. Другое название — гексагон. Он имеет ряд следующих особенностей и признаков:

• Длина стороны равнозначна радиусу описанной вокруг него окружности.
• Длинная диагональ представляет собой диаметр описанной окружности вокруг шестиугольника и её числовое значение — это удвоенная величина стороны.
• Короткая диагональ этой фигуры  больше его стороны в √3 раза.
• Величина каждого из шести углов имеет значение 120 градусов.
• Короткая диагональ гексагона — это перпендикуляр к одной из его сторон.
• Прямоугольный треугольник, который образуется посредством одной из сторон данной фигуры, а также его диагоналями — короткой и длинной, — имеет острые углы 30 и 60 градусов.
• Если провести 6 длинных диагоналей, то образуется 6 правильных треугольников. Все их углы будут по 60 градусов, а каждая высота равнозначна радиусу окружности, вписанной в данную фигуру.

Вариантов нахождения периметра гексагона существует множество. Например, с использованием диагоналей и площади. Ведь по условию не всегда известна длина стороны.

• Периметр правильного шестиугольника через площадь
• Периметр правильного шестиугольника через короткую диагональ
• Периметр правильного шестиугольника через длинную диагональ
• Периметр правильного шестиугольника через радиус описанной окружности
• Периметр правильного шестиугольника через радиус вписанной окружности
• Периметр правильного шестиугольника через сторону

Через площадь

Если по условию известна только площадь, то и с этим исходным значением получится найти периметр данной фигуры. Формула используется для этого следующая: a=sqrt(2/3*S/sqrt(3)).

Вычислив значение «a», можно отыскать периметр, расчёт выглядит так:

P = 6*a

В данной и последующих формулах sqrt — это обозначение квадратного корня.

Площадь правильного шестиугольника — это одна из основных числовых характеристик фигуры. С её помощью могут вычисляться другие параметры, значение которых нужно найти в задании.

Находится по формуле: S=(3√3*a²)/2, где S обозначается площадь правильного шестиугольника; «а» — длина его стороны.

Площадь (S):

мм²см²дм²м²

Цифр после запятой:

012345678910Результат в: ммсмдмм

Через короткую диагональ

Меньшая диагональ гексагона — это величина отрезка, который соединяет одну его вершину с другой, находящейся через один угол. Она в √3 раз больше его стороны. Отрезок отсекает в шестиугольнике треугольник, который получается равнобедренным.
Для нахождения периметра в этом случае используют следующую формулу:

P = 6 * (d/√3)

где d — короткая диагональ.

Диагональ (d):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Через длинную диагональ

Длинная диагональ гексагона является отрезком, который проходит из одной вершины многоугольника до противоположной. Противоположная вершина находится через два угла.

P = 3 * d

Большая диагональ шестиугольника правильной формы является диаметром описанной вокруг него окружности и равна сумме двух его сторон. Соответственно, чтобы найти его периметр данным способом, нужно умножить известную величину на 3.

Диагональ (D):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Через радиус описанной окружности

Радиус — отрезок, который идет из центра окружности к любой точке, расположенной на окружности.

Радиус описанной окружности вокруг гексагона равен длине одной его стороны.
Отсюда следует, что

P = 6 * r

где r — радиус описанной окружности.
Вокруг каждой правильной геометрической фигуры можно описать окружность или вписать её внутрь. Правильный шестиугольник имеет только одну описанную окружность. Периметр равен шести радиусам этой окружности.

Радиус (R):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Через радиус вписанной окружности

Также можно рассчитать периметр данной фигуры, если нам известен радиус вписанной в многоугольник окружности . Искомая величина равна произведению четырёх корней из трёх и радиуса вписанной окружности. Математическая формула выглядит так:

P = 4 * √3 * r

где r — радиус вписанной окружности.

Радиус (r):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Через сторону

Периметр — это суммарная величина длин всех сторон плоской фигуры. Так как рассматривается шестиугольник правильной формы, требуется измерить только одну из его сторон (здесь и далее она обозначается как «а») и умножить на 6.

Р = 6 * a

Сторона (a):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Данный способ очень простой, используется часто, но не является единственным. Так как значение стороны может быть неизвестно, а по условию задачи будут доступны другие исходные данные.

Найти периметр любой фигуры легко, если знать необходимые формулы и правила, а также свойства и признаки фигур. Иногда недостаточно применять только способ сложения длин всех сторон. Для этого может не хватать исходных данных по условию, поэтому используют формулы с участием иных терминов. Необходимо понимать и применять аксиомы, теоремы для решения подобных и других задач. Формулы, разобранные выше, основаны на свойствах прямоугольных треугольников. (Теорема Пифагора, синусы углов, косинусы углов и другие.)

Лестницы. Входная группа. Материалы. Двери. Замки. Дизайн

Как найти периметр основания треугольника. Как найти периметр треугольника если известны не все стороны. Вычисление периметра треугольника с использованием радиуса окружности, вписанной в него

Периметром треугольника , как в прочем и любой фигуры, называется сумма длин всех сторон. Довольно часто это значение помогает найти площадь или используется для расчета других параметров фигуры.

Формула периметра треугольника выглядит так:

Пример расчета периметра треугольника. Пусть дан треугольник со сторонами a = 4см, b = 6 см, c = 7 см. подставим данные в формулу: см

Формула расчета периметра равнобедренного треугольника будет выглядеть так:

Формула расчета периметра равностороннего треугольника :

Пример расчета периметра равностороннего треугольника. Когда все стороны фигуры равны, то их можно просто умножить на три. Допустим, дан правильный треугольник со стороной 5 см в таком случае: см

В общем, когда все стороны даны, найти периметр довольно просто. В остальных же ситуациях требуется найти размер недостающей стороны. В прямоугольном треугольнике можно найти третью сторону по теореме Пифагора . К примеру, если известны длины катетов, то можно найти гипотенузу по формуле:

Рассмотрим пример расчета периметра равнобедренного треугольника при условии, что мы знаем длину катетов в прямоугольном равнобедренном треугольнике.

Дан треугольник с катетами a =b =5 см. Найти периметр. Для начала найдем недостающую сторону с . см
Теперь посчитаем периметр: см
Периметр прямоугольного равнобедренного треугольника будет равен 17 см.

В случае, когда известна гипотенуза и длина одного катета, можно найти недостающий по формуле:
Если в прямом треугольнике известна гипотенуза и один из острых углов, то недостающая сторона находится по формуле.

Как найти периметр треугольника? Таким вопросом задавался каждый из нас, учась в школе. Попробуем вспомнить все, что мы знаем об этой удивительной фигуре, а также ответить на заданный вопрос.

Ответ на вопрос о том, как найти периметр треугольника, обычно является довольно-таки простым — требуется всего-лишь выполнить процедуру сложения длин всех его сторон. Однако есть ещё несколько простых методов искомой величины.

Советы

В том случае, если радиус (r) окружности, которая вписана в треугольник, и его площадь (S) известны, то ответить на вопрос о том, как найти периметр треугольника, довольно просто. Для этого вам необходимо воспользоваться обычной формулой:

Если известны два угла, допустим, α и β, которые прилегают к стороне, и сама длина стороны, то периметр можно найти с помощью весьма и весьма популярной формулы, которая имеет вид:

sinβ∙а/(sin(180° — β — α)) + sinα∙а/(sin(180° — β — α)) + а

Если вы знаете длины смежных сторон и угол β, находящийся между ними, то для того, чтобы найти периметр, требуется воспользоваться Периметр вычисляется по формуле:

P = b + a + √(b2 + a2 — 2∙b∙а∙cosβ),

где b2 и а2 являются квадратами длин смежных сторон.

Подкоренное выражение — это длина третьей стороны, которая неизвестна, выраженная посредством теоремы косинусов.

Если вы не знаете, как найти периметр то здесь, на самом деле, нет ничего сложного. Вычислите его по формуле:

где b — основание треугольника, а — его боковые стороны.

Для нахождения периметра правильного треугольника следует воспользоваться простейшей формулой:

где а — длина стороны.

Как найти периметр треугольника, если известны только радиусы окружностей, которые описаны около него или вписаны в него? Если треугольник является равносторонним, то тогда следует применить формулу:

P = 3R√3 = 6r√3,

где R и r являются радиусами описанной и вписанной окружности соответственно.

Если треугольник является равнобедренным, то для него применима формула:

P=2R (sinβ + 2sinα),

где α — это угол, который лежит у основания, а β — угол, который противолежит основанию.

Зачастую для решения математических задач требуется глубочайший анализ и специфическое умение находить и выводить требуемые формулы, а это, как многим известно, довольно непростая работа. Хотя некоторые задачи можно решить всего лишь с помощью одной-единственной формулы.

Давайте рассмотрим формулы, которые являются базовыми для ответа на вопрос о том, как найти периметр треугольника, по отношению к самым разнообразным типам треугольников.

Безусловно, главное правило для нахождения периметра треугольника — это данное утверждение: для нахождения периметра треугольника требуется сложить длины всех его сторон по соответствующей формуле:

где b, a и с — это длины сторон треугольника, а Р — периметр треугольника.

Есть несколько частных случаев данной формулы. Допустим, ваша задача формулируется следующим образом: «как найти периметр прямоугольного треугольника?» В таком случае вам следует воспользоваться следующей формулой:

P = b + a + √(b2 + a2)

В этой формуле b и а являются непосредственными длинами катетов прямоугольного треугольника. Несложно догадаться, что вместо стороны с (гипотенузы) используется выражение, полученное по теореме великого ученного древности — Пифагора.

Если требуется решить задачу, где треугольники являются подобными, то логично было бы воспользоваться данным утверждением: отношение периметров соответствует коэффициенту подобия. Допустим, у вас есть два подобных треугольника — ΔABC и ΔA1B1C1. Тогда для нахождения коэффициента подобия необходимо разделить периметр ΔABC на периметр ΔA1B1C1.

В заключение можно отметить, что периметр треугольника можно найти при помощи самых различных методик, в зависимости от тех исходных данных, которые у вас имеются. Необходимо добавить, что существуют некоторые частные случаи для прямоугольных треугольников.

Предварительные сведения

Периметр любой плоской геометрической фигур на плоскости определяется как сумма длин всех его сторон. Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.

Определение 1

Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками (рис. 1).

Определение 2

Точки в рамках определения 1 будем называть вершинами треугольника.

Определение 3

Отрезки в рамках определения 1 будем называть сторонами треугольника.

Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.

В зависимости от отношении сторон друг к другу, треугольники делятся на разносторонние, равнобедренные и равносторонние.

Определение 4

Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.

Определение 5

Треугольник будем называть равнобедренным, если две его стороны равны друг другу, но не равняются третьей стороне.

Определение 6

Треугольник будем называть равносторонним, если все его стороны равняются друг другу.

Все виды этих треугольников Вы можете видеть на рисунке 2.

Как найти периметр разностороннего треугольника?

Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.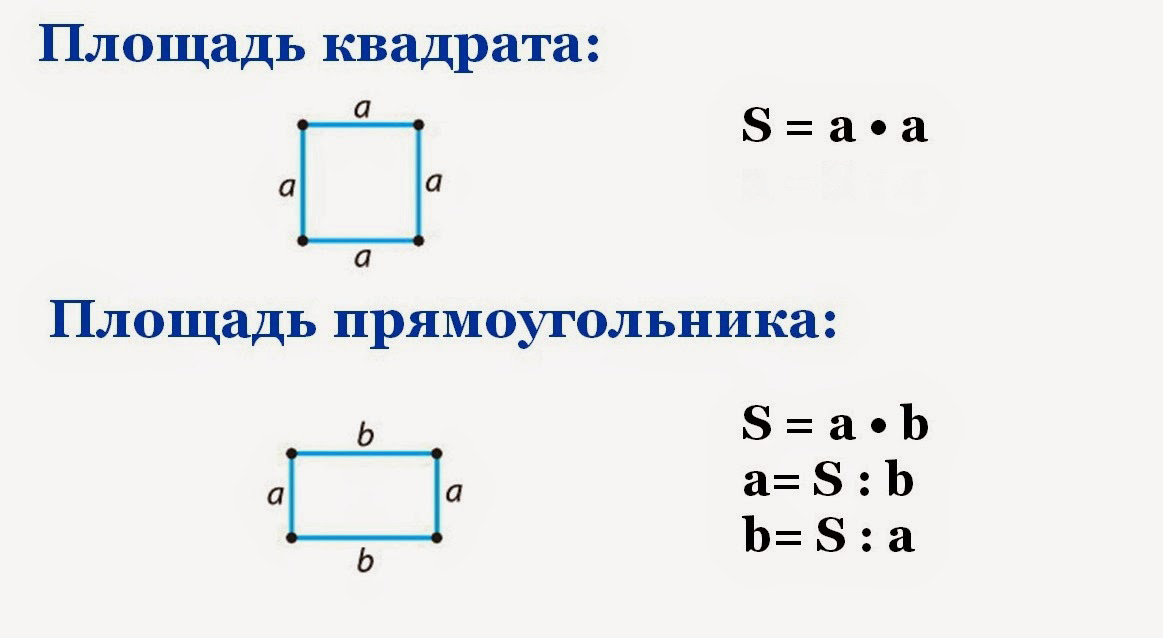

Вывод: Для нахождения периметра разностороннего треугольника надо все длин его сторон сложить между собой.

Пример 1

Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.

$P=34+12+11=57$ см

Ответ: $57$ см.

Пример 2

Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.

Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда

$α=10$ По правилу вычисления периметра разностороннего треугольника, получим

$P=10+8+6=24$ см

Ответ: $24$ см.

Как найти периметр равнобедренного треугольника?

Пусть нам дан равнобедренный треугольник, у которого длины боковых сторон будут равняться $α$, а длина основания равняется $β$.

По определению периметра плоской геометрической фигуры, получим, что

$P=α+α+β=2α+β$

Вывод: Для нахождения периметра равнобедренного треугольника надо удвоенную длину его сторон сложить с длиной его основания.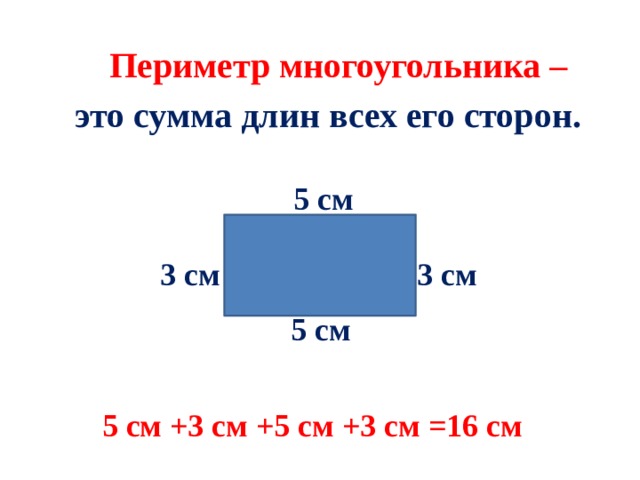

Пример 3

Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.

По рассмотренному выше примеру, видим, что

$P=2\cdot 12+11=35$ см

Ответ: $35$ см.

Пример 4

Найти периметр равнобедренного треугольника, если его высота, проведенная на основание, равняется $8$ см, а основание $12$ см.

Рассмотрим рисунок по условию задачи:

Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.

По теореме Пифагора, из треугольника $ADB$, найдем боковую сторону. Обозначим ее через $α$, тогда

По правилу вычисления периметра равнобедренного треугольника, получим

$P=2\cdot 10+12=32$ см

Ответ: $32$ см.

Как найти периметр равностороннего треугольника?

Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.

По определению периметра плоской геометрической фигуры, получим, что

$P=α+α+α=3α$

Вывод: Для нахождения периметра равностороннего треугольника надо длину стороны треугольника умножить на $3$.

Пример 5

Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.

По рассмотренному выше примеру, видим, что

$P=3\cdot 12=36$ см

Найти периметр треугольника можно не только просуммировав длины его сторон. Что, например, делать, если дана одна сторона и углы треугольника или, к примеру, две стороны и угол, между ними заключённый?»

1. В случае, если известны все три стороны.

Периметр произвольного треугольника равен a+b+c .

Если дан равносторонний (правильный) треугольник, то P=3a , то есть длина стороны, умноженная на три.

Если дан равнобедренный треугольник, то P=2a+c , где а — боковая сторона, а с — основание.

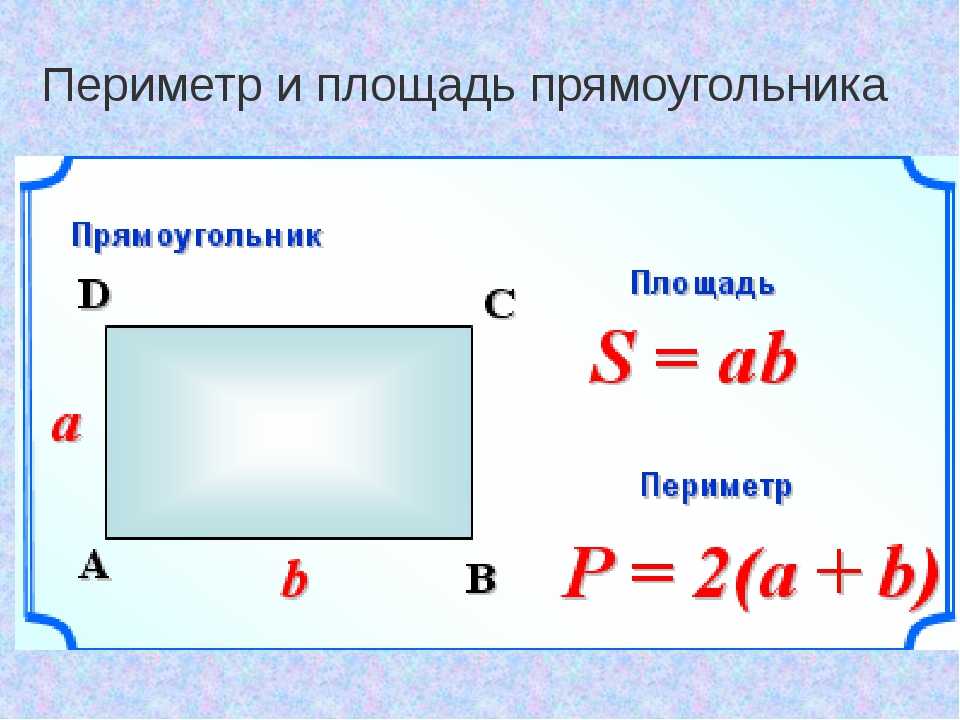
2. Если даны две стороны и значение угла между ними.

Для начала из теоремы косинусов можно узнать третью сторону, лежащую против угла»beta;. Эта сторона (назовём её стороной с) будет равна корню квадратному из выражения a 2 +b 2 -2∙a∙b∙cosbeta;.

Следовательно, периметр равен» a+b+radic;(a 2 +b 2 -2∙a∙b∙cosbeta;) .

3. Если известна сторона и два прилегающих к ней угла.

В этом случае, чтобы найти периметр треугольника, необходимо учитывать теорему синусов.

Тогда формула для расчёта периметра примет вид»а+sinalpha;∙а/(sin(180deg;-alpha;-beta;)) + sinbeta;∙а/(sin(180deg;-alpha;-beta;)) .

4. Если известна площадь треугольника и радиус окружности, вписанной в треугольник.

Найти периметр треугольника тогда можно через отношение удвоенной площади к радиусу вписанной окружности:» P=2S/r.

Частные случаи

(периметр, выраженный через радиусы вписанных и описанных окружностей).

1. Для правильного треугольника P=3Rradic;3=6rradic;3 .

2. Для равнобедренного треугольнка P=2R(2sinalpha;+sinbeta;) .

Треугольник — это одна из базовых фигур, образованная тремя пресекающимися отрезками прямых. Точки пересечения называются вершинами, а сами отрезки сторонами треугольника. Периметр треугольника — это сумма длин его сторон. Находить площадь треугольника учат еще в школе и впоследствии эти знания используются многими людьми включая студентов, математиков и инженеров.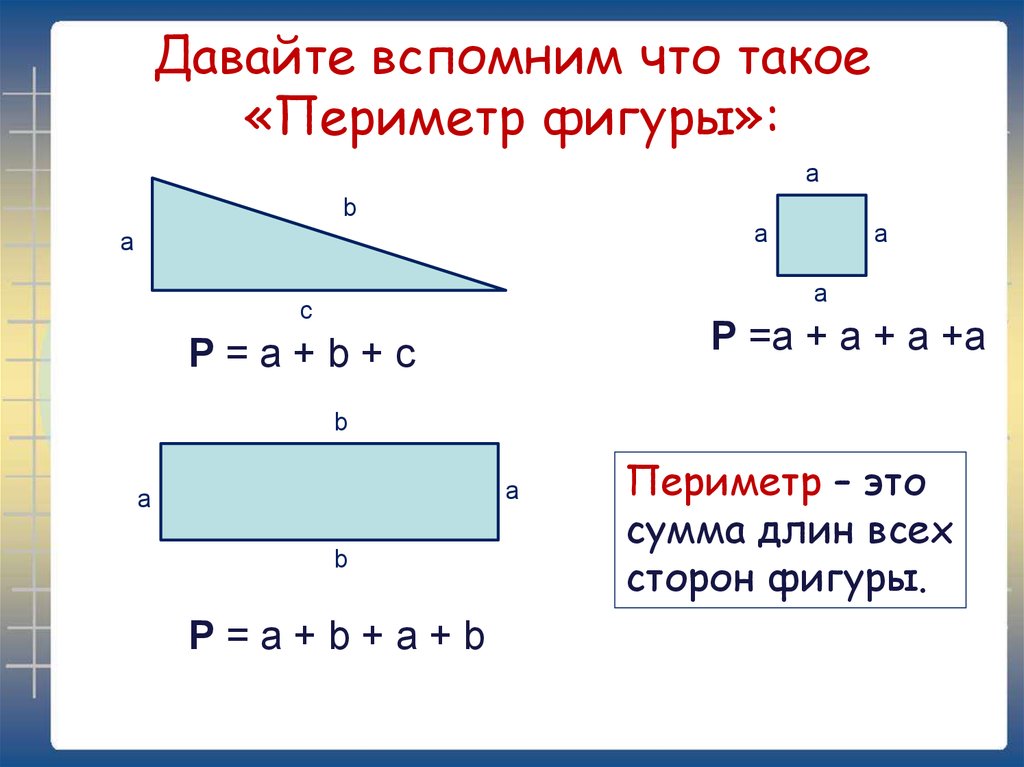 В зависимости от исходный данных площадь треугольника может быть надена различными способами. Рассмотрим их все по порядку.

1 способ Если известны длины всех сторон треугольника a, b и с, то в данном случае периметр определяется как сумма длин всех сторон:

P = a + b + c

где P — периметр треугольника;
a, b, c — длины сторон треугольника.

В частном случае для равнобедренного треугольника данная формула примет следующий вид:

P = 3a

то есть длина стороны, умноженная на три.
Если треугольник будет равнобедренный, то формула может быть записана в виде:

P = 2a + c

где a — боковая сторона, c — основание.

2 способ

Но длины всех сторон могут быть заданы не всегда. Если известны только две стороны и величина угла между ними, то периметр треугольника может быть определен через нахождение третьей стороны, лежащей напротив угла β. Эта сторона (назовем ее с) будет равна квадратному корню из выражения

a2+b2-2∙a∙b∙cosβ

В этом случае периметр треугольника может быть найден по формуле:

P = a+b+√(a2+b2-2∙a∙b∙cosα)

где a, b — длины сторон;
α — величина угла между сторонами a и b.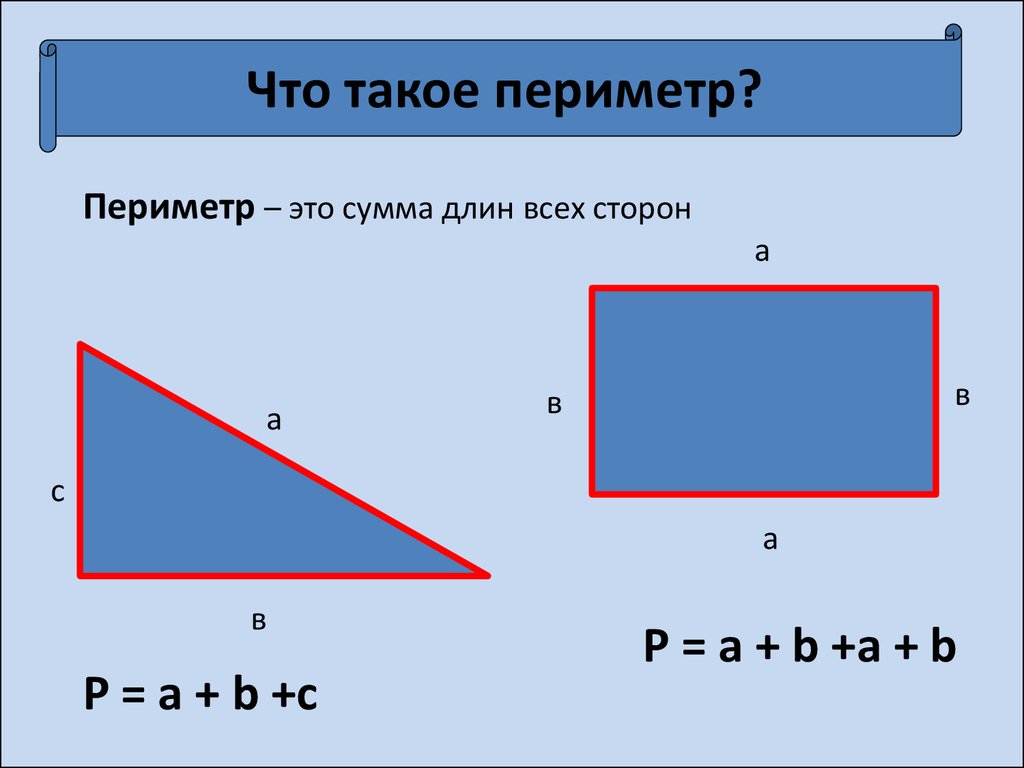

3 способ
Если известна сторона и два прилегающих к ней угла, то периметр треугольника определяется по теореме синусов по формуле:

P = а+sinα∙а/(sin(180°-α-β)) + sinβ∙а/(sin(180°-α-β))

где — a — длина стороны треугольника;
α, β — величина прилегающих к стороне a углов.

4 способ
Если задача предполагает нахождение периметра треугольника по радиусу вписанной в него окружности и площади треугольника, то в данном случае периметр может быть определен по формуле.

Как найти периметр многоугольника (видео и примеры)

Вы когда-нибудь ходили по полигону? Вероятно, нет, так как все полигоны двумерны, а вы трехмерный человек, но если вы когда-либо полностью обходили здание снаружи, вы ощущали периметр многоугольника.

Во-первых, убедитесь, что вы имеете дело с полигоном. Чтобы быть многоугольником, ваша форма должна состоять из трех вещей:

1. Она должна быть двумерной, иметь только высоту и ширину

2. Она должна быть сделана только с прямыми сторонами (без кривых)

3. Она должна быть закрыть в пространстве, как забор вокруг загона для лошадей (без зазоров)

Чтобы быть правильным многоугольником , ваш многоугольник должен также  все стороны быть равными.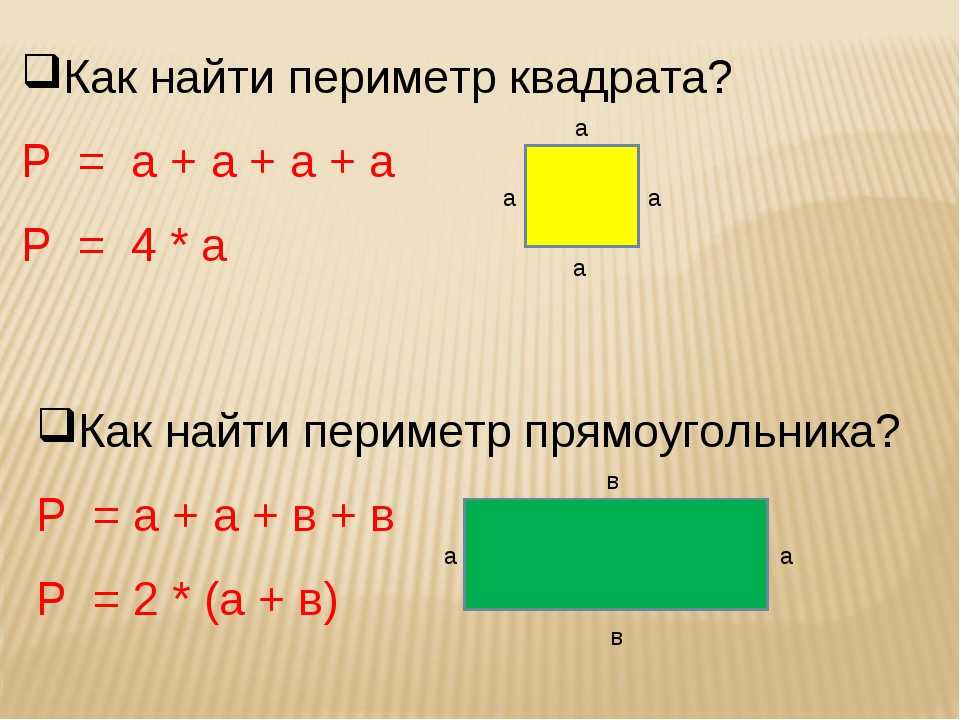 Он также должен иметь все внутренние углы, равные друг другу. Это автоматически сделает внешние углы конгруэнтными (равными).

Периметр многоугольника

Периметр  – это расстояние вокруг внешней стороны любой формы. Вы также можете легко измерить периметр всех многоугольников, будь то правильные или неправильные многоугольники.

Напомним, что многоугольник замыкается в пространстве, поэтому он создает внутреннее и внешнее пространство. Думайте о сторонах многоугольника как о заборах или стенах.

Как найти периметр многоугольника

Представьте себя маленьким двухмерным человечком, который ходит по всему многоугольнику. Ваше путешествие по фигуре — это ее периметр.

Вы начинаете, проводя рукой по внешней стороне каждой стороны, а затем возвращаетесь к исходной точке. Осознаете вы это или нет, но вы сделали один полный оборот и полностью обвели рукой периметр многоугольника.

Для всех многоугольников верным способом вычисления периметра является сложение длин всех сторон. Для треугольника это означает добавление трех чисел; для четырехугольника четыре числа; и так далее.

Предположим, что, обходя многоугольник, вы тщательно измеряете каждую его сторону. Когда вы закончите вращение вокруг фигуры и вернетесь в исходную точку, вы можете сложить все эти измерения, чтобы узнать периметр, в тех же линейных единицах, которые используются для каждой стороны.

Вы не можете вычислить периметр, если не знаете длины всех сторон многоугольника. Это не всегда означает, что каждая сторона будет идентифицирована.

Например, в прямоугольнике вам нужна только одна длина и одна ширина, потому что идентифицирующее свойство прямоугольников состоит в том, что противоположные стороны конгруэнтны. Если вы знаете эти два измерения, вы знаете длины всех четырех сторон.

Как найти периметр многоугольника

Математики записали многие из этих измерений периметра в формулы, чтобы ускорить расчеты. Вот несколько, где P  is the perimeter:

Perimeter of a Polygon Formula

Triangles

For a triangle with sides a , b , c :

Squares

Для квадрата со сторонами s :

Прямоугольники

Для прямоугольника со сторонами l и w 3 ( и ширина):0004 Какая бы единица измерения не использовалась для длины сторон, это та же самая единица измерения для периметра.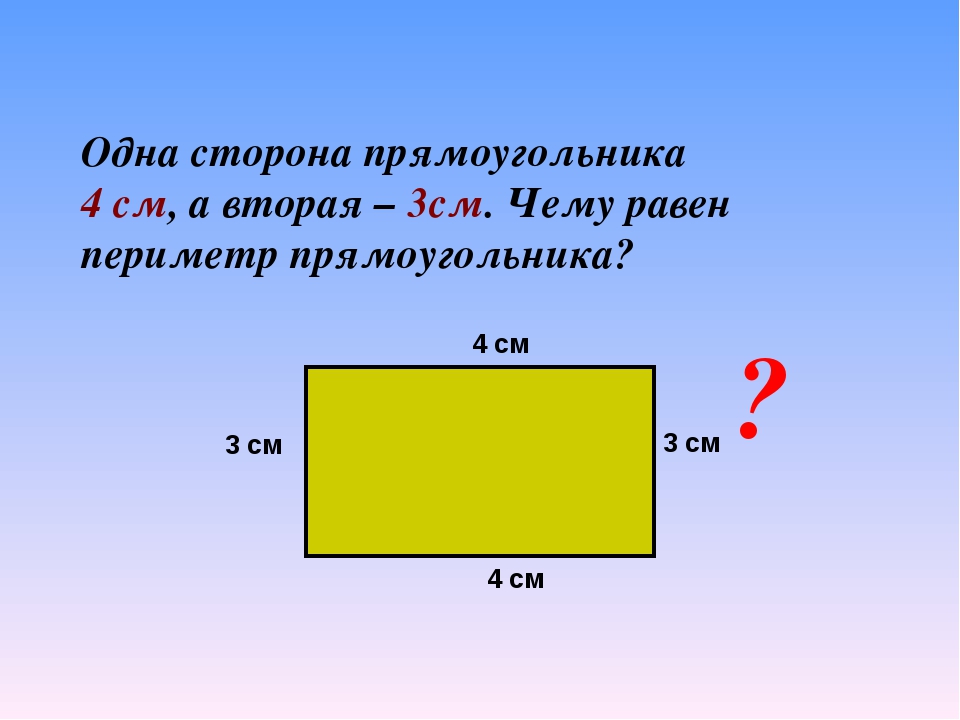 Таким образом, квадрат со стороной 37 метров имеет периметр 148 метров .

Треугольник со сторонами 30 , 40 и 50 миль имеет периметр 120 миль .

Применение формулы периметра многоугольника

Попробуйте найти периметр самостоятельно! Предположим, вы ограждаете прямоугольное пастбище лам площадью 200 метров 9.0036 в длину и 150 метров в ширину. Каков периметр пастбища?

Применение формулы периметра многоугольника Пример

Применение формулы периметра прямоугольника:

Пастбище лам имеет периметр 700 метров . Расчеты периметра часто ложатся в основу многоэтапных задач, таких как расчет примерной стоимости ограждения, если известна цена за метр.

Вычисление периметра неправильных многоугольников

Вычисление периметра не всегда так просто. Неправильный многоугольник, имеющий необычную форму, может потребовать много дополнений.

Предположим, вы отвечаете за оформление банкета, посвященного награждению команды по софтболу. Вы делаете большую домашнюю тарелку, и вам нужно повесить по ее краям гирлянду декоративных огней. Вот украшение вашей домашней тарелки:

Периметр неправильного многоугольника — пример домашней тарелки

Чтобы найти периметр (для правильной длины огней), сложите все стороны:

Вам нужен пакет огней не менее 14′ 6″ , чтобы полностью обойти украшение.

Как найти периметр правильного многоугольника

Уловили наш подлый ход в списке формул? Квадрат является правильным многоугольником. У него четыре равные стороны и четыре равных внутренних угла.

Его формула не похожа на другие. Для квадрата вам нужна была только длина одной стороны, а затем вы умножали на количество сторон.

Формула для вычисления периметра любого правильного многоугольника (от простого равностороннего треугольника до самого причудливого n-угольника, который только можно себе представить) всегда одна и та же.

Формула для периметра правильного многоугольника

Для правильного многоугольника с n сторонами и длиной одной стороны s :

Помните, что единицей периметра будет та же линейная единица, которая используется для измерения сторон многоугольника . Для правильного эннеагона (девятиугольника) с одной стороной 51 см формула будет выглядеть так:

Только после вычисления периметра в тех же единицах, что и стороны, вы можете попытаться преобразовать единицы измерения, если это необходимо. : 459 см = 4,59 м ; 4 метра , 59 сантиметров ; или 4590 мм .

Итоги урока

После просмотра видео, графики и текста вы теперь можете идентифицировать многоугольник на основе его свойств, найти периметр любого многоугольника путем сложения длин всех сторон многоугольника и применить знания о правильном многоугольников для быстрого расчета периметра по формуле

, где n — количество сторон, а  s — длина любой стороны.

Видео-вопрос: нахождение периметра фигуры, состоящей из 4 полукругов

Стенограмма видео

Используйте 3.14, чтобы аппроксимировать 𝜋 и вычислить периметр следующей фигуры.

Давайте начнем с того, что взглянем на диаграмму и посмотрим, какие фигуры мы можем идентифицировать.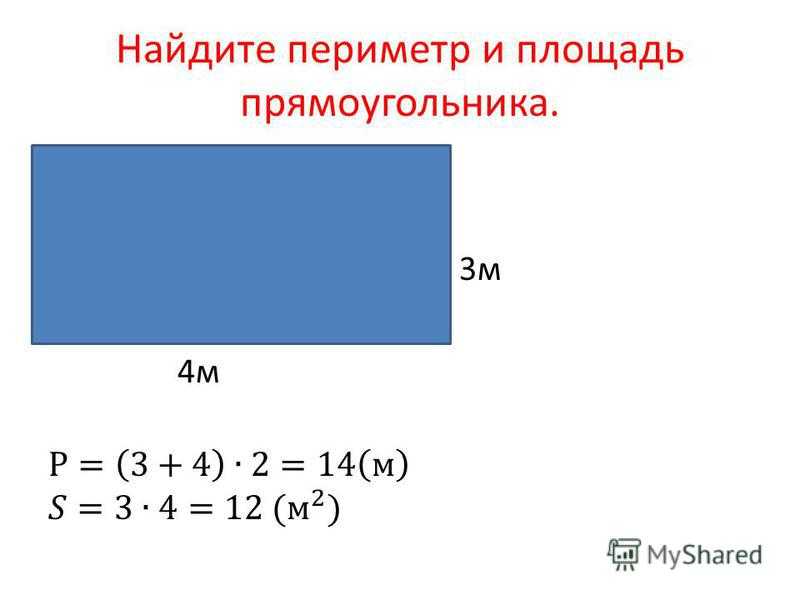 Внешне мы имеем то, что выглядит как четыре полукруга. Но уверены ли мы, что все они будут иметь одинаковый радиус или диаметр? Если мы посмотрим на эту длину, которая отмечена как 15 сантиметров, мы увидим, что центр этого круга, образующего полукруг, задан. Радиус круга здесь имеет две линии. И мы видим, что это верно и для других радиусов трех других окружностей. Следовательно, все четыре полуокружности имеют одинаковый радиус и, следовательно, будут одного размера.

Итак, давайте начнем думать о том, как мы можем вычислить периметр. И мы помним, что периметр — это расстояние вокруг внешней стороны фигуры. Когда дело доходит до нахождения периметра этой фигуры, даже если мы видим, что внутри нее есть квадрат, мы не считаем его частью периметра, поскольку он не находится снаружи фигуры. Когда мы думаем о периметре круга, вместо этого мы используем слово «окружность». Мы находим длину окружности, умножая 𝜋 на диаметр или даже на два раза на 𝜋 на радиус.

Есть два разных подхода к решению задачи нахождения периметра четырех полукругов. Одним из способов было бы рассмотреть, как мы найдем периметр одного полукруга, а затем умножим его на четыре. Второй метод заключается в том, чтобы понять, что если мы соединим два таких полукруга, то получим один круг. А так как у нас их два, то мы найдем периметр или длину окружности, а затем умножим его на два.

Начнем с того, как найти периметр одного полукруга. Мы знаем, что наш периметр будет основан на длине окружности, которая в 𝜋 раз больше диаметра. Но поскольку это только половина, мы делим на два. Мы можем заполнить значения, которые нам даны. И нам говорят использовать 3,14 в качестве приближения для 𝜋, а диаметр круга равен 15. Поскольку мы собираемся использовать здесь некалькуляторный метод, мы можем упростить этот расчет, признав, что 15 делится на два в 7,5 раз. . Вычисление 3,14 умножить на 7,5 даст нам периметр 23,55 сантиметра.

Итак, если это периметр одного полукруга, то чтобы найти весь периметр, нам нужно умножить это значение на четыре. 23,55, умноженное на четыре, дает нам периметр 94,2 сантиметра.

No related posts.