Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
R — большая полуось
r — малая полуось
π ≈ 3.14
Формула площади эллипса, через полуоси:
Калькулятор, вычислить площадь элипса:
1. Формула площади равнобедренной трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S ):
Формула площади равнобедренной трапеции через стороны и угол, (S ):
2.
Формулы площади равнобедренной трапеции если в нее вписана окружность
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
R — радиус вписанной окружности
m — средняя линия
O — центр вписанной окружности
c — боковые стороны
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3.
Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c — боковая сторона
m — средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S ):
a, b, c — стороны треугольника
α, β, γ— противолежащие углы
Площадь треугольника через сторону и два угла (S):
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Зная длины всех трех сторон
и используя формулу Герона можно найти площадь разностороннего треугольника
a, b, c — стороны треугольника
p — полупериметр, p=(a+b+c)/2
Формула (Герона) площади треугольника через полупериметр (
Калькулятор — вычислить, найти площадь треугольника:
a =
b =
c =
S=
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Треугольник это плоская фигура, которая имеет три стороны и три угла.
Сумма всех трех углов, равна 180 градусов.
Высота треугольника это — опущенный перпендикуляр из вершины угла на противоположенную сторону или ее продолжение, которую в этом случае, называют основанием.
Что бы найти площадь треугольника,
для этого надо основание умножить на высоту и разделить на два
1. Площадь разностороннего треугольника
h — высота треугольника
a — основание
Формула площади треугольника (S):
Калькулятор для расчета площади треугольника
Высота, h =
Основание, a =
Количество знаков после запятой: 212461015
Площадь треугольника, S =
2. Площадь треугольника с тупым углом
h — высота треугольника
a — основание
Формула площади треугольника с тупым углом (S):
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Зная у треугольника
две стороны и синус угла между ними, находим по формуле, его площадь
a, b, c — стороны треугольника
α, β, γ — углы
Формулы площади треугольника, через две стороны и угол между ними, (S):
Калькулятор — вычислить, найти площадь треугольника:
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется — гипотенуза
1. Если известны только катеты
a, b — катеты треугольника
Формула площади треугольника через катеты ( S ) :
2. Если известны острый угол и гипотенуза или катет
c — гипотенуза
a, b — катеты
α, β — острые углы
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
то справедливы следующие тождества:
3.
Если известны радиус вписанной окружности и гипотенуза
c — гипотенуза
c1, c2 — отрезки полученные делением гипотенузы, точкой касания окружности
r — радиус вписанной окружности
О — центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу (
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b, (S):
Калькулятор — вычислить, найти площадь треугольника через высоту и основание:
b (основание) =
h (высота)=
S (площадь) =
Формула площади треугольника через, стороны a, b, (S):
Калькулятор — вычислить, найти площадь треугольника через равные стороны и основание:
a (сторона)=
b (основание)=
S (площадь)=
b — основание треугольника
a — равные стороны
h — высота
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Если вы знаете сторону или высоту
вы можете найти площадь равностороннего треугольника
a — сторона треугольника
h — высота
Площадь треугольника через сторону a и высоту h, (S):
Площадь треугольника только через сторону a, (S):
Калькулятор для расчета площади равностороннего треугольника
Площадь треугольника только через высоту h, (S):
Калькулятор для расчета площади равностороннего треугольника
a — сторона треугольника
h — высота
Формулы для треугольника:
Сторона произвольного треугольника
Стороны равнобедренного треугольника
Стороны прямоугольного треугольника
Высота произвольного треугольника
Высота прямоугольного треугольника
Высота, медиана, биссектриса равнобедренного треугольника
Высота=медиана=биссектриса равностороннего треугольника
Биссектриса произвольного треугольника
Биссектриса прямоугольного треугольника
Медиана произвольного треугольника
Медиана прямоугольного треугольника
Все разделы по геометрии
Формула площади круга, диаметр
Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса
Зная диаметр
или радиус круга или длину окружности, можно найти его площадь.
r — радиус круга
D — диаметр круга
π ≈ 3.14
Формула площади круга, (S):
Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через радиус
Радиус окружности, r =
Количество знаков после запятой: 2124610F
Площадь круга, S =
Калькулятор для расчета площади круга через диаметр
Диаметр окружности, D =
Количество знаков после запятой: 2124610F
Площадь круга, S =
L — длина окружности
О — центр круга
π ≈ 3.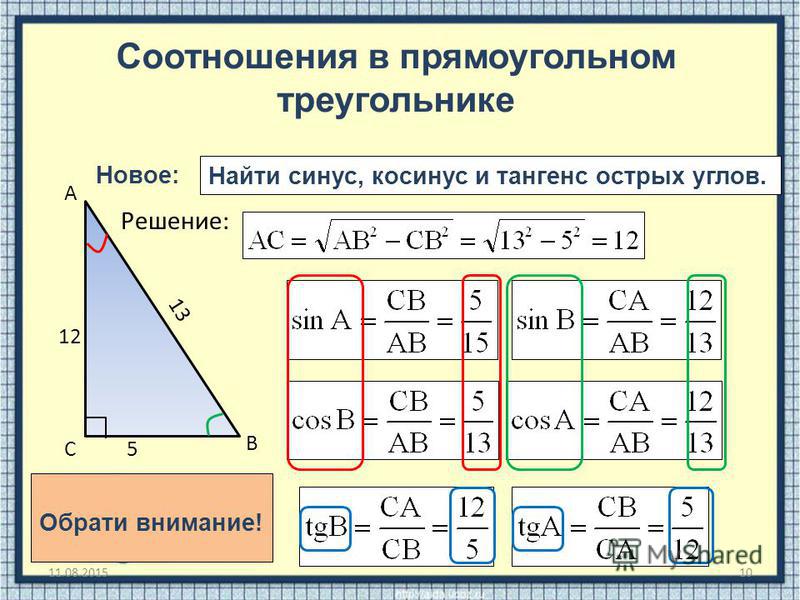
14
Формула площади круга если известна длина окружности, (S):
Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через длину
Длина окружности, L =
Количество знаков после запятой: 2124610F
Площадь круга, S =
Площадь кольца равна — число π, умноженное на разницу квадратов, радиуса внешней окружности и радиуса внутренней окружности
R — радиус внешней окружности
r — радиус внутренней окружности
π ≈ 3.14
Формула площади кольца (S):
Калькулятор — вычислить, найти площадь кольца
R — радиус внешней окружности
r — радиус внутренней окружности
α — угол сектора AOB, в градусах
π ≈ 3.
14
Формула площади сектора кольца (S):
R — радиус круга
α — угол сегмента в градусах
π ≈ 3.14
Формула площади сегмента круга (S), отсекаемая хордой AC:
Калькулятор для расчета длины дуги окружности :
Формулы для окружности и круга:
Длина хорды окружности
Высота сегмента круга
Все разделы по геометрии
Найти площадь сектора круга если даны радиус и длина дуги или радиус и центральный угол
r — радиус круга
L — длина дуги AB
α — угол сектора круга AOB в градусах
π ≈ 3.14
Формула площади сектора круга (S), через длину дуги (L):
Формула площади сектора круга (S), через угол (α):
Формулы для окружности и круга:
Длина хорды окружности
Высота сегмента круга
Все разделы по геометрии
Вычислить площадь ромба, зная: (диагонали) или (сторону и угол между ними) или (диагональ и угол между сторонами)
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы площади ромба через диагонали и углы между сторонами ( S ):
a — сторона ромба
h — высота
r — радиус вписанной окружности
Формула площади ромба через высоту или радиус вписанной окружности ( S ):
1.
Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α, β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):
Калькулятор — вычислить, найти площадь параллелограмма:
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d —меньшая диагональ
α, β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
Калькулятор — вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии
1.
Формула площади трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
m — средняя линия
h — высота трапеции
Формула площади трапеции, (S ):
2. Формула площади трапеции через диагонали и угол между ними
d1, d2 — диагонали трапеции
α, β — углы между диагоналями
Формула площади трапеции, (S ):
3. Формула площади трапеции через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
Формула площади трапеции, (S ):
Зная сторону
или диагональ квадрата, можно найти его площадь
a — сторона квадрата
c — диагональ
Формула площади квадрата через сторону a, (S):
Калькулятор — вычислить, найти площадь квадрата:
Формула площади квадрата через диагональ c, (S):
C (диагональ)=
S=
Зная длину
и ширину прямоугольника, можно вычислить его площадь
b — длина прямоугольника
a — ширина прямоугольника
Формула площади прямоугольника, (S):
Калькулятор — вычислить, найти площадь прямоугольника:
a (длина) =
b (ширина)=
S=
a — сторона многоугольника
n — количество сторон
Формула площади правильного многоугольника, (S):
Калькулятор — вычислить, найти площадь правильного многоугольника
Внешний угол треугольника.
Синус и косинус внешнего углаВ некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом . Если угол острый, то смежный с ним угол — тупой, и наоборот.
Обратите внимание, что:
Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
Легко
доказать, что внешний
угол треугольника равен сумме двух
внутренних углов, не смежных с ним.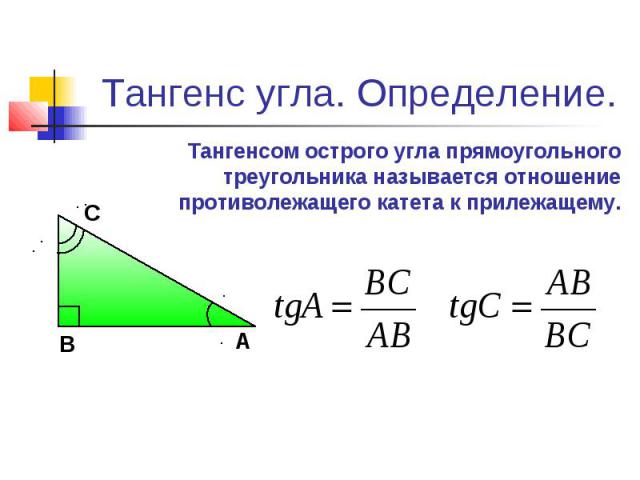
1. В треугольнике угол равен , . Найдите тангенс внешнего угла при вершине .
Пусть — внешний угол при вершине . Имеем:
Зная , найдем по формуле
Получим:
2. В треугольнике угол равен , . Найдите синус внешнего угла при вершине .
Задача решается за четыре секунды. Поскольку сумма углов и равна , . Тогда и синус внешнего угла при вершине также равен .
Вспомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.
В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.
Один
из типов экзаменационных задач В6 в
банке заданий ФИПИ — такие, где
в прямоугольном треугольнике высота
проведена из вершины прямого угла.
Посмотрим, что получается:
Высота проведена к гипотенузе . Она делит треугольник на два прямоугольных треугольника — и . Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.
Мы помним, что сумма двух острых углов прямоугольного треугольника равна . Значит, , то есть угол равен углу . Аналогично, угол .
Иными словами, каждый из трех углов треугольника равен одному из углов треугольника и треугольника . Треугольники , и называются подобными. Давайте нарисуем их рядом друг с другом.
Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?
Возьмем треугольники и . Стороны треугольника длиннее, чем стороны треугольника , в некоторое число раз:
При
решении задач нам пригодится равенство
углов треугольников
,
и
,
а также пропорциональность их сторон.
Обратите также внимание, что площадь
треугольника
можно
записать двумя разными способами: как
половину произведения катетов и как
половину произведения гипотенузы
на проведенную к ней высоту.
1. В треугольнике угол равен , — высота, , . Найдите .
Рассмотрим треугольник . В нем известны косинус угла и противолежащий катет . Зная синус угла , мы могли бы найти гипотенузу . Так давайте найдем :
(поскольку значение синуса острого угла положительно). Тогда:
Рассмотрим прямоугольный треугольник , . Имеем:
Отсюда, поскольку :
и тогда
Ответ: .
2. В треугольнике угол равен , , . Найдите высоту .
Сделайте
чертеж и рассмотрите прямоугольный
треугольник
.
Ответ: .
3. В треугольнике угол равен , , . К гипотенузе проведена высота . Найдите .
Это чуть более сложная задача. Ведь вам неизвестны катеты и .
Зато можно записать теорему Пифагора:
Нам известно также, что
Решая эту систему из двух уравнений, найдем:
Запишем площадь треугольника двумя способами:
и найдем .
Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений.
Тригонометрический идентификатор-калькулятор-Google Suce
ALLBILDERVIDEOSBüchermapSnewshopping
Sucoptionen
Тригонометрическая идентификация STEP-BY-STEP-step-steplify
WWW.
Symbolab.com. -шаг.
Калькулятор и решатель для доказательства тригонометрических тождеств — SnapXam0003
Калькулятор доказательства тригонометрических тождеств. Получите подробные решения ваших математических задач с помощью нашего пошагового калькулятора доказательства тригонометрических тождеств.
Калькулятор и решатель тригонометрических тождеств — SnapXam
www.snapxam.com › калькуляторы › trigonometric-ide…
Получите подробные решения ваших математических задач с помощью нашего пошагового калькулятора тригонометрических тождеств. Практикуйте свои математические навыки и учитесь шаг за шагом с …
Упрощение тригнометрических уравнений, доказательство тождеств и вычисление…
atozmath.com › Тригонометрия
Упрощение тригнометрических уравнений, доказательство тождеств и вычисление функций, шаг за шагом онлайн.
Тригонометрический калькулятор — Microsoft Math Solver
mathsolver.
microsoft.com › trigonometry-calculator
Отсканируйте или напишите свои математические задачи в приложении Microsoft Start и получите пошаговую помощь! Не сейчас. Скачать приложение.
Пошаговая проверка тригонометрических тождеств — Math34.pro
math34.pro › identity
Бесплатный калькулятор тригонометрических тождеств — пошаговая проверка тригонометрических тождеств.
«Тригонометрические тождества» — Бесплатный математический виджет — Wolfram|Alpha
www.wolframalpha.com › виджеты › просмотреть
14.05.2013 · Получите бесплатно виджет «Тригонометрические тождества» для своего сайта, блога, WordPress, Blogger или iGoogle. Найдите другие математические виджеты в …
Калькулятор тригонометрии — решение математических задач
solvemathproblems.org › trigonometry-calculator
Калькулятор тригонометрии — ответьте на любую задачу тригонометрии и получите пошаговые инструкции… Как только вы это сделаете, применение этих тождеств в различных задачах будет стать .
..
Тригонометрия — Проверка триггерных тождеств с помощью калькулятора — YouTube
www.youtube.com › смотреть
25.09.2016 · При работе с тригонометрическими тождествами может быть трудно определить, есть ли у вас эквивалент выражение …
Dauer: 6:14
Прислан: 25.09.2016
Ähnliche Fragen
Как решать тригонометрические тождества?
Может ли Photomath решать триггерные тождества?
Каковы 9 тождеств тригонометрии?
Тригонометрические тождества — Бесплатная помощь по математике
www.freemathhelp.com › trig-identities
Тригонометрические тождества. Используйте эти фундаментальные формулы тригонометрии, чтобы помочь решить проблемы, переписав выражения в другой эквивалентной форме.
Ähnliche Suchanfragen
Trigonometric equations calculator
Proving trig identities calculator with steps free
Solving trigonometric identities
Trigonometric matrix calculator
Symbolab
Trigonometry calculator online
Induction calculator
Complete the identity calculator
| 1 | Найти точное значение | грех(30) | ||
| 2 | Найти точное значение | грех(45) | ||
| 3 | Найти точное значение | грех(30 градусов) | ||
| 4 | Найти точное значение | грех(60 градусов) | ||
| 5 | Найти точное значение | загар (30 градусов) | ||
| 6 | Найти точное значение | угловой синус(-1) | ||
| 7 | Найти точное значение | грех(пи/6) | ||
| 8 | Найти точное значение | cos(pi/4) | ||
| 9 | Найти точное значение | грех(45 градусов) | ||
| 10 | Найти точное значение | грех(пи/3) | ||
| 11 | Найти точное значение | арктический(-1) | ||
| 12 | Найти точное значение | cos(45 градусов) | ||
| 13 | Найти точное значение | cos(30 градусов) | ||
| 14 | Найти точное значение | желтовато-коричневый(60) | ||
| 15 | Найти точное значение | csc(45 градусов) | ||
| 16 | Найти точное значение | загар (60 градусов) | ||
| 17 | Найдите точное значение | сек (30 градусов) | ||
| 18 | Найти точное значение | cos(60 градусов) | ||
| 19 | Найти точное значение | соз(150) | ||
| 20 | Найти точное значение | грех(60) | ||
| 21 | Найти точное значение | cos(pi/2) | ||
| 22 | Найти точное значение | загар (45 градусов) | ||
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | ||
| 24 | Найти точное значение | csc(60 градусов) | ||
| 25 | Найти точное значение | сек (45 градусов) | ||
| 26 | Найти точное значение | csc(30 градусов) | ||
| 27 | Найти точное значение | грех(0) | ||
| 28 | Найти точное значение | грех(120) | ||
| 29 | Найти точное значение | соз(90) | ||
| 30 | Преобразовать из радианов в градусы | пи/3 | ||
| 31 | Найти точное значение | желтовато-коричневый(30) | ||
| 32 | Преобразование градусов в радианы | 45 | 92 | |
| 35 | Преобразовать из радианов в градусы | пи/6 | ||
| 36 | Найти точное значение | детская кроватка(30 градусов) | ||
| 37 | Найти точное значение | арккос(-1) | ||
| 38 | Найти точное значение | арктический(0) | ||
| 39 | Найти точное значение | детская кроватка(60 градусов) | ||
| 40 | Преобразование градусов в радианы | 30 | ||
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | ||
| 42 | Найти точное значение | грех((5pi)/3) | ||
| 43 | Найти точное значение | грех((3pi)/4) | ||
| 44 | Найти точное значение | желтовато-коричневый (пи/2) | ||
| 45 | Найти точное значение | грех(300) | ||
| 46 | Найти точное значение | cos(30) | ||
| 47 | Найдите точное значение | соз(60) | ||
| 48 | Найти точное значение | соз(0) | ||
| 49 | Найти точное значение | соз(135) | ||
| 50 | Найти точное значение | cos((5pi)/3) | ||
| 51 | Найти точное значение | cos(210) | ||
| 52 | Найти точное значение | сек(60 градусов) | ||
| 53 | Найти точное значение | грех(300 градусов) | ||
| 54 | Преобразование градусов в радианы | 135 | ||
| 55 | Преобразование градусов в радианы | 150 | ||
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | ||
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | ||
| 58 | Преобразование градусов в радианы | 89 градусов | ||
| 59 | Преобразование градусов в радианы | 60 | ||
| 60 | Найти точное значение | грех(135 градусов) | ||
| 61 | Найти точное значение | грех(150) | ||
| 62 | Найти точное значение | грех(240 градусов) | ||
| 63 | Найти точное значение | детская кроватка(45 градусов) | ||
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | ||
| 65 | Найти точное значение | грех(225) | ||
| 66 | Найти точное значение | грех(240) | ||
| 67 | Найти точное значение | cos(150 градусов) | ||
| 68 | Найти точное значение | желтовато-коричневый(45) | ||
| 69 | Оценка | грех(30 градусов) | ||
| 70 | Найти точное значение | сек(0) | ||
| 71 | Найти точное значение | cos((5pi)/6) | ||
| 72 | Найти точное значение | КСК(30) | ||
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | ||
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | ||
| 75 | Найти точное значение | желтовато-коричневый(0) | ||
| 76 | Оценить | грех(60 градусов) | ||
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | ||
| 78 | Преобразовать из радианов в градусы | (3 шт. |