Какие бывают числа рациональные: Рациональные числа: что это такое, свойства и примеры

Какие числа бывают

Прежде, чем изучать новые, комплексные числа, давайте вспомним числа, которые мы знаем. Самые простые числа — это натуральные, они обозначаются буквой :

1, 2, 3, 4, 5, 6, …

С помощью этих чисел мы считаем разные объекты. Натуральные числа мы можем складывать и умножать. Целые числа, обозначаемые , расширяют множество натуральных чисел — добавляют нуль и отрицательные числа. Наличие отрицательных чисел позволяет нам вычитать любое число из любого, тогда как «живя» в натуральных числах, при вычитании мы должны были всегда следить, чтобы из большего вычиталось меньшее. Вот примеры целых чисел:

Чтобы рассматривать части целого (например, три восьмых от пирога), были придуманы дробные числа . Их так же называют рациональными:

Кроме сложения, вычитания, умножения рациональные числа можно делить друг на друга и снова получать рациональное число (конечно, на ноль делить при этом нельзя).

Следующее множество чисел, расширяющее множество рациональных чисел — это действительные (вещественные) числа .

Задача 1[8] Задача Архимеда

Докажите, что существуют иррациональные числа.

Рисунок 1. Длина диагонали единичного квадрата иррациональна

Решение.

Замечание: этот подход не является строгим в современном смысле. Нужно дать определение вещественных чисел и доказать, что среди них вообще существуют иррациональные числа. Например, в Фихтенгольце это делается с помощью Дедекиндового сечения, а уж потом доказывается, что корень из двух является примером такого числа.

Точнее эта задача звучит так: докажите, что есть отрезки, длина которых не является рациональным числом. Рассмотрим диагональ единичного квадрата. По теореме Пифагора, квадрат её длины есть

то есть

Докажем, что это число не рационально. Пусть это не так (применяем метод доказательства от противного).

Тогда есть такие натуральные числа и , что

— несократимая дробь. Возведем равенство в квадрат и умножим на :

Отсюда следует, что четное, то есть , где какое-то натуральное число. Получаем:

Из последнего уравнения следует, что тоже четное число. Итак, мы получили, что и четные числа. Но вначале мы предположили, что несократимая дробь. Таким образом, получили противоречие. А значит, наше предположение, что существуют натуральные и такие, что

неверно. Конец решения.

Действительные числа очень обширны, с их помощью можно описывать любое количество вещества, любой объём жидкости, длину любого отрезка. Действительные числа можно складывать, вычитать, умножать, делить (только на ноль делить нельзя). Кроме того, можно брать корни из неотрицательных чисел и вычислять самые разные функции, например, синус, косинус, экспоненту и др.

Действительные числа можно представлять в виде направленной прямой с выделенной точкой . Точке соответствует число . Справа находятся положительные числа, а слева — отрицательные. Такое представление называется «числовой осью»:

Задача 2[8]

а) Может ли сумма двух иррациональных чисел быть рациональна? Если да, то приведите пример двух иррациональных чисел, сумма которых рациональна.

б) Приведите пример двух иррациональных чисел, сумма которых иррациональна. Докажите, что сумма действительно иррациональна.

Решение

а) ;

б) .

Математики проливают свет на минималистскую гипотезу / Хабр

На этой табличке родом из Вавилона, сделанной около 1800 года до н.э., перечислены пифагоровы тройки – целые числа a, b и c, удовлетворяющие полиномиальному уравнению a

2 + b² = c². По сию пору поиск рациональных и целочисленных решений полиномиальных уравнений остаётся серьёзной задачей для математиков

В пятом столетии до н. э. греческий математик сделал открытие, пошатнувшее основы математики, и, по легенде, стоившее ему жизни. Историки считают, что это был Гиппас из Метапонта, и он принадлежал к пифагорейской школе математики, основным догматом которой было то, что любое физическое явление можно выразить целыми числами и их отношениями (тем, что мы называем рациональными числами). Но это предположение развалилось, когда, как считают историки, Гиппас рассматривал длины сторон прямоугольного треугольника, которые должны удовлетворять теореме Пифагора – знаменитому соотношению a² + b

2 = c². Говорят, что Гиппас показал, что при одинаковой длине катетов треугольника, выражаемой рациональным числом, его гипотенузу нельзя выразить рациональным числом.

Согласно одной из версий истории, Гиппас сделал это открытие, находясь в море, и его коллеги, потрясённые этим открытием, сбросили его за борт.

Современные математики уже не смущаются, словно древние греки, иррациональными числами (и вообще открыли, что иррациональных чисел больше, чем рациональных).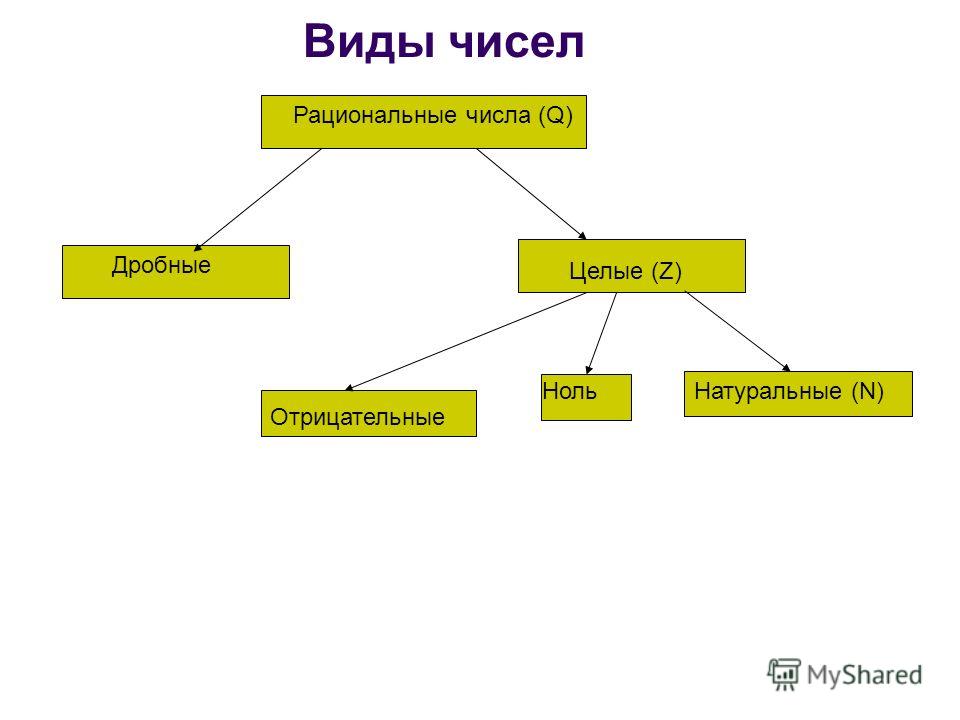 Но любовь пифагорейцев к рациональным решениям уравнений продолжает питать математиков информацией. Она лежит в основе теории чисел, традиционного теоретического ответвления математики, которое, в нашу цифровую эру нашло неожиданно много применений.

Теперь два молодых математика продвинулись на передовой край науки в своём исследовании рациональных решений кубических уравнений. Полиномиальные уравнения, в которых переменные находятся в некоторых степенях, такие, как y = 3x

3 + 4 или x² + y² = 1, принадлежат к числу фундаментальных объектов, изучаемых математиками, и используются в различных практических приложениях, а также в ответвлениях математики.

Полиномиальная вселенная

Легко видеть, что у полиномиального уравнения, в котором степень переменных не превышает 1, типа y = 3x + 4, есть бесконечное число рациональных решений. Любое рациональное значение x даёт рациональное значение y, и наоборот.

Как находить рациональные решения для полиномов со степенью 2, таких, как x² + y² = 1 или y = 3x³ + 2x – 7, известно уже тысячу лет. Они могут вообще не иметь решения, или иметь бесконечно много решений. Графиками таких кривых служат конические сечения – окружности, параболы, эллипсы и гиперболы. Если одна рациональная точка P находится на графике, то есть красивый способ найти все остальные рациональные точки. Нужно просто взять все линии, проходящие через P с рациональным уклоном, и рассчитать второе пересечение этой линии с коническим сечением.

В 1983 году Герд Фолтингс [Gerd Faltings], занимающий сегодня пост директора математического института им. Макса Планка в Бонне, разобрался с полиномиальными уравнениями со степенями более 3. Он показал, что у большинства из них может быть только конечное число рациональных решений. И остались кубические уравнения, упрямые уклонисты вселенной полиномов.

Кубические уравнения сопротивлялись попыткам математиков, классифицировавших их решения. Попытками классификации рациональных решений кубических уравнений – точнее, семейства кубических уравнений, известного, как эллиптические кривые, поскольку именно у них, за исключением нескольких других, могут быть рациональные решения – занимались все великие специалисты по теории чисел, начиная с французского математика XVII столетия Пьера Ферма, говорит Бенедикт Гросс из Гарвардского университета.

У эллиптических кубических уравнений может быть ноль, конечное или бесконечное число решений. Математикам пока удалось лишь догадаться, как часто возникают эти варианты.

У эллиптических кривых есть необъяснимая способность возникать в неожиданных местах, как в теоретической, так и в прикладной математике. Их понимание стало ключевым элементом в доказательстве теоремы Ферма от 1995 года, хотя, кажется, что эллиптические кривые не имеют отношения к её формулировке. Операции, использующие эллиптические кривые, стали центральными компонентами многих криптографических протоколов, кодирующих номера банковских карт в онлайн-транзакциях. Рациональные решения эллиптических кривых находятся в самом центре различных геометрических задач пифагорейского стиля, к примеру, поиска прямоугольных треугольников с рациональными длинами сторон и одновременно рациональной площадью.

«Интеллектуальная стимуляция, прекрасная структура, практические приложения – всё это есть у эллиптических кривых», – говорит Манджул Баргава [Manjul Bhargava] из Принстонского университета.

Баргаве 38 лет, его коллеге, Арулу Шанкару [Arul Shankar] – 26, они работают в институте передовых исследований в Принстоне и уже сделали один из крупнейших шагов за последние несколько десятилетий к пониманию рациональных решений эллиптических кривых.

В их работе не найти рецепта для поиска рациональных решений конкретной эллиптической кривой; вместо этого она объясняет, каковы могут быть наиболее вероятные сценарии для рациональных решений, если выбирать кривую случайным образом.

Открытия Баргавы и Шанкара «начинают проливать свет на крупную область нашей невежественности, – сказал Гросс. – После их работы весь мир выглядит по-другому».

Эллиптическая безопасность

Если взять две рациональные точки на эллиптической кривой, то проходящая через них прямая почти всегда будет пересекать кривую ещё в одной точке, также с рациональными координатами. Очень просто использовать две разные рациональные точки для генерации третьей, но очень сложно сделать наоборот – взять одну рациональную точку и найти две других рациональных точки, которые бы сгенерировали её. Это свойство делает эллиптические кривые полезными для криптографии: на операциях, которые легко сделать в одном направлении и сложно в другом, основана криптографическая безопасность.

«Эллиптические кривые участвуют во многих удивительных вещах, – сказал Питер Сарнак из Принстонского университета. – Они достаточно сложны, чтобы переносить большое количество информации, но достаточно просты для углублённого изучения».

Весёлая поездка

Нахождение рациональных решений эллиптической кривой сводится к нахождению точек на её графике на плоскости xy, таких, что их x и y координаты – рациональные числа. И часто это довольно сложно проделать. Но если вы нашли несколько рациональных точек, становится возможным сгенерировать ещё, при помощи простых процедур, впервые открытых два тысячелетия назад александрийским математиком Диофантом. К примеру, если провести линию через две рациональные точки, обычно она пересечёт кривую ещё ровно в одной точке, также рациональной.

Этот процесс – «очень сложная структура, есть нечто особенное в кубических уравнениях, придающее им глубину», – сказал Баргава.

В 1922 году Луис Морделл доказал нечто поразительное. Для любой эллиптической кривой, даже имеющей бесконечно много рациональных точек, можно сгенерировать все рациональные точки, начав с небольшого их числа, и затем соединяя их между собой. Если количество рациональных точек на эллиптической кривой бесконечно, то минимальное количество точек, необходимое для генерации их всех, называется рангом кривой. Когда количество этих точек конечно, то ранг кривой равен 0.

Десятилетия математики обдумывали минималистскую гипотезу, оценивающую ранг эллиптических кривых, с неоднозначными доказательствами. Гипотеза говорит, что статистически, примерно у половины эллиптических кривых ранг равен 0 (то есть, у них есть либо конечное количество рациональных точек, или нулевое), а у другой половины – 1 (то есть, их бесконечное количество рациональных точек можно сгенерить из одной). Согласно этой гипотезе, количество всех остальных случаев исчезающе мало. Это не значит, что исключений не бывает, или даже что их конечное число – но если брать всё более крупные коллекции эллиптических кривых, то кривых, попадающие в другие категории, в процентном отношении будет становиться всё меньше, и их количество будет стремиться к 0%.

Это предположение впервые сформулировал в 1979 Дориан Голдфелд [Dorian Goldfeld] из Колумбийского университета, имея в виду определённый класс эллиптических кривых. «Оно уже давно стало фольклорным», – говорит Барри Мазур из Гарвардского Университета.

Частично минималистскую гипотезу поддерживает распространённая вера в то, что у эллиптических кривых не должно быть слишком много рациональных точек. Ведь на числовой прямой рациональных чисел меньшинство.

«Рациональные точки эллиптических кривых – случайные жемчужины математики, и очень сложно представить, чтобы таких драгоценных случайностей было слишком много», – писал Мазур и его три соавтора в 2007 году для журнала Bulletin of the American Mathematical Society.

На первый взгляд это говорит о том, что большинство эллиптических кривых должно обладать рангом 0. Но многие математики верят в гипотезу паритета, предполагающую, что эллиптические кривые с чётными и нечётными рангами встречаются 50 на 50. Если скомбинировать гипотезу паритета с редкостью рациональных точек, то мы получим минималистскую гипотезу – разделение 50 на 50 между нижайшими из возможных рангов, 0 и 1.

В поддержку минималистской гипотезы говорят и экспериментальные данные, согласно которым эллиптическим кривым действительно сложно обладать высокими рангами. Специалисты по построению эллиптических кривых использовали компьютеры для поиска кривых с высокими рангами. Текущий рекорд установлен на отметке 28 – но таких кривых очень мало и их коэффициенты гигантские.

Но другие расчётные данные уже не такие вдохновляющие. Математики подсчитывали ранги сотен тысяч эллиптических кривых, и пока что 20% всех кривых обладают рангом 2. У небольшого, но не очень маленького процента кривых ранг равен 3. Согласно минималистской гипотезе их процент должен стремиться к нулю, если принять во внимание все эллиптические кривые. «Судя по всему, данные противостоят предположению», – сказал Мазур.

Обычно, когда данные не соответствуют гипотезе, правильно будет отбросить её. Но множество математиков цепляется за минималистскую гипотезу. И хотя компьютеры переработали множество примеров, математики указывают на то, что эти подсчёты – лишь верхушка айсберга. «Может случиться и так, что пока мы не докажем гипотезы, никакие собранные нами данные, даже и весьма солидные по количеству, не успокоят теоретиков», – писал Мазур с коллегами.

Также они добавили, что довольно крупная часть подсчитанных эллиптических кривых с рангом более 1 аналогична тёмной материи в физике. «Эта большая масса рациональных точек явно находится там. У нас нет сомнений на этот счёт. Мы сомневаемся лишь в том, как дать удовлетворительное объяснение тому, что они там есть».

Из-за конфликта данных и теории, пишут они, десятилетия минималистская гипотеза «то отвергалась, то принималась на веру».

Новые методы

До недавнего времени Манджул Баргава, восходящая звезда математического мира, находился в стане сомневающихся. Один из журналов Popular Science причислил его к «десятке гениев» в 2002 году, а в следующем году в 28 лет он стал одним из самых молодых людей, получивших звание профессора в Принстонском университете. Его коллеги восторгаются не только его математическими достижениями, но и его добрым и творческим нравом.

Манджул Баргава в 38 лет

«Манджул весьма необычный парень, – сказал Гросс. – Он смотрит на вещи отличным от большинства людей способом, в этом и состоит его гений».

Баргава, специалист по теории чисел, заинтересовался явным контрастом между расчётными данными и минималистской гипотезой. «Это говорит о том, что там происходит что-то интересное», – сказал он. «Я пошёл к коллеге, Питеру Сарнаку, и спросил его: „Как ты можешь верить в это предположение?“ – вспоминает Баргава. „Для меня оно выглядело смешным“.

Но Сарнак считал, что данные в результате начнут склоняться в противоположную сторону, когда можно будет обсчитать эллиптические кривые с гораздо большими коэффициентами. „Он был весьма уверен в этой гипотезе“, – сказал Баргава.

Баргава решил так или иначе выяснить что-либо определённое по поводу гипотезы. „Настало время что-нибудь доказать“, – говорит он. Он начал изучать наборы алгоритмов, подсчитывающих ранги эллиптических кривых, берущие начало в процедуре, введённой Ферма в XVII веке. Это семейство алгоритмов, зовущихся алгоритмами спуска – для каждого из целых чисел больше 2 существует по алгоритму – работали со знанием дела и находили эллиптические кривые с рациональными точками. Но несмотря на многочисленные попытки, никто не смог доказать, что эти алгоритмы всегда будут работать.

Баргава решил попробовать другой подход. „У меня была идея попробовать алгоритм спуска для всех эллиптических кривых одновременно, и потом доказать, что в большинстве случаев он будет работать“, – сказал Баргава. Ведь для исследования минималистской гипотезы не обязательно знать, как выглядит каждая эллиптическая кривая – достаточно знать, к какому виду они стремятся.

Такой подход включал работу в области геометрии чисел, занимающейся подсчётом узлов решётки в различных фигурах (узел решётки – точка с целочисленными координатами). У простейших форм типа круга или квадрата число узлов решётки примерно соответствует площади фигуры. Но задача Баргавы касалась более сложных фигур, и когда у фигуры есть непростые особенности, типа щупалец, у неё может оказаться гораздо больше или меньше узлов решётки, чем предсказывает её площадь.

Арул Шанкар в 26 лет

Перед тем, как приняться за такие формы, Баргава поставил схожую, но простую задачу перед Арулом Шанкаром, его аспирантом. Частенько аспиранты годами сражаются с задачами из диссертаций, но Шанкар принёс решение всего через три месяца. Поэтому, говорит Баргава, „я спросил его, не хочет ли он присоединиться ко мне“.

Баргава и Шанкар выработали набор новых техник, чья важность, вероятно, выйдет далеко за пределы изначальной решаемой ими задачи, как говорит Мазур. „Геометрия чисел всегда была глубоким и мощным методом, и теперь они серьёзно увеличили его мощность“. Он добавил, что гениальность их техники „открывает новые возможности в теории чисел“.

Эти новые техники „будут влиять на теорию чисел ещё много лет“, – соглашается Гросс.

Чёткая закономерность

Если минималистская гипотеза верна, то средний ранг эллиптических кривых должен быть ½, но до работы Баргавы и Шанкара математики не могли даже доказать, что среднее значение будет конечным. Используя алгоритм спуска 2 порядка, Баргава и Шанкар смогли показать, что средний ранг для всех эллиптических кривых не превышает 1,5. Используя порядки 3, 4 и 5 для некоторых кривых, не обработанных на предыдущем шаге, они смогли снизить верхнюю планку до 0,88.

И хотя между этим значением и средним числом, предсказанным минималистской гипотезой, пока есть разрыв, открытие Баргавы и Шанкара представляют собой скачок вперёд. „Это только первый шаг, но уже очень большой, – говорит Сарнак. – Здорово видеть, как активно продвигаются двое настолько молодых людей“.

Более того, показав, что средний ранг меньше 1, Баргава и Шанкар доказали, что довольно большой кусок эллиптических кривых – не менее 12% — обладают рангом 0 (поскольку иначе среднее было бы выше). Они использовали это, чтобы показать, что та же часть кривых удовлетворяет знаменитой гипотезе Бёрча — Свиннертон-Дайера, старому вопросу об эллиптических кривых, за ответ на который математическим институтом Клэя назначена награда в миллион долларов.

На лекции Баргавы в институте Клэя один из слушателей в шутку спросил, не полагается ли Баргаве и Шанкару теперь 12% от приза в миллион. „Представители института были на лекции, и они сразу же сказали, что нет, не полагается“, – печально заметил Баргава.

Открытия Баргавы и Шанкара переполошили специалистов по теории чисел, многие из которых не ожидали прогресса в области среднего ранга. „Спроси вы меня за месяц до того, как Манджул рассказал мне о своей работе, – говорит Гросс, – я бы ответил вам, что это безнадёжно“. Теперь, по его словам, минималистская гипотеза выглядит всё более многообещающей. „Я бы поставил на неё деньги“.

Один из возможных путей – который, вероятно, потребует вливания новых идей, как говорят математики – попробовать использовать алгоритмы спуска порядков выше, чем 5, чтобы всё больше уточнять границы среднего ранга. „С использованием спусков 2, 3, 4 и 5 порядков возникла чёткая закономерность, и скорее всего, она продолжится“, – сказал Баргава.

Баргава не считает себя единоличным обладателем прав на эту идею, и надеется, что их работа вдохновит молодых математиков на дальнейшие исследования в области рациональных точек эллиптических кривых. „Минималистская гипотеза – не самоцель, – говорит он. – Каждый раз, открывая дверь, оказывается, что нужно открыть ещё множество дверей. Чем больше людей этим занимаются, тем больше дверей мы сможем открыть“.

1.3: Рациональные числа — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

19851

• Дэвид Арнольд
• College of the Redwoods

Начнем с определения рационального числа.

Рациональные числа

Любое число, которое может быть представлено в виде \(p/q\), где \(p\) и \(q\) — целые числа, \(q \neq 0\), называется рациональным количество. Буква \(\mathbb{Q}\) используется для обозначения набора рациональных чисел. То есть:

\[\mathbb{Q}=\left\{\dfrac{p}{q} : p \text { и } q \text {являются целыми числами, } q \neq 0\right\} \nonumber \]

Поскольку \(-2/3\), \(4/5\) и \(123/(-12)\) имеют вид \(p/q\), где \(p\) и \( q\) — целые числа, каждое из которых является примером рационального числа. Если вы думаете, что слышите слово «дробь», когда мы говорим «рациональное число», вы правы в своих размышлениях. Любое число, которое можно представить в виде дроби, где числитель и знаменатель являются целыми числами, является рациональным числом. Каждое целое также является рациональным числом. Возьмем, к примеру, целое число \(-12\). Есть несколько способов выразить \(-12\) в виде дроби с целыми числителем и знаменателем, \(-12/1\), \(24/(-2)\) и \(-36/ 3\) несколько.

Приведение дробей к наименьшим членам

Сначала мы определим, что подразумевается под наибольшим общим делителем двух целых чисел.

Наибольший общий делитель

Для двух целых чисел \(a\) и \(b\), наибольшим общим делителем чисел \(a\) и \(b\) является наибольшее целое число, которое делится без остатка ) как в \(a\), так и в \(b\). Обозначение \(\operatorname{GCD}(a, b)\) используется для представления наибольшего общего делителя \(a\) и \(b\).

Например, \(\operatorname{GCD}(12,18)=6, \operatorname{GCD}(32,40)=8,\) и \(\operatorname{GCD}(18,27)=9\).

Теперь мы можем определить, когда дробь сокращается до наименьших членов.

Наименьшие члены

Говорят, что дробь \(a/b\) приводится к наименьшим членам тогда и только тогда, когда \(\operatorname{GCD}(a, b)=1\).

Обычный метод приведения дроби к наименьшему члену состоит в делении числителя и знаменателя на их наибольший общий делитель.

Пример \(\PageIndex{1}\)

Уменьшить \(8/12\) до минимального значения.

Раствор

Обратите внимание, что \(\operatorname{GCD}(8,12)=4\). Разделите числитель и знаменатель на \(4\).

\[\begin{aligned} \dfrac{8}{12} &=\dfrac{8 \div 4}{12 \div 4} \quad \color{Red} \text{Числитель и знаменатель разделить на } \ operatorname{GCD}(8,12)=4 \\ &=\dfrac{2}{3} \quad \color{Red} \text{Упростить числитель и знаменатель.}\\ \text{Таким образом, } 8/12 &= 2/3 \end{align} \nonumber\]

Упражнение \(\PageIndex{1}\)

Уменьшить: \(-48 / 60\).

Ответить

\(-4 / 5\)

Вспомним определение простого числа .

Простое число

Натуральное число больше единицы является простым тогда и только тогда, когда его единственные делители равны единице и самому себе.

Например, \(7\) простое число (его делителями являются только \(1\) и \(7\)), а \(14\) нет (его делителями являются \(1\), \( 2\), \(7\) и \(14\)). Точно так же \(2\), \(3\) и \(5\) являются простыми, но \(6\), \(15\) и \(21\) не являются простыми.

Пример \(\PageIndex{2}\)

Уменьшить \(10/40\) до наименьшего значения.

Решение

Обратите внимание, что \(\operatorname{GCD}(10,40)=10\). Разделите числитель и знаменатель на \(10\).

\[\begin{aligned} \dfrac{10}{40} &=\dfrac{10 \div 10}{40 \div 10} \quad \color{Red} \text{Числитель и знаменатель разделить на } \ operatorname{GCD}(10,40)=10 \\ &=\dfrac{1}{4} \quad \color{Red} \text{Упростить числитель и знаменатель.}\\ \text{Таким образом, } 10/40 &= 1/4 \end{выровнено} \nonumber\]

Альтернативное решение

Используйте деревья множителей , чтобы выразить числитель и знаменатель как произведение простых множителей.

Рисунок \(\PageIndex{1}\)

Следовательно, \(10=2 \cdot 5\) и \(40=2 \cdot 2 \cdot 2 \cdot 5\). Теперь, чтобы сократить \(10/40\) до наименьших членов, замените числитель и знаменатель их простыми факторизациями, затем сократите множители, которые являются общими для числителя и знаменателя.

\[\begin{align}
\dfrac{10}{40} &=\dfrac{2 \cdot 5}{2 \cdot 2 \cdot 2 \cdot 5} \quad \color{Red} \text{ Числитель и знаменатель простого множителя.} \\
&=\dfrac{{\color{Red}\not}2 \cdot {\color{Red}\not}5}{{\color{Red}\not}2 \ cdot 2 \cdot 2 \cdot {\color{Red}\not}5} \quad \color{Red} \text{Отменить общие множители.} \\
&=\dfrac{1}{4} \quad \color {Red} \text{Упростите числитель и знаменатель.}
\end{aligned}\]

Когда мы исключаем \(2\) из числителя и знаменателя, мы фактически делим и числитель, и знаменатель на \( 2\). Аналогичное утверждение можно сделать и об отмене \(5\). Отмена как \(2\), так и \(5\) эквивалентна делению числителя и знаменателя на \(10\). Это объясняет \(1\) в числителе, когда все множители сокращаются.

Упражнение \(\PageIndex{2}\)

Сократите \(18/24\) до наименьших значений. .

Ответить

\(3/4\)

Пример \(\PageIndex{2}\) демонстрирует важный момент.

Когда все факторы сокращаются

Когда все множители сокращаются в числителе или знаменателе, результирующий числитель или знаменатель равен единице.

Умножение дробей

Во-первых, определение.

Умножение дробей

Если \(a/b\) и \(c/d\) две дроби, то их произведение определяется следующим образом:

\[\dfrac{a}{b} \cdot \ dfrac{c}{d}=\dfrac{a c}{b d} \nonumber \]

Таким образом, чтобы найти произведение \(a/b\) и \(c/d\), просто перемножьте числители и умножьте знаменатели. Например:

\[\dfrac{1}{2} \cdot \dfrac{3}{4}=\dfrac{3}{8} \quad \text { и } \quad -\dfrac{2}{ 5} \cdot \dfrac{7}{3}= -\dfrac{14}{15} \quad \text { и } \quad -\dfrac{5}{8} \cdot \left(-\dfrac{1 {6} \right)=\dfrac{5}{48} \nonumber \]

Подобно целочисленному умножению, одинаковые знаки дают положительный ответ, а разные знаки дают отрицательный ответ. Конечно, при необходимости не забывайте сокращать свой ответ до минимума.

Пример \(\PageIndex{3}\)

Упрощение: \(-\dfrac{14}{20} \cdot \dfrac{10}{21}\).

Решение

Умножьте числители и знаменатели, затем приведите к наименьшему числу.

\[\begin{align}
-\dfrac{14}{20} \cdot \dfrac{10}{21} &=-\dfrac{140}{420} \quad \color{Red} \text{ Умножить числители и знаменатели}\
&=-\dfrac{2 \cdot 2 \cdot 5 \cdot 7}{2 \cdot 2 \cdot 3 \cdot 5 \cdot 7} \quad \color{Red} \text{Prime factor.} \\
&=-\dfrac{{\color{Red}\not}2 \cdot {\color{Red}\not}2 \cdot {\color{Red}\not}5 \cdot {\color{Red}\not } 7}{{\color{Red}\not}2 \cdot {\color{Red}\not}2 \cdot 3 \cdot {\color{Red}\not}5 \cdot {\color{Red}\ not}7} \quad \color{Red} \text{Отменить общие множители.} \\
&=-\dfrac{1}{3} \quad \color{Red} \text{Упростить.}
\end{ выровнено} \nonumber \]

Обратите внимание, что когда все множители исключаются из числителя, у вас остается \(1\). Таким образом, \((-14/20)\cdot (10/21) = -1/3\).

Упражнение \(\PageIndex{3}\)

Упрощение: \(-\dfrac{8}{9} \cdot\left(-\dfrac{27}{20}\right)\).

Ответить

\(6/5\)

Правило отмены

При умножении дробей сокращать общие множители по следующему правилу: «Сокращать множитель в числителе ради такого же множителя в знаменателе».

Правило «отменить что-то сверху ради чего-то снизу». Таким образом, альтернативный подход к умножению дробей состоит в том, чтобы множить числители и знаменатели на месте, а затем отменять множитель в числителе для идентичного множителя в знаменателе.

Пример \(\PageIndex{4}\)

Упрощение: \(\dfrac{15}{8} \cdot\left(-\dfrac{14}{9}\right)\).

Решение

Расставьте числители и знаменатели на месте, затем сократите общие множители в числителях для общих множителей в знаменателях.

\[\begin{align}
\dfrac{15}{8} \cdot\left(-\dfrac{14}{9}\right) &=\dfrac{3 \cdot 5}{2 \cdot 2 \cdot 2} \cdot\left(-\dfrac{2 \cdot 7}{3 \cdot 3}\right) \quad \color{Red} \text{Числители и знаменатели множителей. } \\
&=\dfrac{{\color{Red}\not}3 \cdot 5}{{\color{Red}\not}2 \cdot 2 \cdot 2} \cdot\left(-\dfrac{{\color {Red}\not}2 \cdot 7}{{\color{Red}\not}3 \cdot 3}\right) \quad \color{Red} \text{Отменить множитель в числителе для общего множителя в знаменатель.} \\
&=-\dfrac{35}{12} \quad \color{Red} \text{Умножение числителей и знаменателей.}
\end{aligned} \nonumber \]

Обратите внимание, что в отличие от знаков дают отрицательный продукт. Таким образом, \((15/8)\cdot (-14/9) = -35/12\).

Упражнение \(\PageIndex{4}\)

Упростить: \(-\dfrac{6}{45} \cdot\left(-\dfrac{35}{14}\right)\)

Ответ

\(1/3\)

Деление дробей

Каждое ненулевое рациональное число имеет обратное мультипликативное или обратное .

Обратное число

Если \(a\) является любым ненулевым рациональным числом, то \(1/a\) называется мультипликативным обратным или обратным числом \(a\), и:

\[a \cdot \ dfrac{1}{a}=1 \nonumber \]

Обратите внимание, что:

\[2 \cdot \dfrac{1}{2}=1 \quad \text { and } \quad \dfrac{3}{5} \cdot \dfrac{5}{3}= 1 \quad \text { and } \quad -\dfrac{4}{7} \cdot\left(-\dfrac{7}{4}\right)=1 \nonumber \]

Таким образом, обратная величина \ (2\) равно \(1/2\), обратная величина \(3/5\) равна \(5/3\), а обратная величина \(-4/7\) равна \(-7/ 4\). Обратите внимание: чтобы найти обратную величину числа, просто инвертируйте число (переверните его вверх ногами). Теперь мы можем определить частное двух дробей.

Деление дробей

Если \(a/b\) и \(c/d\) две дроби, то их частное определяется следующим образом:

\[\dfrac{a}{b} \div \dfrac{c}{ d}=\dfrac{a}{b} \cdot \dfrac{d}{c} \nonumber \]

Приведенное выше определение деления резюмируется фразой «обратить и умножить».

Пример \(\PageIndex{5}\)

Упрощение: \(-\dfrac{35}{21} \div\left(-\dfrac{10}{12}\right)\).

Решение

Обратить и умножить, затем поставить на множители и исключить общие множители в числителе для общих множителей в знаменателе.

\[\begin{align}
-\dfrac{35}{21} \div\left(-\dfrac{10}{12}\right) &=-\dfrac{35}{21} \cdot\ left(-\dfrac{12}{10}\right) \quad \color{Red} \text{Инвертировать и умножить.} \\
&=-\dfrac{5 \cdot 7}{3 \cdot 7} \ cdot\left(-\dfrac{2 \cdot 2 \cdot 3}{2 \cdot 5}\right) \quad \color{Red} \text{Prime factor. } \\
&=-\dfrac{{\ color{Red}\not}5 \cdot {\color{Red}\not}7}{{\color{Red}\not}3 \cdot {\color{Red}\not}7} \cdot\left( -\dfrac{{\color{Red}\not}2 \cdot 2 \cdot {\color{Red}\not}3}{{\color{Red}\not}2 \cdot {\color{Red}\ not}5}\right) \quad \color{Red} \text{Отменить общие множители.} \\
&=\dfrac{2}{1} \quad \color{Red} \text{Умножить числители и знаменатели.} \\ &=2 \quad \color{Red} \text{Упростить.} \end{aligned} \nonumber \]

Обратите внимание, что когда все множители в знаменателе сокращаются, остается \(1\). Таким образом, \((-35/21)÷(-10/12) = 2\). Заметим также, что подобные знаки дают положительный результат.

Упражнение \(\PageIndex{5}\)

Упрощение: \(-\dfrac{4}{9} \div \dfrac{27}{81}\).

Ответить

\(-4/3\)

Добавление дробей

Сначала определение.

Сложение дробей

Если две дроби имеют общий знаменатель, сложите числители и поместите результат над общим знаменателем. В символах:

\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \nonumber \]

Например:

\[-\ dfrac{3}{5}+\dfrac{7}{5}=\dfrac{4}{5} \quad \text { и } \quad-\dfrac{4}{3}+\left(-\dfrac {7}{3}\right)=-\dfrac{11}{3} \quad \text { и } \quad \dfrac{4}{7}+\left(-\dfrac{5}{7}\ справа)=-\dfrac{1}{7} \nonumber \]

Если дроби не имеют общего знаменателя, сначала составить эквивалентные дроби с наименьшим общим знаменателем, а затем сложить по приведенному выше правилу.

Наименьший общий знаменатель

Если дроби \(a/b\) и \(c/d\) не имеют общего знаменателя, наименьший общий знаменатель для \(b\) и \(d\), записывается \(\mathrm{LCD}(b, d)\) определяется как наименьшее число, которое делится как на \(b\), так и на \(d\).

Пример \(\PageIndex{6}\)

Упрощение: \(-\dfrac{3}{8}+\dfrac{5}{12}\).

Решение

Наименьшим общим знаменателем в этом случае является наименьшее число, которое делится как на \(8\), так и на \(12\). В этом случае \(\mathrm{LCD}(8,12)=24\). Сначала нам нужно составить эквивалентные дроби с общим знаменателем \(24\).

\[\begin{align} -\dfrac{3}{8}+\dfrac{5}{12} &=-\dfrac{3}{8} \cdot \dfrac{\color{Red}3} {\color{Red}3}+\dfrac{5}{12} \cdot \dfrac{\color{Red}2}{\color{Red}2} \quad \color{Red} \text{Сделайте эквивалентную дробь с общим знаменателем } 24 \\ &=-\dfrac{9}{24}+\dfrac{10}{24} \quad \color{Red} \text{Умножение числителей и знаменателей.}\\ &=\dfrac{1}{24} \quad \color{Red} \text {Add: } -9+10=1 \end{aligned} \nonumber\]

Обратите внимание, как мы складываем числители на последнем шаге, помещая результат над общим знаменателем. Таким образом, \(-3/8+5/12 = 1/24\).

Упражнение \(\PageIndex{6}\)

Упрощение: \(-\dfrac{5}{6}+\dfrac{1}{9}\).

Ответить

\(-13/18\)

Порядок действий

Рациональные числа подчиняются тем же Правилам, определяющим порядок действий, что и целые числа.

Правила, определяющие порядок операций

При вычислении выражений действуйте в следующем порядке.

1. Сначала вычислить выражения, содержащиеся в символах группировки. Если символы группировки являются вложенными, сначала вычислите выражение в самой внутренней паре символов группировки.
2. Вычислить все показатели степени, встречающиеся в выражении.
3. Выполнить все операции умножения и деления в порядке их появления в выражении, двигаясь слева направо.
4. Выполнять все операции сложения и вычитания в порядке их появления в выражении слева направо.

Пример \(\PageIndex{7}\)

Учитывая \(x = 2/3\), \(y = -3/5\) и \(z = 10/9\), оцените \( ху + yz\).

Решение

После Советы по вычислению алгебраических выражений, сначала замените все вхождения переменных в выражение \(xy + yz\) открытыми круглыми скобками. Затем подставьте заданные значения переменных (\(2/3\) вместо \(x\), \(-3/5\) вместо \(y\) и \(10/9\) вместо \(z \)) в открытых скобках.

\[\begin{align} x y+y z &=()(\;\;)+(\;\;)(\;\;) \quad \color{Red} \text{Замените переменные скобками }\\ &=\left(\dfrac{2}{3}\right)\left(-\dfrac{3}{5}\right)+\left(-\dfrac{3}{5}\right) \left(\dfrac{10}{9}\right) \quad \color{Red} \text{Замените: } 2/3 \text{ вместо } x, -3/5 \text{ вместо } y, \text { и } 10 сентября\text{ for } z \end{aligned} \nonumber \]

Используйте правила , определяющие порядок операций , для упрощения.

\[\begin{align}
&=-\dfrac{6}{15}+\left(-\dfrac{30}{45}\right) \quad \color{Red} \text{Multiply}\ \
&=-\dfrac{2}{5}+\left(-\dfrac{2}{3}\right) \quad \color{Red} \text{Reduce} \\
&=-\dfrac{ 2}{5} \cdot \dfrac{3}{3}+\left(-\dfrac{2}{3} \cdot \dfrac{5}{5}\right) \quad \color{Red} \text {Составьте эквивалентные дроби с помощью }\\
&=-\dfrac{6}{15}+\left(-\dfrac{10}{15}\right) \quad \color{Red} \text{Наименьший общий знаменатель }\\
&=-\dfrac{16}{15} \quad \color{Red} \text{Add}
\end{aligned} \nonumber \]

Таким образом, если \(x=2 / 3, y=- 3/5,\) и \(z=10/9,\), затем \(x y+y z=-16/15\)

Упражнение \(\PageIndex{7}\)

Дано \(a= -1 / 2, b=2 / 3\) и \(c=-3 / 4\), вычислить выражение \(a+bc\) и упростить результат. {3}=27/125\), учитывая \(x=-3/5\). 9{2}=9 / 4\)
\[=\dfrac{16}{9}+\dfrac{2}{1}\left(-\dfrac{4}{3}\right)\left(-\ dfrac{3}{2}\right)-\dfrac{3}{1}\left(\dfrac{9}{4}\right) \nonumber \]

Затем выполните умножение и уменьшение.

\[\begin{array}{l}{=\dfrac{16}{9}+\dfrac{24}{6}-\dfrac{27}{4}} \\ {=\dfrac{16} {9}+4-\dfrac{27}{4}}\end{array} \nonumber \]

Составьте эквивалентные дроби с общим знаменателем, затем сложите.

\[\begin{array}{l}{=\dfrac{16}{9} \cdot {\color{Red} \dfrac{4}{4}}+4 \cdot {\color{Red} \ dfrac {36} {36}} — \ dfrac {27} {4} \ cdot {\ color {Red} \ dfrac {9{2}\).

Ответить

\(-31/400\)

Дроби на графическом калькуляторе

Мы всегда должны помнить, что графический калькулятор — это «аппроксимирующая машина». В небольшом числе ситуаций он способен дать точный ответ, но для большинства вычислений лучшее, на что мы можем надеяться, — это приблизительный ответ.

Однако калькулятор дает точные результаты для операций с дробями, если мы не используем дроби со слишком большими знаменателями, чтобы калькулятор мог дать точный ответ.

Пример \(\PageIndex{10}\)

С помощью графического калькулятора упростите каждое из следующих действийУпростите с помощью графического калькулятора:

1. \(\dfrac{2}{3}+\dfrac{1}{2 }\)
2. \(\dfrac{2}{3} \cdot \dfrac{5}{7}\)
3. \(\dfrac{3}{5} \div \dfrac{1}{3}\)

Решение

Вводим каждое выражение по очереди.

1. Правила , определяющие порядок операций , говорят нам, что мы должны выполнять деление перед сложением. Таким образом, выражение \(2/3+1/2\) эквивалентно:
   \[\begin{aligned} 2 / 3+1 / 2 &=\dfrac{2}{3}+\dfrac{1}{2} \quad \color{Red} \text{Сначала разделить.}\\ &=\dfrac{4}{6}+\dfrac{3}{6} \quad \color{Red} \text{Эквивалентные дроби с ЖК-дисплеем.}\\ &=\dfrac{7}{6} \quad \ color{Red} \text{Add. } \end{aligned} \nonumber \]Введите выражение \(2/3+1/2\) на калькуляторе, затем нажмите клавишу ENTER. Результат показан на первом изображении на рисунке \(\PageIndex{2}\). Затем нажмите кнопку MATH, затем выберите 1:Frac (см. второе изображение на рисунке \(\PageIndex{2}\)) и снова нажмите клавишу ENTER. Обратите внимание, что результат, показанный на третьем изображении на рисунке \(\PageIndex{2}\), соответствует правильному ответу \(7/6\), найденному выше.

Рисунок \(\PageIndex{2}\): Расчет \(2/3+1/2\).

2. Правила , определяющие порядок операций , говорят нам, что нет предпочтения деления перед умножением или наоборот. Мы должны выполнять деление и умножение по мере их возникновения, двигаясь слева направо. Отсюда: \[\begin{aligned}
   2/3 \times 5/7 &=\dfrac{2}{3} \times 5/7 \quad \color{Red} \text{Divide: } 2/3= \dfrac{2}{3}\\
   &=\dfrac{10}{3} / 7 \quad \color{Red} \text{Multiply: } \dfrac{2}{3}\times 5=\dfrac {10}{3}\\
   &=\dfrac{10}{3} \times \dfrac{1}{7} \quad \color{Red} \text{Инвертировать и умножить. }\\
   &=\dfrac{10}{21} \ quad \color{Red} \text{Multiply: } \dfrac{10}{3}\times \dfrac{1}{7}=\dfrac{10}{21}
   \end{aligned} \nonumber \] Это точно такой же результат, который мы получаем, когда мы выполняем следующее вычисление. \[\dfrac{2}{3} \times \dfrac{5}{7}=\dfrac{10}{21} \quad \color{Red} \text{Умножение числителей и знаменателей.} \nonumber \] Следовательно : \[2 / 3 \times 5 / 7 \quad \text { эквивалентно } \quad \dfrac{2}{3} \times \dfrac{5}{7} \nonumber \]Введите выражение \(2 /3×5/7\) на вашем калькуляторе, затем нажмите клавишу ENTER. Результат показан на первом изображении на рисунке \(\PageIndex{3}\). Затем нажмите кнопку MATH, затем выберите 1:Frac (см. второе изображение на рисунке \(\PageIndex{3}\)) и снова нажмите клавишу ENTER. Обратите внимание, что результат, показанный на третьем изображении на рисунке \(\PageIndex{3}\), соответствует правильному ответу \(10/21\), найденному выше.

Рисунок \(\PageIndex{3}\): Расчет \(2/3×1/2\).

3. Этот пример демонстрирует необходимость постоянного напоминания о Правилах, определяющих порядок операций . Мы знаем, что нам нужно инвертировать и умножать в этой ситуации. \[\begin{align} \dfrac{3}{5} \div \dfrac{1}{3}&= \dfrac{3}{5} \times \dfrac{3}{1} \quad \color{ Красный} \text { Инвертировать и умножить. } \\ &=\dfrac{9}{5} \quad \color{Red} \text { Умножение числителей и знаменателей. } \end{выровнено} \nonumber \]
   Итак, правильный ответ 9/5. Введите выражение \(3/5/1/3\) на калькуляторе, затем нажмите клавишу ENTER. Выберите 1:Frac в меню MATH и снова нажмите клавишу ENTER. Обратите внимание, что результат на первом изображении на рисунке \(\PageIndex{4}\) не соответствует правильному ответу \(9/5\), найденному выше. Что мы сделали не так? Если мы будем следовать Правилам , определяющим порядок операций точно , тогда: \[\begin{aligned}
   3 / 5 / 1 / 3 & =\dfrac{3}{5} / 1 / 3 \quad \color{Red } \text {Разделить: } 3/5=\dfrac{3}{5} \\
   & =\dfrac{3}{5} / 3 \quad \color{Red} \text { Разделить: } \dfrac{3}{5} / 1=\dfrac{3}{5} \\
   & = \dfrac{3}{5} \times \dfrac{1}{3} \quad \color{Red} \text {Инвертировать и умножить. } \\
   & =\dfrac{1}{5} \quad \color {Red} \text {Multiply: } \dfrac{3}{5} \times \dfrac{1}{3}=\dfrac{1}{5}
   \end{aligned} \nonumber\] Это объясняет ответ на первом изображении на рисунке \(\PageIndex{4}\). Однако это также показывает, что: \[ 3 / 5 / 1 / 3 \quad \text { не эквивалентно } \quad \dfrac{3}{5} \div \dfrac{1}{3} \nonumber \] Мы можем решить эту проблему, используя символы группировки. \[\begin{aligned} (3 / 5) /(1 / 3) &=\dfrac{3}{5} / \dfrac{1}{3} \quad \color{Red} \text { Сначала скобки. } \\ &=\dfrac{3}{5} \div \dfrac{1}{3} \quad \color{Red} \text { эквивалентно } \div \end{aligned} \nonumber \] Следовательно: \[(3 / 5) /(1 / 3) \quad \text { эквивалентно } \quad \dfrac{3}{5} \div \dfrac{1}{3} \nonumber \]Введите выражение \ ((3/5)/(1/3)\) на калькуляторе, затем нажмите клавишу ENTER. Выберите 1:Frac в меню MATH и снова нажмите клавишу ENTER. Обратите внимание, что результат на втором изображении на рисунке \(\PageIndex{4}\) соответствует правильному ответу \(9/5\).

Рисунок \(\PageIndex{4}\): Расчет \((3/5)/(1/3)\).

Упражнение \(\PageIndex{10}\)

Упростите с помощью графического калькулятора: \(-\dfrac{4}{5}+\dfrac{8}{3}\).

Ответить

\(28/15\)

Авторы

---

Эта страница под названием 1.3: The Rational Numbers распространяется под лицензией CC BY-NC-ND 3.0 и была создана, изменена и/или курирована Дэвидом Арнольдом с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Дэвид Арнольд

   Лицензия

   CC BY-NC-ND

   Версия лицензии

   3,0

   Показать страницу TOC

   нет

2. Теги

   1. источник@https://math. libretexts.org/@api/deki/files/80188/ElementaryAlgebra.pdf

Что такое рациональные числа? — GeeksforGeeks

Система счисления включает в себя различные типы чисел, например, простые числа, нечетные числа, четные числа, рациональные числа, целые числа и т. д. Эти числа используются в различных арифметических операциях, таких как сложение, вычитание, умножение, деление, процент, и т. д., чтобы определить определенное значение. Эти числа могут быть выражены как цифрами, так и словами соответственно.

Числа используются в различных арифметических операциях, таких как сложение, вычитание, умножение и т. д., которые применимы в повседневной деловой и торговой деятельности. Цифры или числа — это математические значения, используемые для подсчета, измерения, маркировки или распознавания времени и для многих других действий. Числа обычно также известны как цифры.

Числа — это математические или арифметические числа, используемые для счета, измерения и других арифметических вычислений. Некоторыми примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.

A Система счисления или Система счисления определяется как стандартизированная система для выражения чисел. Это уникальный способ представления, в котором числа представлены в арифметической и алгебраической структуре.

Типы чисел

Существуют различные типы чисел, которые подразделяются на наборы по системе счисления. Типы описаны ниже:

1. Натуральные числа: Натуральные числа представляют собой набор чисел, считая от 1 до бесконечности. Множество натуральных чисел обозначается буквой «N». Это числа, которые мы обычно используем для счета. Набор натуральных чисел на
2. дано N=1,2,3,4,5,6,7,……………
3. Целые числа : Целые числа — это набор натуральных чисел, включая ноль, который считается от 0 до бесконечности. Целые числа не включают дроби или десятичные дроби. Множество целых чисел обозначается буквой «W». Набор целых чисел определяется как W=0,1,2,3,4,5,………………
4. Целые числа : Целые числа представляют собой набор чисел, включающий все положительные натуральные числа, а также ноль. как и все отрицательные числа, которые считают от отрицательной бесконечности до положительной бесконечности. В наборе нет дробей и десятичных знаков. Множество целых чисел обозначается Z. Набор целых чисел задается Z=………..,-5.-4,-3,-2,-1,0,1,2,3,4,5,………….
5. Десятичные числа: Любое числовое значение, состоящее из десятичной точки, является десятичным числом. Оно может быть выражено как 2,5, 0,567 и т. д.
6. Действительное число: Действительные числа — это заданные числа, не содержащие мнимых значений. Он включает в себя все положительные целые числа, отрицательные целые числа, дроби и десятичные значения. Обычно обозначается буквой «R».
7. Комплексный номер: Комплексные числа — это набор чисел, включающий мнимые числа. Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается буквой «С».
8. Рациональные числа : Рациональные числа — это числа, которые могут быть выражены как отношение двух целых чисел. Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается буквой Q.
9. Иррациональные числа: Иррациональные числа — это числа, которые не могут быть выражены дробями или отношениями целых чисел. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается буквой «П».

Что такое рациональные числа?

Числа, которые могут быть выражены в виде дробей двух целых чисел и могут быть записаны как положительное число, отрицательное число, простое число и даже нуль, называются рациональными числами.

Это может быть выражено как p/q, где q ≠ 0

Например, 2/3 — это рациональное число, выражающее деление 2 целых чисел на 3 целых числа.

Рациональные числа могут быть представлены дробями, десятичными знаками и даже нулем. Поскольку все числа с ненулевым знаменателем, которые можно записать в форме p/q, являются рациональными числами.

Давайте посмотрим на различные выражения рациональных чисел

В форме дроби

Рациональное число — это отношение двух целых чисел, которое может быть записано в виде p/q, где q не равно нулю. Следовательно, любая дробь с ненулевым знаменателем является рациональным числом.

Например:

2/5 — рациональное число, где 2 — целое число, деленное на ненулевое целое число, равное 5.

В десятичной форме

Рациональное число также может быть записано в десятичной форме, если десятичное значение является определенным или имеет повторяющиеся цифры после запятой.

Например:

0,3 — рациональное число. Поскольку значение 0,3 может быть далее выражено в виде отношения или дроби, как p/q

0,3 = 3/10

, что является отношением двух определенных целых чисел.

0 является рациональным числом, как?

0 также входит в рациональное число, так как имеет ненулевой знаменатель. Если мы представим 0 в виде p/q

=>0=0/1

где 0 — целое число, деленное на целое число 1.

Свойства рациональных чисел

Переместительное свойство

Ассоциативное свойство

Разрушающее свойство

Эти свойства при различных операциях обсуждаются ниже:

Свойство замыкания

Дополнение: Сумма двух рациональных чисел всегда является рациональным числом. Например, 2 и 3 — рациональные числа, а 2+3=5 — тоже рациональное число.

Вычитание: Разность двух рациональных чисел всегда является рациональным числом. Например, 5 и 2 — рациональные числа, и их разность составляет 5-2=3, что также является рациональным числом.

Умножение: Произведение двух рациональных чисел всегда является рациональным числом. Например: 2 и 3 — рациональные числа, а их произведение равно 2×3=6, что также является рациональным числом.

Деление: Деление двух рациональных чисел также является рациональным числом, если только знаменатель отношения не равен нулю. Например, p и q — два рациональных числа p/q=r, r будет рациональным числом, если q не равно нулю.

Переместительное свойство

Дополнение: Сумма двух рациональных чисел может быть выражена в любом порядке. Например: если p и q — два рациональных числа и p+q=q+p

Вычитание: Вычитание не показывает коммутативное свойство, поскольку разность двух рациональных p и q равна p ≠q, тогда p-q≠q-p тогда как, если p=q, то p-q=q-p

Умножение: Произведение двух рациональных чисел может быть выражено в любом порядке. Например: если p и q — два рациональных числа, pxq=qxp

Деление: Деление также не показывает свойство перестановочности, как если бы p и q — два рациональных числа, тогда p/q≠q/p

Ассоциативное свойство

Дополнение: Сумма трех рациональных чисел может быть выражена в любом порядке. Например: если p, q и r — три рациональных числа, то (p+q)+r= p+ (q+r)

Вычитание: Разность трех рациональных чисел p, q и r выражается как (p-q)-r=p-(q-r)=0

Умножение: Произведение трех рациональных чисел можно сгруппировать в Любой заказ. Если p, q и r — три рациональных числа, то px(qxr)=(pxq)xr

Деление: Если p, q и r — три рациональных числа. Тогда их выражение будет (p÷q)÷r≠p÷(q÷r)

Разрушающее свойство

Разрушающее свойство показывает, что произведение сумм или разностей рациональных чисел равно сумме или разности их товары. Этот порядок выражается как p.(q+r)= p.q+q.r

Обратное свойство

Когда к числу добавляется отрицательное рациональное число, чтобы его значение равнялось 0, это аддитивное обратное свойство. Ибо рациональное число p, (-P) является аддитивно обратным. Например: 2+(-2)=0.

Свойство идентичности

Произведение любого рационального числа на 1 и есть само рациональное число. Если p — рациональное число, его произведение на 1 даст px1=p. Следовательно, 

Аналогичные вопросы

Вопрос 1. Какие рациональные числа находятся между 3 и 5?

Ответ:

Рациональные числа между 3 и 5: 31/10, 32/10, 33/10, 34/10, 35/10, 36/10,…………..,49 /10.

Чтобы найти набор рациональных чисел между двумя числами, предположим A и B, нам нужно выразить числа A и B в рациональных числах.

Доказательство:

Представим рациональные числа 3 и 5 следующим образом: между 3 и 5 — 30/10, а 50/10 — 31/10, 32/10, 33/10, 34/10, 35/10, 36/10, 37/10, 38/10, 39/10, 40/10, …………..49/10.

Вопрос 2: Какие пять рациональных чисел находятся между 0 и 1?

Ответ:

Пять рациональных чисел от 0 до 1: 12, 21, 34, 41 и 51.

Вопрос 3: Является ли 2,6 рациональным числом?

Ответ:

Да, 2,6 — рациональное число. Поскольку рациональные числа могут быть выражены как десятичными значениями, так и дробями. Число также может быть записано как 26/10, что является отношением двух целых чисел.

Взгляните на доказательство ниже.

Доказательство:

Число 2.6 может быть представлено, как показано ниже:

=> 2,6 = 26/10

Далее это число можно разбить следующим образом:

=> 260/100=13/5

Число 13/5 — это отношение двух целых чисел, состоящих из 13 целых чисел, деленное на 5 целых чисел и выраженное в форме дроби (как p/q, где q не равно 0).

Вопрос 4. Является ли 4,5 рациональным числом?

Ответ:

Да, число 4,5 — рациональное число. Поскольку рациональные числа также могут быть представлены в виде десятичных дробей с повторяющимися цифрами после запятой.

Взгляните на приведенное ниже доказательство:

Доказательство:

Данное число 4.5 можно выразить как

=> 45/10

Это можно далее разбить как

=> 450/100=9 /2

Число 9/2 — это отношение двух целых чисел, состоящих из 9 целых чисел, деленное на целое число 2.

No related posts.