Что такое иррациональное число: суть, примеры, свойства
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Что такое иррациональное число: суть, примеры, свойства
Бесконечные дроби бывают периодическими и непериодическими. Последние называются иррациональными числами.
Их суть, как следует из названия, заключается в том, что они не является рациональным, т.е. не могут быть представлены в виде обыкновенной дроби
m/n
, где m и n – это целые числа, а n ≠ 0.
Самый распространенный вид иррациональных чисел (но не единственный) – квадратный корень из любого натурального числа, которое не является точным квадратом.
Примеры:
- √2 = 1,414213562373…
- √3 = 1,732050807568…
- e = 2,718281828459…
Множество иррациональных чисел обозначается латинской буковой “I“.
Свойства:
1. Суммой двух иррациональных чисел может быть рациональное число.
2. Между двумя любыми числами есть иррациональное.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Элементарная математика с точки зрения высшей, Т.
1. Арифметика. Алгебра. Анализ Элементарная математика с точки зрения высшей, Т.1. Арифметика. Алгебра. Анализ
ОглавлениеПРЕДИСЛОВИЕ РЕДАКТОРАВВЕДЕНИЕ АРИФМЕТИКА I. ДЕЙСТВИЯ НАД НАТУРАЛЬНЫМИ ЧИСЛАМИ 2. Основные законы арифметических действий 3. Логические основы теории целых чисел 4. Практика счета с целыми числами II. ПЕРВОЕ РАСШИРЕНИЕ ПОНЯТИЯ ЧИСЛА 1. Отрицательные числа 3. Иррациональные числа III. ОСОБЫЕ СВОЙСТВА ЦЕЛЫХ ЧИСЕЛ 1. Роль теории чисел в школьном и университетском преподавании 2. Простые числа и разложение на множители 3. Обращение простых дробей в десятичные 4. Непрерывные дроби 5. Пифагоровы числа. Великая теорема Ферма 6. Задача о делении окружности на равные части 7. Доказательство невозможности построения правильного семиугольника циркулем и линейкой IV.  n = wНевозможность деления угла на три равные части. 2. Уравнение диэдра 3. Уравнения тетраэдра, октаэдра и икосаэдра 4. Продолжение; вывод уравнений 5. О решении нормальных уравнений 6. Униформизация нормальных уравнений посредством трансцендентных функций Тригонометрическое решение кубического уравнения. 7. Разрешимость в радикалах 8. Сведение общих уравнений к нормальным АНАЛИЗ 1. Систематика алгебраического анализа 2. Историческое развитие учения о логарифме Непер и Бюрги: уравнение в конечных разностях. XVII столетие: площадь гиперболы. Эйлер и Лагранж: алгебраический анализ. XIX столетие: функции комплексной переменной. 3. Некоторые замечания о школьном преподавании 4. Точка зрения современной теории функций II. О ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЯХ 1. Теория тригонометрических функций в связи с учением о логарифме 2. Тригонометрические таблицы В. Логарифмо-тригонометрические таблицы. 3. Применения тригонометрических функций В.  Учение о малых колебаниях, в частности, о колебаниях маятника.С. Изображение периодических функций посредством рядов из тригонометрических функций (тригонометрические ряды). D. Общее понятие функции. III. ИСЧИСЛЕНИЕ БЕСКОНЕЧНО МАЛЫХ В СОБСТВЕННОМ СМЫСЛЕ СЛОВА 1. Общие замечания относительно исчисления бесконечно малых Реакция против предельных переходов и бесконечно малых; исчисление производных Лагранжа. О преподавании исчисления бесконечно малых в школе. 2. Теорема Тейлора Оценка погрешности. Проблемы интерполирования и разностного исчисления. 3. Замечания исторического и педагогического характера ПРИЛОЖЕНИЯ I. ТРАНСЦЕНДЕНТНОСТЬ ЧИСЕЛ e И pi 2. Доказательство трансцендентности числа e 3. Доказательство трансцендентности числа pi 4. Трансцендентные и алгебраические числа II. УЧЕНИЕ О МНОЖЕСТВАХ 1. Мощность множества Счетность множества рациональных и алгебраических чисел.  Несчетность континуума. Мощность континуумов высших измерений. Множества более высоких мощностей. 2. Порядок элементов множества Инвариантность числа измерений при непрерывном отображении. 3. Заключительные замечания о значении учения о множествах и о преподавании в школе ПРИМЕЧАНИЯ АЛГЕБРА АНАЛИЗ |
Написанная в форме лекций для учителей, книга и за давностью лет не потеряла своей значимости,, свежести, привлекательности.
Узнайте об иррациональных числах в математике
Математику можно разделить на две широкие категории: рациональные и иррациональные. Иррациональные числа нельзя разбить на дроби. С другой стороны, рациональные числа могут быть.
Пи — пожалуй, самый известный пример иррационального числа. Число пи невозможно записать в виде дроби, оно никогда не заканчивается и не повторяется в десятичной форме. Это может показаться незначительным отличием, но на самом деле это очень важно!
Давайте определим, что такое иррациональное число, и узнаем, что отличает иррациональные числа от их рациональных аналогов и почему они так интригуют математиков.
Оставайтесь с нами, чтобы узнать больше об этой увлекательной теме!
Что такое иррациональное число?
Иррациональное число — это действительное число, которое нельзя записать в виде дроби или отношения двух целых чисел. Это бесконечное неповторяющееся десятичное число, которое никогда не заканчивается и не имеет шаблона.
Иррациональные числа не могут быть вычислены точно и должны быть аппроксимированы для решения математических задач. Примеры иррациональных чисел включают π (пи), √2 и e или число Эйлера.
Эти числа не совпадают с их рациональными эквивалентами, которые можно записать в виде дроби. Рациональные числа — это любые числа, которые можно записать в виде a/b, где a и b — целые числа (целые числа) без общих делителей, кроме 1.
Примеры иррациональных чисел
Иррациональные числа — это, по существу, неповторяющиеся, не заканчивающиеся десятичные числа, которые не могут быть представлены в виде дроби. Некоторые примеры включают число пи (3,14159.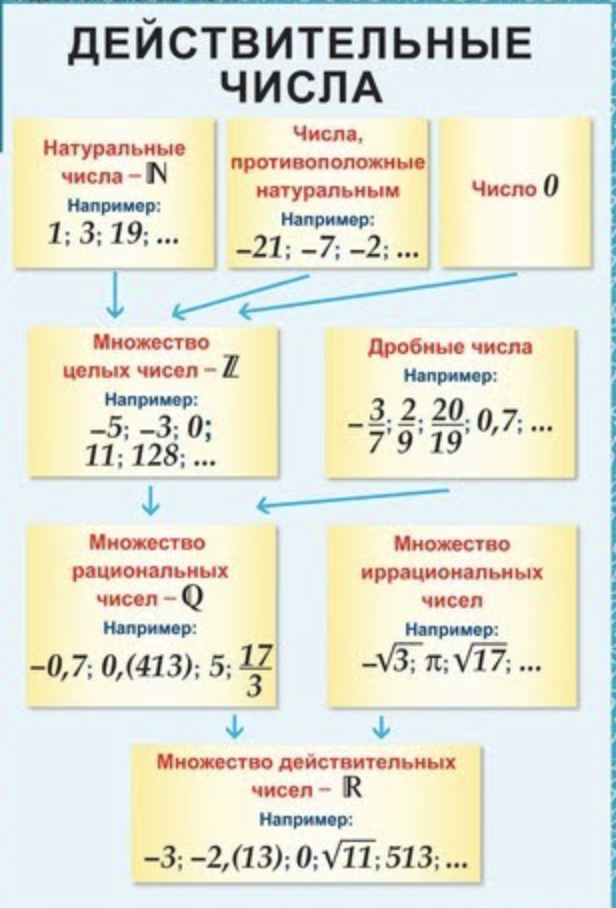
..), квадратный корень из двух (1,414213…) и золотое сечение (1,618033…).
Хотя иррациональные числа могут использоваться для описания измерений природы, они также могут демонстрировать отношения между различными объектами или между объектом и его окружением.
Например, в архитектуре последовательность Фибоначчи часто используется для определения эстетически приятных пропорций, демонстрирующих иррациональное число, такое как 1,61803… совпадающее с абсолютной математической точностью золотого сечения.
Число Эйлера, обозначаемое как e (2,71828…), является иррациональным числом, которое используется во многих областях математики и физики, таких как экспоненциальный рост или затухание, сложные проценты и число возможных конфигураций системы.
Как видите, иррациональные числа используются не только для расчетов, но и для создания визуально приятных форм и пропорций. Вот почему они так увлекательны — их можно применять в самых разных областях и помочь нам понять Вселенную во всей ее полноте.
Почему их называют «иррациональными»
Иррациональные числа, или числа, которые не могут быть выражены простыми дробями, получили название «иррациональные» из-за невозможности представить их в простейшей форме.
В то время как дробь может представлять совершенно рациональное число, такое как 1/2, некоторые другие числа, такие как , считаются иррациональными, потому что они бесконечно длинные и не могут быть точно записаны в дробной форме.
Из-за этого иррациональные числа имеют бесконечное количество цифр после запятой, что затрудняет работу с ними или их использование в математике.
Например, число пи, обозначаемое греческой буквой π, является иррациональным числом, часто используемым в геометрии. Пи составляет около 3,14159 и записывается как бесконечная строка цифр, которые не повторяются после запятой. Итак, пи всегда будет «иррациональным» числом, потому что его никогда нельзя записать точно в виде простой дроби.
В математике есть много способов приблизиться к иррациональным числам и работать с ними, чтобы упростить вычисления.
В зависимости от ситуации и того, насколько точным должен быть ответ, эти методы могут варьироваться от разложения в ряд до численных приближений.
Как иррациональные числа используются в математике?
Иррациональные числа используются в математике для описания множества понятий, и они встречаются почти во всех областях предмета. В алгебре иррациональные числа можно использовать для решения уравнений или вычисления площади определенных фигур.
В исчислении иррациональные числа полезны для вычисления пределов и производных. Они также появляются в геометрии и тригонометрии при вычислении расстояний, углов и площадей.
Кроме того, иррациональные числа появляются при изучении вероятностей и статистики. Их можно использовать для расчета вероятностей или моделирования случайных явлений, таких как броуновское движение. Наконец, они важны для решения уравнений, не имеющих решения в рациональных числах. Выразив решение в иррациональных числах, уравнение можно решить аналитически.
В целом, иррациональные числа являются фундаментальной частью математики и могут использоваться для решения многих типов задач. Они могут появиться практически в любой математической области и могут помочь нам ответить на вопросы об окружающем нас мире.
Изучаете ли вы инженерное дело, экономику или физику, иррациональные числа являются ключевой частью понимания сложности Вселенной.
Как вычислять иррациональные числа
Одним из наиболее распространенных способов вычисления иррациональных чисел является разложение в ряды. Расширение ряда включает выражение числа в виде суммы членов, где каждый член представляет собой дробную часть целого числа. Например, чтобы вычислить число пи, можно использовать следующую формулу:
Эта формула является примером ряда Тейлора, который можно использовать для вычисления значений множества различных иррациональных чисел. Некоторые численные приближения, такие как метод деления пополам и итерация Ньютона-Рафсона, также могут использоваться для определения иррациональных чисел.
Помимо чисел, для вычисления иррациональных чисел можно использовать геометрические идеи, такие как теорема Пифагора и золотое сечение. Эти геометрические методы отлично подходят для определения значений, зависящих от форм, углов и других геометрических свойств.
Например, площадь круга равна пи, умноженному на квадрат его радиуса, а пи — иррациональное число. Золотое сечение также можно использовать для расчета длин сторон правильного пятиугольника или других подобных фигур.
Наконец, иррациональные числа также можно вычислять с помощью алгебраических методов. Нахождение точек пересечения по оси x алгебраического уравнения, как и квадратного уравнения, является распространенным способом определения значения иррационального числа. Затем x-перехваты используются для определения значения иррационального числа.
Алгебра также используется для решения уравнений с несколькими переменными, таких как нахождение недостающей стороны в треугольнике или вычисление длины окружности.
Примеры использования иррациональных чисел в реальном мире
Примером использования иррациональных чисел в реальном мире является измерение длины окружности. Формула для нахождения длины окружности требует иррационального числа пи (π).
Пи — иррациональное число с бесконечным числом цифр, которые никогда не повторяются и не могут быть выражены в виде дроби или десятичной дроби, что делает невозможным измерение длины окружности без использования числа Пи.
Формула для нахождения длины окружности: 2πr, где r — радиус окружности. Чтобы вычислить это, вы должны использовать число Пи, чтобы получить точный ответ. Зная, как использовать иррациональные числа при решении математических уравнений и задач, мы можем получить представление об их применении в реальном мире.
Например, число «пи» используется в технике для расчета длины окружности колеса или для измерения расстояния вокруг дорожки или поля. В архитектуре число Пи может помочь нам рассчитать размер колонн и балок, используемых при строительстве зданий.
Пи также часто используется в физике, например, чтобы выяснить, как движутся планеты и куда они движутся.
Пи можно найти не только в технике и архитектуре, но и в природе. Например, соотношение между лепестками цветка и его центром основано на числе Пи. В биологии было замечено, что нити ДНК следуют схеме, связанной с числом пи.
Понимание иррациональных чисел (с небольшой помощью)
Понятие иррациональных чисел может быть немного трудным для понимания, но с небольшой помощью эксперта понимание чисел, таких как пи, может стать проще.
С опытными репетиторами по математике Learner учащиеся могут связаться с репетитором, обладающим знаниями и опытом, который поможет им лучше понять иррациональные числа, такие как число пи. Наши преподаватели знают, как помочь учащимся, у которых возникли проблемы, лучше понять сложные идеи.
Мы в Learner считаем, что обучение должно доставлять удовольствие, и наши репетиторы по математике стремятся сделать процесс максимально интерактивным и увлекательным.
С их помощью и экспертными знаниями учащиеся узнают больше об иррациональных числах и смогут использовать полученные знания в различных областях математики.
Наши репетиторы по математике могут помочь не только понять иррациональные числа. Они также могут помочь с такими вещами, как методы решения задач, алгебра, геометрия и даже более сложные темы, такие как исчисление и тригонометрия. Это гарантирует, что учащиеся получат наиболее полный доступный учебный опыт.
Свяжитесь с нами сегодня, чтобы узнать больше о том, как они могут помочь вам понять и преуспеть в работе с иррациональными числами. Наша опытная команда будет усердно работать, чтобы гарантировать, что вы достигнете своих целей. Мы будем рады помочь вам добиться успеха!
Что такое иррациональные числа? | Live Science
Когда вы совершаете покупку по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот как это работает.
Иррациональные числа — это действительные числа, которые при выражении в виде десятичной дроби всегда идут после десятичной дроби и никогда не повторяются.
(Изображение предоставлено Shutterstock)Иррациональные числа — это числа, которые нельзя представить как отношение двух целых чисел. Это противоположно рациональным числам, таким как 2, 7, одна пятая и -13/9, которые могут выражаться и выражаются как отношение двух целых чисел. При выражении в виде десятичного числа иррациональные числа всегда идут после десятичной точки и никогда не повторяются.
Связанный: 9 самых больших существующих чисел
Кто вычислил иррациональные числа?
Греческому математику Гиппасу из Метапонта приписывают открытие иррациональных чисел в V веке до нашей эры, согласно статье Кембриджского университета . Говорят, что во время работы над отдельной задачей Гиппас наткнулся на тот факт, что у равнобедренного прямоугольного треугольника, длина двух сторон которого равна 1 единице, гипотенуза равна √2, что является иррациональным числом. (Это можно показать с помощью знаменитой теоремы Пифагора a^2 + b^2 = c^2.
)
Легенда гласит, что Гиппас был брошен в море в награду за его великое открытие. Это потому, что он был членом пифагорейцев, квазирелигиозного ордена, которые верили, что «все есть число» и что вселенная состоит из целых чисел и их соотношений. Обеспокоенные открытием Гиппаса, группа приговорила его к смертной казни через утопление.
Связанный: Фотографии: Большие числа, определяющие Вселенную
Страх перед иррациональными числами позже утих, и в конце концов они были включены в математику. Вместе рациональные и иррациональные числа составляют число 9.0103 действительные числа , которые включают любое число на числовой прямой и в которых отсутствует мнимое число i.
Большинство действительных чисел иррациональны. Немецкий математик Георг Кантор окончательно доказал это в 19 веке, показав, что рациональные числа счетны , а действительные числа несчетны. Это означает, что существует больше реальных, чем рациональных, согласно веб-сайту по истории, математике и другим темам от образовательного карикатуриста Чарльза Фишера Купера.
Поскольку иррациональные числа — это все те действительные числа, которые не являются рациональными, иррациональные числа значительно перевешивают рациональные числа; они составляют все остальные несчетные действительные числа.
Известные иррациональные числа:
Квадратный корень из 2
Несмотря на судьбу Гиппаса, √2 является одним из самых известных иррациональных чисел и иногда называется константой Пифагора, согласно веб-сайту Wolfram MathWorld .
Постоянная Пифагора равна 1,4142135623… (точки означают, что она продолжается вечно).
Все это может звучать теоретически, но число имеет и очень конкретное применение. Международные форматы бумаги включают √2. Международная организация по стандартизации (ИСО) 216, определение серии размеров бумаги A, гласит, что длина листа, деленная на его ширину, должна составлять 1,4142. Это приводит к тому, что лист бумаги формата А1, разделенный пополам по ширине, дает два листа бумаги формата А2.
Пи
Пи — это отношение длины окружности к ее диаметру. Математикам известно число пи со времен древних вавилонян, 4000 лет назад.
Пи равно 3,1415926535…
Некоторые фанаты числа Пи очень гордятся тем, что могут запомнить как можно больше цифр числа Пи. Суреш Кумар Шарма из Индии установил мировой рекорд в 2015 году, запомнив 70 030 цифр числа Пи, согласно Всемирному рейтингу числа Пи .
Phi
Phi также известен как золотое сечение . Его можно найти, взяв палку и разломив ее на две части; если соотношение между этими двумя частями такое же, как соотношение между общей палочкой и большим сегментом, говорят, что части находятся в золотом сечении.
Фи равняется 1,6180339887…
На протяжении столетий вокруг понятия фи накопилось множество преданий, например идея о том, что оно представляет совершенную красоту или может быть найдено повсюду в природе.
e
Основание натуральных логарифмов называется e в честь своего тезки, швейцарского математика 18-го века Леонарда Эйлера.
e равно 2,7182818284…
Наряду с логарифмами, e появляется в уравнениях , включающих комплексных чисел и экспоненциальный рост. Подобно тому, как День Пи отмечается 14 марта (14 марта), 90 103 e День 90 106 отмечается 7 февраля (7 февраля) или 27 января (27 января), в зависимости от того, какую календарную систему вы используете.
Дополнительные ресурсы:
- В Академии Хана есть много полезных видеороликов, объясняющих иррациональные числа. Вот с чего начать: « Вступление в рациональные и иррациональные номера . «
- Говоря о знаменитых числах, ознакомьтесь с этим списком чисел, которые более оланговы
Будьте в курсе последних научных новостей, подписавшись на нашу рассылку Essentials.
