Что такое угол? Определение, виды, как обозначают, примеры
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
Что такое вершина и стороны угла
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.
Иногда встречается обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
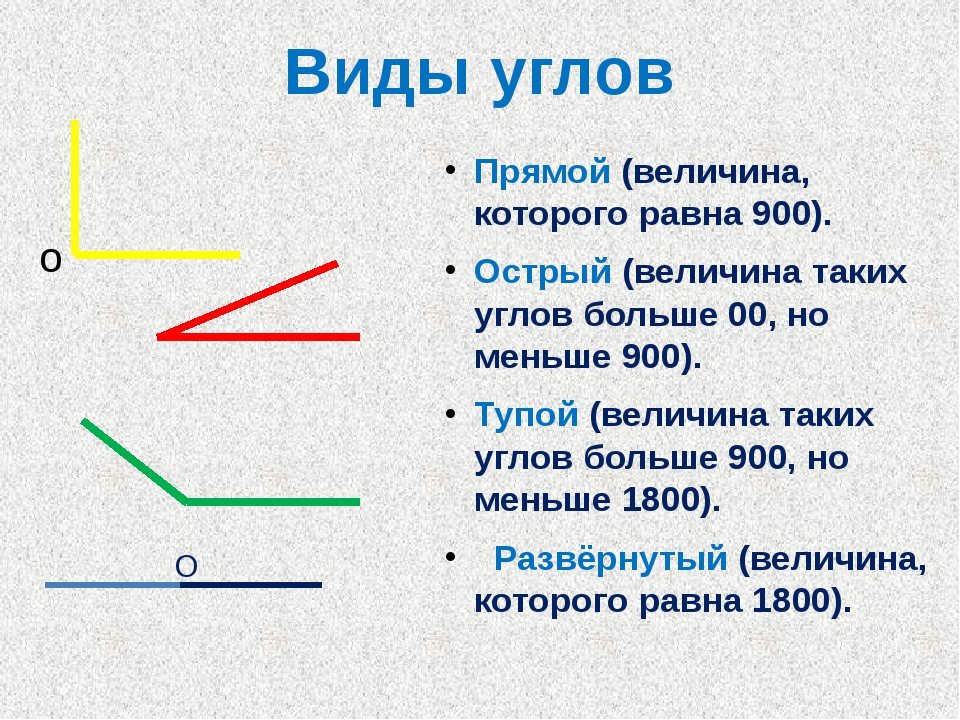
Виды углов
Есть разные типы углов и у каждого своё название:
- острый
- прямой
- тупой
- развернутый
- выпуклый
- полный
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Определять можно на глаз или с помощью линейки.
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Острый угол — это угол, который меньше прямого угла, то есть < 90°.
Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол, показано на первой картинке.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.
Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.
Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.
Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.
Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.
Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.
Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:
- ∠AOC = ∠AOB − ∠COB,
- ∠COB = ∠AOB − ∠AOC.
Запоминаем!
Угол называется прямым, если он равен 90°, острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол равен 180°.
Развернутый угол равен 180°.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Сравнение углов
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
При этом развернутые углы всегда являются равными.
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.
- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.
Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот как он выглядит:
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается ´.
Секунда — 1/60 часть минуты. Обозначается ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.
Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.
Равные углы имеют равную градусную меру.
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:
Вот что важно запомнить при обозначении лучей и углов:
- Равные углы обозначают одинаковым количеством дуг.
- Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
На чертеже отмечены три неравных угла:
Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.
Острый угол
Содержание:
- Какой угол называется острым в математике
- Определение, основные признаки и свойства
- Примеры решения задач
Содержание
- Какой угол называется острым в математике
- Определение, основные признаки и свойства
- Примеры решения задач
Какой угол называется острым в математике
Угол представляет собой геометрическую фигуру, которая образована с помощью пары лучей. Данные линии называют сторонами. Они берут начало в одной точке, называемой вершиной. Согласно основным признаком геометрической фигуры, можно сформулировать ее понятие.
Данные линии называют сторонами. Они берут начало в одной точке, называемой вершиной. Согласно основным признаком геометрической фигуры, можно сформулировать ее понятие.
Определение
Угол является геометрической фигурой, состоящей из пары лучей в виде ее сторон, которые выходят из одной точки или вершины.
Данные фигуры в геометрии подразделяют на типы в зависимости от градусной величины, расположению относительно друг друга и относительно окружности. Основными видами являются:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- прямой;
- тупой;
- острый;
- развернутый.
Градусная мера, которой обладает острый угол, менее 90 градусов. Данный вид геометрической фигуры можно встретить в каждом четырехугольнике, если он не является прямоугольным квадратом или произвольным параллелограммом. Острый угол можно полностью вписать во внутреннее пространство прямого, а одна из его сторон является биссектрисой. Пример острого угла АОВ изображен на рисунке:
Острый угол можно полностью вписать во внутреннее пространство прямого, а одна из его сторон является биссектрисой. Пример острого угла АОВ изображен на рисунке:
Определение, основные признаки и свойства
Определение
Острый угол – это геометрическая фигура, градусная мера которой составляет менее 90 градусов. Источник: webmath.ruДля всех острых углов характерна градусная мера в интервале от 0 до 90 градусов. Простым способом распознавания типа угла является использование предмета, который имеет прямой угол. Его прикладывают к искомому элементу таким образом, чтобы их вершины были совмещены. Примером такого инструмента является линейка. Возможно два варианта результата измерений:
- прямой угол целиком вмещает в себя начерченный, тогда измеряемый угол является острым;
- нарисованный угол помещает в себя прямой, тогда рассматриваемый угол является тупым.

Точным инструментом для измерения градусной меры является транспортир, который состоит из линейки и полуокружности. Пользоваться им несложно. Достаточно приложить центр транспортира к вершине фигуры таким образом, чтобы любой из его сторон совпадал с гранью линейки. Второй луч покажет градусы, соответствующие геометрической фигуре.
Транспортир также применяют, когда необходимо начертить тупой или острый угол:
- провести один луч;
- начало линии совместить с центром инструмента;
- приложить линейку к нужному числу градусов и провести линию.
Особенности рассматриваемой геометрической фигуры:
- если один из смежных углов острый, то второй в любом случае окажется тупым;
- каждый треугольник обладает как минимум одним острым углом;
- есть треугольники, все углы которых являются острыми, их называют остроугольными.
Примеры решения задач
Задача 1
С помощью рисунка необходимо найти острые углы.
Решение
Стороны фигуры, изображенной на первом рисунке, перпендикулярны друг другу. Поэтому его нельзя назвать острым. На втором рисунке начерчен угол, который меньше, чем прямой.
Источник: webmath.ruСогласно определению, данный угол является острым. Если сравнить угол, который изображен на третьем рисунке, с прямым, то можно сделать вывод, что он тупой, так как его градусная мера составляет больше, чем 90 градусов.
Источник: webmath.ruОтвет: острым является угол, который изображен на втором рисунке.
Задача 2
Имеется пара смежных углов. Один из них больше, чем второй на 30 градусов. Требуется определить, какой из этих углов является острым.
Решение
Обозначим меньший угол буквой х. Тогда (х+30) является большим углом. Известно, что сумма смежных углов составляет 180 градусов. Можно записать справедливое равенство:
х + (х + 30) = 180
2х = 150
х = 75
75 < 90
Ответ: меньший угол, который составляет 75 градусов, будет острым.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Как выглядят острые и тупые углы. Острый угол. Введение в понятие геометрического угла
26 июня 2013
Давайте начнем с определения того, что такое угол. Во-первых, он является геометрической фигурой. Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера тупого угла всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить смежные углы, проведя из его вершины один или несколько лучей в любых направлениях.
На нем можно построить смежные углы, проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов.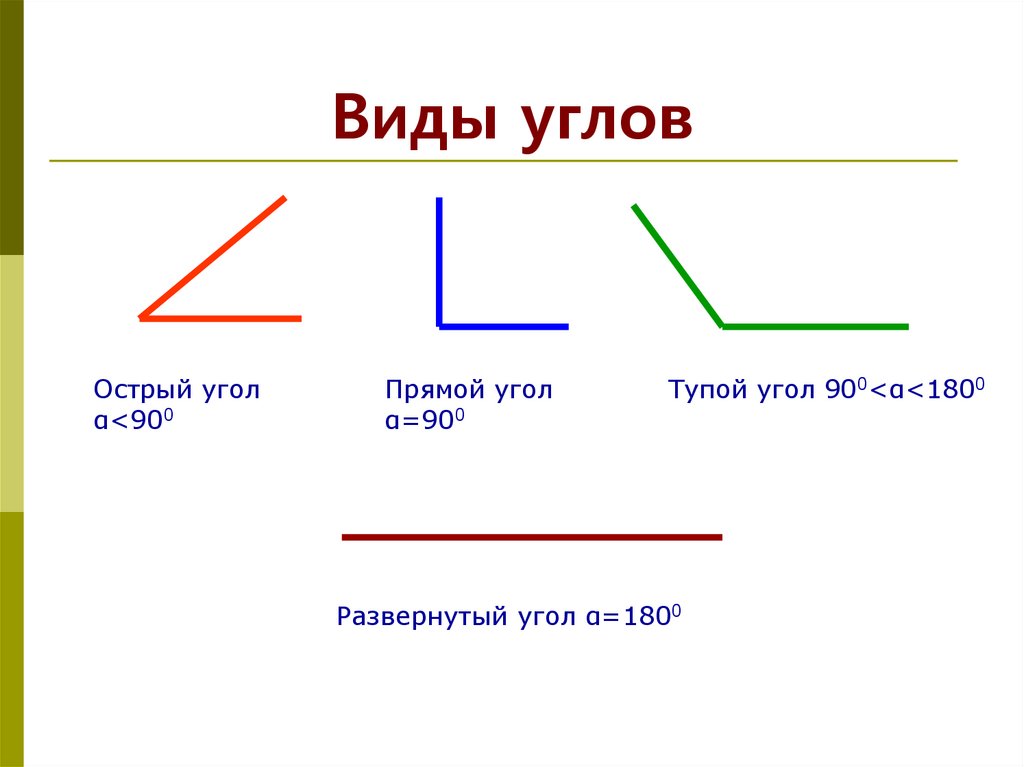 Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Источник: fb.ru
Актуально
Разное
Разное
В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.
Навигация по странице.
Определение угла.
Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.
Дадим сначала определение луча.
Пусть нам дана некоторая прямая на плоскости. Обозначим ее буквой a . Пусть O – некоторая точка прямой a . Точка O разделяет прямую a на две части. Каждая из этих частей вместе с точкой О называется лучом , а точка О называется началом луча . Еще можно услышать, что луч называют полупрямой .
Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p или луч k ), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА или луч СD ). Покажем изображение и обозначение лучей на чертеже.
Теперь мы можем дать первое определение угла.
Определение.
Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом.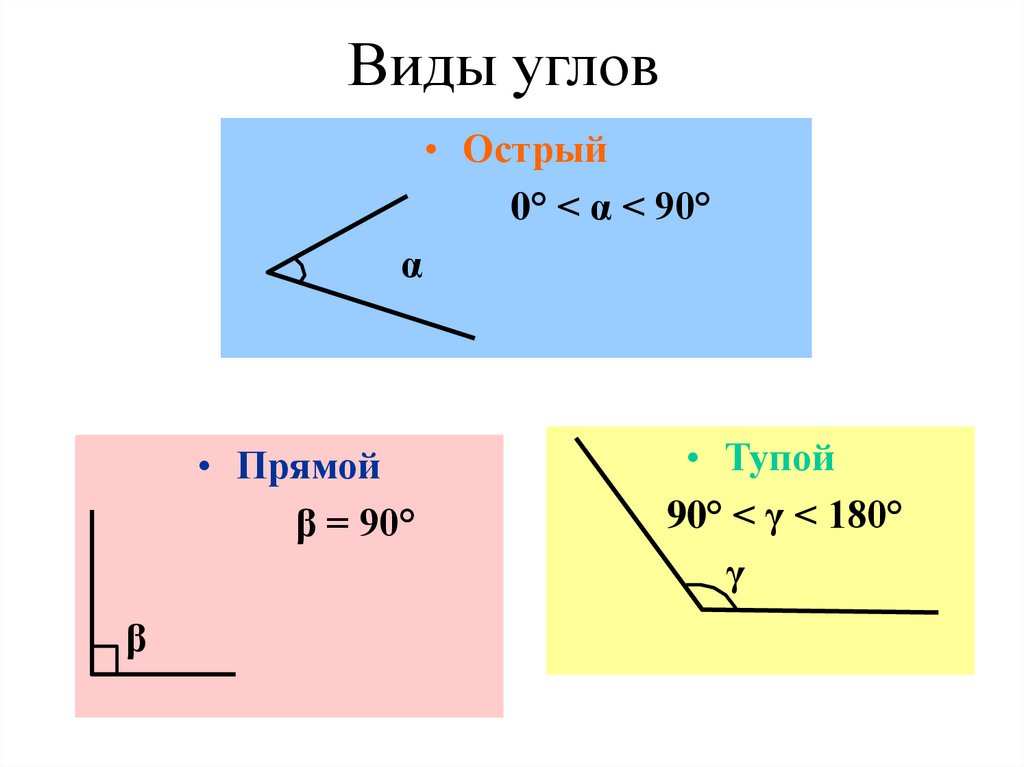 Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Возможен случай, когда стороны угла составляют прямую линию. Такой угол имеет свое название.
Определение.
Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым .
Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.
Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k
, а другая h
), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA
, а вторая сторона угла OB
), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ).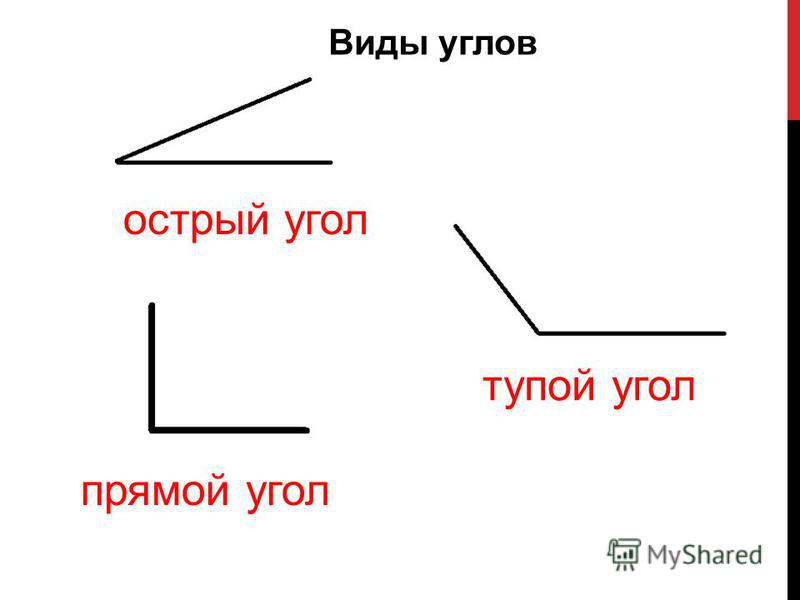 Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла , а другую – внешней областью угла . Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая — внешней.
Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.
Определение внутренней области угла приводит нас ко второму определению угла.
Определение.
Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.
Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Дадим еще определения смежных и вертикальных углов.
Определение.
Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.
Из определения следует, что смежные углы дополняют друг друга до развернутого угла.
Определение.
Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.
На рисунке изображены вертикальные углы.
Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.
Сравнение углов.
В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим.
Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением.
Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»?
Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными .
Если же две другие стороны углов не совместятся, то углы называются неравными , причем меньшим считается тот угол, который составляет часть другого (большим является тот угол, который полностью содержит другой угол).
Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.
Измерение углов.
Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла.
Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.
Одной из единиц измерения углов является градус .
Определение.
Один градус – это угол, равный одной сто восьмидесятой части развернутого угла.
Градус обозначают символом «», следовательно, один градус обозначается как .
Таким образом, в развернутом угле мы можем уложить 180 углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180 равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла.
При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180 раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30 раз (такой угол составляет шестую часть развернутого угла) и ровно 90 раз (половина развернутого угла).
Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения). Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определение.
Минута – это одна шестидесятая часть градуса.
Определение.
Секунда – это одна шестидесятая часть минуты.
Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600 секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17 градусов 3 минуты и 59 секунд, можно обозначить как .
Определение.
Градусной мерой угла называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле.
Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна .
Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир.
Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110 ), то используют краткую запись вида и говорят: «Угол АОВ равен ста десяти градусам».
Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180] (в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют прямым углом . Угол меньший 90 градусов называется острым углом . Угол больший девяноста градусов называется тупым углом . Итак, мера острого угла в градусах выражается числом из интервала (0, 90) , мера тупого угла – числом из интервала (90, 180) , прямой угол равен девяноста градусам. Приведем иллюстрации острого угла, тупого угла и прямого угла.
Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов.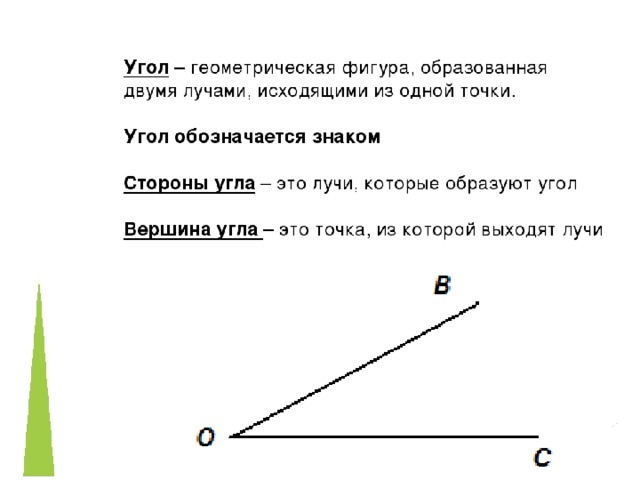 На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
Таким образом, сумма смежных углов равна ста восьмидесяти градусам , так как они составляют развернутый угол.
Из этого утверждения следует, что . Действительно, если углы АОВ и СОD – вертикальные, то углы АОВ и ВОС — смежные и углы СОD и ВОС также смежные, поэтому, справедливы равенства и , откуда следует равенство .
Наряду с градусом удобна единица измерения углов, называемая радианом . Радианная мера широко используется в тригонометрии. Дадим определение радиана.
Определение.
Угол в один радиан – это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности.
Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA (как и радиуса OB ) равна длине дуги AB , поэтому, по определению угол AOB равен одному радиану.
Для обозначения радианов используют сокращение «рад». Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой.
Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса.
Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно.
Обозначение углов на чертеже.
На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой.
Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное.
Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства.
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.

- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.

- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.
- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4.
 Вычислите полученные углы.
Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х. Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚.
 Ответ: 36˚ и 144˚.
Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
Каждый угол, в зависимости от его величины, имеет своё название:
| Вид угла | Размер в градусах | Пример |
|---|---|---|
| Острый | Меньше 90° | |
| Прямой | Равен 90°. На чертеже прямой угол, обычно обозначают символом , проведённым от одной стороны угла до другой. | |
| Тупой | Больше 90°, но меньше 180° | |
| Развёрнутый | Равен 180° Развёрнутый угол равен сумме двух прямых углов, а прямой угол составляет половину развёрнутого угла. | |
| Выпуклый | Больше 180°, но меньше 360° | |
| Полный | Равен 360° |
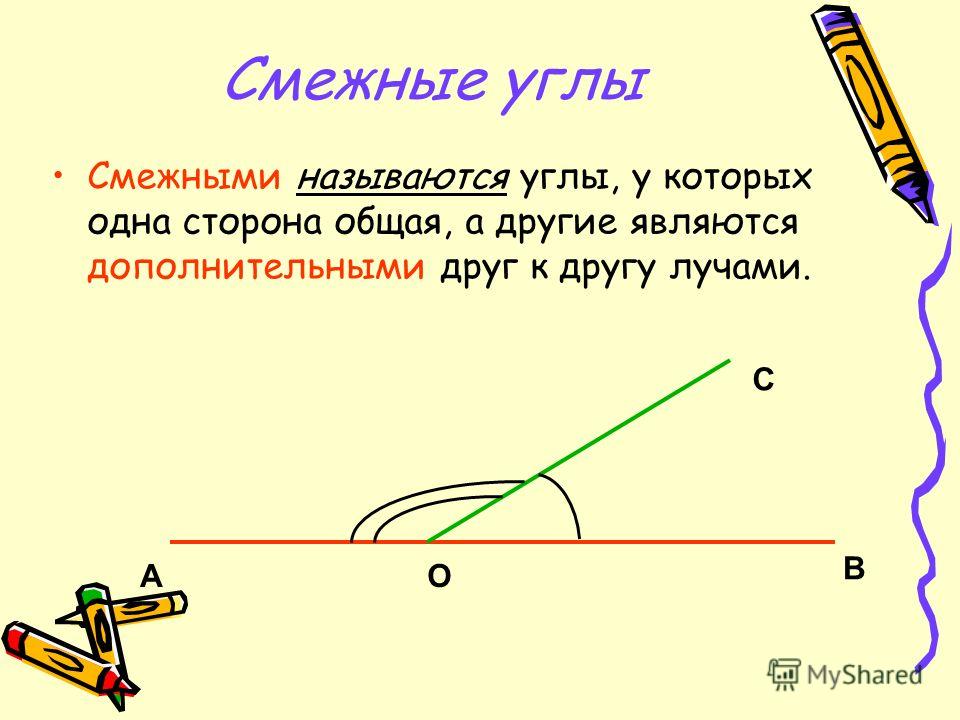
Два угла называются смежными , если у них одна сторона общая, а две другие стороны составляют прямую линию:
Углы MOP и PON смежные, так как луч OP — общая сторона, а две другие стороны — OM и ON составляют прямую.
Общая сторона смежных углов называется наклонной к прямой , на которой лежат две другие стороны, только в том случае, когда смежные углы не равны между собой. Если смежные углы равны, то их общая сторона будет перпендикуляром .
Сумма смежных углов равна 180°.
Два угла называются вертикальными , если стороны одного угла дополняют до прямых линий стороны другого угла:
Углы 1 и 3, а также углы 2 и 4 — вертикальные.
Вертикальные углы равны.
Докажем, что вертикальные углы равны:
Сумма ∠1 и ∠2 составляет развёрнутый угол. И сумма ∠3 и ∠2 составляет развёрнутый угол. Значит, эти две суммы равны:
∠1 + ∠2 = ∠3 + ∠2.
В этом равенстве слева и справа есть по одинаковому слагаемому — ∠2. Равенство не нарушится, если это слагаемое в левой и в правой части опустить. Тогда мы получаем.
Острый угол это угол градусная мера которого до 90 градусов.
Прямой угол это угол градусная мера которого 90 градусов
Тупой
угол это угол градусная мера которого
больше 90 градусов. Острый
угол — это угол меньше 90°. Тупой угол —
это угол больше 90°, но меньше 180°. Прямой
угол — это угол = 90°.
Острый
угол — это угол меньше 90°. Тупой угол —
это угол больше 90°, но меньше 180°. Прямой
угол — это угол = 90°.
20. Какие углы называются смежными? Чему равна их сумма?
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая) . Сумма смежных углов равна 180°. Или
Два угла называются смежными , если у них одна сторона общая, а другие стороны являются дополнительными лучами. сумма смежных углов равна 180°. Каждый из этих углов дополняет другой до развернутого угла.
21. Какие углы называются вертикальными? Каким свойством они обладают?
Вертикальные
углы — два угла, у которых стороны одного
являются продолжениями сторон другого.
Вертикальные углы равны. (Вертикальными
называются углы, образованные пересекающимися прямыми
и не являющиеся прилегающими друг к
другу, то есть общей стороны у них нет,
но вертикальные углы имеют вершину в
одной точке. Вертикальные углы равны
между собой).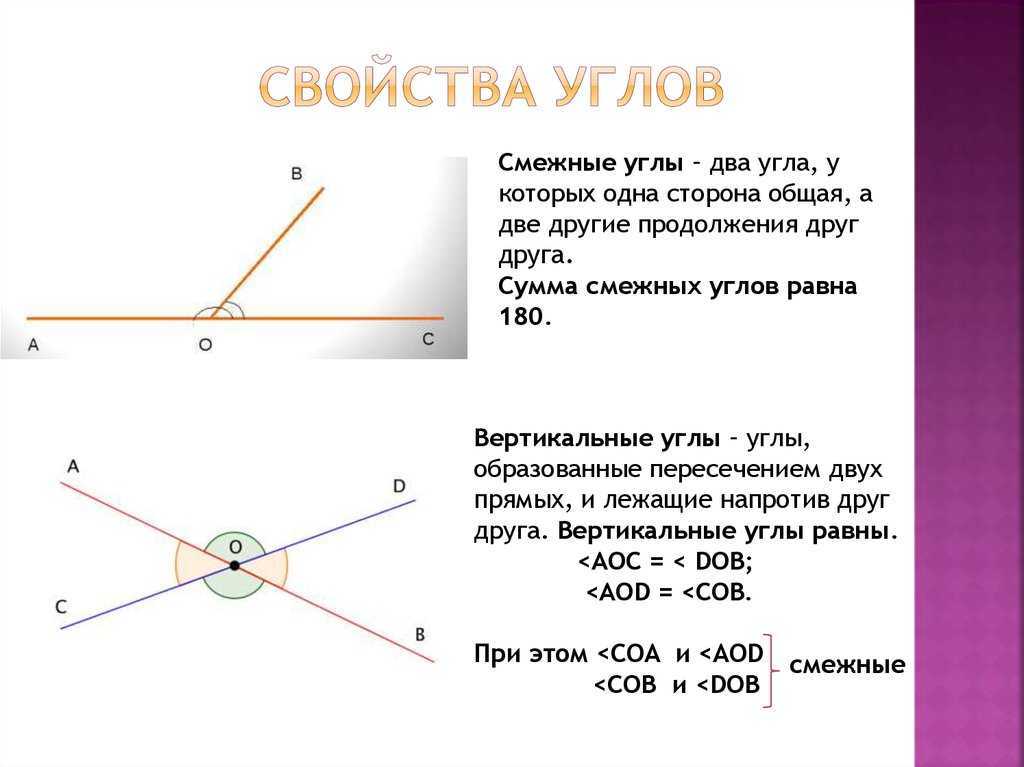
22. Какие прямые называются перпендикулярными? Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла. Или Перпендикулярные прямые это прямые пересекающиеся под углом 90 градусов. Или Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.
23. Объясните, какой отрезок называется перпендикуляром, проведенным из данной точки к данной прямой. Что такое основание перпендикуляра? называется отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения. Конец отрезка, лежащий на данной прямой, называется основанием перпендикуляра.
24.
Что такое теорема и доказательство
теоремы? В
математике утверждение, справедливость
которого устанавливается путем
рассуждений, называется теоремой,
а само рассуждение – доказательством
теоремы.
Теоре́ма — утверждение, для которого в рассматриваемой теории существует доказательство (иначе говоря, вывод) . В отличие от теорем, аксиомами называются утверждения, которые, в рамках конкретной теории, принимаются истинными без всяких доказательств или обоснований. Доказательство — это утверждение, объясняющее теорему. Теорема — такая гипотеза, которую требуется доказать;Гипотеза всегда требует доказательства. Доказательство — доводы, подтверждающие действенность, правильность теоремы.
Какие углы называют смежными свойство смежных углов. Смежные и вертикальные углы. Перпендикулярные прямые
Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Образование углов
Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.
Острым называется угол, мера которого не превышает 90 градусов.
Тупым является угол, превышающий 90 градусов.
Угол называется прямым в том случае, когда его градусная мера равна 90.
В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:
Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:
- Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
- Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.
Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.
Вертикальные углы
Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.
При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
Что такое смежный угол
Угол – это геометрическая фигура (рис.1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла).
СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.
Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.
Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
рис. 2
На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.
рис. 3
На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.
Теорема о смежных углах
Теорема: сумма смежных углов равна 180°
Доказательство:
Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.
Теорема доказана.
Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.
Определение 1.1. Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи:
Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.
Определение 3. Прямой угол — это угол величиной в 90 градусов.
Определение 4. Угол, меньший 90 градусов, называется острым углом.
Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.
Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.
Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.
рис. 4
Связь математики с музыкой
«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства. «
«
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т.е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a: l ,
где а — коэффициент, характеризующий физические свойства струны.
Так же предложу вашему внимаю забавную пародию про спор двух математиков =)
Геометрия вокруг нас
Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились.
Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов.
Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились.
Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов.
Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
Задание 1.
1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?
Задание 2.
Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.
Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.
Задание 3.
Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.
Решение задач
1) Даны два угла, относящиеся друг к другу как 1: 2, а смежные с ними — как 7: 5. Нужно найти эти углы.
2) Известно, что один из смежных углов больше другого в 4 раза. Чему равны смежные углы?
3) Необходимо найти смежные углы, при условии, что один из них на 10 градусов больше от второго.
Математический диктант на повторение ранее выученного материала
1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а — через а1 и а2, а прямой b — через b1 i b2.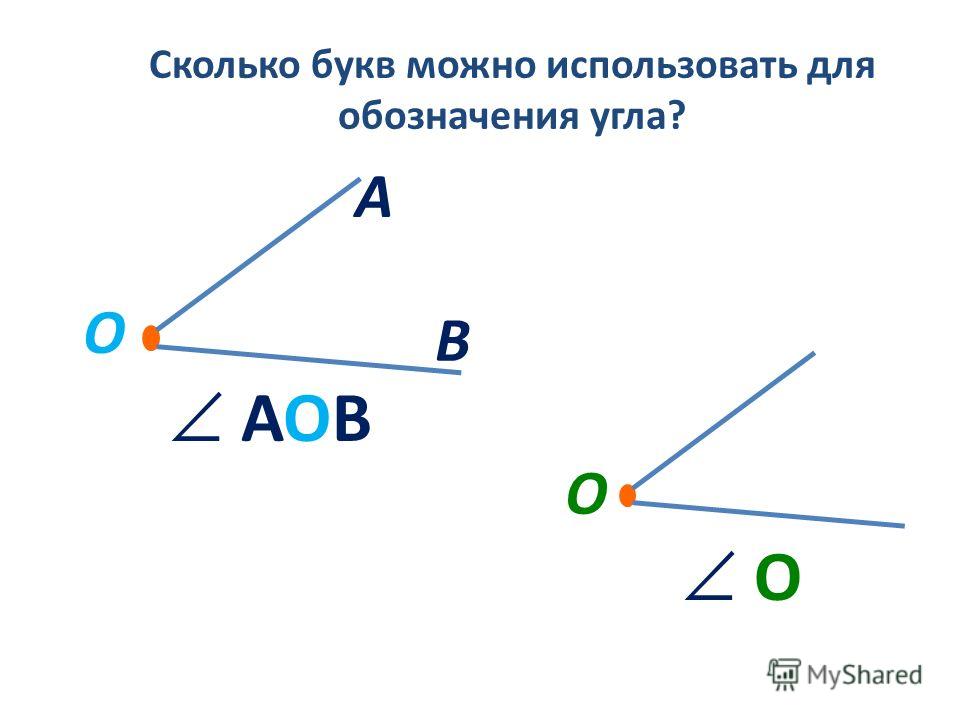
2) Пользуясь выполненным рисунком, впишите нужные значения и объяснения в места пропусков в тексте:
а) угол 1 и угол …. смежные, поскольку…
б) угол 1 и угол …. вертикальные, поскольку…
в) если угол 1 = 60°, то угол 2 = …, потому что…
г) если угол 1 = 60°, то угол 3 = …, потому что…
Решите задачи:
1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.
3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:
а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.
Итог урока
1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.
Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.
Домашнее задание:
1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1: 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.
Вопросы:
- Что такое угол?
- Какие бывают типы углов?
- Какая особенность смежных углов?
Предмети > Математика > Математика 7 класс
Вопрос 1. Какие углы называются смежными?
Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a 1 b) и (a 2 b) смежные. У них сторона b общая, а стороны a 1 и a 2 являются дополнительными полупрямыми.
Вопрос 2. Докажите, что сумма смежных углов равна 180°.
Ответ. Теорема 2.1. Сумма смежных углов равна 180°.
Доказательство. Пусть угол (a 1 b) и угол (a 2 b) — данные смежные углы (см. рис.31). Луч b проходит между сторонами a 1 и a 2 развёрнутого угла. Поэтому сумма углов (a 1 b) и (a 2 b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.
Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.
Из теоремы 2.1 следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a 1 b) и (c 1 d) равны. Нам нужно доказать, что углы (a 2 b) и (c 2 d) тоже равны.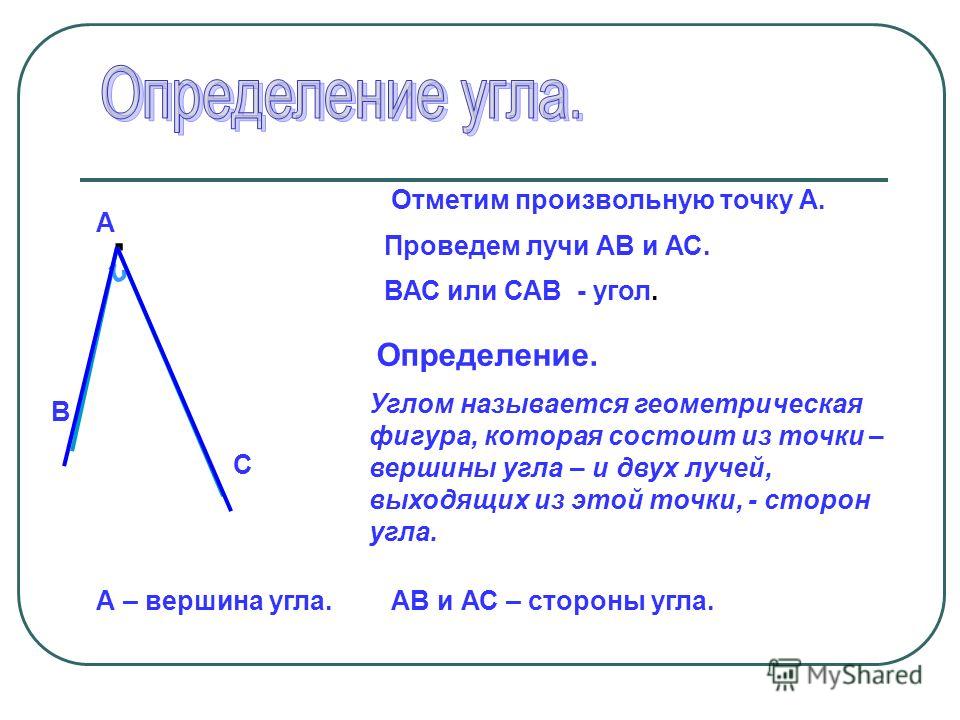
Сумма смежных углов равна 180°. Из этого следует, что a 1 b + a 2 b = 180° и c 1 d + c 2 d = 180°. Отсюда, a 2 b = 180° — a 1 b и c 2 d = 180° — c 1 d. Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° — a 1 b = c 2 d. По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.
Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.
Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол.
Ответ. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол: x + 90° = 180°, x= 180° — 90°, x = 90°.
Вопрос 6. Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.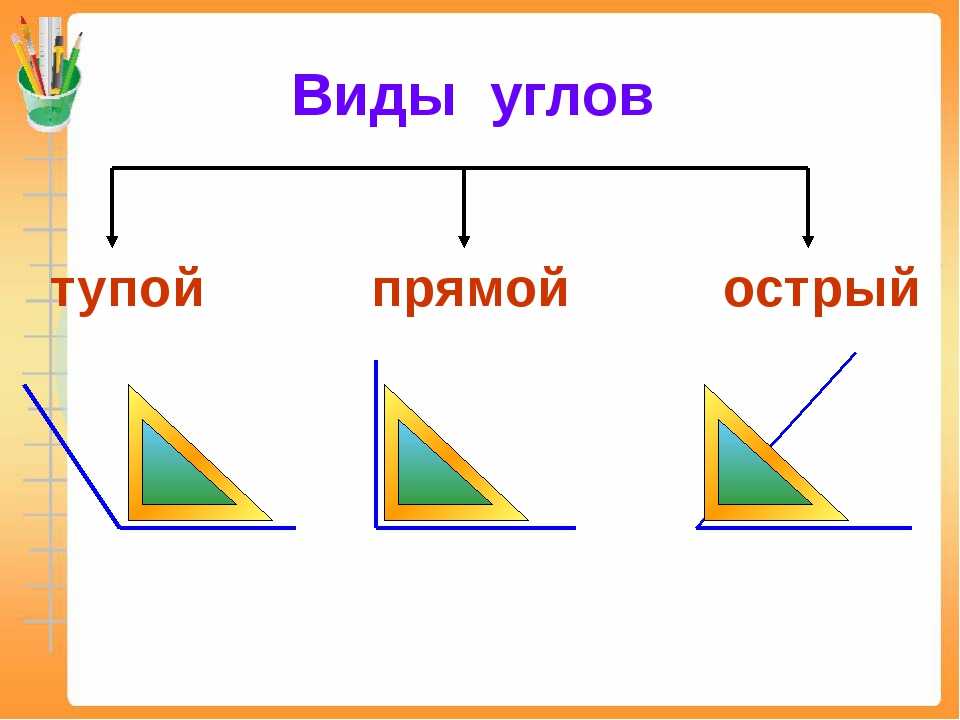
Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a 1 b 1) и (a 2 b 2)- данные вертикальные углы (рис. 34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т.е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.
Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
Что и требовалось доказать.
Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».
Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3. Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.
Доказательство. Пусть a — данная прямая и A — данная точка на ней. Обозначим через a 1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a.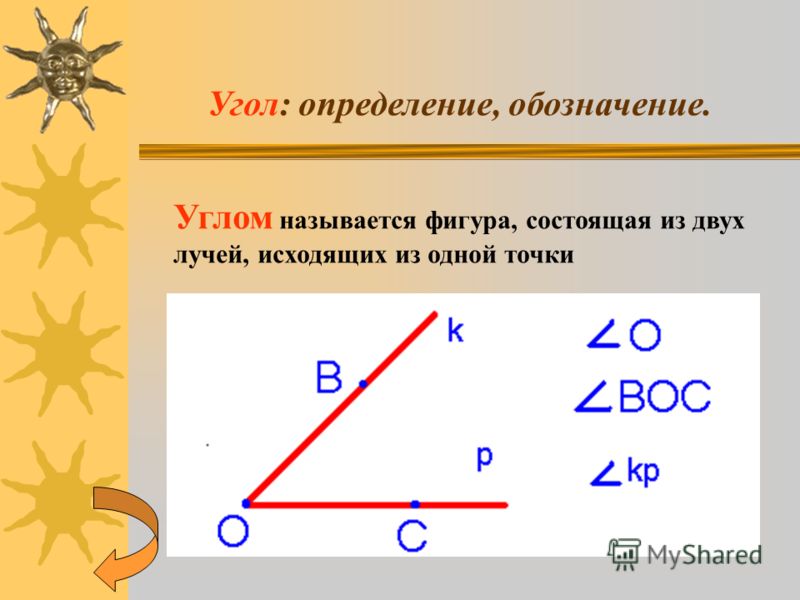 Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Углы (a 1 b 1) и (a 1 c 1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a 1 . Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.
Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме.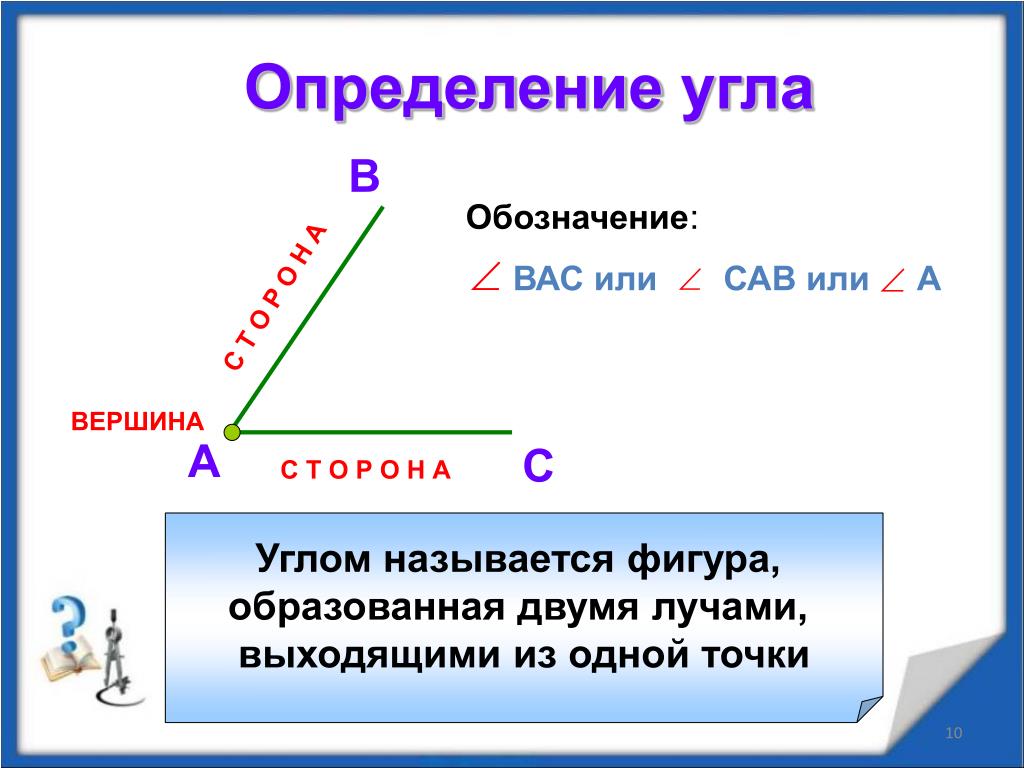 На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (рис. 72): ∠АВС и ∠СВD, у которых одна сторона ВС общая, а две другие, АВ и ВD, составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, ∠АDF и ∠FDВ — углы смежные (рис. 73).
Смежные углы могут иметь самые разнообразные положения (рис. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 180°
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 54°, то второй угол будет равен:
180° — 54° = l26°.
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На рисунке 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть ∠1 = \(\frac{7}{8}\) ⋅ 90°(рис. 76). Смежный с ним ∠2 будет равен 180° — \(\frac{7}{8}\) ⋅ 90°, т. е. 1\(\frac{1}{8}\) ⋅ 90°.
Таким же образом можно вычислить, чему равны ∠3 и ∠4.
∠3 = 180° — 1\(\frac{1}{8}\) ⋅ 90° = \(\frac{7}{8}\) ⋅ 90°;
∠4 = 180° — \(\frac{7}{8}\) ⋅ 90° = 1\(\frac{1}{8}\) ⋅ 90° (рис. 77).
Мы видим, что ∠1 = ∠3 и ∠2 = ∠4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.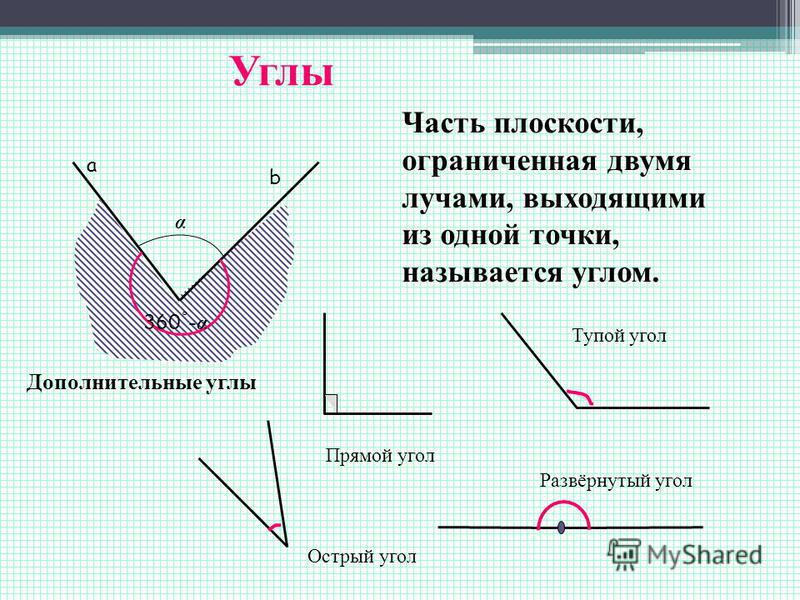
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём доказательства.
Доказательство можно провести следующим образом (рис. 78):
∠a + ∠c = 180°;
∠b + ∠c = 180°;
(так как сумма смежных углов равна 180°).
∠a + ∠c = ∠b + ∠c
(так как и левая часть этого равенства равна 180°, и правая его часть тоже равна 180°).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: ∠a = ∠b , т. е. вертикальные углы равны между собой.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 ∠1, ∠2, ∠3 и ∠4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
В сумме эти углы составляют развёрнутый угол, т. е.
∠1 + ∠2 + ∠3 + ∠4 = 180°.
На чертеже 80 ∠1, ∠2, ∠3, ∠4 и ∠5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.
Другие материалы
Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, / АDF и / FDВ — углы смежные (черт. 73).
Смежные углы могут иметь самые разнообразные положения (черт. 74).
74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:
2d — 3 / 5 d = l 2 / 5 d .
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт. 77).
Мы видим, что / 1 = / 3 и / 2 = / 4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт. 78):
/ a + / c = 2d ;
/ b + / c = 2d ;
(так как сумма смежных углов равна 2d ).
/ a + / c = / b + / c
(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).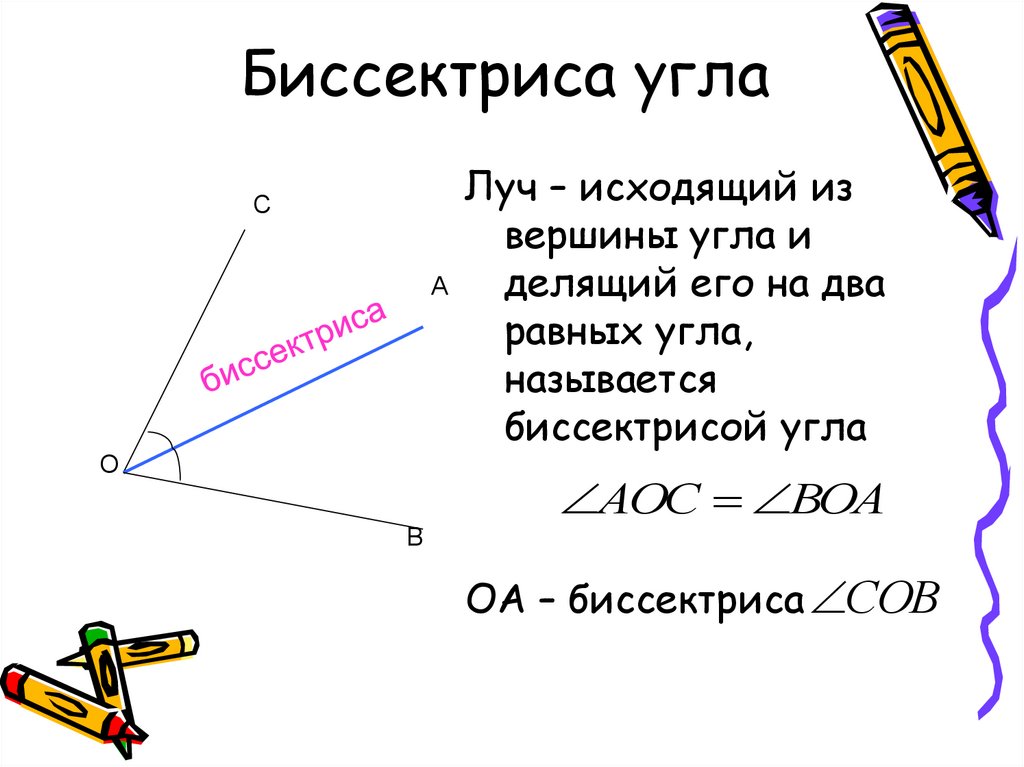
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.
2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.
3. Доказать, что если два угла равны, то равны и их смежные углы.
4. Сколько пар смежных углов на чертеже 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?
6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?
Какие углы острые.
 Полный угол
Полный уголДавайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .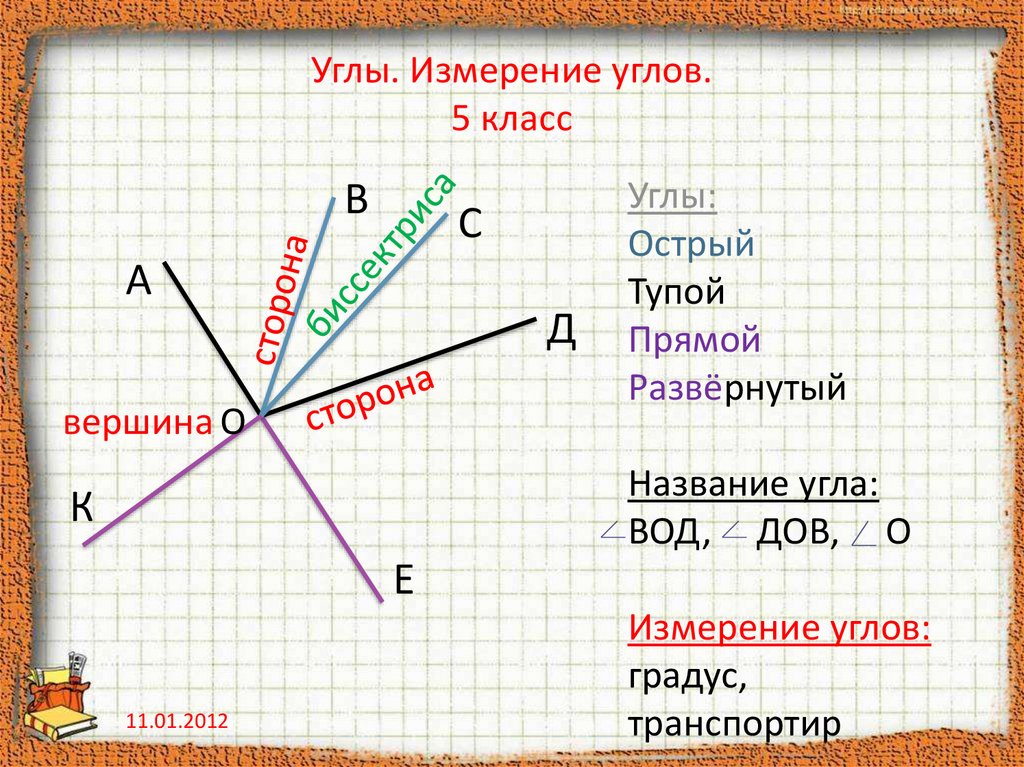
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
С понятием угол учащиеся знакомятся еще в начальной школе. Но как геометрическую фигуру, имеющую определенные свойства, начинают изучать его с 7-го класса в геометрии. Кажется, довольно простая фигура , что о ней можно сказать. Но, приобретая новые знания, школьники всё больше понимают, что можно узнать о ней довольно интересные факты.
Вконтакте
Когда изучаются
Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию. В каждом из них немалое внимание уделяется углам :
В каждом из них немалое внимание уделяется углам :
- В планиметрии дается их основное понятие, происходит знакомство с их видами по величине. Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
- В стереометрии изучаются пространственные углы – двугранные и трехгранные.
Внимание! В данной статье рассматриваются все виды и свойства углов именно в планиметрии.
Определение и измерение
Приступая к изучению, первоначально определяют, что такое угол в планиметрии.
Если на плоскости взять определённую точку и провести от нее два произвольных луча, то получим геометрическую фигуру – угол, состоящую из следующих элементов:
- вершина – та точка, из которой и проводились лучи, обозначается заглавной буквой латинского алфавита;
- стороны – полупрямые, проведенные из вершины.

Все элементы, образующие рассматриваемую нами фигуру, разбивают плоскость на две части :
- внутренняя — в планиметрии не превышает 180 градусов;
- внешняя.
Принцип измерения углов в планиметрии объясняют на интуитивной основе. Для начала знакомят учащихся с понятием развернутый угол.
Важно! Угол называется развернутым, если полупрямые, выходящие из его вершины, образуют прямую линию. Неразвернутый угол это все остальные случаи.
Если его разделить на 180 равных частей, то принято считать меру одной части равной 10. В таком случае говорят, что измерение производится в градусах, а градусная мера такой фигуры составляет 180 градусов.
Основные виды
Виды углов подразделяются по таким критериям, как градусная мера, характер их образования и представленные ниже категории.
По величине
Учитывая величину, углы разделяют на:
- развернутый;
- прямой;
- тупой;
- острый.

Какой угол называется развернутым, было представлено выше. Определимся с понятием прямого.
Его можно получить при делении развернутого на две равные части. В этом случае легко ответить на вопрос: прямой угол, сколько градусов составляет?
180 градусов развернутого делим на 2 и получаем, что прямой угол равен 90 градусам . Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.
Имеет она и свои особенности в обозначении. Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.
Углы, которые получаются при делении произвольным лучом прямого, называют острыми. По логике вещей следует, что острый угол меньше прямого, но его мера отлична от 0 градусов. То есть, он имеет величину от 0 до 90 градусов.
Тупой угол больше прямого, но меньше развернутого. Его градусная мера варьируется в интервале от 90 до 180 градусов.
Данный элемент можно разбить на разные виды рассматриваемых фигур, исключая развёрнутый.
Вне зависимости от того, как разбивается неразвернутый угол, всегда пользуются базовой аксиомой планиметрии — «основное свойство измерения».
При разделении угла одним лучом или несколькими, градусная мера данной фигуры равна сумме мер углов, на которые она разбита.
На уровне 7-го класса виды углов по их величине на этом заканчиваются. Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов.Их называют выпуклыми.
Фигуры при пересечении прямых
Следующие типы углов, с которыми знакомятся учащиеся – элементы, образованные при пересечении двух прямых. Фигуры, которые размещаются друг напротив друга, называют вертикальными. Их отличительное свойство – они равны.
Элементы, которые прилегают к одной и той же прямой, называют смежными. Теорема, отображающая их свойство, говорит о том, что смежные углы в сумме дают 180 градусов .
Элементы в треугольнике
Если рассматривать фигуру как элемент в треугольнике, то углы подразделяют на внутренний и внешний.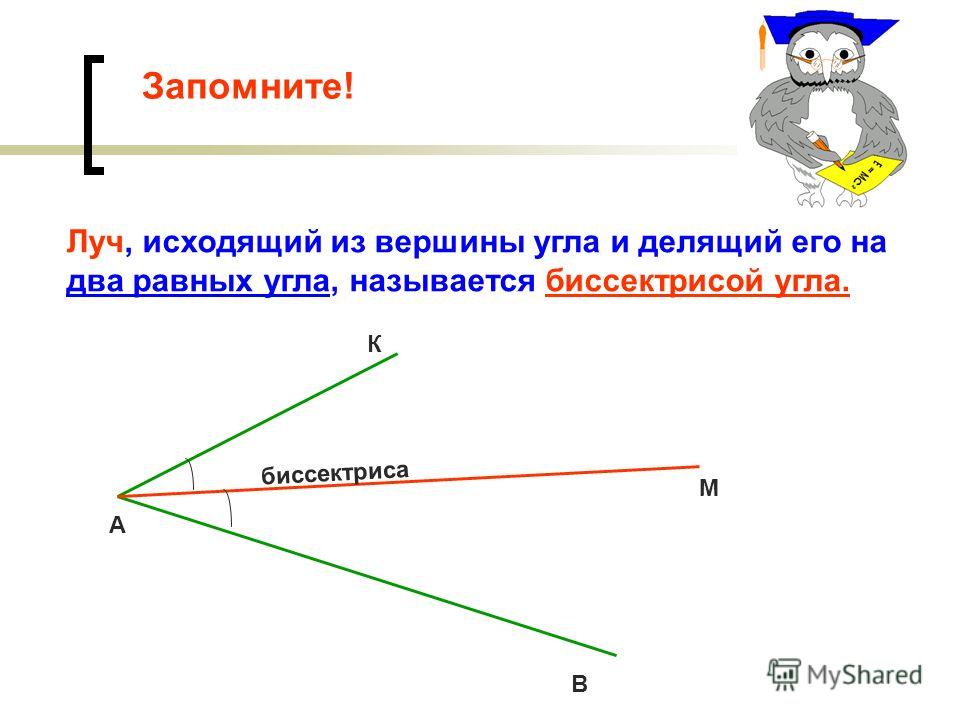 Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними .
Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними .
Если взять любой внутренний элемент при любой вершине и продлить любую сторону, то угол, который образовался и является смежным с внутренним, называется внешним. Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.
Пересечение двух прямых секущей
Пересечение прямых
При пересечении двух прямых секущей также образуются углы , которые принято распределять по парам. Каждая пара элементов имеет свое название. Выглядит это следующим образом:
- внутренние накрест лежащие:∟4 и ∟6, ∟3 и ∟5;
- внутренние односторонние: ∟4 и ∟5, ∟3 и ∟6;
- соответствующие: ∟1 и ∟5, ∟2 и ∟6, ∟4 и ∟8, ∟3 и ∟7.
В том случае, когда секущая пересекает две
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла.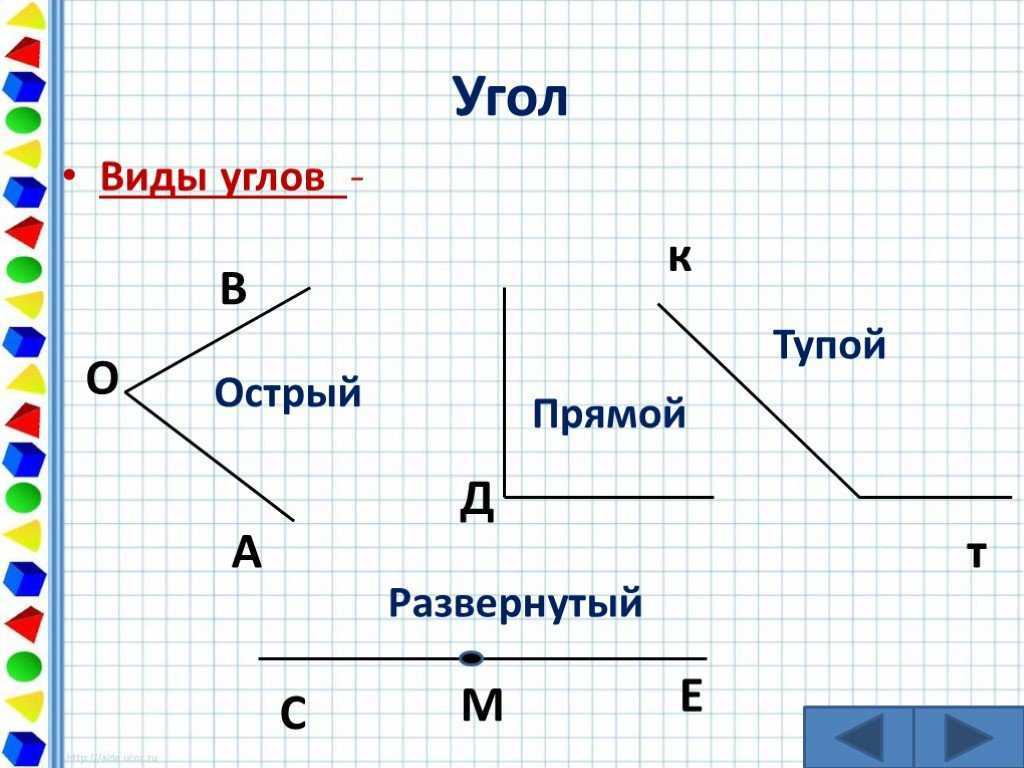 Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Yandex.RTB R-A-339285-1 Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита.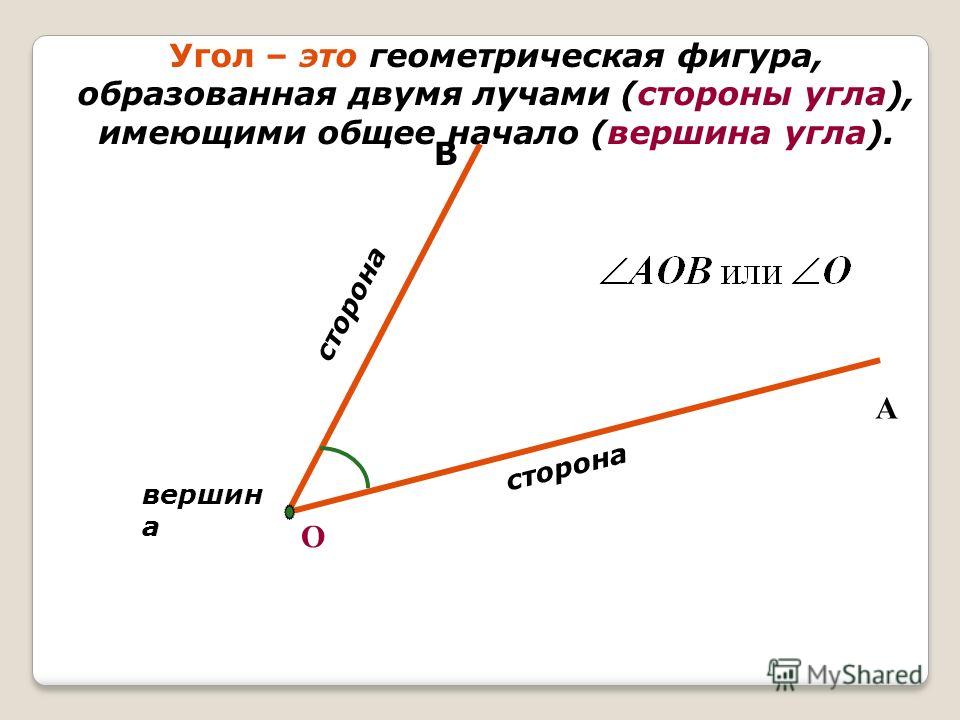 При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение 6
Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Ниже показано на рисунке.
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус .
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.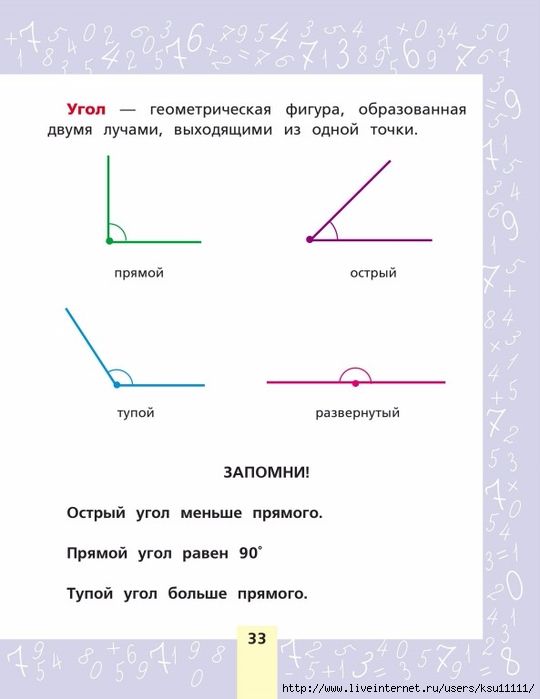
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение:
1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» .
Определение 11
Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.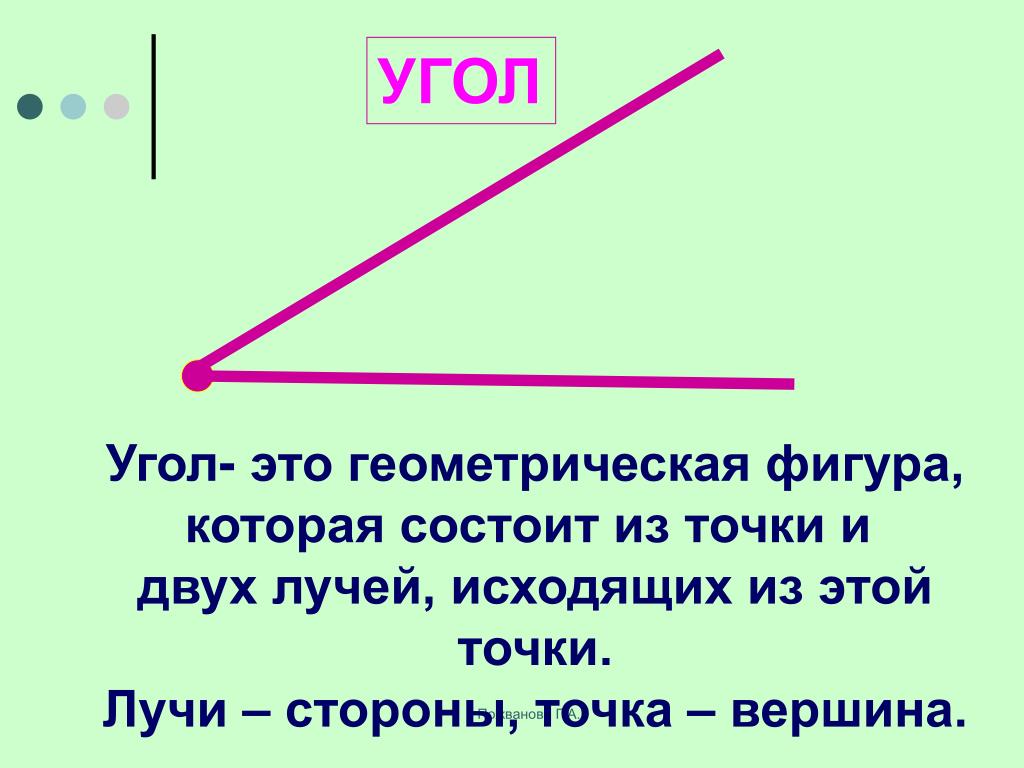
Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного.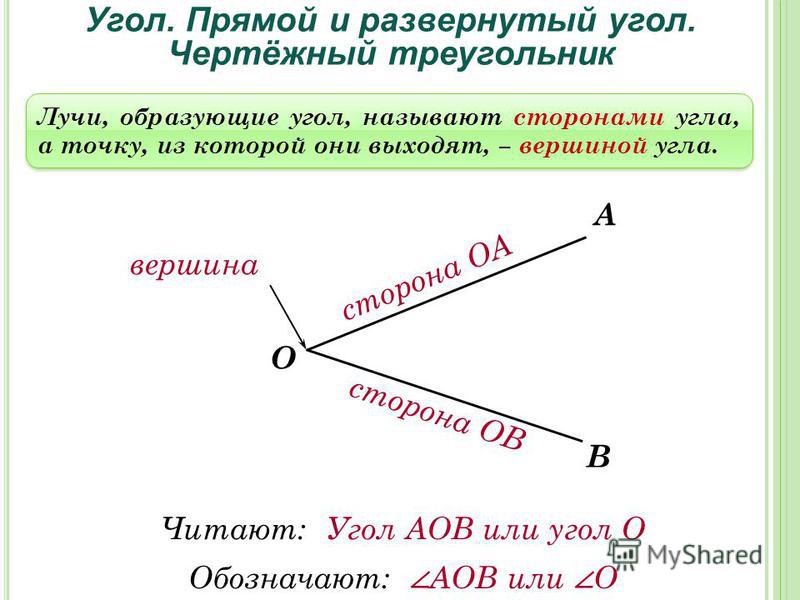 На чертеже изображено правильное обозначение острых, равных и неравных углов.
На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки.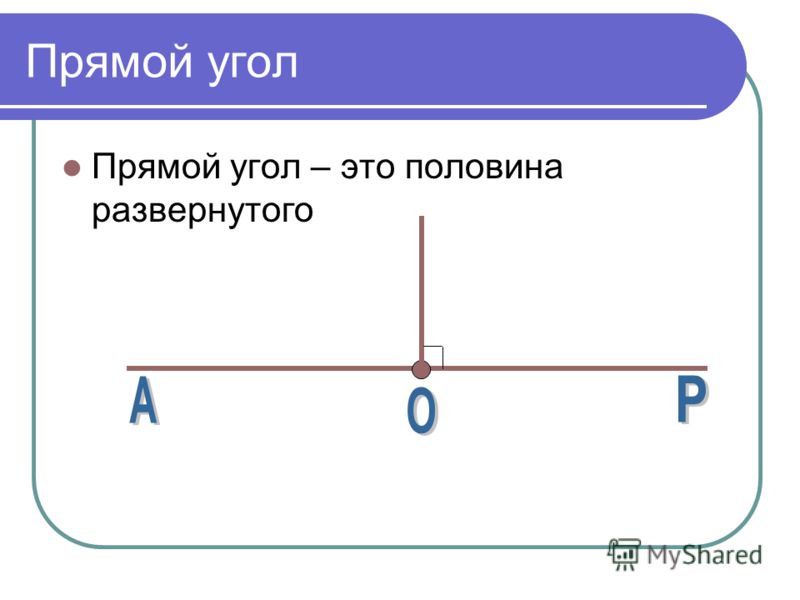 Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.
- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.

Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.

- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х. Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
Сколько градусов в остром угле — nehomesdeaf
Сколько градусов прямой, тупой и острый углы?
Сколько градусов прямой угол ?
Сколько градусов тупой угол?
Сколько градусов острый угол ?
Углом в геометрии называют точку, из которой выходят два луча.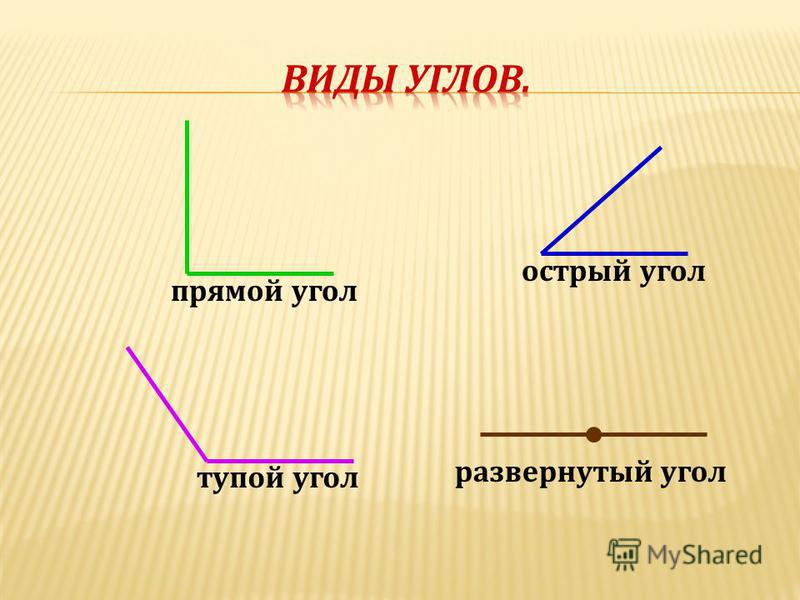
В зависимости от того, насколько отличаются направления лучей, определяются характеристики самого угла.
Мера углов меряется в градусах.
Если лучи угла расходятся один от одного под угол в 90 градусов — это прямой угол.
Если лучи угла расходятся один от одного под угол больше 90 градусов (от 90 до 180 градусов, потому как 180 градусов — это развернутый угол), то угол тупой.
Если лучи угла расходятся меньше чем угол 90 градусов (от 0 до 90 градусов) — угол острый.
Прямой угол собой представляет половину развернутого. А потому как величина развернутого угла в градусах равна 180-ти, то градусная мера прямого угла равна 90°.
Углы, меньшие 90°, называют острыми. Углы же, чья градусная мера превосходит все те же 90 градусов, однако при этом меньше 180°, называют тупыми.
Подобным образом, величина острого угла в градусах может принимать любое значение из диапазона (0; 90), ну а тупого — исходя из этого из диапазона (90; 180).
И только прямой угол из всех обозначенных в вопросе имеет вполне конкретную (не колеблющуюся ни в каких диапазонах) градусную меру — 90.
Какой угол именуется острым, прямым, тупым?
Какой угол в геометрии именуется острым, прямым, тупым? Сколько градусов в остом угле, тупом угле, прямом угле? Как определить острый угол, прямой угол, тупой угол?
Угол грамотный пересечением 2-ух поперечных прямых именуется прямым. Также прямой угол может появиться при делении окружности на ровные 4-ре части (1/4 окружности).
Прямой угол равён 90 градусам.
Когда стороны угла совпадают, подобный угол именуется нулевым
Нулевой угол равён 0 градусам.
Все углы, значения в градусах которых больше нулевого и меньше прямого именуется острыми.
Острый угол — больше 0 градусов и меньше 90 градусов.
Если стороны угла лежат в разных направлениях и создают прямую, подобный угол именуется развернутым и равён он 180 градусам.
Углы, значения в градусах которых больше прямого и меньше развернутого называются тупыми.
Тупой угол — больше 90 градусов и меньше 180 градусов.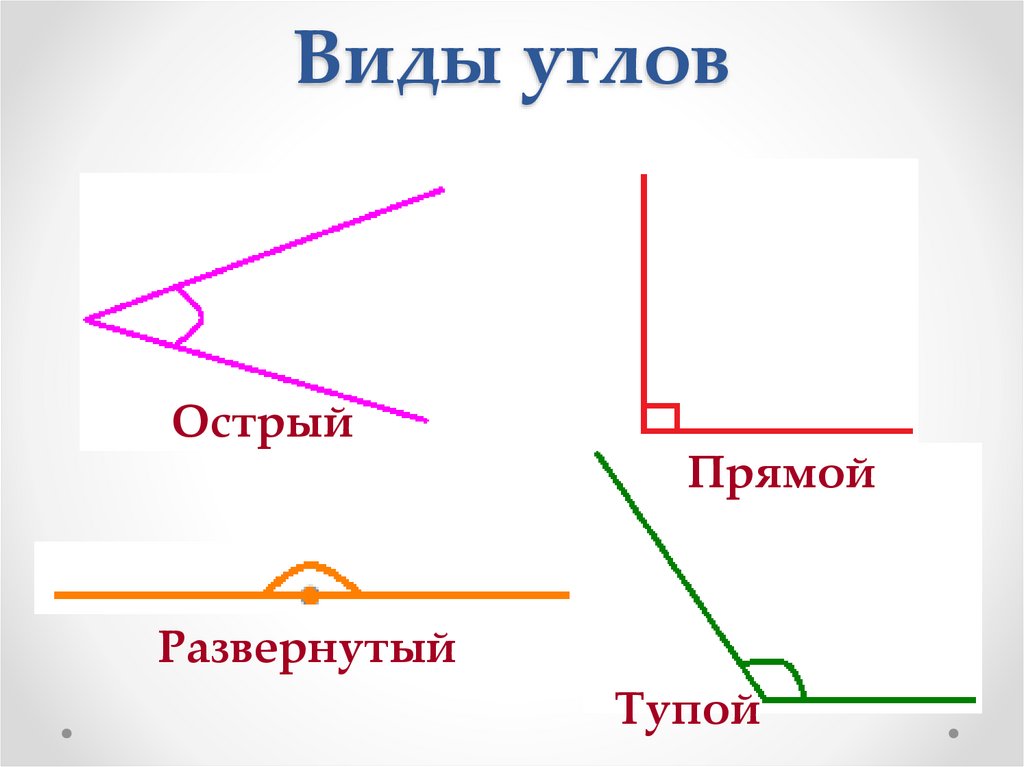
Всех их соединяет одно:
острый, прямой и тупой углы — они все рельефные.
Все очень просто. Проведём аналогию с обыкновенными часами. Если одну из стрелок установить таким образом, чтобы она указывала на двенадцать часов, а другою, чтобы указывала на три — то они создают прямой угол в 90 градусов. Если же начать двигать стрелку указывающую на 3 часа в обратном направлении( в двухчасовой метки на циферблате) — то она будет образовывать, одновременно со второй стрелкой, острые углы(менее 90 градусов). Когда же стрелки будут указывать в одну точку — они создают нулевой угол в ноль градусов.А если вернуть вторую стрелку к исходной( трехчасовой отметке) и начать перемещать её вперед по циферблату — то аж до шестичасовой метки она одновременно с первой будут образовывать тупые углы( более 90 градусов). Когда стрелки будут указывать, одна на 12, а остальная на 6 — это будет, говоря иначе, развёрнутый угол в 180 градусов.
Острый угол сколько градусов
Добрый день!
Как понять острый угол сколько градусов равён? Как можно усвоить?
Благодарю!
Усвоить и разобраться очень легко. Начинаем учиться на циферблате обыкновенных часов.
Начинаем учиться на циферблате обыкновенных часов.
Установим одну стрелку так, что она будет указывать на 12- часов, а остальная будет указывать на 3 часа. В этом положении стрелки создают прямой угол, который равён девяносто град.
Начинаем сдвигать стрелку, которая указывает на 3 часа, против хода часовой стрелки, о есть к двенадцати часам через 2 часа и один час. В этом случае две стрелки будут образовывать острый угол, который окажется меньшей 90 град., но больше 0 град.
Если же стрелки объединить на одной цифре, к примеру, на двенадцати, то стрелки создают угол в ноль град., другими словами нулевой.
Если же первую стрелку оставить на 12-ти часах, а вторую опять уместить на 3 часа и начать двигать по ходу часовой стрелки, другими словами через определения четырех, пяти до 6-ти часов, то полученные углы будут тупыми (больше 90 и меньше 180 градусов).
Когда вторая стрелка будет стоять на 6-ти часах, то подобный угол будет равным 180 градусов, а его называют развернутым.
Полный оборот циферблата равён 360 градусам.
Надеюсь, этот подход поможет Вам хорошо разобраться и усвоить какой из углов каким должен быть и скольким градусам быть равным.
Острый, прямой и тупой углы
Что такое острый угол? Определение, свойства, формулы и примеры
Что такое угол?
В геометрии два луча, имеющие общий конец, образуют угол. Общий конец называется вершиной, а два луча называются плечами угла.
Типы углов
Существует три основных типа углов: острый угол, прямой угол и тупой угол.
Острый угол: угол меньше 90°
Прямой угол: угол, равный точно 90°
Тупой угол: угол, размер которого больше 90°
Определение острого угла
Любой угол, величина которого больше 0° и меньше 90°, называется острым углом.
∠ABC равна 30°, следовательно, это острый угол.
Примеры острых углов
Острые углы меньше 90°
Следовательно, 67°, 45°, 23°, 52°, 86°, 14° являются примерами острых углов.
Разделив прямой угол (90˚), мы получим два или более острых угла, так как каждый вновь образованный угол будет меньше 90˚.
- ПРАВИЛЬНЫЙ КОНГ
ПРАВИЛЬНЫЙ УГОЛ ДВА ОТКРЫТЫЙ УГОЛОДОГО СОЗДАНИЯ ОТДЕЛ БАЗ
Разделение правого угла.
Реальные примеры острых углов
Если мы нарежем пиццу на 5 или более кусочков, каждый кусок пиццы будет образовывать острый угол.
Каждый кусочек пиццы образует острый угол.
Другой пример — настенные часы. Стрелки настенных часов в несколько часов дня образуют острые углы. Например, 10 часов.
Часовая и минутная стрелки образуют острый угол в положении «10 часов».
Пара открытых ножниц, открытый рот аллигатора и клюв птиц образуют острые углы.
Остроугольный треугольник
Треугольник, образованный всеми углами меньше 90˚, также известен как остроугольный треугольник. Например, в равностороннем треугольнике все три угла равны 60°, что делает его остроугольным.
Например, в равностороннем треугольнике все три угла равны 60°, что делает его остроугольным.
Остроугольный треугольник
Интересные факты
1. По крайней мере два угла любого треугольника являются острыми углами.
2. В угле 180˚, если один угол тупой (больше 90˚), другой угол всегда будет острым (меньше 90˚).
Решенные примеры
Вопрос 1: Измерение трех углов:0004 Укажите тип угла в каждом случае.
Ответ:
- Острый угол- так как 75° меньше 90°
- Тупой угол- так как 112° больше 90°
- Острый угол- так как 17° меньше 90° 1 009 00
- Question 2: Measure of some angles are given below:
.∠A ∠B ∠C ∠D ∠E 71° 17° 93° 102 ° 45 °  Вопрос 3: Состояние Верно или Ложно :
Вопрос 3: Состояние Верно или Ложно :- Угол, равный 45°, является прямым.
- Угол, равный 85°, является острым углом.
- Угол, равный 90°, является тупым углом.
- Угол, равный 15°, является острым.
Решение:
- False
- True
- False
- True
Практические задачи
I & III
I & II
II & III
I & II
II & IV
I & II
II & IV
9 : I & II
Первый и второй углы острые, потому что они меньше 90°.луч
линия
угол
отрезок прямой
Правильный ответ: угол
Угол образуется, когда два луча имеют общий конец.полный угол
прямой угол
прямой угол
Ни один из этих
Правильный ответ: Ни один из этих
Не было бы угла, образованного с 0°. Таким образом, ответ будет вариантом d.
Таким образом, ответ будет вариантом d.Заключение
Острый угол — это угол, который меньше 90°, и эти углы можно измерить с помощью транспортира. На этом уроке мы узнали об острых углах творчески. Откройте для себя и изучите больше интересных тем по математике на SplashLearn.
Часто задаваемые вопросы
Как определить острый угол?
Угол, величина которого меньше 90°, называется острым углом. Г-образная форма образует угол 90 °, поэтому, если стороны угла раскрываются меньше, чем буква «L», образуется острый угол.
Что вы подразумеваете под остроугольным треугольником?
Остроугольный треугольник — это треугольник, в котором каждый угол меньше 90°. Даже если один угол треугольника равен 90°, это не остроугольный треугольник. Например, равносторонний треугольник всегда остроугольный, потому что все углы (60°) меньше 90°.
Какие бывают виды углов в геометрии?
Виды углов в геометрии следующие:
- Острый угол, который больше 0°, но меньше 90°
- Прямой угол, образующий 90°
- Тупой угол, больше 90°, но меньше 180°
- Угол рефлекса больше 180°, но меньше 360°
- Полный угол, образующий 360°
Острый угол — определение, свойства, градус , Формула, Примеры
Острый угол — это тип угла, размер которого меньше 90°.
 Например, когда время 11 часов, угол, образованный между часовой и минутной стрелками, является острым углом. Другими словами, 30°, 40°, 57° и т. д. — все это острые углы.
Например, когда время 11 часов, угол, образованный между часовой и минутной стрелками, является острым углом. Другими словами, 30°, 40°, 57° и т. д. — все это острые углы.1. Что такое острый угол? 2. Реальные примеры острых углов 3. Свойства остроугольного треугольника 4. Часто задаваемые вопросы об остром угле Что такое острый угол?
Угол образуется, когда два луча встречаются в вершине. Когда этот угол меньше 90°, его называют острым углом. На рисунке ниже угол, образованный между «Лучами 1» и «Лучами 2», является острым. Кроме того, когда прямой угол делится на два, он образует два острых угла.
Определение острого угла
Острый угол определяется как угол, размер которого меньше 90 градусов, т. е. его размер составляет от 0° до 90°.
 Некоторые из примеров: 60 °, 30 °, 45 градусов и т. Д. Треугольник, образованный всеми внутренними углами, меньшими 90 °, называется остроугольным треугольником. Например, равносторонний треугольник является остроугольным, так как его внутренние углы равны 60°.
Некоторые из примеров: 60 °, 30 °, 45 градусов и т. Д. Треугольник, образованный всеми внутренними углами, меньшими 90 °, называется остроугольным треугольником. Например, равносторонний треугольник является остроугольным, так как его внутренние углы равны 60°.Острый угол Градус
В предыдущем разделе мы читаем, что угол, который измеряется меньше 90 градусов, то есть меньше прямого угла, является острым углом. Примеры градусов острого угла: 63°, 31°, 44°, 68°, 83°, 85°. Следовательно, градус острого угла лежит в пределах от 0° до менее 9°.0°. Вот несколько схематических изображений острых углов.
Реальные примеры острых углов
Мы знаем, что углы, размеры которых больше 0° и меньше 90°, в геометрии называются острыми углами. Следовательно, 45°, 5°, 28°, 49°, 89° являются примерами острых углов.
Вот несколько реальных примеров острых углов.
- Ломтик арбуза, разрезанный на небольшие части, как показано ниже.
- Несколько примеров образования углов между часовой и минутной стрелками часов.

- Клюв птицы, когда он открыт.
- Угол образуется при открытой пасти крокодила.
Свойства остроугольного треугольника
В остроугольном треугольнике все углы меньше 90°. Когда все три угла треугольника равны 60°, он образует особый треугольник, называемый равносторонним треугольником. Остроугольные треугольники можно разделить на остроугольные, равнобедренные и равнобедренные. Существует много типов треугольников, и остроугольный треугольник является одним из них. В показанном ниже треугольнике все внутренние углы меньше 90°. Поэтому его называют остроугольным треугольником.
Формула острого угла
Точно так же, как теорема Пифагора для прямоугольных треугольников, у нас есть формула треугольника острого угла, которая часто известна как теорема неравенства треугольников для остроугольных треугольников. Он гласит, что сумма квадратов двух сторон треугольника больше, чем квадрат наибольшей стороны.
 В Δ ABC, если стороны измеряются a,b,c так, что c является наибольшей стороной, то a 2 + b 2 > с 2 . Другими словами, в треугольнике, если a 2 + b 2 > c 2 , треугольник является остроугольным.
В Δ ABC, если стороны измеряются a,b,c так, что c является наибольшей стороной, то a 2 + b 2 > с 2 . Другими словами, в треугольнике, если a 2 + b 2 > c 2 , треугольник является остроугольным.☛Темы, связанные с острым углом
Ознакомьтесь с некоторыми интересными темами, связанными с острым углом.
- Геометрия
- Уголки
- Треугольники
- Тупой угол
- Транспортир
Примеры острого угла
Пример 1: Выберите углы, которые можно классифицировать как острые.
Решение:
Вариант а) и вариант d) измеряют менее 90°. Следовательно, это острые углы.
Пример 2: Посмотрите на часы, показанные ниже, и определите моменты времени, когда стрелки образуют острый угол.

Решение:
Мы можем заметить, что в 10 часов и 11 часов угол, образованный между часовой и минутной стрелками, является острым углом. Таким образом, часы, которые показывают 10 и 11 часов, образуют острый угол.
Пример 3: Является ли следующий треугольник остроугольным?
Решение:
Все 3 угла внутри остроугольного треугольника должны быть меньше 90°. Из рисунка видно, что два угла равны 45° каждый, а ∠Y равен 90°. Следовательно, это не остроугольный треугольник.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по острому углу
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об остром угле
Что такое острый угол?
Острый угол — это угол, градусная мера которого меньше 90°.
 Его можно измерить с помощью транспортира. Например, 35°, 60°, 72° и т. д. — все это острые углы.
Его можно измерить с помощью транспортира. Например, 35°, 60°, 72° и т. д. — все это острые углы.Каковы некоторые примеры острых углов?
Острые углы — это углы, градусная мера которых меньше 90°. Таким образом, 10°, 30°, 45°, 70° являются примерами острых углов.
Как найти меру острого угла?
Острые углы можно измерять с помощью транспортира. Чтобы измерить острый угол, поместите нижнюю линию транспортира на базовую линию и поместите центр транспортира на вершину, где пересекаются линии двух углов. Теперь рассмотрим нижнюю шкалу транспортира и измерим угол.
Что такое остроугольный треугольник?
Остроугольный треугольник — это треугольник, в котором все внутренние углы меньше 90°. Например, у равностороннего треугольника все внутренние углы равны 60°. Таким образом, его можно назвать остроугольным треугольником.
Каковы свойства остроугольного треугольника?
Есть несколько важных свойств, которые отличают остроугольный треугольник от других типов треугольников.

- Три внутренних угла остроугольного треугольника в сумме дают 180°.
- Треугольник не может быть остроугольным и прямоугольным одновременно.
- Треугольник не может быть одновременно тупоугольным и остроугольным.
- Все три угла остроугольного треугольника всегда меньше 90° или лежат между (от 0° до 90°).
Каковы характеристики острого угла?
Основная характеристика острого угла состоит в том, что его измерение лежит в пределах от 0° до 9°0°. В случае остроугольного треугольника мера всех трех внутренних углов остроугольного треугольника лежит в пределах от 0° до 90°, но сумма всех внутренних углов всегда равна 180°.
Какое наименьшее количество острых углов у прямоугольного треугольника?
В прямоугольном треугольнике должно быть не менее двух острых углов. Один угол должен быть равен 90°, а два других всегда лежат в пределах от 0° до 90°.
Как выглядит острый угол?
Размер острого угла лежит между 0° и 9°0°.
 Пара открытых ножниц выглядит как острый угол. Стрелки часов образуют острый угол в положении 11 часов.
Пара открытых ножниц выглядит как острый угол. Стрелки часов образуют острый угол в положении 11 часов.Запишите несколько градусов острого угла?
Когда величина угла находится в диапазоне от 0° до 90° и меньше 90°, это острый угол. Несколько градусов острого угла составляют 45°, 65°, 75°, 85°, 89°.
Является ли прямоугольный треугольник остроугольным треугольником?
Нет, прямоугольный треугольник не является остроугольным. У прямоугольного треугольника один из внутренних углов равен 90°, а два других угла по 45° каждый. Чтобы треугольник был остроугольным, все внутренние углы должны быть меньше 90°. Таким образом, мы можем сказать, что прямоугольный треугольник не является остроугольным треугольником.
В чем разница между тупым и острым углами?
Тупые углы больше 90° (но меньше 180°), а острые углы меньше 90°. Например, 110° — тупой угол, а 50° — острый угол.
Острый угол Определение и значение
- Основные определения
- Викторина
- Подробнее об остром угле
- Примеры
- Культура
Сохраните это слово!
Угол, величина которого лежит в пределах от 0° до 90°.
 Сравните тупой угол.
Сравните тупой угол.ВИКТОРИНА
Сыграем ли мы в «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?
Следует ли вам пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!
Вопрос 1 из 6
Какая форма используется для указания обязательства или обязанности кого-либо?
Слова рядом с острым углом
острый живот, острый акцент, острая адренокортикальная недостаточность, острая африканская сонная болезнь, острый алкоголизм, острый угол, острый передний полиомиелит, острый арочный паралич, острый восходящий паралич, острый плечевой радикулит, острое поражение головного мозга
Научный словарь American Heritage® Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
ПОДРОБНЕЕ ОБ ОСТРОМ УГЛЕ
Что такое
острый угол ?Острый угол — это угол, размеры которого составляют от 90° до 0°, что означает, что он меньше прямого угла (в форме буквы «L»), но имеет по крайней мере некоторое пространство между двумя образующими его линиями.
 Форма «V» является примером острого угла .
Форма «V» является примером острого угла . Угол – это пространство между двумя пересекающимися линиями или плоскостями (поверхностями) или фигура, образованная таким пересечением. Углы обычно измеряются в градусах (°). (Они не связаны с градусами, используемыми для измерения температуры.)
Острые углы — это основная концепция геометрии с большим количеством приложений. Инженерия и архитектура полагаются на знание углов и способов их точного измерения.
Почему
острых угла важны в геометрии?Вы когда-нибудь пользовались транспортиром? Если да, то вы, вероятно, помните, что использовали его для измерения углов. Три основных вида углов: прямые углы, тупые углы, , и острые углы. Если базовая геометрическая фигура состоит из прямых линий (извините, кругов), она содержит по крайней мере один из этих трех типов углов.
В квадрате четыре внутренних угла являются четырьмя углами квадрата.
 Все эти углы прямые (каждый равен 90°). Если вы возьмете один из этих углов и переместите одну линию ближе к другой, сузив пространство между ними, угол будет меньше 90° и будет острым углом. Угол больше 90° называется тупой угол. Если продолжать увеличивать угол, в конечном итоге он составит 180° и будет выглядеть точно как прямая линия.
Все эти углы прямые (каждый равен 90°). Если вы возьмете один из этих углов и переместите одну линию ближе к другой, сузив пространство между ними, угол будет меньше 90° и будет острым углом. Угол больше 90° называется тупой угол. Если продолжать увеличивать угол, в конечном итоге он составит 180° и будет выглядеть точно как прямая линия.Понимание разницы между углами — один из первых уроков геометрии, а понимание этой основной идеи — отправная точка для изучения более сложных геометрических понятий. Острые углы (а также прямые и тупые углы) важны во многих областях, которые полагаются на геометрию и точное измерение форм. Просто подумайте о том, сколько углов в вашем доме, и вы поймете, насколько важны углы для архитектуры.
Знаете ли вы… ?
Сумма трех углов треугольника всегда равна 180°. Это означает, что по крайней мере два угла треугольника всегда будут острыми углами. Треугольник, состоящий из трех одинаковых острых углов по 60°, называется равносторонним треугольником.

Каковы реальные примеры
острых углов ?Как только вы узнаете, как выглядят острые углы, вы, вероятно, начнете замечать их в повседневных предметах.
Matisfun.com
Линия роста волос Дрейка действительно раньше была острым углом??? 💀 https://t.co/gyHLB7gW0Z
— Джон (@__Cephei) 15 ноября 2019 г.
Каждый раз, когда я сгибаю колено под острым углом, я чувствую натяжение и легкий щелчок/хлопок за правым коленом 😂
— Trap Money 🐂 (@fwitter_life) 15 ноября 2019 г.
Какие еще слова связаны с
острый угол ?Проверьте себя!
Острый угол это угол, который равен:
A. Равен 90°
B. Меньше 90°
C. Больше 90°Как использовать острый угол в предложении
- 4 Мой капитан на лодке, Бразакка, хотел, чтобы я сделал этот хемингуэевский отрывок с белой щетиной, и он хотел, чтобы я снялся в героическом ракурсе.

История улыбки Ли Марвина Liberty Valance Smile|Роберт Уорд|3 января 2015 г.|DAILY BEAST
Эксплуатация жертв торговли людьми может быть наиболее острой в конфликтных и прилегающих регионах, но она не ограничивается этими районами.
ИГИЛ, Боко Харам и растущая роль торговли людьми в терроризме 21-го века|Луиза И. Шелли|26 декабря 2014 г.|DAILY BEAST
Другой ракурс, который Робинов предлагает в качестве возможного для Питера Паркера/Человека-паука, перезагрузка франшизы, в которой Паучок становится… взрослым.
Эксклюзив: Sony Hack раскрывает подробные планы студии по еще одной перезагрузке «Человека-паука»|William Boot|13 декабря 2014 г.|DAILY BEAST
как и иранцы.
Катар, союзник США, укрывает джихадистов от денег|Джейми Деттмер|10 декабря 2014|DAILY BEAST
Это чувство уязвимости, конечно, еще более остро ощущается в таких микрогосударствах, как Ямайка.
Как Мориса Томлинсона выгнали на Ямайке и отправили в изгнание|Джей Майклсон|9 декабря 2014 г.
 |DAILY BEAST
|DAILY BEASTПри остром и хроническом паренхиматозном нефрите их количество обычно очень велико.
Руководство по клинической диагностике|Джеймс Кэмпбелл Тодд
В центре многих комнат играл небольшой фонтан; в других их было четыре, по одному в каждом углу.
Blackwood’s Edinburgh Magazine, Volume 60, No. 372, October 1846|Various
При паренхиматозном нефрите, особенно при острой форме, большое количество почечных клеток.
Руководство по клинической диагностике|Джеймс Кэмпбелл Тодд
Остальное делается путем срезания двух верхних и четырех нижних зубов и замены вставных под нужным углом.
Шах и мат|Джозеф Шеридан Ле Фаню
В комнате царила острая дисгармония, хотя совсем недавно была хотя бы видимая гармония.
The Wave|Algernon Blackwood
- Автор Varsha
- Последнее изменение 19-07-2022
- Автор Варша
- Последнее изменение 19-07-2022
- Вершина: Точка, в которой пересекаются две прямые, называется вершиной.

- Плечи: Плечи — это сегментация или две линии, исходящие из вершины и образующие угол.
- Разделив один прямой угол, мы получим два или более острых угла.
- Все равносторонние треугольники являются треугольниками с острыми углами.
- Любой угол больше 90 градусов не подпадает под категорию острого угла.
- Два угла любого треугольника будут острыми.
- Буква V образует острый угол
- Когда часы бьют в 1 или 2 часа, они образуют острый угол
- Кусок пиццы образует острый угол
- Несколько дорожных знаков, указывающих направления, образуют острый угол
- Несколько поз для упражнений образуют острый угол
- Что такое острый угол?
- Острые треугольники
- Комплементарные углы
- Острый угол Определение угла
- Острый угол Пример угла
- $0,0001$ градусов
- $15$ градусов
- $45$ градусов
- $75$ градусов
- $89,9999$ градусов.
- $\frac{1}{1000} \pi$
- $\frac{1}{10} \pi$
- $\frac{3}{ 8} \pi$
- $\frac{2}{5} \pi$
- $\frac{49}{100} \pi$.

- У треугольника есть два угла, сумма градусов которых составляет $91$ градусов. Является ли треугольник остроугольным? Почему или почему нет? Можете ли вы использовать этот пример, чтобы вывести общее правило для определения того, является ли треугольник остроугольным, на основе двух угловых величин?
- Какое наименьшее количество острых углов необходимо для получения окружности?
- Докажите, что единственный возможный остроугольный многоугольник — треугольник.
 То есть докажите, что у любого n-угольника с более чем тремя сторонами все углы не могут быть острыми.
То есть докажите, что у любого n-угольника с более чем тремя сторонами все углы не могут быть острыми. - Пусть $ABC$ — треугольник, в котором угол $ABC$ больше угла $BCA$. Докажите, что угол $BCA$ острый.
- Докажите, что дополнение к любому тупому углу является острым.
- Этот треугольник не обязательно остроугольный. Хотя третий угол стоит $180-91 = 89$ градусов и, следовательно, острый, никогда не указывалось, что меньшие углы составляют в сумме $91$ градусов. Возможно, треугольник правильный. Например, он может иметь прямой угол и угол в $1$ градуса. Это может быть даже тупым, потому что градусные меры непрерывны. Если бы он имел, например, один угол величиной $0,5$, а другой — $90,5$ градусов, он был бы тупым.
Но если сумма двух острых углов равна $91$ градусу, то треугольник остроугольный. В общем, если два меньших угла треугольника (которые всегда должны быть острыми) имеют градусную меру большую, чем градусная мера прямого угла, треугольник является острым.
- $5$ необходимы острые углы.
- Докажите от противного. Пусть $n$ — натуральное число, большее или равное $4$. Тогда сумма внутренних углов должна быть равна $180(n-2) = 180n-360$.
Предположим, что все углы n-угольника меньше прямого угла. В градусах их мера составляет менее $90$ градусов. Тогда сумма внутренних углов $\alpha$ меньше $90n$.
Но сумма внутренних углов равна $180n-360$. Следовательно, $180n-360 < 90$. Перемещение членов $n$ влево, а остальных членов вправо дает $90n < 360$. Тогда деление дает $n<4$.
Но единственный многоугольник, у которого меньше $4$ сторон, — это треугольник. Следовательно, единственный остроугольный многоугольник — это треугольник. - Наименьшие два угла любого треугольника острые. Таким образом, $ABC$ — либо больший из двух острых углов, а $BCA$ — меньший из двух, либо $ABC$ — наибольший угол треугольника, а $BCA$ — один из двух меньших острых углов. В последнем случае, независимо от того, является ли $ABC$ острым, тупым или правильным, $BCA$ остается острым.
 В первом случае $BCA$ тоже острый. Следовательно, угол должен быть острым, если он не является наибольшим углом.
В первом случае $BCA$ тоже острый. Следовательно, угол должен быть острым, если он не является наибольшим углом. - Тупой угол больше прямого угла, и угловая добавка работает вместе с другим углом, чтобы получить прямой угол. В градусах прямой угол равен $180$ градусам. Дополнение любого угла имеет размер $180-\alpha$. Если $\alpha$ тупая, то $\alpha > 90$ градусов. Следовательно, $180-\alpha < 90$. Таким образом, дополнение составляет менее $90$ градусов и, следовательно, тупое.
- Мы видим, что острые углы наклонены в правильном направлении.
- Прямые углы всегда образуют L-образную форму.
- Тупые углы выходят за пределы формы «L» и наклоняются влево.
- Пицца, нарезанная на 6 или 8 ломтиков, будет иметь ломтики с острыми углами. Это имеет смысл, потому что каждый срез будет иметь угловую меру либо 45 90 328 o 90 329, либо 60 90 328 o 90 329., соответственно.
- Треугольные знаки, подобные показанному выше, будут содержать три внутренних угла, каждый из которых является острым.

- Открытые ножницы также могут образовывать острые углы, если их не открывать слишком широко.
- Два острых угла могут быть дополнительными (в сумме получается 90 o ), но никогда не могут быть дополнительными (в сумме 180 o ).
- Это также означает, что два острых угла могут образовывать прямоугольный треугольник, но никогда не образуют прямой угол.

- Если многоугольник имеет пять или более вершин или сторон, внешний угол многоугольника является острым.
- Когда все внутренние углы треугольника острые, мы называем его остроугольным.
Культурные определения острого угла
острый угол
Угол, размер которого меньше девяноста градусов, но больше нуля градусов.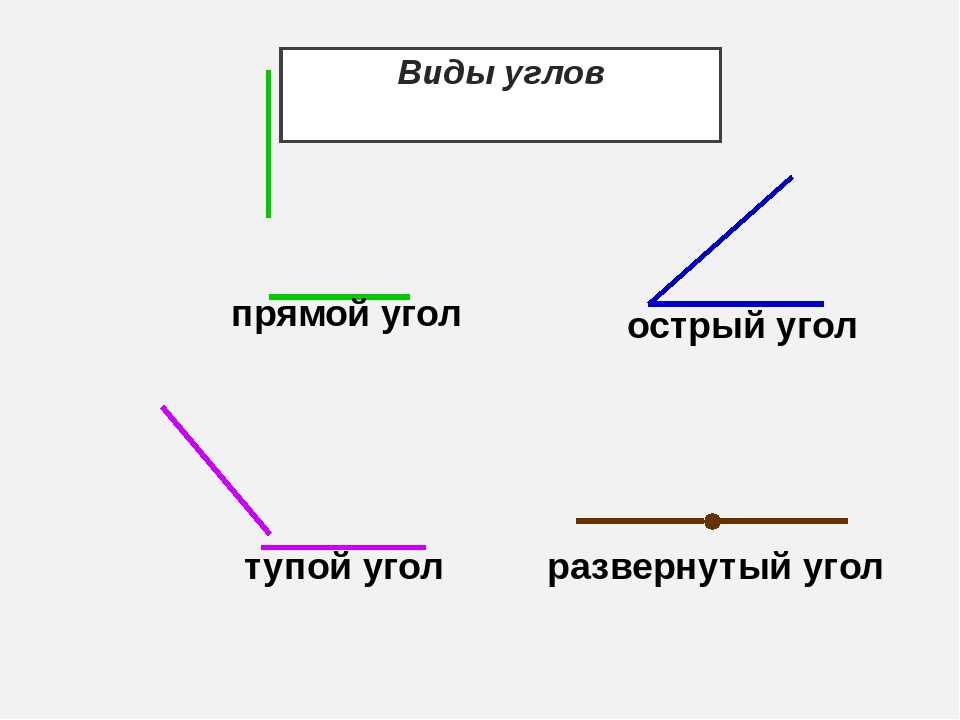 (Сравните тупой угол и прямой угол.)
(Сравните тупой угол и прямой угол.)
Новый словарь культурной грамотности, третье издание Авторское право © 2005 г., издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Определение, факты, формулы, типы и примеры
Острый угол : В математике две прямые пересекаются в одной точке, образуя угол. В геометрии существует много типов углов, таких как острый, тупой, прямой и т. Д. Острый угол — это угол, который меньше 90 °. Многоугольники, такие как треугольник, параллелограмм, трапеция и т. д., будут иметь по крайней мере один острый угол.
На этой странице мы предоставили всю необходимую информацию о том, что такое острый угол, а также определения, формулы и примеры. Читай дальше, чтобы узнать больше.
Острый угол Определение : Угол меньше 90° называется острым углом. Острым углом иначе называют угол, который меньше прямого угла. Острый угол обозначается символом «∠» и измеряется с помощью транспортира в градусах.
Изучите концепции 11-го экзамена CBSE
Примеры острого угла : Несколько примеров острых углов в градусах — ♂80 O , ♂55 O , ♂70 O , ▲25 O , ♂83 282829992899289928992899289892898989898992898989928989898989898989928998989992898998999928989999999999999928929н. , ∠15 о , ∠12 о , ∠28 о .
A ∠45 o острый угол можно нарисовать следующим образом:
Представление острого угла
Каждый угол состоит из двух компонентов: стороны и вершины. Точно так же острый угол также имеет две составляющие стороны и вершину. Представление острого угла.
Треугольник с острым углом
Если внутренние углы треугольника меньше 90 градусов, то такой треугольник называется остроугольным. Равнобедренные треугольники имеют острые углы.
Параллелограмм острого угла
Параллелограмм — это не что иное, как четырехугольник, противоположные стороны которого параллельны и равны. Каждый параллелограмм имеет два острых угла, угол которых меньше 90 градусов.
Источник: Книга НЦЭРТ.Здесь ∠SPQ и ∠QRS — острые углы.
Практика 11-го экзамена CBSE Вопросы
Остроугольная трапеция
Трапеция – это параллелограмм, у которого две противоположные стороны параллельны друг другу. Каждая трапеция имеет 2 острых угла.
Здесь ∠DCB и ∠ADC — острые углы.
Формула острого угла
Для остроугольного треугольника справедливо следующее соотношение длин сторон:
| Q 2 + P 2 > R 2 P 2 + R 2 > Q 2 + R 2 > Q 2 + R 2 > Q 2 + R 2 > Q 2 + R 2 > Q 2 + R 2 > Q 2 + R 2 >. 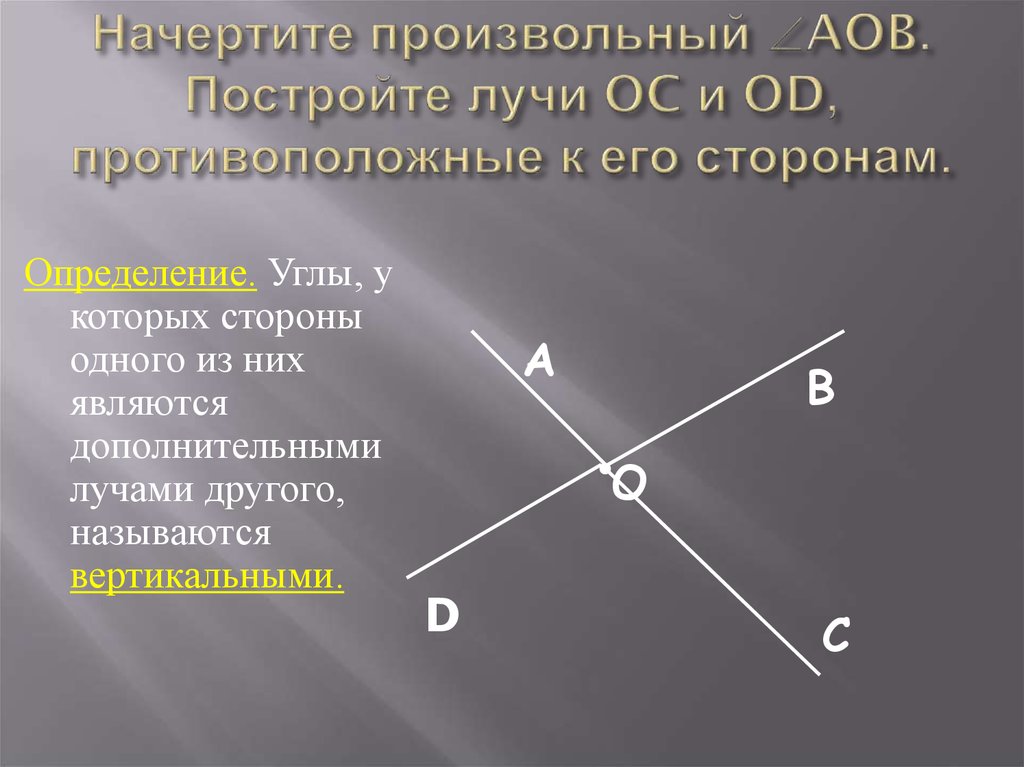 2 2 |
Где p, q и r — длины сторон.
Свойства острого угла
Свойства острых углов приведены ниже:
Попытка 11-го экзамена CBSE Пробные тесты
Примеры острого угла в реальной жизни
Ниже приведены несколько реальных примеров острых углов:
Вопросы об остром ракурсе
Ниже приведены несколько решенных вопросов по острым углам:
В. Что из следующего является возможным измерением острого угла? Что из следующего является возможным измерением острого угла? Опции: 90 градусов 45 градусов 180 градусов 360 градусов Ответ: 45 градусов — острый угол. |
| В. Какая из следующих букв содержит острый угол? Опции: E F H V A. Буква «V» содержит острый угол. |
| В. Является ли 1 час острым углом? A. Да, 1 час — это острый угол. |
| В. Что такое острый угол? A. Угол от 0 до 90 градусов называется острым. |
| В. Острый угол равен 0 градусов? A. Да, 0 градусов — это острые углы. |
| В. Напишите 5 примеров острого угла в градусах? A.  5 примеров острых углов в градусах: ∠70 o , ∠25 o , ∠83 o , ∠89 o , ∠15. 5 примеров острых углов в градусах: ∠70 o , ∠25 o , ∠83 o , ∠89 o , ∠15. |
Вы также можете воспользоваться Решениями NCERT по математике для 6 класса, , которые будут полезны при подготовке к экзамену.
СКАЧАТЬ MATHS NCERT SOLUTIONS ЗДЕСЬ
Кроме того, решайте вопросы по математике и проходите бесплатные пробные тесты по математике на Embibe:
Мы надеемся, что эта подробная статья об остром угле будет вам полезна. Если у вас есть какие-либо вопросы, связанные с этой страницей, напишите нам через раздел комментариев ниже, и мы свяжемся с вами как можно скорее.
Практические вопросы по острому углу с советами и решениями
Острый угол – объяснение и примеры
Острый угол – это угол, больший нулевого угла и меньший прямого угла.
Острый угол в градусах больше $0$ градусов и меньше $90$ градусов.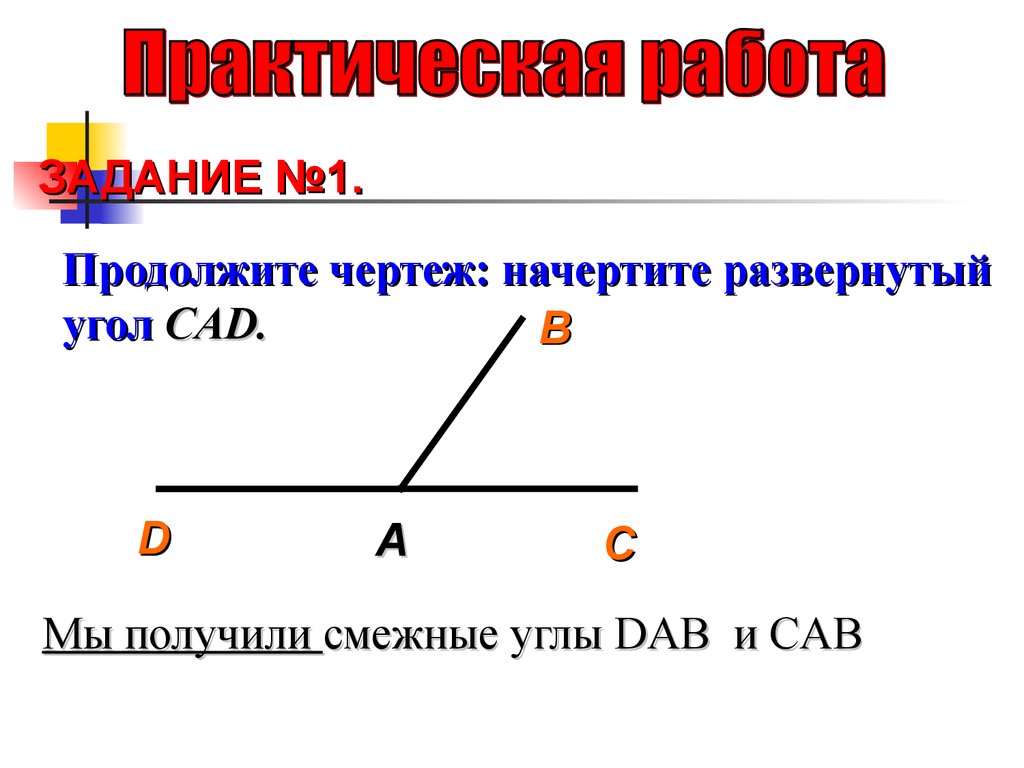 В радианах острым углом считается угол, градусная мера которого больше $0$ радиан и меньше $\frac{\pi}{2}$ радиан.
В радианах острым углом считается угол, градусная мера которого больше $0$ радиан и меньше $\frac{\pi}{2}$ радиан.
Острые углы используются математически в геометрии, тригонометрии и исчислении. Они также находят применение в науке и технике, включая астрономию и архитектуру.
Прежде чем перейти к этому разделу, обязательно ознакомьтесь со свойствами и типами углов. Также может помочь краткий обзор треугольников.
В этом разделе рассматриваются:
Что такое угол с острым углом?
Острый угол — это угол с мерой меньше, чем мера прямого угла. Поскольку во многих системах (включая те, которые используются для тригонометрических функций) используются отрицательные углы, определения обычно предусматривают, что острый угол также должен быть больше нулевого угла.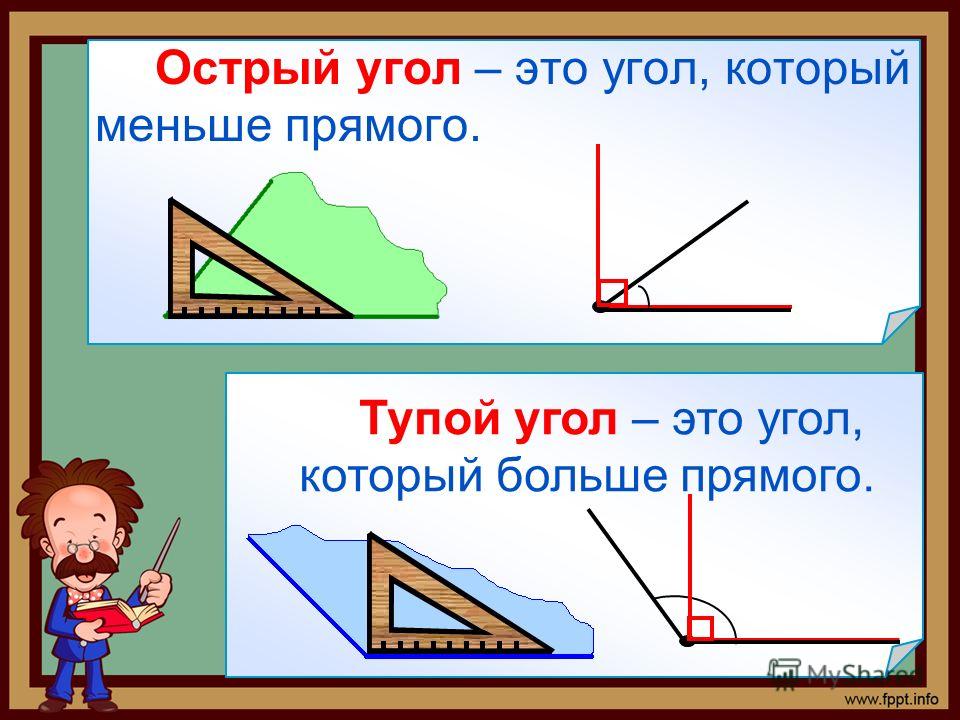
В градусах острый угол $\alpha$ имеет размер от $0$ до $90$ градусов. В радианах мера альфа находится в пределах от $0$ до $\frac{\pi}{2}$ радиан.
Легкая мнемоника для запоминания определения остроты в английском языке происходит от общего использования слова «милый» для описания чего-то маленького, например, щенка. Следовательно, острые углы — это малые углы.
Остроугольный треугольник
Все треугольники имеют как минимум два острых угла.
Это потому, что треугольник с двумя прямыми углами имеет третий угол с мерой $0$, поэтому такой «треугольник» на самом деле является прямой линией. Если треугольник имеет два или более тупых угла, мера его внутреннего угла превышает $180$ градусов.
Таким образом, мера третьего угла используется для классификации треугольников по типам углов. Если третий угол больше прямого, то треугольник тупоугольный. Точно так же, если третий угол прямой, то треугольник прямоугольный.
Если же все три угла острые, то треугольник остроугольный. Это может произойти, если, например, каждый угол равен $60$ градусам. Внутренний угол такого треугольника равен $180$ градусам, но каждый из его отдельных углов меньше прямого угла.
Это может произойти, если, например, каждый угол равен $60$ градусам. Внутренний угол такого треугольника равен $180$ градусам, но каждый из его отдельных углов меньше прямого угла.
Дополнительные углы
Дополнительные углы — это два угла, которые вместе имеют градус прямого угла.
Если предположить, что оба угла положительны, два дополнительных угла будут оба острыми.
Острый угол Определение
Острый угол — это угол, меньший прямого, но больший нулевого угла.
Такой угол имеет размер от $0$ до $90$ градусов не включительно или от $0$ до $\frac{\pi}{2}$ радиан не включительно.
Острый угол Пример
Существует бесконечно много острых углов, поскольку существует бесконечно много чисел между $0$ и $90$ или $0$ и $\frac{\pi}{2}$.
В градусах примеры острых углов включают:
Примеры острых углов в радианах:
Распространенные примеры
В этом разделе рассматриваются распространенные примеры задач на острые углы и их пошаговые решения.
Пример 1Классифицируйте каждый угол как острый или неострый.
A. $\frac{27}{53} \pi$ радиан
B. $\frac{23}{51} \pi$ радиан
C. $-2$ градусов
D. $2$ градусов
Решение
В этом случае углы B и D острые, а углы A и C нет.
Для задач, связанных с радианами, посмотрите на коэффициент $\pi$. Если он меньше $\frac{1}{2}$ и больше $0$, угол острый.
В этом случае рассмотрим $\frac{27}{53}$. Половина от $53$ составляет $26,5$. Поскольку $27 > 26,5$, $\frac{27}{53}$ больше, чем $\frac{1}{2}$. Таким образом, $\frac{27}{53}\pi$ больше, чем $\frac{\pi}{2}$. Следовательно, угол тупой.
Но половина от 51$ составляет 25,5$. Поскольку $23$ меньше $25,5$, $\frac{23}{51}$ меньше половины. Следовательно, $\frac{23}{51}\pi$ меньше, чем $\frac{\pi}{2}$, поэтому угол B острый.
C — отрицательная градусная мера. Это означает, что угол меньше нулевого угла, поэтому он не острый. Обратите внимание, что это имеет значение только тогда, когда имеет значение ориентация угла в пространстве или при алгебраическом использовании.
Последний угол, D, однако, находится между $0$ и $90$ градусами включительно. Поэтому он острый.
Пример 2Является ли следующий треугольник остроугольным? Почему или почему нет?
Решение
Этот треугольник остроугольный.
Хотя даны только два угла, информации достаточно, чтобы определить, что третий угол острый. Так как данные два угла также острые, то все три угла острые. Следовательно, треугольник остроугольный.
Почему?
Напомним, что внутренние углы треугольника (в градусах) составляют в сумме $180$ градусов. Это означает, что мера третьего угла равна $180-(87,7+56,5) = 180-144,2 = 35,8$ градусов.
Так как $35,8$, $56,5$ и $87,7$ меньше, чем $90$ градусов, треугольник должен быть остроугольным.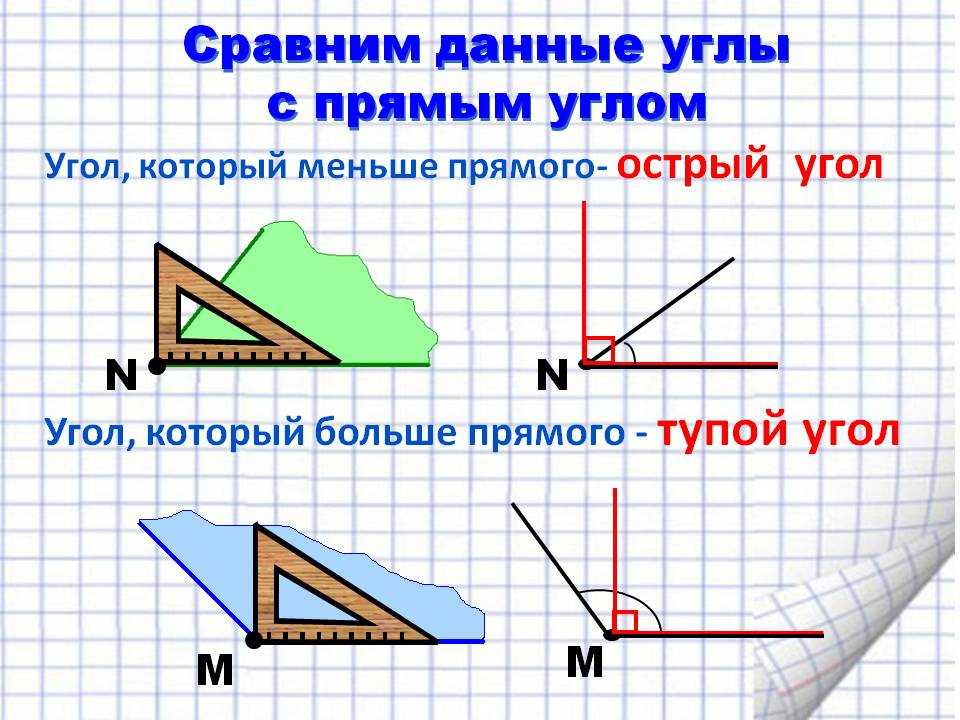
Найдите дополнение угла для угла с мерой $\frac{4}{9} \pi$ радиан.
Решение
Угловое дополнение к углу — это еще один угол, который можно добавить к первому, чтобы получить прямой угол.
Заданный угол $\frac{4}{9} \pi$ радиан меньше прямого угла, поскольку $4$ меньше, чем $4,5$, а $\frac{4,5}{9} \pi = \frac{1 }{2} \pi$ радианы, мера прямого угла в радианах.
В этом случае дополнением является разница между $\frac{\pi}{2}$ радиан и $\frac{4}{9} \pi$ радиан.
Это равно:
$\frac{4.5}{9} \pi – \frac{4}{9} \pi = \frac{0.5}{9} \pi = \frac{1}{18 } \пи$.
Таким образом, дополнение к углу имеет меру $\frac{1}{18} \pi$ радиан.
Пример 4Какое наименьшее количество острых углов необходимо для получения прямого угла?
Решение
Напомним, что прямой угол равен двум прямым углам. В градусах это $180$ градусов. Он также равен $\pi$ радианам.
Поскольку каждый острый угол меньше $90$ градусов или $\frac{\pi}{2}$ радиан, два острых угла должны иметь градусную меру меньше $180$ градусов или меньше $\pi$ радиан.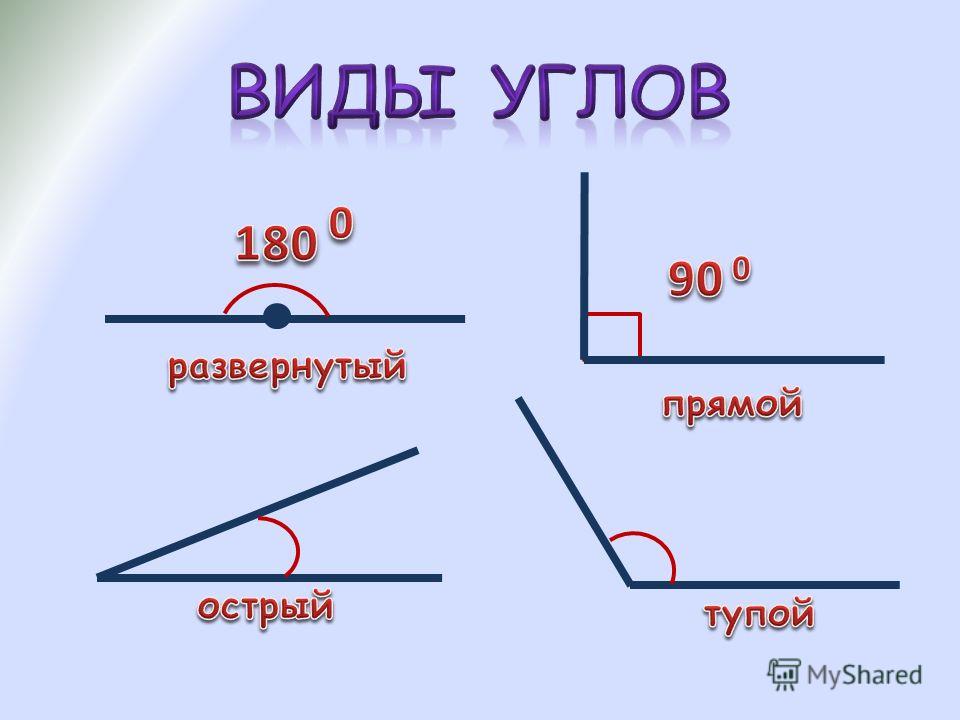
То есть два острых угла всегда будут меньше прямого угла. Но два острых угла, близких к прямому, плюс один малый угол могут равняться прямой линии.
Например, два угла с размерами $89$ градусов и $88$ градусов имеют сумму $177$ градусов. Дополнительный угол в $3$ даст прямую линию.
Аналогично, угол $\frac{49}{100} \pi$ радиан и угол $\frac{47}{100} \pi$ радиан имеют общую меру $\frac{97}{100} \ пи$ радиан. Но дополнительного угла $\frac{3}{100}\pi$ радиан было бы достаточно, чтобы создать прямую линию.
Пример 5Рассмотрим окружность с центром $A$ и двумя различными точками $B$ и $C$ на окружности.
Докажите, что угол $ACB$ острый для любой точки $C$ на окружности треугольника.
Решение
Во-первых, обратите внимание, что отрезки $AC$ и $AB$ имеют одинаковую длину, поскольку оба являются радиусами одной и той же окружности.
Следовательно, треугольник $ABC$ всегда будет как минимум равнобедренным, а иногда и равносторонним.
Но в равнобедренном треугольнике углы при основании всегда равны. Это означает, что углы $ACB$ и $ABC$ всегда будут равны, независимо от того, где на окружности находится угол $C$.
Эти два угла не могут быть тупыми, потому что тогда общий внутренний угол треугольника будет больше двух прямых углов.
Точно так же оба угла не могут быть прямыми, потому что тогда угол $CAB$ был бы нулевым углом. Это означает, что $C$ и $B$ должны лежать на одной прямой по одну сторону от $A$ и на окружности. Тогда в таком случае $C$ и $B$ будут одной и той же точкой. Однако в постановке этой задачи указано, что точки $C$ и $B$ должны быть разными.
Следовательно, оба угла должны быть острыми. В частности, тогда $ACB$ является острым для любой отдельной точки $C$ на окружности.
Другие примеры с пояснениямиИзображения/математические чертежи создаются с помощью GeoGebra.
Острые углы (что это такое и как они выглядят)
Острые углы — это углы, градусная мера которых меньше 90 o . От латинского термина acutus , что означает что-то острое или заостренное, острые углы известны своей заостренной формой. Чаще всего острые углы, с которыми вы столкнетесь, имеют V-образную форму. Попробуйте подумать о реальных примерах, демонстрирующих эту форму, и вы, вероятно, уже сталкивались с острыми углами раньше.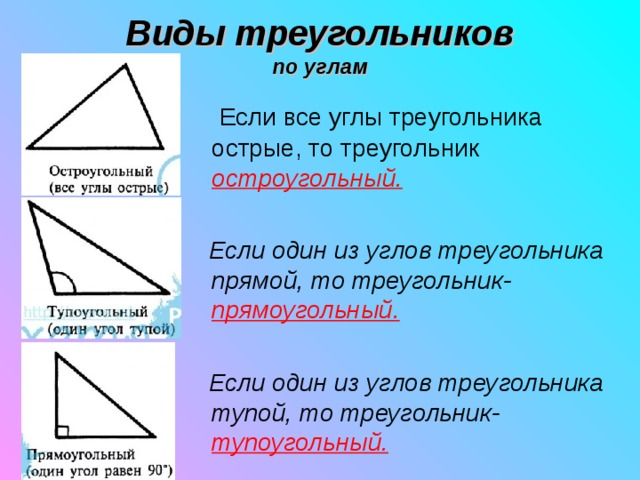
В этой статье мы покажем вам компоненты и основное определение острых углов. Мы также покажем вам размеры углов и реальные примеры острых углов, чтобы вы лучше ознакомились с тем, как выглядят острые углы. В этом обсуждении также будут рассмотрены определения и свойства остроугольных треугольников, что покажет вам, насколько важны острые углы в основе геометрии.
Что такое острые углы?
Острые углы — это углы, размер которых меньше 90 o или просто прямые углы. Это означает, что любой угол между 0 o и 90 o считается острым углом. Давайте посмотрим на острый угол, показанный ниже.
Мы видим, что острый угол образован двумя плечами или лучами, и они встречаются в общей точке, которую мы называем вершиной. На приведенной выше диаграмме острый угол \угол AOB, измеряемый в \тета градусах, образован лучами \overline{AB} и \overline{AO}. Чтобы \угол AOB был острым углом, \theta должен быть между 0 или и 90 или .
Чтобы лучше понять, что делает острые углы уникальными, давайте покажем вам три распространенных типа углов: острый, прямой и тупой.
Показывая вам, как выглядит острый угол по сравнению с прямым и тупым углами, он помогает вам понять и идентифицировать острые углы с одного взгляда.
Вы, вероятно, также сталкивались с острыми углами в прошлом, не зная, что они содержат острые углы. Изображения, показанные выше, являются тремя из многих примеров острых углов в реальном мире.
Еще несколько примеров можно придумать самостоятельно. Важно, чтобы вы привыкли определять форму, образованную острыми углами. А пока давайте попробуем разминку, чтобы проверить ваше понимание острых углов.
Проблема 1
На изображениях, показанных ниже, вы видите транспортир — удобный инструмент, который мы можем использовать для измерения и построения углов. Для каждого элемента определите, является ли выделенный угол действительно острым или нет.
а.
Сторона угла опирается на угол 30°, поэтому градусная мера угла AOB равна 30°. Напомним, что все острые углы имеют размеры от 0 до 90°, поэтому наш угол острый. В дополнение к его размеру, форма угла также подтверждает, что это острый угол.
б.
При осмотре может показаться сложным определить этот угол, так как он близок к прямому. Но, увидев его реальную меру, мы подтвердим, острый угол или нет.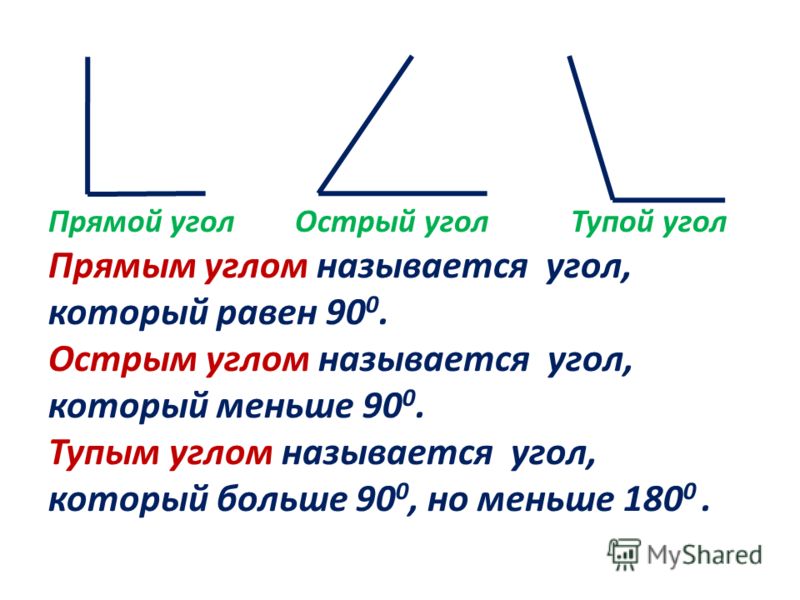 Так как конечная позиция угла AOB приземляется на 85o. Так как 85\степень < 90\градус,\угол AOB - острый угол.
Так как конечная позиция угла AOB приземляется на 85o. Так как 85\степень < 90\градус,\угол AOB - острый угол.
в.
Только по его наброску видно, что угол AOB наклонен влево и проходит отметку 90°. Транспортир измеряет угол AOB как 120°. Это выходит за пределы углов, которые можно определить как острый угол, поэтому угол AOB не является острым углом. На самом деле это тупой угол.
Теперь, когда мы рассмотрели основы того, что делает острые углы уникальными, давайте расширим наши знания, изучив свойства острых углов и их применение.
Другие свойства острых углов
Острые углы обладают интересными свойствами, которые пригодятся позже. Давайте рассмотрим эти основы для вас, чтобы убедиться, что вы знаете все основы острых углов.
Задача 2
Определите, верны или нет следующие утверждения.
а. У шестиугольника всегда будут внешние углы, каждый из которых является острым.
Мы упоминали, что многоугольники, содержащие пять или более сторон, такие как шестиугольники (шестигранные многоугольники), всегда будут иметь острые внешние углы. Например, если у нас есть правильный шестиугольник, показанный ниже, у нас есть внешние углы, показанные ниже.
Это подтверждает, что утверждение верно.
б. Когда прямой угол делится на биссектрису угла, он возвращает один острый угол и один тупой угол.
Мы знаем, что прямой угол всегда будет иметь угловую меру 90°. Когда биссектриса делит угол, она делит его на два равных угла.
Это означает, что мы разделим 90 градусов на 2, поэтому каждый угол будет иметь размер 45 градусов.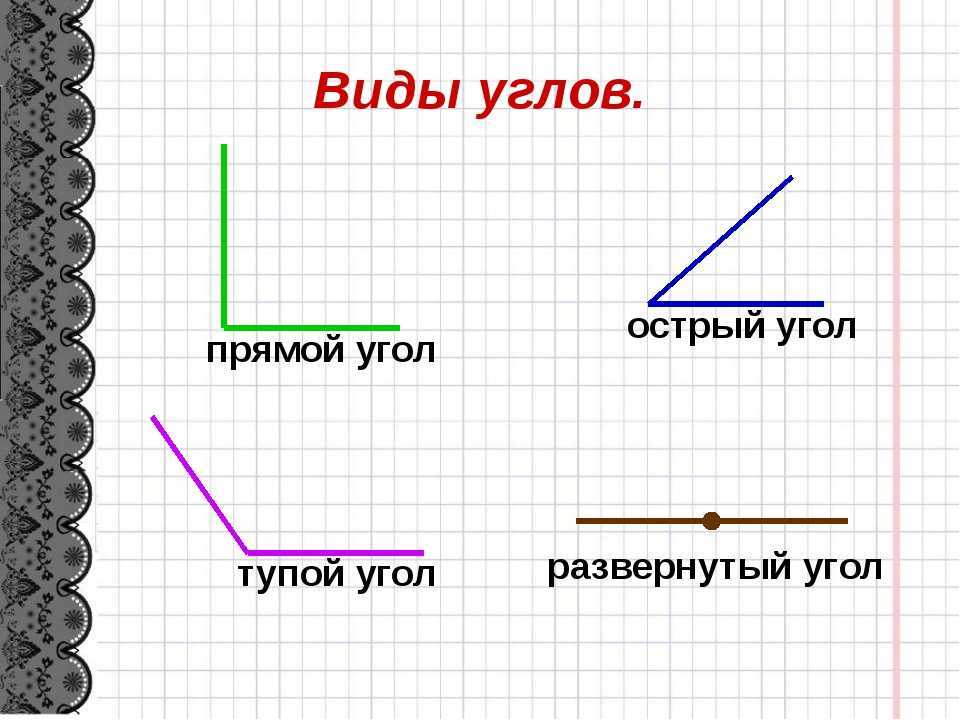 Это меньше, чем 90° (это ожидаемо, поскольку мы делим 90° на 2), поэтому мы можем подтвердить, что результирующие углы будут острыми, что делает утверждение верным.
Это меньше, чем 90° (это ожидаемо, поскольку мы делим 90° на 2), поэтому мы можем подтвердить, что результирующие углы будут острыми, что делает утверждение верным.
Теперь, когда мы знаем некоторые интересные факты об острых углах, давайте теперь сосредоточимся на остроугольных треугольниках. Эти треугольники также демонстрируют интересное поведение из-за того, что они содержат острые углы.
Что такое остроугольные треугольники?
Как мы уже отмечали, остроугольные треугольники — это просто треугольники, содержащие внутри три острых угла. Это означает, что остроугольный треугольник имеет внутренние углы, каждый из которых меньше 90°. Вот несколько примеров остроугольных треугольников:
Каждый остроугольный треугольник содержит острые углы внутри его внутренних углов. Взгляните на третий треугольник: мы называем его равносторонним треугольником. Это особый тип остроугольного треугольника, каждый из внутренних углов которого равен 60°.
Это означает, что когда треугольник содержит три острых угла, мы можем сразу идентифицировать его как остроугольный треугольник.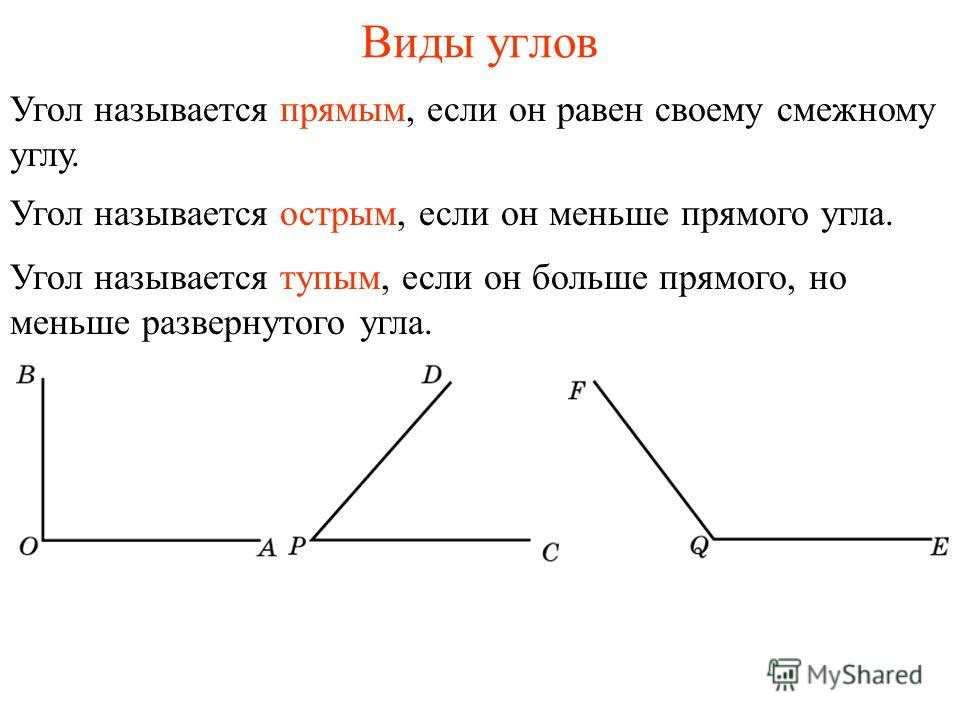 Этот треугольник также проявляет интересные свойства с точки зрения его сторон — мы называем это соотношение формулой остроугольного треугольника. 92 \конец{выровнено}
Этот треугольник также проявляет интересные свойства с точки зрения его сторон — мы называем это соотношение формулой остроугольного треугольника. 92 \конец{выровнено}
Вот почему мы также можем назвать эту формулу неравенством треугольника для остроугольных треугольников. На словах эта формула острого треугольника означает, что квадрат суммы меньших сторон всегда будет больше, чем квадрат самого длинного знака. Давайте теперь применим то, что мы узнали и поработали над проблемами ниже.
Задача 3
Покажите, что острый угол может иметь следующие стороны, как показано ниже.
Напомним, что остроугольный треугольник удовлетворяет показанному ниже неравенству. 92\\100 + 64 &> 144\\164 &> 144\\&\Стрелка вправо \text{Остроугольный треугольник} \end{выравнивание}
Поскольку стороны удовлетворяют неравенству, стороны действительны и могут образовывать остроугольный треугольник.
Задача 4
Еще один особый остроугольный треугольник — золотой треугольник — остроугольный равнобедренный треугольник.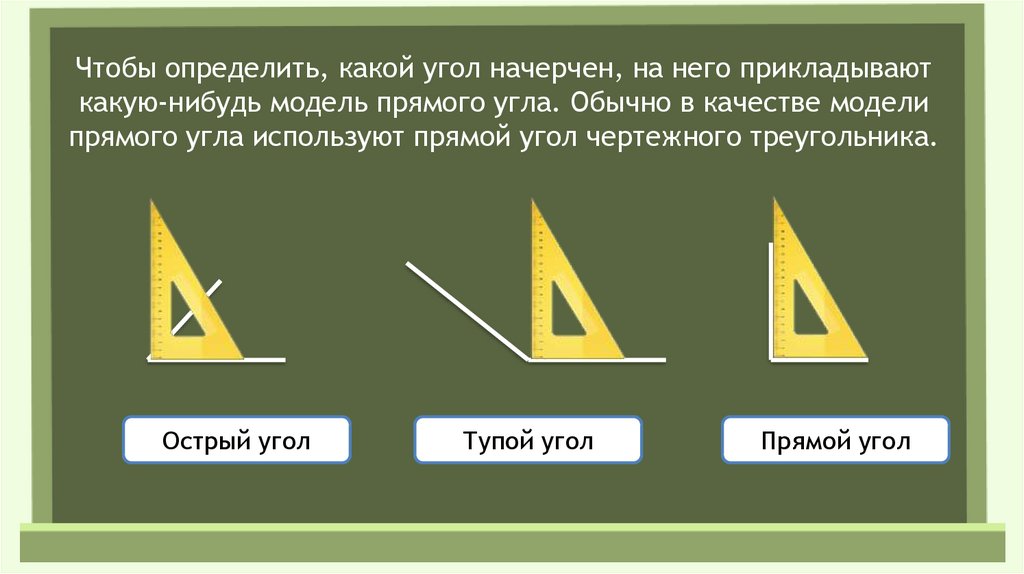



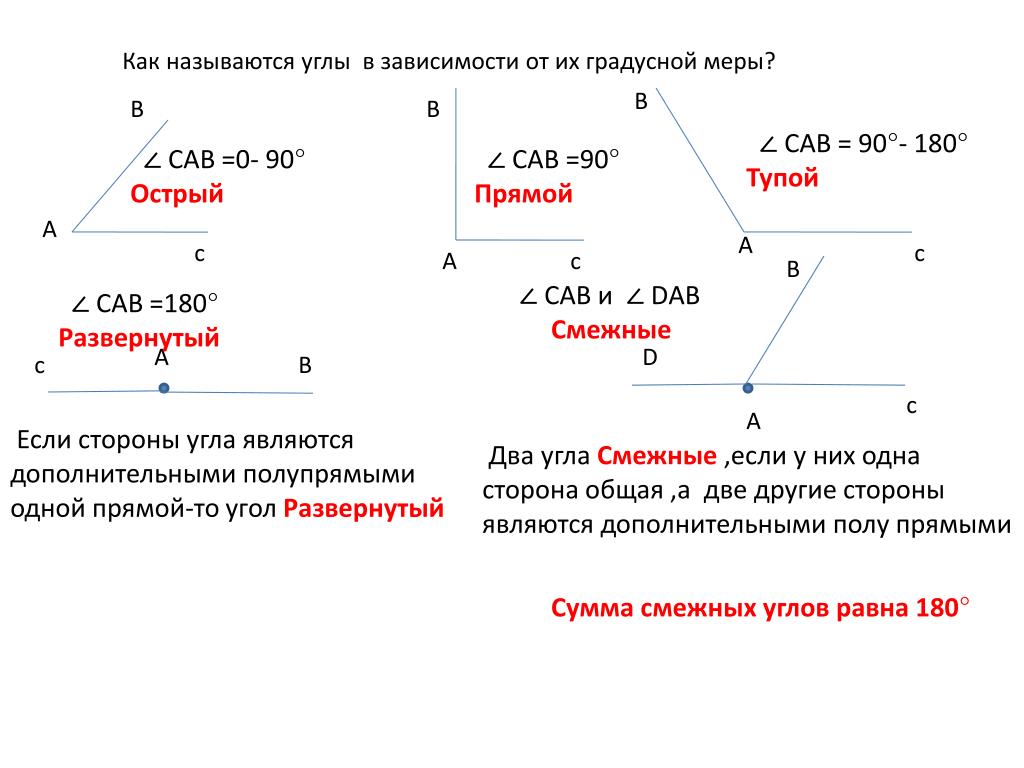 Вычислите полученные углы.
Вычислите полученные углы.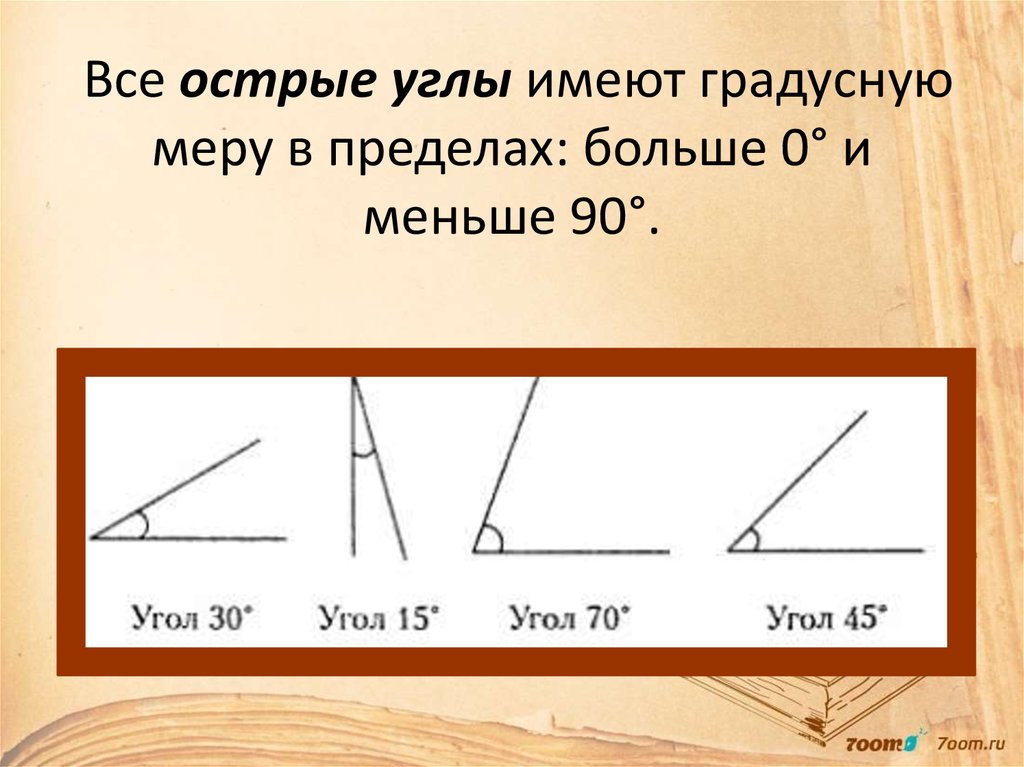 Ответ: 36˚ и 144˚.
Ответ: 36˚ и 144˚.
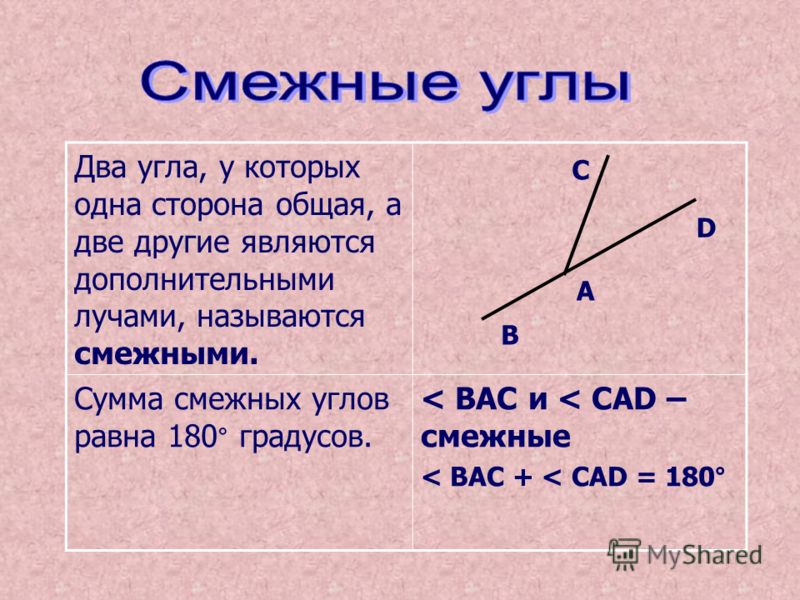

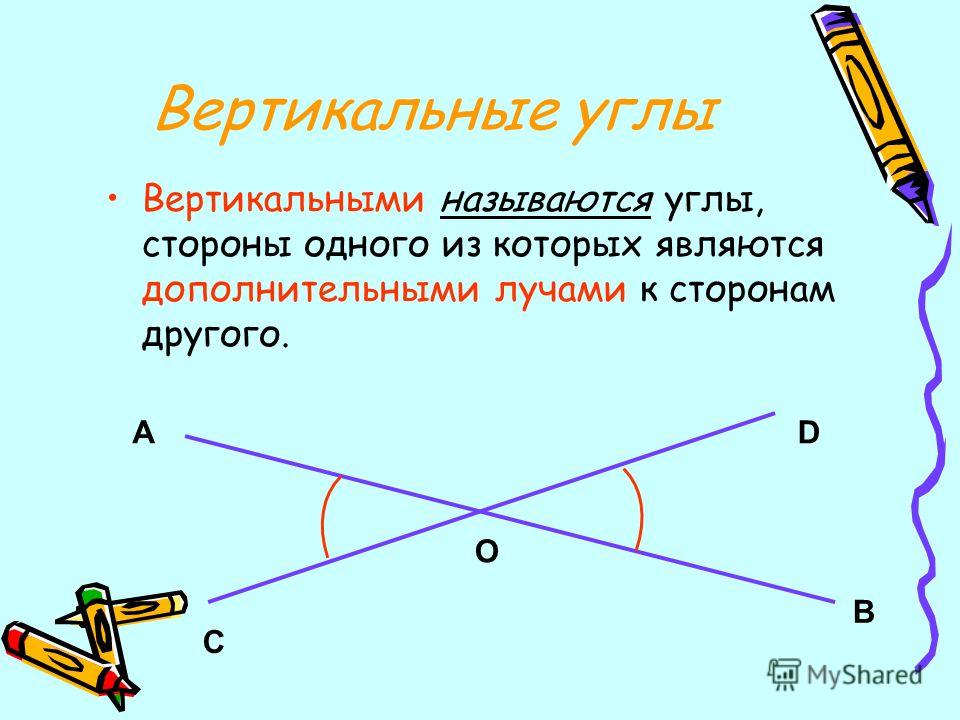
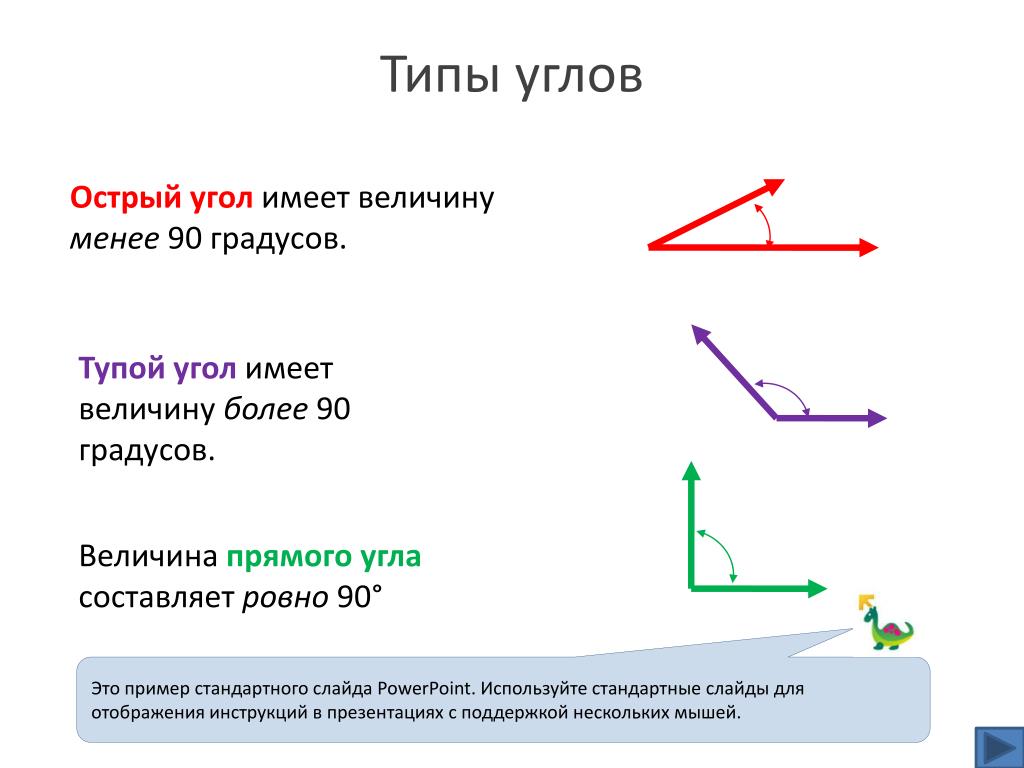 Вопрос 3: Состояние Верно или Ложно :
Вопрос 3: Состояние Верно или Ложно : Таким образом, ответ будет вариантом d.
Таким образом, ответ будет вариантом d.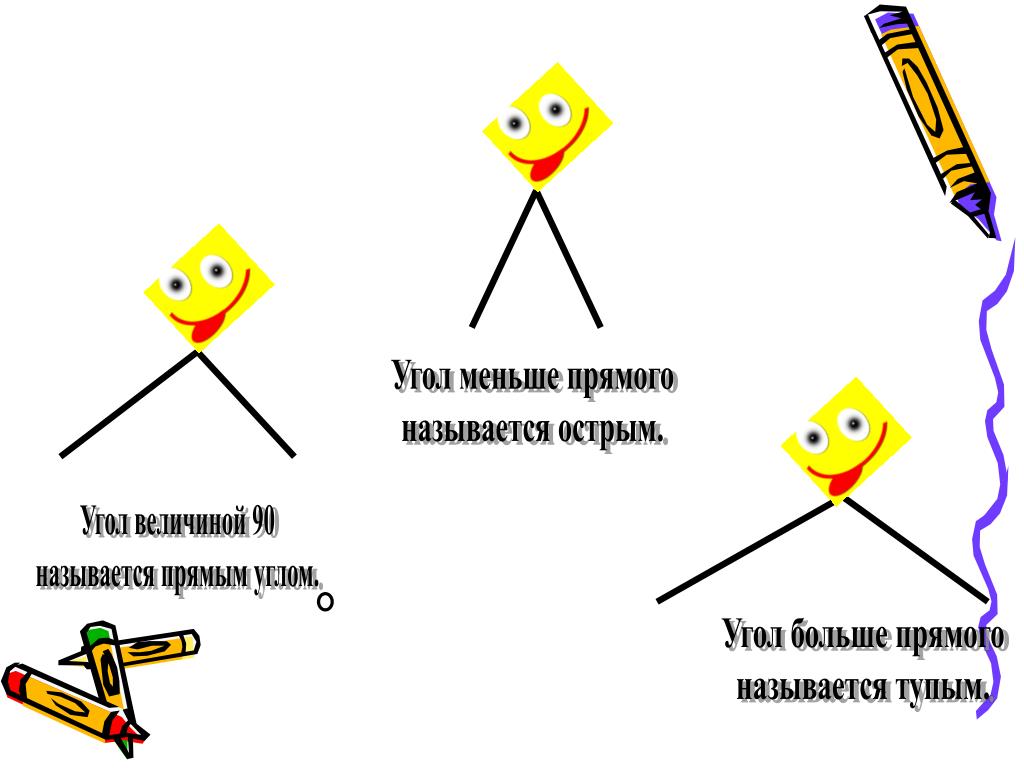 Например, когда время 11 часов, угол, образованный между часовой и минутной стрелками, является острым углом. Другими словами, 30°, 40°, 57° и т. д. — все это острые углы.
Например, когда время 11 часов, угол, образованный между часовой и минутной стрелками, является острым углом. Другими словами, 30°, 40°, 57° и т. д. — все это острые углы.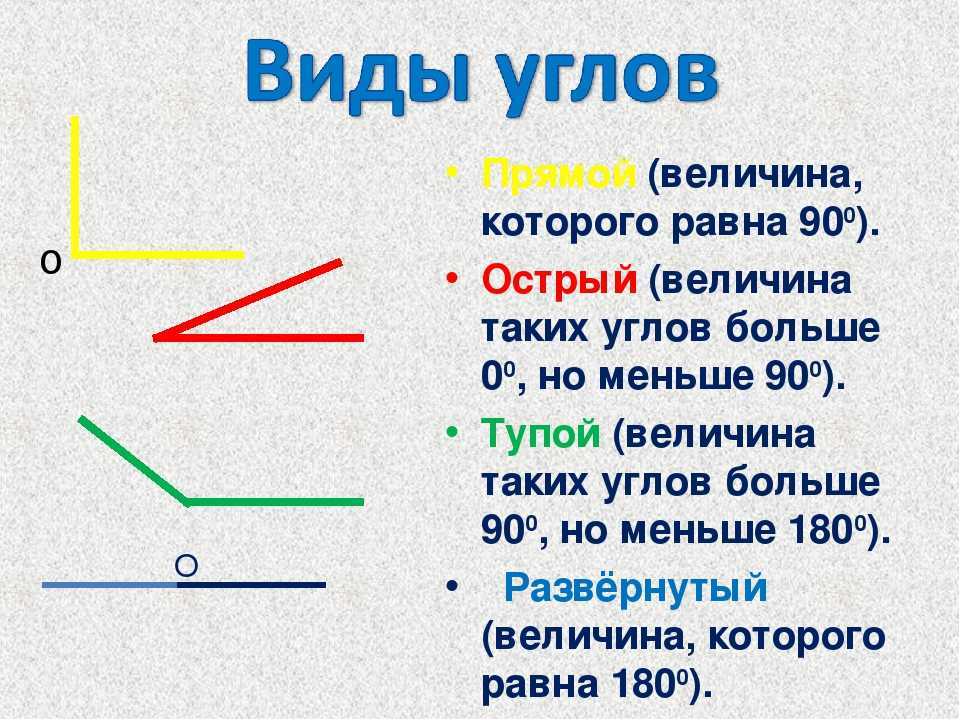 Некоторые из примеров: 60 °, 30 °, 45 градусов и т. Д. Треугольник, образованный всеми внутренними углами, меньшими 90 °, называется остроугольным треугольником. Например, равносторонний треугольник является остроугольным, так как его внутренние углы равны 60°.
Некоторые из примеров: 60 °, 30 °, 45 градусов и т. Д. Треугольник, образованный всеми внутренними углами, меньшими 90 °, называется остроугольным треугольником. Например, равносторонний треугольник является остроугольным, так как его внутренние углы равны 60°.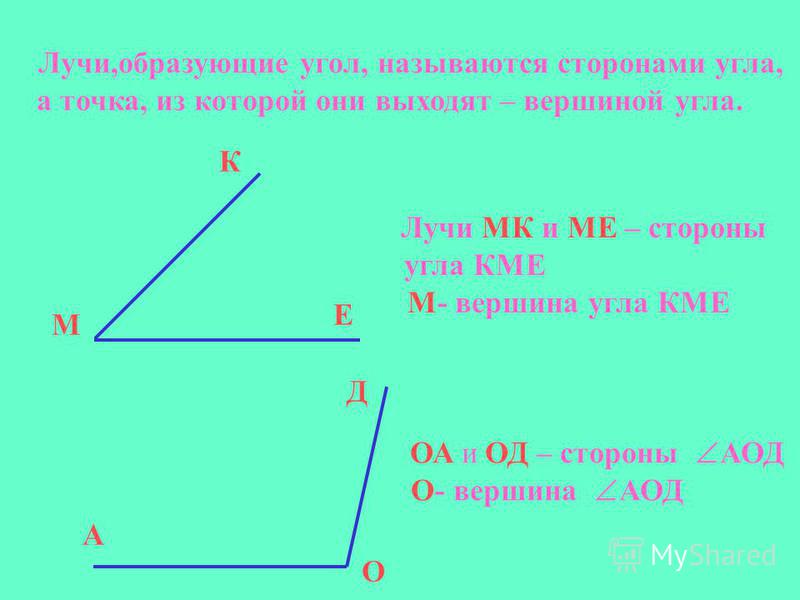
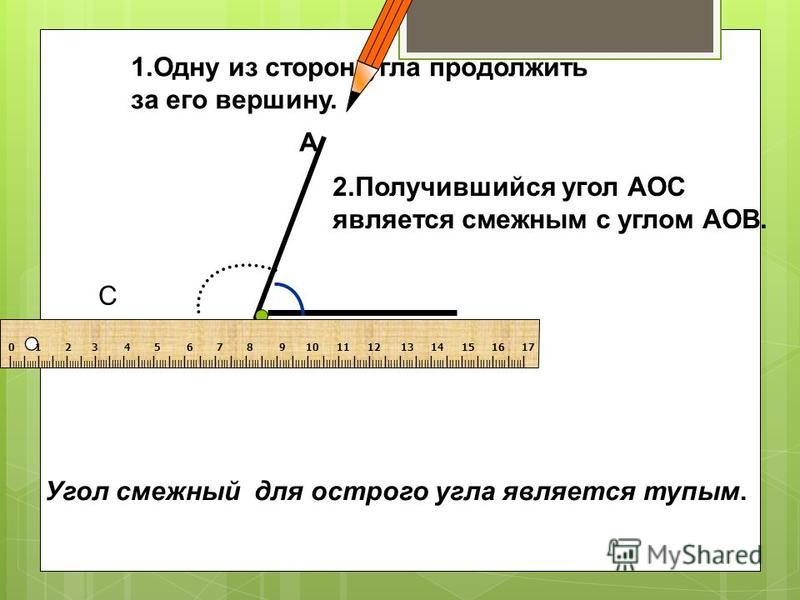 В Δ ABC, если стороны измеряются a,b,c так, что c является наибольшей стороной, то a 2 + b 2 > с 2 . Другими словами, в треугольнике, если a 2 + b 2 > c 2 , треугольник является остроугольным.
В Δ ABC, если стороны измеряются a,b,c так, что c является наибольшей стороной, то a 2 + b 2 > с 2 . Другими словами, в треугольнике, если a 2 + b 2 > c 2 , треугольник является остроугольным.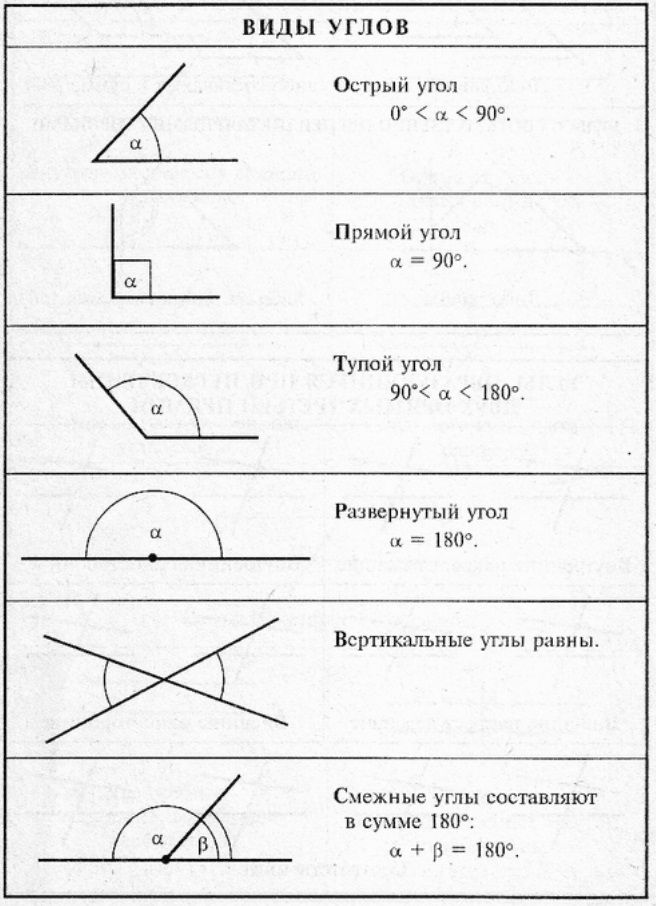
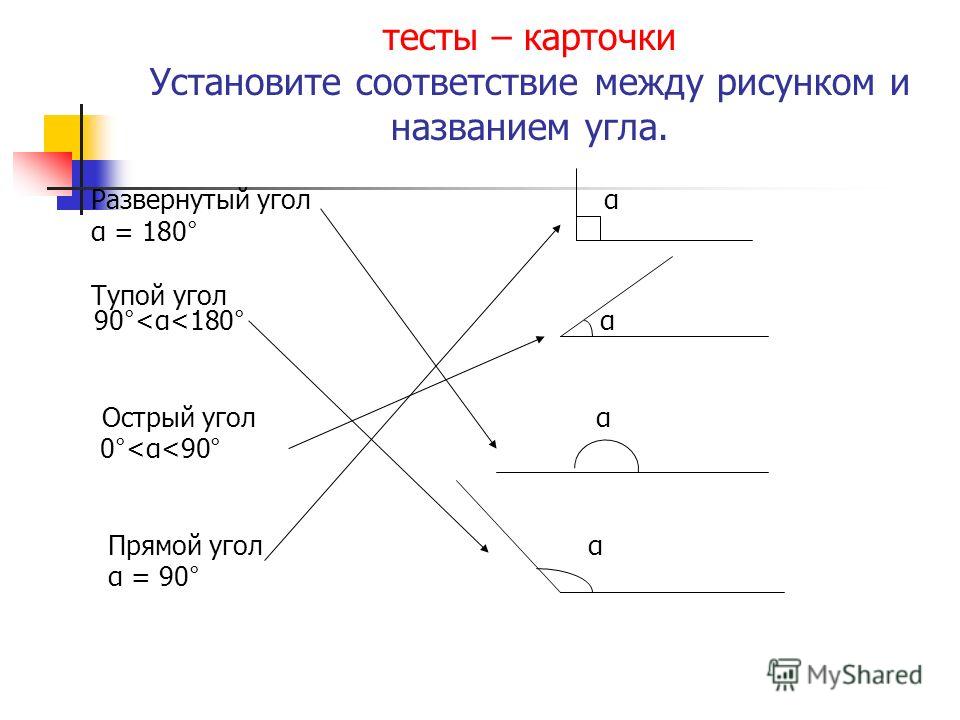 Его можно измерить с помощью транспортира. Например, 35°, 60°, 72° и т. д. — все это острые углы.
Его можно измерить с помощью транспортира. Например, 35°, 60°, 72° и т. д. — все это острые углы.
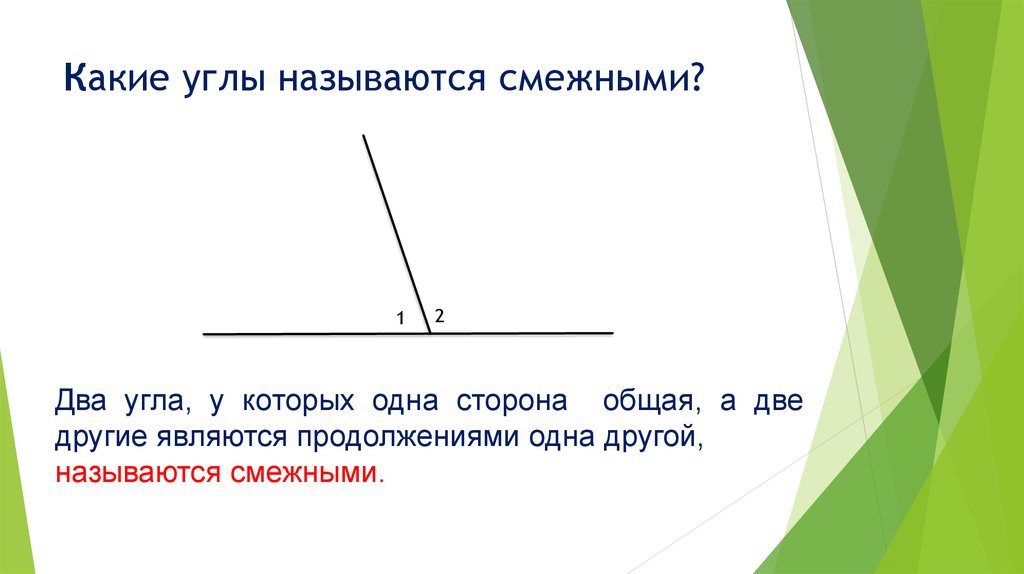 Пара открытых ножниц выглядит как острый угол. Стрелки часов образуют острый угол в положении 11 часов.
Пара открытых ножниц выглядит как острый угол. Стрелки часов образуют острый угол в положении 11 часов. Сравните тупой угол.
Сравните тупой угол. Форма «V» является примером острого угла .
Форма «V» является примером острого угла .  Все эти углы прямые (каждый равен 90°). Если вы возьмете один из этих углов и переместите одну линию ближе к другой, сузив пространство между ними, угол будет меньше 90° и будет острым углом. Угол больше 90° называется тупой угол. Если продолжать увеличивать угол, в конечном итоге он составит 180° и будет выглядеть точно как прямая линия.
Все эти углы прямые (каждый равен 90°). Если вы возьмете один из этих углов и переместите одну линию ближе к другой, сузив пространство между ними, угол будет меньше 90° и будет острым углом. Угол больше 90° называется тупой угол. Если продолжать увеличивать угол, в конечном итоге он составит 180° и будет выглядеть точно как прямая линия.

 |DAILY BEAST
|DAILY BEAST
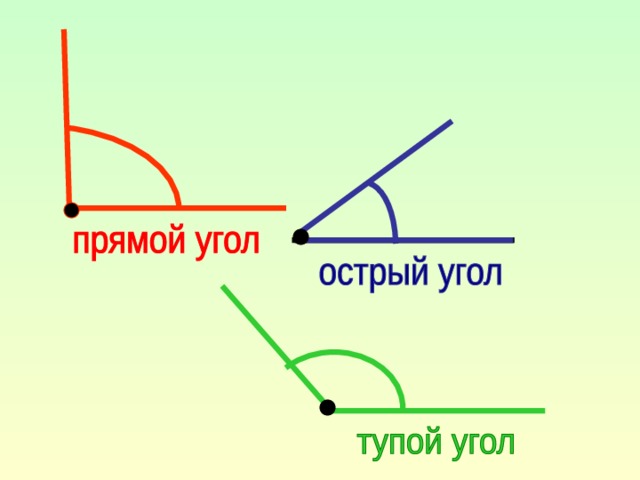
 То есть докажите, что у любого n-угольника с более чем тремя сторонами все углы не могут быть острыми.
То есть докажите, что у любого n-угольника с более чем тремя сторонами все углы не могут быть острыми.
 В первом случае $BCA$ тоже острый. Следовательно, угол должен быть острым, если он не является наибольшим углом.
В первом случае $BCA$ тоже острый. Следовательно, угол должен быть острым, если он не является наибольшим углом.
