Какое предложение не является высказыванием никакая причина: Какое предложение не является высказыванием? а) Никакая причина не извиняет невежливость б) Обязательно стань отличником

Тест по информатике Математические основы информатики 8 класс

Тест по информатике Математические основы информатики предназначен для учащихся 8 класса. Тест содержит 20 вопросов. В конце теста имеются ответы.

1. Совокупность знаков, при помощи которых записываются числа, называется:

а) системой счисления
б) цифрами системы счисления
в) алфавитом системы счисления
г) основанием системы счисления

2. Чему равен результат сложения двух чисел, записанных римскими цифрами: МСМ + LXVIII?

а) 1168
б) 1968
в) 2168
г) 1153

3. Число 301011 может существовать в системах счисления с основаниями:

а) 2 и 10
б) 4 и З
в) 4 и 8
г) 2 и 4

4. Двоичное число 100110 в десятичной системе счисления записывается как:

а) 36
б) 38
в) 37
г) 46

5. В классе 110010₂% девочек и 1010₂ мальчиков. Сколько учеников в классе?

а) 10
б) 20
в) 30
г) 40

6. Сколько цифр 1 в двоичном представлении десятичного числа 15?

а) 1
б) 2
в) 3
г) 4

7. Чему равен результат сложения чисел 110₂ и 12₈?

а) 6₁₀
б) 10₁₀
в) 10000₂
г) 17₈

8. Ячейка памяти компьютера состоит из однородных элементов, называемых:

а) кодами
б) разрядами
в) цифрами
г) коэффициентами

9. Количество разрядов, занимаемых двухбайтовым числом, равно:

а) 8
б) 16
в) 32
г) 64

10. В знаковый разряд ячейки для отрицательных чисел заносится:

а) +
б) —
в) 0
г) 1

11. Вещественные числа представляются в компьютере в:

а) естественной форме
б) развёрнутой форме
в) нормальной форме с нормализованной мантиссой
г) виде обыкновенной дроби

12.

Какое предложение не является высказыванием?

а) Никакая причина не извиняет невежливость
б) Обязательно стань отличником
в) Рукописи не горят
г) 1011₂ = 1 х 2³ + 0 х 2² + 1 х 2¹ + 1 х 2⁰

13. Какое высказывание является ложным?

а) Знаком v обозначается логическая операция ИЛИ
б) Логическую операцию ИЛИ иначе называют логическим сложением
в) Дизъюнкцию иначе называют логическим сложением
г) Знаком v обозначается логическая операция конъюнкция

14. Для какого из указанных значений числа X истинно высказывание
((X ?

а) 1
б) 2
в) 3
г) 4

15. Для какого символьного выражения верно высказывание:

«НЕ (Первая буква согласная) И НЕ (Вторая буква гласная)»?

a) abcde
б) bcade
в) babas
г) cabab

16. Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент:
сканер — 200
принтер — 250
монитор — 450
Сколько сайтов будет найдено по запросу принтер | сканер | монитор, если по запросу принтер | сканер было найдено 450 сайтов, по запросу принтер & монитор — 40, а по запросу сканер & монитор — 50?

а) 900
6) 540
в) 460
г) 810

17. Какому логическому выражению соответствует следующая таблица истинности?

A B F
0 0 1
0 1 1
1 0 1
1 1 0

18. Когда сломался компьютер, его хозяин сказал: «Оперативная память не могла выйти из строя». Сын хозяина компьютера предположил, что сгорел процессор, а жёсткий диск исправен. Пришедший специалист по обслуживанию сказал, что, скорее всего, с процессором всё в порядке, а оперативная память неисправна. В результате оказалось, что двое из них сказали всё верно, а третий — всё неверно. Что же сломалось?

а) оперативная память
б) процессор
в) винчестер
г) процессор и оперативная память

19. На перекрёстке произошло дорожно-транспортное происшествие, в котором участвовали автобус (А), грузовик (Г), легковой автомобиль (Л) и маршрутное такси (М). Свидетели происшествия дали следующие показания. Первый свидетель считал, что первым на перекрёсток выехал автобус, а маршрутное такси было вторым. Другой свидетель полагал, что последним на перекрёсток выехал легковой автомобиль, а вторым был грузовик. Третий свидетель уверял, что автобус выехал на перекрёсток вторым, а следом за ним — легковой автомобиль. В результате оказалось, что каждый из свидетелей был прав только в одном из своих утверждений. В каком порядке выехали машины на перекрёсток? В вариантах ответов перечислены подряд без пробелов первые буквы названий транспортных средств в порядке их выезда на перекрёсток.

а) АМЛГ
б) АГЛМ
в) ГЛМА
г) МЛГА

20. Какое логическое выражение соответствует следующей схеме?

Ответы на тест по информатике Математические основы информатики
1-а, 2-б, 3-в, 4-б, 5-б, 6-г, 7-в, 8-б, 9-б, 10-г, 11-в, 12-б, 13-г, 14-а, 15-а, 16-г, 17-в, 18-б, 19-б, 20-г

PDF-версия
Тест Математические основы информатики(102 Кб, pdf)

Математические основы информатики. Тестовые задания для самоконтроля.

---

Информатика. 8 класса. Босова Л.Л. Оглавление

---

1. Совокупность знаков, с помощью которых записываются числа, называется:

• а) системой счисления
• б) цифрами системы счисления
• в) алфавитом системы счисления
• г) основанием системы счисления

2. Чему равен результат сложения двух чисел, записанных римскими цифрами: МСМ + LXVIII?

• а) 1168
• б) 1968
• в) 2168
• г) 1153

3. Число 301011 может существовать в системах счисления с основаниями:

• а) 2 и 10
• б) 4 и 3
• в) 4 и 8
• г) 2 и 4 4

4. Двоичное число 100110 в десятичной системе счисления записывается как:

• а) 36
• б) 38
• в) 37
• г) 46

5. В классе 1100102% девочек и 10102 мальчиков. Сколько учеников в классе?

• а) 10
• б) 20
• в) 30
• г) 40

6. Сколько цифр 1 в двоичном представлении десятичного числа 15?

• а) 1
• б) 2
• в) 3
• г) 4

7. Чему равен результат сложения чисел 1102 и 128?

• а) 6₁₀
• б) 10₁₀
• в) 10000₂
• г) 17₈

8. Ячейка памяти компьютера состоит из однородных элементов, называемых:

• а) кодами
• б) разрядами
• в) цифрами
• г) коэффициентами

9. Количество разрядов, занимаемых двухбайтовым числом, равно:

• а) 8
• б) 16
• в) 32
• г) 64

10. В знаковый разряд ячейки для отрицательных чисел заносится:

• а) +
• б) —
• в) 0
• г) 1

11. Вещественные числа представляются в компьютере в:

• а) естественной форме
• б) развёрнутой форме
• в) экспоненциальной форме с нормализованной мантиссой
• г) виде обыкновенной дроби

12. Какое предложение не является высказыванием?

• а) Никакая причина не извиняет невежливость.
• б) Обязательно стань отличником.
• в) Рукописи не горят.
• г) 1011₂ = 1 • 2³ + 0 • 2² + 1 • 2¹ + 1 • 2⁰

13. Какое высказывание является ложным?

• а) Знаком v обозначается логическая операция ИЛИ.
• б) Логическую операцию ИЛИ также называют логическим сложением.
• в) Дизъюнкцию также называют логическим сложением.
• г) Знаком v обозначается логическая операция конъюнкция.

14. Для какого из указанных значений числа X истинно высказывание
((X < 5) ? (X < 3)) ? ((X < 2) ? (X < 1)) ?

• а) 1
• б) 2
• в) 3
• г) 4

15. Для какого символьного выражения верно высказывание:
«НЕ (Первая буква согласная) И НЕ (Вторая буква гласная)»?

• а) abcde
• б) bcade
• в) babas
• г) cabab

16. Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент:

Сколько сайтов будет найдено по запросу принтер | сканер | монитор, если по запросу принтер | сканер было найдено 450 сайтов, по запросу принтер & монитор — 40, а по запросу сканер & монитор — 50?

• а) 900
• б) 540
• в) 460
• г) 810

17. Какому логическому выражению соответствует следующая таблица истинности?

18. Когда сломался компьютер, его хозяин сказал: «Оперативная память не могла выйти из строя». Сын хозяина компьютера предположил, что вышел из строя процессор, а жёсткий диск исправен. Пришедший специалист по обслуживанию сказал, что, скорее всего, с процессором всё в порядке, а оперативная память неисправна. В результате оказалось, что двое из них сказали всё верно, а третий — всё неверно. Что же сломалось?

• а) оперативная память
• б) процессор
• в) жёсткий диск
• г) процессор и оперативная память

19. На перекрёстке произошло дорожно-транспортное происшествие, в котором участвовали автобус (А), грузовик (Г), легковой автомобиль (Л) и маршрутное такси (М). Свидетели происшествия дали следующие показания. Первый свидетель считал, что первым на перекрёсток выехал автобус, а маршрутное такси было вторым. Другой свидетель полагал, что последним на перекрёсток выехал легковой автомобиль, а вторым был грузовик. Третий свидетель уверял, что автобус выехал на перекрёсток вторым, а следом за ним — легковой автомобиль. В результате оказалось, что каждый из свидетелей был прав только в одном из своих утверждений. В каком порядке выехали машины на перекрёсток? В вариантах ответов перечислены подряд без пробелов первые буквы названий транспортных средств в порядке их выезда на перекрёсток:

• а) АМЛГ
• б) АГЛМ
• в) ГЛМА
• г) МЛГА

20. Какое логическое выражение соответствует следующей схеме?

---

Математические основы информатики. Ответы тестовые задания для самоконтроля.

---

Оглавление

§ 1.3. Элементы алгебры логики

Тестовые задания для самоконтроля

§ 2.1. Алгоритмы и исполнители

---

Что такое заявления? Определение и примеры

Давайте рассмотрим несколько примеров утверждений и не-утверждений, чтобы определить, какие предложения образуют утверждения.

© Патрик Жирар, Университет Окленда

Говоря об утверждениях, мы начнем с нескольких примеров утверждений и не-утверждений.

Выписки	Неутверждения
Поезда всегда опаздывают.	Добро пожаловать в Оклендский университет!
Прыжки в багажник — основная причина автомобильных аварий.	Как перестать прятаться?
Я люблю бананы, потому что в них нет костей.	Когда машина впереди достигает объекта, убедитесь, что вы можете сосчитать до четырех крокодилов , прежде чем вы достигнете того же объекта.

Итак, что делает что-то заявлением?

• Определение : Утверждения — это предложения, которые либо истинны, либо ложны.

Таким образом, утверждение является утверждением о том, что нечто имеет место или не имеет место. Утверждение истинно, если то, что оно утверждает, имеет место, и ложно, если то, что оно утверждает, не имеет места.

Например, утверждение «Поезда всегда опаздывают» истинно только в том случае, если оно описывает случай, т. е. если на самом деле случай, что поезда всегда опаздывают. Это ложь в Окленде. Иногда поезда приходят вовремя, а иногда рано. Кто-то может нетерпеливо жаловаться, что поезда всегда опаздывают, чтобы выразить свое недовольство системой поездов, но, строго говоря, то, что они говорят, — ложь.

Это правда, что у бананов нет костей, и я люблю бананы, но я люблю бананы, потому что они вкусные и полезные, а не потому, что у них нет костей. Таким образом, я бы сказал что-то ложное, если бы сказал: «Мне нравятся бананы, потому что в них нет костей». Вот почему «мне нравятся бананы, потому что в них нет костей» — это утверждение. Это предложение, которое либо истинно, либо ложно, в данном случае ложно.

Однако говорить о том, что фраза «Добро пожаловать в Оклендский университет!» не имеет смысла! является либо истинным, либо ложным. Разве вы не были бы озадачены, если бы кто-то ответил «правда» в ответ на приветствие? Это не будет подходящим ответом. «Как мне перестать прятаться?» это вопрос; предложение не выражает ничего истинного или ложного.

Наконец, «Когда машина впереди достигает объекта, убедитесь, что вы можете сосчитать до четырех крокодилов , прежде чем доберетесь до того же объекта». это совет. Он советует вам убедиться, что вы можете сосчитать до четырех крокодилов (один крокодил, два крокодила,…, четыре крокодила), прежде чем вы достигнете того же объекта, что и машина впереди вас. Попробуй! Вы будете гораздо более безопасным водителем (это верное утверждение!).

Таким образом, предложения, которые могут быть истинными или ложными, являются высказываниями. Достаточно просто. Но все может быть сложнее. Посмотрим, как.

Что-то может быть утверждением, даже если мы не знаем, истинно оно или ложно. Все, что имеет значение в утверждениях, это то, что они могут быть истинными или ложными, а не то, что мы знаем, истинны они или ложны. Например:

• Иван Слотвский, знаменитый ирландский строитель Мадрида, в этот самый момент ест бифштексы с ветчиной и чатни.

Правда или ложь? Я не знаю. Но это то, что может быть правдой или ложью.

Вот еще один:

• Когда-нибудь в следующие 39 лет у меня будет жуткая соседка.

Пока все хорошо. Мне повезло, и у меня не было жуткого соседа по соседству. Но это утверждение верно, если однажды в следующие 39 лет у меня появится жуткий сосед. В противном случае утверждение ложно.

Но я не знаю, верно это утверждение или нет. Независимо от того, что имеет значение, так это то, что это предложение является истинным или ложным.

Другой пример:

• Vero входит в состав Promina

Я понятия не имею, что такое Веро или Промина. Но предложение выражает нечто, что либо истинно, либо ложно.

Одно и то же утверждение может быть истинным в одних случаях и ложным в других. То есть утверждения не всегда истинны или всегда ложны.

Вот пример:

• Я киви.

Это утверждение верно для Тима и неверно для Патрика. Или заявление

• Патрик счастлив в браке.

было ложным до того, как Патрик женился, оно верно сейчас (пока я это печатаю) и может стать ложным в будущем.

Одна из трудностей с утверждениями состоит в том, что иногда они могут выражать две разные вещи. Мы называем эти

неоднозначных утверждения . Вот пример:

• Джон приветствовал всех с улыбкой.

Какие два состояния дел может описывать это утверждение? Попробуйте ответить на этот вопрос для себя, прежде чем продолжить.

Ответ:

1. Джон улыбался, а затем поприветствовал всех. В данном случае это правда, что он всех встречал улыбкой – своей улыбкой.
2. Может быть, были улыбающиеся и не улыбающиеся люди, а Джон приветствовал только тех, кто улыбался.

Таким образом, предложение «Джон приветствовал всех с улыбкой» можно использовать для описания двух разных вещей. Вот что делает его двусмысленным.

Будьте осторожны с этим. Если вы используете двусмысленные утверждения, вы рискуете, что другие неправильно поймут то, что вы говорите. В некоторых случаях то, что другие думают, что вы говорите, может сильно отличаться от того, что вы пытались выразить. Например, Тим — ранняя пташка. Каждое утро он встает рано и всегда раньше жены. Теперь предположим, что он попытался выразить это, сказав:

• Я избиваю свою жену каждый день.

Это наверняка будет воспринято неправильно. Старайтесь не использовать двусмысленные предложения!

Во втором списке не утверждений у нас были вопросы и команды, и обычно это не утверждения.

• Если люди произошли от обезьян, почему у нас до сих пор есть обезьяны?

Этот вопрос не выражает ничего, что может быть истинным или ложным. Нет смысла отвечать «правда» или «ложь», когда вы это слышите. Это не заявление. Обратите внимание, что часть предложения является утверждением, а именно «люди произошли от обезьян». Это ложное утверждение. Люди не эволюционировали от обезьян. Люди, обезьяны и человекообразные обезьяны в целом имеют общего предка, которого больше нет. Несмотря на то, что часть вопроса содержит ложное утверждение, это не делает сам вопрос чем-то истинным или ложным.

Однако иногда, в особом контексте, один и тот же вопрос может использоваться для выражения утверждения. Можете ли вы представить себе контекст, в котором кто-то мог бы использовать этот вопрос, чтобы выразить что-то, что является правдой или ложью? Если это так, то, по-видимому, человек использовал бы вопрос, чтобы выразить, что утверждение о том, что люди произошли от обезьян, ложно, поскольку обезьяны все еще существуют. Мы называем вопросы, которые используются для выражения утверждений риторический вопрос . Когда вы видите риторический вопрос, вы всегда должны перефразировать его как утверждение. В нашем случае заявление будет примерно таким:

• Люди не произошли от обезьян, потому что у нас все еще есть обезьяны.

Таким образом, утверждения являются типами предложений, которые либо истинны, либо ложны. Предложения неоднозначны, если они могут использоваться для выражения нескольких утверждений. Когда у вас есть двусмысленное предложение, вам нужно решить, для выражения какого утверждения оно используется. Вопросы, команды и советы обычно не являются утверждениями, потому что они не выражают ничего истинного или ложного. Но иногда люди используют их риторически для выражения заявлений. Мы видели пример вопроса, который сам по себе не является утверждением, но может использоваться для выражения утверждения. Когда вы видите риторические вопросы, всегда перефразируйте их как утверждения.

© Патрик Жирар, Университет Окленда

Заявления 3A

Заявления 3A

ГЛАВА 3

ЛОГИКА

Логика несколько уникальна среди разделов математики. В логике мы не столько изучаем окружающий мир, сколько изучаем, как работает наш собственный разум; требуется хороший самоанализ. Действительно, можно утверждать, что вся математика начинается с логики, ибо без некоторого понимания правил рассуждений как мы можем заниматься логическими рассуждениями?

Заявления 3A

	Ожидает ли он, что поверят?

Утверждение — это сообщение, которое можно классифицировать как истинное или ложное. Предложение «Сегодня четверг» либо истинно, либо ложно и, следовательно, является утверждением; однако предложения «Как дела сегодня» и «Пожалуйста, передайте масло» не являются ни истинными, ни ложными и, следовательно, не являются утверждениями. Когда мы хотим передать информацию, мы обычно говорим утверждениями, но когда мы хотим узнать информацию или попросить кого-то сделать что-то, мы обычно переключаемся на другие способы речи.

Когда мы делаем утверждение, мы обычно намереваемся интерпретировать его как точное описание реальности, то есть мы хотим, чтобы слушатель принял это утверждение как истинное. Если кто-то говорит: «Меня зовут Джон», он полностью имеет в виду, что предложение «Меня зовут Джон» истинно. Неявное намерение правдивости понимается имплицитно, иначе было бы бесполезно вообще что-либо говорить. Конечно, бывают случаи, когда мы нарушаем норму, делая утверждения, которые, как мы ожидаем, будут восприняты как ложные, — например, когда мы шутим или иронизируем, — но в этих случаях наша цель, возможно, не столько в том, чтобы передать информацию, сколько в том, чтобы повлиять на слушателя. каким-то другим образом. На самом деле можно сказать, что неотъемлемая часть устной комедии заключается в нарушении правил дискурса путем высказывания заведомо невероятных утверждений.

пример 1

Предложения внизу слева являются утверждениями, а предложения справа — нет:

A.  Гавайи находятся в Атлантическом океане.		E. Привет, Долли.
Б.  2 + 3 = 5		Ф.  О боже мой!
C. Завтра будет дождь.		Г.  Где твоя мама?
D. На Марсе существует жизнь.		H. На углу поверните налево.

Заметьте, что утверждение не обязательно должно быть истинным — действительно, утверждение А несомненно ложно, тогда как В истинно. Кроме того, правдивость утверждения может быть не сразу очевидна. Утверждение C либо истинно, либо ложно, но что именно, мы узнаем только завтра. Утверждение D будет сбивать нас с толку еще дольше.

---

В логике принято использовать буквы p, q, r и т. д. для обозначения утверждений. Каждое утверждение имеет так называемое истинностное значение . Значение истинности истинного утверждения равно 90 190 истинного 90 191 (обозначается как T), а значение истинности ложного утверждения равно 90 190 ложного 90 191 (обозначается как F). Для любого утверждения p существует другое утверждение, связанное с p, обозначаемое ~p и называемое отрицанием p; это то утверждение, истинностное значение которого обязательно противоположно истинностному значению p. (Символ «~» в этом контексте читается как «не»; таким образом, «~р» читается как «не р».) Вот некоторые утверждения с их отрицаниями непосредственно под ними:

р : идет дождь		q : Ген мужского пола		г : 4 + 3 = 7
~p : дождя нет		~q : Женский ген		~r : 4 + 3 ≠ 7

В каждом случае истинностное значение утверждения должно быть противоположно истинностному значению его отрицания. Например, если q истинно, то Джин — мужчина, поэтому он не женщина, а утверждение ~q ложно; с другой стороны, если q ложно, то Джин не мужчина, поэтому она женщина, а ~ q истинно.

Таблица истинности для отрицания р ~р Т Ф Ф Т

Таблица слева представляет собой таблицу истинности для отрицания . В левой колонке таблицы перечислены возможные значения истинности общего высказывания p, а в правой колонке — соответствующие значения истинности его отрицания ~p.

Не всегда очевидно, как составить отрицание высказывания. Иногда противоречивых утверждений смешивают как отрицания друг друга. Два утверждения противоречат друг другу, если оба они не могут быть истинными. Например, утверждения «Анне 20 лет» и «Анне 22 года» противоречивы, так как только одно из них может быть верным; однако ни то, ни другое не является отрицанием другого. В самом деле, если Анне 21 год, то утверждения не противоположны по истинностному значению, поскольку оба они ложны. Часто самый простой способ опровергнуть утверждение — вставить слово «не» в стратегической позиции. Предложение «Энн нет 20 лет» является допустимым отрицанием предложения «Энн 20 лет».

Такие слова, как «некоторые», «все», «каждый», «каждый» и «нет», называются квантификаторами . Чтобы отрицать операторы с кванторами, нужно немного подумать. Сначала мы должны договориться о том, что подразумевается под словом «некоторые» — означает ли оно больше, чем ничего, больше одного, больше двух, по крайней мере пять или что? Чтобы устранить любую двусмысленность, в целях нашего логического обсуждения мы постановим, что «некоторые» означают «по крайней мере один».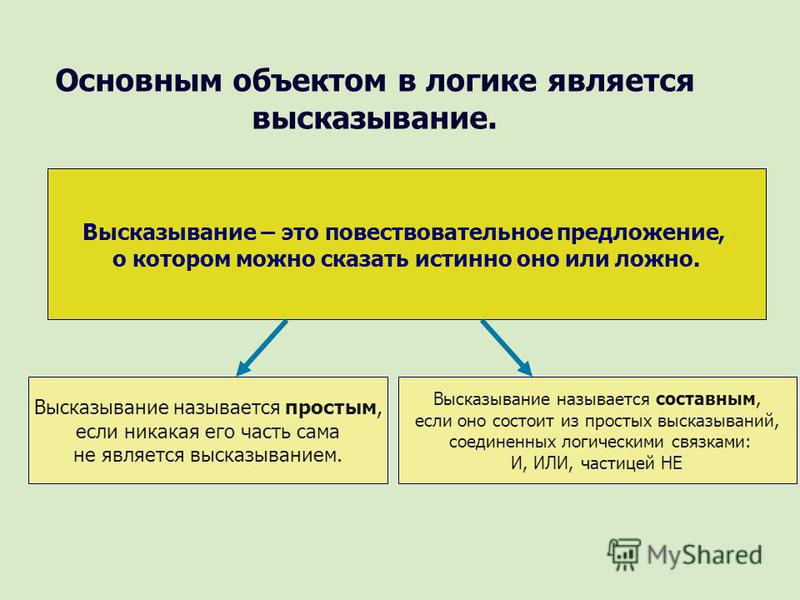 Это соглашение полезно, поскольку упрощает отрицание утверждений, содержащих квантификаторы.

пример 2

	Коричневый Огр

Отвергнем утверждение

p: некоторые огры коричневые.

Согласно нашему соглашению о «некоторых», утверждение означает, что по крайней мере один огр коричневый. Чтобы утверждение было ложным, никакой людоед не может быть коричневым. Таким образом, кандидатом на отрицание является

.

~p : людоед не коричневый .

Теперь, если ваш мозг устроен правильно, вы должны согласиться с тем, что если p истинно, то ~p ложно, а если p ложно, то ~p истинно; таким образом, предлагаемое нами отрицание является правильным. Распространенная ошибка состоит в том, что ошибочно принимают за отрицание p утверждение

.

«некоторые огры не коричневые».

Однако это утверждение и p были бы и истинными, если бы некоторые огры были коричневыми, а некоторые зелеными.

Далее мы отрицаем утверждение

q : все огры коричневые .

Еще одна распространенная ошибка состоит в том, что в качестве отрицания предполагается, что «людоеды не коричневые». Однако тогда мы имеем только противоречивые утверждения. Несмотря на то, что только одно из этих двух утверждений может быть истинным, возможно, что оба они могут быть ложными — как было бы в случае, если бы некоторые огры были коричневыми, а некоторые — зелеными. Чуть более глубокое созерцание приводит к правильному отрицанию «хоть один людоед не коричневый», или, опять же по нашему соглашению о «некоторых»,

~q: некоторые огры не коричневые.

Вы должны убедиться, что если q истинно, то ~q ложно, а если q ложно, то ~q истинно.

---

Ниже слева приведены утверждения, содержащие кванторы, а справа их отрицания:

ЗАЯВЛЕНИЕ		ОТРИЦАНИЕ
У меня нет бананов.		У меня есть бананы.
Курица не умеет плавать.		Некоторые куры умеют плавать.
Некоторые яблоки красные.		Яблоки не красные.
Беа пройдёт как минимум 4 курса.		Беа возьмет менее 4 блюд.
Иногда мне грустно.		Мне никогда не грустно.
Энди всегда готов к вечеринке.		Иногда Энди не готов к вечеринке.
У каждой рыбы есть жабры.		У некоторых рыб нет жабр.
Иногда Ева не носит шляпу.		Ева всегда носит шляпу.
Все максы булы.		Некоторые макси не булы.
Аллигаторов нельзя гладить.		Некоторых аллигаторов можно погладить.
Некоторые колибри очень громкие.		Колибри не шумит.
Каждая из моих кошек ловит мышей.		Некоторые из моих кошек не ловят мышей.

Здесь нет бананов

Как мы узнали на уроках английского, двойные отрицания отменяют друг друга. Отрицание «у меня есть бананы» — это «у меня нет бананов». Если вы говорите «у меня нет бананов», то вы отрицаете утверждение «у меня нет бананов», поэтому вывод должен заключаться в том, что у вас есть бананы. Соответствующее правило логики здесь выражается в формуле

~(~p) ≡ p  .

Таблица истинности для Двойное отрицание р ~р ~(~р) Т Ф Т Ф Т Ф

Символ «≡» означает «эквивалент», и формула утверждает, что «отрицание отрицания» утверждения эквивалентно исходному утверждению. Хотя эта формула в значительной степени соответствует здравому смыслу, мы можем официально проверить ее с помощью таблицы истинности. Таблица справа состоит из трех столбцов; мы начинаем с p, инвертируем его, чтобы получить ~p, а затем снова инвертируем, чтобы получить ~(~p). Поскольку столбцы под p и ~(~p) идентичны, утверждения p и ~(~p) всегда имеют одно и то же значение истинности и поэтому считаются «логически эквивалентными» утверждениями.

пример 3

Забавно начинать с утверждения, отрицать его, а затем снова отрицать, пытаясь получить утверждение, эквивалентное оригиналу, но в совершенно другой форме. Вот иллюстрации :

р : Я вегетарианец		q : Все дипломаты вежливы
~p : Я ем мясо		~q : Некоторые дипломаты невежливы
~(~p): я не ем мясо		~(~q) : Ни один дипломат не вежлив
r : Король мертв		s : Никто не виноват
~r : Король жив		~s : Кто-то виноват
~(~r): Короля нет в живых		~(~s) : Все безупречны.

Обратите внимание, что в каждом случае двойное отрицание означает то же самое, что и исходное.

---

УПРАЖНЕНИЯ 3A

1. Определите, можно ли считать предложение утверждением:
   1. Космические пришельцы похитили меня и отвезли на встречу с Элвисом.
   2. Не забудьте сегодня взять зонтик.
   3. Валовой национальный продукт США увеличился в прошлом году.
   4. Ты закончил обедать?
   5. Ей-богу, мисс Молли!
   6. Бразилия — страна в Африке.
   7. Дождь в Испании идет в основном на равнине.
   8. Мне нравятся детективы.
   9. Алоха!
   10. Это предложение ложно.
   
   
2. Какие пары утверждений противоречат друг другу?
   1. Все собаки ненавидят кошек.
      Моя собака любит кошек.
   2. Аарону больше 18 лет.
      Аарону больше 21 года.
   3. Салли продает ракушки.
      Салли продает страховку.
   4. Честность — лучшая политика.
      Замалчивание — лучшая политика.
   5. Мэри специализируется на биологии.
      Мэри ненавидит биологию.
   6. Сегодня понедельник.
      Сегодня вторник.
   7. Сегодня понедельник.
      Вчера не было воскресенья.
   8. Дик Чейни — президент.
      Джордж Буш — вице-президент.
   9. 2 + 3 = 4
      2 + 3 = 6
   10. Дэн Иноуэ представляет Гавайи в сенате США.
       Дэн Акака представляет Гавайи в сенате США.
   
   

Сформулируйте отрицание утверждения: Джордж Вашингтон не был первым президентом. Температура не менее 90 градусов. Все мои друзья верны. Ни один человек не может жить одним хлебом. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт