Алгебра
24 минут назад
Помогите пожалуйста решить Sin (x+3pi/2)=1Алгебра
1 час назад
Помогите дз алгебраАлгебра
2 часа назад
Алгебра 7 классАлгебра
3 часа назад
Найдите все точки, которые принадлежат графику функции y=x²Алгебра
5 часов назад
a) F(x) = -x ³45, 8) F (Ax) = sinx+3₁ Fex)= x F(x) = — cosx + 3x 75X+2Алгебра
5 часов назад
Срочно! Решить уравнение х^2-2х-1=0Алгебра
6 часов назад
Допоможіть будь ласка благаю .
2 Визначити: a) значення функції, якщо значення аргументу дорівнює 2,5; б) значення аргументу, якщо значення функції дорівнює 169; в) чи проходить графік даної функції через точку A(13; 125).Алгебра
7 часов назад
Помогите с алгеброй пожалуйстаАлгебра
7 часов назад
!!ДАМ 80 БАЛЛОВ!! Необязательно всё, хотя-бы с 1 до 5-6 задания пожалуйстаАлгебра
7 часов назад
Між числами 243 і 1 вставте чотири такі числа, щоб вони разом із заними числами утворювали геометричну прогресіюАлгебра
8 часов назад
Математика Помогите построить косинусоидуАлгебра
8 часов назад
Доведіть нерівністьx²+4y²+9≥2x²y+3x²+6yАлгебра
8 часов назад
Алгебра, 10 класс.
Тангенс, котангенс, синус и косинус. ПОМОГИТЕ, СОВСЕМ НИЧЕГО НЕ ПОНИМАЮВсе предметы
English
United States
Polski
Polska
Bahasa Indonesia
Indonesia
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Português
Brasil
Русский
Россия
How much to ban the user?
1 hour 1 day
Координатная прямая — что это, определение и ответ
Координатная прямая – это прямая, имеющая направление, начало отсчета и заданный масштаб.
Начало координат соответствует координате \(= 0\), а положительное направление указано стрелочкой.
Единичный отрезок – это расстояние между соседними делениями на координатной прямой. Единичный отрезок показывает масштаб координатной прямой.
ТОЧКА НА КООРДИНАТНОЙ ПРЯМОЙ:
Любая точка, соответствующая числу на координатной прямой, имеет координату, равную этому числу.
Например:
Точка А соответствует числу 2. В таком случае говорят, что существует точка А с координатой 2 или записывают её как А(2). Если точка не обозначается буквой, можно сказать, что существует точка 2.
На координатной прямой можно отмечать не только целые числа, но и дробные.
Например:
Теперь координата точки В\(\left( — \frac{3}{4} \right)\) дробная и отрицательная:
С помощью координатной прямой удобно сравнивать числа. Любое число справа будет больше, чем число слева.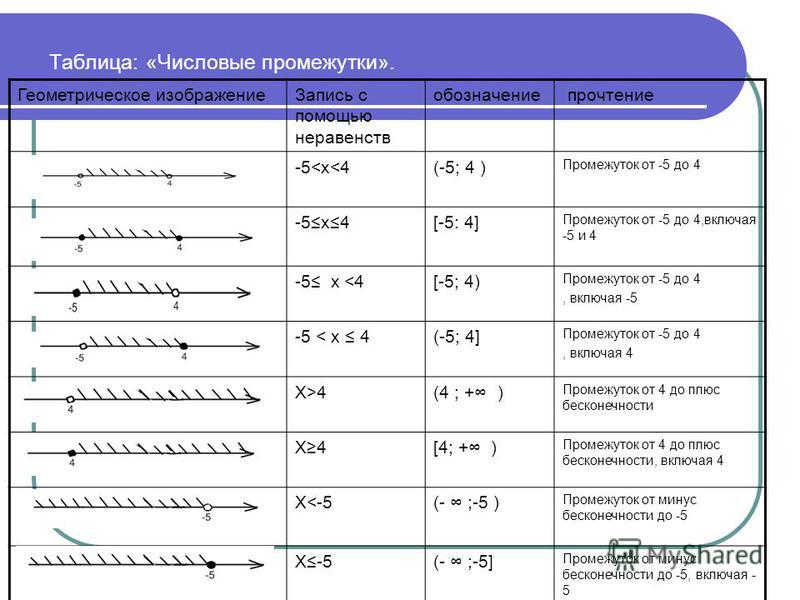
ПРОМЕЖУТКИ НА КООРДИНАТНОЙ ПРЯМОЙ:
На координатной прямой можно отмечать сразу совокупность точек, входящие в тот или иной промежуток.
Числовой промежуток – это множества чисел, обозначенные на координатной прямой с помощью луча, интервала или отрезка.
Луч – это открытый числовой промежуток с помощью которого обозначается множество чисел больше или меньше какого-то числа.
Например:
Отметим на координатной прямой все значения \(x > 2\):
Само число 2 не может быть больше себя же, поэтому точка, которой отмечается эта координата остается пустой или выколотой. Такой точке соответствует круглая скобка.
Таким образом любое число на закрашенной области соответствует заданному неравенству, а обозначить его можно как
\(x \in (2; + \infty)\)
Закрытый луч – это луч на координатной прямой, точка начала которого входит в заданный промежуток
Например:
Отметим на координатной прямой все значения \(x \leq 2\):
Число 2 равно самому себе, поэтому точка 2 входит в заданный промежуток.
Такая точка закрашивается и называется вколотой. Такой точке соответствует квадратная скобка. Промежуток обозначается как
\(x \in (–\infty;\left. \ 2 \right\rbrack\).
Отрезок – числовой промежуток, который имеют ограничения с двух сторон, при этом точки, ограничивающие отрезок, в него входят.
Например:
Отметим на координатной прямой все значения \(- 3 \leq x \leq 1\):
Точки -3 и 1 входят в этот промежуток и являются вколотыми. Все числа, обозначенные на координатной прямой, удовлетворяют неравенству. Такой промежуток обозначается как
\(x \in \left\lbrack — 3;1 \right\rbrack\)
Интервал – числовой промежуток, который имеют ограничения с двух сторон. Разница с отрезком заключается в том, что граничные точки НЕ входят в интервал. В интервал входит все, что между этими точками.
Например:
Отметим на координатной прямой все значения \(- 3 < x < 1\):
Поменялись только точки, но описывается уже совсем другая математическая ситуация.
\(x \in ( — 3;1)\)
Полуинтервал – числовой промежуток, одна граница которого в него входит, а вторая нет. При чем не важно с какой стороны находится пустая точка.
Например:
Отметим на координатной прямой все значения \(0 < x \leq 2\):
Точки такого полуинтервала будут вколоты и выколоты в соответствии с условием: 0 не входит в полуинтервал – точка выколота, 2 – входит в интервал – точка вколота. Тогда полуинтервал записывается так:
\(x \in (0;\left. \ 2 \right\rbrack\)
3-8Неравенство 3 3 (3,5] (3, 3 7.
Отправить вопрос Перейти к ответуВопрос
Пошаговый ответ
Для интервалов значений введите ответ, используя обозначение интервала. Вот несколько примеров того, как запись интервала связана с неравенствами: Неравенство 3
< х < 5 Interva…Для интервалов значений введите ответ, используя обозначение интервала. Вот несколько примеров того, как запись интервала связана с неравенствами: Неравенство 3 < х < 5 Обозначение интервала (3,5) 3 < с < 5 х > 3 (3,5] (3, 3 < х < 5 0r 7 < х < 9(3,5) У (7,9) С неравенствами мы используем «меньше» (<) или «больше» (>), чтобы исключить конечную точку интервала. В интервальных обозначениях мы используем круглые скобки: ( , ) С неравенствами мы используем «меньше или равно» (<) или «больше или равно» (2), чтобы включить конечную точку интервала. В интервальных обозначениях мы используем квадратные скобки: [J. Чтобы объединить два интервала, используйте U (буква U в верхнем регистре) для объединения: U Используйте 00 (две буквы 0 в нижнем регистре) для бесконечности: 0_ ПОПРОБУЙТЕ СЕЙЧАС: введите интервал, эквивалентный 2 < 1 < 5 O € >
Отправить вопрос Перейти к ответуВидеоответ:
Решено проверенным экспертом
Вопрос о наилучшем совпадении:
Для интервалов значений введите ответ, используя обозначение интервалов. Вот несколько примеров того, как запись интервала связана с неравенствами: Неравенство 3 < х < 5 Обозначение интервала (3,5) 3 < с < 5 х > 3 (3,5] (3, 3 < x < 5 0r 7 < x < 9 (3,5) U (7,9) С неравенствами мы используем «меньше» (<) или «больше» (>), чтобы исключить конечную точку интервала. В интервальных обозначениях мы используем круглые скобки: ( , ) С неравенствами мы используем «меньше или равно» (<) или «больше или равно» (2), чтобы включить конечную точку интервала. В интервальных обозначениях мы используем квадратные скобки: [J. Чтобы объединить два интервала, используйте U (буква U в верхнем регистре) для объединения: U Используйте 00 (две буквы 0 в нижнем регистре) для бесконечности: 0_ ПОПРОБУЙТЕ СЕЙЧАС: введите интервал, эквивалентный 2 < 1 < 5 O € >
7.
Отправить вопрос Перейти к ответуРекомендуемые видео
Стенограмма
Таким образом, в этом решении в основном нам нужно, а затем в проблеме эквивалентно этому конкретному влиянию, и мы дали некоторую информацию, связанную с различным неравенством, и его обозначения проблем, как на заднем плане, нужно изучить В нашем обозначении дано, что X меньше или равно пяти, вперед X равно семи. Итак, согласно обозначению, если избыточный свет живет, будет три и 5. Итак, на этот раз горечь от 3 до 5. В три он открыт, а в пять закрыт, потому что X может быть прямо здесь. Это можно записать как X тоже относится к открытому в беде. И закрывающая таблица пять и или может использоваться как объединение. А если X больше семи, то если мы посмотрим на этот интервал неравенства доступа позже, чем на три. Так что это может вернуть нас просто открыть и удвоить три до бесконечности. Так это можно горечь просто открыть и путешествовать семь к бесконечности. Это требуется в беде. Нам нужно войти сюда.