Высота прямоугольного треугольника Калькулятор | Вычислить Высота прямоугольного треугольника
✖Высота прямоугольного треугольника равна длине перпендикулярной стороны прямоугольного треугольника, примыкающей к основанию.ⓘ Высота прямоугольного треугольника [h] | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Основание прямоугольного треугольника — это длина стороны основания прямоугольного треугольника, примыкающей к перпендикулярной стороне. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Высота прямоугольного треугольника — это длина вертикального расстояния от гипотенузы до вершины, образованной соединением основания и высоты прямоугольного треугольника. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Высота прямоугольного треугольника Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.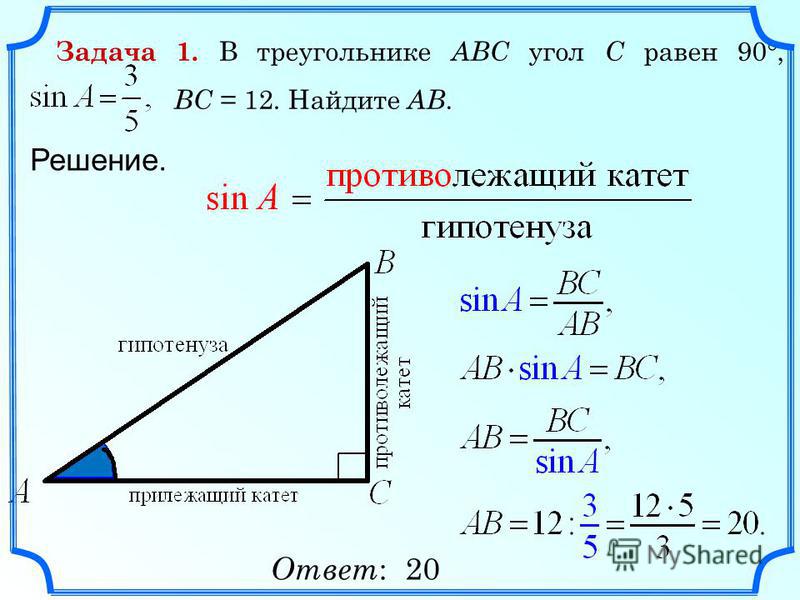 2)
2)
Что такое прямоугольный треугольник?
Прямоугольный треугольник или прямоугольный треугольник, или, более формально, ортогональный треугольник — это треугольник, в котором один угол является прямым. Соотношение между сторонами и углами прямоугольного треугольника является основой тригонометрии. Сторона, противолежащая прямому углу, называется гипотенузой.
Share
Copied!
Гипотенуза в прямоугольном треугольнике — как её найти, зная катеты?
Гипотенуза — сторона в прямоугольном треугольнике, находящаяся напротив прямого угла. Две других стороны — катеты. В прямоугольном треугольнике гипотенуза всегда длиннее катетов.
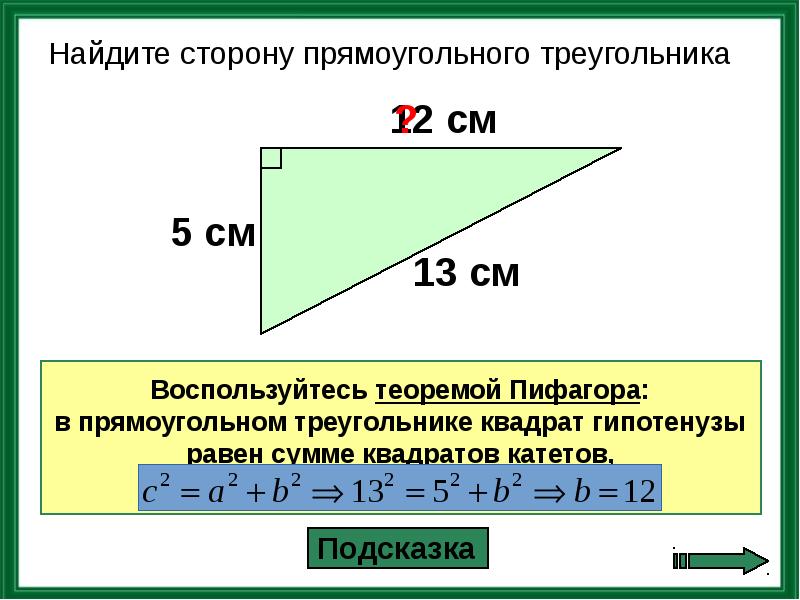
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов (формула: c² = a² + b², где c — гипотенуза, a и b — катеты). Очень часто для вычисления гипотенузы используется именно эта теорема.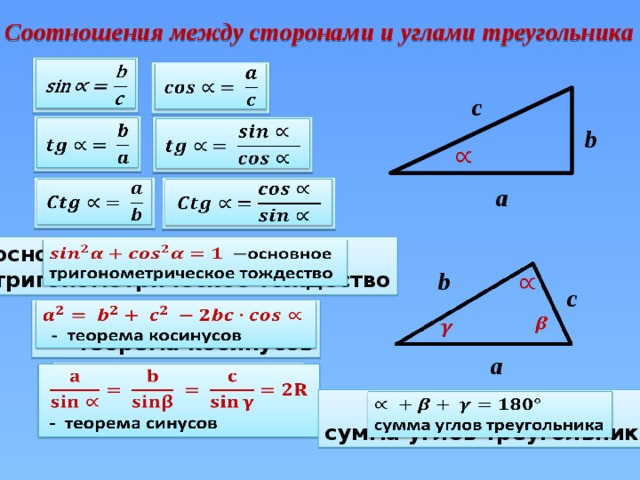
Как найти гипотенузу, зная катеты?
Если известны оба катета (две другие стороны прямоугольного треугольника), можно применить Теорему Пифагора.
Теорема Пифагора — в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Формула: c² = a² + b² (при c — гипотенуза, a и b — катеты).
Например:
Один катет равен 3 см, другой — 4 см. Таким образом, а = 3, b = 4, подставляем в формулу:
c² = 3² + 4² <=> c² = 9 + 16 <=> c² = 25 <=> c = √25 <=> c = 5.
Ответ: длина гипотенузы 5 см (или x = 5).
Как найти
катет в прямоугольном треугольникеПо той же формуле можно найти и длину одного неизвестного катета, нужно только немного её изменить:
Начальная формула: c² = a² + b² (при c — гипотенуза, a и b — катеты), и найти катет можно по этой:
(c — гипотенуза, a и b — катеты)Например: Один катет равен 3 см, а гипотенуза — 5 см. Нужно узнать длину второго катета.
Применяем формулу b = √c² — a² ⇔
b = √5² — 3² ⇔ b = √25 — 9 ⇔ b = √16 ⇔ b = 4.
Как найти гипотенузу, зная катет и угол?
Если есть противолежащий катет — теорема синусов
Если в условии задачи дан угол и противолежащий катет, то ищем гипотенузу по Теореме синусов: стороны треугольника пропорциональны синусам противолежащих углов.
Примечание: гипотенуза есть только в прямоугольном треугольнике, однако теорему синусов можно применять к любым треугольникам (не только к прямоугольным).
Формула:
Например:
Известна одна сторона треугольника 𝐴𝐶 = √2 и ∠β = 45º.
∠α = 90º (т.к. мы ищем гипотенузу, то второй угол в треугольнике прямой, значит имеет 90º).
Так как во всех треугольниках сумма всех углов равна 180º, то можем узнать оставшийся ∠c.
Значит: ∠c = 180º — (90º + 45º) = 45º.
Подставляем в формулу (a/sinα = b/sinβ = c/sinγ) известные:
BC/sin90º = AC/sin45º = AB/sin45º
В таблице вы найдёте значения для синуса:
| sin 45º | √2/2 |
| sin 60º | √3/2 |
| sin 90º | 1 |
В условии задачи нам дано: 𝐴𝐶 = √2, значит:
BC/sin90º = √2/sin45º = AB/sin45º
Подставляем значения синуса из таблицы:
BC/1 = √2/(√2/2) = AB/(√2/2) (забудем на время про катет AB) ⇔
BC = √2/(√2/2) ⇔ BC = 2 (гипотенуза равна 2)
Если хотите вычислить катет, уже зная другой катет и гипотенузу:
AB/(√2/2) = 2 ⇔ AB = √2
Ответ: гипотенуза BC равна 2 см, а катет AB √2 см.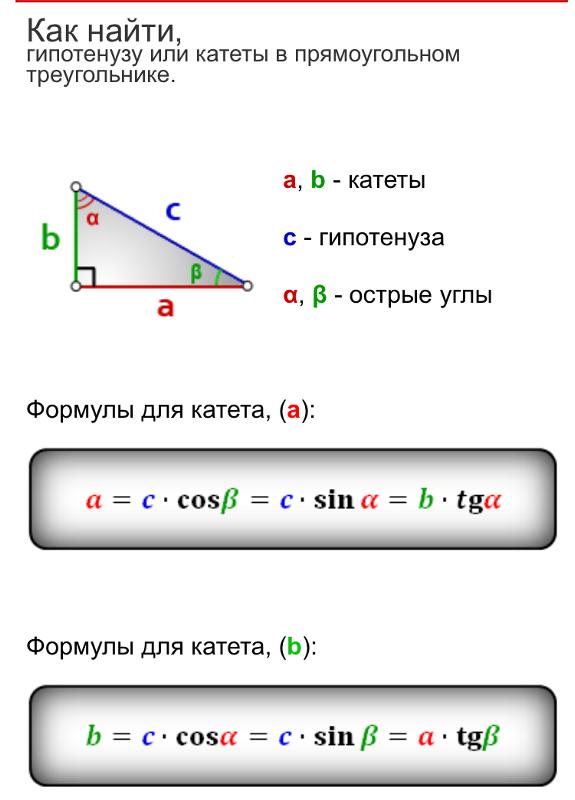
Если есть прилежащий катет — по косинусу
Если в условии задачи дан угол и прилежащий катет, то ищем гипотенузу по косинусу (в прямоугольном треугольнике, косинус острого угла (cos) — это отношение прилежащего катета (b) к гипотенузе(c), таким образом cos a = b/c, из этого получается c = b / cos α).
Т.е. гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α.
Например:
Известна одна сторона треугольника AB = 1 и ∠β = 45º. Нужно вычислить гипотенузу (BC).
Помним, что гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α. Т.е.: BC = AB / cosβ ⇔ BC = 1/ cos 45º.
Смотрим в таблице, чему равен cos 45º.
BC = 1/ (√2/2) = √2
Ответ: гипотенуза BC равна √2 см.
Как найти гипотенузу равнобедренного треугольника
В равнобедренном треугольнике есть гипотенуза только в том случае, если он одновременно и прямоугольный, т.к. гипотенуза есть только в прямоугольных треугольниках (и его основание будет гипотенузой).
Чтобы найти такую гипотенузу, нужно любой из двух одинаковых катетов возвести в квадрат, умножить на 2 и посчитать квадратный корень: b = √2a² (где b — гипотенуза, а — катет). Это следствие из теоремы Пифагора.
Например:
Катет равнобедренного треугольника равен 7см. Нужно найти гипотенузу.
Формула b = √2a². Подставляем:
b = √2*7² = √2*49 ≈ √98 ≈ 9.899
Если забудете эту формулу, можно использовать уже знакомую формулу Пифагора для гипотенузы (c² = a² + b²):
c² = a² + b²
c² = 7² + 7²
c² = 49 + 49
c² = 98
c = √98
c ≈ 9.899
Ответ: гипотенуза равна 9.899.
Узнайте больше про Теорему Пифагора, Теорему косинусов, а также, что такое Тангенс и Аксиома.
Калькулятор треугольника
Укажите, что вы знаете о треугольнике:
Треугольник:
Калькулятор решает треугольник, заданный тремя его свойствами. Каждый треугольник имеет шесть основных характеристик: три стороны a, b, c и три угла (α, β, γ).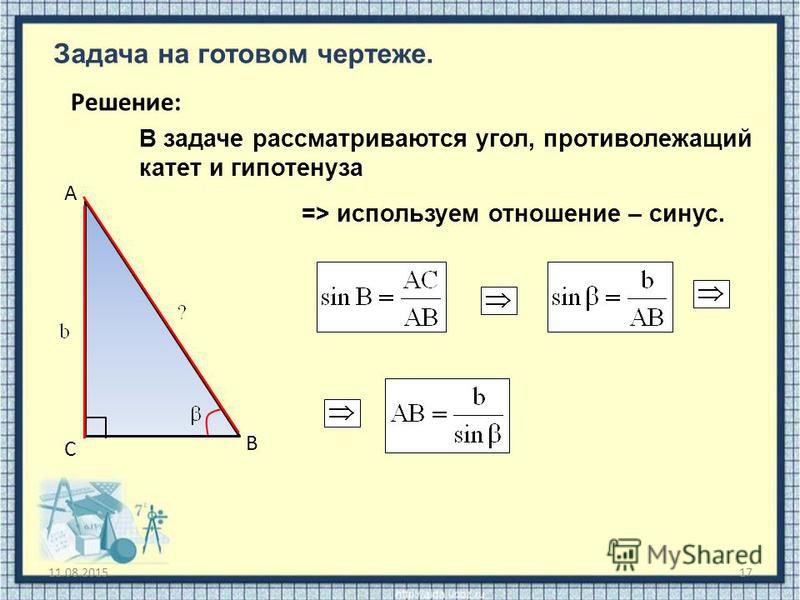 Классическая задача тригонометрии состоит в том, чтобы указать три из этих шести характеристик и найти остальные три. Конечно, наш калькулятор решает треугольники из комбинаций основных и производных свойств, таких как площадь, периметр, высота, медиана и т. д.
Обычно по длине трех сторон (SSS), сторона-угол-сторона или угол-сторона-угол.
Классическая задача тригонометрии состоит в том, чтобы указать три из этих шести характеристик и найти остальные три. Конечно, наш калькулятор решает треугольники из комбинаций основных и производных свойств, таких как площадь, периметр, высота, медиана и т. д.
Обычно по длине трех сторон (SSS), сторона-угол-сторона или угол-сторона-угол.
Как этот калькулятор решает треугольник?
Расчет общего треугольника состоит из двух фаз:
- Экспертная фаза различна для разных задач. Калькулятор пытается по введенным данным вычислить размеры трех сторон треугольника. Он постепенно применяет базу знаний к введенным данным, которая представлена, в частности, отношениями между отдельными параметрами треугольника.
Они последовательно применяются и комбинируются, и вычисляются параметры треугольника. Калькулятор повторяется до тех пор, пока треугольник не вычислит все три стороны.
Например, соответствующая высота вычисляется из заданной площади треугольника и соответствующей стороны. По известным высоте и углу можно рассчитать прилегающую сторону и т. д.
Калькулятор использует знания, например, формулы и отношения, такие как теорема Пифагора, теорема синусов, теорема косинуса и формула Герона.
По известным высоте и углу можно рассчитать прилегающую сторону и т. д.
Калькулятор использует знания, например, формулы и отношения, такие как теорема Пифагора, теорема синусов, теорема косинуса и формула Герона. - Второй этап — вычисление свойств треугольника по имеющимся длинам трех его сторон.
Примеры ввода треугольника:
a=3 b=4 c=5 … расчет треугольника по трем сторонам a,b,c.
B=45 c=10 a=9 … треугольник вычисляется по двум сторонам a,c и углу B.
A=25 C=80 b=22
A=35 C=26 a=10
a=3 C=90 c=5 … как ввести прямоугольный треугольник.
a=3 β=25 γ=45 … расчет треугольника, если известны сторона и два угла.
a=3 β=25 T=12 … расчет треугольника, если известны сторона, угол и площадь треугольника.
T=2.5 c=2 b=4 … найти сторону a, если известны стороны b, c и площадь треугольника T.
ma=1 b=2.5 c=2 … вычисление треугольника, если мы знаем одну медиану и любые две стороны.
ma=1 mb=2. 5 mc=2 … расчет треугольника по трем медианам.
5 mc=2 … расчет треугольника по трем медианам.
ha=220, hb=165 hc=132 … треугольник вычисляется по трем высотам.
a=7 β=40 mc=5 … расчет треугольника по одной стороне, одному углу и одной медиане.
a:b:c=2:3:4 T=2.5 … треугольник, где известно отношение сторон и его площадь.
A:B:C=1:4:5 a=2 … расчет треугольника, если известно отношение внутренних углов к одной стороне.
Что означают символы?a, b, c... стороны BC, AC, AB
A, B, C или α, β, γ... внутренние углы
ha, hb, hc... высоты
ma, mb, mc. .. медианы
T ... площадь
p ... периметр
s ... полупериметр
Треугольники в текстовых задачах:
- Стороны 7
Стороны треугольника равны 5,2, 4,6 и x. Если ПЕРИМЕТР треугольника равен 11,2 фута, какова длина неизвестной стороны? (подсказка: нарисуй картинку) - Равнобедренный 2
Равнобедренный треугольный каркас имеет длину 72 метра по ножкам и 18 метров по основанию. Найдите периметр рамки.
Найдите периметр рамки. - Пересечение 64854
Нарисуйте любой треугольник. Сделайте оси двух его сторон. Их пересечение представляет собой точку S. (а) Измерьте расстояние точки S от всех трех вершин (б) Проведите ось третьей стороны. - Вычислить
Вычислить площадь треугольника ABE AB = 38 мм и высоту E = 42 мм Ps: попробуйте выполнить быстрый расчет - Диагональ
Может ли это быть диагональный ромб в два раза длиннее его стороны? - Высота прямого RT
Прямоугольный треугольник ABC имеет гипотенузу c длиной 9 см и часть гипотенузы cb = 3 см. Какова высота этого прямоугольного треугольника? - Площадь RT 2
Вычислите площадь прямоугольного треугольника, катеты которого равны 6,2 см и 9,8 см. - Треугольник 8
Треугольник имеет основание 9,2 фута и высоту 4,8 фута. Чему равна площадь треугольника? - Площадь ST
Дан квадрат DBLK со стороной |BL|=13. Вычислите площадь треугольника DKU, если вершина U лежит онлайн LB.
- Диагональ
Может ли ромб иметь одинаковую длину, диагональ и сторону? - Лестница
Лестница имеет длину 3,5 метра. Он прислонен к стене, поэтому нижний конец находится в 2 метрах от стены. Найдите высоту лестницы. - Прямоугольный
Мы построили квадрат такой же площади, как прямоугольный треугольник с катетами 12 см и 20 см. Какой длины будет сторона квадрата? - Sss треугольник 2
Постройте треугольник ABC, в котором |AB|=5см, |AC|=6см и |BC|=9см - QuizQ
Две стороны равнобедренного треугольника равны 7 км и 39 км. Какой длины третья сторона? - В треугольнике 2
В треугольнике XYZ, если угол X=40°, а угол Y=75°. Какая сторона треугольника длиннее и почему?
больше задач на треугольник »
Посмотрите также коллекцию математических задач и вопросов нашего друга:
- triangle
- right triangle
- Heron’s formula
- The Law of Sines
- The Law of Cosines
- Pythagorean theorem
- triangle inequality
- similarity of triangles
- The right triangle altitude theorem
See more information about треугольники или более подробную информацию о решении треугольников.
Калькулятор треугольника
Укажите, что вы знаете о треугольнике:
Калькулятор решает треугольник, заданный тремя его свойствами. Каждый треугольник имеет шесть основных характеристик: три стороны a, b, c и три угла (α, β, γ). Классическая задача тригонометрии состоит в том, чтобы указать три из этих шести характеристик и найти остальные три. Конечно, наш калькулятор решает треугольники из комбинаций основных и производных свойств, таких как площадь, периметр, высота, медиана и т. д.
Обычно по длине трех сторон (SSS), сторона-угол-сторона или угол-сторона-угол.
Как этот калькулятор решает треугольник?
Расчет общего треугольника состоит из двух фаз:
- Экспертная фаза различна для разных задач. Калькулятор пытается по введенным данным вычислить размеры трех сторон треугольника. Он постепенно применяет базу знаний к введенным данным, которая представлена, в частности, отношениями между отдельными параметрами треугольника.
 Они последовательно применяются и комбинируются, и вычисляются параметры треугольника. Калькулятор повторяется до тех пор, пока треугольник не вычислит все три стороны.
Они последовательно применяются и комбинируются, и вычисляются параметры треугольника. Калькулятор повторяется до тех пор, пока треугольник не вычислит все три стороны.
Например, соответствующая высота вычисляется из заданной площади треугольника и соответствующей стороны. По известным высоте и углу можно рассчитать прилегающую сторону и т. д. Калькулятор использует знания, например, формулы и отношения, такие как теорема Пифагора, теорема синусов, теорема косинуса и формула Герона. - Второй этап — вычисление свойств треугольника по имеющимся длинам трех его сторон.
Примеры ввода треугольника:
a=3 b=4 c=5 … расчет треугольника по трем сторонам a,b,c.
B=45 c=10 a=9 … треугольник вычисляется по двум сторонам a,c и углу B.
A=25 C=80 b=22
A=35 C=26 a=10
a=3 C=90 c=5 … как ввести прямоугольный треугольник.
a=3 β=25 γ=45 … расчет треугольника, если известны сторона и два угла.
a=3 β=25 T=12 . .. расчет треугольника, если известны сторона, угол и площадь треугольника.
.. расчет треугольника, если известны сторона, угол и площадь треугольника.
T=2.5 c=2 b=4 … найти сторону a, если известны стороны b, c и площадь треугольника T.
ma=1 b=2.5 c=2 … вычисление треугольника, если мы знаем одну медиану и любые две стороны.
ma=1 mb=2.5 mc=2 … расчет треугольника по трем медианам.
ha=220, hb=165 hc=132 … треугольник вычисляется по трем высотам.
a=7 β=40 mc=5 … расчет треугольника по одной стороне, одному углу и одной медиане.
a:b:c=2:3:4 T=2.5 … треугольник, где известно отношение сторон и его площадь.
A:B:C=1:4:5 a=2 … расчет треугольника, если известно отношение внутренних углов к одной стороне.
Что означают символы?a, b, c... стороны BC, AC, AB
A, B, C или α, β, γ... внутренние углы
ha, hb, hc... высоты
ma, mb, mc. .. медианы
T ... площадь
p ... периметр
s ... полупериметр
Треугольники в текстовых задачах:
- Стороны 7
Стороны треугольника равны 5,2, 4,6 и x. Если ПЕРИМЕТР треугольника равен 11,2 фута, какова длина неизвестной стороны? (подсказка: нарисуй картинку)
Если ПЕРИМЕТР треугольника равен 11,2 фута, какова длина неизвестной стороны? (подсказка: нарисуй картинку) - Равнобедренный 2
Равнобедренный треугольный каркас имеет длину 72 метра по ножкам и 18 метров по основанию. Найдите периметр рамки. - Пересечение 64854
Нарисуйте любой треугольник. Сделайте оси двух его сторон. Их пересечение представляет собой точку S. (а) Измерьте расстояние точки S от всех трех вершин (б) Проведите ось третьей стороны. - Вычислить
Вычислить площадь треугольника ABE AB = 38 мм и высоту E = 42 мм Ps: попробуйте выполнить быстрый расчет - Диагональ
Может ли это быть диагональный ромб в два раза длиннее его стороны? - Высота прямого RT
Прямоугольный треугольник ABC имеет гипотенузу c длиной 9 см и часть гипотенузы cb = 3 см. Какова высота этого прямоугольного треугольника? - Площадь RT 2
Вычислите площадь прямоугольного треугольника, катеты которого равны 6,2 см и 9,8 см. - Треугольник 8
Треугольник имеет основание 9,2 фута и высоту 4,8 фута.

 ⓘ Основание прямоугольного треугольника [B]
ⓘ Основание прямоугольного треугольника [B]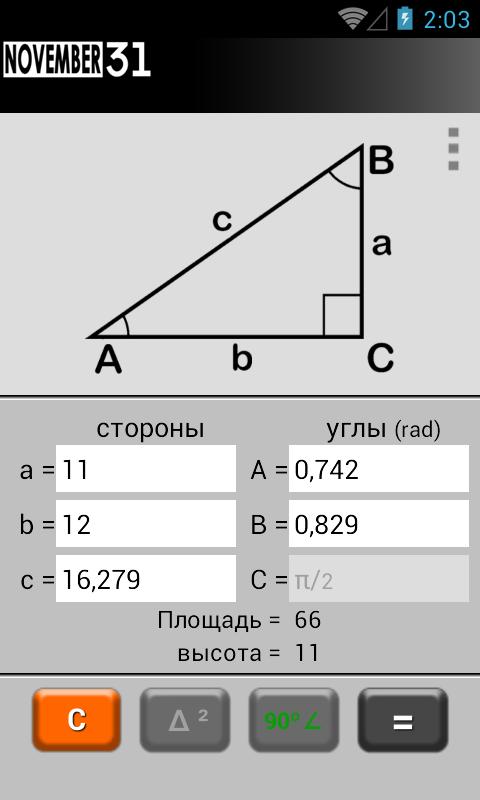
 По известным высоте и углу можно рассчитать прилегающую сторону и т. д.
Калькулятор использует знания, например, формулы и отношения, такие как теорема Пифагора, теорема синусов, теорема косинуса и формула Герона.
По известным высоте и углу можно рассчитать прилегающую сторону и т. д.
Калькулятор использует знания, например, формулы и отношения, такие как теорема Пифагора, теорема синусов, теорема косинуса и формула Герона.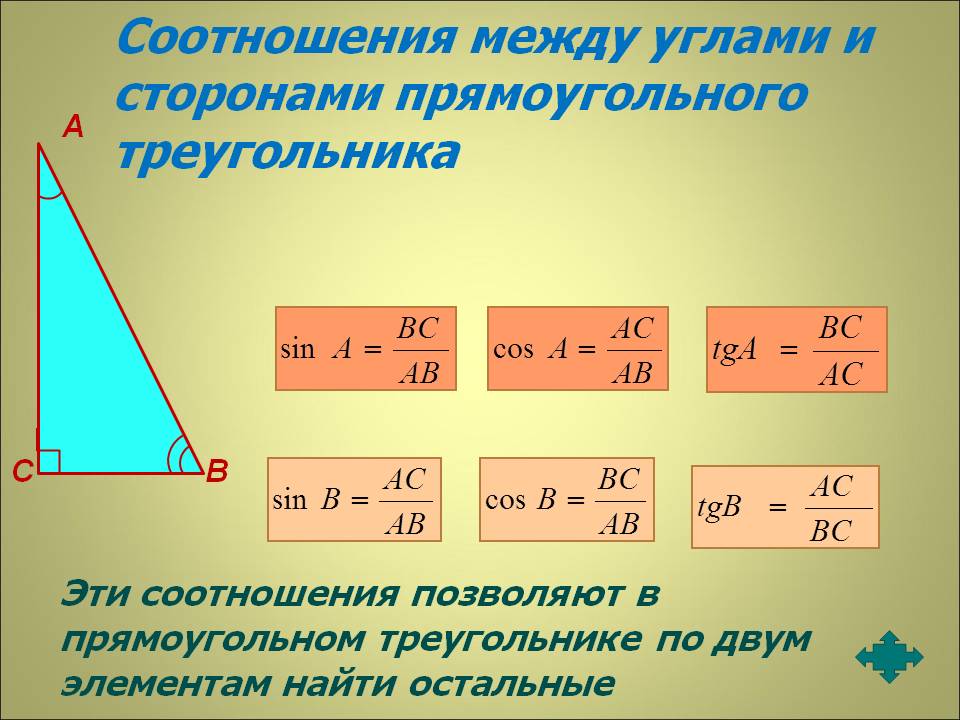 Найдите периметр рамки.
Найдите периметр рамки.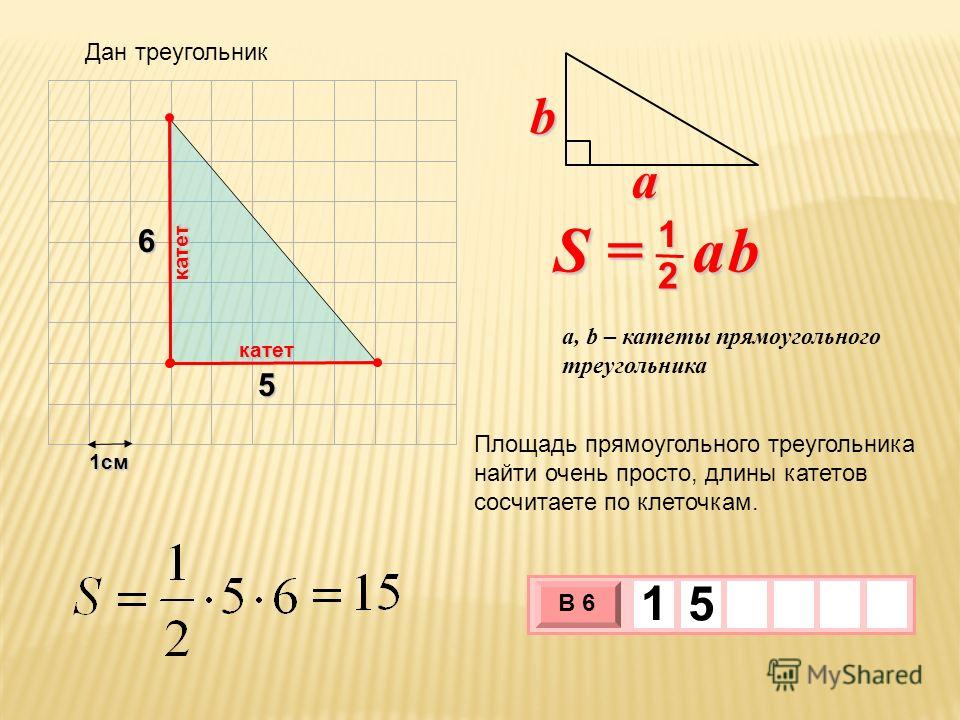
 Они последовательно применяются и комбинируются, и вычисляются параметры треугольника. Калькулятор повторяется до тех пор, пока треугольник не вычислит все три стороны.
Они последовательно применяются и комбинируются, и вычисляются параметры треугольника. Калькулятор повторяется до тех пор, пока треугольник не вычислит все три стороны.  Если ПЕРИМЕТР треугольника равен 11,2 фута, какова длина неизвестной стороны? (подсказка: нарисуй картинку)
Если ПЕРИМЕТР треугольника равен 11,2 фута, какова длина неизвестной стороны? (подсказка: нарисуй картинку)