Калькулятор e в степени x: Возведение экспоненты в степень | Онлайн калькулятор

Путешествие в калькулятор / Хабр

Ничто так не скрыто от нас, как то, что лежит на поверхности.
Сунь Цзы и Чжугэ Лян (вольный перевод)

Случилось сие в одном из роликов на YouTube. При просмотре программистского урока нужно было срочно перевести 377 в десятичную систему. Мы не стали раскладывать это на тройки бит, представлять степени восьмёрки или просто не обращать на это внимание и пропустить этот неважный момент. Мы запустили калькулятор в операционной системе, пододвинули его окно к центру экрана и там всё выяснили. Да, это оно — число 255.

Конечно, не нужно рассказывать, что бывает в более сложных случаях. Порой дело доходит до листика в тетради, лежащей рядом с компьютером как раз для таких случаев. У каждого найдётся парабола или что-то около того, пересекающее что-то около того.

Как и следовало ожидать, при использовании Emacs на протяжении месяцев или просто многих лет наступает Emacs головного мозга. Поэтому такие случаи не проходят даром и среди ночи в голове возникает вопрос: «Как же всё-таки в Emacs’е перевести 377? Он хотя бы это умеет? Ну, хотя бы 8 возведёт в степень?».

Наутро, зарядившись энергией в виде чая с горстью шоколадных конфет, мы открываем Emacs и начинаем его исследование.

Начинаем с операций

Понятно, что введя Alt + x и calc , мы первым делом видим обычный стековый калькулятор, которых писали, наверное, штук сто вот этими вот руками. И как бы не хотелось повторять этот путь в сто первый раз, обнаружив, что он не умеет ничего.

Методом тыка сначала делаем + — * /

5 <RET> 7 <RET> +

5 <RET> 7 <RET> —

5 <RET> 7 <RET> *

5 <RET> 7 <RET> /

Потом

8 <RET> 8 <RET> *


О! А вот и квадрат восьмёрки! А где квадрат, там и куб!

Открываем хелп

Конечно, все знают, что русский человек (сссрский, имперский и др.) не будет начинать с инструкции, а сначала попробует всё сломать, потом починить, а потом уже инструкцию читать в поисках пропущенных секретов.

Не скажу, что в этот раз с инструкции всё началось, так как в отличие от многих я не отключаю меню Emacs’а, а пользуюсь им для вспоминания сочетаний клавиш во всяких редких режимах.

Вот и в этот раз я начал обзор с меню калькулятора

Для того, чтобы открыть хелп, нужно ввести Ctrl + x + * + i . А чтобы открыть туториал, нужно ввести Ctrl + x + * + t .

Их по-разному можно открыть, но, как показала практика, сочетание Ctrl + x + * + <клавиша> используется очень часто и сделано специально для удобного управления калькулятором в процессе другой работы.

Поэтому открыть калькулятор можно через Ctrl + x + * + c , а запустить калькулятор в текущем буфере можно через Ctrl + x + * + e .

Описание клавиш

calc-dispatch-help is an interactive compiled Lisp function.

(calc-dispatch-help ARG)

C-x* is a prefix key sequence; follow it with one of these letters:

For turning Calc on and off:
C calc. Start the Calculator in a window at the bottom of the screen.
O calc-other-window. Start the Calculator but don't select its window.
B calc-big-or-small. Control whether to use the full Emacs screen for Calc.


Q quick-calc. Use the Calculator in the minibuffer.
K calc-keypad. Start the Calculator in keypad mode (X window system only).
E calc-embedded. Use the Calculator on a formula in this editing buffer.
J calc-embedded-select. Like E, but select appropriate half of => or :=.
W calc-embedded-word. Like E, but activate a single word, i.e., a number.
Z calc-user-invocation. Invoke Calc in the way you defined with `Z I' cmd.
X calc-quit. Turn Calc off.

For moving data into and out of Calc:
G calc-grab-region. Grab the region defined by mark and point into Calc.
R calc-grab-rectangle. Grab the rectangle defined by mark, point into Calc.
: calc-grab-sum-down. Grab a rectangle and sum the columns.
_ calc-grab-sum-across. Grab a rectangle and sum the rows.
Y calc-copy-to-buffer.

Copy a value from the stack into the editing buffer.

For use with Embedded mode:
A calc-embedded-activate. Find and activate all :='s and =>'s in buffer.
D calc-embedded-duplicate. Make a copy of this formula and select it.
F calc-embedded-new-formula. Insert a new formula at current point.
N calc-embedded-next. Advance cursor to next known formula in buffer.
P calc-embedded-previous. Advance cursor to previous known formula.
U calc-embedded-update-formula. Re-evaluate formula at point.
` calc-embedded-edit. Use calc-edit to edit formula at point.

Documentation:
I calc-info. Read the Calculator manual in the Emacs Info system.
T calc-tutorial. Run the Calculator Tutorial using the Emacs Info system.
S calc-summary. Read the Summary from the Calculator manual in Info.

Miscellaneous:
L calc-load-everything. Load all parts of the Calculator into memory.

M read-kbd-macro. Read a region of keystroke names as a keyboard macro.
0 (zero) calc-reset. Reset Calc stack and modes to default state.

Press `*' twice (`C-x * *') to turn Calc on or off using the same
Calc user interface as before (either C-x * C or C-x * K; initially C-x * C).

Поднимаем планку

Примерно день ушёл на проверку всех опций из меню. Среди них есть такие, как нахождение следующего простого числа, поэтому такое нельзя было просто пропустить, хотелось убедиться, что это действительно работает.

Наибольший общий делитель (НОД) теперь можно не писать, здесь он просто есть. Надо ввести два числа и нажать k g, где k означает комбинаторику, а g — gcd (Greatest Common Divisor).

Факториал 3000 (своеобразная проверка на скорость) вычисляется не без труда, но всё же вычисляется секунд за пятнадцать.

Транспонирование матрицы, нахождение её определителя или скалярное умножение векторов выполняется легко и со свистом.

На минуту я забыл, за чем пришёл, выполняя операции одну за другой, не веря собственным глазам. А за чем же я пришёл?

Продолжаем

На второй день стало интересно, вычислит ли он систему уравнений методом Крамера. Раз определители есть, то и решение методом Крамера можно найти. Раньше-то я в редакторе это писал много раз, даже навыки уже сложились по вычислению определителей в редакторе.

Но это не потребовалось. Оказалось, что достаточно просто ввести три уравнения, а потом запросить их решение. Да, прямо как в Вольфраме.

Найдём первую попавшуюся систему

 2y +  x +  z = -1
 -z -  y + 3x = -1


-2x + 3z + 2y =  5


Надо просто её выделить Ctrl + x + h , скопировать Alt + w , перейти в калькулятор Ctrl + x + * + * , вставить её Ctrl + y , упаковать уравнения в вектор 3 v p , нажать a P и в ответ на вопрос «По каким переменным искать корни?» ввести x y z .

В стеке появится вектор с ответами, дальше мы просто нажимаем y и вектор с ответами вставляется в позицию курсора в исходном буфере с уравнениями.

[[ 0., -2., 3. ]] 2y +  x +  z = -1
 -z -  y + 3x = -1
-2x + 3z + 2y =  5


Если бы мы курсор оставили в конце системы уравнений, то ответ вставился бы туда.

Сила стека

При пользовании калькулятором в течение какого-то времени становится неудобно от того, что в стеке начинают накапливаться значения. При этом ты не знаешь, возможно ли их удалить, так как среди них есть нужные, поэтому любой эксперимент может закончится потерей.

Так идут часы, пока в одну прекрасную минуту ты не решаешься всё-таки открыть хелп и потратить время на его чтение. К счастью, все комбинации подобраны максимально удобно, так что там даже присутствует и поддерживается некая симметрия действий.

Вот эти числа с двоеточиями в стеке в начале каждой строки являются как бы адресами. Во многих командах ввод положительного аргумента означает «несколько штук», а ввод отрицательного аргумента означает «такой-то номер».

К примеру, есть у нас число пять в стеке

1: 5


Если мы нажмём <RET> (Enter), то оно скопируется и у нас будет

2: 5
1: 5


Вот эта двойка равна количеству элементов в стеке, она же является адресом первого числа пять, а число 1 является адресом второго числа пять.

У команды <RET> есть аргумент, который по умолчанию равен 1. Когда мы нажимаем <RET> , он копирует столько элементов от вершины стека (вершина — в самом низу). Поэтому, если мы введём Alt + 2 + <RET> , он возьмёт два элемента и скопирует их

4: 5
3: 5
2: 5
1: 5


Если же аргумент отрицательный, то он берёт элемент с таким адресом (если минус убрать). Поэтому, если мы введём теперь Alt + — + 4 + <RET> , он скопирует элемент по адресу 4

5: 5
4: 5
3: 5
2: 5
1: 5


Большинство основных операций работают по той же схеме. Если нужно удалить три элемента, то пишем Alt + 3 + <DEL> , где <DEL> — это backspace. Если же нужно удалить элемент с адресом 3, то пишем Alt + — + 3 + <DEL> .

Если почитать хелп ещё более подробно, то к этим операциям можно найти такие своеобразные операции из антимира, состоящие из чёрной материи.

Например, для <RET> существует операция Ctrl + j , для <DEL> существует Alt + <DEL> , а для <TAB> существует Alt + <TAB> .

Смысл этих операций точно такой же, только аргумент меняется по знаку. Поэтому, если ввести Alt + 3 + Ctrl + j , то он не три элемента скопирует, а элемент с адресом 3, а если ввести отрицательный аргумент, то он скопирует не элемент с адресом 3, а три элемента.

Если нужно очистить весь стек, то нужно нажать Alt + 0 + <DEL> .

Есть множество путей

Поначалу кажется, что всё можно делать только одним способом, который надо просто выучить. Но со временем открываются многие способы достижения одного и того же результата.

Например, как можно ввести матрицу?

Самое первое, что приходит на ум, — это написать её в буфере и потом просто скопировать.

Вот это

[[1, 2, 3], [4, 5, 6], [7, 8, 9]]


Превращается вот в это

1: [ [ 1, 2, 3 ]
  &nbsp  [ 4, 5, 6 ]
  &nbsp  [ 7, 8, 9 ] ]


Второе, что приходит на ум, — это использование внутреннего средства.

Матрица — это три вектора

1 <RET> 2 <RET> 3 <RET> 3 v p
4 <RET> 5 <RET> 6 <RET> 3 v p
7 <RET> 8 <RET> 9 <RET> 3 v p
3 v p


Третье, что приходит на ум, — это использование внутреннего и удобного средства.

1 <RET> 2 <RET> 3 <RET> 4 <RET> 5 <RET> 6 <RET> 7 <RET> 8 <RET> 9 <RET>
[3, 3]
v p


И четвертое, что приходит на ум, — «А её нельзя просто ввести?»

[ 1 <SPC> 2 <SPC> 3 ; 4 <SPC> 5 <SPC> 6 ; 7 <SPC> 8 <SPC> 9 ] ]


У команды pack есть симметричная — unpack, поэтому, если нужно разложить матрицу на векторы или вектор разложить на числа, то мы просто нажимаем v u .

Привлекаем внешние средства

По мере ковыряния в калькуляторе вдруг начинаешь обращать внимание на окружающие буферы и постепенно возникает вопрос: «А какие средства обычного Emacs’а можно привлечь при работе в калькуляторе?»

Поначалу мы просто находим n-ую производную многочлена путём записи макроса и повторения его n раз через аргумент макроса. 2 + 24

Если же мы нажмём Ctrl + x + z , а потом z z , то мы постепенно получим ноль.

Уходим во внешний мир

Через какое-то время калькулятор закрывается и мы возвращаемся к нашей обычной работе, к нашим обычным развлечениям.

И вот в один прекрасный момент мы читаем, в Emacs’е естественно, историю про лису, которая прыгала-прыгала через ленивую собаку и прыгнула 1024 раза. Постойте, скажете вы, разве лиса может прыгнуть столько раз прямо точь в точь, если она не компьютерная? Надо это дело исправить.

У нас имеется следующий текст

The quick brown fox has jumped over the lazy dog 1024 times.


Наводим курсор на 1024 и осторожно нажимаем Ctrl + x + * + w . Дальше нажимаем Q, а потом так же осторожно нажимаем Ctrl + x + * + w .

И у нас получается

The quick brown fox has jumped over the lazy dog 32 times.


Вот это уже больше похоже на правду. То есть, чтобы что-то вычислить, калькулятор совсем не обязательно открывать, достаточно лишь понажимать какие-то кнопки. -24 yocto

(**) When in TeX or LaTeX display mode, the TeX specific unit
names will not use the `tex’ prefix; the unit name for a
TeX point will be `pt’ instead of `texpt’, for example.
To avoid conflicts, the unit names for pint and parsec will
be `pint’ and `parsec’ instead of `pt’ and `pc’.

x$ с «нуля» (построенный на числовой библиотеке произвольной точности, такой как GMP) с более быстрой сходимостью, чем аппроксимации ряда Тейлора/полиномиала, я бы разработал аппроксимацию непрерывной дроби/рациональной функции.

Подобно тому, как точность известного ряда Тейлора может быть увеличена, если требуется, с помощью дополнительных членов, точно так же и разложение непрерывной дроби даст любую требуемую точность с помощью дополнительных подходящих чисел.

Сначала может показаться, что оценка приближения цепной дроби влечет за собой существенный недостаток по сравнению со степенным рядом. К частичным суммам степенного ряда можно добавить дополнительные члены, чтобы получить последовательные приближения слева направо. Существует способ добиться того же эффекта с непрерывными дробями, а именно путем преобразования частичных числителей и знаменателей в подходящие с помощью рекуррентного соотношения. 92$ в расширении).

Хотя аппроксимация экспоненциальной функции цепной дробью или рядом Тейлора может сходиться для произвольных действительных (или комплексных) значений, скорость сходимости неравномерна. Ряд Тейлора сходится тем быстрее, чем ближе аргумент к нулю. Таким образом, сокращение диапазона важно для выражения экспоненциальной функции при произвольном действительном значении через значение в некотором интервале, таком как $[0,1]$. Например, если арифметика с плавающей запятой двоичная (основание 2), может быть особенно удобно использовать знакомый закон показателей с кратными $\ln 2$: 9x$, который необходимо вычислить с точностью до изменения двоичной степени, используя аппроксимацию, быстро сходящуюся над $[0,\ln 2]$.

Объединив эти две идеи (симметрия, сокращение диапазона), скорость сходимости можно ограничить интервалом $[0, \ln 2/2]$. Ограничение интервала оценки может позволить вам заранее определить, сколько членов непрерывной дроби или разложения в ряд Тейлора необходимо сохранить для получения желаемой точности. Когда это известно, оценка может быть выполнена более эффективно (обратная рекурсия для непрерывных дробей или метод Хорнера для усеченных рядов/многочленов Тейлора), чем если бы мы были вынуждены постоянно вводить новые члены, пока не будет достигнута желаемая точность.

Добавлено:

Я имел в виду формулу (11.1.2) «более быстрой» цепной дроби:

[Справочник цепных дробей для специальных функций (Cuyt et al, 2008)]
http:// books.google.com/books?id=DQtpJaEs4NIC&dq=exponential+function+continued+fraction+convergence

Их ссылка на эту современную классику:

Применение непрерывных дробей и их обобщений к задачам теории приближения
А.Н. Хованского, 1963 (P.Noordhoff)

На аккуратном веб-сайте Андреаса Лаушке, основанном на математике, представлены некоторые идеи по ускорению сходимости непрерывных дробей с помощью «сокращений». IP-адрес время от времени меняется, и его нельзя использовать в качестве ссылки внутри StackExchange, но вы можете найти его в Google:

[Ускорение конвергенции с помощью канонических сокращений непрерывных дробей: Экспоненциальная функция — Andreas Lauschke Consulting]

У меня есть несколько заметок о его формулах (полученных путем сокращения из приведенной выше), если это будет полезно. Некоторый связанный материал был предоставлен для демонстраций Wolfram.

Вычисление константы $\ln 2$

Поколения студентов-математиков познакомились с понятием условной и абсолютной сходимости на примере знакопеременного гармонического ряда:

$$\ln 2 = 1 — 1/ 2 + 1/3 — 1/4 + …$$

Конечно, этот ряд, полученный из степенного ряда $\ln x$ вокруг $x = 1$, имеет такую ​​медленную сходимость, что даже если мы объединим последовательные пары термов:

$$\ln 2 = 1/2 + 1/12 + 1/30 + …$$

полученный абсолютно сходящийся ряд бесполезен для получения произвольных значений точности $\ln 2$. Для удобства первые семь частичных сумм:

 0,50000000...
0,58333333...
0,61666666...
0,63452381...
0,64563492...
0,65870518...
 

Поскольку $\ln 2$ равно 0,69314718…, у нас есть ошибка около трети единицы в первом десятичном разряде. Другими словами, не намного больше сходимости, чем правильный один десятичный знак.

Таким образом, это разительно контрастирует с прекрасной сходимостью разложения непрерывной дроби того же значения:

$$\ln 2 = \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{3 + \cfrac{4}}{4 + \cfrac{4}{5 + \cfrac {9}{6 + \cfrac{9}{7 + …}}}}}}}$$

Первые семь подходящих элементов:

 0,66666666...
0,70000000...
0,69230769...
0,69333333...
0,69312169...
0,69315245...
 

Ошибка здесь составляет около половины единицы в пятом знаке после запятой.

Как делать экспоненты на калькуляторе iPhone (полное руководство)

Многим пользователям iPhone неизвестно, что приложение-калькулятор может выполнять сложные вычисления, такие как ручной или офисный научный калькулятор. Вам нужно выполнить математическое уравнение, но вы забыли дома научный калькулятор? Не волнуйтесь, так как ваш калькулятор iPhone может решить большинство из этих вычислительных задач, включая экспоненциальные вычисления.

Итак, как вы делаете экспоненты на калькуляторе iPhone?

Мы подготовили эту статью, чтобы показать вам, как делать экспоненты на калькуляторе iPhone и другие полезные приемы.

Содержание

1. Как выполнять экспоненциальные вычисления на калькуляторе iPhone?
2. Как ввести экспоненты на iPhone?
3. Заключение
4. Часто задаваемые вопросы

Как выполнять экспоненциальные вычисления на калькуляторе iPhone?

Чтобы вычислить степень на калькуляторе iPhone, вам нужно повернуть экран, чтобы вызвать научный калькулятор, который доступен только в альбомной ориентации. Выполните следующие действия, чтобы включить альбомную ориентацию на вашем телефоне:

1. Проведите по экрану снизу вверх, чтобы открыть Центр управления на главном экране вашего iPhone.
2. Проверьте значок ориентации экрана; если это красный , « блокировка вращения » включена.
3. Чтобы отключить его, коснитесь значка поворота экрана. Он станет белым с символ открытия замка .
4. Теперь ваш телефон будет принимать альбомную ориентацию при повороте. Кроме того, вы получите уведомление « Блокировка портретной ориентации: выкл. ».

Выполните следующие действия, чтобы вычислить степень на вашем iPhone:

1. Откройте приложение Calculator . Вы можете запустить приложение калькулятора из Центра управления , ярлыка приложения на главном экране или выполнить поиск в строке поиска.
2. После запуска калькулятора поверните его в альбомную ориентацию.
3. Появится научный калькулятор с дополнительными функциями.
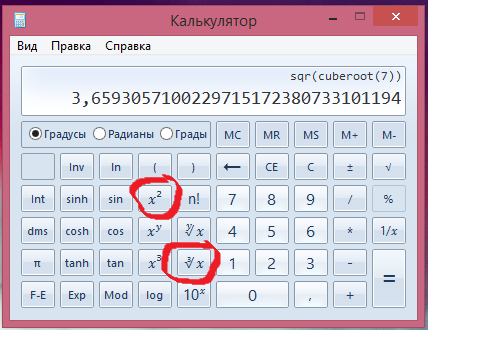
4. Для выполнения экспоненциальных функций используйте либо x ² ,x ³ , либо x ^y . Например, если вы хотите возвести 7 в квадрат, нажмите 7, затем x ² и, наконец, знак равенства (=) ; число на экране — ваш ответ.
5. Повторите ту же процедуру, чтобы найти куб числа, но вместо этого используйте x ³   .
6. Для экспоненциальной функции, превышающей степень трех, выполните ту же процедуру, но используйте x ^{y , где «x» — базовое число, а y — показатель степени. Предположим, вы хотите возвести 10 в степень 7. Вам нужно нажать 10, коснуться x y , нажать 7 и, наконец, th e знак равенства , и вот вам ответ.}

В качестве альтернативы вы можете использовать функцию « EE » для выполнения экспоненциальных вычислений. Однако этот метод подходит, когда показатель степени равен 10 ^x , где x — положительное или отрицательное число. Например, вы можете использовать метод EE для расчета 89 x10 ^-5 .

Выполните следующие шаги, чтобы сделать экспоненты на iPhone с помощью функции EE:

1. Введите базовый номер ; в нашем примере базовое число равно 89.
2. Нажмите функцию « EE» .
3. Введите показатель степени ; в нашем случае показатель степени равен -5.
4. Нажми на знак равенства . Число, которое появляется на экране, является вашим ответом.

Как ввести экспоненты на iPhone?

Предположим, вы хотите написать своему приятелю по колледжу сообщение о математической задаче и вам нужно ввести показатель степени на клавиатуре вашего iPhone. Большинству людей сложно включить эти функции в обычный текст, потому что они отсутствуют на стандартной клавиатуре. К счастью, вы можете скопировать эти функции с веб-страницы и вставить их в свой текст.

В качестве альтернативы вы можете создать текстовый ярлык на клавиатуре, если вы регулярно используете функции в своих текстах. Вот как сделать ярлык: 92).

Наконец, сохраните ярлык.

Заключение

Можно использовать калькулятор iPhone для выполнения сложных экспоненциальных вычислений. Запустите приложение-калькулятор и поверните экран телефона, чтобы добиться альбомной ориентации. В альбомной ориентации отображается научный калькулятор с показателями, включающими x ² , x ³ и x ^y , где «y» — любой показатель степени выше трех. Кроме того, вы можете использовать функцию «EE» для экспоненциальных вычислений с 10 ^x в качестве показателя степени.

Часто задаваемые вопросы

Чтобы вычислить отрицательную составляющую на калькуляторе iPhone, выполните следующие действия:

1. Нажмите основное число.
2. Коснитесь функции EE.
3. Введите показатель степени.
4. Коснитесь знака «-»; показатель степени становится отрицательным.
5. Нажмите знак равенства.
6. Число, которое появляется на экране, является вашим ответом.