Слоупок ФМ №13. Код Хэмминга на дисплее калькулятора: sevabashirov — LiveJournal
?- Психология
- Техника
- Cancel
И, как всегда, не сразу до меня дошло, что семисегментный индикатор — это визуализация для классического кода Хэмминга (7; 4). Того самого, который автоматически корректирует одиночную ошибку ценой добавления 3 проверочных символов к 4 исходным.
Так вот, повертев исходную таблицу, изо всего множества вариантов (не стал лезть в комбинаторику и считать) выбрал на мой взгляд наиболее гармоничный. Во-первых, симметричный относительно вертикальной оси (зеркальная пара к любому символу присутствует в наборе), во-вторых, полноширинный (нет символов, умещающихся в одной «стенке» индикатора). Ну и из двух оставшихся вариантов выбрал тот, в котором «кружок» в нижней части, а не в верхней. Вот этот набор:
Чем не шестнадцатеричные цифры?
P.S. А можно и к социотипам прикрутить… 7 из 15 признаков Рейнина, если вы понимаете, о чем я.
Tags: ©, Слоупок ФМ, рацпредложение, соционика, числа
SubscribeСлоупок ФМ №24.
 Судоку
СудокуВдруг дошло, что разновидность классического судоку с 9 цветами, где помимо трех обычных ограничений (разные цифры в строках, столбцах и квадратах)…
Слоупок ФМ №23. Wordle
Совсем недавно узнал, что у игры «быки и коровы со словами» появилась популярная веб-реализация — Wordle. А ведь правила можно…
Слоупок ФМ №22. Полгода совсем никуда
Я один только сейчас понял, что 24 февраля — это ровно 6 месяцев в любую сторону от Дня Незалежності, 24 августа? Нет ли в этой дате недвусмысленного…
Photo
Hint http://pics.livejournal.com/igrick/pic/000r1edq
Слоупок ФМ №24. Судоку
Вдруг дошло, что разновидность классического судоку с 9 цветами, где помимо трех обычных ограничений (разные цифры в строках, столбцах и квадратах)…
Слоупок ФМ №23. Wordle
Совсем недавно узнал, что у игры «быки и коровы со словами» появилась популярная веб-реализация — Wordle.
 А ведь правила можно…
А ведь правила можно…Слоупок ФМ №22. Полгода совсем никуда
Я один только сейчас понял, что 24 февраля — это ровно 6 месяцев в любую сторону от Дня Незалежності, 24 августа? Нет ли в этой дате недвусмысленного…
Диаграммы Эйлера-Венна — Готовые рефераты
ВВЕДЕНИЕ
ДИАГРАММЫ ЭЙЛЕРА-ВЕННА
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
Круги Эйлера – геометрическая схема, которая позволяет показать взаимосвязь между подмножествами для визуального представления. Схемы были изобретены Леонардом Эйлером. Они используются в математике, логике, управлении и других прикладных областях.
Важным частным случаем эйлеровых кругов являются диаграммы Эйлера-Венна, представляющие все 2n комбинаций из n свойств, то есть конечную булеву алгебру. При n = 3 диаграмма Эйлера-Венна обычно изображается в виде трех окружностей, центрированных по вершинам равностороннего треугольника и одинакового радиуса, приблизительно равных длине стороны треугольника.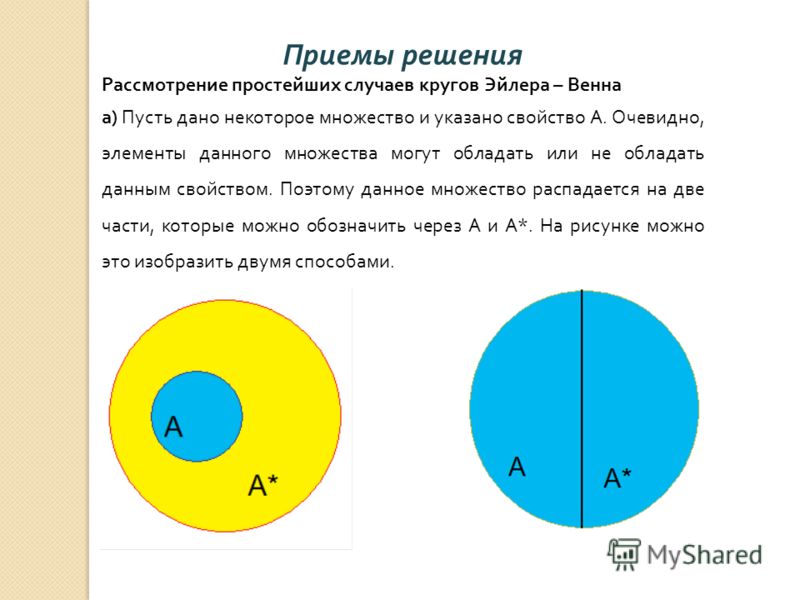
Решая ряд проблем, Леонард Эйлер использовал идею представления множеств с помощью кружков. Однако еще до Эйлера этот метод использовался выдающимся немецким философом и математиком Готфридом Вильгельмом Лейбницем (1646-1716). Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но в то же время предпочитал использовать линейные схемы.
Но Л. Эйлер разработал этот метод довольно тщательно. Метод кругов Эйлера был также использован немецким математиком Эрнстом Шрёдером (1841-1902) в его книге «Алгебра логики». Графические методы достигли особой высоты в трудах английского логика Джона Венна (1843–1923), который подробно описал их в книге «Символическая логика», опубликованной в Лондоне в 1881 году. Поэтому такие схемы иногда называют диаграммой Эйлера-Венна.
ДИАГРАММЫ ЭЙЛЕРА-ВЕННА
Леонард Эйлер (1707-1783, Санкт-Петербург, Российская Империя) – математик, механик, физик. Адъюнкт по физиологии, профессор физики, профессор высшей математики, внесший значительный вклад в развитие математики, а также механики, физики, астрономии и многих прикладных наук.
Эйлер является автором более 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и т. д. [6, c, 200]
Он провел почти половину своей жизни в России, где он внес значительный вклад в развитие российской науки. В 1726 году его вызвали на работу в Санкт-Петербург, куда он переехал год спустя. С 1711 по 1741, а также с 1766 года он был академиком в Санкт-Петербургской академии наук (1741-1766 работал в Берлине, оставаясь почетным членом Петербургской академии). Он свободно говорил по-русски и публиковал некоторые свои работы (особенно учебники) на русском языке. Первые русские академики по математике (С. К. Котельников) и астрономы (С. Я. Румовский) были учениками Эйлера. Некоторые из его потомков до сих пор живут в России.
Джон Венн (1834-1923), английский логик. Он работал в области классовой логики, где создал специальный графический аппарат (так называемые диаграммы Венна), который нашел применение в логико-математической теории «формальных нейронных сетей».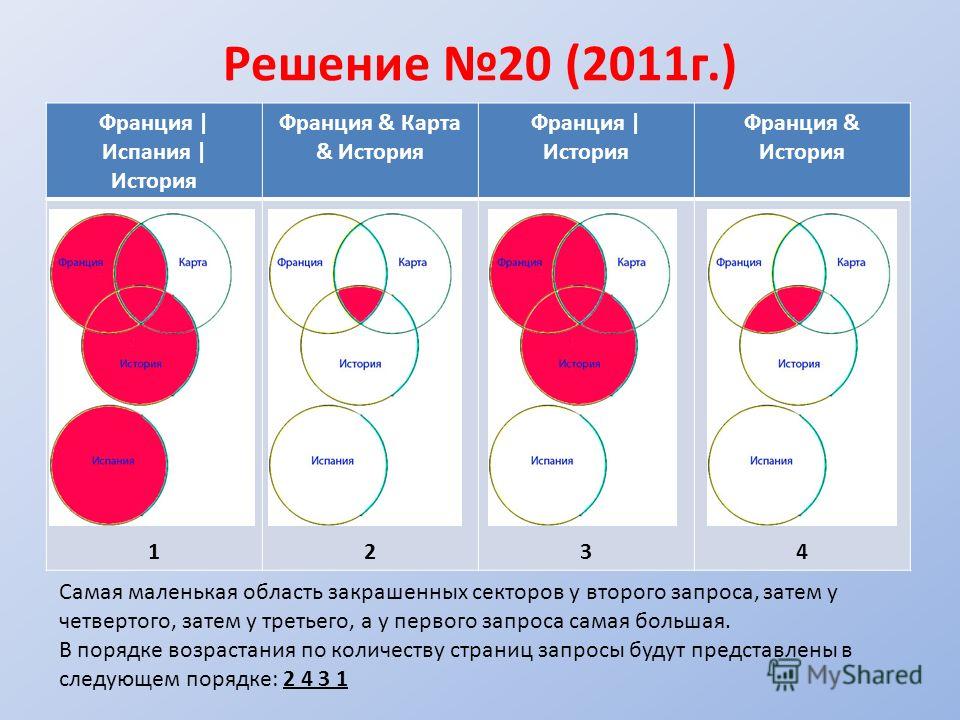 Венну принадлежит обоснование обратных операций в логическом исчислении Дж. Буля. Основным интересом Джона была логика, и он опубликовал три статьи на эту тему. Это была «Логика случая», в которой в 1866 г. была представлена интерпретация частоты или частотная теория вероятностей; «Символьная логика», в которой представлены диаграммы Венна в 1881 году; «Принципы эмпирической логики» 1889 года, в которой обосновано использование обратных операций в булевой логике. [5, c. 40]
Венну принадлежит обоснование обратных операций в логическом исчислении Дж. Буля. Основным интересом Джона была логика, и он опубликовал три статьи на эту тему. Это была «Логика случая», в которой в 1866 г. была представлена интерпретация частоты или частотная теория вероятностей; «Символьная логика», в которой представлены диаграммы Венна в 1881 году; «Принципы эмпирической логики» 1889 года, в которой обосновано использование обратных операций в булевой логике. [5, c. 40]
ЗАКЛЮЧЕНИЕ
Диаграммы Эйлера-Венна являются геометрическими представлениями множеств. Простая конструкция диаграммы дает наглядное представление универсального множества U, а внутри него – кругов (или других замкнутых фигур), представляющих множества. Фигуры пересекаются в наиболее общем случае, необходимом для задачи, и соответствуют образному изображению. Точки, лежащие в разных областях диаграммы, можно рассматривать как элементы соответствующих множеств. Имея построенную диаграмму, можно затенять определенные области, чтобы указать вновь сформированные наборы.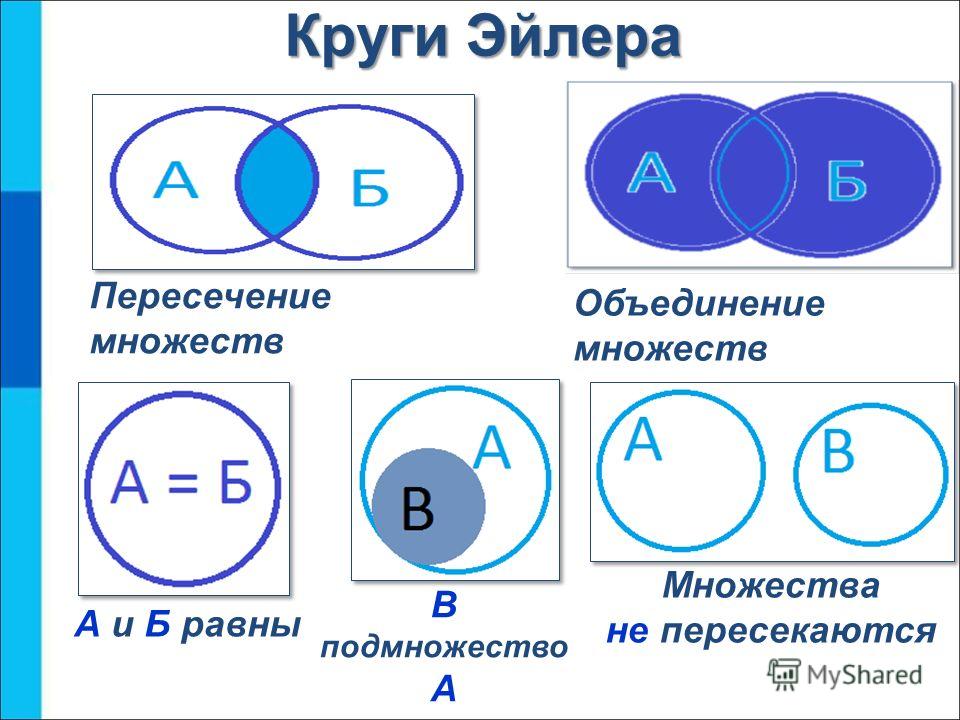 Это дает нам наиболее полную картину проблемы и ее решения. Простота диаграмм Эйлера-Венна позволяет использовать эту технику в таких областях, как математика, логика, управление и другие прикладные области.
Это дает нам наиболее полную картину проблемы и ее решения. Простота диаграмм Эйлера-Венна позволяет использовать эту технику в таких областях, как математика, логика, управление и другие прикладные области.
1. Ивин, А.А. Логика для журналистов. Учебное пособие/ А.А. Ивин. – М.: Аспект Пресс, 2002. – 224 с.
2. Ивин, А.А., Никифоров, А.Л. Словарь по логике / А.А. Ивин, А.Л. Никифоров. – М.: Туманит, изд. центр ВЛАДОС, 1997. – 384 с.
3. Кузичев, А. С. Диаграммы Венна. История и применения / А.С. Кузичев. – М.: Наука, 1968. – 249 с.
4. Нефедов, В.Н., Осипова, В.А. Курс дискретной математики / В.Н. Нефедов, В.А. Осипова. – М.: МАИ, 1992. – 264 с.
5. Никифоров, А.Л. Общедоступная и увлекательная книга по логике / А.Л. Никифоров. – М.: Гнозис, 1996. – 240 с.
6. Столл, Р. Множества, логика, аксиоматические теории / Р. Столл. – М.: Мир, 1968. – 231 с.
7. Челпанов, Г.И. Учебник логики / Г.И. Челпанов. – М.: «Прогресс», 1994. – 248 с.
8. About Eric Weisstein, Creator of MathWorld http://mathworld. wolfram.com/.
wolfram.com/.
| Онлайн-инструмент для построения диаграмм Эйлера
Creately уже используют более 10 миллионов человек и тысячи команд.
ВИЗУАЛИЗИРУЙТЕ
Создавайте диаграммы Эйлера без усилий
Шаблоны диаграмм Эйлера для различных сценариев.
Используя пользовательские цветовые темы и шрифты, выделяйте и маркируйте контуры и зоны.
Нарисуйте диаграммы Эйлера с невыпуклыми контурами, используя рисунок от руки.
Импортируйте или перетаскивайте изображения, графику и т. д. для создания визуально динамичных диаграмм Эйлера.
ПОДКЛЮЧАЙТЕ И ОРГАНИЗУЙТЕ
Добавьте больше контекста к вашей диаграмме Эйлера
Добавьте больше информации о различных зонах с интегрированными примечаниями.

библиотек форм для более чем 50 типов диаграмм для дальнейшего расширения диаграмм Эйлера.
Создавайте интерактивные презентации с помощью встроенных инструментов, таких как рамки, режим просмотра и т. д.
СОТРУДНИЧАТЬ
Сотрудничайте с другими в любое время и в любом месте
Совместная работа в режиме реального времени для работы со студентами или коллегами на общем холсте.
Комментарий с контекстом, чтобы обсуждения и последующие действия были на одном холсте. Асинхронно!
Автономная синхронизация для постоянной синхронизации вашей работы.
Экспортируйте свои диаграммы в несколько форматов изображений для встраивания, печати или совместного использования.
Что такое диаграмма Эйлера?
Диаграмма Эйлера — это графическое изображение, обычно используемое для иллюстрации отношений между наборами или группами; диаграммы обычно рисуются в виде кругов или овалов, хотя их можно рисовать и в других формах.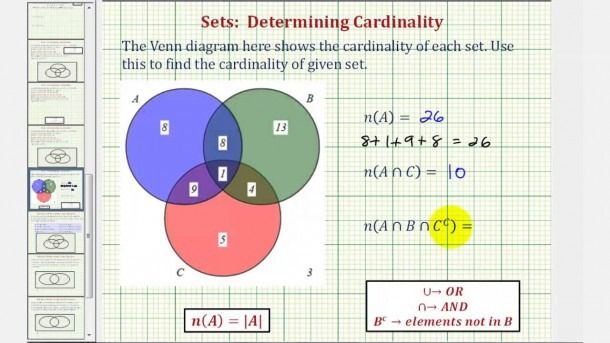 Диаграммы Эйлера могут быть полезны в ситуациях, когда диаграммы Венна могут быть слишком сложными или неясными, и они предлагают более гибкий и адаптируемый способ представления множеств и отношений.
Диаграммы Эйлера могут быть полезны в ситуациях, когда диаграммы Венна могут быть слишком сложными или неясными, и они предлагают более гибкий и адаптируемый способ представления множеств и отношений.
Что такое генератор диаграмм Эйлера?
Генератор диаграмм Эйлера — это онлайн-инструмент, который позволяет легко создавать диаграммы Эйлера и делиться ими. Они предоставляют формы, цветовые темы, параметры импорта и экспорта изображений, а также готовые шаблоны для настройки и быстрого старта.
Как пользоваться генератором диаграмм Эйлера от Creately?
Создатель диаграмм Эйлера от Creately прост в использовании и интуитивно понятен. Он поставляется с множеством шаблонов диаграмм Эйлера, разработанных для нескольких сценариев, и возможностями настройки диаграмм для создания динамических диаграмм Эйлера. Вы можете сразу начать с одного из готовых шаблонов диаграммы Эйлера или начать с нуля, перетащив круги на холст. Затем приступайте к дальнейшей настройке, добавляя цвета, изображения или значки.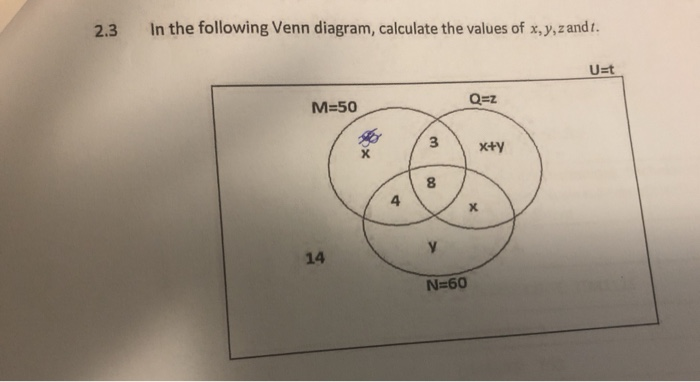
Как я могу поделиться своей диаграммой Эйлера?
Генератор диаграмм Эйлера от Creately предоставляет несколько вариантов обмена диаграммами Эйлера. Вы можете экспортировать свою диаграмму Эйлера в формате PNG, SVG, JPEG или PDF для встраивания в документы или презентации, или вы можете поделиться ссылкой с правами редактирования или просмотра с человеком, с которым вы хотите поделиться диаграммой. Вы также можете использовать ссылку для встраивания, чтобы встроить диаграмму Эйлера на любой сайт или в интранет, или использовать режим просмотра в редакторе, чтобы сразу представить диаграмму.
Оптимизируйте свои рабочие процессы за счет интеграции с любимыми инструментами
Creately интегрируется с инструментами, которые ваши команды используют каждый день, и беспрепятственно поддерживает рабочий процесс вашей команды.
Начать пробную версию
Почему Creately является лучшим генератором диаграмм Эйлера
Creately — это интеллектуальная визуальная платформа, обеспечивающая визуальную совместную работу, управление знаниями и выполнение проектов.
Более 100 фирменных функций обеспечивают гибкую, не требующую кода визуальную платформу, профессионально настроенную для простоты использования.
Бесконечный визуальный холст
Визуально создавайте и организуйте любую структуру, которую вы себе представляете. Перетаскивайте фигуры или наборы данных, встраивайте внешний контент.
Совместная работа в режиме реального времени
Работайте удаленно или гибридно с отслеживанием курсора в реальном времени, синхронизированным предварительным просмотром и правильными контекстными комментариями и задачами.
Пользовательские базы данных
Создавайте пользовательские базы данных для любого вида информации, от задач, кадровых записей до вопросов для юридических фирм.
Документы, управляемые данными
Создавайте документы и заметки, чтобы углубиться в визуальные представления высокого уровня. Двусторонняя ссылка на другие документы, фигуры или данные с помощью @mentions.
Профессиональное построение диаграмм
Более 50 типов стандартных схем с более чем 1000 специально разработанных форм и соединителей обеспечивают молниеносное построение диаграмм.
Управление проектами и задачами
Используйте встроенные инструменты гибкого управления проектами или интегрируйте их с вашими любимыми инструментами управления проектами, чтобы обеспечить бесперебойную работу.
Масштабируемость предприятия
От SSO, SCIM до четко определенных рабочих процессов адаптации и увольнения сотрудников Creately может масштабироваться для удовлетворения различных потребностей предприятия.
Мощное визуальное моделирование
Визуальные элементы, поддерживаемые базами данных, обновляются один раз, отражают рабочие процессы в нескольких представлениях.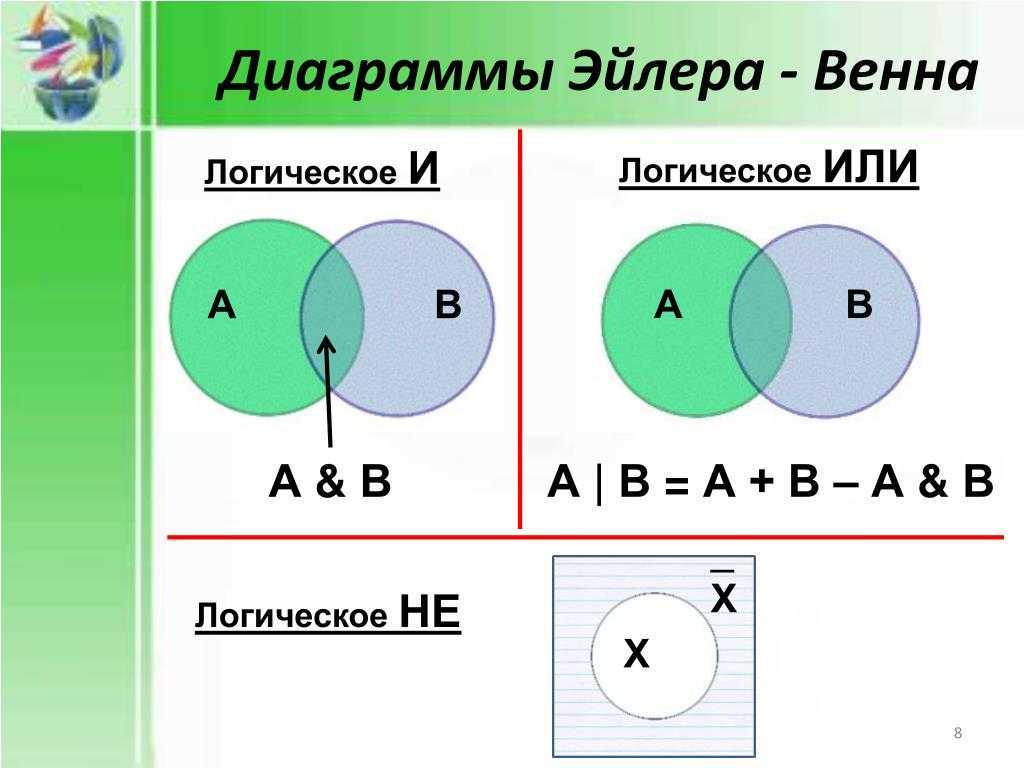
Безопасность и соответствие требованиям корпоративного уровня
Мы обеспечиваем конфиденциальность и информационную безопасность как клиентов, так и пользователей с помощью усиленных мер безопасности данных, соответствующих отраслевым стандартам безопасности. Creately соответствует требованиям GDPR и предназначен для обеспечения конфиденциальности, безопасности и сохранности ваших данных. Создать безопасность
Просто подключи и работай
Простой в использовании интерфейс с минимальными затратами на обучение. Просто войдите в систему, используя свой рабочий адрес электронной почты, чтобы автоматически добавить членов команды в корпоративный план. Установка не требуется.
Зарегистрируйте бесплатную учетную запись сегодня.
Формула Эйлера для комплексных чисел
(Есть еще одна «Формула Эйлера» о геометрии ,
эта страница посвящена формуле, используемой в комплексных числах)
Во-первых, вы, возможно, видели известную «Тождество Эйлера»:
e
Кажется совершенно волшебным, что такое аккуратное уравнение объединяет:
- 9014 7 e (число Эйлера)
- i (мнимый номер блока)
- π (знаменитое число пи, которое встречается во многих интересных областях)
- 1 (первое счетное число)
- 0 (ноль)
А также основные операции сложения, умножения и возведения в степень!
Но если вы хотите совершить интересное путешествие по математике, вы узнаете, как она возникает.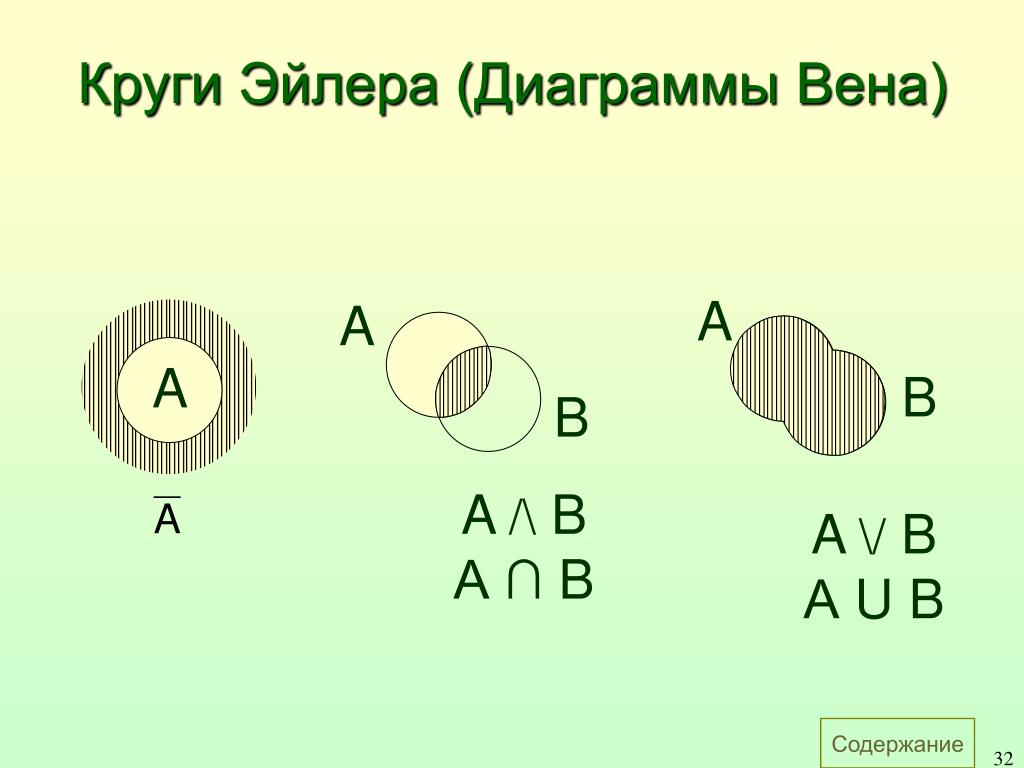
Заинтересованы? Читай дальше!
Открытие
Это было около 1740 года, и математики интересовались мнимыми числами.
Воображаемое число, возведение в квадрат которого дает отрицательный результат
Обычно это невозможно (попробуйте возвести в квадрат некоторые числа, помня, что умножение отрицательных чисел дает положительный результат, и посмотрите, сможете ли вы получить отрицательный результат), но просто представьте, что вы может сделать это!
И у нас может быть этот специальный номер (называемый i для воображаемого):
i 2 = −1
Леонард Эйлер однажды развлекался, играя с воображаемыми числа (или мне так кажется!), и он взял этот известный ряд Тейлора (почитайте о них, они очаровательны):
e x = 1 + x + x 2 2! + х 3 3! + х 4 4! + х 5 5! + . ..
..
И он положил в него i :
e ix = 1 + ix + (ix) 2 9 0230
А потому что i 2 = −1 , это упрощается до:
e ix = 1 + ix − x 2 2! − ix 3 3! + х 4 4! + ix 5 5! − …
Теперь сгруппируйте все термины i в конце:
e ix = ( 1 − x 90 157 2 2! + х 4 4! − … ) + i( x − x 3 3! + x 5 5! − . .. )
.. )
А вот и чудо… две группы на самом деле являются рядом Тейлора для cos и sin :
| cos x = 1 − x 2 2 ! + х 4 4! — … |
| sin x = x − x 3 3! + х 5 5! — … |
Таким образом, это упрощается до:
e i x = cos x + i 9 0150 sin x
Должно быть, он был так счастлив, когда обнаружил это!
И теперь она называется Формула Эйлера .
Давайте попробуем:
Пример: когда x = 1,1
e i x = cos x + i sin x
e 1.1i = cos 1. 1 + i sin 1.1
1 + i sin 1.1
e 1.1i = 0,45 + 0,89 i (до 2 знаков после запятой)
Примечание. Мы используем радианы, а не градусы.
Ответ представляет собой комбинацию действительного и мнимого чисел, которые вместе называются комплексным числом.
На комплексной плоскости можно нанести такое число (действительные числа идут слева направо, а мнимые вверх-вниз):
Здесь мы показываем число 0,45 + 0,89 i
То же, что и e 1.1i
Давайте построим еще!
Круг!
Да, нанесение формулы Эйлера на этот график дает круг:
e i x дает круг радиусом 1
И когда мы включаем радиус r , мы можем повернуть любую точку (например, 3 + 4i ) в re i x найдите правильное значение x и r :
Пример: число
3 + 4iПревратить 3 + 4i в re i x делаем декартово преобразование в полярное:
- r = √(3 2 + 4 2 9 0162 ) = √(9+16) = √25 = 5
- x = тангенс -1 ( 4 / 3 ) = 0,927 (до 3 десятичных знаков)
Таким образом, 3 + 4i также может быть 5 e 0,927 i
900 05
Это другая форма
По сути, это еще один способ получить комплексное число.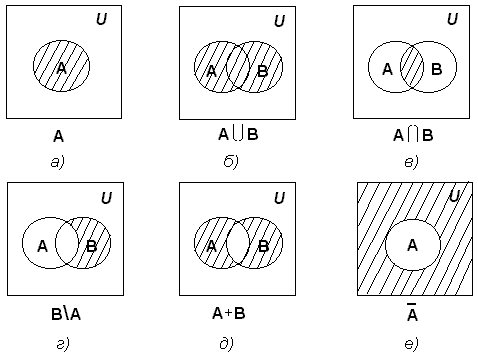

 Судоку
Судоку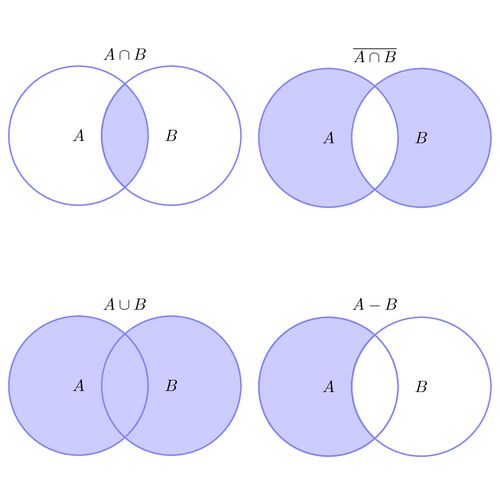 А ведь правила можно…
А ведь правила можно…