Запись десятичных дробей целыми числами по образцу. 7-й класс
- Доркина Людмила Владимировна, учитель математики
Разделы: Математика
Класс: 7
Программа: – Программа специальных коррекционных общеобразовательных учреждений VIII вида 5-9 классы (сборник 1), 2000 год, под редакцией В.В.Воронковой
Учебник: Т.В.Алышева “Математика”. 7 класс. Учебник для специальных (коррекционных) образовательных учреждений VIII вида. Москва “Просвещение” 2005 г.
Цели урока:
- Закрепить знания о десятичной дроби.

- Повторить определения по данной теме, закрепить умение переводить именованные числа в десятичные дроби.
- Познакомить с новым приемом перевода десятичной дроби в целое число, выраженное именованным числом.
- Развивать речь посредством математических терминов, учить делать выводы.
- Развивать умение комментировать свои действия.
Ход урока
“Человек подобен дроби: в знаменателе – то, что он о себе думает, в числителе – то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь”
Л.Н. Толстой
1. Орг. момент.
Ребята, у нас сегодня необычный урок. Вы видите,
что у нас гости. И мне хотелось бы , что бы вы
работали хорошо на уроке. Давайте проверим , с
каким настроением вы пришли на урок? И с каким
настроением мы начинаем работать? У каждого на
столе лежат смайлики.
.
И мы постараемся в ходе урока “отличное настроение” не ухудшить, а равнодушие и плохое настроение улучшить.
Обратить внимание на слова Толстого, как понимают?
Записываем число и классная работа.
2. Сообщение темы и цели урока.
– Какие бывают дроби? (обыкновенные и десятичные)
– Чем отличаются? (ответ) (памятки)
– Что показывает числитель дроби?
– Что показывает знаменатель?
3 ц 5 кг = 3,05 ц
1 км 265 м = 1,265 км
4,2 дм = …дм …см ? (проблема)
Как вы думаете чем мы будем заниматься на уроке? (Переводить десятичную дробь в целое число)
3.
 Изучение нового.
Изучение нового.
Вспомним и составим таблицу:
Десятая доля метра? … дм
Десятая доля дм? ….см
Десятая доля см? …мм
Десятая доля тонны?….ц0,1 м = 1 дм
0,1 дм = 1 см
0,1 см = 1 мм
0,1 т = 1 ц
Выполняем по образцу:
4,2 дм = 4 дм 2 см ( с пояснение) (1 ДМ = 10 СМ, 1 см =1/10 дм, целая часть 4 – это дм, десятая 2 – это см)
Работа с учебником. № 703 (3) по рядам а) первый ряд; б) второй ряд; в) третий ряд.
3 человека у доски. Проверка.
4. Физминутка.
5. Закрепление.
№ 707 (чертеж с пояснением) – практическое применение.
АВ = 6,3 см = 6 см 3 мм
ВС = 1,1 дм = 1 дм 1 см = 11 см и т. д.
6. Итог урока.
Собрать правило:
десятые доли метра = центнер
десятые доли дециметра = миллиметр
десятые доли сантиметра = дециметр
десятые доли тонны = сантиметр
7.
 Рефлексия.
Рефлексия.
– Чем занимались на уроке?
– Что нового узнали? Чему научились?
– Кто был активным на уроке?
– Какие оценки поставим?
– С каким настроением закончили урок? (смайлики)
Обратиться к словам Толстого : согласны с его высказыванием и почему? (попробовать обосновать, высказать свое мнение)
Оценки.
Спасибо всем за урок.
Как сравнить разные дроби. Персонажи, используемые для записи в калькуляторе
Вчера термометр показывал 15˚ C, а сегодня показывает 20˚ C. Сегодня теплее, чем вчера. Число 15 меньше числа 20, можем записать так: 15
А сейчас рассмотрим отрицательные температуры. Вчера на улице было -12˚ C, а сегодня -8˚ C. Сегодня теплее, чем вчера. Поэтому считают, что число -12 меньше числа -8. На горизонтальной координатной прямой точка со значением -12 расположена левее точки со значением -8. Можем записать так: -12
На горизонтальной координатной прямой точка со значением -12 расположена левее точки со значением -8. Можем записать так: -12
Итак, если сравнивать числа с помощью горизонтальной координатной прямой, из двух чисел меньшим считается то, изображение которого на координатной прямой расположено левее, а большим то, изображение которого расположено правее. Например, у нас на рисунке А > B и C, но B > C.
На координатной прямой положительные числа располагаются справа от нуля, а отрицательные – слева от нуля, всякое положительное число больше нуля, а всякое отрицательное меньше нуля, и поэтому всякое отрицательное число меньше всякого положительного числа.
Значит, первое на что необходимо обратить внимание при сравнении чисел, – это знаки сравниваемых чисел. Число с минусом (отрицательное) всегда меньше положительного.
Если же мы сравниваем два отрицательных числа, то нужно сравнить их модули: большим будет то число, модуль которого меньше, а меньшим то число, модуль которого меньше. Например, -7 и -5. Сравниваемые числа – отрицательные. Сравниваем их модули 5 и 7. 7 больше чем 5, значит -7 меньше чем -5. Если отметить на координатной прямой два отрицательных числа, то левее окажется меньшее число, а большее будет расположено правее. -7 расположено левее -5, значит -7
Например, -7 и -5. Сравниваемые числа – отрицательные. Сравниваем их модули 5 и 7. 7 больше чем 5, значит -7 меньше чем -5. Если отметить на координатной прямой два отрицательных числа, то левее окажется меньшее число, а большее будет расположено правее. -7 расположено левее -5, значит -7
Сравнение обыкновенных дробей
Из двух дробей с одинаковыми знаменателями меньше та, у которой меньше числитель, и больше та, у которой больше числитель.
Можно сравнивать дроби только с одинаковыми знаменателями.
Алгоритм сравнения обыкновенных дробей
1) Если у дроби есть целая часть, сравнение начинаем именно с неё. Большей будет та дробь, у которой целая часть больше. Если целой части у дробей нет или они равны, переходим к следующему пункту.
2) Если дроби с разными знаменателями необходимо привести их к общему знаменателю.
3) Сравниваем числители дробей. Большей будет та дробь, у которой числитель больше.
Обратите внимание, дробь с целой частью всегда будет больше дроби без целой части.
Сравнение десятичных дробей
Десятичные дроби можно сравнивать только с одинаковым количеством цифр (знаков) справа от запятой.
Алгоритм сравнения десятичных дробей
1) Обращаем внимание на количество знаков справа от запятой. Если количество цифр одинаковое, можем приступать к сравнению. Если – нет, дописываем нужное количество нулей в одной из десятичных дробей.
2) Сравниваем десятичные дроби слева направо: целые с целыми, десятые с десятыми, сотые с сотыми и т.д.
3) Большей будет та дробь, в которой одна из частей окажется больше, чем в другой дроби (сравнение начинаем с целых чисел: если целая часть одной дроби больше, значит, и вся дробь больше).
Например, сравним десятичные дроби:
1) Допишем в первой дроби необходимое количество нулей, чтобы уравнять количество знаков после запятой
57,300 и 57,321
2) Сравнивать начинаем слева направо:
целые с целыми: 57 = 57;
десятые с десятыми: 3 = 3;
сотые с сотыми: 0
Так как сотые первой десятичной дроби оказались меньше, вся дробь и будет меньше:
57,300
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Сравнить две дроби – значит определить, какая из дробей больше, какая меньше или установить, что дроби равны.
Сравнение дробей с одинаковыми числителями
При сравнении двух дробей, у которых одинаковые числители, больше будет та дробь, у которой знаменатель меньше.
Например, больше , так как количество взятых долей в обеих дробях одинаковое, но первая дробь содержит более крупные доли, чем вторая:
Сравнение дробей с одинаковыми знаменателями
При сравнении двух дробей, у которых одинаковые знаменатели, больше будет та дробь, у которой числитель больше.
Например, меньше , так как первая дробь содержит меньше взятых долей, чем вторая:
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После приведения дробей к общему знаменателю, их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.
Например, сравним две дроби: и . Приводим их к общему знаменателю:
Приводим их к общему знаменателю:
Теперь сравниваем их:
так как , значит
Равенство дробей
Две обыкновенные дроби считаются равными, если равны их числители и знаменатели или, если они выражают одну и ту же часть единицы.
Сравнение дроби с натуральным числом
Правильная дробь меньше любого натурального числа.
Чтобы сравнить неправильную дробь с натуральным числом, нужно натуральное число представить в виде неправильной дроби, затем привести дроби к общему знаменателю. После приведения дробей к общему знаменателю, их сравнивают по правилу сравнения дробей с одинаковыми знаменателями.
Пример. Сравним неправильную дробь с числом 5.
1. Переводим натуральное число в неправильную дробь:
2. Приводим дроби к общему знаменателю:
3. Сравниваем:
так как , значит
Онлайн калькулятор сравнения дробей
Данный калькулятор поможет вам сравнить обыкновенные дроби. Просто введите две дроби и нажмите кнопку.
описание
Вам не нужно иметь навыки программирования для написания сложных сценариев или тратить время на классифицирование классифицированных программ — Excel или Word.
Как сравнить фракции
Теперь вы можете использовать готовые решения в повседневной работе.
Алгоритм поможет сразу отсортировать значения в алфавитном и обратном порядке, чтобы строить данные по количеству символов в слове или любому значению символа.
инструкции
Инструмент отлично справляется с добавленной стоимостью в столбце и отдельными словами, заданными запятой или пробелом.
Скопируйте данные, необходимые для сортировки в левом окне, укажите одну из четырех функций и нажмите кнопку Сортировать по .
По умолчанию он доступен Алфавитный порядок (A — R / 0 — 9) .
По выбору Обратный порядок (H — A / 9 — 0) , алгоритм сразу отображает матрицу в обратном направлении.
черты Значения на длину (от малого до большого) и Значения по длине (от более высокой до нижней) работайте по аналогичному принципу, но сортировка основана на количестве символов в строке.
Написать комментарий
Для меня важно знать, как работает служба и как ее можно улучшить. Написать комментарий по почте [email protected] или в нижней форме.
Как работать с калькулятором регулярных фракций?
Калькулятор предназначен для спасения простые фракции и фракции с целыми числами (смешанный ). Функция десятичных дробей запланирована в будущем, но в настоящее время она недоступна.
Чтобы начать работу с частичным калькулятором, вам нужно понять очень простой принцип ввод данных.
Все целые числа вводятся с помощью больших кнопок слева. Все счетчики вводятся с маленькими белыми кнопками, расположенными в верхней правой части цифр. Все символы вводятся нажатием кнопки в правом нижнем углу. Метод ввода данных является своего рода инновационным, поскольку он четко описывает весь числитель и знаменатель, который позволяет проводить расчеты, экономит время и позволяет более эффективно взаимодействовать с использованием. », а затем на номер шесть на главной клавиатуре.
», а затем на номер шесть на главной клавиатуре.
В результате мы получаем готовый пример:
в настоящее время Нажмите эквивалентную кнопку и перейдите стоимость результата .
В приведенном выше примере показан почти весь арсенал дробных калькуляторов. Вы можете сделать то же самое так же размножение, деление и вычитание фракций , так же просто, как алгебраические, с одинаковыми и разными знаменателями, целыми числами и т. д.
Калькулятор также может рассчитывать фракции из фракций, что не часто требуется, но тем не менее очень важно решить ряд неотложных проблем.
Чтобы получить положительное отрицательное число, сначала введите номер и нажмите кнопку «+/-».
После этого число или часть автоматически завертываются в скобки с отрицательным значением или наоборот (в зависимости от начального состояния номера). Чтобы удалить число, счетчик или знаменатель, используйте соответствующую стрелку возврат на одну позицию , который находится в блоке как числителя, так и знаменателя.
Стрелки работают одинаково, а затем удаляют номера или символы на экране компьютера.
Управляйте частичным калькулятором с клавиатуры.
Используйте его Калькулятор веб-фракций не только с компьютерной мышью, но и с клавиатурой.
Логика очень проста:
- Все вводится как обычно, нажимая цифровые клавиши.
- Все счетчики вводятся путем добавления клавиши CTRL (например, CTRL + 1).
- Все знаменатели вводятся путем добавления клавиши ALT (например, ALT + 2).
Меры умножения, деления, добавления и вычитания, а также запуска соответствующих клавиш на клавиатуре, если они есть (обычно расположены с правой стороны, так называемая область Numpad).
Удаление выполняется нажатием клавиши Backspace. Очистка (красная кнопка «C») запускается нажатием клавиши «C». Квадратный корень — нажатием соседней клавиши «V».
Удаление выполняется нажатием клавиши Backspace.
Зачем вам нужен онлайн-калькулятор?
Дробный калькулятор онлайн предназначен для обработки гладкий и смешанный дробей (с целым числом).
Решение фракций часто необходимо для студентов и студентов, а также для инженеров и выпускников. Наш калькулятор позволяет создавать следующие действия с частицами: расщепление фракций, умножение фракций, добавление фракций и вычитание фракций . Калькулятор также может работать с корнями и ставками, а также с отрицательными числами, что делает его несколько раз превышает аналогичные веб-приложения.
Простой калькулятор фракционной дроби онлайн поможет вам решить дела с фракциями, поэтому вам не нужно беспокоиться о том, как противодействовать фракции.
Он становится здесь автоматически , поскольку само приложение вычисляет общий знаменатель и, наконец, показывает конечный результат.
Каковы преимущества этого метода для решения фракций?
калькулятор поддерживает работу с скобками , что позволяет решать фракции, даже в сложных математических случаях. Кампании часто необходимы для скобок алгебраические дроби или отрицательные фракции , над которыми мы должны постоянно избегать всех учащихся средних школ.
Калькулятор для сравнения фракций
Кроме того, вы можете использовать этот калькулятор сокращение фракций или дробные растворы с разными знаменателями . Кроме того, этот калькулятор, в отличие от многих других бесплатных сервисов, может работать с двумя, тремя, четырьмя и вообще с любым количеством дробей и чисел.
Калькулятор регулярных фракций абсолютно бесплатно и не требует регистрации.
Вы можете использовать его в любое время дня и ночи. Вы можете сделать это с помощью мыши или непосредственно с клавиатуры (это относится к числу и действиям). Мы попытались реализовать максимум удобный интерфейс частичные вычисления, которые делают сложные математические расчеты меняющимися в одно удовольствие!
Сравнение обыкновенных дробей
Удобный и простой онлайн-калькулятор фракций с точным решением вы можете:
- Складывайте, вычитайте, размножайте и размещайте фрагменты в Интернете,
- Получите частичное решение изображения и просто загрузите его.

Результат фракций будет здесь …
Наш калькулятор онлайн-калькуляторов имеет быстрый ввод .
Например, если вы хотите получить частичное решение , просто введите 1/2 + 2/7 в калькулятор и нажмите кнопку «Rescue Faction».
Калькулятор напишет вам детальное решение фракций и вопросы легко скопировать изображение .
Персонажи, используемые для записи в калькуляторе
Вы можете ввести пример решения с клавиатуры или с помощью кнопки.
Характеристики калькулятора веб-фракций
Калькулятор фракций может выполнять операции только с двумя простыми фракциями.
Они могут быть правильными (счетчик меньше знаменателя) или неверны (счетчик больше знаменателя). Числа в числителе и знаменателе не должны быть отрицательными и больше 999.
Наш онлайн-калькулятор принимает решения по фракциям и направляет ответ на правильный формат — уменьшает долю и, при необходимости, назначает всю часть.
Просто используйте свойства минус, чтобы сохранить отрицательные части. При умножении и делении отрицательных дробей знак плюс добавляет плюс. Это означает, что продукт и распределение отрицательных дробей идентичны произведению и распределению того же положительного. Если фракция отрицательная, если вы ее умножаете или делите, удалите минус и добавьте ее в ответ. При добавлении отрицательных фракций результат будет таким же, как добавление одинаковых положительных пропорций.
При умножении и делении отрицательных дробей знак плюс добавляет плюс. Это означает, что продукт и распределение отрицательных дробей идентичны произведению и распределению того же положительного. Если фракция отрицательная, если вы ее умножаете или делите, удалите минус и добавьте ее в ответ. При добавлении отрицательных фракций результат будет таким же, как добавление одинаковых положительных пропорций.
Если вы добавите одну отрицательную долю, то это то же самое, что и вычесть тот же самый положительный результат.
При вычитании отрицательных дробей результат будет таким же, как если бы они были изменены в местах и стали положительными.
Сравнение фракций
Это означает, что минус минус в этом случае дает плюс, и сумма не изменяется от суммы. Те же правила, которые мы используем при подсчете фракций, один из которых отрицателен.
Чтобы решить смешанные фракции (фракции, в которых размещена вся часть), просто заполните всю фракцию во фракцию.
Чтобы сделать это, умножьте всю часть на знаменатель и добавьте его в счетчик.
Если вы хотите сохранить 3 или более акций в Интернете, они должны быть приняты. Во-первых, подсчитайте первые две фракции, затем с полученным ответом определите следующую долю и так далее. Выполните операции на линии 2 фракций, и в конце вы получите правильный ответ.
Зачем принимать решения в калькуляторе
Решения в калькуляторе должны узнать, как сохранить дроби.
Калькулятор не имеет намерения решать фракции для вас.
Это не универсальный резак, это инструмент обучения. Это поможет вам понять решение, так что вы можете легко решить фракции самостоятельно. В дополнение к учебному калькулятору мы также рекомендуем изучить наши материалы: «Как разрешить фракции». Решение фракций. «
Если вы заметили какие-либо ошибки или неудобства при использовании калькулятора, пожалуйста, свяжитесь с нами в комментариях. Насколько это возможно, мы закончим калькулятор!
Онлайн калькулятор. Сравнение фракций.
Студент видит на экране несколько номеров с интересной цветовой схемой. Эти числа расположены в случайном порядке. Ребенок, который знает правильный порядок учетной записи, должен отредактировать от малого до большого. Проблема с упражнением заключается в том, что цифры, показанные на рисунке, не обязательно идут один за другим.
Эти числа расположены в случайном порядке. Ребенок, который знает правильный порядок учетной записи, должен отредактировать от малого до большого. Проблема с упражнением заключается в том, что цифры, показанные на рисунке, не обязательно идут один за другим.
Фактически, промежутки между ними могут быть важными. Но студент, который выполняет эту задачу, должен помнить, какой из чисел больше и меньше. Когда ребенок создает последовательность, он немедленно переходит на следующий уровень (если ответ правильный) или после просмотра правильной опции — если он совершает ошибку.
Это упражнение не только развивает логическое мышление, оно учит вас анализировать и готовить последовательные выводы из образа, но также помнить о правильной последовательности чисел при подсчете.
Порядок увеличения является естественным для многих партий, поэтому ребенок может легко обнаружить его.
Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.
Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.
Yandex.RTB R-A-339285-1
Сравнение дробей с одинаковыми знаменателями
Когда производится сравнение дробей с одинаковыми знаменателями, мы работаем только с числителем, а значит, сравниваем доли числа. Если имеется дробь 3 7 , то она имеет 3 доли 1 7 , тогда дробь 8 7 имеет 8 таких долей. Иначе говоря, если знаменатель одинаковый, производится сравнение числителей этих дробей, то есть 3 7 и 8 7 сравниваются числа 3 и 8 .
Отсюда следует правило сравнения дробей с одинаковыми знаменателями:из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.
Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.
Пример 1
Произвести сравнение заданных дробей 65 126 и 87 126 .
Решение
Так как знаменатели дробей одинаковые, переходим к числителям. Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87 126 больше 65 126 .
Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87 126 больше 65 126 .
Ответ: 87 126 > 65 126 .
Сравнение дробей с разными знаменателями
Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.
Если имеются дроби с разными знаменателями, для их сравнения необходимо:
- найти общий знаменатель;
- сравнить дроби.
Рассмотрим данные действия на примере.
Пример 2
Произвести сравнение дробей 5 12 и 9 16 .
Решение
В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16 . Это число 48 . Необходимо надписать дополнительные множители к первой дроби 5 12 , это число находится из частного 48: 12 = 4 , для второй дроби 9 16 – 48: 16 = 3 . Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 .
Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 .
После сравнения дробей получаем, что 20 48
Ответ: 5 12
Имеется еще один способ сравнения дробей с разными знаменателями. Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби a b и c d , приводим к общему знаменателю, тогда b · d , то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a · d b · d и c · b d · b . Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a · d и c · b . Отсюда получаем правило сравнения дробей с разными знаменателями:если a · d > b · c , тогда a b > c d , но если a · d
Пример 3
Произвести сравнение дробей 5 18 и 23 86 .
Решение
Данный пример имеет a = 5 , b = 18 , c = 23 и d = 86 . Тогда необходимо вычислить a · d и b · c . Отсюда следует, что a · d = 5 · 86 = 430 и b · c = 18 · 23 = 414 . Но 430 > 414 , тогда заданная дробь 5 18 больше, чем 23 86 .
Отсюда следует, что a · d = 5 · 86 = 430 и b · c = 18 · 23 = 414 . Но 430 > 414 , тогда заданная дробь 5 18 больше, чем 23 86 .
Ответ: 5 18 > 23 86 .
Сравнение дробей с одинаковыми числителями
Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.
Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.
Рассмотрим на примере.
Пример 4
Произвести сравнение дробей 54 19 и 54 31 .
Решение
Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31 . Это понятно, исходя из правила.
Ответ: 54 19 > 54 31 .
Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 1 2 пирога, анна другой 1 16 . Если съесть 1 2 пирога, то насытишься быстрей, нежели только 1 16 . Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.
Если съесть 1 2 пирога, то насытишься быстрей, нежели только 1 16 . Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.
Сравнение дроби с натуральным числом
Сравнение обыкновенной дроби с натуральным числом идет как и сравнение двух дробей с записью знаменателей в виде 1 . Для детального рассмотрения ниже приведем пример.
Пример 4
Необходимо выполнить сравнение 63 8 и 9 .
Решение
Необходимо представить число 9 в виде дроби 9 1 . Тогда имеем необходимость сравнения дробей 63 8 и 9 1 . Далее следует приведение к общему знаменателю путем нахождения дополнительных множителей. После этого видим, что нужно сравнить дроби с одинаковыми знаменателями 63 8 и 72 8 . Исходя из правила сравнения, 63
Ответ: 63 8
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.
Она позволит новичку почувствовать себя учёным в белом халате.
Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.
Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются , такими как больше (>) или меньше (
Ученые-математики уже позаботились о готовых правилах, позволяющие сразу ответить на вопрос какая дробь больше, а какая меньше. Эти правила можно смело применять.
Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.
Содержание урока
Сравнение дробей с одинаковыми знаменателямиДроби, которые нужно сравнить, попадаются разные. Самый удачный случай это когда у дробей одинаковые знаменатели, но разные числители. В этом случае применяют следующее правило:
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. И соответственно меньше будет та дробь, у которой числитель меньше.
Например, сравним дроби и и ответим, какая из этих дробей больше. Здесь одинаковые знаменатели, но разные числители. У дроби числитель больше, чем у дроби . Значит дробь больше, чем . Так и отвечаем. Отвечать нужно с помощью значка больше (>)
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем пиццы:
Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с одинаковыми числителямиСледующий случай, в который мы можем попасть, это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.
Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:
пиццы больше, чем пиццы:
Каждый согласиться с тем, что первая пицца больше, чем вторая.
Сравнение дробей с разными числителями и разными знаменателями
Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями.
Например, сравнить дроби и . Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.
Приведём дроби и к одинаковому (общему) знаменателю. Найдём (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.
Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:
Теперь найдём второй дополнительный множитель. Разделим НОК на знаменатель второй дроби . НОК это число 6, а знаменатель второй дроби это число 3. Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:
Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:
Умножим дроби на свои дополнительные множители:
Мы пришли к тому, что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.
После выделения целой части в дроби , получим следующее выражение:
Теперь можно легко понять, почему больше, чем . Давайте нарисуем эти дроби в виде пицц:
2 целые пиццы и пиццы, больше чем пиццы.
Вычитание смешанных чисел. Сложные случаи.Вычитая смешанные числа, иногда можно обнаружить, что всё идёт не так гладко, как хотелось бы. Часто случается так, что при решении какого-нибудь примера ответ получается не таким, каким он должен быть.
При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.
Например, 10−8=2
10 — уменьшаемое
8 — вычитаемое
2 — разность
Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.
А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5−7=−2
5 — уменьшаемое
7 — вычитаемое
−2 — разность
В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.
Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.
С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.
Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.
Например, решим пример .
Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем
поэтому смело можем вернуться к примеру и решить его:
Теперь решим такой пример
Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:
В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.
Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .
Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать, как это сделать. Если испытываете затруднения, обязательно повторите .
Не будем подробно расписывать, как это сделать. Если испытываете затруднения, обязательно повторите .
После приведения дробей к одинаковому знаменателю, получаем следующее выражение:
Теперь нужно сравнить дроби и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .
А это значит, что уменьшаемое больше, чем вычитаемое
А значит мы можем вернуться к нашему примеру и смело решить его:
Пример 3. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю.
Продолжаем изучать рациональные числа. В данном уроке мы научимся сравнивать их.
Из предыдущих уроков мы узнали, что чем правее число располагается на координатной прямой, тем оно больше. И соответственно, чем левее располагается число на координатной прямой, тем оно меньше.
И соответственно, чем левее располагается число на координатной прямой, тем оно меньше.
Например, если сравнивать числа 4 и 1, то можно сразу ответить, что 4 больше чем 1. Это вполне логичное утверждение и каждый с этим согласится.
В качестве доказательства можно привести координатную прямую. На ней видно, что четвёрка лежит правее единицы
Для этого случая есть и правило, которое при желании можно использовать. Выглядит оно следующим образом:
Из двух положительных чисел больше то число, модуль которого больше.
Чтобы ответить на вопрос какое число больше, а какое меньше, сначала нужно найти модули этих чисел, сравнить эти модули, а потом уже ответить на вопрос.
Например, сравним те же числа 4 и 1, применяя вышеприведенное правило
Находим модули чисел:
|4| = 4
|1| = 1
Сравниваем найденные модули:
4 > 1
Отвечаем на вопрос:
4 > 1
Для отрицательных чисел существует другое правило, выглядит оно следующим образом:
Из двух отрицательных чисел больше то число, модуль которого меньше.
Например, сравним числа −3 и −1
Находим модули чисел
|−3| = 3
|−1| = 1
Сравниваем найденные модули:
3 > 1
Отвечаем на вопрос:
−3
Нельзя путать модуль числа с самим числом. Частая ошибка многих новичков. К примеру, если модуль числа −3 больше, чем модуль числа −1, это не означает, что число −3 больше, чем число −1.
Число −3 меньше, чем число −1 . Это можно понять, если воспользоваться координатной прямой
Видно, что число −3 лежит левее, чем −1 . А мы знаем, что чем левее, тем меньше.
Если сравнивать отрицательное число с положительным, то ответ будет напрашиваться сам. Любое отрицательное число будет меньше любого положительного числа. Например, −4 меньше, чем 2
Видно, что −4 лежит левее, чем 2. А мы знаем, что «чем левее, тем меньше».
Здесь в первую очередь нужно смотреть на знаки чисел. Минус перед числом будет говорить о том, что число отрицательное. Если знак числа отсутствует, то число положительное, но вы можете записать его для наглядности. Напомним, что это знак плюса
Напомним, что это знак плюса
Мы рассмотрели в качестве примера целые числа, вида −4, −3 −1, 2. Сравнить такие числа, а также изобразить на координатной прямой не составляет особого труда.
Намного сложнее сравнивать другие виды чисел, такие как обыкновенные дроби, смешанные числа и десятичные дроби, некоторые из которых являются отрицательными. Здесь уже в основном придётся применять правила, потому что точно изобразить такие числа на координатной прямой не всегда возможно. В некоторых случаях, число надо будет , чтобы сделать его более простым для сравнения и восприятия.
Пример 1. Сравнить рациональные числа
Итак, требуется сравнить отрицательное число с положительным. Любое отрицательное число меньше любого положительного числа. Поэтому не теряя времени отвечаем, что меньше, чем
Пример 2.
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то, модуль которого меньше.
Находим модули чисел:
Сравниваем найденные модули:
Пример 3. Сравнить числа 2,34 и
Сравнить числа 2,34 и
Требуется сравнить положительное число с отрицательным. Любое положительное число больше любого отрицательного числа. Поэтому не теряя времени отвечаем, что 2,34 больше, чем
Пример 4. Сравнить рациональные числа и
Находим модули чисел:
Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём в неправильные дроби и приведём к общему знаменателю
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Пример 5.
Требуется сравнить ноль с отрицательным числом. Ноль больше любого отрицательного числа, поэтому не теряя времени отвечаем, что 0 больше, чем
Пример 6. Сравнить рациональные числа 0 и
Требуется сравнить ноль с положительным числом. Ноль меньше любого положительного числа, поэтому не теряя времени отвечаем, что 0 меньше, чем
Пример 7 . Сравнить рациональные числа 4,53 и 4,403
Сравнить рациональные числа 4,53 и 4,403
Требуется сравнить два положительных числа. Из двух положительных чисел больше то число, модуль которого больше.
Сделаем в обеих дробях количество цифр после запятой одинаковым. Для этого в дроби 4,53 припишем в конце один ноль
Находим модули чисел
Сравниваем найденные модули:
Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число 4,53 больше, чем 4,403 потому что модуль числа 4,53 больше, чем модуль числа 4,403
Пример 8. Сравнить рациональные числа и
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше.
Находим модули чисел:
Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём смешанное число в неправильную дробь, затем приведём обе дроби к общему знаменателю:
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Сравнивать десятичные дроби намного проще, чем обыкновенные дроби и смешанные числа. В некоторых случаях, посмотрев на целую часть такой дроби, можно сразу ответить на вопрос какая дробь больше, а какая меньше.
Чтобы сделать это, нужно сравнить модули целых частей. Это позволит быстро ответить на вопрос в задаче. Ведь как известно, целые части в десятичных дробях имеют вес больший, чем дробные.
Пример 9. Сравнить рациональные числа 15,4 и 2,1256
Модуль целой части дроби 15,4 больше, чем модуль целой части дроби 2,1256
поэтому и дробь 15,4 больше, чем дробь 2,1256
15,4 > 2,1256
Другими словами, нам не пришлось тратить время на дописывание нулей дроби 15,4 и сравнивать получившиеся дроби, как обычные числа
154000 > 21256
Правила сравнения остаются всё теми же. В нашем случае мы сравнивали положительные числа.
Пример 10. Сравнить рациональные числа −15,2 и −0,152
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей
Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей
Видим, что модуль целой части дроби −15,2 больше, чем модуль целой части дроби −0,152.
А значит рациональное −0,152 больше, чем −15,2 потому что модуль целой части числа −0,152 меньше, чем модуль целой части числа −15,2
−0,152 > −15,2
Пример 11. Сравнить рациональные числа −3,4 и −3,7
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей. Но проблема в том, что модули целых чисел равны:
В этом случае придётся пользоваться старым методом: найти модули рациональных чисел и сравнить эти модули
Сравниваем найденные модули:
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное −3,4 больше, чем −3,7 потому что модуль числа −3,4 меньше, чем модуль числа −3,7
−3,4 > −3,7
Пример 12. Сравнить рациональные числа 0,(3) и
Сравнить рациональные числа 0,(3) и
Требуется сравнить два положительных числа. Причем сравнить периодическую дробь с простой дробью.
Переведём периодическую дробь 0,(3) в обыкновенную дробь и сравним её с дробью . После перевода периодической дроби 0,(3) в обыкновенную, она обращается в дробь
Находим модули чисел:
Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно приведём к общему знаменателю:
Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число больше, чем 0,(3) потому что модуль числа больше, чем модуль числа 0,(3)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Все правила с дробями и целыми числами. Чем полезны десятичные дроби. Арифметические действия над десятичными дробями
Калькулятор дробей предназначен для быстрого расчета операций с дробями, поможет легко дроби сложить, умножить, поделить или вычесть.
Современные школьники начинают изучение дробей уже в 5 классе, с каждым годом упражнения с ними усложняются. Математические термины и величины, которые мы узнаем в школе, редко могут пригодиться нам во взрослой жизни. Однако дроби, в отличие от логарифмов и степеней, встречаются в повседневности достаточно часто (измерение расстояния, взвешивание товара и т.д.). Наш калькулятор предназначен для быстрого проведения операций с дробями.
Для начала определим, что такое дроби и какие они бывают. Дробями называют отношение одного числа к другому, это число, состоящее из целого количества долей единицы.
Разновидности дробей:
- Обыкновенные
- Десятичные
- Смешанные
Пример обыкновенных дробей:
Верхнее значение является числителем, нижнее знаменателем. Черточка показывает нам, что верхнее число делится на нижнее. Вместо подобного формата написания, когда черточка находится горизонтально, можно писать по-другому. Можно ставить наклонную линию, например:
1/2, 3/7, 19/5, 32/8, 10/100, 4/1
Десятичные дроби являются самой популярной разновидностью дробей. Они состоят из целой части и дробной, отделенные запятой.
Они состоят из целой части и дробной, отделенные запятой.
Пример десятичных дробей:
0,2, или 6,71 или 0,125
Состоят из целого числа и дробной части. Чтобы узнать значение этой дроби, нужно сложить целое число и дробь.
Пример смешанных дробей:
Калькулятор дробей на нашем сайте способен быстро в онлайн-режиме выполнить любые математические операции с дробями:
- Сложение
- Вычитание
- Умножение
- Деление
Для осуществления расчета нужно ввести цифры в поля и выбрать действие. У дробей нужно заполнить числитель и знаменатель, целое число может не писаться (если дробь обыкновенная). Не забудьте нажать на кнопку «равно».
Удобно, что калькулятор сразу предоставляет процесс решения примера с дробями, а не только готовый ответ. Именно благодаря развернутому решению вы можете использовать данный материал при решении школьных задач и для лучшего освоения пройденного материала.
Вам нужно осуществить расчет примера:
После введения показателей в поля формы получаем:
Чтобы сделать самостоятельный расчет, введите данные в форму.
Калькулятор дробей
Введите две дроби:
| + — * : | |||||||
Сопутствующие разделы.
Примеры с дробями – один из основных элементов математики. Существует много разных типов уравнений с дробями. Ниже приведена подробная инструкция по решению примеров такого типа.
Как решать примеры с дробями – общие правила
Для решения примеров с дробями любых типов, будь то сложение, вычитание, умножение или деление, необходимо знать основные правила:
- Для того чтобы сложить дробные выражения с одинаковым знаменателем (знаменатель – число, находящееся в нижней части дроби, числитель – в верхней), нужно сложить их числители, а знаменатель оставить тем же.
- Для того чтобы вычесть от одного дробного выражения второе (с одинаковым знаменателем), нужно вычесть их числители, а знаменатель оставить тем же.

- Для того чтобы сложить или вычесть дробные выражения с разными знаменателями, нужно найти наименьший общий знаменатель.
- Для того чтобы найти дробное произведение, нужно перемножить числители и знаменатели, при этом, если есть возможность, сократить.
- Для того чтобы разделить дробь на дробь, нужно умножить первую дробь на перевернутую вторую.
Как решать примеры с дробями – практика
Правило 1, пример 1:
Вычислить 3/4 +1/4.
Согласно правилу 1, если у дробей двух (или больше) одинаковый знаменатель, нужно просто сложить их числители. Получим: 3/4 + 1/4 = 4/4. Если у дроби числитель и знаменатель одинаковы, такая дробь будет равна 1.
Ответ: 3/4 + 1/4 = 4/4 = 1.
Правило 2, пример 1:
Вычислить: 3/4 – 1/4
Пользуясь правилом номер 2, для решения этого уравнения нужно от 3 отнять 1, а знаменатель оставить тем же. Получаем 2/4. Так как два 2 и 4 можно сократить, сокращаем и получаем 1/2.
Ответ: 3/4 – 1/4 = 2/4 = 1/2.
Правило 3, Пример 1
Вычислить: 3/4 + 1/6
Решение: Пользуясь 3-м правилом, находим наименьший общий знаменатель. Наименьшим общим знаменателем называется такое число, которое делится на знаменатели всех дробных выражений примера. Таким образом, нам нужно найти такое минимальное число, которое будет делиться и на 4, и на 6. Таким числом является 12. Записываем в качестве знаменателя 12. 12 делим на знаменатель первой дроби, получаем 3, умножаем на 3, записываем в числителе 3*3 и знак +. 12 делим на знаменатель второй дроби, получаем 2, 2 умножаем на 1, записываем в числителе 2*1. Итак, получилась новая дробь со знаменателем, равным 12 и числителем, равным 3*3+2*1=11. 11/12.
Ответ: 11/12
Правило 3, Пример 2:
Вычислить 3/4 – 1/6. Этот пример очень схож с предыдущим. Проделываем все те же действия, но в числителе вместо знака +, пишем знак минус. Получаем: 3*3-2*1/12 = 9-2/12 = 7/12.
Ответ: 7/12
Правило 4, Пример 1:
Вычислить: 3/4 * 1/4
Пользуясь четвертым правилом, умножаем знаменатель первой дроби на знаменатель второй и числитель первой дроби на числитель второй. 3*1/4*4 = 3/16.
3*1/4*4 = 3/16.
Ответ: 3/16
Правило 4, Пример 2:
Вычислить 2/5 * 10/4.
Данную дробь можно сократить. В случае произведения сокращаются числитель первой дроби и знаменатель второй и числитель второй дроби и знаменатель первой.
2 сокращается с 4. 10 сокращается с 5. получаем 1 * 2/2 = 1*1 = 1.
Ответ: 2/5 * 10/4 = 1
Правило 5, Пример 1:
Вычислить: 3/4: 5/6
Пользуясь 5-м правилом, получим: 3/4: 5/6 = 3/4 * 6/5. Сокращаем дробь по принципу предыдущего примера и получаем 9/10.
Ответ: 9/10.
Как решать примеры с дробями – дробные уравнения
Дробными уравнениями называются примеры, где в знаменателе есть неизвестное. Для того чтобы решить такое уравнение нужно пользоваться определенными правилами.
Рассмотрим пример:
Решить уравнение 15/3x+5 = 3
Вспомним, нельзя делить на ноль, т.е. значение знаменателя не должно равняться нулю. При решении таких примеров, это нужно обязательно указывать. Для этого существует ОДЗ (область допустимых значений).
Таким образом, 3x+5 ≠ 0.
Отсюда: 3x ≠ 5.
x ≠ 5/3
При x = 5/3 уравнение просто не имеет решения.
Указав ОДЗ, наилучшим способом решить данное уравнение будет избавиться от дробей. Для это сначала представим все не дробные значения в виде дроби, в данном случае число 3. Получим: 15/(3x+5) = 3/1. Чтобы избавиться от дроби нужно умножить каждую из них на наименьший общий знаменатель. В данном случае таковым будет (3x+5)*1. Последовательность действий:
- Умножаем 15/(3x+5) на (3x+5)*1 = 15*(3x+5).
- Раскрываем скобки: 15*(3x+5) = 45x + 75.
- То же самое проделываем с правой частью уравнения: 3*(3x+5) = 9x + 15.
- Приравниваем левую и правую часть: 45x + 75 = 9x +15
- Переносим иксы влево, числа вправо: 36x = – 50
- Находим x: x = -50/36.
- Сокращаем: -50/36 = -25/18
Ответ: ОДЗ x ≠ 5/3 . x = -25/18.
Как решать примеры с дробями – дробные неравенства
Дробные неравенства по типу (3x-5)/(2-x)≥0 решаются при помощи числовой оси. Рассмотрим данный пример.
Рассмотрим данный пример.
Последовательность действий:
- Приравниваем числитель и знаменатель к нулю: 1. 3x-5=0 => 3x=5 => x=5/3
2. 2-x=0 => x=2 - Чертим числовую ось, расписывая на ней получившиеся значения.
- Под значение рисуем кружок. Кружок бывает двух типов – заполненный и пустой. Заполненный кружок означает, что данное значение входит в ареал решений. Пустой круг говорит о том, что данное значение не входит в ареал решений.
- Так как знаменатель не может быть равным нулю, под 2-ой будет пустой круг.
- Чтобы определить знаки, подставляем в уравнение любое число больше двух, например 3. (3*3-5)/(2-3)= -4. значение отрицательное, значит над областью после двойки пишем минус. Затем подставляем вместо икса любое значение интервала от 5/3 до 2, например 1. Значение опять отрицательное. Пишем минус. То же самое повторяем с областью, находящейся до 5/3. Подставляем любое число, меньшее чем 5/3, например 1. Опять минус.

- Так как нас интересуют значения икса, при котором выражение будет больше или равно 0, а таких значений нет (везде минусы), это неравенство не имеет решения, то есть x = Ø (пустое множество).
Ответ: x = Ø
В статье покажем, как решать дроби на простых понятных примерах. Разберемся, что такое дробь и рассмотрим решение дробей !
Понятие дроби вводится в курс математики начиная с 6 класса средней школы.
Дроби имеют вид: ±X/Y, где Y — знаменатель, он сообщает на сколько частей разделили целое, а X — числитель, он сообщает, сколько таких частей взяли. Для наглядности возьмем пример с тортом:
В первом случае торт разрезали поровну и взяли одну половину, т.е. 1/2. Во втором случае торт разрезали на 7 частей, из которых взяли 4 части, т.е. 4/7.
Если часть от деления одного числа на другое не является целым числом, ее записывают в виде дроби.
Например, выражение 4:2 = 2 дает целое число, а вот 4:7 нацело не делится, поэтому такое выражение записывается в виде дроби 4/7.
Иными словами дробь — это выражение, которое обозначает деление двух чисел или выражений, и которое записывается с помощью дробной черты.
Если числитель меньше знаменателя — дробь является правильной, если наоборот — неправильной. В состав дроби может входить целое число.
Например, 5 целых 3/4.
Данная запись означает, что для того, чтобы получить целую 6 не хватает одной части от четырех.
Если вы хотите запомнить, как решать дроби за 6 класс , вам надо понять, что решение дробей , в основном, сводится к понимаю нескольких простых вещей.
- Дробь по сути это выражение доли. То есть числовое выражение того, какую часть составляет данное значение от одного целого. К примеру дробь 3/5 выражает, что, если мы поделили что то целое на 5 частей и количество долей или частей это этого целого — три.
- Дробь может быть меньше 1, например 1/2(или по сути половина), тогда она правильная. Если дробь больше 1, к примеру 3/2(три половины или один с половиной), то она неправильная и для упрощения решения, нам лучше выделить целую часть 3/2= 1 целая 1/2.

- Дроби это такие же числа, как 1, 3, 10, и даже 100, только числа это не целые а дробные. С ними можно выполнять все те же операции, что с числами. Считать дроби не сложнее, и далее на конкретных примерах мы это покажем.
Как решать дроби. Примеры.
К дробям применимы самые разные арифметические операции.
Приведение дроби к общему знаменателю
Например, необходимо сравнить дроби 3/4 и 4/5.
Чтобы решить задачу, сначала найдем наименьший общий знаменатель, т.е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей
Наименьший общий знаменатель(4,5) = 20
Затем знаменатель обоих дробей приводится к наименьшему общему знаменателю
Ответ: 15/20
Сложение и вычитание дробей
Если необходимо посчитать сумму двух дробей, их сначала приводят к общему знаменателю, затем складывают числители, при этом знаменатель останется без изменений. Разность дробей считается аналогичным образом, различие лишь в том, что числители вычитаются.
Например, необходимо найти сумму дробей 1/2 и 1/3
Теперь найдем разность дробей 1/2 и 1/4
Умножение и деление дробей
Тут решение дробей несложное, здесь все достаточно просто:
- Умножение — числители и знаменатели дробей перемножаются между собой;
- Деление — сперва получаем дробь, обратную второй дроби, т.е. меняем местами ее числитель и знаменатель, после чего полученные дроби перемножаем.
Например:
На этом о том, как решать дроби , всё. Если у вас остались какие то вопросы по решению дробей , что то непонятно, то пишите в комментарии и мы обязательно вам ответим.
Если вы учитель, то возможно скачать презентацию для начальной школы (http://school-box.ru/nachalnaya-shkola/prezentazii-po-matematike.html) будет вам кстати.
Содержание урока
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3 . Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить без изменения;
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1 . Сложим дроби и
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли.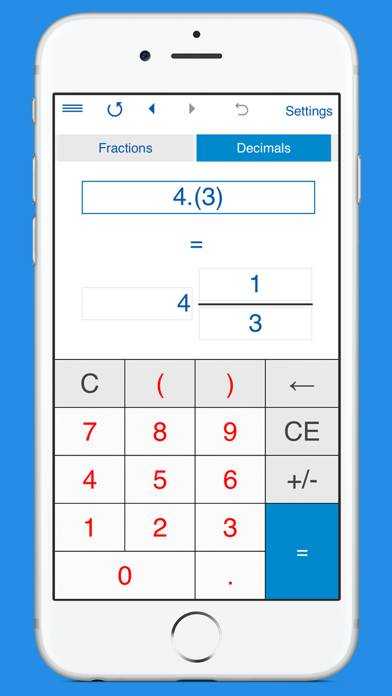 Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2.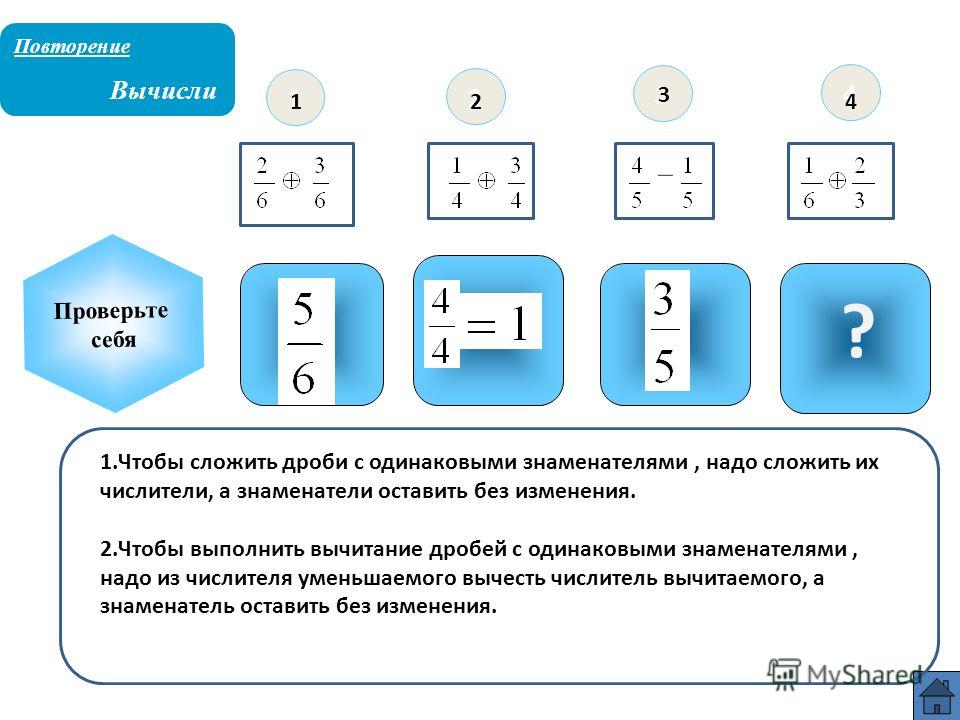 Найти значение выражения .
Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателямиВычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить прежним.
Пример 1 . Умножить дробь на число 1 .
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2 . Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Умножение дробейЧтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Найти значение выражения .
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2 . Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числаСейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2 . Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | Найти объем | сфера (4) | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | 2 1/2÷22000000 | |
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | Перевести в процентное соотношение | 3/9 | |
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Онлайн калькулятор дробей.
 Вычисления с дробями. Сложение, вычитание, умножение и деление дробей
Вычисления с дробями. Сложение, вычитание, умножение и деление дробейМатематика умножение дробей
Используя этот Онлайн калькулятор с дробями, вы сможете Сложить, вычесть, умножить, разделить или возвести в степень обыкновенные дроби, смешанные числа (дроби с целой частью), десятичные дроби и целые числа, соответственно найти их сумму, разность, произведение или частное.
Воспользовавшись онлайн калькулятором дробей, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения задач с дробями и закрепить пройденный на уроках материал.
Калькулятор дробей
| | | 1 | 2 | 3 | ÷ | |
| ( | ) | 4 | 5 | 6 | × | С |
| A 2 | 7 | 8 | 9 | — | | |
| A b | . | 0 | + |
Инструкция использования калькулятора дробей
Для решения вашей задачи выполните следующие действия:
- введите ваш пример в калькулятор; нажмите кнопку для выполнения вычислений.

Ввод данных в калькулятор дробей
В калькулятор дробей можно вводить: целые числа, десятичные дроби, обыкновенные дроби и смешанные числа.
Целые числа. Для ввода целых чисел используйте цифровые клавиши калькулятора или цифровые клавиши вашего компьютера. 1 2 3 4 5 6 7 8 9 0
Десятичные дроби. Десятичные дроби вводятся также как и целые числа, в качестве десятичного разделителя рекомендуется использовать точку .
Обыкновенные дроби: Для ввода обыкновенной дроби нажмите клавишу на клавиатуре калькулятора — после чего введите значения числителя и знаменателя дроби используя числовые клавиши.
Смешанные числа: Используя числовые клавиши введите целую часть смешанной дроби, нажмите клавишу дроби на клавиатуре калькулятора — после чего введите значения числителя и знаменателя дроби используя числовые клавиши.
Отрицательные числа: Перед числом поставьте знак минус — , не забывайте брать отрицательные числа в скобки ( ) . 3)
3)
N. B. Калькулятор поддерживает только целые степени!
N. B. Буквенные выражения, операции извлечения корня калькулятор не поддерживает!
Калькулятор дробей
| | | 1 | 2 | 3 | ÷ | |
| ( | ) | 4 | 5 | 6 | × | С |
| A 2 | 7 | 8 | 9 | — | | |
| A b | . | 0 | + |
Для решения вашей задачи выполните следующие действия:
- введите ваш пример в калькулятор; нажмите кнопку для выполнения вычислений.
В калькулятор дробей можно вводить целые числа, десятичные дроби, обыкновенные дроби и смешанные числа.
Ru. onlinemschool. com
08.08.2019 0:05:54
2019-08-08 00:05:54
Источники:
Https://ru. onlinemschool. com/math/assistance/fraction/fraction_calc/
Умножение и деление дробей, примеры, тесты — обучающие курсы » /> » /> . keyword { color: red; }
keyword { color: red; }
Математика умножение дробей
Для того, чтобы перемножить дроби, необходимо перемножить числители и знаменатели каждой из дробей.
Полученную дробь сократить, если возможно, получить ответ.
В том случае, если дробь задана неявно, сперва преобразовать.
Деление дробей
Для того, чтобы разделить дроби, необходимо перевернуть дробь, на которую делим, после чего деление превращается в умножение дробей. Остается перемножить числители и знаменатели.
Обратите внимание на второй пример. Очень часто требуется разделить дробь на некоторое однозначное число. Трудность не возникает, если помнить, что число можно представить в виде дроби: число деленное на единицу.
Полученную дробь сократить, если возможно, получить ответ.
Fizmat. by
02.11.2017 20:34:34
2017-11-02 20:34:34
Источники:
Http://fizmat. by/math/fraction/division#:~:text=%D0%A3%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5%20%D0%B4%D1%80%D0%BE%D0%B1%D0%B5%D0%B9%20%D0%94%D0%BB%D1%8F%20%D1%82%D0%BE%D0%B3%D0%BE%2C%20%D1%87%D1%82%D0%BE%D0%B1%D1%8B%20%D0%BF%D0%B5%D1%80%D0%B5%D0%BC%D0%BD%D0%BE%D0%B6%D0%B8%D1%82%D1%8C%20%D0%B4%D1%80%D0%BE%D0%B1%D0%B8%2C%20%D0%BD%D0%B5%D0%BE%D0%B1%D1%85%D0%BE%D0%B4%D0%B8%D0%BC%D0%BE,%D0%B5%D1%81%D0%BB%D0%B8%20%D0%B4%D1%80%D0%BE%D0%B1%D1%8C%20%D0%B7%D0%B0%D0%B4%D0%B0%D0%BD%D0%B0%20%D0%BD%D0%B5%D1%8F%D0%B2%D0%BD%D0%BE%2C%20%D1%81%D0%BF%D0%B5%D1%80%D0%B2%D0%B0%20%D0%BF%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D1%82%D1%8C. %20%D0%94%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5%20%D0%B4%D1%80%D0%BE%D0%B1%D0%B5%D0%B9
%20%D0%94%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5%20%D0%B4%D1%80%D0%BE%D0%B1%D0%B5%D0%B9
Как умножать дроби с разными и одинаковыми знаменателями » /> » /> .keyword { color: red; }
Математика умножение дробей
Изучать части целого может быть увлекательно и даже полезно в будущем — все взрослые используют эти знания. Например, когда меняют рубли на доллары. В этой статье расскажем, как перемножать дроби.
О чем эта статья:
5 класс, 6 класс
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой A и B являются числами или выражениями. Существует два формата записи:
- обыкновенный вид — 1/2 или a/b, десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление — в 5 классе уже это знают.
Дроби могут быть двух видов:
Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15. Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя:
Неправильной — ту, у которой числитель больше знаменателя или равен ему:
Такое число называют смешанным, читают как «пять целых одна четвертая», а записывают так: 5 1\4.
Основные правила дробей
- Если делитель равен нулю — у дроби нет значения Дробь равна нулю, если числитель равен нулю, а знаменатель — нет Две дроби a/b и c/d называют равными, если a * d = b * c. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число — получится равная ей дробь.
Умножение дробных чисел
Рассмотрим несколько вариантов умножения обыкновенных дробей.
Как умножить дробь на дробь
Числитель равен произведению числителей обеих дробей, а знаменатель равен произведению знаменателей:
Важно проверить возможность сокращения — так решать будет легче:
Как умножить смешанные дроби
Преобразовать смешанные числа в неправильные, перемножить числители и знаменатели, при необходимости сократить и перевести в смешанную дробь.
Как умножить дробь на натуральное число
Метод 1. Числитель умножить на натуральное число, а знаменатель оставить без изменения. Если в результате произведения получилась неправильная дробь, нужно выделить целую часть, то есть превратить неправильную в смешанную.
Метод 2. Знаменатель разделить на натуральное число, а числитель оставить прежним.
Этот способ будет удобнее предыдущего, если знаменатель делится на натуральное число без остатка.
Решение задач
Ребятам в 5 и 6 классе нужно практиковаться как можно чаще, чтобы решать такие примеры быстро и легко.
Задание 1. Выполнить умножение 2/17 на 5.
Как решаем: перемножим числитель и натуральное число.
Ответ:
Задание 2. Выполнить умножение 4/15 и 55/6.
Как решаем:
Ответ:
Задание 3. Выполнить умножение одной целой трех седьмых на шесть.
Как решаем:
- переводим смешанное число в неправильную дробь, умножаем делимое на натуральное число, сократим полученное, преобразуем в смешанное число.

Ответ:
Онлайн-курсы по математике для детей и подростков — прекрасный способ разобраться в новом материале и закрепить его на практике.
Ответ:
Основные правила дробей
- Если делитель равен нулю — у дроби нет значения Дробь равна нулю, если числитель равен нулю, а знаменатель — нет Две дроби a/b и c/d называют равными, если a * d = b * c. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число — получится равная ей дробь.
Рассмотрим несколько вариантов умножения обыкновенных дробей.
Преобразовать смешанные числа в неправильные, перемножить числители и знаменатели, при необходимости сократить и перевести в смешанную дробь.
Десятичный вид 0,5.
Skysmart. ru
18.12.2017 8:57:32
2017-12-18 08:57:32
Источники:
Https://skysmart. ru/articles/mathematic/umnozhenie-drobej
Дробь на умножение: Умножение дробей
Содержание
Урок 62.
 умножение натурального числа на дробь — Математика — 5 класс
умножение натурального числа на дробь — Математика — 5 классМатематика
5 класс
Урок № 62
Умножение натурального числа на дробь
Перечень рассматриваемых вопросов:
– произведение двух дробей;
– взаимно обратные дроби;
– умножение натурального числа на дробь.
Тезаурус
Произведение двух дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Взаимно обратные дроби – это дроби, произведение которых равно единице.
Обязательная литература
1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС./ С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др.– М.: Просвещение, 2017, стр. 272.
Теоретический материал для самостоятельного изучения
Произведение двух дробей есть дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Например,
Можно ли умножить дробь на натуральное число n? Конечно, да! Натуральное число n можно представить в виде обыкновенной дроби n/1 и применить правило умножения дробей. Итак, чтобы умножить натуральное число на дробь, можно числитель дроби умножить на это натуральное число, а знаменатель оставить тот же.
Например:
Вычислим произведение четырёх пятых и трёх. Умножение можно заменить сложением, то есть три раза сложить дробь четыре пятых. Применяем правило сложения обыкновенных дробей и получаем:
Если произведение дробей равно единице, то такие дроби называют взаимно обратными.
Например,
Дроби ¼ и 4/1 называются взаимно обратными.
Чтобы умножить простую и смешанную дробь, можно записать последнюю в виде неправильной дроби и выполнить умножение обыкновенных дробей.
Например,
Перед возведением в степень смешанную дробь записывают в виде неправильной, и эту дробь возводят в степень.
Решим задачу: в равностороннем треугольнике длина стороны равна 4/7 м. Найдите периметр треугольника.
Найдите периметр треугольника.
Решение. Как мы знаем, периметр – это сумма длин всех сторон. В треугольнике три стороны, а т. к. треугольник равносторонний – стороны равны. Получается, что сумму длин всех сторон можно представить как произведение натурального числа 3 на обыкновенную дробь
Разбор решения заданий тренировочного модуля
№ 1. Вычислите значение выражения, результат запишите в виде смешанной дроби.
Переведём смешанные дроби в неправильные, после чего перемножим числители и знаменатели, а результат запишем в виде смешанной дроби. Получим:
№ 2. Вычислите значение произведения, результат сократите.
Умножим числитель первой дроби на числитель второй дроби, знаменатели тоже перемножим. Получим:
Ответ:
Калькулятор дробей
Как перевести смешанную дробь в обыкновенную
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: i nd = i · d + nd
Например,
5 34 = 5 · 4 + 34 = 234
Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
- Поделить числитель дроби на её знаменатель
- Результат от деления будет являться целой частью
- Остаток отделения будет являться числителем
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Как перевести десятичную дробь в обыкновенную или смешанную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
- Записать дробь в виде десятичная дробь1
- Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
- Найти наибольший общий делитель и сократить дробь.
Например, переведем 0.36 в обыкновенную дробь:
- Записываем дробь в виде: 0.361
- Умножаем на 10 два раза, получим 36100
- Сокращаем дробь 36100 = 925
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).

- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Выполнить сложение дробей путем сложения их числителей.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.

- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.

- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Как умножать дроби с разными и одинаковыми знаменателями
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление — в 5 классе уже это знают.
Дроби могут быть двух видов:
- Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
- Алгебраические — состоят из переменных, например, (x + y)/(x — y).
 В этом случае значение дроби зависит от данных значений букв.
В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя:
Неправильной — ту, у которой числитель больше знаменателя или равен ему:
Такое число называют смешанным, читают как «пять целых одна четвертая», а записывают так: 5 1\4.
Основные правила дробей
|
Умножение дробных чисел
Рассмотрим несколько вариантов умножения обыкновенных дробей.
Как умножить дробь на дробь
Числитель равен произведению числителей обеих дробей, а знаменатель равен произведению знаменателей:
Важно проверить возможность сокращения — так решать будет легче:
Как умножить смешанные дроби
Преобразовать смешанные числа в неправильные, перемножить числители и знаменатели, при необходимости сократить и перевести в смешанную дробь.
Как умножить дробь на натуральное число
Метод 1. Числитель умножить на натуральное число, а знаменатель оставить без изменения. Если в результате произведения получилась неправильная дробь, нужно выделить целую часть, то есть превратить неправильную в смешанную.
Метод 2. Знаменатель разделить на натуральное число, а числитель оставить прежним.
Этот способ будет удобнее предыдущего, если знаменатель делится на натуральное число без остатка.
Решение задач
Ребятам в 5 и 6 классе нужно практиковаться как можно чаще, чтобы решать такие примеры быстро и легко.
Задание 1. Выполнить умножение 2/17 на 5.
Как решаем: перемножим делимое и натуральное число.
Ответ:
Задание 2. Выполнить умножение 4/15 и 55/6.
Как решаем:
- перемножим числители между собой и знаменатели соответственно
- сократим полученное
- выделим целую часть
Ответ:
Задание 3.
 Выполнить умножение одной целой трех седьмых на шесть.
Выполнить умножение одной целой трех седьмых на шесть.Как решаем:
- переводим смешанное число в неправильную дробь,
- умножаем делимое на натуральное число,
- сократим полученное,
- преобразуем в смешанное число.
Ответ:
Если вопрос не ждет и ответ нужно получить как можно быстрее, можно использовать онлайн калькулятор. Умножение будет быстрым и точным:
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Умножение дробей, формулы и примеры решений
Содержание:
Умножение дроби на число
Умножение дроби $\frac{a}{b}$ на число $n$ равносильно сложению одинаковых слагаемых:
Итак, можно сделать вывод, что чтобы умножить дробь на число, надо числитель этой
дроби умножить на это число, а знаменатель оставить без изменения.
Пример
Задание. Найти произведение $\frac{1}{3} \cdot 4$
Решение. Выполним умножение по описанному выше правилу
$\frac{1}{3} \cdot 4=\frac{1 \cdot 4}{3}=\frac{4}{3}=1 \frac{1}{3}$
Ответ. $\frac{1}{3} \cdot 4=1 \frac{1}{3}$
Аналогично выполняется умножения числа на дробь.
Слишком сложно?
Умножение дробей не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Найти произведение 3$\cdot \frac{1}{4}$
Решение. Выполним умножение по описанному выше правилу
$3 \cdot \frac{1}{4}=\frac{3 \cdot 1}{4}=\frac{3}{4}$
Ответ. $3 \cdot \frac{1}{4}=\frac{3}{4}$
Умножение дробей
Определение
Произведением дробей называется такая дробь, числитель которой равен произведению числителей исходных дробей, а знаменатель — произведению их знаменателей:
$\frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}$
Таким образом, чтобы умножить дробь на дробь, надо умножить числитель первой дроби на числитель второй и результат
записать в числитель; а также перемножить знаменатели и результат записать в знаменатель.
Замечание. При выполнении умножения по возможности следует сокращать. Сокращать можно только числа стоящие в числителе с числами, стоящими в знаменателе. Числитель с числителем и знаменатель со знаменателем сокращать нельзя.
Пример
Задание. Найти произведение дробей $\frac{1}{3}$ и $\frac{4}{5}$
Решение. Выполним умножение дробей по описанному выше правилу
$\frac{1}{3} \cdot \frac{4}{5}=\frac{1 \cdot 4}{3 \cdot 5}=\frac{4}{15}$
Ответ. $\frac{1}{3} \cdot \frac{4}{5}=\frac{4}{15}$
Пример
Задание. Умножить $\frac{13}{14}$ на $\frac{14}{39}$
Решение. Необходимо найти произведение $\frac{13}{14} \cdot \frac{14}{39}$ . Как видим, числа 13 и 39 можно сократить на общее число 13. Для этого сами указанные величины зачеркиваем, а над ними пишем число, которое получается после деления. Аналогично поступает со знаменателем первой дроби и числителем второй:
Ответ. $\frac{13}{14} \cdot \frac{14}{39}=\frac{1}{3}$
$\frac{13}{14} \cdot \frac{14}{39}=\frac{1}{3}$
Умножение смешанных дробей
Чтобы перемножить смешанные дроби, нужно представить их в виде неправильных дробей, а затем уже выполнить умножение как обыкновенных дробей.
Пример
Задание. Найти произведение дробей 3$\frac{1}{3} \cdot 4 \frac{2}{5}$
Решение. Выполним умножение смешанных дробей по описанному выше правилу
$3 \frac{1}{3} \cdot 4 \frac{2}{5}=\frac{3 \cdot 3+1}{3} \cdot \frac{4 \cdot 5+2}{5}=\frac{10}{3} \cdot \frac{22}{5}=$
Ответ. $3 \frac{1}{3} \cdot 4 \frac{2}{5}=14 \frac{2}{3}$
Для умножения смешанной дроби на целое число поступают либо аналогично и далее умножают дробь на число, либо на целое число отдельно умножают целую часть, и отдельно дробную часть смешанного числа.
Пример
Задание. Умножить смешанную дробь 3$\frac{3}{4}$ на 2
Решение. Выполним умножение смешанной дроби на число по описанному выше правилу
Либо
$=(6+1)+\frac{1}{2}=7+\frac{1}{2}=7 \frac{1}{2}$
Ответ. $3 \frac{3}{4} \cdot 2=7 \frac{1}{2}$
$3 \frac{3}{4} \cdot 2=7 \frac{1}{2}$
Читать следующую тему: деление дробей.
Умножение и деление обыкновенных дробей. Онлайн калькулятор
Умножение дробей
Чтобы умножить одну обыкновенную дробь на другую, нужно умножить числитель первой дроби на числитель второй дроби (это произведение будет числителем результата), и знаменатель первой дроби на знаменатель второй дроби (это произведение будет знаменателем результата):
Правило умножения обыкновенных дробей в виде формулы:
Для упрощения вычислений, ещё до выполнения умножения дробей, можно сокращать любой множитель числителя с любым множителем знаменателя на общий делитель.
При сокращении числителей со знаменателями их обычно зачёркивают и рядом пишут число, которое получилось после сокращения:
В примере мы сократили 25 и 20 на общий делитель — 5, а 27 и 12 на общий делитель — 3.
Умножение дроби на натуральное число
Чтобы умножить натуральное число на обыкновенную дробь или наоборот — умножить дробь на натуральное число, можно числитель дроби умножить на это натуральное число, а знаменатель оставить без изменений:
Пример.
Деление дробей
При делении одной обыкновенной дроби на другую, нужно перевернуть вторую дробь и после этого умножить первую дробь на вторую, т. е. нужно числитель первой дроби умножить на знаменатель второй (это произведение будет числителем результата), а знаменатель первой дроби умножить на числитель второй (это произведение будет знаменателем результата):
Для проверки правильности выполненного деления, можно полученное частное умножить на делитель и посмотреть, получится ли у нас делимое, если делимое получено верно, значит деление было выполнено правильно:
Теперь осталось только сократить полученную дробь:
Правило деления обыкновенных дробей в виде формулы:
Иногда могут встретиться записи такого вида:
Так как дробная черта означает деление, то такие записи можно переписать в более удобном виде:
В записях, в которых дробная черта используется несколько раз, знак =
ставится у дробной черты, означающей последнее по порядку действие деления:
Деление дроби на натуральное число
Чтобы обыкновенную дробь разделить на натуральное число или наоборот — натуральное число разделить на дробь, нужно просто представить натуральное число в виде дроби.
Примеры.
Калькулятор умножения и деления дробей
Данный калькулятор поможет вам выполнить умножение или деление обыкновенных дробей. Просто введите две дроби, выберите нужную операцию и нажмите кнопку Вычислить
.
правила, примеры, решения, умножение дробей с разными знаменателями
Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Как умножить одну обыкновенную дробь на другую
Запишем сначала основное правило:
Определение 1
Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a/b и c/d это можно выразить как ab·cd=a·cb·d.
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 14 и 18 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8·4=32). Соответственно, площадь каждого из них будет равна 132 от площади всей фигуры, т.е. 132 кв. единицы.
Далее нам надо выделить цветом часть исходного квадрата так, как это сделано на рисунке:
У нас получился закрашенный фрагмент со сторонами, равными 58 числовой единицы и 34 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 58·34 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15, значит, общая площадь составляет 1532 квадратных единиц.
Поскольку 5·3=15 и 8·4=32, мы можем записать следующее равенство:
58·34=5·38·4=1532
Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как ab·cd=a·cb·d. Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.
Пример 1
Умножьте 711 на 98.
Решение
Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9. У нас получилось 63. Затем вычислим произведение знаменателей и получим: 11·8=88. Составим их двух чисел ответ: 6388.
Все решение можно записать так:
711·98=7·911·8=6388
Ответ: 711·98=6388.
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Пример 2
Вычислите произведение дробей 415 и 556.
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:
Запись решения будет выглядеть так:
415·556=4·5515·6=22090
Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10.
Выполним сокращение дроби: 22090 НОД (220, 90)=10, 22090=220:1090:10=229. В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 229=249.
Ответ: 415·556=249.
Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a·cb·d. Разложим значения переменных на простые множители и одинаковые из них сократим.
Поясним, как это выглядит, используя данные конкретной задачи.
Пример 3
Вычислите произведение 415·556.
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
415·556=4·5515·6
Поскольку как 4=2·2, 55=5·11, 15=3·5 и 6=2·3, значит,4·5515·6=2·2·5·113·5·2·3.
Далее мы можем просто сократить некоторые множители и получить следующее: .
Нам осталось подсчитать несложные произведения в числителе и знаменателе и выделить целую часть из получившейся в итоге неправильной дроби:
2·113·3=229=249
Ответ: 415·556=249.
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
ab·cd=cd·ab=a·cb·d
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Определение 2
Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби ab на натуральное число n можно записать в виде формулы ab·n=a·nb.
Умножение некоторой дроби ab на натуральное число n можно записать в виде формулы ab·n=a·nb.
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
ab·n=ab·n1=a·nb·1=a·nb
Поясним нашу мысль конкретными примерами.
Пример 4
Вычислите произведение 227 на 5.
Решение
В результате умножения числителя исходной дроби на второй множитель получим 10. В силу правила, указанного выше, мы получим в результате 1027. Все решение приведено в этой записи:
227·5=2·527=1027
Ответ: 227·5=1027
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.
Пример 5
Условие: вычислите произведение 8 на 512.
Решение
По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 512·8=5·812=4012. Итоговая дробь имеет признаки делимости на 2, поэтому нам нужно выполнить ее сокращение:
В итоге получаем, что 512·8=5·812=4012. Итоговая дробь имеет признаки делимости на 2, поэтому нам нужно выполнить ее сокращение:
НОК(40, 12)=4, значит, 4012=40:412:4=103
Теперь нам осталось только выделить целую часть и записать готовый ответ: 103=313.
В этой записи можно видеть все решение целиком: 512·8=5·812=4012=103=313.
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Ответ: 512·8=313.
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
ab·n=n·ab=a·nb
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Пример 6
Умножьте четыре обыкновенные дроби 120, 125, 37 и 58.
Решение: для начала сделаем запись произведения. У нас получится 120·125·37·58. Нам надо перемножить между собой все числители и все знаменатели: 120·125·37·58=1·12·3·520·5·7·8.
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
1·12·3·520·5·7·8=1·(2·2·3)·3·52·2·5·5·7(2·2·2)=3·35·7·2·2·2=9280
Ответ: 1·12·3·520·5·7·8=9280.
Пример 7
Перемножьте 5 чисел 78·12·8·536·10.
Решение
Для удобства мы можем сгруппировать дробь 78 с числом 8, а число 12 с дробью 536, поскольку при этом нам будут очевидны будущие сокращения. В итоге у нас получится:
В итоге у нас получится:
78·12·8·536·10=78·8·12·536·10=7·88·12·536·10=71·2·2·3·52·2·3·3·10==7·53·10=7·5·103=3503=11623
Ответ: 78·12·8·536·10=11623.
Правила умножения дробей
Для того чтобы произвести арифметические действия умножения над дробями, следует перемножить их числители и знаменатели, а результат записать в соответствующей форме.
Умножение простой дроби на число
При умножении простой дроби на натуральное число, ее числитель следует умножить на этот множитель, а знаменатель оставить без изменения.
3 8 |
× | 4 | = | 3 × 4 8 |
= | 12 8 |
= | 1 | 4 8 |
= | 1 | 1 2 |
Умножение смешанной дроби на число
При необходимости умножения смешанной дроби на натуральное число следует произвести данное арифметическое действие с целым числом этой дроби и её числителем.
| 1 | 2 5 |
× | 3 | = | 1 × 3 | + | 2 × 3 5 |
= | 3 | 6 5 |
= | 4 | 1 5 |
Умножение дроби на дробь
Когда нужно умножить простую дробь на простую дробь, следует перемножить числители, а затем знаменатели.
3 6 |
× | 4 8 |
= | 3 × 4 6 × 8 |
= | 12 48 |
= | 1 4 |
Умножение смешанной дроби на смешанную дробь
При выполнении операции умножения смешанных чисел, их следует записать в виде неправильных дробей, после чего перемножить их по соответствующим правилам.
| 2 | 1 3 |
× | 4 | 3 5 |
= | 7 3 |
× | 23 5 |
= | 7 × 23 3 × 5 |
= | 161 15 |
= | 10 | 11 15 |
Калькулятор дробей
Использование калькулятора
Используйте этот калькулятор дробей для сложения, вычитания, умножения и деления дробей. Ответы представляют собой дроби в наименьшем значении или смешанные числа в сокращенном виде.
Ответы представляют собой дроби в наименьшем значении или смешанные числа в сокращенном виде.
Введите правильные или неправильные дроби, выберите математический знак и нажмите Рассчитать. Это калькулятор дробей с шагами, указанными в решении.
Если у вас отрицательные дроби, вставьте знак минус перед числителем.Итак, если одна из ваших дробей -6/7, вставьте -6 в числитель и 7 в знаменатель.
Иногда в математических задачах используется слово «из», например Что такое 1/3 от 3/8? Of означает, что вам нужно умножить, поэтому вам нужно решить 1/3 × 3/8.
Для математических вычислений со смешанными числами (целыми и дробными) используйте Калькулятор смешанных чисел.
Математика в дробях с разными знаменателями
Есть 2 случая, когда вам нужно знать, имеют ли ваши дроби разные знаменатели:
- если складываете дроби
- , если вы вычитаете дроби
Как сложить или вычесть дроби
- Найдите наименьший общий знаменатель
- Вы можете использовать ЖК-калькулятор, чтобы найти наименьший общий знаменатель для набора дробей
- Для первой дроби найдите, на какое число нужно умножить знаменатель, чтобы получить наименьший общий знаменатель.

- Умножьте числитель и знаменатель вашей первой дроби на это число
- Повторите шаги 3 и 4 для каждой фракции
- Для сложения уравнений добавьте числители дробей
- Для уравнений вычитания вычтите числители дробей
- Преобразовать неправильные дроби в смешанные числа
- Уменьшить дробь до наименьшего значения
Как умножать дроби
- Умножить все числители вместе
- Умножить все знаменатели вместе
- Уменьшить результат до минимума
Как разделить дроби
- Перепишите уравнение, как в «Сохранить, изменить, перевернуть»
- Оставить первую дробь
- Поменять знак деления на умножение
- Переверните вторую дробь, переключив верхнее и нижнее числа
- Умножить все числители вместе
- Умножить все знаменатели вместе
- Уменьшить результат до минимума
Формулы фракций
Есть способ складывать или вычитать дроби, не находя
наименьший общий знаменатель (ЖКД). Этот метод предполагает перекрестное умножение дробей. См. Формулы ниже.
Этот метод предполагает перекрестное умножение дробей. См. Формулы ниже.
Вы можете обнаружить, что проще использовать эти формулы, чем производить математические вычисления, чтобы найти наименьший общий знаменатель.
Формулы для умножения и деления дробей следуют тому же процессу, что и описанный выше.
Формула сложения дробей:
\ (\ dfrac {a} {b} + \ dfrac {c} {d} = \ dfrac {ad + bc} {bd} \)
Пример шагов:
\ (\ dfrac {2} {6} + \ dfrac {1} {4} = \ dfrac {(2 \ times4) + (6 \ times1)} {6 \ times4} \)
\ (= \ dfrac {14} {24} = \ dfrac {7} {12} \)
Формула вычитания дробей:
\ (\ dfrac {a} {b} — \ dfrac {c} {d} = \ dfrac {ad — bc} {bd} \)
Пример шагов:
\ (\ dfrac {2} {6} — \ dfrac {1} {4} = \ dfrac {(2 \ times4) — (6 \ times1)} {6 \ times4} \)
\ (= \ dfrac {2} {24} = \ dfrac {1} {12} \)
Формула умножения дробей:
\ (\ dfrac {a} {b} \ times \ dfrac {c} {d} = \ dfrac {ac} {bd} \)
Пример шагов:
\ (\ dfrac {2} {6} \ times \ dfrac {1} {4} = \ dfrac {2 \ times1} {6 \ times4} \)
\ (= \ dfrac {2} {24} = \ dfrac {1} {12} \)
Формула деления дробей:
\ (\ dfrac {a} {b} \ div \ dfrac {c} {d} = \ dfrac {ad} {bc} \)
Пример шагов:
\ (\ dfrac {2} {6} \ div \ dfrac {1} {4} = \ dfrac {2 \ times4} {6 \ times1} \)
\ (= \ dfrac {8} {6} = \ dfrac {4} {3} = 1 \ dfrac {1} {3} \)
Сопутствующие калькуляторы
Для выполнения математических операций над смешанными дробями чисел используйте нашу
Калькулятор смешанных чисел. Этот калькулятор также может преобразовывать неправильные дроби в смешанные числа и показывает проделанную работу.
Этот калькулятор также может преобразовывать неправильные дроби в смешанные числа и показывает проделанную работу.
Если вы хотите упростить отдельную дробь до наименьших значений, используйте наш Упростите калькулятор дробей.
Для объяснения того, как множить числа, чтобы найти наибольший общий множитель (GCF), см. Калькулятор наибольшего общего коэффициента.
Если вы вручную упрощаете большие дроби, вы можете использовать Длинное деление с калькулятором остатков, чтобы найти целые числа и остатки.
Банкноты
Этот калькулятор выполняет вычисление сокращения быстрее, чем другие калькуляторы, которые вы можете найти. Основная причина в том, что он использует алгоритм Евклида для уменьшения дробей, который можно найти на Математический форум.
Умножение дробей
Умножьте вершины, умножьте основания.
Есть 3 простых шага для умножения дробей
1. Умножьте верхние числа (числители , ).
Умножьте верхние числа (числители , ).
2. Умножьте нижние числа (знаменатели ).
3. При необходимости упростите дробь.
Пример:
1 2 × 2 5
Шаг 1 . Умножьте верхние числа:
1 2 × 2 5 знак равно 1 × 2 знак равно 2
Шаг 2 .Умножаем нижние числа:
1 2 × 2 5 знак равно 1 × 2 2 × 5 знак равно 2 10
Шаг 3 . Упростим дробь:
2 10 знак равно 1 5
С пиццей
Вот с пиццей …
Вы видите, что половина двух пятых — это две десятых?
Вы также видите, что две десятых проще одной пятой?
С ручкой и бумагой
А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):
Другой пример:
1 3 × 9 16
Шаг 1 . Умножьте верхние числа:
Умножьте верхние числа:
1 3 × 9 16 знак равно 1 × 9 знак равно 9
Шаг 2 . Умножаем нижние числа:
1 3 × 9 16 знак равно 1 × 9 3 × 16 знак равно 9 48
Шаг 3 .Упростим дробь:
9 48 знак равно 3 16
(На этот раз мы упростили, разделив верхнюю и нижнюю части на 3)
Рифма
♫ «Умножение дробей: нет большой проблемы,
Верхнее умножение сверху на нижнее умножение на низ.
« И не забудьте упростить,
Прежде, чем пришло время прощаться »♫
Дроби и целые числа
А как насчет умножения целых чисел на дроби и ?
Превратите целое число в дробь, поставив его над единицей.
Затем продолжайте, как прежде.
Пример:
2 3 × 5
Превратите 5 в 5 1 :
2 3 × 5 1
А теперь как обычно.
Умножение вершин и оснований:
2 3 × 5 1 знак равно 2 × 5 3 × 1 знак равно 10 3
Дробь уже настолько проста, насколько это возможно.
Ответ = 10 3
Или вы можете просто представить себе целое число как «верхнее» число:
Пример:
3 × 2 9
Умножение вершин и оснований:
3 × 2 9 знак равно 3 × 2 9 знак равно 6 9
Упростить:
6 9 знак равно 2 3
Смешанные фракции
Вы также можете прочитать, как умножить смешанные дроби
Умножение дробей — методы и примеры
Как умножать дроби?
В этой статье обсуждаются все шаги, которые необходимо знать при умножении дробей, включая умножение правильных и неправильных дробей, смешанную дробь и умножение дроби на целое число. Вот шаги для умножения дробей:
Вот шаги для умножения дробей:
- Умножьте числители вместе и поместите произведение поверх полученной дроби
- Умножьте знаменатели вместе и запишите результат внизу новой дроби
- Уменьшите или упростите результат, если возможно
Пример 1:
1/2 × 2/5
Шаг 1. Умножьте числители:
1/2 × 2/5 = 1 × 2 = 2
Шаг 2 .Умножьте знаменатели:
2 x 5 = 10
Шаг 3. Упростите дробь:
2/10 = 1/5
Пример 2:
1/3 × 9/16
Шаг 1. Умножьте числители:
1/3 × 9/16 = 1 × 9 = 9
Шаг 2. Умножьте знаменатели:
3 × 16 = 48
Шаг 3. Упростите дробь:
9 / 48 = 3/16
Пример 3:
Умножение: 4/5 x 7/6
Сначала умножьте числители, чтобы получить: 4 × 7 = 28.
Затем умножьте знаменатели, чтобы получить: 5 × 9 = 45.
Результат = 28/45
Поскольку нет общих делителей 28 и 45, эта дробь уже находится в самом низком выражении. Окончательный ответ — 28/45.
Окончательный ответ — 28/45.
Пример 4:
Умножение: 9/4 x 14/15
Вы можете выполнить все операции в одной математической строке. Не забудьте поставить числитель вверху, а знаменатели — внизу.
9/4 x 14/15 = (9 x 14) / (4 x 15) = 126/60
Умножение более чем на 2 дроби
Отмена — отличный способ умножения с более чем двумя множителями.
Пример 5:
Умножение (1/2) × (2/3) × (3/4) × (4/5).
Начните с исключения общих факторов.
(1/2) × (2/3) × (3/4) × (4/5).
= 1/5
Как умножить дроби на целые числа?
Дроби можно умножать на целые числа точно так же, как умножаются другие дроби.Самая важная процедура состоит в том, чтобы переписать целое число как дробь, введя знаменатель 1. Затем можно применить те же методы умножения дроби.
Целое число N можно преобразовать в дробь со знаменателем 1 следующим образом:
N = N / 1
Пример 6:
Умножение: 3/5 × 60.
3/5 × 60 = 3/5 x 60/1
Умножьте числители:
3 x 60 = 180
Умножьте знаменатели:
1 x 5 = 5
Результат — 180/5, упростите ответ до минимально возможного термины.
180/5 = 36.
Как умножить смешанные дроби?
Смешанная фракция — это фракция, состоящая из целой и дробной части. Например, 7½ — это смешанная дробь, состоящая из целого числа 7 и дробной части ½.
Ниже приведены ключевые шаги при умножении смешанных дробей или смешанной дроби на правильную или неправильную дробь:
- Первым шагом является преобразование всех дробей в неправильную дробь.
- Умножьте числители и поместите произведение вверху.
- Умножьте знаменатели и поместите произведение внизу.
- По возможности упростите результат.
Пример 7:
Умножение: 2 5 / 6 x 3 1 / 4
Начните с преобразования каждой смешанной дроби в эквивалентную неправильную дробь.
2 5 / 6 x 3 1 / 4 = 17/6 x 13/4 = 221/24
Окончательный ответ можно упростить или преобразовать обратно в смешанное число путем деления.Преобразование обратно в смешанную дробь похоже на деление с остатком. Частное становится целой частью, а остаток становится новым числителем.
Как умножить отрицательные дроби?
Те же правила умножения отрицательных чисел применяются при умножении дробей:
- + x + = +
- + x — = —
- — x — = +
Пример 8:
Умножение : 2/3 × (–3/4)
2/3 × (–3/4) = –6/12 = –1/2.
Пример 9:
Умножение: (–4/3) × (–7/5)
(–4/3) × (–7/5) = 28/15.
Практические вопросы
Умножьте следующие дроби:
- 1/3 × 4/5
- –3/7 × 2/11
- 9/10 × 35/36
- 3/8 × 10
- 5 / 3 × 7/2 × 6/7
- 6 × 4¾
- –11/3 × (–3/11)
- Мой грузовик проезжает 10 2 / 3 миль на галлон.
 Предположим, что бак пуст и я заправляю его 5 1 / 2 галлонов, как далеко я могу уехать с грузовиком?
Предположим, что бак пуст и я заправляю его 5 1 / 2 галлонов, как далеко я могу уехать с грузовиком? - Для рецепта требуется 1/2 столовой ложки соли.Сколько нужно соли, чтобы приготовить 20 подобных рецептов?
Предыдущий урок | Главная страница | Следующий урок
Что такое умножение дробей? — Определение, факты и примеры
Умножение дробей
Дробь — это часть целого .
Яблочный пирог, разрезанный на 4 равных ломтика и один ломтик, отделенный друг от друга, как показано на рисунке.
Здесь яблочный пирог разрезан на 4 равные части, каждая из которых составляет одну четвертую часть пирога. Сколько будет яблочного пирога в 5 таких кусочках?
Это будет произведение 5 × 1 4. Мы также можем оценить умножение как повторное сложение, и это проще.
Мы также можем оценить умножение как повторное сложение, и это проще.
5 × 1 4 = 1 4 + 1 4 + 1 4 + 1 4 + 1 4 = 5 4
Мы также можем преобразовать это в смешанное число, 5 4 = 1 1 4. Следовательно, из 5 кусочков пирога будет одна с четвертью яблочного пирога.
Но повторное сложение — не всегда более простой метод, особенно когда множитель также является дробью.
Рассмотрим произведение 2 5 × 3 4.
Дробь 3 4 может быть представлена следующим образом:
Теперь требуемый продукт составляет две пятых этой заштрихованной части.
Чтобы найти это, вам нужно разделить эти три заштрихованные части на 5 равных частей. Более простой способ сделать это — разделить каждую из этих 4 частей на 5 равных частей.
Итак, две пятых от трех четвертых — это две заштрихованные части из каждой из этих трех частей, то есть 6 заштрихованных частей из 20, как показано.
Другой способ геометрического представления:
В дроби, представляющей произведение, целое делится на 20 равных частей, и заштрихованные части, общие для обоих факторов, являются знаменателем, а 6 представляет числитель произведения.
Алгебраически правило умножения двух дробей:
Шаг 1 : Умножьте числители дробей множителя.
Шаг 2 : Умножьте знаменатели.
Шаг 3 : При необходимости упростите продукт.
Пример:
5 6 x 3 8 = 5 x 3 6 x 8 = 15 48
Здесь 3 — общий множитель числителя и знаменателя. Итак, чтобы упростить дробь, разделите числитель и знаменатель на 3.
15 ÷ 3 48 ÷ 3 = 5 6
Таким образом, 5 6 x 3 8 = 5 16.
Правило:
| Если a b и c d дроби с b, d ≠ 0, то a b x c d = ac bd |
Интересные факты
|
Обзор дробей: умножение и деление дробей
Purplemath
Умножать дроби просто: вы умножаете верхние числа и умножаете нижние числа.Например:
Когда это возможно, вы уменьшаете дробь, отбрасывая общие множители; то есть вы вычеркиваете любые множители с одной стороны дробной линии, которые дублируются с другой стороны линии. Однако в приведенном выше примере ничего не уменьшается, потому что 8 и 45 не имеют общих множителей.
MathHelp.com
Если вы не уверены, можно ли что-то отменить, вы всегда можете разложить числитель и знаменатель на множители и проверить наличие повторяющихся множителей:
Ничего не дублируется между верхом и низом, поэтому ничего не отменяется.
Однако часто что-то отменяется:
Упростить
Для умножения я умножаю все верхние числа (числители) друг на друга и умножаю все нижние числа (знаменатели) друг на друга. Однако, чтобы немного облегчить себе жизнь, я сначала исключу все факторы, общие как для числителей, так и для знаменателей:
Тогда упрощенный продукт —
7 / 2 .
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в умножении дробей. Попробуйте введенное упражнение, введите свое упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления.)
Разделить дроби так же просто, как и умножить их; есть только один дополнительный шаг.Когда вы делите на дробь, первое, что вы делаете, — это «перевернуть-п-умножить». То есть вы берете вторую дробь, переворачиваете ее вверх ногами (то есть «находите обратную»), а затем умножаете первую дробь на эту перевернутую дробь.
Упростить
Моим первым шагом будет преобразовать это в умножение, перевернув 9 / 4 , чтобы получить 4 / 9 .Затем я могу продолжить простое умножение, исключив все повторяющиеся множители:
Тогда мой упрощенный ответ:
4 / 15 .
Упростить
Это немного сложно, но я могу справиться с целым числом 5, преобразовав его в дробь.Помните, что любое целое число является дробью, если вы поставите его над «1». Итак, я преобразовываю 5 в дробь 5 / 1 и переверну с умножением:
Тогда мой упрощенный ответ:
1 / 6 .
Упростить
Для этого упражнения мне сначала нужно преобразовать смешанные числа в (неправильную) дробную форму.(Умножение и деление дробей — это места, где дроби оооочень намного лучше, чем смешанные числа!) Как только у меня есть дроби, я могу перевернуть-n-умножить.
Тогда мой ответ смешанный:
1 37 / 68 .
Примечание. Когда входные данные представляют собой смешанные числа, как в последнем примере выше, книга (или преподаватель, или оценщик) обычно также ожидает смешанные числа на выходе. Итак, если ваш ответ является неправильной дробью, вам нужно будет преобразовать ее обратно в форму смешанного числа.Не забывайте этот шаг!
Итак, если ваш ответ является неправильной дробью, вам нужно будет преобразовать ее обратно в форму смешанного числа.Не забывайте этот шаг!
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в делении дробей. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления.)
Далее мы переходим к гораздо более сложному сложению и вычитанию дробей …
URL: https://www.purplemath.com/modules/fraction3.htm
Каковы правила умножения дробей?
Обновлено 21 декабря 2020 г.
Лиза Мэлони
Умножение — одна из самых простых операций, которые вы можете выполнять с дробями, потому что вам не нужно беспокоиться о том, имеют ли дроби одинаковый знаменатель или нет; просто умножьте числители вместе, умножьте знаменатели вместе и, если необходимо, упростите полученную дробь. Однако есть несколько вещей, на которые следует обратить внимание, включая смешанные числа и отрицательные знаки.
Однако есть несколько вещей, на которые следует обратить внимание, включая смешанные числа и отрицательные знаки.
Умножение прямо через
Первое и самое важное правило умножения дробей состоит в том, что вы умножаете только числитель на числитель и знаменатель на знаменатель. Если у вас есть две дроби 2/3 и 4/5, их умножение даст новую дробь:
\ frac {2 × 4} {3 × 5}
\ frac {8} {15}
При этот момент вы бы упростили, если бы могли, но, поскольку 8 и 15 не имеют общих множителей, эту дробь нельзя упростить дальше.
Чтобы увидеть больше примеров, включая умножение дробей, которые необходимо уменьшить, посмотрите видео ниже:
Следите за отрицательными знаками
Если вы умножаете дроби с отрицательными членами, убедитесь, что у вас есть эти отрицательные знаки через ваши расчеты. Например, если вам даны две дроби -3/4 и 9/6, вы должны умножить их вместе, чтобы получить новую дробь:
Например, если вам даны две дроби -3/4 и 9/6, вы должны умножить их вместе, чтобы получить новую дробь:
\ frac {-3 × 9} {4 × 6}
\ frac {-27} {24}
Поскольку -27 и 24 имеют общий делитель 3, вы можете вынести 3 из числителя и знаменателя, в результате получится:
\ frac {-9} {8}
Обратите внимание, что -9/8 представляет собой значение, сильно отличающееся от 9/8.Если бы этот отрицательный знак потерялся по пути, ваш ответ был бы неправильным.
Да, неправильные дроби можно умножать
Еще раз взгляните на только что приведенный пример. Вторая дробь, 9/6, неправильная дробь. Или, другими словами, его числитель был больше, чем знаменатель. Это никак не меняет способ работы вашего умножения, хотя в зависимости от вашего учителя или ограничений задачи, над которой вы работаете, вы можете предпочесть упростить результат последнего примера, который сам является неправильной дробью, до смешанное число:
\ frac {-9} {8} = -1 \, \ frac {1} {8}
Умножение смешанных чисел
Это прекрасно ведет к обсуждению того, как умножать смешанные числа: Преобразование смешанное число на неправильную дробь и умножьте как обычно, как описано в последнем примере. Например, если вам нужно умножить дробь 4/11 и смешанное число 5 2/3, вы сначала умножите целое число 5 на 3/3 (это число 1 в виде дроби знаменатель которого совпадает со знаменателем дробной части смешанного числа), чтобы преобразовать его в дробь:
Например, если вам нужно умножить дробь 4/11 и смешанное число 5 2/3, вы сначала умножите целое число 5 на 3/3 (это число 1 в виде дроби знаменатель которого совпадает со знаменателем дробной части смешанного числа), чтобы преобразовать его в дробь:
5 × \ frac {3} {3} = \ frac {15} {3}
Затем добавьте дробную часть смешанного числа, что дает вам:
5 \, \ frac {2} {3} = \ frac {15} {3} + \ frac {2} {3} = \ frac {17} {3}
Теперь вы готовы умножить две дроби вместе:
\ frac {17} {3} × \ frac {4} {11}
Умножение числителя и знаменателя дает:
\ frac {17 × 4} { 3 × 11}
\ frac {68} {33}
Вы не можете больше упрощать члены этой дроби, но при желании можете преобразовать ее обратно в смешанное число:
2 \, \ frac {2} {33}
Умножение — это обратное деление
Вот удобный Уловка: если вы знаете, как умножать на дроби, вы уже знаете, как делить на дроби.Просто переверните вторую дробь вверх дном и умножьте ее, вместо того чтобы делить. Итак, если у вас есть:
Итак, если у вас есть:
\ frac {3} {4} ÷ \ frac {2} {3}
Это то же самое, что писать:
\ frac {3} {4} × \ frac {3} { 2}
, которые затем можно умножить как обычно.
Умножение дробей — ChiliMath
Чтобы умножить дроби, достаточно выполнить 3 предложенных ниже шага. Понятно, что ни одна дробь не может иметь знаменатель \ color {red} 0, потому что это будет неопределенный член.
Шаги в умножении дробей
Даны две дроби с ненулевыми знаменателями:
Шаг 1: Умножьте числители.
- Это будет числитель «новой» дроби.
Шаг 2: Умножьте знаменатели.
- Это будет знаменатель «новой» дроби.
Шаг 3: Упростите полученную дробь, уменьшив ее до наименьшего члена, если необходимо.
Прежде чем мы рассмотрим некоторые примеры, есть другие способы обозначить умножение.
- Точечный символ как оператор умножения
- Скобка как оператор умножения
Примеры умножения дробей
Пример 1 : Умножение.
Умножьте числители дробей.
Аналогичным образом умножьте знаменатели.
Результирующая дробь после умножения уже имеет уменьшенную форму, поскольку наибольший общий делитель числителя и знаменателя равен \ color {blue} +1.Это и станет нашим окончательным ответом!
Пример 2 : Умножение.
Шаг 1. Умножьте верхние числа.
Шаг 2: Умножьте нижние числа.
Шаг 3. Упростите ответ, сократив его до наименьшего члена.
Разделите верхнюю и нижнюю на наибольший общий коэффициент (GCF), равный 10.
Пример 3 : Умножьте.
Вы можете столкнуться с проблемой, когда вам будет предложено умножить три дроби.
Общая идея остается такой же, как и при умножении двух дробей, как показано в предыдущих примерах.
Шаг 1. Рассчитайте произведение числителей.
Шаг 2: Вычислите произведение знаменателей.
Шаг 3. Уменьшите дробь до ее простейшего вида.
Разделите числитель и знаменатель на наибольший общий делитель, равный 12.
Пример 4 : Умножьте целое число на дробь.
Калькуляторы дробей
Научитесь складывать, вычитать, умножать и делить дроби. Сократите дроби до минимума, упростите, сравните и упорядочите дроби. Преобразовывайте дроби в десятичные и проценты, работайте со смешанными числами и неправильными дробями и находите X в уравнениях дробей с помощью онлайн-калькуляторов дробей CalculatorSoup ® .
Дробные операции и манипуляции
Калькулятор дробей
Действия над правильными и неправильными дробями. Включает формулы для сложения, вычитания, умножения и деления дробей.
Сложение и вычитание дробей.
Сложите или вычтите до 10 дробей за раз и посмотрите работу по поиску ответа.
Смешанные номера
Смешанные числа, целые числа и дроби . Операции над целыми числами, целыми, смешанными числами, правильными дробями и неправильными дробями. Показывает уравнения и работу в результатах калькулятора.
Операции над целыми числами, целыми, смешанными числами, правильными дробями и неправильными дробями. Показывает уравнения и работу в результатах калькулятора.
Смешанные фракции
(То же, что и смешанные номера)
Упрощение дробей
Преобразование неправильных дробей в смешанные числа. Упростите правильные и неправильные дроби, показав произведение и ответ в виде дроби или смешанного числа.
Упрощение калькулятора сложных дробей
Упростить дроби по числителям и знаменателям любых двух смешанных чисел (смешанных дробей), правильных дробей, неправильных дробей или целых чисел.
Калькулятор сложных дробей
Сложение, вычитание, умножение и деление сложных дробей, содержащих смешанные числа, дроби или целые числа.
Десятичная дробь
Преобразование десятичной дроби в дробь.
Дробь к десятичной
Преобразование дроби в десятичную.
Дробь в процент
Преобразование дроби в проценты.
Проценты в дроби
Преобразование процентов в дроби.
Наименьший общий знаменатель ( LCD )
Находит LCD дробей, целых и смешанных чисел. Показывает дроби и эквивалентные дроби с ЖК-дисплей .
Наименее распространенное кратное ( ЛКМ )
Находит LCM целых и целых чисел.
Наибольший общий делитель ( GCF )
Находит GCF набора чисел, показывающих работу с использованием факторизации, простой факторизации и алгоритма Евклида.
Калькулятор соотношения
Решите задачи на отношение и пропорцию для отсутствующего значения отношения в форме A:B = C:D (или эквивалентной A/B = C/D). Сравните два отношения эквивалентности, ИСТИНА или ЛОЖЬ.
Калькулятор отношения к дроби
Преобразование пропорций в дроби. Введите отношение части к части или части к целому и найдите дробные эквиваленты.
Упрощение отношения
Упростить и уменьшить соотношение в виде A : B. Показана работа с шагами.
Золотое сечение
Введите одно значение в формулу золотого сечения (A+B : A = A : B), и другие значения будут сгенерированы с геометрическим представлением.
Эквивалентные дроби
Создать набор дробей, эквивалентных заданной дроби, смешанному числу или целому числу.
Неправильные дроби в смешанных числах
Преобразуйте неправильные дроби в смешанные числа и посмотрите, сколько работы потребуется для преобразования. Упростите дроби и приведите к наименьшим терминам.
Смешанные числа в неправильные дроби
Преобразуйте смешанные числа в неправильные дроби и посмотрите, сколько работы потребуется для преобразования.
Смешанные числа в десятичные
Преобразуйте смешанные числа, дроби или целые числа в десятичные числа и проследите за работой, связанной с преобразованием.
Смешанные числа в процентах
Преобразуйте смешанные числа, дроби или целые числа в проценты и посмотрите, сколько работы потребуется для преобразования.
Порядок дробей
Упорядочивание и сортировка дробей, целых и смешанных чисел, чтобы определить, равны ли они, больше или меньше друг друга ( = или > или < ). Показывает затраченную работу и преобразует входные данные в эквивалентные дроби с ЖК-дисплей .
Показывает затраченную работу и преобразует входные данные в эквивалентные дроби с ЖК-дисплей .
Сравнение дробей
Сравнение дробей, целых и смешанных чисел для демонстрации равенства или неравенства ( = или < или > ). Показывает входные данные, преобразованные в эквивалентные дроби с ЖК-дисплей .
Решение для X в дробях
Найдите неизвестные X , такие как Х/12 = 4/16 . Этот калькулятор может решить для X в дробях в виде равенств и неравенств: < или ≤ или > или ≥ или = . Показывает работу для перекрестного умножения.
Оценка сумм и разностей
Оценка сумм и разностей для положительных правильных дробей, n/d, где n ≤ d и 0 ≤ n/d ≤ 1. Включает таблицу дробей порядка половин, четвертей, восьмых и шестнадцатых с их десятичными эквивалентами.
Усреднение дробей
Вычислить среднее значение набора дробей. Находит среднее положительных и отрицательных, правильных и неправильных дробей, целых и смешанных чисел. Включает возможность показать работу, связанную с вычислением результата.
Таблица фракций
Дроби в порядке от 0 до 1 для половин до шестнадцатых. Включает десятичные эквиваленты дробей.
Число дробей Строка
Дробные части размером от шестнадцатых долей.
Преобразование дробей, десятичных знаков и процентов
Конвертер десятичных дробей в дроби
Конвертер десятичных чисел в проценты
Конвертер дробей в десятичную
Конвертер дробей в проценты
Конвертер процентов в десятичные числа
Конвертер процентов в дроби
Конвертер смешанных чисел в десятичные числа
Конвертер смешанных чисел в проценты
Смешанные числа в неправильные дроби
Неправильные дроби в смешанных числах
Калькулятор смешанных чисел — преобразование целых чисел в дроби
Онлайн-калькулятор смешанных чисел — это бесплатный и лучший инструмент, который позволяет вам складывать, вычитать, умножать и делить дробь смешанных чисел. Проще говоря, этот калькулятор дробей и целых чисел позволяет решать задачи дробей с целыми числами и дробями. Этот калькулятор не только упрощает дроби смешанных чисел, но также показывает пошаговый расчет и результат в десятичном виде, соответствующем заданным входам.
Проще говоря, этот калькулятор дробей и целых чисел позволяет решать задачи дробей с целыми числами и дробями. Этот калькулятор не только упрощает дроби смешанных чисел, но также показывает пошаговый расчет и результат в десятичном виде, соответствующем заданным входам.
В этом посте мы поможем вам понять, как складывать (+), вычитать (-), умножать (×) и делить (÷) вручную и с помощью онлайн-калькулятора. Но пришло время изучить некоторые основные термины, знаете что? Читать дальше!
Что такое смешанный номер?Смешанное число можно определить как комбинацию целого числа и правильной дроби, существующих вместе. Из-за такой смеси калькулятор смешанных дробей может складывать, вычитать, умножать и делить каждое смешанное число, чтобы легко решать математические задачи. Кроме того, смешанные числа обычно обозначают цифру, которая существует среди любых двух целых чисел. Его можно создать, объединив 3 части, а именно:
- Целый номер
- Числитель
- Знаменатель
На основании этой комбинации смешанное число признается частично целым числом и частично дробью. Например, если смешанное число равно 2 (1/5), то:
Например, если смешанное число равно 2 (1/5), то:
- Целое число: 2
- Числитель: 1
- Знаменатель: 5
Онлайн-калькулятор смешанных чисел — это инструмент, который помогает выполнять вычисления с 3 частями смешанных чисел: «целым числом», «знаменателем» и «знаменателем».
Как складывать смешанные дроби?Смешанные числа также известны как смешанные дроби. Сложение смешанных дробей удобно выполнять с помощью простой алгебраической формулы, если вы выполняете расчеты вручную. Кроме того, онлайн-калькулятор сложения смешанных чисел позволяет мгновенно складывать смешанные дроби. Формула:
- (A разделить на b) + (c разделить на d) = (a умножить на d) + (b умножить на c)/ (b умножить на d)
Пример:
Если у нас есть два смешанных числа:
- 1 (4 / 6)
- 2 (2/4)
Подставьте значения в приведенную выше формулу:
- 1 (4 / 6) + 2 (2 / 4) = 10 / 6 + 10 / 4
- (10*6) + (10*4)/6*4
(60) плюс (40) разделить на (24) = 100 на 24
- При упрощении: 100 / 24 = 25 / 6
- 4 (1/6)= 4,16
Однако для сложения смешанных дробей с помощью калькулятора смешанных дробей можно получить быстрые и безошибочные результаты.
Вычитание смешанных дробей звучит сложно, но вы можете сделать это вручную с помощью формулы. Сложение и вычитание смешанных чисел можно выполнять таким же образом с аналогичным уравнением формулы, но с измененными знаками. Все, что вам нужно сделать, это заменить знак сложения на знак вычитания в приведенной выше формуле:
(A разделить на B) – (C разделить на D)= (A умножить на D) – (B умножить на C) / ( B умножить на D)
Пример:
Если у нас есть два смешанных числа:
- 1 (4 / 6)
- 2 (2/4)
Подставьте значения в приведенную выше формулу:
- 1 (4/6) – 2 (2/4) = 10/6 – 10/4
- (10*4) – (10*6)/6*4
- (40)– (60) разделить на 24 = – 20 разделить на 24
- При упрощении: – 5 / 6 = – 0,8333
Однако вы можете легко складывать и вычитать смешанные числа с помощью нашего онлайн-калькулятора смешанных чисел.
Умножение смешанных дробей можно выполнить в три простых шага:
- Преобразовать все неправильные дроби в правильные.
- Примените алгебраическую формулу умножения дробей со смешанными числами: a / b * c / d = a * c / b * d.
- Упростите и уменьшите дробь до возможного значения.
Пример :
Если у нас есть два смешанных числа:
- 1 (4 / 6)
- 2 (2/4)
Примените формулу и подставьте в нее значения: a / b * c / d = a * c / b * d.
- 10/ 6 * 10/ 4 = 10 * 10/ 6 * 4
- 100/24
При упрощении уравнения: 100/24 = 26/6 = 4 (1/6)
В десятичных дробях: 4,166.
Тем не менее, умножение смешанных чисел с помощью калькулятора смешанных дробей является наиболее подходящим вариантом для выполнения таких сложных вычислений.
Как делить смешанные дроби? Хватит волноваться! Онлайн-калькулятор деления смешанных дробей позволяет делить смешанные дроби за доли секунд. Но, если вы хотите показать свою работу в классе (пошагово) по делению смешанных дробей, то мы поможем вам на примере решить такие сложные вычисления вручную.
Но, если вы хотите показать свою работу в классе (пошагово) по делению смешанных дробей, то мы поможем вам на примере решить такие сложные вычисления вручную.
Пример :
Два смешанных числа:
1 (4 / 6)
2 (2 / 4)
Формула деления смешанных чисел: A / b разделить на c / d = a * d /б*с
Подставив значения в приведенную выше формулу, мы получим: 10 / 6 разделить на 10 / 4 = 10 * 4 / 10 * 6 = 40 / 60
0n упростив, мы получим: 2 / 3 = 0,6667
О Калькулятор смешанных чисел:Этот онлайн-калькулятор смешанных дробей — это умный инструмент, который поможет вам складывать, вычитать, умножать и делить дробь смешанных чисел. Этот калькулятор для простых смешанных дробей и позволяет заменить смешанное число на неправильную/правильную дробь или наоборот.
Как использовать этот калькулятор смешанных чисел (сложение, вычитание, умножение и деление): Калькулятор упрощения смешанных дробей — это 100% бесплатный инструмент, который упрощает заданное число смешанных дробей в мгновение ока, просто следуйте инструкциям. данный шаг для достижения мгновенных результатов:
данный шаг для достижения мгновенных результатов:
Входы:
- Все, что вам нужно ввести значения смешанной дроби в соответствующие поля этого калькулятора
- Далее вам просто нужно выбрать знак оператора, с помощью которого вы хотите упростить смешанные числа, это может быть (+, -, ×, ÷)
Помните: Если ваше число смешанных дробей состоит из минуса или знака минус (-), то все, что вам нужно, это поставить минус (-) при добавлении значения в данные поля этого калькулятора.
Выводы:
Итак, после того, как вы заполнили вышеуказанные поля, просто нажмите на кнопку расчета, этот калькулятор покажет:
- Упрощение чисел смешанной дроби
- Пошаговый расчет для заданных смешанных фракций
- Смешанная числовая дробь для данного результата (если возможно)
- Десятичное число предоставленного результата (если возможно)
Кроме того, вы также можете преобразовать смешанное число в неправильную дробь, используя наш бесплатный онлайн-калькулятор смешанных чисел в неправильную дробь.
Все, что вам нужно, это нажать «1» на вашем калькуляторе, а затем знак «плюс» (+). «1» символизирует целое число смешанной дроби и добавляет числитель или верхнее число дроби.
Что такое 8 4 как смешанное число?Наибольший общий делитель числа 8/4 равен 2, поэтому при делении и числителя, и знаменателя на 2 мы получили ответ 2/1, значит только 2. Значит, 2 дальше не выражаются смешанным числом.
Что такое 7/4 как смешанное число?7/4 выражается в смешанном числе или смешанной дроби как 1 3/4, 1 считается целым числом, 3 — числителем, а 4 — знаменателем.
Какие примеры смешанных чисел можно привести?Смешанным числом называется комбинация целого числа и дроби. Например: если у вас есть две целые груши и одна половина груши, вы можете представить это как смешанное число: 2 + 1/2 груши или 2 1/2 груши.
Что такое 9 4 как смешанное число? 9/4 выражается в смешанном числе как 2 1/4, 2 указывается как целое число, 1 как числитель и 4 как знаменатель.
3/2 выражается смешанной дробью/числом как 1 1/2, 1 обозначается как целое число, 1 — числитель, а 2 — знаменатель соответственно.
Что такое 4/3 как смешанное число?4/3 выражается в смешанном числе как 1 1/3.
Что такое 7 3 как смешанное число?7/3 выражается в смешанном числе как 2 1/3.
Что такое 8 на 3 как смешанное число?8 больше 3 или 8/3 выражается в смешанном числе как 2 2/3.
Что такое 11 3 как смешанное число?1 1/3 в виде смешанного числа выражается как 3 2/3.
Еда на вынос: Калькулятор смешанных чисел дает вам пошаговую процедуру сложения, вычитания, умножения и деления для всех заданных смешанных чисел. Более того; он также может мгновенно обрабатывать несколько дробей, а также целые числа. Он может служить решателем дробей и даже калькулятором смешанных дробей. Вот почему это полная поддержка для студентов и профессионалов, занимающихся вычислениями смешанных чисел, чтобы сэкономить их время и энергию, а также получить точные и точные результаты.
Вот почему это полная поддержка для студентов и профессионалов, занимающихся вычислениями смешанных чисел, чтобы сэкономить их время и энергию, а также получить точные и точные результаты.
Из источника по математике (wikia): Основное математическое определение смешанного числа
Авторизованный источник онлайн-обучения математике, содержащий: Преобразование смешанных чисел в неправильные дроби и наоборот
Из источника splashlearn вы можете узнать все о: Упрощении смешанных чисел — Определение с примерами
Из источника greenemath: Операции со смешанными числами Урок — Как складывать, вычитать, умножать и делить смешанные числа
Калькулятор дробей — Вычисление дробей
Вычисление дробей — это специальный калькулятор для умножения, деления, сложения и вычитания двух или более дробей и целых чисел. Он может обрабатывать несколько дробей и целых чисел одновременно. Затем он отображает пошаговые решения любой операции, которую он обработал. Иногда мало кто назовет его решателем дробей, в то время как другие могут сказать, что это калькулятор смешанных чисел или калькулятор смешанных дробей. Это онлайн-калькулятор с кнопкой дроби. На данный момент он может вычислять до десяти дробей и смешанных чисел. Это полезно для всех учащихся всех классов. Его можно использовать в качестве справочника для всех учителей математики и даже для тех специалистов, которые часто используют дроби на работе или дома.
Иногда мало кто назовет его решателем дробей, в то время как другие могут сказать, что это калькулятор смешанных чисел или калькулятор смешанных дробей. Это онлайн-калькулятор с кнопкой дроби. На данный момент он может вычислять до десяти дробей и смешанных чисел. Это полезно для всех учащихся всех классов. Его можно использовать в качестве справочника для всех учителей математики и даже для тех специалистов, которые часто используют дроби на работе или дома.
Упростить
Backspace
Целые числа
Числители
Знаменатели
Как использовать?
Этот калькулятор был разработан для удобства использования.
- Сложение двух дробей
- Нажмите любую цифру из кнопок числителя.
- Нажмите любую цифру из кнопок знаменателя.
- Нажмите кнопку добавления (+) .
- Нажмите любую цифру из кнопок числителя для второй дроби.
- Нажмите любую цифру из кнопок знаменателя для второй дроби.

- Нажмите кнопку равно (=) , чтобы вычислить ответ. Ответ и решение будут отображаться выше.
- Повторите шаги, описанные выше, за исключением последнего шага.
- Нажмите кнопку добавления (+) .
- Нажмите любую цифру из кнопок числителя для третьей дроби.
- Нажмите любое число из кнопок знаменателя для третьей дроби.
- Нажмите кнопку равно (=) , чтобы вычислить ответ, или нажмите кнопку добавления (+) , чтобы добавить другие дроби.
- Тот же процесс будет использован для четвертой, пятой или любого количества фракций. Просто нажмите кнопку равно (=) для вычисления.
- Следуйте инструкциям по сложению дробей, но вместо нажатия кнопки добавления (+) нажмите кнопку вычитания (-) .
- Следуйте инструкциям по сложению дробей, но вместо нажатия кнопки добавления (+) нажмите кнопку умножения (x) для умножения и деления (÷) кнопку для разделение.

Важно помнить, что при работе со смешанными числами при использовании этого калькулятора никогда не забывайте вводить целые числа. Кнопки целых чисел в калькуляторе больше, чем кнопки числителя и знаменателя. Вам нужно только сначала нажать кнопку целого числа, а затем дробь, после чего вы можете перейти к любой операции, которую хотите.
- Нажмите кнопку целого числа, если ваша дробь состоит из целого числа, или вы можете напрямую нажать кнопку числителя, если вам не нужно целое число. Вы не можете нажать кнопку знаменателя, если вы не нажали целое число или кнопку знаменателя. Это означает, что вам нужно сначала нажать кнопку целого числа или числителя. После нажатия кнопки числителя вы больше не можете нажимать кнопку целого числа. Вы можете нажать кнопку целого числа еще раз только в том случае, если вы удалите числитель, нажав кнопку возврата.
 Нули не должны быть нажаты первыми. Нули будут нажаты после нажатия ненулевых чисел.
Нули не должны быть нажаты первыми. Нули будут нажаты после нажатия ненулевых чисел. - Нажмите кнопку знаменателя для вашего знаменателя. После нажатия вы не можете снова нажать кнопку целого числа или числителя. Вы можете нажать кнопку числителя только в том случае, если вы удалите знаменатель, нажав кнопку возврата.
- Выберите любую операцию.
- Нажмите кнопку Равно , если вы закончили с дробью. Решение будет отображаться выше.
- Нажмите Backspace , если вы хотите удалить по одному номеру за раз.
- Нажмите Кнопка AC для очистки уравнения дроби.
- На данный момент этот калькулятор ограничен только 10 дробями.
Расчет дробей на мобильных телефонах Android
Выпущен наш калькулятор дробей для мобильных телефонов Android. Он может обрабатывать базовые и сложные операции с дробями и может отображать решение как методом перекрестного умножения, так и методом LCD (наименьший общий знаменатель). Вы можете получить его из магазина Google Play.
Вы можете получить его из магазина Google Play.
Как был выполнен расчет?
Иногда возникают сомнения в том, как выполняются вычисления при использовании нескольких операций. Используя нотацию MDAS, умножение и деление имеют такой же приоритет, но выше, чем сложение и вычитание. Сложение и вычитание имеют одинаковый приоритет. Сначала обрабатывается более высокий приоритет. Это всегда было правилом, и оно соблюдалось повсеместно. При одинаковом приоритете операция выполняется слева направо.
Калькулятор дроби целого числа
Fraction Calc также является калькулятором целочисленных дробей, потому что он может обрабатывать множество целых чисел. Работа с целыми числами означает, что вам придется больше учиться и делать дополнительные шаги, преобразовывая целые числа в формат, подходящий для математических операций. Выполнение математических операций с целыми числами означает, что вам нужно выполнить дополнительные действия, чтобы получить правильный ответ. Это означает дополнительную энергию и нагрузку для людей, которые оказались в ситуации, когда им нужно решать целые числа и дроби. Вот почему некоторые люди ищут калькулятор дробей и целых чисел не только с целью предоставления простых решений сложных задач, но и для экономии времени и энергии. Экономия времени и энергии на определенной задаче означает, что вы получаете дополнительные ресурсы для выполнения еще более важной задачи, которая была бы очень полезной.
Это означает дополнительную энергию и нагрузку для людей, которые оказались в ситуации, когда им нужно решать целые числа и дроби. Вот почему некоторые люди ищут калькулятор дробей и целых чисел не только с целью предоставления простых решений сложных задач, но и для экономии времени и энергии. Экономия времени и энергии на определенной задаче означает, что вы получаете дополнительные ресурсы для выполнения еще более важной задачи, которая была бы очень полезной.
3 Калькулятор дробей
В большинстве случаев в любой математической арифметике используются только две дроби. Очень редко в какой-либо операции участвуют 3 фракции. Но если это ваш случай, то вам очень повезло, что вы нашли этот инструмент. Вы можете легко использовать этот инструмент в качестве калькулятора 3-х дробей, потому что он может абсолютно решить эту проблему. Это основная цель этого инструмента. Некоторые люди никогда не слышали об этом инструменте, поэтому они специально искали калькулятор с тремя дробями. Но теперь, когда его инструмент создан, я думаю, у них больше нет времени беспокоиться.
Но теперь, когда его инструмент создан, я думаю, у них больше нет времени беспокоиться.
Калькулятор кратных дробей
Большинство созданных калькуляторов имеют ограниченные возможности до такой степени, что могут вычислять только две дроби за раз. Но Fraction Calc может даже больше. Он может решить до 10 целых чисел или дробей вместе взятых. Вот почему многие называют его калькулятором кратных дробей. Это очень специализированный калькулятор с целыми числами. С комбинацией целого числа и дроби трудно иметь дело, но с этим калькулятором кратных дробей вычисления становятся проще. Сложение смешанных чисел, преобразование дробей в целые числа, умножение дробей на целые числа, вычитание смешанных чисел и умножение смешанных дробей — вот некоторые из процессов, которые может выполнять этот калькулятор.
Преимущества и недостатки использования калькулятора дробей.
- Преимущества:
- Он прост в использовании.
- Экономит больше времени и энергии.

- Нет необходимости в ручных вычислениях.
- Вычисленный результат точен и точен.
- Это может затруднить вычисление дробей.
- Вы будете очень зависеть от него в будущем.
- Вы можете забыть правила вычисления.
Правила работы с дробями
- Сложение и вычитание дробей
Сложение и вычитание дробей выполняются по одним и тем же правилам. Они должны иметь одинаковые знаменатели для выполнения выбранной операции. Вы можете сложить или вычесть две дроби, если у них один и тот же знаменатель, если нет; вы должны создать общий знаменатель, прежде чем складывать или вычитать их.
Подобные дроби — это дроби, имеющие одинаковые знаменатели. Чтобы сложить дроби с одинаковым знаменателем, добавьте его числитель. Например, 2/5 + 1/5 = 3/5.
Дроби, имеющие разные знаменатели, не похожи на дроби. Чтобы сложить разные дроби, нужно привести их к общему знаменателю. Самый простой способ сделать это — использовать метод бабочки. Чтобы выполнить метод бабочки, выполните следующие действия.
Самый простой способ сделать это — использовать метод бабочки. Чтобы выполнить метод бабочки, выполните следующие действия.
- Умножьте числитель первой дроби на знаменатель второй дроби. Результатом будет первый числитель дроби.
- Умножьте знаменатель первой дроби на знаменатель второй дроби. Результатом будет новый знаменатель первой дроби.
- Умножьте числитель второй дроби на знаменатель первой дроби. Результатом будет новый числитель второй дроби.
- Умножьте знаменатель второй дроби на знаменатель первой дроби. Результат теперь является новым знаменателем второй дроби.
Например: 2/3 + 3/5.
- 2 х 5 = 10.
- 3 х 5 = 15.
- 3 х 3 = 9.
- 5 х 3 = 15.
Новая фракция: 10/15 и 9/15.
15/10 + 15/9 = 15/19.
Новая дробь 19/15.
Чтобы вычесть дроби с одинаковым знаменателем, просто вычтите числитель второй дроби из числителя первой дроби. Пример: 4/6 – 3/6 = 1/6.
Для дробей с разными знаменателями приведите их к одному знаменателю, используя метод бабочки, а затем выполните вычитание после того, как у них будет одинаковый знаменатель.
Правило умножения двух дробей простое. Умножьте числитель первой дроби на числитель второй дроби и умножьте знаменатель первой дроби на знаменатель второй дроби. Пример: 2/3 х 1/5 = 2/15.
Чтобы разделить две дроби, вы должны сначала инвертировать вторую дробь, а затем начать умножать две дроби. Пример: 2/3 разделить на 1/5 = 2/3 x 5/1 = 10/3.
Когда вы сокращаете неправильную дробь до наименьшего члена, вам нужно изменить ее на смешанное число. Это делается делением числителя на знаменатель. Частное будет целым числом. Остаток будет новым числителем, а знаменатель останется прежним.
При делении или умножении смешанных чисел вам нужно, чтобы оно превратилось в неправильную дробь. Это делается путем умножения целого числа на знаменатель, а затем добавления текущего числителя. Результатом будет новый числитель, а знаменатель останется прежним.
Это делается путем умножения целого числа на знаменатель, а затем добавления текущего числителя. Результатом будет новый числитель, а знаменатель останется прежним.
Для дробей с одинаковыми знаменателями дробь с наибольшим числителем является большей, чем дробь с меньшим числителем.
Для дробей с одинаковыми числителями дробь с наибольшим знаменателем меньше дроби с меньшим знаменателем.
Из темы выше мы уже знаем, что есть равнозначные дроби-дроби, одинаковые по значению, даже если у них разные числители и знаменатели. Упрощение дроби означает использование наименьшего числителя и знаменателя, но одного и того же значения. Дробь имеет простейшую форму, когда нет общего множителя для числителя и знаменателя. Например, вместо использования 7/14 мы можем использовать ½, что является самой простой формой.
Наибольший общий делитель — это наибольшее число, используемое для деления числителя и знаменателя для получения простейшей формы дроби. Например, для дроби 12/30 наибольшее число, на которое можно разделить как числитель, так и знаменатель, равно 6. Разделив его на 6, вы получите его простейшую форму — 2/5.
Например, для дроби 12/30 наибольшее число, на которое можно разделить как числитель, так и знаменатель, равно 6. Разделив его на 6, вы получите его простейшую форму — 2/5.
Факты о дробях
Дроби являются частями целого. Например, один торт на пятерых детей. Итак, торт делится на пять частей. Каждый ребенок получит одну часть торта. Дробь будет 1/5. Каждый ребенок получит 1/5 торта.
Дробь состоит из двух частей. Верхняя половина называется числителем. Нижняя половина называется знаменателем. Числитель — это часть целого, где она используется или с которой в настоящее время имеют дело.
Существуют три типа дробей: правильная дробь, неправильная дробь и смешанные числа.
Правильная дробь — это дробь, числитель которой всегда меньше знаменателя.
Неправильная дробь – это дробь, числитель которой больше или равен знаменателю.
Смешанное число представляет собой целое число плюс дробь.
Равные дроби — это дроби, которые имеют разные числители и знаменатели, но имеют одинаковое значение, например 1/2, 2/4, 7/14, 8/16, 10/20, 20/40 и 50/100.
Как был создан калькулятор дробей?
Когда я был студентом, у меня был предмет по математике. Одна из тем была о дроби. Хотя эта тема сложна, меня очень удивило, почему трудно определить, правильное решение или нет. Вы должны просмотреть его несколько раз, чтобы убедиться, что ваше решение является правильным. Это произошло не только у меня. Я узнал, что большинство студентов испытывали то же самое. Так что с этого момента я мечтаю, что так или иначе буду им помогать. Я помогу им убедиться, что их решение правильное, не просматривая множество обзоров. Именно поэтому я создал этот калькулятор. Этот калькулятор был создан в качестве справочника или руководства только для того, чтобы учащийся получил правильный ответ из своих задач на дроби. От основателя FractionCalc.com
Онлайн-калькулятор смешанных дробей с целыми числами
MiroCalc.net бесплатный онлайн-калькулятор дробей позволяет складывать, вычитать, умножать и делить дроби одним щелчком мыши. Кроме того, вы можете решать задачи с неправильными дробями, целыми числами, а также со смешанными дробями (смешанными числами). Наш калькулятор дробей дает ответы в виде упрощенных дробей в наименьшем выражении.
Кроме того, вы можете решать задачи с неправильными дробями, целыми числами, а также со смешанными дробями (смешанными числами). Наш калькулятор дробей дает ответы в виде упрощенных дробей в наименьшем выражении.
Мы постарались сделать наш калькулятор смешанных дробей максимально удобным для пользователя. Пожалуйста, следуйте приведенным ниже инструкциям, чтобы выполнить желаемую операцию с дробями.
Онлайн-калькулятор дробей целых чисел Инструкции:
Наш онлайн-калькулятор дробей очень прост в использовании и быстр. Вот все, что вам нужно сделать:
- Введите каждую дробь в поля «Первая дробь» и «Вторая дробь». Например: 1/5 (для «одной пятой») или 3 4/7 (для «три и четыре седьмых»). Важно оставить пробел между целым числом и дробным числом: 3 4/7.
- Выберите действие: добавить «+», вычесть «-», умножить «*» или разделить «/»
- Нажмите «Рассчитать»
Например, 1/5 (для «одной пятой») или 3 4/7 (для «три и четыре седьмых»). Важно оставлять пробел между целым числом и дробным числом.
Важно оставлять пробел между целым числом и дробным числом.
Первая фракция
Действие +-*/
Вторая фракция
Результат
Если вам понравился наш калькулятор дробей, мы будем признательны, если вы поделитесь им в социальных сетях:
Как работает наш калькулятор смешанных фракций?
Прежде чем углубляться в детали того, как работает калькулятор дробей Mirocalc.net, давайте объясним основные термины, которые вам необходимо знать, чтобы правильно понять, как работает наш калькулятор дробей:
Дробь является частью целого.
Дробь обычно состоит из числителя (равные части) и знаменателя (части, на которые делится целое).
Числитель — это число выше дробной черты (до косой черты) и знаменателя это число ниже дробной черты (после косой черты).
Произношение дробей звучит следующим образом: «одна пятая» для 1/5 и «три и четыре седьмых» для 3 4/7
Наиболее распространенными формами дробей являются простые дроби, правильные/неправильные дроби , смешанные дроби (смешанные числа).
Простая дробь : 1/5 (где 1 — числитель, 5 — знаменатель, 1 — равная часть 5 частей, составляющих целое
Неправильная дробь : 5/3 (где числитель больше знаменателя).
Смешанная дробь : 3 4/7 (состоит из целого числа и правильной дроби, где 3 — целое число, обозначающее три целых единицы, а 4/7 — дробное число, обозначающее 4 равные части из 7 частей, целое равно разделен на).
Упрощение : математическая операция, при которой числитель и знаменатель делятся на их наибольший общий множитель.
Теперь, когда мы рассмотрели основы, давайте посмотрим, как работает наш калькулятор дробей:
Как калькулятор дробей MiroCalc.net складывает дроби
Чтобы сложить две дроби, калькулятор смешанных дробей MiroCalc.net выполняет ряд шагов:
- Калькулятор дробей проверяет, является ли введенная вами дробь смешанной. Если да, он преобразует его в неправильную дробь. Числитель неправильной дроби больше или равен знаменателю.
 Например, если вы ввели 1 ⅕, наш калькулятор дробей преобразует его в 6/5.
Например, если вы ввели 1 ⅕, наш калькулятор дробей преобразует его в 6/5. - Калькулятор смешанных чисел MiroCalc.net найдет наименьший общий знаменатель, который является наименьшим кратным обоих знаменателей. После нахождения калькулятор смешанной дроби умножает верхние и нижние части каждой дроби на одинаковую величину.
- Наш калькулятор дробей складывает числители и ставит сумму над знаменателем
- Если получена неправильная дробь (это когда числитель больше знаменателя), наш калькулятор дробей упростит результат.
- Результатом, отображаемым нашим калькулятором дробей, может быть число и дробная часть (которая называется смешанной дробью).
Как калькулятор дробей MiroCalc.net вычитает дроби
Чтобы вычесть дроби, калькулятор смешанных дробей MiroCalc.net выполняет почти те же действия, что и при сложении двух дробей:
- Если вы ввели смешанную дробь, калькулятор дробей преобразовать его в неправильный.
- Калькулятор дробей находит наименьший общий знаменатель.
 После нахождения калькулятор смешанной дроби умножает верхние и нижние части каждой дроби на одинаковую величину.
После нахождения калькулятор смешанной дроби умножает верхние и нижние части каждой дроби на одинаковую величину. - Наш калькулятор дробей вычитает числители и подставляет разность к знаменателю
- Калькулятор дробей упрощает дробь
- Онлайн-калькулятор дробей отобразит результат
Как калькулятор дробей MiroCalc.net умножает дроби
Чтобы умножить две дроби, калькулятор смешанных дробей MiroCalc.net выполняет ряд шагов:
- Если вы ввели смешанную дробь, калькулятор дробей преобразует его в неправильный.
- Если дроби не в наименьшем выражении, калькулятор дробей упростит их
- Калькулятор смешанных дробей умножит числители
- Знаменатели также умножаются
- Калькулятор смешанных дробей упрощает результат и отображает его.
Как калькулятор дробей MiroCalc.net делит дроби
Чтобы разделить две дроби, смешанный калькулятор MiroCalc.net для дробей использует алгоритм умножения… с изюминкой:
- Если вы ввели смешанную дробь, калькулятор дробей преобразует ее в неправильную.

- Две дроби упрощаются калькулятором дробей
- Наш калькулятор смешанных дробей переворачивает одну из дробей
- Затем калькулятор смешанных дробей умножает числители
- Знаменатели умножаются
- Результат упрощен и отображен
Преимущества онлайн-калькулятора дробей MiroCalc.net
Когда вы выполняете сложные расчеты для различных задач, онлайн-калькулятор дробей может стать вашим лучшим другом. Имея под рукой простой инструмент, вы сможете значительно сэкономить время, работая над любым проектом, в котором используются расчеты дробей.
Что такое смешанная фракция?
Смешанная дробь состоит из целого числа и дроби. Выглядит это так: 1 1/5 или 45 6/7. Смешанные дроби сложны в работе и требуют определенного времени для расчетов. Калькулятор смешанных дробей упрощает работу. Все, что вам нужно сделать, это ввести дроби и выбрать нужную операцию. Результат появится мгновенно.
Как сравнить две дроби с помощью калькулятора смешанных дробей?
Допустим, у вас есть две дроби с разными знаменателями, например, 8/23 и 9/25, и вам нужно их сравнить. Это выглядит сложно, не так ли? Но не с нашим калькулятором смешанных дробей.
Это выглядит сложно, не так ли? Но не с нашим калькулятором смешанных дробей.
Даже если наш калькулятор целых чисел и дробей позволяет только складывать, вычитать, умножать и делить дроби, вы также можете использовать его для сравнения двух дробей.
Если вы спросите себя как, вот ответ: просто вычтите их. Если результат, выдаваемый калькулятором смешанных дробей, меньше нуля, значит, первая дробь меньше второй. И наоборот, если калькулятор дробей показывает результат больше нуля, это просто означает, что первая дробь больше второй.
Зачем использовать калькулятор смешанных дробей?
Полезным инструментом является калькулятор целых чисел и дробей. Всего за несколько кликов вы можете получить нужные результаты и перейти к следующей задаче. Этот калькулятор целых чисел доступен везде, где есть доступ в Интернет.
Бесплатен ли этот онлайн-калькулятор дробей?
Калькулятор дробей абсолютно бесплатный. Вы можете использовать его для выполнения любого количества расчетов. Ограничений на бесплатное использование нет.
Ограничений на бесплатное использование нет.
В современном мире гаджетов, быстрого интернета и Wi-Fi карманные калькуляторы, как и расчеты вручную, безнадежно устарели. Когда дело доходит до принятия быстрых решений и соблюдения сроков, вы хотите использовать самые быстрые и эффективные инструменты, доступные круглосуточно.
Этот калькулятор целых дробей создан для удовлетворения потребностей абсолютно всех, кому приходится иметь дело с дробями. Независимо от того, пользуетесь ли вы одноразовым приложением или рассчитываете долю ежедневно, этот инструмент предназначен для того, чтобы помочь вам достичь своих целей быстрее, чем у конкурентов.
Самый простой калькулятор дробей для простых и смешанных дробей
С нашим калькулятором дробей вы можете легко складывать, вычитать, умножать или делить дроби и смешанные числа . Вы также можете конвертировать их в десятичные дроби или проценты с помощью нашего конвертера дробей.
Онлайн-калькулятор дробей (плюс смешанные дроби)
В этом калькуляторе есть все: это калькулятор сложения дробей, калькулятор деления дробей, калькулятор умножения дробей и калькулятор вычитания дробей. Кроме того, это калькулятор смешанных дробей, также называемый калькулятором смешанных чисел. Просто выберите предпочтительную операцию и правильный оператор, и вы сможете легко переключаться между сложением, вычитанием, умножением и делением дробей и смешанных чисел.
Калькулятор: преобразование дробей в десятичные числа и проценты
С помощью приведенного ниже приложения вы сможете конвертировать дроби в десятичные числа или проценты одним нажатием кнопки.
Однако лучшее, что вы можете сделать, это узнать, как работают сами дроби. Чтобы лучше понять расчеты, происходящие за кулисами, мы собрали несколько советов, которые вы можете найти здесь
- Сложение дробей
- Вычитание дробей
- Деление дробей
- Умножение дробей
Как преобразовать дроби в десятичные?
Знаете ли вы, что преобразовать дроби в эквивалентные им десятичные числа довольно просто? Понимание указанных преобразований можно найти в разбивке самих дробей. Строка в дроби разделяет эти два значения и может быть переписана как операция. Дроби в их простейших формах представляют собой деление числителя (или верхнего члена) на знаменатель (нижний член), поэтому использование калькулятора может быть лучшим и самым простым способом преобразования дробей в десятичные числа. Однако, как только вы перенастроите свой мозг, чтобы рассматривать линию как символ деления, преобразование дробей в десятичные числа и, в свою очередь, проценты станет проще простого.
Строка в дроби разделяет эти два значения и может быть переписана как операция. Дроби в их простейших формах представляют собой деление числителя (или верхнего члена) на знаменатель (нижний член), поэтому использование калькулятора может быть лучшим и самым простым способом преобразования дробей в десятичные числа. Однако, как только вы перенастроите свой мозг, чтобы рассматривать линию как символ деления, преобразование дробей в десятичные числа и, в свою очередь, проценты станет проще простого.
Возьмем, к примеру, дробь 3/4. Если мы переосмыслим эту дробь и увидим, что мы делим числитель на знаменатель, мы можем прочитать ее как 3, деленное на 4. Отсюда мы можем сказать, что 3, деленное на 4, равно 0,75, что равно 75%.
Таблица дробей и их десятичных и процентных эквивалентов
Ниже приведена таблица часто используемых дробей и их разговорных, десятичных и процентных эквивалентов.
| Записано | Fraction | Percent (Rounded) | Decimal Value | |
|---|---|---|---|---|
| A Half | ½ | 50 % | 0. 50 50 | |
| One third | 1/3 | 33.3 % | 0.333 | |
| A quarter | ¼ | 25 % | 0.25 | |
| A fifth | 1/5 | 20 % | 0.20 | |
| One sixth | 1/6 | 16.67 % | 0.166 | |
| One seventh | 1/7 | 14.29 % | 0.1429 | |
| An eighth | 1/8 | 12.5 % | 0.125 | |
| One ninth | 1/9 | 11.11 % | 0.11 | |
| A tenth | 1/10 | 10 % | 0.10 | |
| One twentieth | 1/20 | 5 % | 0.05 | |
| One twenty-fifth | 1/25 | 4 % | 0.025 | |
| One fiftieth | 1/50 | 2 % | 0.02 | |
| One hundredth | 1/100 | 1 % | 0,01 | |
| Одна тысячная | 1/1000 | 0,1 % | 0,001 | 9 Что такое дроби? Дроби — это еще один способ представления рациональных чисел , это числовые значения , которые могут быть частью целого количества . Дробь=\frac{Часть}{Целое}=\frac{Верхнее}{Низ}=\frac{Числитель}{Знаменатель} Например, в случае дроби ½ 1 — это числитель, а 2 — знаменатель, и при попытке преобразовать это значение в десятичную дробь или процент можно представить его как 1, деленное на 2. Не только дроби могут представлять части целого, но и в реальных сценариях, их можно использовать для описания различных контекстов жизни. С точки зрения времени, можно сказать, что это половина (1/2) третьего, то есть 3:30 утра/пополудни или четверть (¼) третьего или 4:15 утра/пополудни. Метод расчета: как складывать дробиЕсли знаменатели совпадают, можно просто сложить числители, чтобы знаменатель не изменился при сложении двух дробей. Например, \frac{1}{4}+\frac{2}{4}=\frac{3}{4} Если знаменатели разные, нам нужно скорректировать складываемые дроби, чтобы можно было общий знаменатель, и мы можем следовать горизонтальному сложению числителей, как обсуждалось выше. \frac{1}{4}+\frac{1}{16}=\frac{4}{16}+\frac{1}{16}=\frac{5}{16} Примечание. 1/4 * 4/4 = 4/16, что означает, что 1/4 = 4/16, потому что было выполнено умножение на 1, и в соответствии со свойством мультипликативной идентичности, когда вы умножаете число на 1, продукт сам / оригинал количество. Вы все еще запутались? Вот ссылка на видео о том, как складывать дроби с разными знаменателями: Метод вычисления: как вычитать дробиЕсли знаменатели совпадают, можно просто вычесть числители прямо, а знаменатель сохранить. соответствует с вычитанием двух дробей друг из друга. Например, \frac{2}{4}-\frac{1}{4}=\frac{1}{4} Если знаменатели разные , нам нужно настроить вычитаемые дроби так, чтобы мог быть общий знаменатель, и мы могли следовать горизонтальному вычитанию числителей, как обсуждалось выше. \frac{1}{4}-\frac{1}{16}=\frac{4}{16}-\frac{1}{16}=\frac{3}{16} Примечание. 1/4 * 4/4 = 4/16, что означает, что 1/4 = 4/16, потому что было выполнено умножение на 1 (или 4/4) и согласно свойству мультипликативной идентичности, когда вы умножаете число на 1, продукт сам по себе/ исходный номер. Вы все еще запутались? Вот ссылка на видео о том, как вычитать дроби с разными знаменателями: Метод вычисления: умножение дробейК счастью, умножать дроби намного проще, чем складывать или вычитать их! Неважно, совпадают знаменатели или нет, вам просто нужно умножить числители прямо и знаменатели прямо. Чтобы лучше понять это, давайте визуализируем это следующим образом: \frac{2}{4}*\frac{1}{2}=\frac{2}{8} Выше мы видим, что прямое умножение числителей дает нам 2 x 1 = 2, в результате в 2 наверху 2/8, и умножение знаменателей прямо поперек дает нам 4 x 2 = 8- вот почему в нижней половине результирующей дроби 2/8 есть 8. Если вы все еще не знаете, как умножать дроби, посмотрите это видео: Метод расчета: деление дробейДелить дроби так же просто, как и умножать их, если знать правильный прием. При делении дробей надо брать обратную вторую из двух дробей, и вместо их деления мы изменим операцию на умножение. Другими словами, вам просто нужно «перевернуть» числитель и знаменатель СЕКУНД двух дробей и написать символ умножения вместо символа деления между двумя дробями. Как только вы закончите применять этот трюк, вы можете просто умножать числители и знаменатели прямо. Изобразим это, чтобы лучше представить сказанное выше. \frac{3}{8}\div\frac{1}{4}\rightarrow\frac{3}{8}*\frac{4}{1}=\frac{12}{8} Примечание: мы «переворачиваем» ВТОРУЮ из двух дробей, поэтому ¼ становится 4/1 и превращаем символ деления в умножение. Если это все еще неясно, посмотрите это видео для большей практики: Часто задаваемые вопросыКак вы считаете дроби?Преобразование дроби в ее десятичный эквивалент может быть таким же простым, как деление числителя на знаменатель. Следуйте этому калькулятору для лучшего понимания. Как делить дроби? Если вы хотите разделить дроби, вы можете просто умножить первую дробь на обратную вторую. Обратная величина образуется путем перестановки числителя и знаменателя дроби. Как преобразовать десятичные дроби в дроби? Требуется всего несколько шагов, чтобы преобразовать конечное десятичное число (число точек), например 1,572, в дробь. Сначала возьмите соответствующее десятичное число и удалите десятичную дробь (или символ точки), что в нашем примере будет соответствовать превращению 1,572 в 1572. Затем напишите 1 в знаменателе дроби, а затем напишите столько же нулей после 1 в знаменателе, так как есть знаки после запятой соответствующего числа. В нашем случае 1,572 имеет три десятичных разряда после «.», что означает, что наш знаменатель будет содержать значение: 1000 (три нуля для трех десятичных разрядов). Следовательно, эквивалент дроби 1,572 равен 1572/1000. Как соотносятся десятичные дроби и понятие времени? Преобразование десятичных чисел в часы и минуты (и наоборот) в основном используется в промышленности и в реальных сценариях и используется для учета и записи времени. Как преобразовать дроби в десятичные? Существует два основных способа преобразования дроби в десятичное число. Калькулятор смешанных фракций — Fractioncalculation.com
Правда в том, что дроби не кажутся большинству учащихся легкими. Одна из вещей, которую вам нужно понять, это то, что существует два основных типа дробей:
Узнайте, как складывать дроби. Теперь, когда вы понимаете, что дроби бывают двух разных типов, сегодня мы решили рассмотреть самые сложные из них — несоставные дроби. Итак, чтобы у вас больше не возникало проблем, когда вам нужно выполнять с ними математические операции, мы решили не только добавить на эту страницу калькулятор дробных смешанных чисел, который вы можете видеть вверху, так как мы также собираемся чтобы объяснить вам, как именно вы можете выполнять все математические операции со смешанными дробями, не используя наш калькулятор смешанного числа дробей. Использование нашего калькулятора смешанных чисел дробейЕсли вы посмотрите вверху этой страницы, вы увидите наш простой в использовании калькулятор. Надеюсь, вы сможете использовать его не только тогда, когда вам нужно просто быстро выполнить математическую операцию со смешанными дробями, но и для подтверждения своих результатов. Как мы только что сказали, наш калькулятор целых чисел дробей очень прост в использовании, и у вас не должно возникнуть проблем с ним. Тем не менее, когда вы хотите выполнить математическую операцию со смешанными дробями, вам нужно убедиться, что вы выбрали правильный тип дроби. В этом случае вам нужно будет выбрать второй тип. Как видите, наш калькулятор целых чисел сразу показывает вам все пустые поля, которые вам нужно заполнить своими смешанными дробями. Как только вы заполните все поля, вы можете нажать кнопку «Рассчитать», чтобы получить результат. Одна из вещей, которую вы заметите при использовании нашего калькулятора, заключается в том, что вы получите свои результаты как в виде дроби, так и в виде десятичного числа. Еще одна вещь, которую стоит отметить в нашем калькуляторе целых чисел дробей, это то, что вы можете без проблем складывать, вычитать, умножать и делить смешанные дроби. Все, что вам нужно сделать, это нажать на стрелку, которая стоит между обеими дробями, и выбрать математическую операцию, которую вы хотите выполнить. Итак, теперь, когда мы уже описали вам, как работает наш калькулятор, пришло время проверить несколько практических примеров. Чтобы вы полностью поняли процесс, мы покажем вам примеры для каждой из различных математических операций — сложения, вычитания, умножения и деления. Сложение с помощью нашего калькулятора смешанных чисел дробей – практические примеры Как мы упоминали выше, с помощью нашего калькулятора целых чисел дробей вы можете легко складывать смешанные дроби. Практический пример #1: Допустим, вы хотите добавить: 5 (7/8) + 3 (2/5) Итак, как мы уже упоминали, первое, что вам нужно сделать, это сделать убедитесь, что вы выбрали смешанные дроби, а не обычные дроби. Затем вам просто нужно заполнить калькулятор смешанными дробями, которые вы хотите добавить. Убедитесь, что у вас выбрано дополнение, и как только вы это сделаете, вам просто нужно нажать на кнопку «Рассчитать», чтобы получить результат. Итак, в этом случае вам нужно будет сложить дроби: 5 (7/8) и 3 (2/5). И вы получите следующий результат: 5 (7/8) + 3 (2/5) = 9 (11/40) = 9,28 Не знаете, как умножать правильные дроби? Практический пример #2: Теперь предположим, что вы хотите добавить: 2 (7/4) + 1 (2/9) Итак, как мы упоминали, первое, что вам нужно сделать, это убедитесь, что выбраны смешанные дроби, а не обычные дроби. Итак, в этом случае вам нужно будет сложить дроби: 2 (7/4) и 1 (2/9). И вы получите следующий результат: 2 (7/4) + 1 (2/9) = 4 (35/36) = 4,97 Узнайте, как делить правильные дроби. Вычитание с помощью нашего калькулятора смешанных дробей – практические примерыКак мы упоминали выше, с помощью нашего калькулятора целых чисел дробей вы можете легко вычитать смешанные дроби. Практический пример №1: Допустим, вы хотите вычесть: 4 (1/8) – 1 (1/5) Итак, как мы уже упоминали, первое, что вам нужно сделать, это убедиться, что вы выбрали смешанные дроби, а не правильные дроби. Затем вам просто нужно заполнить калькулятор смешанными дробями, которые вы хотите вычесть. Убедитесь, что у вас выбрано вычитание, и как только вы это сделаете, вам просто нужно нажать кнопку «Рассчитать», чтобы получить результат. Итак, в данном случае вам нужно будет вычесть дроби: 4 (1/8) и 1 (1/5). И вы получите следующий результат: 4 (1/8) – 1 (1/5) = 2 (37/40) = 2,92 Практический пример №2: Теперь допустим, что вы хотите вычесть: 2 (8/3) – 1 (5/6) Итак, как мы уже упоминали, первое, что вам нужно сделать, это убедиться, что вы выбрали смешанные дроби, а не правильные дроби. Затем вам просто нужно заполнить калькулятор смешанными дробями, которые вы хотите вычесть. Убедитесь, что у вас выбрано вычитание, и как только вы это сделаете, вам просто нужно нажать кнопку «Рассчитать», чтобы получить результат. Итак, в этом случае вам нужно будет вычесть дроби: 2 (8/3) и 1 (5/6). И вы получите следующий результат: 2 (8/3) – 1 (5/6) = 2 (5/6) = 2,83 Узнайте, как перейти от дроби к десятичной. Умножение с помощью нашего калькулятора смешанных дробей – практические примеры Как мы упоминали выше, с помощью нашего калькулятора целых чисел дробей вы можете легко умножать смешанные дроби. Практический пример №1: Допустим, вы хотите умножить: 3 (5/8) X 1 (2/5) Итак, как мы уже упоминали, первое, что вам нужно сделать, это убедиться, что вы выбрали смешанные дроби, а не правильные дроби. Затем вам просто нужно заполнить калькулятор смешанными дробями, которые вы хотите умножить. Убедитесь, что у вас выбрано умножение, и как только вы это сделаете, вам просто нужно нажать кнопку «Рассчитать», чтобы получить результат. Итак, в данном случае вам нужно будет перемножить дроби: 3 (5/8) и 1 (2/5). И вы получите следующий результат: 3 (5/8) X 1 (2/5) = 5 (3/40) = 5,08 Узнайте, как перейти от процентов к дробям. Практический пример #2: Допустим, вы хотите умножить: 2 (4/3) X 3 (1/2) Итак, как мы уже упоминали, первое, что вам нужно сделать, это сделать убедитесь, что вы выбрали смешанные дроби, а не обычные дроби. Затем вам просто нужно заполнить калькулятор смешанными дробями, которые вы хотите умножить. Итак, в данном случае вам нужно будет перемножить дроби: 2 (4/3) и 3 (1/2). И вы получите следующий результат: 2 (4/3) X 3 (1/2) = 11 (2/3) = 11,67 Деление с использованием нашего калькулятора дробей смешанных чисел – практические примерыКак мы упоминали выше , с нашим калькулятором целых чисел дробей вы можете легко делить смешанные дроби. Практический пример №1: Допустим, вы хотите разделить: 1 (3/5) ÷ 1 (4/7) Итак, как мы уже упоминали, первое, что вам нужно сделать, это убедиться, что вы выбрали смешанные дроби, а не правильные дроби. Затем вам просто нужно заполнить калькулятор смешанными дробями, которые вы хотите разделить. Убедитесь, что у вас выбрано деление, и как только вы это сделаете, вам просто нужно нажать на кнопку «Рассчитать», чтобы получить результат. Итак, в данном случае вам нужно будет разделить дроби: 1 (3/5) и 1 (4/7). 1 (3/5) ÷ 1 (4/7) = 1 (1/55) = 1,02 Посмотрите, как легко передать десятичную дробь. Практический пример #2: Предположим теперь, что вы хотите разделить: 4 (1/3) ÷ 2 (9/5) Итак, как мы упоминали, первое, что вам нужно сделать, это убедитесь, что выбраны смешанные дроби, а не обычные дроби. Затем вам просто нужно заполнить калькулятор смешанными дробями, которые вы хотите разделить. Убедитесь, что у вас выбрано деление, и как только вы это сделаете, вам просто нужно нажать на кнопку «Рассчитать», чтобы получить результат. Итак, в этом случае вам нужно будет разделить дроби: 4 (1/3) и 2 (9/5). И вы получите следующий результат: 4 (1/3) ÷ 2 (9/5) = 1 (8/57) = 1,14 Как видите, пользоваться нашим калькулятором довольно просто. Однако мы считаем, что также важно, чтобы вы знали, как выполнять эти расчеты вручную. Сложение смешанных дробей вручнуюyoutube.com/embed/pynfj2bYRms?start=11&feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Допустим, вы хотите узнать результат: 1 (3/4) + 2 (3/8) Итак, как вы можете выполнить эти вычисления вручную? Первое, что вам нужно сделать, это переписать уравнение: 1 (3/4) + 2 (3/8) = 1 + 3/4 + 2 + 3/8 Здесь вы можете легко убедитесь, что у вас есть два целых числа и две правильные дроби. Следовательно, вы можете сложить их по отдельности: 1 + 2 = 3 и 3/4 + 3/8 Поскольку у этих правильных дробей разные знаменатели, вам нужно будет найти наименьший общий знаменатель. В данном случае это 8. Итак, вам нужно будет умножить первое уравнение на 2, а второе на 1: 3/4 + 3/8 = [(3 X 2) / (4 X 2)] + [(3 X 1) / (8 X 1)] = = 6/8 + 3/8 = (6+3)/8 = 9/8 Упрощая 9/8, вы получаете: 9/8 = 1 (1/8) Теперь вам нужно объединить целую и дробную части : 3 + 1 + 1/8 = 4 (1/8) Узнайте разницу между правильными и неправильными дробями. |








 В этом случае значение дроби зависит от данных значений букв.
В этом случае значение дроби зависит от данных значений букв.